中国剩余定理及应用

中国剩余定理（模板+详解）问题：今有物不知其数，三三数之剩⼆，五五数之剩三，七七数之剩⼆。

问物⼏何？简单点说就是，存在⼀个数x，除以3余2，除以5余三，除以7余⼆，然后求这个数。

上⾯给出了解法。

再明⽩这个解法的原理之前，需要先知道⼀下两个定理。

定理1：⼏个数相加，如果存在⼀个加数，不能被整数a整除，那么它们的和，就不能被整数a整除。

定理2：两数不能整除，若除数扩⼤（或缩⼩）了⼏倍，⽽被除数不变，则其商和余数也同时扩⼤（或缩⼩）相同的倍数（余数必⼩于除数）。

以上两个定理随便个例⼦即可证明！现给出求解该问题的具体步骤：1、求出最⼩公倍数lcm=3*5*7=1052、求各个数所对应的基础数（1）105÷3=3535÷3=11......2 //基础数35（2）105÷5=2121÷5=4 (1)定理2把1扩⼤3倍得到3，那么被除数也扩⼤3倍，得到21*3=63//基础数633、105÷7=1515÷7=2 (1)定理2把1扩⼤2倍得到2，那么被除数也扩⼤2倍，得到15*2=30//基础数30把得到的基础数加和（注意：基础数不⼀定就是正数）35+63+30=1284、减去最⼩公倍数lcm（在⽐最⼩公倍数⼤的情况下）x=128-105=23那么满⾜题意得最⼩的数就是23了。

⼀共有四个步骤。

下⾯详细解释每⼀步的原因。

（1）最⼩公倍数就不解释了，跳过（记住，这⾥讨论的都是两两互质的情况）（2）观察求每个数对应的基础数时候的步骤，⽐如第⼀个。

105÷3=35。

显然这个35是除了当前这个数不能整除以外都能够被其他数整除，就是其他数的最⼩公倍数。

相当于找到了最⼩的起始值，⽤它去除以3发现正好余2。

那么这个基础数就是35。

记住35的特征，可以整除其他数但是不能被3整除，并且余数是2。

体现的还不够明显，再看下5对应的基础数。

21是其他数的最⼩公倍数，但是不能被5整除，⽤21除以5得到的余数是1，⽽要求的数除以5应该是余1的。

使得 一口（ ｏ ， 关 于模 ｍ 是 唯一 的 ， 中 ｒ ｄｍ ） 且 ｏ 其
ｍ ｍ ｌ ，ｍ ２ … ，ｍ ｋ ０
其 中ห้องสมุดไป่ตู้ｕ为展 开 式 中 提 出公 因 子 ｇ （ 第 一 项 １之 除
外） 后所 剩 的多 项 式 。利用 上 述 引 理 可 以类 似 地 得
到在 Ｋ ］ ［ 上的中国剩余定理 。
ｑ ） 唯一 的 。 （ 是
２
［ 上的中 国剩余定理 ］
引理 设 ｑ （ ， ） … ， ） Ｋ［ 内互 。 ） ｑ （ ， ｑ （ 为 ］
素且次 数 ≥１的多项 式 ， 对 任一 ｉ１ ）存 在 则 （ ≤ ≤ｋ ， 多项式 ｈ（ ）∈ ］使 得 Ｋ［ ，
ｈ（ 一１ ｍ ｄｑ（ ） ） （ ｏ ） ，
１ 传统 的中 国剩余定理
定理 １ … 设 ，。ｍ：… ， ｋ 两两 互 素 的 孔， ， ｍ 是 个
且有 ｈ 兀 （ 一ｕ ｉ） （ １ ｊ）＝１＋ｑ ｑ ｉ ｕ
Ｊ≠ ‘
正 整数 ， 任给 ｋ个整 数 ０ ， … ， 必 存 在 整 数 ， 口 ， Ⅱ ，
１ ｍｏ 。 （ ｄｑ）
５６ ９６
科
学
技
术
与
工
程
ｌ Ｏ卷
（ 。 ） ＿ ）令 『 ≠ ＝∑ （） ， （）则对每 １ 个 （≤
≤ ， ） 有 （ ｈ （ （ （ ｏ ） ） ） ） ｒ ｄｑ（ 。 ｏ ） 而 当ｊ 时 ， （ ）ｊ ｘ －ｏ ｒ ｄｑ（ ） 于是 ＃ｉ ｆ ｘ ｈ（ ） （ ｏ ｉ ｊ ｏ ） ， （ ＾ （ ） ｆ（ ） 戈 － ， ）＋， （ ｑ（ ， （ ） （ 一 他 ） ｉ ｆ 戈 ） ） ｊ

中国剩余定理的实际应用：
有一个年级的同学,每9人一排多5人,每7人一排多1人, 每5人一排多2人,问这个年级至少有多少人?
求数学高手详细解答!剩余定理是什么意思?
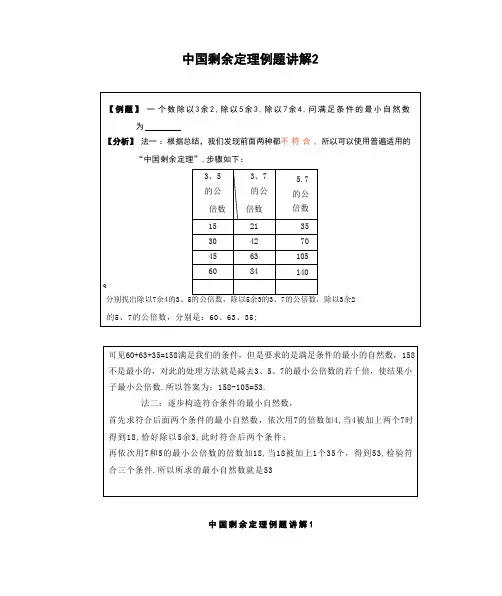
5 和 9 的公倍数依次是 45、90、135、180、225 ……
这些公倍数中，被7除余1的数是 225
9 和 7 的公倍数依次是 63、126、189、252……
这其中，被5除余2的是 252
5 和 7 的公倍数是 35、70、105、140、……
其中被9除余5的数是 140
把以上 225 252 140 三个数相加，求得
225 + 252 + 140 = 617
5 7 9 三个数的最小公倍数是 5*7*9=315
617-315 = 302
因此 302 就是这个年级至少人数。

1.韩信点兵：有兵一队，若列成五行纵队，则末行一人，成六行纵队，则末行五人，成七行纵队，则末行四人，成十一行纵队，则末行十人.求兵数.
2.有一堆棋子，三个三个地数剩下2个，五个五个地数剩下4个，七个七个地数剩下6个.问这堆棋子最少有多少个？（用两种方法解）
3.某数除以7余3，除以8余4，除以9余5.从小到大求出适合条件的十个数.
4.某数除以5余2，除以7余4，除以11余8.求适合条件的最小数.
5.一猴子数一堆桃子.两个两个地数剩下1个，三个三个地数剩下1个，五个五个地数剩下3个，七个七个地数剩下3个.问这堆桃子最少是多少个？。

m = n / w[i];
d = extended_euclid(w[i], m, x, y);
ret = (ret + y*m*b[i]) % n;
}
return (n + ret%n) % n;
}
模板:最大公约数
int gcd(int a,int b) {
if(0 == a )
return b;
int flag;
while (scanf ("%I64d", &n) != EOF){
scanf ("%I64d%I64d", &m1, &a1);
n--; flag = 0;
while (n--) {
scanf ("%I64d%I64d", &m2, &a2);
d = exGcd (m1, m2, x, y);
e==-1 && d==-1)){
j++;
k=(p*5544+e*14421+i*1288-d+21252)%21252;
if(k>0)
printf("Case %d: the next triple peak occurs in %d days、
\n",j,k);
else
printf("Case %d: the next triple peak occurs in 21252 days、
一些关于中国剩余定理得定理:
定理2:二数不能整除,若被除数扩大(或缩小) 了几倍,而除数不变,则其余数也同时扩大(或 缩小)相同得倍数(余数必小于除数)。

中国剩余定理内涵及其简单应用
中国剩余定理是数论中的一个重要定理，它提供了求解一类线性同余方程组的方法。

所谓线性同余方程组，是指一组形如x ≡ a1 (mod m1), x ≡ a2 (mod m2), …, x ≡ an (mod mn)的方程，其中x是未知数，a1, a2, …, an是已知数，而m1, m2, …, mn是不同的正整数。

中国剩余定理的内涵是：当所给线性同余方程组的模m1, m2, …, mn 两两互素时，存在唯一解x ≡ X (mod M)，其中X是x的一个解，而M = m1 * m2 * … * mn。

简单来说，中国剩余定理告诉我们，当模数两两互素时，我们可以通过对每个方程求解，再通过一定的运算，得到原方程组的解。

中国剩余定理的应用非常广泛，特别是在密码学和计算机科学中。

例如，当我们需要对一个数进行加密和解密时，可以使用中国剩余定理来进行模运算，从而快速计算得到加密后的结果。

此外，在计算机科学中，中国剩余定理也常用于优化算法和并行计算。

由于中国剩余定理能够将一个大问题拆分成多个小问题并行求解，因此可以显著提高计算效率。

总之，中国剩余定理作为数论中的重要定理，不仅具有深刻的理论意义，还具有广泛的实际应用。

通过它，我们可以快速求解线性同余方程组，加密和解密数据，优化算法等，从而提高计算效率和保护数据安全。

(i = 1, 2,L , n)
1 n( n − 1)(2n − 1) 6
2 2 2 2
当 f ( x) 的次数不超过 M ( x)( M ( x) = m1 ( x)m2 ( x)m3 ( x)L mn ( x)) 的次 数时， f ( x) 唯一确定 . 特 别 地， 当 mi ( x) = x − bi ∈ Q[ x]或R[ x] ， bi (i = 1, 2,L , n) 是不相等的常数，从而 mi ( x)(i = 1, 2,L , n) 也就是两两互素的 多项式，由余数定理可知 mi ( x) ≡ mi (bi )(mod x − bi ), (i = 1, 2,L , n) ， 从而定理可叙述为一定存在多项式 f ( x) ，使得
⎪f(x) ≡ a (x)(modm (x)) ⎪ 2 2 ⎨ ⎪LLLLLLLLLL ⎪ ⎩f(x) ≡ an (x)(modm n (x))
1 1
(n − 0)(n − 1)(n − 3) (n − 0)(n − 1)(n − 2) + 5× (2 − 0)(2 − 1)(2 − 3) (3 − 0)(3 − 1)(3 − 2)
⎧x ⎪x ⎪ ⎨ ⎪x ⎪ ⎩x ≡ 1(mod 5) ≡ 5(mod 6) ≡ 4(mod 7)
≡ 10(mod11)
按照中国属于定理的记号
M = 5 × 6 × 7 × 11 = 2310, M 1 = 6 × 7 × 11 = 462, M 2 = 5 × 7 × 11 = 385,
有正整数解 x ≡ M 1α1c1 + M 2α 2c2 + L + M nα n cn (mod M ) 且解唯一； 其中 α i 是满足 M iα i ≡ 1(mod mi ), k = 1, 2,L , n) 的一个整 数（参阅 [3]）. 下面我们先给出裴蜀恒等式和一个性质，然后证明中国 剩余定理 . 裴蜀恒等式 如果两个数的最大公约数是 d ，则必定存 在两个整数 x, y 使得等式 ax + by = d 成立（参阅 [4]）. 性质 同余式组 a ≡ b(mod m j ), j = 1, 2,L , n 同时成立的 充要条件是 a ≡ b(mod[m1 , m2 ,L , mn ]) （参阅 [5]）. 证明： 先证存在性： M 因为 m1 , m2 ,L , mn ，两两互素， M = m ， 故 ( M k , mk ) = 1, k = 1, 2,L , n ， 由 裴 蜀 恒 等 式 可 知 一 定 存 在 整 数 α k , βk 使 得 M kα k + β k mk = 1 ，即 M kα k = − β k mk + 1 ，因此必定存在 α k ，使

中国剩余定理的历史价值和应用
中国剩余定理（Chinese Remainder Theorem，简称CRT）是古老的数学定理，来源于古印度人拉穆卡尼的《数书大全》，但最早由中国宋朝数学家董仲舒来提出。

CRT是一种快速求解模不互质整数方程组的方法，其历史价值和应用非常广泛。

中国剩余定理可以求解n阶不同进制的数的同余式。

由于CRT的效率高，因此，它在工业上有较多的应用，如计算机硬件中，解数论中的模运算问题时，通常都使用CRT法求解。

例如，在压缩视频时，经典加密算法RSA 就是使用CRT法进行加速计算的。

此外，CRT在许多领域中也有着广大应用，如在凸优化中有测试剩余定理的实验，在几何中的研究的有使用剩余定理的技巧，在模数几何学中也有CRT的计算和推导应用。

而且，CRT在高斯消元法、矩阵计算、主元计算中也有应用可以设计的有关计算的算法。

因此可见，中国剩余定理在古老中国宋朝就已经诞生，它的历史价值和应用十分广泛，它不仅在计算机软件、电子工程中有着重要的地位，而且在许多领域也得到了广大应用，是一种弥足珍贵的古老定理。

中国剩余定理例题讲解2
【例题】一个数除以3余2,除以5余3,除以7余4,问满足条件的最小自然数
为
【分析】法一：根据总结，我们发现前面两种都不符合，所以可以使用普遍适用的
“中国剩余定理”,步骤如下：
Q
3、5
的公
倍数
3、7
的公
倍数
5.7的公
倍数
15
21
35
30
42
70
45
63
105
60
84
140
分别找出除以7余4的3、5的公倍数，除以5余3的3、7的公倍数，除以3余2
代，数学家程大位把这个问题的算法编成了四句歌诀：
三人同行七十稀，
五树梅花廿一枝；
O
七子团圆正半月，
除百零五便得知，
用现在的话来说就是：一个数用3除，除得的余数乘70;用5除，除得的余数乘21;用7除，除得的余数乘15.最后把这些乘积加起来再减去105的倍数，算法是；
11除余7,由于[3,5,11]=165,所以这个数最小是165+7=172.
法二：事实上，如果没有“大于10”这个条件，7即可符合条件，所以只需要在7的
基础上加上3、5、11的最小公倍数，得到172即为所求的数.
什么是中国剩余定理?
“物不知数问题”一般解题步骤：
o
①凑“多”相同，即把余数处理成相同条件；余数与除数的和相同
不相互影响各自被对应除数除后所得的余数，
即70a+213+15c是被3除余a,被5除余b,被7除余c的数，
得到18,恰好除以5余3,此时符合后两个条件；
再依次用7和5的最小公倍数的倍数加18,当18被加上1个35个，得到53,检验符

中国剩余定理的应用一、有余数除法的定理定理1：如果被除数加上（或减去）除数的整数倍，除数不变，则余数不变。

定理2：如果被除数扩大（或缩小）几倍，除数不变，则余数也扩大（或缩小）同样的倍数。

定理3：如果整数a除以自然数b（b≠0），余数r仍不小于b，则r除以b的余数等于a除以b所得余数。

二、例题例1 某数如果加上5就能被6整除，减去5就能被7整除，这个数最小是几？这样想：这个数除以6余几？除以7几？根据题意可知：某数除以6余1，除以7余5。

解：7÷6＝……1, 7是满足6的条件。

6÷7＝……6，余数6×2是满足7的条件。

所以7＋6×2＝19，19不大于6和7的最小公倍数，是要求的数。

例2 一个数除以5余3，除以7余1，求这个数最小是几？解：7÷5＝……2（想2乘几除以5余3呢？2×4能满足这个条件，所以，7×4＝28是满足这个条件的数）。

5÷7＝……5（想5乘几除以7余1呢？5×3能满足这个条件，所以，5×3＝15是满足这个条件的数）。

那么，28＋15＝43是满足除以5余3，除以7余1的条件。

但是，不是题目要求的“最小的”这个条件。

因为43大于5和7的最小公倍数，所以，必须从43里减去5 和7的最小公倍数，即：43－35＝8，这个数是8 。

例3 某数除以5余2，除以6余3，求符合条件的最小数？这样想：这个数如果加上3就能同时被5和6整除（能同时被5和6整除的最小数应该是它们的最小公倍数），所以，满足这个条件的最小数应该是5和6的最小公倍数减去3的数。

5和6的最小公倍数：5×6＝30,30－3＝27。

答：27是符合条件的最小数。

例4 某数除以5余3，除以6也余3。

求符合条件的最小数是多少？这样想：这个数如果加上3就能同时被5和6整除，能同时被5和6整除的最小数应该是它们的最小公倍数，即30，所以题目要求的数为30＋3＝33。

浅谈“中国剩余定理”在小学数学学习中的运用中国剩余定理是数论中的一个重要定理，它在数学领域有着重要的应用价值。

而在小学数学学习中，中国剩余定理也可以通过一些简单的案例来引导学生理解和运用。

本文将从中国剩余定理的基本概念、小学数学中的应用以及学生学习中的启示三个方面来探讨中国剩余定理在小学数学学习中的运用。

一、中国剩余定理的基本概念中国剩余定理是由中国古代数学家孙子约公元7世纪所著的《孙子定理》中提出的，它是一个关于模的定理。

主要内容是：如果m1,m2,…,mn 是两两互质的正整数，a1,a2,…,an 是任意整数，那么模方程组x≡a1(mod m1)x≡a2(mod m2)⋯x≡an(mod mn)有唯一的解。

这就是中国剩余定理的基本内容。

一个简单的例子可以帮助我们了解中国剩余定理的基本概念：例：假设一条囚犯刑期是365天，他想用一个长度在35-45之间的鞭认了当前日子。

该如何完成。

解：这个问题可以看作是一个中国剩余定理的实际问题。

因为365=5*73 。

那么鞭的长度模5的余数必须是0。

因为365=8*45+25 ，所以鞭的长度模8的余数必须是5。

通过中国剩余定理可以知道，模45的余数是25的数只有70。

所以囚犯只需要找一个长度为70的鞭。

（这是一个简单的例子，通过它我们可以初步了解中国剩余定理的基本思想和原理。

）二、小学数学中的应用在小学数学学习中，我们可以通过一些简单的案例来引导学生理解和运用中国剩余定理。

可以引导学生用中国剩余定理解决一些有关时间、距离等实际问题。

这样做不仅可以使学生更加深入地理解中国剩余定理的概念和原理，还可以锻炼学生的数学建模能力和解决问题的能力。

一般来说，小学数学的教学案例其实很简单，可以通过直观的案例引导学生理解和运用中国剩余定理。

以时间问题为例，可以设计这样的案例：某人一次修行时间为3天，另一次修行时间为4天，他已经做了第一次修行，那么他接下来需要再修行多久才能修满一年呢？通过这样的案例，学生可以逐步了解并掌握中国剩余定理的基本方法和步骤。

中国剩余定理的典型例题中国剩余定理是一个强大的数论工具，可以用来解决各种复杂的问题。

在计算机科学、统计学和密码学中都有广泛的应用。

中国剩余定理也被称为“中国余数定理”或“中国余数定理”，它源于中国古代学者Sunzi Suanjing 所著《孙子算经》，该书收录了中国古代数学家对于解决一类特殊方程的研究。

中国剩余定理的典型例题如下：1. 已知正整数a、b、m，求满足a≡x (mod m) 且b≡x (mod m)的整数x的取值范围。

由中国剩余定理可知，a≡x (mod m) 且b≡x (mod m) 等价于 a-b ≡ 0 (mod m)，即x = a-b+km, k∈Z，所以x的取值范围为x ∈ {a-b+km | k∈Z} 。

2. 已知a、b、N，求满足a≡b (mod N)的整数x的最小正整数解。

由中国剩余定理可知，a≡b (mod N) 等价于 a-b ≡ 0 (mod N)，即x = a-b+kN, k∈Z，所以最小正整数解为x = a-b+N。

3. 已知三个整数a、b、c，求满足a≡b (mod c)的整数x的最小正整数解。

由中国剩余定理可知，a≡b (mod c) 等价于 a-b ≡ 0 (mod c)，即x = a-b+kc, k∈Z，所以最小正整数解为x = a-b+c。

4. 已知三个整数a、b、N，求满足a≡b (mod N)且x>0的整数x的最小正整数解。

由中国剩余定理可知，a≡b (mod N) 等价于 a-b ≡ 0 (mod N)，即x = a-b+kN, k∈Z，所以最小正整数解为x = a-b+N，而且x > 0，所以最小正整数解为x = a-b+N，其中N > 0。

以上就是中国剩余定理的典型例题，可以看出，中国剩余定理是一个强大的数论工具，可以用来解决复杂的问题，被广泛应用于计算机科学、统计学和密码学中。

浅谈“中国剩余定理”在小学数学学习中的运用
一、解决同余方程问题
同余方程是小学数学中比较重要的一个知识点，其求解过程很类似中国剩余定理。

因此，可以通过中国剩余定理的教学，进一步帮助学生深入理解同余方程的解法，加深对同余方程的认识。

二、培养学生的数学思维
在教学中，运用中国剩余定理的解题方法，可以帮助学生发掘问题背后的规律，培养其逻辑思维和数学思考能力。

例如，通过求解同余方程组，学生可以逐步了解中国剩余定理应用的基本思想，同时还能增强学生的数学思维能力。

三、加深学生对整除、余数等概念的理解
中国剩余定理的应用还能帮助学生更加深入地理解整除和余数等相关概念，提高自己的数学素养。

例如，当学生在解决同余方程组问题时，不仅仅能够知道余数的含义，还能对这些数值有更为深入的认识。

四、拓展学生的数学知识
五、培养学生的实际应用能力
总的来说，中国剩余定理作为数学中的重要方法之一，其应用不仅局限于大数学，而在小学数学教学中也有着不可忽视的作用。

通过引导学生使用中国剩余定理进行解题，能够促进学生的数学素养、实际应用能力以及创新能力的全面提升。

因此，加强中国剩余定理在小学数学教学中的应用，对于提高学生的数学水平，具有重要的现实意义。

浅谈“中国剩余定理”在小学数学学习中的运用【摘要】中国剩余定理是一种数学定理，可以帮助我们解决关于整数的问题。

在小学数学学习中，了解和运用中国剩余定理对培养学生的逻辑思维和数学能力具有重要意义。

本文通过介绍中国剩余定理和小学数学学习的重要性，探讨了中国剩余定理在小学数学中的应用、实例解析、小学生的理解和运用方法以及教授方法，以及中国剩余定理对小学生数学思维的启发。

结合这些内容，文章总结了中国剩余定理在小学数学学习中的重要作用，并展望了未来它在小学教育中的发展。

这篇文章旨在为小学生提供更深入的数学学习体验，促进他们在数学领域的进步和发展。

【关键词】中国剩余定理、小学数学学习、应用、实例解析、理解、运用、教授、启发、意义、未来发展、作用、数学思维、小学生1. 引言1.1 介绍中国剩余定理中国剩余定理是中国古代数学的一项重要成就，也是整数论中的一个重要定理。

它由中国数学家孙子在《孙子算经》中首次提出，后来被用于解决关于同余方程组的问题。

中国剩余定理的核心思想是：如果给定两个或多个整数的模数两两互质，那么可以通过这些整数在对应模数下的余数来确定一个解。

这个解将是原方程组所有解的一个代表。

中国剩余定理在数论、密码学、编码理论等领域有广泛的应用。

而在小学数学学习中，虽然小学生可能不会直接学习中国剩余定理的证明和推导过程，但可以通过具体的例子和练习来理解和运用这个定理。

通过学习中国剩余定理，学生可以培养逻辑思维能力、数学建模能力和解决问题的能力。

1.2 小学数学学习的重要性数学在现代社会中的应用广泛。

无论是工程、科学、经济、医学等各个领域，都需要数学知识的支撑。

小学阶段对数学的学习不仅可以为将来的学习和就业奠定基础，还可以帮助学生更好地适应未来社会的发展需求。

数学还有助于培养学生的观察力、耐心和合作精神。

在解决数学问题的过程中，学生需要仔细观察、耐心思考，并且有时还需要和同学一起合作来解决难题。

这些素质对学生终身发展都具有重要的意义。

crt中国剩余定理CRT（中国剩余定理）是一种数论中的重要定理，它在解决一类特殊的模线性方程问题中发挥着重要的作用。

本文将从定理的定义、应用场景、解题步骤和数学原理等几个方面对CRT进行详细介绍。

一、定义CRT，全称为中国剩余定理，是中国古代数学家孙子所提出的一种解决模线性方程组的方法。

它适用于一类特殊的线性同余方程组，即方程组的模数两两互质。

CRT的核心思想是通过对模数的分解，将原问题转化为一系列模数互质的小问题，再用模运算的方法求解，最后通过合并得到原问题的解。

二、应用场景CRT在计算机科学、密码学、编码理论等领域有广泛的应用。

比如在计算机图形学中，我们需要对色彩进行混合叠加，而每个颜色的取值范围是有限的。

这时可以利用CRT将颜色的分量分别处理，再合并得到最终的颜色值。

在密码学中，CRT可以用来加密和解密数据，提高安全性和效率。

三、解题步骤要运用CRT解决问题，首先要保证模数两两互质。

接下来，需要对模数进行分解，并求解每个小问题的解。

最后，通过合并每个小问题的解，得到原问题的解。

具体步骤如下：1. 确定模数m1、m2、...、mn，且保证它们两两互质。

2. 对于方程x≡a1 (mod m1)、x≡a2 (mod m2)、...、x≡an (mod mn)，分别求解每个同余方程的解。

3. 求解同余方程x≡ai (mod mi)的解可以利用扩展欧几里得算法，求得系数xi和mi的乘积pi，即xi×mi=pi，其中pi是模mi的倒数。

4. 最后，将每个小问题的解合并，得到原问题的解x。

四、数学原理CRT的数学原理基于中国剩余定理。

中国剩余定理是指：若m1、m2、...、mn两两互质，则对于任意的整数a1、a2、...、an，同余方程组x≡a1 (mod m1)x≡a2 (mod m2)...x≡an (mod mn)必定存在一个解x，并且解存在于模m1、m2、...、mn的一个完全剩余系中。

我国剩余定理和拉格朗日插值公式是数学中重要的概念和定理。

它们在代数、数论、离散数学等领域都有重要应用。

本文将对这两个概念和定理进行介绍和讨论，以期帮助读者更深入地了解它们的原理和应用。

一、我国剩余定理我国剩余定理是我国古代数学的一个重要成果，其核心思想是：如果我们知道一个数除以几个数的余数，那么根据这些余数我们就可以推断出这个数模某个数的值。

这个定理在密码学、编码理论、计算机科学等领域有着广泛的应用。

我国剩余定理的具体表述如下：设m1,m2,...,mk是两两互质的正整数，即对任意i≠j，都有gcd(mi,mj)=1。

那么对于任意给定的整数a1,a2,...,ak和模数m1,m2,...,mk，我国剩余定理保证了下面这个方程组：x≡a1(modm1)x≡a2(modm2)...x≡ak(modmk)有唯一解。

这个定理在数论中有着重要的应用，比如在寻找解模的整数时，我国剩余定理能够更加高效地解决问题。

二、拉格朗日插值公式拉格朗日插值公式是代数学中非常重要的一个公式，它的作用是通过已知的n个数据点，构造一个n-1次多项式，使得这个多项式在这n 个点上与已知的数据完全一致。

拉格朗日插值公式在数值计算、信号处理、图像处理等领域有着广泛的应用。

拉格朗日插值公式的具体表述如下：设(x1,y1),(x2,y2),...,(xn,yn)是n 个不同的数对。

那么存在一个n-1次多项式P(x)，使得对于任意i，P(xi)=yi。

具体构造方法是通过拉格朗日基本多项式：Lk(x)=∏i≠k(x-xi)/(xk-xi)这样，我们就可以得到n个不同的拉格朗日基本多项式，它们的线性组合：P(x)=∑ykLk(x)就是我们所需要的插值多项式。

这个插值多项式能够在给定的n个数据点上完全地还原原始的函数值，从而能够方便地进行数据的插值和拟合。

我国剩余定理和拉格朗日插值公式是数学中非常重要的概念和定理，它们在代数、数论、离散数学等领域有着广泛的应用。

浅谈“中国剩余定理”在小学数学学习中的运用中国剩余定理，又称孙子定理，是中国古代数学家孙子在《孙子算经》中提出的一种数学定理，该定理在小学数学学习中有着丰富的运用。

中国剩余定理的表述是：如果我们知道一个数除以几个不同的数的余数，并且这些除数互质，那么我们可以通过这些余数以及除数的乘积之积恢复出这个数。

在小学数学学习中，中国剩余定理可以应用在许多问题中，例如：1. 节省运算步骤：使用中国剩余定理可以将一个大的除法问题转化为若干小的除法问题，并最后合并答案。

这样可以大大节省运算的步骤，减小计算量，提高计算效率。

2. 解决同余方程问题：同余方程是小学数学中的一个重要概念，中国剩余定理提供了一个有效的求解方法。

通过建立同余方程组并应用中国剩余定理，可以解决例如“小明今年的年龄是一个不大于12的正整数，除以3余2，除以4余3，除以5余4”的问题。

3. 推理规律性：小学数学学习中，推理规律性是一个重要的能力培养目标。

通过运用中国剩余定理，可以帮助学生建立数学模型，观察问题中的规律，通过归纳和演绎思维进行推理分析。

运用中国剩余定理的例子：例子一：小明买苹果。

他买了苹果，每袋15个粒，还剩2个苹果；如果每袋20个粒，还剩3个苹果；如果每袋32个粒，还剩7个苹果。

问小明买了多少个苹果？解答：我们可以建立如下的方程组：x ≡ 2 (mod 15)x ≡ 3 (mod 20)x ≡ 7 (mod 32)其中符号≡表示同余。

由中国剩余定理，我们可以解得：x ≡ 17 (mod 480)所以小明买了480个苹果。

例子二：某个居民小区购买新的电梯。

共有100户居民，为了满足居民的需求，电梯安装在了离每一栋楼房最近的位置。

电梯间隔每4个楼房就有一台电梯，间隔每7个楼房就有一台电梯。

问这个小区共安装了多少部电梯？所以这个小区共安装了28部电梯。

通过以上两个例子，我们可以看到中国剩余定理在小学数学学习中的灵活运用。

它能够使学生在解决问题时灵活思考，培养学生观察规律、建立数学模型、进行推理分析的能力。

LUOYANG NORMAL UNIVERSITY 2012届本科毕业论文中国剩余定理的归纳及其应用院（系）名称数学科学学院专业名称数学与应用数学学生姓名任晓燕学号*********指导教师王众杰讲师完成时间2012.5中国剩余定理的归纳及其应用任晓燕数学科学学院 数学与应用数学 学号：080414001指导老师：王众杰摘要：中国剩余定理又称为孙子定理,它的数学思想在近代数学中占有非常重要的地位.本文归纳了中国剩余定理并给出证明,并给出相关的经典例,并在此基础上对其在同余式组,多项式定理、赋值定理、密码学以及生活中的应用进行初步的讨论和分析.关键词：中国剩余定理； 同余式组； 多项式； 密码学 引言中国古代著名数学著作<孙子算经>记载,"今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二,问物几何?"此问题为中国剩余定理的原型.解法和答案用算式表示为70×2+21×3+15×2-105×2=23.即得到适合题意的最小整数是23."物不知其数"开创了一次同余式研究的先河,但真正从完整的计算程序和理论上解决这个问题的事南宋时期的数学家秦九韶,秦九韶在他的《数书九章》中提出了一个数学方法"大衍求一术" .1876年,德国人马蒂生首先指出这一解法与19世纪高斯《算术探究》中关于一次同余式组的解法完全一致.从此,中国古代数学这一创造受到世界学者瞩目,并在西方数学史著中正式称为"中国剩余定理" ..1 中国剩余定理及其证明设122,,,...n n m m m 两两互素的正整数,令121122......,n n n M m m m m M m M m M ====则同余式组()()()1122mod mod ........................mod n n x c m x c m x c m =⎧⎪=⎪⎨⎪⎪=⎩有正整数解()111222...mod n n n x M a c M a c M a c M =++且解唯一；其中i a 是满足()()1mod ,1,2,...i i i M a m i n ≡=的一个整数.下面我们先给出裴蜀恒等式和一个性质,然后证明中国剩余定理.在数论中，裴蜀定理是一个关于最大公约数（或最大公约式）的定理。