九年级上册第一单元测试题

部编版语文九年级上册第一单元测试卷考试时间120分钟满分120分第Ⅰ卷（30分）一、基础知识及课外现代文阅读（每小题3分,合计30分）1．下列加点字的读音全部正确的一项是( )(3分)A ．妖娆．(ráo)折．腰(shé)可汗．(hán) 娉．婷(pīnɡ)B ．分．外(fèn) 风骚．(sāo)鲜妍．(yàn) 莽．莽(mǎnɡ)C ．稍逊．(xùn) 摇曳．(yè)冠．冕(ɡuān) 枉．然(wǎnɡ)D ．红晕．(yùn) 呢喃．(nán)黎．明(lí) 丰润．(yùn)2、下列词语中没有错别字的一项是( )(3分 )A ．邮票折腰天娇喉咙B ．妖饶滔滔嘶哑黎明C ．凝望鲜研漫游海峡D ．坟墓呢喃飘逸忧戚3．下列加点词语使用不正确的一项是( )(3分)A ．红日白雪交相辉映,祖国就像一位红装素裹．．．．的少女,格外娇艳多姿。

B ．张学良对我国历史产生了巨大影响,他是一位地地道道的风流人物．．．．。

C ．你娉婷婉约的风姿,娇艳俏丽的容貌,妩媚得体的举止,优雅大方的谈吐,令我刮目相看．．．．。

D ．我们当代的青少年是一代天骄．．．．,肩负着建设祖国的伟大使命。

4．依次填入下面一段文字横线处的语句,衔接最恰当的一项是( )(3分)“南国之秋,当然是也有它的特异的地方的……可是色彩不浓,回味不永。

比起北国的秋来,正像是黄酒之与白干,稀饭之与馍馍,鲈鱼之与大蟹,黄犬之与骆驼。

”这就不但在情调上,而且在语言上把雅趣和俗趣统一起来了。

__________。

__________。

__________。

________。

________。

①但是,郁达夫却在这里构成了和谐的统一情调②前面就有茅房、耗子,这里又有稀饭、馍馍、黄犬、大蟹,等等③这是因为他的情感特点,本身就是把大雅和大俗融为一体的④这些话语本来就是缺乏诗意的,用在这充满古典的、高雅趣味的文章中,是要冒不和谐的风险的⑤郁达夫把秋天写得这么有诗意,赋予它一系列诗意的高雅的话语,然而不时又穿插一些平民的俗语进去A ．②①⑤④③B ．⑤②④①③C ．②⑤①④③D ．③⑤②④①5．下列句中没有语病的一项是( )(3分)A ．科学家应该用专业的知识去传播科学理性的精髓,让科学获得最广泛公众的支持和理解,这是科学家的责任,也是一种担当。

九年级语文上册第一单元测试卷一、基础知识及运用。

（ 27 分）1．以下加点字注音有误的一项为哪一项（B）（ 2 分）A．稍逊 (x ùn)格外(fèn)风骚（sāo）济慈(cí)．．．．B．喑哑 ( ān)丝缕(1ǚ)襁褓（qiánɡbǎo）折腰(zhé)．．．．．C．闪耀 (shu ò)．D．静谧 (mì)．发抖(ch ．联想(xi ．àn) 凝视（ nínɡ）．á) 栖息（ qī）．留滞 (zh ì)．角落 (jiǎo)．2．选出以下加点字音、形、义正确的一项(A)(2分)A．妖娆 (r áo) ：娇艳美好。

．留滞：即滞留，逗留不流通。

B．田圃 (f ǔ) ：田地。

．丝缕．(l ǚ)：丝线。

C．成吉思汗．(h án) ：元太祖铁木真。

折腰：鞠躬，倾倒。

襁褓 (qi ǎnɡb ǎo)．．监禁：约束，强力限制。

凝视 (n ínɡw ànɡ)．．喧嚷 (xu án) ：高声喊。

．冻僵．(jián)风流人物：这里指能立功立业的英豪人物。

D．发抖 (ch án d óu) 。

．．微漾 (y ànɡ) ：微波涟漪。

．枯黄：枯竭焦黄。

唯余莽莽：只剩下白茫茫的一片。

3．以下诗句与原作完整一致的是（B）（ 2 分）A．需晴天，看红妆素裹，格外妖娆。

B．当鱼塘寒浅留滞着游鱼C．小燕子见了我就笑斜了翅膀啊D．明月撒下它的光芒，给四周的全部披上盛装。

4．指出以下句子运用的修辞。

(4 分 )(1)山舞银蛇，原驰蜡象，欲与天公试比高。

( 比喻 )( 拟人 )(2)惜秦皇汉武，略输文采；唐宗宋祖，稍逊风骚。

一代天骄，成吉思汗，只识弯弓射大雕。

( 比喻 )( 对偶 )5．以下作家、作品、出处搭配有误的一项为哪一项 (D)(2分 ) A．毛泽东——《沁园春雪》——《毛泽东诗词集》B．郑愁予——《雨说》——《郑愁予诗的自选I 》C．江河——《星星变奏曲》——《上海文学》D．济慈——《夜》——《世界派别诗选》6．以下表述错误的一项为哪一项(C)(2分)A．《沁园春雪》经过对北国雪景的描述，表达了诗人对祖国大好河山的热爱以及对历代封建统治者的批判和对他们缺乏文采的痛惜这一主题思想。

【导语】考试的⽅法有笔试、⼝试、⾯试和操作考试等，可根据不同的测试⽬标和测试内容选择合适的⽅式。

下⾯是⽆忧考为您整理的《九年级上册数学第⼀章单元测试题》，仅供⼤家参考。

【篇⼀】 ⼀、选择题(每⼩题5分，共25分) 1.反⽐例函数的图象⼤致是() 2.如果函数y=kx-2(k0)的图象不经过第⼀象限，那么函数的图象⼀定在A.第⼀、⼆象限B.第三、四象限C.第⼀、三象限D.第⼆、四象限 3.如图，某个反⽐例函数的图像经过点P，则它的解析式为() A.B. C.D. 4.某村的粮⾷总产量为a(a为常数)吨，设该村的⼈均粮⾷产量为y 吨，⼈⼝数为x，则y与x之间的函数关系式的⼤致图像应为() 5.如果反⽐例函数的图像经过点(2，3)，那么次函数的图像经过点()A.(-2,3)B.(3,2)C.(3,-2)D.(-3,2) ⼆、填空题 6.已知点(1，-2)在反⽐例函数的图象上，则k=. 7.⼀个图象不经过第⼆、四象限的反⽐例函数的解析式为. 8.已知反⽐例函数，补充⼀个条件：后，使得在该函数的图象所在象限内，y随x值的增⼤⽽减⼩. 9.近视眼镜的度数y与镜⽚焦距x(⽶)成反⽐例.已知400度近视眼镜镜⽚的焦距为0.25⽶，则眼镜度数y与镜⽚焦距x之间的函数关系式是. 10.如图，函数y=-kx(k0)与y=-的图像交于A、B两点.过点 A作AC垂直于y轴，垂⾜为C，则△BOC的⾯积为. 三、解答题(共50分) 11.(8分)⼀定质量的氧⽓，其密度(kg/m,)是它的体积v(m,)的反⽐例函数.当V=10m3时甲=1.43kg/m. (1)求与v的函数关系式;(2)求当V=2m3时，氧⽓的密度. 12.(8分)已知圆柱的侧⾯积是6m2，若圆柱的底⾯半径为x(cm)，⾼为ycm). (1)写出y关于x的函数解析式; (2)完成下列表格： (3)在所给的平⾯直⾓坐标系中画出y关于x的函数图像. 13.(l0分)在某⼀电路中，保持电压不变，电流I(安培)与电阻R(欧姆)成反⽐例.当电阻R=5欧姆时，电流I=2安培. (l)求I与R之间的函数关系式; (2)当电流I=0.5安培时，求电阻R的值; (3)如果电路中⽤电器的可变电阻逐渐增⼤，那么电路中的电流将如何变化? (4)如果电路中⽤电器限制电流不得超过10安培，那么⽤电器的可变电阻应控制在什么范围内? 14.(12分)某蓄⽔池的排⽔管每⼩时排⽔飞12m3,8h可将满池⽔全部排空. (1)蓄⽔池的容积是多少? (2)如果增加排⽔管，使每⼩时的排⽔量达到x(m3)，那么将满池⽔排空所需的时间y(h)将如何变化? (3)写出y与x之间的关系式; (4)如果准备在6h内将满池⽔排空，那么每⼩时的排⽔量⾄少为多少? (5)已知排⽔管每⼩时的排⽔量为24m3，那么最少多长时间可将满池⽔全部排空? 15.(12分)反⽐例函数和⼀次函数y=mx+n的图象的⼀个交点A(-3，4)，且⼀次函数的图像与x轴的交点到原点的距离为5. (1)分别确定反⽐例函数与⼀次函数的解析式; (2)设⼀次函数与反⽐例函数图像的另⼀个交点为B，试判断AOB(点O为平⾯直⾓坐标系原点)是锐⾓、直⾓还是钝⾓?并简单说明理由. 【篇⼆】 ⼀、选择题(每⼩题3分，共30分) 1、两个直⾓三⾓形全等的条件是()A、⼀锐⾓对应相等B、两锐⾓对应相等C、⼀条边对应相等D、两条边对应相等 2、如图，由∠1=∠2，BC=DC，AC=EC，得△ABC≌△EDC的根据是()A、SASB、ASAC、AASD、SSS 3、等腰三⾓形底边长为7，⼀腰上的中线把其周长分成两部分的差为3，则腰长是()A、4B、10C、4或10D、以上答案都不对 4、如图，EA⊥AB，BC⊥AB，EA=AB=2BC，D为AB中点，有以下结论： (1)DE=AC;(2)DE⊥AC;(3)∠CAB=30°;(4)∠EAF=∠ADE。

九年级语文上册第一单元测试卷本试卷分为Ⅰ卷、Ⅱ卷和Ⅲ卷三部分。

满分120分，考试时间150分钟。

第Ⅰ卷(选择题共30分)一、基础·积累(每小题3分，共12分)1．下列各组词语书写和加点字的读音全部正确的一项是( )A．妖娆．(ráo)娉婷．(tín)丰润．(rùn)红装素裹．(guǒ)B．鲜妍．(yán) 摇曳．(yè) 呢喃．(lán) 新颖．别至(yǐnɡ)C．汹．涌(xiōng) 飘逸．(yì) 冠冕．(miǎn) 不屈不挠．(náo)D．凝．望(níng) 忧戚．(qī) 滔．滔(tāo) 成吉思汗．(hàn)2．下列句子中加点成语的使用正确的一项是( )A．电影《战狼2》，以场面的气势恢宏、情节的抑扬顿挫．．．．和风格的奇异独特，赢得了广大观众的一致好评。

B．他们是一对孪生兄弟，因此长得惟妙惟肖．．．．。

C．家风是一种软约束，通过潜滋暗长．．．．的影响，有效约束家庭成员的行为、作风和操守。

D．村干部因地制宜．．．．，大力发展生态农业，带领村民走上致富道路。

3．(广元中考)下列句子没有语病的一项是( )A．所有学校都要关爱留守儿童，利用一切契机激励他们，锻炼他们，培养他们自立自强。

B．10月23日是世界读书日，各地读者纷纷来到图书馆、书店等地，阅读图书，品味书香。

C．为了营造良好的安全环境，各级部门切实加强安全生产执法检查和应急管理工作水平。

D．嘉陵第一小学采取了各种预防措施，防止师生不患春季流感，确保全校师生健康安全。

4．(襄阳中考)下面语句的顺序排列恰当的一项是( )①全民阅读率的上升，显然是一件好事。

②因此，全民阅读质量的真正提升之路还很漫长。

③但有必要思考的是：现在提升的到底是整体式阅读还是碎片式阅读，到底是深阅读，还是浅阅读？④或者把问题进一步简化为：到底是高质量的阅读还是低质量的阅读？⑤在这些方面，并没有准确的数字区分，但就我们眼中所见而言，高质量阅读，可能并不尽如人意。

九年级数学上册第一单元测试卷一、选择题（每题3分，共30分）1. 下列哪个数是无理数？A. 2.5B. πC. 0.333...D. √42. 已知函数f(x) = 2x + 3，求f(-1)的值。

A. -1B. 1C. 3D. 53. 一个直角三角形的两直角边分别为3和4，斜边的长度是多少？A. 5B. 6C. 7D. 84. 以下哪个不等式是正确的？A. 3 < 4 < 5B. 3 > 4 > 5C. 3 < 5 < 4D. 4 > 3 > 25. 一个圆的半径为5，它的面积是多少？A. 25πB. 50πC. 25D. 506. 如果一个数的平方等于81，那么这个数是多少？A. 9B. ±9C. 3D. ±37. 一个数的立方根是2，这个数是多少？A. 8B. 6C. 4D. 28. 以下哪个是二次根式？A. √9B. √(-4)C. √3D. √19. 一个多项式f(x) = ax^2 + bx + c，当a < 0时，抛物线的开口方向是什么？A. 向上B. 向下C. 向左D. 向右10. 一个等差数列的首项是3，公差是2，第5项是多少？A. 11B. 13C. 15D. 17二、填空题（每题2分，共20分）11. 圆的周长公式是C = 2πr，其中r是________。

12. 一个数的绝对值是它与0的距离，例如|-5| = ________。

13. 一个二次方程ax^2 + bx + c = 0的判别式是________。

14. 如果一个角是直角的一半，那么这个角的度数是________。

15. 一个数的相反数是________。

16. 一个数的倒数是1除以这个数，例如5的倒数是________。

17. 一个等比数列的首项是2，公比是3，第4项是________。

18. 一个函数y = kx + b，当k = 0时，函数的图像是一条________。

部编版九年级语文上册第一单元测试卷（附答案解析）一、语言文字积累与运用（共29分）（一）单项选择题（共12分，每小题3分）1.下列加点字注音全部正确的一项是( )A. 嘶．哑(sī) 分．外(fèn) 娉．婷(pìng) 浮．动(fú)B. 摇曳．(yè) 折．腰(zhé) 鲜妍．(yán) 可．汗(kě)C. 妖娆．(náo) 海峡．(xiá) 红晕．(yùn) 凝．望(níng)D. 冠．冕(guān) 枉．然(wǎng) 飘逸．(yì) 轻灵．(líng)【答案】D【解析】字音重点考核多音字、形声字、形似字、音近字、方言、生僻字等。

D项注音全部正确。

A娉婷(pīng)。

B可汗(kè)。

C妖娆(ráo)。

2.下列词语中没有错别字的一项是( )A. 妖娆优戚生机勃发呢喃软语B. 黎明流盼屏气凝神江山多娇C. 汹涌丰润暴风骤雨尽态极颜D. 坟墓喉咙涛涛不绝稍逊风骚【答案】B【解析】字形题从表象上看主要考核双音节词语和成语，有时会考核三字的专业术语和熟语。

B项词语中没有错别字。

A忧戚。

C尽态极妍。

D滔滔不绝。

3. 填入下面横线上的句子，排列顺序最恰当的一项是( )商务印书馆创始人张元济先生有一句简单而朴素的话：“天下第一件好事还是读书。

”________。

①从个人角度而言，腹有诗书气自华。

②从国家层面来说，倡导全民阅读提升整个民族的素质。

③历史证明，全世界一步步从野蛮走向文明，无不是建立在知识的积累之上。

④的确，读书可以明理，阅读铸就灵魂。

A. ①④②③B. ③①②④C. ④①②③D. ④②③①【答案】C【解析】C项排列顺序最恰当。

推敲各句之间的逻辑关系；④句承前解说张元济先生话语的意思，注意“的确”二字；①②两句从个人到国家层面依次展开，具体说明读书的作用；③句总结放最后。

部编版语文9年级上册第1单元基础测试时间：120分钟满分：120分班级__________姓名__________得分__________一、选择题(共18分)1．(本题3分)下列加点字的注音和各组词语的字形全都正确的一项是（）A．沁．园春（qìng）分外妖娆原驰蜡象B．成吉思汗．（hán）江山多骄山舞银蛇C．还看今朝．（cháo）略输文彩竞折腰D．稍逊风骚．（sāo）风流人物红装素裹2．(本题3分)下列词语书写全部正确的一项是（）A．黄昏折腰喉咙汹涌B．悲愤坟墓邮票翅冀C．月圆鹅黄海狭柔嫩D．季节红晕寂静慢游3．(本题3分)下列句中加点词语解释不正确的一项是（）A．须晴日，看红装素裹．．．．，分外妖娆。

（形容雪后天晴，红日和白雪交相辉映的壮丽景色）B．哦，逝去的多少欢乐和忧戚．．，我枉然在你的心胸里描画！（忧伤）C．百花的冠冕．．你戴着，你是/天真，庄严，你是夜夜的月圆。

（礼帽）D．数风流人物．．．．，还看今朝。

（指能建功立业的英雄人物）4．(本题3分)下列句子中的标点符号使用不正确．．．的一项是（）A．看了媒体发布的收视报道，我才知道今年的电视剧《都挺好》有多火。

B．人生，只有一条路不能选择，那就是放弃；只有一条路不能拒绝，那就是成长。

C．大诗人苏轼曾经说过：“古之立大事者，不惟有超世之才，亦必有坚韧不拔之志。

”D．应该关注的是传统文化的形式？还是传统文化的内涵？这值得我们认真思考。

5．(本题3分)下面对《艾青诗选》内容的表述不正确的一项是（）A．从“活着就要斗争，在斗争中前进”可以体会到作者对革命的崇高热情、不懈努力。

B．“在死亡没有来临，把能量发挥干净”可以看出诗人对生命的热爱、赞叹、赞赏。

C．《礁石》中“含着微笑，看着海洋”的礁石，象征着坚韧不拔、高傲自负的人们。

D．“然后我死了，连羽毛也腐烂在土地里面”这两诗形象地表达了诗人对土地的眷恋。

6．(本题3分)下列句子中，没有语病的一项是（）A．4月20日，“齐鲁时代楷模”发布仪式在济南举行，山东省委宣传部追授莱芜市明利特色蔬菜种植专业合作社理事长陈明利同志“齐鲁时代楷模”荣誉称号。

九年级上册英语第一单元测试卷及答案（经典版）编制人：__________________审核人：__________________审批人：__________________编制单位：__________________编制时间：____年____月____日序言下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。

文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢!并且，本店铺为大家提供各种类型的经典范文，如演讲致辞、规章制度、策划方案、合同协议、条据文书、心得体会、职业规划、教学资料、作文大全、其他范文等等，想了解不同范文格式和写法，敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!Moreover, our store provides various types of classic sample essays for everyone, such as speeches, rules and regulations, planning plans, contract agreements, documentary evidence, insights, career planning, teaching materials, complete essays, and other sample essays. If you want to learn about different sample formats and writing methods, please pay attention!九年级上册英语第一单元测试卷及答案九年级上册英语第一单元测试卷及答案免费九年级英语第一单元学习是很重要的，学生们要在课后主动做英语第一单元试卷，英语考试才会取得好成绩。

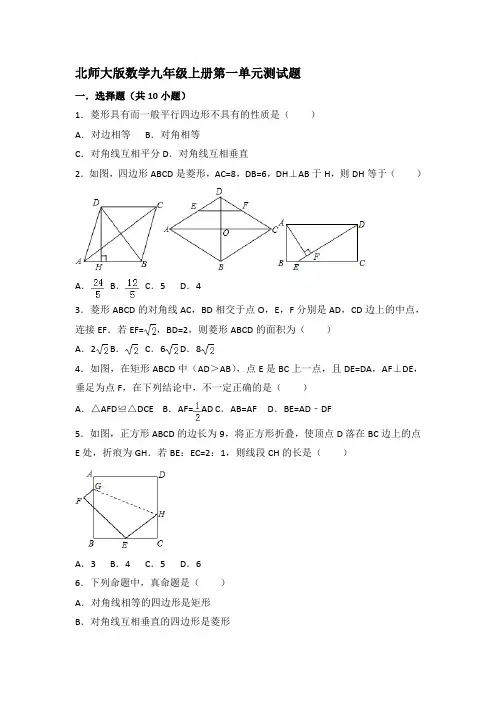
北师大版数学九年级上册第一单元测试题一．选择题（共10小题）1．菱形具有而一般平行四边形不具有的性质是（）A．对边相等B．对角相等C．对角线互相平分 D．对角线互相垂直2．如图，四边形ABCD是菱形，AC=8，DB=6，DH⊥AB于H，则DH等于（）A．B．C．5 D．43．菱形ABCD的对角线AC，BD相交于点O，E，F分别是AD，CD边上的中点，连接EF．若EF=，BD=2，则菱形ABCD的面积为（）A．2 B．C．6 D．84．如图，在矩形ABCD中（AD＞AB），点E是BC上一点，且DE=DA，AF⊥DE，垂足为点F，在下列结论中，不一定正确的是（）A．△AFD≌△DCE B．AF=AD C．AB=AF D．BE=AD﹣DF5．如图，正方形ABCD的边长为9，将正方形折叠，使顶点D落在BC边上的点E处，折痕为GH．若BE：EC=2：1，则线段CH的长是（）A．3 B．4 C．5 D．66．下列命题中，真命题是（）A．对角线相等的四边形是矩形B．对角线互相垂直的四边形是菱形C．对角线互相平分的四边形是平行四边形D．对角线互相垂直平分的四边形是正方形7．如图，在周长为12的菱形ABCD中，AE=1，AF=2，若P为对角线BD上一动点，则EP+FP的最小值为（）A．1 B．2 C．3 D．48．如图，四边形ABCD中，对角线相交于点O，E、F、G、H分别是AD、BD、BC、AC的中点，要使四边形EFGH是菱形，则四边形ABCD需满足的条件是（）A．AB=AD B．AC=BD C．AD=BC D．AB=CD9．如图，在正方形ABCD中，H是BC延长线上一点，使CE=CH，连接DH，延长BE交DH于G，则下面结论错误的是（）A．BE=DH B．∠H+∠BEC=90°C．BG⊥DH D．∠HDC+∠ABE=90°10．如图，正方形ABCD中，点E、F分别在BC、CD上，△AEF是等边三角形，连接AC交EF于G，下列结论：①BE=DF；②∠DAF=15°；③AC垂直平分EF；④BE+DF=EF；⑤S△CEF=2S△ABE，其中正确结论有（）A．2个 B．3个 C．4个 D．5个二．填空题（共10小题）11．如图，在菱形ABCD中，对角线AC与BD相交于点O，AC=8，BD=6，OE⊥BC，垂足为点E，则OE=．12．如图，菱形ABCD的对角线AC、BD相交于点O，E为AD的中点，若OE=3，则菱形ABCD的周长为．13．如图，将正方形纸片按如图折叠，AM为折痕，点B落在对角线AC上的点E 处，则∠CME=．14．如图，在正方形ABCD中，点E，N，P，G分别在边AB，BC，CD，DA上，点M，F，Q都在对角线BD上，且四边形MNPQ和AEFG均为正方形，则的值等于．15．菱形的两条对角线长分别为16和12，则它的面积为．16．如图，矩形ABCD的对角线AC，BD相交于点O，CE∥BD，DE∥AC．若AC=4，则四边形CODE的周长是．17．如图，在矩形ABCD中，AB=2，BC=4，对角线AC的垂直平分线分别交AD、AC于点E、O，连接CE，则CE的长为．18．如图，在矩形ABCD中，AD=9cm，AB=3cm，将其折叠，使点D与点B重合，则重叠部分（△BEF）的面积为．19．如图，O是矩形ABCD的对角线AC的中点，M是AD的中点，若AB=6，AD=8，则四边形ABOM的周长为．20．矩形ABCD中，AB=5，BC=4，将矩形折叠，使得点B落在线段CD的点F处，则线段BE的长为．三．解答题（共10小题）21．如图，在▱ABCD中，BC=2AB=4，点E、F分别是BC、AD的中点．（1）求证：△ABE≌△CDF；（2）当四边形AECF为菱形时，求出该菱形的面积．22．如图，在菱形ABCD中，对角线AC、BD相交于点O，过点D作对角线BD 的垂线交BA的延长线于点E．（1）证明：四边形ACDE是平行四边形；（2）若AC=8，BD=6，求△ADE的周长．23．如图，AC是矩形ABCD的对角线，过AC的中点O作EF⊥AC，交BC于点E，交AD于点F，连接AE，CF．（1）求证：四边形AECF是菱形；（2）若AB=，∠DCF=30°，求四边形AECF的面积．（结果保留根号）24．如图，菱形ABCD的对角线AC，BD相交于点O，且DE∥AC，AE∥BD．求证：四边形AODE是矩形．25．如图，四边形ABCD是正方形，点E是BC的中点，∠AEF=90°，EF交正方形外角的平分线CF于F．求证：AE=EF．26．已知，如图，正方形ABCD中，E为BC边上一点，F为BA延长线上一点，且CE=AF．连接DE、DF．求证：DE=DF．27．如图，在正方形ABCD中，E是边AB的中点，F是边BC的中点，连结CE、DF．求证：CE=DF．28．如图，已知菱形ABCD的对角线相交于点O，延长AB至点E，使BE=AB，连结CE，若∠E=50°，求∠BAO的大小．29．如图，在△ABC中，∠ACB=90°，BC的垂直平分线DE交BC于D，交AB于E，F在DE上，并且AF=CE．（1）求证：四边形ACEF是平行四边形；（2）当∠B满足什么条件时，四边形ACEF是菱形？请回答并证明你的结论．30．如图，在矩形ABCD中，对角线BD的垂直平分线MN与AD相交于点M，与BD相交于点O，与BC相交于N，连接BM，DN．（1）求证：四边形BMDN是菱形；（2）若AB=2，AD=4，求MD的长．01月18日dxzxshuxue的初中数学组卷参考答案与试题解析一．选择题（共10小题）1．（2016•莆田）菱形具有而一般平行四边形不具有的性质是（）A．对边相等B．对角相等C．对角线互相平分 D．对角线互相垂直【分析】由菱形的性质可得：菱形的对角线互相平分且垂直；而平行四边形的对角线互相平分；则可求得答案．【解答】解：∵菱形具有的性质：对边相等，对角相等，对角线互相平分，对角线互相垂直；平行四边形具有的性质：对边相等，对角相等，对角线互相平分；∴菱形具有而一般平行四边形不具有的性质是：对角线互相垂直．故选D．【点评】此题考查了菱形的性质以及平行四边形的性质．注意菱形的对角线互相平分且垂直．2．（2016•枣庄）如图，四边形ABCD是菱形，AC=8，DB=6，DH⊥AB于H，则DH等于（）A．B．C．5 D．4【分析】根据菱形性质求出AO=4，OB=3，∠AOB=90°，根据勾股定理求出AB，再根据菱形的面积公式求出即可．【解答】解：∵四边形ABCD是菱形，∴AO=OC，BO=OD，AC⊥BD，∵AC=8，DB=6，∴AO=4，OB=3，∠AOB=90°，由勾股定理得：AB==5，∵S=，菱形ABCD∴，∴DH=，故选A．【点评】本题考查了勾股定理和菱形的性质的应用，能根据菱形的性质得出S菱=是解此题的关键．形ABCD3．（2016•宁夏）菱形ABCD的对角线AC，BD相交于点O，E，F分别是AD，CD 边上的中点，连接EF．若EF=，BD=2，则菱形ABCD的面积为（）A．2 B．C．6 D．8【分析】根据中位线定理可得对角线AC的长，再由菱形面积等于对角线乘积的一半可得答案．【解答】解：∵E，F分别是AD，CD边上的中点，EF=，∴AC=2EF=2，又∵BD=2，∴菱形ABCD的面积S=×AC×BD=×2×2=2，故选：A．【点评】本题主要考查菱形的性质与中位线定理，熟练掌握中位线定理和菱形面积公式是关键．4．（2016•荆门）如图，在矩形ABCD中（AD＞AB），点E是BC上一点，且DE=DA，AF⊥DE，垂足为点F，在下列结论中，不一定正确的是（）A．△AFD≌△DCE B．AF=AD C．AB=AF D．BE=AD﹣DF【分析】先根据已知条件判定△AFD≌△DCE（AAS），再根据矩形的对边相等，以及全等三角形的对应边相等进行判断即可．【解答】解：（A）由矩形ABCD，AF⊥DE可得∠C=∠AFD=90°，AD∥BC，∴∠ADF=∠DEC．又∵DE=AD，∴△AFD≌△DCE（AAS），故（A）正确；（B）∵∠ADF不一定等于30°，∴直角三角形ADF中，AF不一定等于AD的一半，故（B）错误；（C）由△AFD≌△DCE，可得AF=CD，由矩形ABCD，可得AB=CD，∴AB=AF，故（C）正确；（D）由△AFD≌△DCE，可得CE=DF，由矩形ABCD，可得BC=AD，又∵BE=BC﹣EC，∴BE=AD﹣DF，故（D）正确；故选B．【点评】本题主要考查了矩形和全等三角形，解决问题的关键是掌握矩形的性质：矩形的四个角都是直角，矩形的对边相等．解题时注意：在直角三角形中，若有一个锐角等于30°，则这个锐角所对的直角边等于斜边的一半．5．（2016•毕节市）如图，正方形ABCD的边长为9，将正方形折叠，使顶点D 落在BC边上的点E处，折痕为GH．若BE：EC=2：1，则线段CH的长是（）A．3 B．4 C．5 D．6【分析】根据折叠可得DH=EH，在直角△CEH中，设CH=x，则DH=EH=9﹣x，根据BE：EC=2：1可得CE=3，可以根据勾股定理列出方程，从而解出CH的长．【解答】解：设CH=x，则DH=EH=9﹣x，∵BE：EC=2：1，BC=9，∴CE=BC=3，∴在Rt△ECH中，EH2=EC2+CH2，即（9﹣x）2=32+x2，解得：x=4，即CH=4．故选（B）．【点评】本题主要考查正方形的性质以及翻折变换，折叠问题其实质是轴对称变换．在直角三角形中，利用勾股定理列出方程进行求解是解决本题的关键．6．（2016•内江）下列命题中，真命题是（）A．对角线相等的四边形是矩形B．对角线互相垂直的四边形是菱形C．对角线互相平分的四边形是平行四边形D．对角线互相垂直平分的四边形是正方形【分析】A、根据矩形的定义作出判断；B、根据菱形的性质作出判断；C、根据平行四边形的判定定理作出判断；D、根据正方形的判定定理作出判断．【解答】解：A、两条对角线相等且相互平分的四边形为矩形；故本选项错误；B、对角线互相垂直的平行四边形是菱形；故本选项错误；C、对角线互相平分的四边形是平行四边形；故本选项正确；D、对角线互相垂直平分且相等的四边形是正方形；故本选项错误；故选C．【点评】本题综合考查了正方形、矩形、菱形及平行四边形的判定．解答此题时，必须理清矩形、正方形、菱形与平行四边形间的关系．7．（2016•龙岩模拟）如图，在周长为12的菱形ABCD中，AE=1，AF=2，若P为对角线BD上一动点，则EP+FP的最小值为（）A．1 B．2 C．3 D．4【分析】作F点关于BD的对称点F′，则PF=PF′，由两点之间线段最短可知当E、P、F′在一条直线上时，EP+FP有最小值，然后求得EF′的长度即可．【解答】解：作F点关于BD的对称点F′，则PF=PF′，连接EF′交BD于点P．∴EP+FP=EP+F′P．由两点之间线段最短可知：当E、P、F′在一条直线上时，EP+FP的值最小，此时EP+FP=EP+F′P=EF′．∵四边形ABCD为菱形，周长为12，∴AB=BC=CD=DA=3，AB∥CD，∵AF=2，AE=1，∴DF=AE=1，∴四边形AEF′D是平行四边形，∴EF′=AD=3．∴EP+FP的最小值为3．故选：C．【点评】本题主要考查的是菱形的性质、轴对称﹣﹣路径最短问题，明确当E、P、F′在一条直线上时EP+FP有最小值是解题的关键．8．（2016•蜀山区二模）如图，四边形ABCD中，对角线相交于点O，E、F、G、H分别是AD、BD、BC、AC的中点，要使四边形EFGH是菱形，则四边形ABCD 需满足的条件是（）A．AB=AD B．AC=BD C．AD=BC D．AB=CD【分析】由点E、F、G、H分别是任意四边形ABCD中AD、BD、BC、CA的中点，根据三角形中位线的性质，可得EF=GH=AB，EH=FG=CD，又由当EF=FG=GH=EH时，四边形EFGH是菱形，即可求得答案．【解答】解：∵点E、F、G、H分别是任意四边形ABCD中AD、BD、BC、CA的中点，∴EF=GH=AB，EH=FG=CD，∵当EF=FG=GH=EH时，四边形EFGH是菱形，∴当AB=CD时，四边形EFGH是菱形．故选：D．【点评】此题考查了中点四边形的性质、菱形的判定以及三角形中位线的性质．此题难度适中，注意掌握数形结合思想的应用．9．（2016•曹县校级模拟）如图，在正方形ABCD中，H是BC延长线上一点，使CE=CH，连接DH，延长BE交DH于G，则下面结论错误的是（）A．BE=DH B．∠H+∠BEC=90°C．BG⊥DH D．∠HDC+∠ABE=90°【分析】根据正方形的四条边都相等，角都是直角，先证明△BCE和△DCH全等，再根据全等三角形对应边相等，全等三角对应角相等，对各选项分析判断后利用排除法．【解答】解：在正方形ABCD中，BC=CD，∠BCD=∠DCH=90°，在△BCE和△DCH中，，∴△BCE≌△DCH（SAS），∴BE=DH，故A选项正确；∠H=∠BEC，故B选项错误；∠EBC=∠HDC，∴∠EBC+BEC=∠HDC+DEG，∵BCD=90°，∴∠EBC+BEC=90°，∴∠HDC+DEG=90°，∴BG⊥DH，故C选项正确；∵∠ABE+∠EBC=90°，∴∠HDC+∠ABE=90°，故D选项正确．故选B．【点评】本题主要利用正方形的和三角形全等的性质求解，熟练掌握性质是解题的关键．10．（2016•新华区一模）如图，正方形ABCD中，点E、F分别在BC、CD上，△AEF是等边三角形，连接AC交EF于G，下列结论：①BE=DF；②∠DAF=15°；③AC垂直平分EF；④BE+DF=EF；⑤S△CEF=2S△ABE，其中正确结论有（）A．2个 B．3个 C．4个 D．5个【分析】通过条件可以得出△ABE≌△ADF，从而得出∠BAE=∠DAF，BE=DF，由正方形的性质就可以得出EC=FC，就可以得出AC垂直平分EF，设EC=x，BE=y，由勾股定理就可以得出x与y的关系，表示出BE与EF，利用三角形的面积公式分别表示出S△CEF 和2S△ABE，再通过比较大小就可以得出结论．【解答】解：∵四边形ABCD是正方形，∴AB=BC=CD=AD，∠B=∠BCD=∠D=∠BAD=90°．∵△AEF等边三角形，∴AE=EF=AF，∠EAF=60°．∴∠BAE+∠DAF=30°．在Rt△ABE和Rt△ADF中，，Rt△ABE≌Rt△ADF（HL），∴BE=DF（故①正确）．∠BAE=∠DAF，∴∠DAF+∠DAF=30°，即∠DAF=15°（故②正确），∵BC=CD，∴BC﹣BE=CD﹣DF，即CE=CF，∵AE=AF，∴AC垂直平分EF．（故③正确）．设EC=x，由勾股定理，得EF=x，CG=x，AG=AEsin60°=EFsin60°=2×CGsin60°=x，∴AC=，∴AB=，∴BE=﹣x=，∴BE+DF=x﹣x≠x，（故④错误），=x2，∵S△CEFS△ABE=x2，∴2S=x2=S△CEF，（故⑤正确）．△ABE综上所述，正确的有4个，故选：C．【点评】本题考查了正方形的性质的运用，全等三角形的判定及性质的运用，勾股定理的运用，等边三角形的性质的运用，三角形的面积公式的运用，解答本题时运用勾股定理的性质解题时关键．二．填空题（共10小题）11．（2016•内江）如图，在菱形ABCD中，对角线AC与BD相交于点O，AC=8，BD=6，OE⊥BC，垂足为点E，则OE=．【分析】先根据菱形的性质得AC⊥BD，OB=OD=BD=3，OA=OC=AC=4，再在Rt△OBC中利用勾股定理计算出BC=5，然后利用面积法计算OE的长．【解答】解：∵四边形ABCD为菱形，∴AC⊥BD，OB=OD=BD=3，OA=OC=AC=4，在Rt△OBC中，∵OB=3，OC=4，∴BC==5，∵OE⊥BC，∴OE•BC=OB•OC，∴OE==．故答案为．【点评】本题考查了菱形的性质：菱形具有平行四边形的一切性质；菱形的四条边都相等；菱形的两条对角线互相垂直，并且每一条对角线平分一组对角．也考查了勾股定理和三角形面积公式．12．（2016•扬州）如图，菱形ABCD的对角线AC、BD相交于点O，E为AD的中点，若OE=3，则菱形ABCD的周长为24．【分析】由菱形的性质可得出AC⊥BD，AB=BC=CD=DA，再根据直角三角形斜边上的中线等于斜边的一半得出AD的长，结合菱形的周长公式即可得出结论．【解答】解：∵四边形ABCD为菱形，∴AC⊥BD，AB=BC=CD=DA，∴△AOD为直角三角形．∵OE=3，且点E为线段AD的中点，∴AD=2OE=6．C菱形ABCD=4AD=4×6=24．故答案为：24．【点评】本题考查了菱形的性质以及直角三角形的性质，解题的关键是求出AD=6．本题属于基础题，难度不大，解决该题型题目时，根据菱形的性质找出对角线互相垂直，再通过直角三角形的性质找出菱形的一条变成是关键．13．（2016•龙岩）如图，将正方形纸片按如图折叠，AM为折痕，点B落在对角线AC上的点E处，则∠CME=45°．【分析】由正方形的性质和折叠的性质即可得出结果．【解答】解：∵四边形ABCD是正方形，∴∠B=90°，∠ACB=45°，由折叠的性质得：∠AEM=∠B=90°，∴∠CEM=90°，∴∠CME=90°﹣45°=45°；故答案为：45°．【点评】本题考查了正方形的性质、折叠的性质；熟练掌握正方形和折叠的性质是解决问题的关键．14．（2016•天津）如图，在正方形ABCD中，点E，N，P，G分别在边AB，BC，CD，DA上，点M，F，Q都在对角线BD上，且四边形MNPQ和AEFG均为正方形，则的值等于．【分析】根据辅助线的性质得到∠ABD=∠CBD=45°，四边形MNPQ和AEFG均为正方形，推出△BEF与△BMN是等腰直角三角形，于是得到FE=BE=AE=AB，BM=MN=QM，同理DQ=MQ，即可得到结论．【解答】解：在正方形ABCD中，∵∠ABD=∠CBD=45°，∵四边形MNPQ和AEFG均为正方形，∴∠BEF=∠AEF=90°，∠BMN=∠QMN=90°，∴△BEF与△BMN是等腰直角三角形，∴FE=BE=AE=AB，BM=MN=QM，同理DQ=MQ，∴MN=BD=AB，∴==，故答案为：．【点评】本题考查了正方形的性质，等腰直角三角形的性质，正方形的面积的计算，熟练掌握等腰直角三角形的性质是解题的关键．15．（2016•白云区校级二模）菱形的两条对角线长分别为16和12，则它的面积为96．【分析】由菱形的两条对角线长分别为16和12，根据菱形的面积等于对角线积的一半，即可求得答案．【解答】解：∵菱形的两条对角线长分别为16和12，∴它的面积为：×16×12=96．故答案为：96．【点评】此题考查了菱形的性质．注意菱形的面积等于对角线积的一半．16．（2016•河源校级一模）如图，矩形ABCD的对角线AC，BD相交于点O，CE ∥BD，DE∥AC．若AC=4，则四边形CODE的周长是8．【分析】先证明四边形CODE是平行四边形，再根据矩形的性质得出OC=OD，然后证明四边形CODE是菱形，即可求出周长．【解答】解：∵CE∥BD，DE∥AC，∴四边形CODE是平行四边形，∵四边形ABCD是矩形，∴OC=AC=2，OD=BD，AC=BD，∴OC=OD=2，∴四边形CODE是菱形，∴DE=CEOC=OD=2，∴四边形CODE的周长=2×4=8；故答案为：8．【点评】本题考查了菱形的判定与性质以及矩形的性质；证明四边形是菱形是解决问题的关键．17．（2016•临沭县校级一模）如图，在矩形ABCD中，AB=2，BC=4，对角线AC 的垂直平分线分别交AD、AC于点E、O，连接CE，则CE的长为．【分析】由矩形的性质得出CD=AB=2，AD=BC=4，∠D=90°，由线段垂直平分线的性质得出CE=AE，设CE=AE=x，则DE=4﹣x，由勾股定理得出方程，解方程即可．【解答】解：∵四边形ABCD是矩形，∴CD=AB=2，AD=BC=4，∠D=90°，∵EF是AC的垂直平分线，∴CE=AE，设CE=AE=x，则DE=4﹣x，在Rt△CDE中，由勾股定理得：CD2+DE2=CE2，即22+（4﹣x）2=x2，解得：x=，∴CE=；故答案为：．【点评】本题考查了矩形的性质、线段垂直平分线的性质、勾股定理；熟练掌握矩形的性质，并能进行推理计算是解决问题的关键．18．（2016•抚顺模拟）如图，在矩形ABCD中，AD=9cm，AB=3cm，将其折叠，使点D与点B重合，则重叠部分（△BEF）的面积为7.5cm2．【分析】设DE=xcm，由翻折的性质可知DE=EB=x，则AE=（9﹣x）cm，在Rt△ABE中，由勾股定理求得ED的长；由翻折的性质可知∠DEF=∠BEF，由矩形的性质可知BC∥AD，从而得到∠BFE=∠DEF，故此可知∠BFE=∠FEB，得出FB=BE，最后根据三角形的面积公式求解即可．【解答】解：设DE=xcm．由翻折的性质可知DE=EB=x，∠DEF=∠BEF，则AE=（9﹣x）cm．在Rt△ABE中，由勾股定理得；BE2=EA2+AB2，即x2=（9﹣x）2+32．解得：x=5．∴DE=5cm．∵四边形ABCD为矩形，∴BC∥AD．∴∠BFE=∠DEF．∴∠BFE=∠FEB．∴FB=BE=5cm．∴△BEF的面积=BF•AB=×3×5=7.5（cm2）；故答案为：7.5cm2．【点评】本题主要考查的是翻折的性质、勾股定理的应用，等腰三角形的判定、三角形的面积公式，证得△BEF为等腰三角形，从而得到FB的长是解题的关键．19．（2016•苏州校级二模）如图，O是矩形ABCD的对角线AC的中点，M是AD的中点，若AB=6，AD=8，则四边形ABOM的周长为18．【分析】根据矩形的性质，直角三角形斜边中线性质，三角形中位线性质求出BO、OM、AM即可解决问题．【解答】解：∵四边形ABCD是矩形，∴AD=BC=8，AB=CD=6，∠ABC=90°，∴AC==10，∵AO=OC，∴BO=AC=5，∵AO=OC，AM=MD=4，∴OM=CD=3，∴四边形ABOM的周长为AB+OB+OM+AM=6+5+3+4=18．故答案为18．【点评】本题看成矩形的性质、三角形中位线定理、直角三角形斜边中线性质等知识，解题的关键是灵活应用中线知识解决问题，属于中考常考题型．20．（2016•天桥区三模）矩形ABCD中，AB=5，BC=4，将矩形折叠，使得点B 落在线段CD的点F处，则线段BE的长为 2.5．【分析】根据翻转前后，图形的对应边和对应角相等，可知EF=BF，AB=AE，故可求出DE的长，然后设出FC的长，则EF=4﹣FC，再根据勾股定理的知识，即可求出BF的长．【解答】解：∵四边形ABCD是矩形，∴∠B=∠D=90°，∵将矩形折叠，使得点B落在线段CD的点F处，∴AE=AB=5，AD=BC=4，EF=BF，在Rt△ADE中，由勾股定理，得DE=3．在矩形ABCD中，DC=AB=5．∴CE=DC﹣DE=2．设FC=x，则EF=4﹣x．在Rt△CEF中，x2+22=（4﹣x）2．解得x=1.5．∴BF=BC﹣CF=4﹣1.5=2.5，故答案为：2.5．【点评】本题考查了矩形的性质、勾股定理的运用以及翻转变换的知识，属于基础题，注意掌握图形翻转前后对应边和对应角相等是解题关键．三．解答题（共10小题）21．（2016•安顺）如图，在▱ABCD中，BC=2AB=4，点E、F分别是BC、AD的中点．（1）求证：△ABE≌△CDF；（2）当四边形AECF为菱形时，求出该菱形的面积．【分析】第（1）问要证明三角形全等，由平行四边形的性质，很容易用SAS证全等．第（2）要求菱形的面积，在第（1）问的基础上很快知道△ABE为等边三角形．这样菱形的高就可求了，用面积公式可求得．【解答】（1）证明：∵在▱ABCD中，AB=CD，∴BC=AD，∠ABC=∠CDA．又∵BE=EC=BC，AF=DF=AD，∴BE=DF．∴△ABE≌△CDF．（2）解：∵四边形AECF为菱形，∴AE=EC．又∵点E是边BC的中点，∴BE=EC，即BE=AE．又BC=2AB=4，∴AB=BC=BE，∴AB=BE=AE，即△ABE为等边三角形，▱ABCD的BC边上的高为2×sin60°=，∴菱形AECF的面积为2．【点评】考查了全等三角形，四边形的知识以及逻辑推理能力．（1）用SAS证全等；（2）若四边形AECF为菱形，则AE=EC=BE=AB，所以△ABE为等边三角形．22．（2016•苏州）如图，在菱形ABCD中，对角线AC、BD相交于点O，过点D 作对角线BD的垂线交BA的延长线于点E．（1）证明：四边形ACDE是平行四边形；（2）若AC=8，BD=6，求△ADE的周长．【分析】（1）根据平行四边形的判定证明即可；（2）利用平行四边形的性质得出平行四边形的周长即可．【解答】（1）证明：∵四边形ABCD是菱形，∴AB∥CD，AC⊥BD，∴AE∥CD，∠AOB=90°，∵DE⊥BD，即∠EDB=90°，∴∠AOB=∠EDB，∴DE∥AC，∴四边形ACDE是平行四边形；（2）解：∵四边形ABCD是菱形，AC=8，BD=6，∴AO=4，DO=3，AD=CD=5，∵四边形ACDE是平行四边形，∴AE=CD=5，DE=AC=8，∴△ADE的周长为AD+AE+DE=5+5+8=18．【点评】此题考查平行四边形的性质和判定问题，关键是根据平行四边形的判定解答即可．23．（2016•贺州）如图，AC是矩形ABCD的对角线，过AC的中点O作EF⊥AC，交BC于点E，交AD于点F，连接AE，CF．（1）求证：四边形AECF是菱形；（2）若AB=，∠DCF=30°，求四边形AECF的面积．（结果保留根号）【分析】（1）由过AC的中点O作EF⊥AC，根据线段垂直平分线的性质，可得AF=CF，AE=CE，OA=OC，然后由四边形ABCD是矩形，易证得△AOF≌△COE，则可得AF=CE，继而证得结论；（2）由四边形ABCD是矩形，易求得CD的长，然后利用三角函数求得CF的长，继而求得答案．【解答】（1）证明：∵O是AC的中点，且EF⊥AC，∴AF=CF，AE=CE，OA=OC，∵四边形ABCD是矩形，∴AD∥BC，∴∠AFO=∠CEO，在△AOF和△COE中，，∴△AOF≌△COE（AAS），∴AF=CE，∴AF=CF=CE=AE，∴四边形AECF是菱形；（2）解：∵四边形ABCD是矩形，∴CD=AB=，在Rt△CDF中，cos∠DCF=，∠DCF=30°，∴CF==2，∵四边形AECF是菱形，∴CE=CF=2，∴四边形AECF是的面积为：EC•AB=2．【点评】此题考查了矩形的性质、菱形的判定与性质以及三角函数等知识．注意证得△AOF≌△COE是关键．24．（2016•吉林）如图，菱形ABCD的对角线AC，BD相交于点O，且DE∥AC，AE∥BD．求证：四边形AODE是矩形．【分析】根据菱形的性质得出AC⊥BD，再根据平行四边形的判定定理得四边形AODE为平行四边形，由矩形的判定定理得出四边形AODE是矩形．【解答】证明：∵四边形ABCD为菱形，∴AC⊥BD，∴∠AOD=90°，∵DE∥AC，AE∥BD，∴四边形AODE为平行四边形，∴四边形AODE是矩形．【点评】本题考查了矩形的判定以及菱形的性质，还考查了平行四边形的判定，掌握平行四边形的判定方法是解题的关键．25．（2016•通辽）如图，四边形ABCD是正方形，点E是BC的中点，∠AEF=90°，EF交正方形外角的平分线CF于F．求证：AE=EF．【分析】先取AB的中点H，连接EH，根据∠AEF=90°和ABCD是正方形，得出∠1=∠2，再根据E是BC的中点，H是AB的中点，得出BH=BE，AH=CE，最后根据CF是∠DCG的角平分线，得出∠AHE=∠ECF=135°，从而证出△AHE≌△ECF，即可得出AE=EF．【解答】证明：取AB的中点H，连接EH；∵∠AEF=90°，∴∠2+∠AEB=90°，∵四边形ABCD是正方形，∴∠1+∠AEB=90°，∴∠1=∠2，∵E是BC的中点，H是AB的中点，∴BH=BE，AH=CE，∴∠BHE=45°，∵CF是∠DCG的角平分线，∴∠FCG=45°，∴∠AHE=∠ECF=135°，在△AHE和△ECF中，，∴△AHE≌△ECF（ASA），∴AE=EF．【点评】此题考查了正方形的性质和全等三角形的判定与性质，解题的关键是取AB的中点H，得出AH=EC，再根据全等三角形的判定得出△AHE≌△ECF．26．（2016•无锡）已知，如图，正方形ABCD中，E为BC边上一点，F为BA延长线上一点，且CE=AF．连接DE、DF．求证：DE=DF．【分析】根据正方形的性质可得AD=CD，∠C=∠DAF=90°，然后利用“边角边”证明△DCE和△DAF全等，再根据全等三角形对应边相等证明即可．【解答】证明：∵四边形ABCD是正方形，∴AD=CD，∠DAB=∠C=90°，∴∠FAD=180°﹣∠DAB=90°．在△DCE和△DAF中，，∴△DCE≌△DAF（SAS），∴DE=DF．【点评】本题考查了正方形的性质，全等三角形的判定与性质，利用全等三角形对应边相等证明线段相等是常用的方法之一，一定要熟练掌握并灵活运用．27．（2016•乐山）如图，在正方形ABCD中，E是边AB的中点，F是边BC的中点，连结CE、DF．求证：CE=DF．【分析】欲证明CE=DF，只要证明△CEB≌△DFC即可．【解答】证明：∵ABCD是正方形，∴AB=BC=CD，∠EBC=∠FCD=90°，又∵E、F分别是AB、BC的中点，∴BE=CF，在△CEB和△DFC中，，∴△CEB≌△DFC，∴CE=DF．【点评】本题考查正方形的性质、全等三角形的判定和性质，解题的关键是熟练掌握正方形的性质以及全等三角形的判定和性质，属于基础题，中考常考题型．28．（2016•长春二模）如图，已知菱形ABCD的对角线相交于点O，延长AB至点E，使BE=AB，连结CE，若∠E=50°，求∠BAO的大小．【分析】根据菱形的四条边都相等可得AB=BC，从而得到BC=BE，再根据等腰三角形的性质求出∠CBE，然后根据两直线平行，同位角相等可得∠BAD=∠CBE，再根据菱形的对角线平分一组对角线可得∠BAO=∠BAD，问题得解．【解答】解：菱形ABCD中，AB=BC，∵BE=AB，∴BC=BE，∴∠BCE=∠E=50°，∴∠CBE=180°﹣50°×2=80°，∵AD∥BC，∴∠BAD=∠CBE=80°，∴∠BAO=∠BAD=×80°=40°．【点评】本题考查了菱形的性质，等腰三角形的性质，平行线的性质，熟记各性质并准确识图是解题的关键．29．（2016•哈尔滨模拟）如图，在△ABC中，∠ACB=90°，BC的垂直平分线DE 交BC于D，交AB于E，F在DE上，并且AF=CE．（1）求证：四边形ACEF是平行四边形；（2）当∠B满足什么条件时，四边形ACEF是菱形？请回答并证明你的结论．【分析】（1）ED是BC的垂直平分线，根据中垂线的性质：中垂线上的点线段两个端点的距离相等，则EB=EC，故有∠3=∠4，在直角三角形ACB中，∠2与∠4互余，∠1与∠3互余，则可得到AE=CE，从而证得△ACE和△EFA都是等腰三角形，又因为FD⊥BC，AC⊥BC，所以AC∥FE，再根据内错角相等得到AF∥CE，故四边形ACEF是平行四边形；（2）由于△ACE是等腰三角形，当∠1=60°时△ACE是等边三角形，有AC=EC，有平行四边形ACEF是菱形．【解答】解：（1）∵ED是BC的垂直平分线∴EB=EC，ED⊥BC，∴∠3=∠4，∵∠ACB=90°，∴FE∥AC，∴∠1=∠5，∵∠2与∠4互余，∠1与∠3互余∴∠1=∠2，∴AE=CE，又∵AF=CE，∴△ACE和△EFA都是等腰三角形，∴∠5=∠F，∴∠2=∠F，∴在△EFA和△ACE中∵，∴△EFA≌△ACE（AAS），∴∠AEC=∠EAF∴AF∥CE∴四边形ACEF是平行四边形；（2）当∠B=30°时，四边形ACEF是菱形．证明如下：∵∠B=30°，∠ACB=90°∴∠1=∠2=60°∴∠AEC=60°∴AC=EC∴平行四边形ACEF是菱形．【点评】本题综合利用了中垂线的性质、等边对等角和等角对等边、直角三角形的性质、平行四边形和判定和性质、菱形的判定求解，有利于学生思维能力的训练．涉及的知识点有：有一组邻边相等的平行四边形是菱形．30．（2016•会宁县一模）如图，在矩形ABCD中，对角线BD的垂直平分线MN 与AD相交于点M，与BD相交于点O，与BC相交于N，连接BM，DN．（1）求证：四边形BMDN是菱形；（2）若AB=2，AD=4，求MD的长．【分析】（1）根据矩形性质求出AD∥BC，推出∠MDO=∠NBO，∠DMO=∠BNO，证△DMO≌△BNO，推出OM=ON，得出平行四边形BMDN，推出菱形BMDN；（2）根据菱形性质求出DM=BM，在Rt△AMB中，根据勾股定理得出BM2=AM2+AB2，即可列方程求得．【解答】（1）证明：∵四边形ABCD是矩形∴AD∥BC，∠A=90°，∴∠MDO=∠NBO，∠DMO=∠BNO，∵在△DMO和△BNO中∴△DMO≌△BNO（ASA），∴OM=ON，∵OB=OD，∴四边形BMDN是平行四边形，∵MN⊥BD，∴平行四边形BMDN是菱形．（2）解：∵四边形BMDN是菱形，∴MB=MD，设MD长为x，则MB=DM=x，在Rt△AMB中，BM2=AM2+AB2即x2=（4﹣x）2+22，解得：x=，答：MD长为．【点评】本题考查了矩形性质，平行四边形的判定，菱形的判定和性质，勾股定理等知识点的应用，对角线互相平分的四边形是平行四边形，对角线互相垂直的平行四边形是菱形．。

一元二次方程单元测试题（满分120分）一、选择题（每题3分，共30分） 1、下列方程中，是一元二次方程的是（ ）A. 0y x 3x 22=-+B.06x 5x 23=--C.4x 4x 2++D.03x2x 2=++2、如果01x 3）x 2（m 2=+++是一元二次方程，则m 的取值范围是 （ ） A. 0m = B.2m -=C.2m -≠D.0m ≠ 3、1x =是下列哪个方程的一个解？（ ）A.01x 3x 22=-+B.03x 5x 22=--C.05x 4x 2=-+D.03x 2x 2=-- 4、方程x x 2=的解是（ ）A.0x =B.1x =C.1x ±=D.0x =或者1x =5、用配方法解一元二次方程13x 12x 2=-时，等号左右两边应同时加上（ ）A.212B.12C.26D.6 6、一元二次方程05x 4x 2=+-的根的情况是（ ）A.有两个不相等的根B.有一个根C.有两个相等的根D.无实根7、一元二次方程02m x 22=+-x 有两个不相等的实根，则m 的取值范围是 （ ）A.4m >B.4m -<C.44<<-mD.4m 4m >-<或者8、已知一个三角形的底比高多2，如果这个三角形的面积是24，则它的底是（ ）A.8B.6C.4D.29、已知方程08x 6x 2=+-的两个根分别是等腰三角形的底和腰，则它的周长是 （ ） A.8 B.10 C.8或10 D.610、一次排球比赛中每两队之间都要进行一次比赛，一共比赛了45场，则参赛的队伍一共有多少个？ （ ） A.8 B.9 C.10 D.11二、填空题（每小题4分，共28分）11、一元二次方程9x 5x 42=-的二次项系数是_____________，常数项是____________。

12、如果2x =是方程08x 2mx 2=+-的一个解，那么=m ______________。