当前位置：文档之家 › 趋势面分析实验报告

趋势面分析实验报告

  • 格式：doc
  • 大小：220.00 KB
  • 文档页数：3

下载文档原格式

  / 3

合集下载

第四章 趋势面分析

第四章 趋势面分析
方法原理及研究过程与多项式趋势面相同， 方法原理及研究过程与多项式趋势面相同 ， 不 付立叶级数。 同之处是数学模型 — 付立叶级数。故仅对作如下 说明： 说明： 一、趋势面分析的功能 调和趋势面分析的数学模型是正弦和余弦函数的 调和趋势面分析的数学模型是正弦和余弦函数的 组合，它具有波动的特征。 组合，它具有波动的特征。
2tπ x 2kπ y 2tπ x 2kπ y + Ctk sin z = F(x, y) = ∑∑[ Etk cos cos cos L H L H t =0 k =0 2tπ x 2kπ y 2tπ x 2kπ y +Ptk cos sin +Wtk sin sin ] L H L H
r s
20
1 1 X= M 1
x1 M
y1 x12 M M
x1 y1 M
3 y12 x1 x12 y1 x1 y12
2 2 3 2 2 x2 y2 x2 x2 y2 y2 x2 x2 y2 x2 y2
M
M
M
M
2 2 3 2 2 xn yn xn xn yn yn xn xn yn xn yn
16
中划分正异常时， 或 为异常下限 为异常下限， 从∆zi+中划分正异常时，e+ (或2s+)为异常下限， ∆zi+ >异常下限为正异常点 。 异常下限为正异常点 异常下限为 为异常上限， 中划分负异常时， 或 从∆zi-中划分负异常时，e-(或-2s-)为异常上限， 为异常上限 ∆zi- <异常上限为负异常点 。 异常上限为负异常点 异常上限为 根据异常上、下限可以在偏差图上圈出正、负异 根据异常上、下限可以在偏差图上圈出正、 常区，即趋势面异常分布图。 常区， 趋势面异常分布图。 注意：异常限仅仅是一个统计估计值， 注意：异常限仅仅是一个统计估计值，因此它可 统计估计值 以被修正。实际工作中可根据资料情况改变其大小。 以被修正。实际工作中可根据资料情况改变其大小。 一般控制异常点数<总点数的 总点数的20% 。 一般控制异常点数 总点数的

2 趋势面分析

2 趋势面分析
三次：z b 0 b 1 x b 2 y ＋ b 3 x 2 b 4 xy b 5 y 2 ＋ b6x
3
b 7 x y b 8 xy
2
2
b 9y
3
………………………………………………
15
z b 0 b 1 x b 2y
1 趋势面分析的概念及类型
(3) 三元趋势分析
(4)
21
2 多项式趋势面分析的数学模型及计算
矩阵形式为：
n n xi i 1 n y i i 1

i 1 i 1 n
n
xi xi
2
i 1 n
xi yi
b0 n yi zi i 1 ni 1 n b1 xi yi zi xi i 1 i 1 n b n 2 2 y i z i y i i 1 i 1
n
(5 )
22
2 多项式趋势面分析的数学模型及计算
结果： 解(5)得 ，从而得二元一次趋势面方程并可计算出各观 察点的趋势值：
z i b 0 b1 x i b 2 y i ( i 1, 2 , n ) (6)
它就表示空间一个平面，其等值线图为一组平行线。偏 差值为：
ei z i z i
i 1 n
i 1

3
i 1 n
b 0 i 1 n 2 x i y i b1 i 1 n 3 yi b2 i 1 n 2 2 x i y i b3 i 1 n 3 x i y i b 4 i 1 n 4 y i b 5 i 1

第三章趋势面分析

第三章趋势面分析
的回归显著性检验
离差来源
（K+1） 次回归 （K+1） 次剩余
K次回归
K次剩余
由K次增 高至
（K+1） 次的回归总离差源自平方和SSR(K 1)
SSD(K 1)
SS
(K R
)
SSD(K )
自由度
均方差
F检验
p n–p–1
q n–q–1
MS
(K R
1)
SSR(K !)
/
p
MSD(K 1)
SSD(K !) /(n p 1)
第三章 地理学中的经典统计分析 方法
第6节 趋势面分析方法
➢趋势面分析的用途 ➢趋势面分析的一般原理 ➢趋势面模型的适度检验 ➢趋势面分析应用实例 ➢趋势面分析的软件实现
一、趋势面分析的用途
❖ 趋势面分析(trend surface analysis, TSA)的主要功 能是找出研究区域内变量的空间分布格局。描述地理要
二、趋势面分析的一般原理
空间趋势面是一种光滑的数学曲面，它能集中地代表地理 数据在大范围内的空间变化趋势。它与实际上的地理曲面不 同，它只是实际曲面的一种近似值。 趋势面是一种抽象的 数学曲面，它抽象并过滤掉了一些局域随机因素的影响，使 地理要素的空间分布规律明显化。
实际曲面=趋势面+剩余曲面。趋势面反映了区域性的变化规 律，它受大范围的系统性因素影响，属于确定性因素作用的 结果。而剩余面反映局部性变化特点，它受局部因素和随机 因素的影响。
图3.6.2 某流域降水量的三次多项式趋势面
模型检验
(1)趋势面拟合适度的R2检验: 根据R2检验 方法计算，结果表明，二次趋势面的判定系数 为R22=0.839，三次趋势面的判定系数为 R32=0.965，可见二次趋势面回归模型和三次 趋势面回归模型的显著性都较高，而且三次趋 势面较二次趋势面具有更高的拟合程度。

第四章 趋势面分析

第四章 趋势面分析

n
偏差平方和
SD
i 1
(z
i
2 zi)
设p次趋势面分析的系数个数为k(不包括b0)， 假设(因变量和自变量及其高次幂和交叉乘 积幂之间不相关，则偏回归系数全为0)：
H 0 : b1 b2 bk 0
统计量：
SR k F ~ F k, n k 1) ( SD (n k 1)
结果
（１）趋势面方程
ˆ z b0 b1 x b2 y
（２）残差
ˆ ei zi zi
做出趋势面和残差 图
3926500
3926000
3925500
3925000
20487000
20487500
20488000
20488500
20489000
20489500
三、有关趋势面系数


的几点说明 多项式中 Ｐ次多项式包含Ｐ－１次多项式 对于Ｐ次多项式
ˆ z b0 b1 x b2 y b3 x b4 xy b5 y bk y
2 2
p
p与k有如下关系： k=(p+1+2)p/2=(p+3)p/2
第三节 趋势面分析的系数检验
２、趋势面方程
ˆ z b0 b1 x b2 y
对每个点有
ˆ zi b0 b1 xi b2 yi
i=1 ,2,．．．n

3、关键
求取最符合真实面的最隹方程，即求 取最隹的 b0,b1 ,b2
4、方法
(1)最小二乘法
ˆ Q (Z i zi ) (Z i b0 b1 xi b2 yi )

趋势面分析实验报告

趋势面分析实验报告

趋势⾯分析实验报告
趋势⾯分析实验报告
实验⽬的:
趋势⾯分析是利⽤数学曲⾯模拟地理系统要素在空间上的分布以及变化趋势的⼀种⽅法。

趋势⾯分析⽅法常常被⽤来模拟资源，环境⼈⼝及经济要素在空间上的分布规律。

利⽤趋势分析的⽅法来检测各个数据在空间分布上的特点。

实验要求：
对某城市郊区垃圾占⽤农⽥⾯积的数量在平⾯上的分布规律进⾏计算和分析。

实验步骤：
步骤⼀：导⼊数据EXCEL格式
步骤三：建⽴趋势⾯模型，分析，回归，线性输⼊⾃变量和因变量，算出⼆次拟合⽅程
Z=2.160+0.638x-0.80y-0.52x*x+0.07xy-0.011y*y
(R的平⽅=0.593 F=2.620)
步骤四：三次趋势⾯分析，求出X6,X7,X8,X9,建⽴三次趋势⾯模型
4
Z=-5.571+2.002x+3.889y-0.154x*x-0.182xy-0.573y*y-0.001x*x*x+0.015x*x*y+0.001x*y *y+0.024y*y*y
(R的平⽅=0.921 F=6.474)
步骤五：模型检验
(1)结果表明⼆次趋势⾯的判定系数为0.593，三次的趋势⾯判定系数为0.921，可见三次
趋势⾯回归模型的拟合程度⾼。

(2)趋势⾯适度的显著性F检验。

⼆次和三次的趋势⾯的F值分别为2.620和6.474 。

⼆
次趋势⾯F=2.2620Fa(9,5),检验显著。

(3)趋势⾯适度的逐次检验。

从回归值与实测值的差值（残差）看，三次趋势⾯残差的绝对
值也显著少于⼆次趋势⾯。

因此三次趋势⾯⽅程可以形象的表⽰出该城市郊区垃圾点占地的规律。

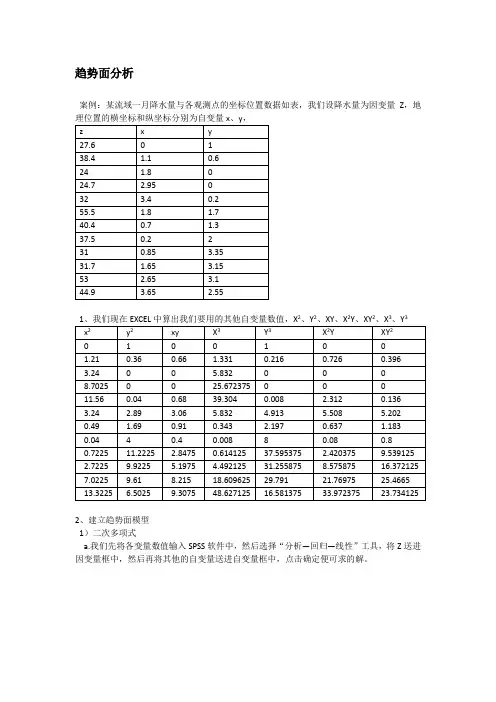
趋势面分析

趋势面分析

趋势面分析案例：某流域一月降水量与各观测点的坐标位置数据如表，我们设降水量为因变量Z，地2、Y2、XY、X22、X3、Y32、建立趋势面模型1）二次多项式a.我们先将各变量数值输入SPSS软件中，然后选择“分析—回归—线性”工具，将Z送进因变量框中，然后再将其他的自变量送进自变量框中，点击确定便可求的解。

b.运行结果如下图1图1中B列的数据为拟合方程的各系数，根据表中的数值及所对应的常量，我们求得的拟合方程为：Z=5.998+17.438X+29.787Y-3.588X2+0.357XY-8.070Y2图2图2显示该拟合二次趋势面的判定系数R2=0.839，显著性F=6.2322）三次多项式a.方法与二次多项式类似，将所有的变量输入SPSS，选择“分析—回归—线性”工具，将Z 送进因变量框中，然后再将其他的自变量送进自变量框中，点击确定便可求解。

b.运行结果如下图1图1中数列B的数据为拟合方程的各系数，根据表中的数值及所对应的常量，我们求得的拟合方程为：Z=-48.810+37.557X+130.130Y+8.389X2-33.166XY-62.740Y2-4.133X3+6.138X2Y+2.566XY2+9.785Y3图2图2显示，该拟合二次趋势面的判定系数R2=0.965，显著性F=6.0543、检验模型1）趋势面拟合适度检验。

根据两次拟合的输出结果表明，二次趋势面的判定系数为R2=0.839，三次趋势面的判定系数为R2=0.965，可见二者趋势面回归模型的显著性都较高（>0.8），且三次趋势面较二次趋势面具有更高的拟合程度（数值更大）。

2）趋势面适度的显著性检验。

根据两次拟合的输出结果表明，两者趋势面的F值分别为F2=6.236、和F3=6.054，在置信水平a=0.05下，查F分布表得F2a=F0.05(5,6)=4.53，F3a=F0.05(9,2)=19.4，我们得出F2>F2a F3 < F3a，因此我们判定用二次趋势面进行拟合比较合理。

趋势面分析方法在下大兴安岭加勒河—科多蒂河一带1：5万水系沉积物剩余异常图方面的应用

趋势面分析方法在下大兴安岭加勒河—科多蒂河一带1：5万水系沉积物剩余异常图方面的应用本文针对大兴安岭地区下加勒河—科多蒂河一带1：5万水系沉积物数据，通过趋势面分析方法确定剩余异常值，利用Surfer软件和MapGIS软件来绘制剩余异常图，圈定成矿远景区，为进一步野外地质工作提供方向。

标签：趋势面分析;大兴安岭;剩余异常图;远景区圈定引言：趋势面分析法是用数学方法研究地质变量空间分布及变化规律的一种多元统计分析方法。

趋势面分析方法则充分考虑到这种区域背景的规律性变化，并根据元素含量的空间分布特征，求出趋势值，拟合趋势面，用趋势面作为区域背景来表现元素含量的区域规律性变化，从而避免统一背景值所圈异常造成的信息损失，从而可以避免漏掉一些由矿化引起的弱小异常。

本文选取大兴安岭地区下加勒河—科多蒂河一带1：5万水系沉积物数据，通过Surfer软件和MapGIS软件来实现剩余异常等值线图的绘制。

利用趋势面分析手段来模拟趋势背景面，并由算出剩余异常值绘制等值线图，最后结合区域成矿地质条件，评价异常区找矿潜力，为确定研究区下一步找矿工作方向提供科学依据。

1 研究区概括研究区位于额尔古纳地块的东段，大地构造位置处于大兴安岭额尔古纳地块与大兴安岭早古生代陆缘增生带结合部位。

前中生代受古亚洲洋构造域控制，中生代受滨太平洋构造域控制。

调查区地质发展历史漫长，地质构造复杂，沉积作用、岩浆作用十分发育。

研究区属大兴安岭Pb、Zn、Mo等多金属成矿带有利成矿部位。

区内地层有倭勒根岩群大网子岩组、上石炭统新伊根河组、上侏罗统白音高老组、下白垩统光华组地层，其中以上侏罗统白音高老组地层为主，大网子岩组、新伊根河组及光华组地层零星分布在研究区的中南部。

区内侵入岩较发育，岩浆活动频繁。

从研究区中部向周围，岩石由老至新。

有早寒武世、早石炭世、晚石炭世、晚侏罗世、早白垩世花岗岩。

其中以晚侏罗世花岗岩为主，区内构造较发育，有南北向布拉卡蒂河及诺库大河、北东向塔哈河、北西向下加勒河活动性断裂。

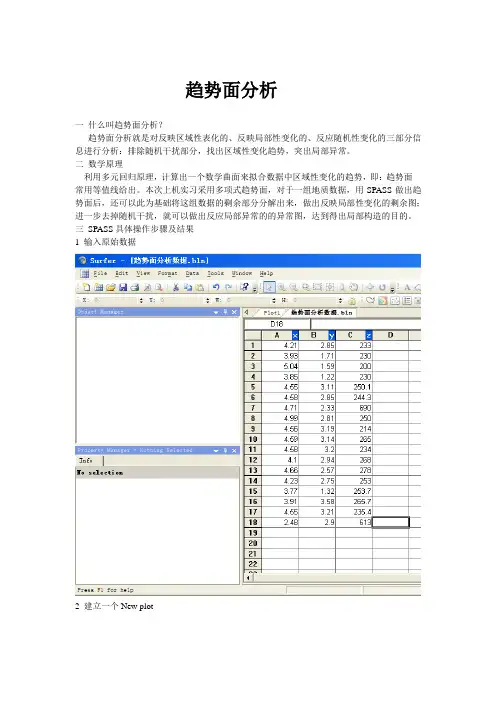
07 趋势面分析

总离差 SST
pq
( ( MSRI ) / MSDK 1)
表1 多项式趋势面的逐次检验
四、实例分析
以下是某地18口钻井资料，Z2层的厚度变化如表所示。
编号 1 2 3 4 坐标 x 4.21 3.93 5.04 3.85 y 2.85 1.7 1.55 1.11 厚度z/m 231 248.5 196 211 编号 10 11 12 13 坐标 x 4.59 4.59 4.1 4.68 y 3.22 3.23 2.84 2.75 厚度z/m 259 259.8 261.5 272
统计分析方法
—趋势面分析
一、趋势面分析原理
通常许多地理数据都包括以下三部分信息： ①反映区域性变化的：数据中反映总体的规律性变 化的部分，如由地质区域构造、区域岩相、区域背景等 大区域因素所决定。 ②反映局部性变化的：它反映局部范围的变化特征。 ③反映随机性变化的：它是由各种随机因素造成的 偏差。 趋势面是一种抽象的数学曲面，它抽象并过滤掉了 一些随机因素的影响，使地理要素的空间分布规律明显 化，以便找出区域性变化趋势，突出局部异常。
趋势面分析的基本原则：所选择的趋势面模型应
该是剩余值最小，而趋势值最大，这样拟合度精度才
能达到足够的准确性。 通常采用的拟合曲面有两种：一种是多项式趋势 面，另一种是以傅里叶级数为基础得出的拟合面，叫 做调和趋势面，它常用于具有周期性变化的地理数据。
二、多项式趋势面的计算
计算多项式趋势面与计算多项式回归在数学上是完全 一样的，现以一次趋势面为例进行分析计算。 设有一组(n个点)地理观测数据，观测点的横坐标为xi， 纵坐标为yi，观测值为zi,（i=1,2,···，n）,现用一次 趋势面
( ( MSRK 1) / MSDK 1)

趋势面分析

趋势面分析一什么叫趋势面分析？趋势面分析就是对反映区域性表化的、反映局部性变化的、反应随机性变化的三部分信息进行分析：排除随机干扰部分，找出区域性变化趋势，突出局部异常。

二数学原理利用多元回归原理，计算出一个数学曲面来拟合数据中区域性变化的趋势，即：趋势面---常用等值线给出。

本次上机实习采用多项式趋势面，对于一组地质数据，用SPASS做出趋势面后，还可以此为基础将这组数据的剩余部分分解出来，做出反映局部性变化的剩余图；进一步去掉随机干扰，就可以做出反应局部异常的的异常图，达到得出局部构造的目的。

三SPASS具体操作步骤及结果1 输入原始数据2 建立一个New plot然后在Plot界面用Grid打开之前建立的数据（可以修改各种参数设定）之后得到一个grid格式的数据和一个分析报告，下一步使用，进行趋势面绘制，用Map工具打开该数据Active Data: 18Univariate Statistics————————————————————————————————————————————X Y Z ————————————————————————————————————————————Count: 18 18 181%%-tile: 2.48 1.22 2005%%-tile: 2.48 1.22 20010%%-tile: 3.77 1.32 21425%%-tile: 3.93 2.33 23350%%-tile: 4.55 2.85 25075%%-tile: 4.58 3.11 26590%%-tile: 4.71 3.2 27895%%-tile: 4.99 3.21 61399%%-tile: 4.99 3.21 613Minimum: 2.48 1.22 200 Maximum: 5.04 3.58 690Mean: 4.29388888889 2.62611111111 289.288888889 Median: 4.55 2.85 250.05 Geometric Mean: 4.24766170066 2.51385012227 271.255793835 Harmonic Mean: 4.19054009746 2.37707222857 260.43837365 Root Mean Square: 4.33183756236 2.71356980951 317.188853664 Trim Mean (10%%): N/A N/A N/A Interquartile Mean: 4.36555555556 2.79 246.5 Midrange: 3.76 2.4 445 Winsorized Mean: 4.33166666667 2.61 248.566666667 TriMean: 4.4025 2.785 249.5Variance: 0.346589869281 0.494472222222 17916.0433987 Standard Deviation: 0.588718837206 0.703187188608 133.85082517 Interquartile Range: 0.65 0.78 32Range: 2.56 2.36 490Mean Difference: 0.610392156863 0.771045751634 104.483660131 Median Abs. Deviation: 0.33 0.315 16.55Average Abs. Deviation: 0.401666666667 0.498333333333 59.2111111111 Quartile Dispersion: 0.0763807285546 0.1433823529410.0642570281124Relative Mean Diff.: 0.142153691597 0.293607436628 0.3611741209Standard Error: 0.138762360667 0.165742809836 31.5489420484 Coef. of Variation: 0.137106211278 0.267767493018 0.462689132943 Skewness: -1.44662719199 -0.822714806649 2.2207762572 Kurtosis: 5.36832306757 2.26851523564 6.39084247191Sum: 77.29 47.27 5207.2Sum Absolute: 77.29 47.27 5207.2Sum Squares: 337.7667 132.5423 1810957.84 Mean Square: 18.7648166667 7.36346111111 100608.768889 ————————————————————————————————————————————Inter-Variable Covariance————————————————————————————————X Y Z ————————————————————————————————X: 0.34658987 0.041551307 -30.09019Y: 0.041551307 0.49447222 2.7437778Z: -30.09019 2.7437778 17916.043 ————————————————————————————————Inter-Variable Correlation————————————————————————————————X Y Z ————————————————————————————————X: 1.000 0.100 -0.382Y: 0.100 1.000 0.029Z: -0.382 0.029 1.000 ————————————————————————————————Inter-Variable Rank Correlation————————————————————————————————X Y Z ————————————————————————————————X: 1.000 0.010 -0.097Y: 0.010 1.000 0.113Z: -0.097 0.113 1.000 ————————————————————————————————Principal Component Analysis————————————————————————————————————————PC1 PC2 PC3 ————————————————————————————————————————X: 0.216419756651 0.216419756651 0.976298964503Y: 0.976300385716 0.976300385716 -0.216419808238Z: 0.000213968453371 0.000213968453371 -0.216419808238Lambda: 17916.0943565 0.504284372067 0.285819896505 ————————————————————————————————————————Planar Regression: Z = AX+BY+CFitted Parameters ————————————————————————————————————————A B C ————————————————————————————————————————Parameter Value: -88.3733860188 12.9750614884 634.680436047 Standard Error: 54.3839287184 45.5310389559 253.339971028 ————————————————————————————————————————Inter-Parameter Correlations ————————————————————————————A B C ————————————————————————————A: 1.000 -0.100 -0.874B: -0.100 1.000 -0.379C: -0.874 -0.379 1.000 ————————————————————————————ANOVA Table ————————————————————————————————————————————————————Source df Sum of Squares Mean Square F ————————————————————————————————————————————————————Regression: 2 45811.1345603 22905.56728021.32779942978Residual: 15 258761.603217 17250.7735478Total: 17 304572.737778 ————————————————————————————————————————————————————Coefficient of Multiple Determination (R^2): 0.150411146101 Nearest Neighbor Statistics—————————————————————————————————Separation |Delta Z| —————————————————————————————————1%%-tile: 0.022********* 2.35%%-tile: 0.022********* 2.310%%-tile: 0.022********* 5.825%%-tile: 0.05 2050%%-tile: 0.128062484749 21.475%%-tile: 0.261725046566 2890%%-tile: 0.667607669219 41295%%-tile: 0.810246875958 41299%%-tile: 0.810246875958 412Minimum: 0.022********* 2.3Maximum: 1.58344561005 490Mean: 0.300678589751 107.561111111 Median: 0.135094594392 22.55Geometric Mean: 0.150505839521 34.1962482825 Harmonic Mean: 0.0760795138321 15.183145853Root Mean Square: 0.484349506498 198.11587939Trim Mean (10%%): N/A N/AInterquartile Mean: 0.156027058614 22.4333333333 Midrange: 0.802903144915 246.15Winsorized Mean: 0.241874303774 103.422222222 TriMean: 0.141962504016 22.7Variance: 0.152668408352 29308.774281 Standard Deviation: 0.390728049098 171.198055716 Interquartile Range: 0.211725046566 8Range: 1.56108493028 487.7Mean Difference: 0.367671560345 153.080392157 Median Abs. Deviation: 0.111396166834 6.55Average Abs. Deviation: 0.230993279821 91.9277777778 Quartile Dispersion: 0.6792044749 0.166666666667 Relative Mean Diff.: 1.2228059226 1.42319459678Standard Error: 0.0920954843723 40.3517687077 Coef. of Variation: 1.29948743415 1.59163524761 Skewness: 2.020******** 1.28865622044 Kurtosis: 6.73356292285 2.76519475547Sum: 5.41221461551 1936.1Sum Absolute: 5.41221461551 1936.1Sum Squares: 4.2227 706498.23Mean Square: 0.234594444444 39249.9016667 —————————————————————————————————Complete Spatial RandomnessLambda: 2.97934322034Clark and Evans: 1.0379*******Skellam: 79.0479539757Gridding RulesGridding Method: KrigingKriging Type: PointPolynomial Drift Order: 0Kriging std. deviation grid: noSemi-Variogram ModelComponent Type: LinearAnisotropy Angle: 0Anisotropy Ratio: 1Variogram Slope: 1Search ParametersNo Search (use all data): trueOutput GridGrid File Name: C:\Documents and Settings\Administrator\桌面\趋势面分析数据.grdGrid Size: 92 rows x 100 columnsTotal Nodes: 9200Filled Nodes: 9200Blanked Nodes: 0Blank Value: 1.70141E+038Grid GeometryX Minimum: 3.22X Maximum: 4.95X Spacing: 0.017474747474747Y Minimum: 1.66Y Maximum: 2.49Y Spacing: 0.0091208791208791Univariate Grid Statistics——————————————————————————————Z ——————————————————————————————Count: 92001%%-tile: 243.6708247515%%-tile: 270.52537986610%%-tile: 289.3649401625%%-tile: 320.7816334150%%-tile: 346.69170079275%%-tile: 403.41375589490%%-tile: 501.89518357495%%-tile: 550.0838342899%%-tile: 623.854749712Minimum: 231.02350996Maximum: 684.239353028Mean: 371.755313657Median: 346.697198378Geometric Mean: 363.519621072Harmonic Mean: 356.180238449Root Mean Square: 380.919972359Trim Mean (10%%): 365.903516549Interquartile Mean: 351.617078065Midrange: 457.631431494Winsorized Mean: 368.205042418TriMean: 354.394697722Variance: 6898.76197525Standard Deviation: 83.0587862616Interquartile Range: 82.6321224834Range: 453.215843068Mean Difference: 87.9557978576Median Abs. Deviation: 36.2856362208Average Abs. Deviation: 59.6216971292Quartile Dispersion: 0.114101972622Relative Mean Diff.: 0.236595939927Standard Error: 0.865947707481Coef. of Variation: 0.223423265816Skewness: 1.19083933754Kurtosis: 4.0676520973Sum: 3420148.88565Sum Absolute: 3420148.88565Sum Squares: 1334920233.15Mean Square: 145100.025342 ——————————————————————————————然后得到趋势面：然后加上颜色表示地下：还可以重点突出某一小区域的构造，改变参数即可; 两趋势面的对比如下:然后做出三维模型：这就是局部构造。

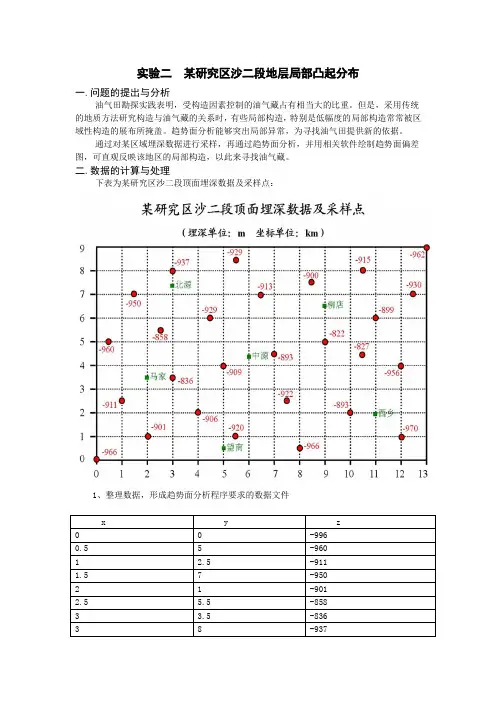
数学地质实验二 趋势面分析

实验二某研究区沙二段地层局部凸起分布
一.问题的提出与分析
油气田勘探实践表明，受构造因素控制的油气藏占有相当大的比重。

但是，采用传统的地质方法研究构造与油气藏的关系时，有些局部构造，特别是低幅度的局部构造常常被区域性构造的展布所掩盖。

趋势面分析能够突出局部异常，为寻找油气田提供新的依据。

通过对某区域埋深数据进行采样，再通过趋势面分析，并用相关软件绘制趋势面偏差图，可直观反映该地区的局部构造，以此来寻找油气藏。

二.数据的计算与处理
下表为某研究区沙二段顶面埋深数据及采样点：
1、整理数据，形成趋势面分析程序要求的数据文件
2、利用给定的趋势面计算程序，分别进行2-4次趋势面分析计算；（1）进行2次趋势面分析，得以下数据：
利用Surfer 软件绘制沙二段顶面2次趋势剩余(正偏差)图：
利用Surfer 软件绘制沙二段顶面3次趋势剩余(正偏差)图：
三.数据分析及结论
通过对该地区进行2-4次趋势面分析，并利用Surfer 软件绘制沙二段顶面2-4次趋势剩余(正偏差
)图可分析该地区的局部构造。

由以上三幅偏差图可以看出，在马家及柳店-西乡一带均出现大面积的正异常区。

而根据实际经验，大部分油气田位于正异常区，由此可以初步推断，在马家及柳店-西乡一带可能存在油气藏。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

趋势面分析实验报告
实验目的:
趋势面分析是利用数学曲面模拟地理系统要素在空间上的分布以及变化趋势的一种方法。

趋势面分析方法常常被用来模拟资源，环境人口及经济要素在空间上的分布规律。

利用趋势分析的方法来检测各个数据在空间分布上的特点。

实验要求：
对某城市郊区垃圾占用农田面积的数量在平面上的分布规律进行计算和分析。

实验步骤：
步骤一：导入数据EXCEL格式
步骤三：建立趋势面模型，分析，回归，线性输入自变量和因变量，算出二次拟合方程
Z=2.160+0.638x-0.80y-0.52x*x+0.07xy-0.011y*y
(R的平方=0.593 F=2.620)
步骤四：三次趋势面分析，求出X6,X7,X8,X9,建立三次趋势面模型
4
Z=-5.571+2.002x+3.889y-0.154x*x-0.182xy-0.573y*y-0.001x*x*x+0.015x*x*y+0.001x*y *y+0.024y*y*y
(R的平方=0.921 F=6.474)
步骤五：模型检验
(1)结果表明二次趋势面的判定系数为0.593，三次的趋势面判定系数为0.921，可见三次
趋势面回归模型的拟合程度高。

(2)趋势面适度的显著性F检验。

二次和三次的趋势面的F值分别为2.620和6.474 。

二
次趋势面F=2.2620<Fa(5,9),则不显著。

三次趋势面F=6.474>Fa(9,5),检验显著。

(3)趋势面适度的逐次检验。

从回归值与实测值的差值（残差）看，三次趋势面残差的绝对
值也显著少于二次趋势面。

因此三次趋势面方程可以形象的表示出该城市郊区垃圾点占地的规律。