最新相交线、平行线复习课教案

相交线与平行线学期复习教案一、教学目标1. 复习相交线与平行线的定义及性质。

2. 巩固学生对平行公理及推论的理解。

3. 提高学生解决实际问题的能力。

4. 培养学生的空间想象能力和逻辑思维能力。

二、教学内容1. 相交线与平行线的定义及性质。

2. 平行公理及推论。

3. 实际问题中的应用。

三、教学重点与难点1. 相交线与平行线的性质。

2. 平行公理及推论的应用。

3. 解决实际问题。

四、教学方法1. 采用讲解、演示、练习、讨论相结合的方法。

2. 利用多媒体课件辅助教学，增强学生的空间想象力。

3. 引导学生运用所学知识解决实际问题，提高学生的应用能力。

五、教学过程1. 导入新课：回顾上节课的内容，引导学生复习相交线与平行线的定义及性质。

2. 讲解与演示：利用多媒体课件，讲解相交线与平行线的性质，展示平行公理及推论。

3. 练习与讨论：布置练习题，让学生独立完成，进行讨论，解答疑难问题。

4. 实际问题应用：给出实际问题，让学生运用所学知识解决，引导学生将理论应用于实践。

5. 总结与反思：对本节课的内容进行总结，强调重点难点，鼓励学生反思自己的学习过程。

六、课后作业1. 巩固相交线与平行线的定义及性质。

2. 熟练运用平行公理及推论解决实际问题。

3. 总结本节课的学习收获，提出疑问。

七、教学评价1. 课堂表现：观察学生在课堂上的参与程度、提问回答等情况，了解学生的学习状态。

2. 练习与作业：检查学生的练习和课后作业，评估学生对知识的掌握程度。

3. 实际问题解决：评估学生在解决实际问题时的能力，考察学生的应用水平。

八、教学资源1. 多媒体课件：展示相交线与平行线的性质、平行公理及推论。

2. 练习题：提供不同难度的练习题，巩固所学知识。

3. 实际问题：选取与生活相关的实际问题，引导学生运用知识解决。

九、教学进度安排1. 课时：2课时。

2. 教学内容：相交线与平行线的定义及性质（第1课时），平行公理及推论（第2课时）。

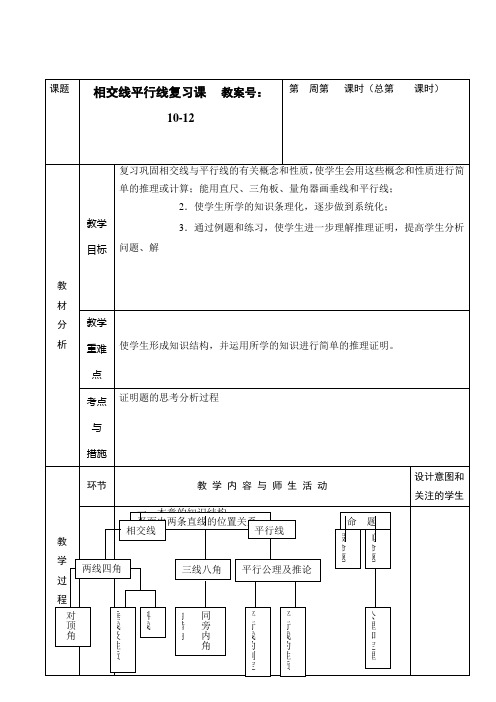
相交线与平行线复习学案［教学目标］1 .经历对本章所学知识回顾与思考的过程,将本章内容条理化、系统化，梳理本章的知识结构；2 .通过对知识的疏理,进一步加深对所学概念的理解,进一步熟悉和掌握几何语言,能用几何语言说明几何图形；3 .认识平面内两条直线的位置关系,在研究平行线时,,能通过有关的角来判断直线平行和反映平行线的性质.理解平移的性质,能利用平移设计图案.【教学重点】更习平面内两条直线的相交和平行的位置关系,以及相交平行的综合应用.【教学难点】垂直、平行的性质和判定的综合应用.一、画出思维导图，加深理解：二、典例精析，释疑解惑专题一相交线【例1】如图,力必（好点Q直线以过0点，Nzf的65° ,求的度数.【练习】如图,月爪CD、夕湘交于点0, N4U700 ,如平分则zcoe= ^专题二点到直线的距离血2】如图，9为△/低的高，能表示点到宜线（线段）的距离的线段有（）A. 2条B.3条 C 4条 D. 5条练习：如图力CL用CDLABTHD, CI>∖. 8cm, AC=6cm, βC=8cm,则点C 到/份的距离是cm;点力到质的距离是cm;点砥必C的距离是_____ cm专题三平行线的性质和判定【例3】如图所示,N1=72° ,N2=72° ,N3=60° ,求N4的度数.练习：己规 NDAUZACBDFE=I80" ,来证：EF"BCD FC 专题四平移【例4】如图所示，卜列四组图形中，有一组中的两个图形经过平移其相交线与平行线复习三、课堂检测，巩固提高1.下列选项中，Nl与N2互为邻补角的是（）3.如图,已知点O在直线AB上,CO_LDO于点0,若Nl = 145° ,则N34.如图,AD_LBD, BC±CD,ΛB=6 cm, BC=4 cm,则BD的长度的取值范围是（）A.大于4 cmB.小于6 cmC.大于4 Cnl或小于6 cmD.大于4 Cnl且小于6 cm5.如图，在已标注数字的角中，与N4是同旁内角的是与/4是同位角的是.与/4是内错角的是.6.下列说法：①过一点有且只有一条直线与已知真线平行；②平移不改变图形的大小和形状：③垂直于同一直线的直线平行.其中正确有（）A. 3个B. 2个 C. 1个 D. O个7,已知：EF±AB, CD±ΛB, ZEFB=ZGDC,求证：Z AGD=ZACB O证明：•・• EFlAB, CDlAB （已知）Λ EF/7 CD （）・•・ZEFB= ZDCB （两直线平行，同位角相等）V ZEFB=ZGD C（已知）Λ ZDC B=ZGDC().•・DG〃BC (内错角相等,两直线平行)：.NAGD=/ACB ( )四、螺旋上升，拓展应用：8.如图，已知/.W¾4+N创＞乙VO=360° .⑴求证物〃，修(2)若/力皮=70° , Z.ACE=Z^ ,BP,别平分//劭，ZACE,求/游曲度数.9,已知直线a〃无将一块含30°角的三角尺力比按图所示方式放置(/ 砌CN(T ),并且顶点4 C分别落在直线多6上.若NI=I8° ,则/2的度数是.五、学后反思：本节课你有什么收获?课后作业：1、如图,直线44〃09,分/月4〃/1与4° ,求/2的度数.2、如图,点力,B、C,麻一条宣线上，也与6校于点G N∕1=N1,CE//DF. 试说明：NE=N之3、如图，已知Nl + N2=180° , N3 = N反试判断N血〃与NC的大小关系，并对结论进行说明.。

相交线与平行线复习课最新教案和讲义模版一、教学目标1. 复习巩固相交线与平行线的基本概念及性质。

2. 提高学生运用相交线与平行线解决实际问题的能力。

3. 培养学生的空间想象能力和逻辑思维能力。

二、教学内容1. 相交线与平行线的定义及性质。

2. 平行线的判定与证明。

3. 相交线的判定与证明。

4. 平行线与相交线在实际问题中的应用。

5. 巩固练习及拓展思考。

三、教学重点与难点1. 教学重点：相交线与平行线的基本概念、性质及应用。

2. 教学难点：平行线的判定与证明，相交线的判定与证明。

四、教学方法1. 采用问题驱动法，引导学生主动探究相交线与平行线的性质。

2. 利用多媒体辅助教学，直观展示相交线与平行线的关系。

3. 结合实例，让学生体会相交线与平行线在实际问题中的应用。

4. 采用小组讨论与合作交流的方式，提高学生的参与度。

五、教学过程1. 导入新课：回顾上节课的内容，引导学生复习相交线与平行线的基本概念。

2. 知识讲解：讲解相交线与平行线的性质，并通过多媒体展示实例，让学生直观理解。

3. 课堂互动：设置问题，让学生判断直线的位置关系，巩固平行线与相交线的判定方法。

4. 应用拓展：结合实际问题，让学生运用相交线与平行线解决实际问题，培养学生的应用能力。

5. 课堂练习：布置针对性的练习题，让学生巩固所学知识。

7. 课后作业：布置适量的课后作业，巩固所学知识。

六、教学评价1. 课堂表现评价：观察学生在课堂上的参与程度、提问回答等情况，了解学生的学习状态。

2. 练习完成情况评价：检查学生课堂练习和课后作业的完成质量，评估学生对知识的掌握程度。

3. 小组讨论评价：评价学生在小组讨论中的表现，包括合作意识、交流能力等。

七、教学资源1. 多媒体教学课件：制作精美的课件，展示相交线与平行线的图形和实例。

2. 练习题库：准备一定数量的练习题，包括判断题、解答题等，用于巩固所学知识。

3. 教学素材：收集相关的实际问题，用于引导学生运用相交线与平行线解决实际问题。

相交线与平行线复习课最新教案和讲义模版一、教学目标：1. 让学生掌握相交线与平行线的定义及性质。

2. 培养学生运用相交线与平行线解决实际问题的能力。

3. 提高学生对几何图形的认识，培养学生的空间想象能力。

二、教学内容：1. 相交线的定义及性质。

2. 平行线的定义及性质。

3. 平行公理及推论。

4. 相交线与平行线在实际问题中的应用。

三、教学重点与难点：1. 重点：相交线与平行线的定义、性质及应用。

2. 难点：相交线与平行线的判定与证明。

四、教学方法：1. 采用问题驱动法，引导学生主动探究相交线与平行线的性质。

2. 利用几何画板软件，直观展示相交线与平行线的变化过程。

3. 结合实际例子，让学生学会运用相交线与平行线解决实际问题。

五、教学过程：1. 导入新课：通过复习旧知识，引导学生回顾相交线与平行线的定义及性质。

2. 讲解与演示：利用几何画板软件，展示相交线与平行线的性质及变化过程。

3. 练习与讨论：让学生自主完成相关练习题，教师引导学生讨论解题思路。

4. 应用拓展：结合实际例子，让学生运用相交线与平行线解决实际问题。

6. 布置作业：布置相关练习题，巩固所学知识。

附：讲义模版一、相交线的定义及性质1. 相交线的定义：在同一平面内，两条直线相交于一点，称这两条直线为相交线。

2. 相交线的性质：（1）相交线交点处的内角和为180度。

（2）相交线交点将两条直线分为两对对应角，对应角相等。

（3）相交线交点将两条直线分为两条对称轴。

二、平行线的定义及性质1. 平行线的定义：在同一平面内，永不相交的两条直线称为平行线。

2. 平行线的性质：（1）平行线之间的距离相等。

（2）平行线上的对应角相等。

（3）平行线上的内角和为180度。

三、平行公理及推论1. 平行公理：经过直线外一点，有且只有一条直线与已知直线平行。

2. 平行公理的推论：（1）平行线上的任意一对对应角相等。

（2）平行线上的任意一对内角和为180度。

（3）平行线之间的距离相等。

相交线与平行线复习教案一、教学目标1. 知识与技能：（1）能识别和画出相交线和平行线；（2）理解平行线的性质和判定；（3）掌握相交线的性质和判定。

2. 过程与方法：（1）通过实例和练习，提高学生对相交线和平行线的识别能力；（2）运用几何画图工具，巩固画图技能；（3）培养学生的逻辑思维能力和问题解决能力。

3. 情感态度价值观：（1）激发学生对几何学科的兴趣；（2）培养学生的团队合作意识和交流能力；（3）渗透数学美感，提高学生的审美素养。

二、教学内容1. 相交线与平行线的概念及性质；2. 平行线的判定与性质；3. 相交线的性质与判定；4. 平行线和相交线在实际问题中的应用。

三、教学重点与难点1. 教学重点：（1）相交线与平行线的识别；（2）平行线的性质和判定；（3）相交线的性质和判定。

2. 教学难点：（1）平行线的判定；（2）相交线的性质和判定。

四、教学准备1. 教具：黑板、粉笔、几何画图工具；2. 学具：学生用书、练习本、铅笔、橡皮。

五、教学过程1. 导入新课：（1）复习相关知识：直线、射线、线段的概念及性质；（2）引入相交线与平行线的概念，引导学生回顾已学知识。

2. 知识讲解：（1）讲解相交线与平行线的性质；（2）讲解平行线的判定与性质；（3）讲解相交线的性质与判定。

3. 课堂练习：（1）根据教师提供的题目，学生独立完成练习；（2）学生相互交流答案，教师进行点评。

4. 应用拓展：（1）提出实际问题，引导学生运用所学的知识解决问题；（2）学生分组讨论，展示解题过程和答案。

5. 课堂小结：（1）教师引导学生总结本节课所学内容；（2）学生分享学习收获和体会。

6. 布置作业：（1）巩固所学知识，提高平行线和相交线的识别和应用能力；（2）培养学生的自主学习能力。

六、教学策略1. 采用问题驱动的教学方法，引导学生通过观察、思考、探究，发现相交线与平行线的性质和判定方法；2. 利用几何画图工具，直观展示相交线与平行线的特点，增强学生的空间想象力；3. 通过小组合作、讨论交流，培养学生团队合作意识和交流能力；4. 设计富有思考性的练习题，激发学生的思维，提高学生解决问题的能力。

一．课题 相交线与平行线复习二．教学目标 1、利用相关知识学会进行有关推理和计算．2、会借助长方体了解直线与直线、直线与平面、平面与平面的位置关系．三．重难点四．考点及考纲要求教学内容教学反思一、回忆所学过的知识点（一）点，线，角1．点、直线、面（不定义概念）及其表示；2．射线、线段、线段的中点及其表示；3．两点确定一条直线；★ 4．两点之间线段最短（两点之间的距离）；★ 5．角、角的顶点、边、角平分线的表示及其性质； 6．角的分类（锐角、直角、钝角、平角、周角）、度量（度、分、秒）及计算． （二）关系角及其性质 1．对顶角、余角、补角（邻补角）、同位角，内错角、同旁内角；2．对顶角相等；★3．同角（或等角）的余角（或补角）相等．★（三）相交线、平行线 1．垂线、垂线段最短（点到直线的距离）； 2．过一点（直线上或直线外）有且只有一条直线和已知直线垂直；★3．会过一点画（作）已知直线的垂线；（一落，二靠，三画） 4．过直线外一点，有且只有一条直线与已知直线平行；★5．如果两条直线都与第三条直线平行，那么这两条直线也互相平行．★6．三线八角与平行线的关系；★①判定公理： 同位角相等，两直线平行． ∵ ∠1=∠2， ∴ a ∥b ．②判定定理1：内错角相等，两直线平行． ∵ ∠1=∠2， ∴ a ∥b ．③判定定理2：同旁内角互补，两直线平行． ∵∠1+∠2=1800 ， ∴ a ∥b ．④性质公理： 两直线平行，同位角相等． ∵ a ∥b ， ∴∠1=∠2．⑤性质定理1：两直线平行，内错角相等． ∵ a ∥b ， ∴∠1=∠2．⑥性质定理2：两直线平行，同旁内角互补． ∵ a ∥b ， ∴ ∠1+∠2=1800．7．平行线之间的距离；8．会过直线外一点，画已知直线的平行线．三、框图疏理，再现知识点知识结构相交相交线两条直线相交四、基础训练，理解知识点1、直线AB 、CD 相交与于O,图中有几对 对顶角？邻补角?当一个角确定了, 另外三个角的大小确定了吗?2.直线AB 、CD 、EF 相交与于O,图中有几对对顶角？ ∠AOC 的对顶角是__∠BOD_____∠CO F 的对顶角是__∠DOE______∠AOC 的邻补角是__∠COB, ∠AOD__ ∠EOD 的邻补角是__∠DOF, ∠COE__3、已知直线AB 、CD 、EF 相交于点O ，4、1、下列命题是真命题的有（ ） A 、相等的角是对顶角B 、不是对顶角的角不相等C 、对顶角必相等平行线两条直线被第三条直线所截 相交线 平行线邻补角、对顶角 垂线及性质 对顶角相等 点到直线的距离 同位角、内错角、同旁内角 平行公理平移 判定 性质O ABC D1 23 4 009036DOE AOE ∠=∠=，BOE BOC ∠∠求、的度数。

相交线与平行线复习课最新教案和讲义模版一、教学目标：1. 复习并巩固学生对相交线与平行线的概念、性质和判定方法。

2. 提高学生解决实际问题的能力，培养学生的空间想象和逻辑思维能力。

3. 培养学生合作学习、积极探究的学习态度。

二、教学内容：1. 相交线与平行线的定义和性质。

2. 相交线与平行线的判定方法。

3. 实际问题中的应用。

三、教学重点与难点：1. 重点：相交线与平行线的概念、性质和判定方法。

2. 难点：相交线与平行线在实际问题中的应用。

四、教学方法：1. 采用问题驱动法，引导学生主动探究相交线与平行线的性质和判定方法。

2. 利用多媒体辅助教学，展示实例，增强学生的空间想象力。

3. 组织学生进行小组讨论，培养学生的合作学习能力。

4. 结合练习题，巩固所学知识，提高学生的解题能力。

五、教学过程：1. 导入新课：回顾相交线与平行线的定义和性质，引导学生思考相交线与平行线在实际生活中的应用。

2. 知识讲解：讲解相交线与平行线的判定方法，并通过实例进行分析。

3. 课堂练习：布置相关的练习题，让学生独立完成，并及时给予解答和指导。

4. 小组讨论：组织学生进行小组讨论，分享各自的解题方法和心得。

5. 总结提升：总结本节课所学内容，强调相交线与平行线在实际问题中的应用。

6. 布置作业：布置适量的作业，让学生巩固所学知识。

六、教学评价：1. 通过课堂练习和课后作业，评价学生对相交线与平行线的掌握程度。

2. 观察学生在小组讨论中的表现，评价其合作学习和探究能力。

3. 结合学生的课堂表现和作业完成情况，对学生的学习态度和积极性进行评价。

七、教学资源：1. 多媒体教学课件：包括相交线与平行线的图片、实例和动画等。

2. 练习题：包括选择题、填空题和解答题等，覆盖本节课所学内容。

3. 小组讨论材料：提供相关的问题和实例，引导学生进行小组讨论。

八、教学进度安排：1. 第1-2课时：复习相交线与平行线的定义和性质。

2. 第3-4课时：讲解相交线与平行线的判定方法，并进行实例分析。

相交线与平行线（复习课）教案一、教学目标1. 知识与技能：（1）能够识别和画出相交线与平行线；（2）理解平行线的性质，能够运用平行线的性质解决问题；（3）掌握相交线的性质，能够运用相交线的性质解决问题。

2. 过程与方法：（1）通过观察、操作、交流等活动，提高学生的空间想象能力；（2）培养学生运用数学知识解决实际问题的能力。

3. 情感态度价值观：（1）培养学生对数学的兴趣，激发学生学习数学的积极性；（2）培养学生合作交流的意识，提高学生的团队协作能力。

二、教学内容1. 相交线与平行线的定义；2. 平行线的性质；3. 相交线的性质；4. 运用相交线与平行线的性质解决问题。

三、教学重点与难点1. 教学重点：（1）相交线与平行线的定义；（2）平行线的性质；（3）相交线的性质；（4）运用相交线与平行线的性质解决问题。

2. 教学难点：（1）平行线的性质；（2）相交线的性质。

四、教学准备1. 教具：黑板、粉笔、直尺、三角板；2. 学具：学生用书、练习本、铅笔、橡皮。

五、教学过程1. 导入新课（1）复习相关知识：直线、射线、线段的概念及特点；（2）引导学生回顾上节课所学内容：相交线与平行线的定义及性质；（3）提问：相交线与平行线在实际生活中有哪些应用？2. 探究与交流（1）分组讨论：让学生分组探讨相交线与平行线的性质，并总结出规律；（2）各组汇报：让学生代表汇报本组的讨论成果；（3）教师点评：对学生的讨论成果进行评价，并给予表扬。

3. 知识拓展（1）引导学生思考：在实际生活中，我们为什么需要学习和应用相交线与平行线；（2）举例说明：如建筑设计、道路规划等领域的应用。

4. 巩固练习（1）让学生独立完成练习题，检测对本节课知识的理解和掌握程度；（2）教师批改：及时批改学生的练习题，给予反馈和指导。

5. 总结与反思（1）让学生回顾本节课所学内容，总结相交线与平行线的性质及应用；（2）教师点评：对学生的学习情况进行评价，并提出改进意见。

相交线与平行线（复习课）教案一、教学目标1. 知识与技能：（1）能够识别和理解相交线与平行线的概念；（2）能够运用相交线与平行线的性质和判定定理解决实际问题。

2. 过程与方法：（1）通过观察、实践、探索等活动，加深对相交线与平行线性质的理解；（2）培养学生的空间想象能力、逻辑思维能力和解决问题的能力。

3. 情感态度与价值观：（2）培养学生团队协作、积极参与的精神风貌。

二、教学内容1. 相交线的概念及性质2. 平行线的概念及性质3. 相交线与平行线的判定定理4. 相交线与平行线在实际问题中的应用三、教学重点与难点1. 教学重点：（1）相交线与平行线的概念及性质；（2）相交线与平行线的判定定理及应用。

2. 教学难点：（1）相交线与平行线的判定定理的灵活运用；（2）解决实际问题中相交线与平行线的应用。

四、教学方法1. 采用问题驱动法，引导学生主动探究相交线与平行线的性质；2. 利用多媒体课件辅助教学，直观展示相交线与平行线的关系；3. 创设实践环节，让学生亲自动手操作，加深对知识的理解；4. 采用小组讨论法，培养学生的团队协作能力和解决问题的能力。

五、教学过程1. 导入新课：通过复习相关定义，引导学生回顾相交线与平行线的概念。

2. 知识讲解：（1）讲解相交线的性质，如相交线的夹角、对顶角等；（2）讲解平行线的性质，如平行线的距离、同位角等；（3）讲解相交线与平行线的判定定理，如同位角相等、内错角相等等。

3. 案例分析：展示实际问题，让学生运用所学的相交线与平行线的性质和判定定理解决问题。

4. 课堂练习：设计相关练习题，让学生巩固所学知识，并及时给予解答和反馈。

5. 总结提升：对本节课的主要内容进行总结，强调相交线与平行线在实际问题中的应用。

6. 作业布置：布置适量作业，让学生进一步巩固所学知识。

六、教学评价1. 课堂表现评价：观察学生在课堂上的参与程度、提问回答情况，以及小组讨论中的表现，评价学生的积极性、合作能力和问题解决能力。