运用超级画板探索圆锥曲线的切线实例

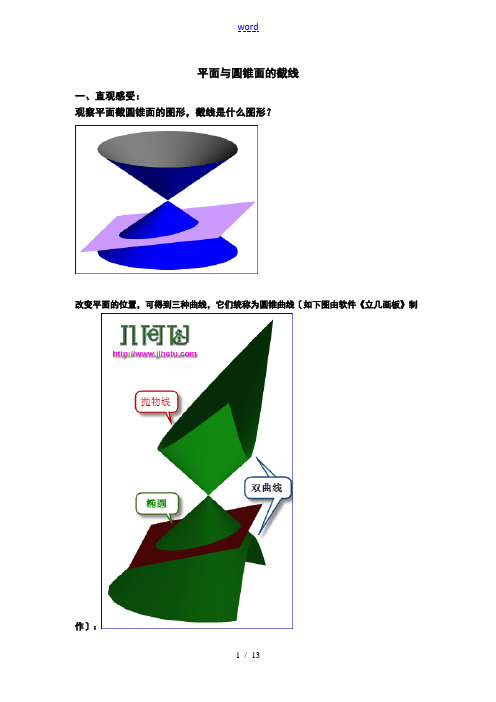
平面与圆锥面的截线一、直观感受：观察平面截圆锥面的图形，截线是什么图形？改变平面的位置，可得到三种曲线，它们统称为圆锥曲线〔如下图由软件《立几画板》制作〕：二、分类探究：从平面图形入手，开始讨论一条直线与等腰三角形的位置关系：将等腰三角形拓广为圆锥，直线拓广为平面。

如果用一平面去截一个正圆锥，而且这个平面不通过圆锥的顶点，会出现哪些情况呢？如如下图：归纳提升：定理在空间中，取直线l为轴，直线l'与l相交于O点，其夹角为α，l'围绕l旋转得到以O为顶点，l'为母线的圆锥面，任取平面π，假如它与轴l交角为β〔π与l平行，记作β＝0〕，如此：〔1〕β＞α，平面π与圆锥的交线为椭圆；〔2〕β＝α，平面π与圆锥的交线为抛物线；〔3〕β＜α，平面π与圆锥的交线为双曲线。

三、证明结论：利用Dandelin双球〔这两个球位于圆锥的内部，一个位于平面的上方，一个位于平面的下方，并且与平面与圆锥均相切〕证明：β＞α，平面与圆锥的交线为椭圆.如图，利用切线长相等，容易证明 PF1+PF2=PQ1+PQ2＝Q1Q2=定值.下面证明：β＝α时，平面与圆锥面的交线为抛物线。

下面讨论当平面与圆锥面的交线为双曲线时准线的与离心率：换个角度看图：容易知道：截得的圆锥曲线的离心率等于截面和圆锥轴的夹角的余弦与圆锥顶角一半的余弦之比.四、知识运用用图霸制作三维直观图：解答参看如下图：五、图形制作三种曲线的丹迪林Dandelin双球图可以在《几何图霸》中统一到一幅图中，主要制作步骤如下：1.作全自由点O，过点O作平行于z轴上的点B，过B作平行于x轴上的点C，作点B、C关于O的对称点B’、C'.2.选取点O、B、C，作圆锥，选取点O、B’、C’，作圆锥.3.在圆B上任取点D，作D关于B对称点，连接OD，OD’，在OD上任取一点E，以E为圆心画过点D’、D的心点圆，在圆E上任取点F，连EF，它表示截面的位置，可以绕点E转动.4.作角OEF的平分线，与轴BB’交于O1；作角DEF的平分线，与轴BB’交于O2，它们就是双球的球心.5.过球心O1、O2分别作边EF的垂线，垂足分别为F1、F2，它们就是焦点.6.选取点O1、F1，作球O1〔图中显示大圆，光照后显示为球〕，同法作球O2.7.取线EF 上的点G、H，作GDO垂线上的伸缩点I，作点I关于点G的对称点I’，按向量GH平称点I、I’，得点I2、I".添加面II2I"I’，连接四边，表示截面.它的长宽可以用点G、H、I 控制；点F控制其转动.8.添加下底圆上的点J，连结OJ交截面于点K，选取点J、K，添加轨迹，它就是截线，如上图中的椭圆.’平移得点E’，EE’交圆于点G1，EG1平行于母线OD’，添加点F到点G1的动画，名为“抛物线〞.10.参看前面各图添加其它图元.下载图霸文件后在“对象浏览器〞中查看各对象.课件下载：共享文件下载中心相关文章：1 利用丹迪林Dandelin双球证明平面与圆锥面的截线定理2平面与圆柱面的截线更多文章：《几何图霸》文章列表几何图霸：.jihetu.。

基于超级画板的圆锥曲线定义作图张海强;姜堰君【期刊名称】《中学数学月刊》【年(卷),期】2013(000)011【总页数】2页(P39-40)【作者】张海强;姜堰君【作者单位】江苏省宜兴中学 214200;江苏省宜兴中学 214200【正文语种】中文1 引言超级画板是基于代数原理开发的.以数驭形、以形表数是其突出特点.与几何画板相比，超级画板中的变量比几何画板中的参数更易控制，其操作方式比几何画板的操作方式更加灵活，这使超级画板的作图变得异常方便快捷.我们以制作圆锥曲线为例加以说明.2 问题熟悉动态几何软件的人都知道：现有的作圆锥曲线的方法没有用到它们的定义，而是用其他方法（如几何性质）实现的，那么试问用超级画板能否较为便利地实现定义作图呢？3 探究圆锥曲线有多种等价定义，这些定义或再现它的研究历史，或展现它不同的形成过程，或凸显它的工具性，都有着特殊的地位和作用.现将其一一陈述如下，并用超级画板对每一定义直接作出其图形，以此来说明超级画板作图的基本思路，揭示以数驭形、以形表数的深刻内涵，体会超级画板作图的便利与快捷.3.1 阿波罗尼斯在其著作《圆锥曲线论》中的定义·定义平面内与两个定点F1，F2的距离的和等于常数（大于F1F2）的点的轨迹叫做椭圆.平面内与两个定点F1，F2的距离的差的绝对值等于常数（小于F1F2的正数）的点的轨迹叫做双曲线.·作图思路设计从代数的角度思考，设其中一个圆的半径为a＋t，另一个圆的半径为a－t，如果两个圆有交点，那么交点到两个圆心的距离之和即为常数2a.·制作椭圆的主要步骤（1）制作两个可以拖动的坐标点F1（－c，0），F2（c，0），拖动参数c；（2）作坐标点A（a＋c＋t，0），拖动参数t；（3）以F2为圆心，过点A作圆，所作圆的半径为a＋t；（4）作坐标点B（t－a－c，0），拖动参数t；（5）以F1为圆心，过点B作圆，所作圆的半径为a－t；（6）作变量a的变量尺；（7）两个圆的交点为C，D；（8）以A为主动点，分别以C，D为从动点，作点的轨迹；（9）利用属性，把轨迹的像素设为3 000，以使图形显得光滑些，如图1.类似地，也可以作出双曲线，如图2.图1图23.2 欧几里得在其巨著《几何原本》中的定义·定义到定点的距离与到定直线的距离之比是常数e的点的轨迹叫做圆锥曲线.当0＜e＜1时轨迹为椭圆；当e＝1时轨迹为抛物线；当e＞1时轨迹为双曲线.·作图思路设计满足条件的点既在平行于定直线且与定直线距离为r的直线上，又在以定点为圆心，er为半径的圆上，当r变化时，利用“轨迹”功能即可实现定义作图.·制作图形的步骤图3图4图5（1）制作两个可以拖动的点拖动参数p；（2）作坐标点拖动参数r；（3）过A，B分别作x轴的垂线l1，l2，两直线之间的距离即为r；（4）作坐标点拖动参数r；（5）以F为圆心，过C点作圆，所作圆的半径为mr；（6）作变量m的变量尺；（7）直线l2（图中虚线所示）与圆F的交点为D，E；（8）以C为主动点，分别以D，E为从动点，作点的轨迹；（9）利用属性，把轨迹的像素设为3 000；（10）拉动变量m的按钮，改变离心率m的值，形成的曲线分别如图3～5所示.（注：m表示离心率，超级画板中的e默认为常数.）3.3 “直径所对的圆周角是直角”的推广与延伸·定义平面内与两定点的连线的斜率之积是常数k（k≠0）的动点的轨迹分别为圆（k＝－1）；椭圆（k＜0，k≠1）；双曲线（k＞0）.·作图思路设计为生成一个可变的角度，只需在定圆上任取一点；利用“测量”功能测量出一条直线的斜率，再利用“测量”中的“测量表达式”功能计算出另一条直线的斜率，并作出该直线，两条直线的交点即为满足要求的点，最后利用“轨迹”功能即可实现定义作图.·制作图形的主要步骤（1）制作两个可以拖动的点A1（－a，0），A2（a，0），拖动参数a；（2）以A1为圆心、1为半径作圆，并在该圆上任意取点C；（3）作直线A1C，并测量其斜率m000；（4）作变量k的变量尺；（5）过点A2作直线，使其斜率为并与直线A1C交于点M；（6）以C为主动点、M为从动点，作点的轨迹；（7）利用属性，把轨迹的像素设为3 000，使曲线更光滑；（8）拉动变量k的按钮，改变其数值，产生如图6～7的曲线.图6图73.4 制作圆锥曲线绘图仪的依据·定义平面内到定点和定圆（定点不在定圆上）距离相等的点的轨迹为圆锥曲线.注：① 动点到定圆的距离定义为：平面内动点到定圆上各点距离中的最短距离.不难证明这个最短距离所在的直线必过定圆的圆心；② 当定点与定圆的圆心重合时，动点的轨迹为圆；③ 当定圆与x轴的交点为圆心在x轴上，且半径为无穷大的圆，定点为时，动点所对应的轨迹为抛物线.·作图思路设计本定义的最大优点是便于尺规作图，因此其作图过程偏重于几何.（利用几何性质：线段中垂线上的点到线段两端的距离相等.）·制作图形的主要步骤（1）制作两个可以拖动的坐标点F1（－c，0），F2（c，0），拖动参数c；（2）以F1为圆心，r为半径作圆，并在该圆上取点C；（3）作变量r的变量尺；（4）作射线F1C；（5）作线段F2C的中垂线，并与射线F1C交于点E；（6）以C为主动点，以E为从动点，作点的轨迹；（7）利用属性，把轨迹的像素设为3 000，使曲线更光滑；（8）拉动变量r的按钮，改变其数值，产生如图8～9的曲线. 图8图94 结语有创意的作品源于作者对数学的深刻理解，源于作者对动态软件原理的高度把握，源于作者的数学眼光和数学素养.《超级画板》的代数设计原理要求设计者更善于从数的角度思考问题，以数驭形、以形表数不仅是设计作品的基本理念，也是制作作品的有效工具，更是数学思想方法（数形结合思想）的集中体现.。

几何画板在《圆锥曲线》中的应用举例高二数学组刘中维在《圆锥曲线方程》这一章中，一些曲线的图像、性质都比较抽象，学生难以理解和接受，如双曲线的渐进线、圆锥曲线的离心率与开都的关系、一些数形结合的题目等，只凭学生的想象力是很难理解掌握有关图像的性质和图像之间的相互关系的，若我们只借助尺规作图的方法画图，一般难以达到满意的效果，还容易把图像画错。

但若我们能利用《几何画板》精确的画图功能、动画功能加以演示，将能引起学生的学习兴趣，帮助学生的理解，提高学生对平面图形的想象思维能力，起到事半功倍的作用。

下面举几个用几何画板解决圆锥曲线问题的例子。

一、在“几何画板”中作直线与圆锥曲线的交点在“几何画板”中可以直接作出直线与直线的交点，直线与圆的交点以及圆与圆的交点．但不能直接作出直线与圆锥曲线的交点．本文介绍直线与圆锥曲线的交点制作、制作原理，该制作过程适合三种圆锥曲线．首先是三个工具的制作：工具一已知直线AP，A在圆锥曲线上，求作直线AP与圆锥曲线的另一个交点B．(以椭圆为例)、、、，作DE与PA交于点L，作AF 作图过程在椭圆上任取4个点C D E F与CD交于点M，作LM与EF的交点N，作NC与直线PA的交点B，则点就是直线PA与椭圆的交点（如图1）．图1 图2制作成工具（命名为工具一）就可以直接使用，先决条件是圆锥曲线、点A、点P，不需要其它的，适合椭圆、双曲线、抛物线．制作原理 任意圆锥曲线的内接六边形的三组对边的交点P 、Q 、R 共线（以椭圆为例，如图2）．（帕斯卡定理）工具二 过圆锥曲线外一点作两条切线．作图过程2.1 若P 为椭圆外任意一点，以1F 为圆心，2a 为半径作辅助圆，以P 为圆心，2PF 为半径作圆与辅助圆交于点Q R 、，分别取2QF 、2RF 的中点A B 、，则PA PB 、为所求的切线，1QF 与PA 的交点、1RF 与PB 的交点为对应切点（如图4）．作图过程2.2 若P 为双曲线外任意一点，以1F 为圆心，2a 为半径作辅助圆，以P 为圆心，2PF 为半径作圆与辅助圆交于点Q R 、，分别取2QF 、2RF 的中点A B 、，PA PB 、为所求的切线． 1QF 与PA 的交点、1RF 与PB 的交点为对应切点（如图5）．作图过程2.3 若P 为抛物线外任意一点，以P 为圆心，PF 为半径作圆与准线交于点Q R 、，分别取QF RF 、的中点A B 、，PA PB 、为所求的切线．过点Q 作准线的垂线与PA 的交点、过点R 作准线的垂线与PB 的交点为对应切点（如图6）．把过圆锥曲线外一点作两条切线的过程制作成工具，需要说明的是要分成两个工具：（1）对于椭圆双曲线，工具先决条件是两个焦点1F 、2F 、长度2a 的线段、点P ；（2）对于抛物线，工具的先决条件是焦点1F ，准线，点P ；为了叙述方便，统一称之为工具二．图4 图5 图6工具三 已知点P 不在圆锥曲线上，求作点P 的极线．(有关极点、极线问题在《高等几何》中有详细地说明，此处利用的是它们的性质)作图过程 在圆锥曲线上任取两点A D 、，利用工具一作直线PA PD 、与圆锥曲线的另一个交点B C 、，连结AC BD 、交于E ，AD BC 、交于F ，就得到了点P 的极线EF （如图7）；如果点P 在圆锥曲线内也按此法，因为圆锥曲线内接四边形ABCD 中，点P 的极线是EF ，点E 的极线是PF ，点F 的极线是PE ．制作成工具(命名为工具三) ，先决条件是圆锥曲线、点P ．作图问题 已知两点P Q 、不在圆锥曲线上，求作PQ 与圆锥曲线的交点A B 、．（1）利用工具三作出点P 的极线，（如图8、图9两种情况）；（2）同理利用工具三作出点Q 的极线，两条极线相交于点R ；图10 图11（3）利用工具二，过点R 作圆锥曲线的两条切线（如图10、图11）； 图7 图9图8、即为所求交点．（4）两切线与直线PQ相交得到交点A B以上过程亦可制作成工具．、，只要能预先作制作原理要想得到直线PQ与圆锥曲线相交的交点A B、为切点的两条切线就可以了，设两切线相交于点R，而过点R作出以交点A B圆锥曲线的切线问题已经由作图问题二解决；这个点R其实是直线ABPQ的极点，根据极线和极点的“点U在点V的极线上移动时，点U的极线也绕点V而、两点的极线的交点来确定．转动”这一性质，我们知道点R也是由P Q二、和两圆都相切的圆心的轨迹（一）、制作结果如图：单击“动画”按钮，D点在圆周上运动，从而圆（C，D）的大小和位置不断发生改变，但始终和圆C1和圆C2相切，圆心C的轨迹是双曲线。

用几何画板探索圆锥曲线的相关性浙江宁波鄞州区钟公庙中学童文虎摘要：对于用几何画板演示圆锥曲线相关性，方法众多，但大都不够完整，不是少了抛物线就是缺了圆。

本文通过探索研究得出的一个实例，十分简明完整地从曲线、准线、离心率、切线、包络等五个方面揭示了圆锥曲线从圆⇔椭圆⇔抛物线⇔双曲线⇔点⇔双曲线的连续演变时的内在关系。

另外也介绍了如何借助函数，补断点，使之演示连续完整。

一、提出问题已知一动点到两定点F1、F2的距离的和等于定长线段MN（MN> F1F2）,求作这个动点的轨迹（椭圆）。

其中一个比较常规的作法如下：1、以F1为圆心，MN为半径作圆，在圆上任取一点A，作线段AF2的中垂线，交直线A F1于点P2、选中点P、A构造轨迹，即得椭圆（如图1）图1 图2 图3 如果移动点F2的位置，我们发现当点F2在圆外时，轨迹是双曲线（如图2）；当点F2与圆心F1重合时，轨迹是圆（如图3）；但就是得不到抛物线，所以把它作为演示圆锥曲线相关性的实例，就显得不够完整。

本文就是针对这个问题，通过探索研究，制作出一个能够完整演示圆锥曲线各种形状并能反映圆锥曲线相关性的实例，同时也渗透介绍一些制作技巧，供同行研讨。

二、探索验证对上述作法稍作变动：把直线F1A绕点F1旋转一个定角，试一下：(1)以F1为圆心，过点A画圆；(2)在平面内任取一点B，作直线F1B，交圆于点C，再在直线F1B和圆上各任取一点D、E，作线段DE的中垂线(3) 在圆上任取一点F，标记角度∠C F1F，以F1为中心旋转点E得点G，作直线F1G，交中垂线于点P(4)选中点P、E构造轨迹。

我们发现点P的轨迹似乎是圆锥曲线，移动点D的位置，或是变动点F、A的位置，曲线的形状都会不断的改变（如图4）图4那么它真的是圆锥曲线吗，它能反映圆锥曲线的各种形状吗，它的形状与点D 、F 、A 的位置又有怎样的关系？下面就来探索这个问题设F 1A= r ，F 1D= m ，∠CF 1F =α。

3.1圆锥曲线切线的定义设直线l '与圆锥曲线相交于P 、Q 两点（对于双曲线P 、Q 在同一支上），将直线绕点P 旋转，使点Q 逐渐靠近点P ，当l '转到直线l 的位置时，点P 与Q 重合，这时直线l 叫做圆锥曲线在点P 的切线，P 叫做切点.经过点P 与切线垂直的直线叫做圆锥曲线在点P 的法线[10].以抛物线为例，作图1如下：3.2圆锥曲线的切线方程（1）过圆锥曲线上一点的切线方程容易得到，过圆锥曲线上一点的切线方程如下：经过椭圆 12222=+by a x 上一点()00,y x P 的切线方程为:12020=+b y y a x x ；经过双曲线12222=-b y a x 、12222=-bx a y 上一点()00,y x P 的切线方程分别为:12020=-b y y a x x 、12020=-bxx a y y ； 经过抛物线px y 22±=、py x 22±=的切线方程分别为:()x x p y y o o +±=、()y y p x x o o +±=.所以经过圆锥曲线上一点()00,y x P 的切线方程，就是把圆锥曲线方程中的2x 和2y'分别为换为0x x 和0y y ,x 和y 分别换为)2(0x x +和)2(0y y +，即“替换法则”. （2）定斜率的切线方程容易证明，对于定斜率圆锥曲线的切线方程如下：斜率为k ，并且和椭圆12222=+by a x 相切的切线方程为:222b k a kx y +±=(不问ab的大小)；斜率为k ，并且和双曲线12222=-b y a x 、12222=-bx a y 相切的切线方程分别为:222b k a kx y -±=(222b k a ≥)、222b k a kx y -±=(222a k b ≤)；斜率为k ，并且和抛物线px y 22±=、py x 22±=相切的切线方程分别为:kp y 2±=（k 0≠）、22pk y =.3.3圆锥曲线切点弦从圆锥曲线外一点向圆锥曲线引两条切线（如果存在），那么经过两切点的圆锥曲线的弦叫做切点弦[11].圆锥曲线外一点()11,P x y 向圆锥曲线引两条切线，求经过两切点的切点弦方程同样可用2x 和2y 分别换为x x 1和y y 1,x 换成21x x +,y 换成21yy +的“替换法则”去求它，即[12]：经过椭圆 12222=+by a x 上一点()11,y x P 的切点弦方程为:12121=+b y y a x x ；经过双曲线12222=-b y a x 、12222=-bx a y 上一点()11,y x P 的切点弦方程分别为:12121=+b y y a x x ,12121=-bxx a y y ； 经过抛物线px y 22±=、py x 22±=上一点()11,y x P 的切点弦方程分别为:()x x p y y o +±=1,()y y p x x o +±=1. 3.4圆锥曲线焦点弦如果经过焦点的直线和圆锥曲线相交于两点，那么经过这两交点的圆锥曲线的弦叫做焦点弦[13]．4 圆锥曲线切线的性质及其应用探讨圆锥曲线有许多共同的优美性质[14].下面我们探讨圆锥曲线的几个简单性质，并给出应用例子，希望这些性质及其应用能有助于初学者对圆锥曲线切线有所了解，从而有效解决相关问题.性质1：在圆锥曲线的准线l （相应准线）上任取一点P ，经过P 点引圆锥曲线的两条切线PA 、PB ，其中A 、B 为切点，则切点弦AB 经过焦点F （相应焦点）且AB 垂直于PF .证明：首先看椭圆的情形.如图2，设椭圆的方程为12222=+b y a x （a ＞b ＞０）,在左准线上任取一点⎪⎪⎭⎫⎝⎛-n c a P ,2，经过P 点所引两条切线PA 、PB ，其中A 、B 为切点，则切点弦AB 的方程为：22222b a ny a x cb a =+- . 又左焦点()0,1c F -满足切点弦AB 的方程，所以点1F 在AB 这条直线上，即切点弦AB 过焦点1F ．又因为2201b cnca c c n k PF -=+-+--= ,cn b n a b a k AB 2222=--=,所以有122-=⋅-=cnb b cn k k ABPF即AB 垂直PF ．同理可证在右准线上的点P 引椭圆的两条切线PA ，PB 的切点弦AB 经过右焦点且AB 垂直PF .同理可证对双曲线12222=-by a x 和12222=-bx a y ，性质1也成立.下面看抛物线的情形.如图3，设抛物线的方程为px y 22=，在其准线上任取一点⎪⎭⎫⎝⎛-n p P ,2，则经过点P 引两切线PA ，PB ，其中A 、B 为切点，则切点弦AB 的方程为：⎪⎭⎫ ⎝⎛+-=x p p ny 2.又因为抛物线px y 22=的焦点为⎪⎭⎫⎝⎛0,2p F ，满足切点弦AB 的方程，所以切点弦AB经过焦点F .又p np p n k PF -=--=22 ,n p k AB = ， 所以有 1-=⋅-=n p p n k k AB PF 即AB 垂直PF .同理可证对于抛物线px y 22-=和py x 22±=，性质1也成立.推论：在圆锥曲线上经过焦点弦AB 两端点的切线的交点P 落在（相应）准线l 上.证明：先看椭圆的情形.设经过椭圆12222=+by a x （a ＞b ＞0）的焦点弦AB 的两端点A 、B 的两条切线相交于()11,y x P ，则直线AB 的方程为12121=+byy a x x . x又因为焦点()0,C F ±的坐标满足切点弦方程121=±acx ，即c a x 21±= ，故P 点落在圆锥曲线的准线上.同理可证对于双曲线、抛物线推论也成立. 下面举例说明性质1及推论的应用.例1[14]：（2006年全国高考题（Ⅱ）理第21题）已知抛物线y x 42=的焦点为F ，A 、B 是抛物线上的两个动点，且−→−−→−=FB AF λ(λ＞0)，过A 、B 两点分别作抛物线的切线，设其交点为M .（1）证明−→−−→−⋅FB FA 为定值；（2）设的△ABM 面积为S ，写出()λf S =的表达式并求S 的最小值. 解法一:详见2006年全国高考题（Ⅱ）理第21题数学试题卷(理科类)答案. 解法二：（1）−→−−→−=FB AF λ∴A 、F 、B 三点共线.即直线AB 经过抛物线y x 42=的焦点F . ∴由性质1知 AB FM ⊥. ∴−→−−→−⊥AB FM . 即0=⊥−→−−→−AB FM .∴−→−−→−⋅FB FA 为定值0.（2） 直线AB 经过抛物线y x 42=的焦点 ∴两切线的交点M 在准线上 −→−−→−⊥AB FM AB FM S ⋅=∴21AB 为定值且4=AB∴要求S 的最小值，需求FM 的最小值∴当且仅当M 在y 轴上时，即()1,0-M 时，S 取得最小值4422121=⨯⨯=⋅=∴AB FM S ∴S 的最小值为4.说明：（1）由性质1的结论知，本题中的M 事实上在准线2py -=上且−→−−→−⊥AB FM ，这样此题便可迎刃而解.（2）由推论知M 在准线上，当且仅当M 在y 轴上，即()1,0-M 时,S 取得最小值.这样来解答相对较简单，节约解题时间.例2[15]:（2006年重庆高考试题文科22题）如图4,对每一个正整数n ,()n n n y x A ,是抛物线y x 42=上的点,过焦点F 的直线n FA 交抛物线于另一点()n n n t s B ,.(1)试证: 4-=n n s x (n ≥1);(2)取n n x 2=,并记n C 为抛物线上分别以n A 与n B 为切点的两切线的交点.试证:122121+-=++++-n n n FC FC FC .下面主要看第二问的解答.解法一:详见2006年全国统一考试(重庆卷)数学试题卷(文科类)答案.解法二:(1)略.(2)nn x 2= ∴42422n n x y ==,则n A 的坐标为⎪⎪⎭⎫⎝4,22n n n A ，所以过n A 的直线的斜率()n n x x y k 22211==='=-. 设()y x C n ,，则直线n n C A 的方程为:()n n nx y 224212-=--.由性质1推论知, n n C A 与n n C B 的交点n C 在相应准线1-=y 上.把1-=y 代入直线n n C A 方程解得1212--=n n x .yx故有⎪⎭⎫⎝⎛----1,21211n n n C ,又()1,0F .∴1121122112122122212------+=⎪⎭⎫ ⎝⎛+=+⎪⎭⎫ ⎝⎛-==n n n n n n n FC .().1222112112121212121122211121221+-=--+--=⎪⎭⎫ ⎝⎛+++++++++=++++---n n n nn n n FC FC FC 说明：此解法优点在于,利用圆锥曲线切线性质求出两切线交点坐标,可大大减少运算量，减少运算时间.由推论知当直线l 过焦点并与圆锥曲线交于A 、B 两点，则经过A 、B 的两切线的交点落在相应的准线上；那么对于任一点()00,y x P 任作直线l 与圆锥曲线交于M 、N 两点,经过M 、N 的两切线的交点是否也落在某一固定的直线上呢？为此通过证明得出性质2.性质2：过圆锥曲线外任一点()00,y x P 作直线l ，交圆锥曲线于M 、N 两点,若圆锥曲线在点M 、N 处切线的交点为Q ，则点Q 在一定直线上.证明：首先来看椭圆的情形.设椭圆的方程为12222=+by a x (a ＞b ＞０),过椭圆外一点()00,y x P 任作直线l 交椭圆于M 、N 两点,椭圆在点M 、N 处切线的交点为Q .设),(11y x M 、),(22y x N ,则两切线的方程分别为:MQ :12121=+b y y a x x ，NQ :12222=+byy a x x . 可解得交点的坐标为：1221122)(y x y x y y a x --=， 1221122)(y x y x x x b y ---=. 设过点()00,y x P 的直线l 的方程为)(00x x k y y -=-,则0011)(y x x k y +-=, 0022)(y x x k y +-=.于是()[][]()()0012002200211221)(y kx x x y x x k x y x x k x y x y x --=+--+-=-，()1212x x k y y -=-.所以()()()00200121221221122)(y kx ka y kx x x x x ka y x y x y y a x -=---=--=, ()()()00200121221221122)(y kx b y kx x x x x b y x y x x x b y --=----=---=. 消去k ,得12020=+b y y a x x .所以点P 在定直线12020=+by y a x x 上. 说明:（1）当点P 在椭圆内部时,任作直线l 与椭圆都有两个交点,此时轨迹为直线12020=+byy a x x .(2）当点P 在椭圆外部时,要使过点P 的直线与椭圆有两个交点,则斜率k 受到限制.同理可证双曲线对性质2也成立.设双曲线方程为12222=-by a x (a ＞0，b ＞０),过双曲线外一点()00,y x P 任作直线l 交双曲线于M 、N 两点,双曲线在点M 、N 处切线的交点为Q ,则点Q 在定直线12020=-byy a x x 上. 说明：当点P 在无穷远处时,过点P 任作直线即为一族平行直线.此时问题变为:斜率为k 一组平行直线交圆锥曲线于M 、N 两点,过M 、N 两点的切线的交点在一定直线上.下面看抛物线的情形.已知抛物线px y 22=，过抛物线外一点()00,y x P 任作直线l 与交抛物线于M 、N 两点,曲线在点M 、N 处的切线交点为Q .设),(11y x M 、),(22y x N ,则两切线的方程分别为:MQ :)(11x x p y y +=,NQ :)(22x x p y y +=.可解得交点的坐标为 ：211221y y y x y x x --=，2121y y x x p y --=.设过()00,y x P 的直线l 的方程为:()00x x k y y -=-.把0011)(y x x k y +-=,0022)(y x x k y +-=代入直线l 的方程解得:kkx y x 00-=，n py =.再消去k ，得()00x x p y y +=.所以点P 在定直线()00x x p y y +=上,故性质2得证. 特别地，当点P 坐标取圆锥曲线的焦点坐标时，该性质变为性质1的推论，即性质2为性质1的推论推广[16].例3：已知抛物线C :2x y =,过点()2,0P 的直线交抛物线于M 、N 两点,曲线C 在点M 、N 处的切线交点为Q ,求点Q 所在的直线.解法一:设()11,y x M , ()22,y x N ,则211x y =,222x y =,过点M 、N 的切线方程分别为()1121y y x x +=，()2221y y x x +=. ∴()11212x x x x y -=- ，()22222x x x x y -=-, 由这两方程解得221x x x +=，21x x y =. 设过点()2,0P 的直线斜率为k ，则方程为2+=kx y (1) 把（1）式代入抛物线方程2x y =，消去y ，得 022=--kx x .由韦达定理得 2,2121-==+x x k x x ,所以2-=y .即点Q 的轨迹在定直线2-=y (x ∈R)上.解法二：由性质2和2x y =知21=p 把00=x ，20=y 代入方程 ()00y y p x x += 得2-=y ，即点Q 的轨迹在定直线2-=y (x ∈R)上.说明：在解题时如果学生懂得性质2，那么就可以直接利用公式来解决，节约做题时间.例4[17]:(2005年江西高考题理科试卷)设抛物线C :2x y =的焦点为F ,动点P 在直线：02=--y x 上的动点，过点P 作抛物线C 的两条切线PA 、PB 且与抛物线C 分别相交于A 、B 两点.（1）求△APB 的重心G 的轨迹方程; （2）证明：∠PFA =∠PFB .解：详见2005年江西高考题理科试卷答案.由（2）的结论和答案激发了一种思想：对于圆锥曲线外一点P 作圆锥曲线的两条切线，切点分别为A 、B .F 为圆锥曲线的其一焦点.当P 点在F 相应的准线上时，由性质1知AB PF ⊥,即∠PFA =∠PFB = 90.当点P 不在准线上时，是否也有∠PFA =∠PFB ？为此通过证明得出性质3.性质3：过圆锥曲线外一点P 作圆锥曲线的两条切线PA ，PB ，其中A 、B 为切点，F 为圆锥曲线的焦点，则PFB PAF ∠=∠.证明：先看椭圆的情形.如图5,设椭圆的方程为12222=+by a x （a ＞b ＞０）,()n m P ,，()11,y x A ，()22,y x B ，则直线AB 的方程为122=+bny a mx ,即 02222=-+b a ny a mx b . 所以 0221212=-+b a ny a mx b ，则有212221amx b b a ny -=. 设F 为左焦点，则()0,c F -，所以()11,y c x FA +=−→−，()n c m FP ,+=−→−,故P=⋅−→−−→−FP FA ()11,y c x +()n c m ,+()()11ny c x c m +++=()()212221a mx b b a c x c m -+++=()()22212a a cm a x a mc c +++=()()2212mc a cx a a ++=⎪⎭⎫ ⎝⎛+⎪⎭⎫⎝⎛+=m ac a x ac a 1()()em a ex a ++=1（e 是椭圆的离心率）.由向量的内积公式PFA FP FA FP FA ∠⋅=⋅−→−−→−−→−−→−cos ||||，所以()()−→−−→−−→−−→−−→−−→−⋅+⋅+=⋅⋅=∠FPFA em a ex a FPFA FPFA PFA 1cos又由椭圆的焦半径公式可知：1||ex a FA +=−→−，所以()()()()−→−−→−+=⋅++⋅+=∠FPem a FPex a em a ex a PFA 11cos同理可得:()−→−+=∠FPem a PFB cos ，所以PFB PFA ∠=∠.说明：当F 为右焦点时，同理可得PFB PFA ∠=∠. 同理可证对双曲线性质3也成立.下面看抛物线的情形.如图6， 设抛物线的方程为：px y 22=，()n m P ,，()1,1y x A ，()2,2y x B ，则直线AB 的方程为: ()x m p ny +=.所以()11x m p ny += ， 又⎪⎭⎫⎝⎛0,2p F ，则⎪⎭⎫ ⎝⎛-=−→−11,2y p x FA ，⎪⎭⎫ ⎝⎛-=−→−n p m FP ,2,故()⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+=++⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=+⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=⋅−→−−→−222222,2,21111111p m p x x m p p m p x ny p m p x n p m y p x FP FA由向量的内积公式 PFA FP FA FP FA ∠⋅=⋅−→−−→−−→−−→−cos ||||，所以||||22||||cos 1−→−−→−−→−−→−−→−−→−⋅⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+=⋅⋅=∠FP FA p m p x FP FA FP FA PFA又由抛物线的焦半径可知：2||1px FA +=−→−，所以 ||2||222||||cos 11−→−−→−−→−−→−−→−−→−⎪⎭⎫ ⎝⎛+=⋅⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+=⋅⋅=∠FP p m FP p x p m p x FP FA FP FA PFA 同理可得：||2cos −→−⎪⎭⎫ ⎝⎛+=∠FP p m PFB ，所以 PFB PFA ∠=∠.说明：如果在教学中教师能引导学生这样分析和探讨得出性质3，那么像例4第二问这样的题目学生在解答时可做到心中有数,且能信心十足地解答好该题[18].性质4：经过圆锥曲线外一点P （双曲线两焦点所在的线段中点除外）作圆锥曲线的两条切线PA 、PB ，切点分别为A 、B .过P 作倾斜角为θ的直线交圆锥曲线于M 、N 两点，与切点弦交于C 点，则直线MN 上的三线段PM 1、PC 1、PN1成等差数列. 证明：首先看椭圆的情形.如图7,设椭圆的方程为12222=+by a x （a ＞b ＞０），椭圆外一点()00,y x P ，两切点为A 、B 两点，则直线AB 的方程为：12020=+by y ax x （1）.设直线MN 的参数方程为 ⎩⎨⎧+=+=θθsin cos 00t y y t x x （t 为参数）（2）,由（1）、（2）式得2020220220sin cos 1b y a x b y a x t +⎪⎪⎭⎫ ⎝⎛+-= 且PC t =. 再将（2）代入椭圆方程12222=+by a x ，得关于t 的方程：01sin cos 2sin cos 220220202022222=-++⎪⎭⎫ ⎝⎛++⎪⎪⎭⎫ ⎝⎛+b y a x b y a x t t b a θθθθ.因为直线与圆锥曲线有两个交点,所以()2002222sin sin sin cos θθθθy x a b --+=∆>0，方程有两根，设两根为1t 、2t ，则PM t =1，PN t =2,所以⎪⎪⎭⎫⎝⎛+-⎪⎭⎫ ⎝⎛+=+=+=+220222020*******sin cos 21111b y a x b y a x t t t t t t PN PM o θθ 由此可发现PCt PN PM 2211==+ 故PM 1、PC 1、PN1成等差数列.同理可证对双曲线性质4也成立.下面看抛物线的情形.如图8，设抛物线的方程为px y 22=，抛物线外一点()00,y x P ，两切点分别为A 、B 两点，则直线AB 的方程为：()x x p yy +=00（1）.设直线MN 的参数方程为⎩⎨⎧+=+=θθsin cos 00t y y t x x （t 为参数）（2）,由（1）、（2）式得:θθcos sin 2020p y y px t --=且PC t = 把（2）带入抛物线方程px y 22=，得关于t 的方程：()()θθcos 2sin 020t x p t y +=+.所以()02cos sin 2sin 02002=-+-+px y t p y θθθ因为直线与圆锥曲线有两个交点,所以∆＞0，方程有两根，设其两根为1t 、2t ，则PM t =1，PN t =2,所以().22cos sin 21111200212121t y px p y t t t t t t PN PM =--=+=+=+θθ 所以PM 1、PC 1、PN1成等差数列. 特别地，当0=θ时，过P 点的直线PM 平行于对称轴与抛物线只有一个交点M ，这时由高等几何的知识，N 可视作无穷远点，因而有01→PN. 即有 PM 1= PC 2, 故M 是PC 的中点.例5[19]：双曲线方程1422=-y x ，)3,1(-P ,ST 为切点弦，过P 点的直线为2+-=x y ，并与双曲线交于A 、B 两点，与切点弦交于C 点.证明三线段PA1、PC 1、PB1成等差数列.证明: ST 的方程为,134=--y x 与2+-=x y 的交点为⎪⎭⎫ ⎝⎛-116,1128C . 11239=∴PC , 392112=PC . 又2+-=x y 与1422=-y x 的交点为()0,2A ，⎪⎭⎫⎝⎛-34,310B . 621=∴PA , 26231=PB ∴PC PB PA 23921126236211==+=+ ∴PA 1、PC 1、PB1成等差数列. 性质5：从圆锥曲线上一点P 引切线和法线分别交x 轴所在直线于T 、N ，交y 轴所在直线于T '、N '，则N P PN T P PT '⋅='⋅.证明：先看椭圆等的情形.如图10，设椭圆的方程为12222=+by a x （a ＞b ＞０）,经过其上一点()ααsin ,cos b a P 的切线与法线方程分为:ab y a x b =⋅+⋅ααsin cos ,()ααααcos sin cos sin 22b a y b x a -=⋅-⋅x它们与长轴所在直线的交点是：⎪⎭⎫ ⎝⎛0,cos αa T ，()⎪⎭⎫⎝⎛-0,cos 122αb a a N .它们与短轴所在直线的交点是：⎪⎭⎫ ⎝⎛'αsin ,0b T ，()⎪⎪⎭⎫ ⎝⎛--'b b a N αsin ,022. 于是有 222222sin sin cos sin cos cos ⎪⎭⎫ ⎝⎛-+⋅+⎪⎭⎫ ⎝⎛-='⋅ααααααb b a b a a T P PTαα2222cos sin b a +=()()2222222222sin sin cos sin cos cos ⎥⎦⎤⎢⎣⎡+++⋅+⎥⎦⎤⎢⎣⎡--='⋅b b a b a b a b a a N P PN αααααα αα2222cos sin b a +=故N P PN T P PT '⋅='⋅其次看双曲线的情形.如图11，设双曲线的方程为12222=-by a x ，过其上一点()θθtan ,sec b a P 的切线与法线方程分为:ab y a x b =⋅-⋅θθtan sec ，()θθθθsec tan sec tan 2⋅+=⋅+⋅b a y b x a .故T 、T '、N 、N '的坐标分别为:⎪⎭⎫ ⎝⎛0,sec θa T ，⎪⎭⎫ ⎝⎛-'θtan ,0b T ，()⎪⎪⎭⎫ ⎝⎛+0,sec 22a b a N θ，()⎪⎪⎭⎫ ⎝⎛+'b b a N θtan ,022 于是有 22222tan tan sec tan sec sec ⎪⎭⎫ ⎝⎛++⋅+⎪⎭⎫ ⎝⎛-='⋅θθθθθθb b a b a a T P PTθθ2222sec tan b a +=22222222tan sec tan sec ⎪⎪⎭⎫ ⎝⎛+⋅+⎪⎪⎭⎫ ⎝⎛='⋅b a a b a b N P PN θθθθ θθ2222sec tan b a += 即N P PN T P PT '⋅='⋅再次看抛物线的情形.如图12，设抛物线的方程为px y 22±=,过其上一点()pt pt P 2,22的切线与法线方程分别为:0222=+-pt ty x ，()22122t pt y tx +-+故T 、T '、N 、N '的坐标分别为:()0,22pt T -，()()0,212t p N +，()pt o T ,'，()()2212,0t pt N +'于是有 ()()()()2222222222pt pt pt pt pt pt T P PT -+⋅++='⋅()222412t t p +=()()[]()()[]22222221222212t pt pt pt t p pt N P PN +-+⋅+-='⋅()222412t t p +=所以N P PN T P PT '⋅='⋅ ，即性质5得证.例6: 椭圆的方程为192522=+y x ，过其上一点⎪⎭⎫ ⎝⎛-59,4P 得切线l 与x 轴、y 轴相交于T 、T '，过点P 的法线l '与x 轴、y 轴相交于N 、N ',求N P PN '⋅的值.分析：由性质5可知//PN PN PT PT ⋅=⋅，要求N P PN '⋅可转化为求T P PT '⋅.解： 直线l 为椭圆的切线，且切点⎪⎭⎫ ⎝⎛-59,4P∴直线l 的方程为1959254=+-yx∴⎪⎭⎫⎝⎛-0,425T ，()5,0T 'x由两点间的距离公式得：20419590442522=⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛+-=PT ，()54145954022=⎪⎭⎫ ⎝⎛-++='T P N P PN T P PT '⋅='⋅ ∴N P PN '⋅=25369541420419=⨯. 总之，在教学过程中引导学生通过探究性学习获得圆锥曲线的一些切线的性质并加以应用，不仅可以让学生进一步加深对圆锥曲线知识的理解，提高解题能力，而且可以培养学生的创造性思维，提高学生的学习数学的兴趣[20].5 结论5.1主要发现圆锥曲线切线的性质及其应用为相关问题的求解和证明提供十分有效的解题思路，有助于学生对圆锥曲线切线知识有更深刻认识.探讨圆锥曲线切线的性质，不仅需要对基础知识熟练掌握，而且要灵活运用相关知识，善于将知识点衔接起来，归纳总结三种圆锥曲线的内在个性特点.只有通过不断地分析典型题目，找出内在规律及它们的一些性质进行总结，才能找出圆锥曲线具有的统一性质.总之，在高考中圆锥曲线切线的相关问题既有一定难度，又有一定的技巧性和整体性，但只要我们善于思考和总结就容易找到解决问题的突破口，也会发现圆锥曲线切线的性质对求解该类问题有着很大的帮助. 5.2启示圆锥曲线切线的性质是解决与圆锥曲线切线相关问题的关键点，理解掌握圆锥曲线切线的性质和证明思路，对解决圆锥曲线的相关问题有极大的帮助.但要理解掌握和灵活运用性质去解决问题时，必须对基础知识熟练掌握，且能够将知识点融会贯通. 5.3局限性本毕业论文提供的仅是有限的几个性质及证明方法，还有许多性质未能得出，限我个人能力有限，不能提供更多的性质以便解决许多相关的问题，同时也没能完全给出相应的应用，这是本毕业论文的不足. 5.4努力方向除了文中所述的几个性质外，根据三种圆锥曲线的内在个性特点可能还有其他的一些性质，这些性质将有待我们作进一步探讨研究，以弥补本论文的不足.参考文献[1] 郑观宝.圆锥曲线的一个共通性质[J].中学数学研究，2006，（8）：44.[2] 人民教育出版社中学数学室.全日制普通高级中学教科书(第二册上)[M].北京：人民教育出版社，2004:91-122.[3] 张留杰. 圆锥曲线的一个性质的证明与推广[J]. 数学通讯，2003，（15）:25-27.[4] 周伟林. 圆锥曲线切点弦的一个性质[J].考试周刊，2007,（3）:49-50.[5] 黄继创. 圆锥曲线的一个几何特征[J].数学通讯，2006,（6）:94-95.[6] 吴翔雁. 圆的重要性质在圆锥曲线上的推广[J].数学通讯，2005,（7）:25-27.[7] 张家瑞.圆锥曲线的一个性质[J].数学教学通讯，2006，（8）:55-56.[8] 潘德党. 圆锥曲线的一个性质及应用[J].数学教学研究，2007,（3）:25-26.[9] 李铭祺.高中几何学习指导[M].西安：陕西人民教育出版社.1987:125-126.[10] 刘膺淳.高中数学知识转化为能力的途径[M].长沙：湖南人民出版社,1988: 115-118.[11] 黄熙宗.圆锥曲线切点弦方程的简易求法[J].苏州教育学院学报,1991，5（3）：18-19.[12] 王保庆，杨振兴，蔡凯.圆锥曲线切点弦方程的性质新探[J]. 数学教学通讯，2009, 5：28-29.[13] 邱昌银.圆锥曲线准切线焦点弦的相关性质[J].数学通讯，2003，（5）：12-13.[14] 杨宣文，杨国平.圆锥曲线的又一性质[J].数学教学通讯，2006,（7）:35-37.[15] 蔡献慧.圆锥曲线切点弦的应用[J].洛阳师范学院学报，2006,5（5）:158-159.[16] 储炳南.圆锥曲线的一个统一性质[J].数学教学，2006，（11）：24—26.[17] 梁平. 圆锥曲线切线性质在高考试题中应用[J].解题研究,2001，(3):34-35.[18] 卢伟峰.圆锥曲线切线的一个性质[J].数学教学通讯，2008，(4)：16-17.[19] 李建明.两道高考题引出的圆锥曲线的一个性质[J].数学通讯，2007，（3）：10-11.[20] 李凤华.相似圆锥曲线的一条优美性质[J]. 数学通讯,2008,(11)：33-34.。

运用《几何画板》探索圆锥曲线的切线性质
陈文斌;储炳南
【期刊名称】《中学数学教学》
【年(卷),期】2008(000)006
【摘要】@@ 1 结论的发现rn受文[1]的启发,笔者利用<几何画板>数学软件探讨抛物线切线的性质时,发现如下一组结论:
【总页数】2页(P21-22)
【作者】陈文斌;储炳南
【作者单位】安徽省巢湖一中,238000;安徽省岳西中学,246600
【正文语种】中文
【中图分类】O1
【相关文献】
1.在几何画板中作圆锥曲线切线的几种方法 [J], 江俊
2.用“几何画板”作圆锥曲线的切线 [J], 赵国藩
3.用《几何画板》作圆锥曲线切线 [J], 徐洪章;刘良志
4.过圆锥曲线上任一点切线的又一尺规作法——圆锥曲线光学性质的应用 [J], 黄伟;
5.用几何画板作圆锥曲线切线的研训导引 [J], 甘大旺
因版权原因，仅展示原文概要，查看原文内容请购买。

《超级画板》帮你教圆锥曲线(1)彭翕成(华中师范大学教育信息技术工程研究中心,湖北　430079)中图分类号:G642.0 文献标识码:A 文章编号:0488-7395(2007)09-0009-04 笔者曾在大学和中学组织过几何画板的培训,感受最深的就是几何画板处理解析几何问题太麻烦,老师们也反应难以掌握.举例来说,平时作两圆的公切线,椭圆切线等,都只要拿尺往圆上一靠,马上就可以用笔画出来了.但在几何画板中,作两圆的公切线要分内公切线和外公切线两种情况,作椭圆的切线要分点在椭圆上和椭圆外两种情况,而且这些作法相当复杂,除了需要较深的数学功底之外,还要熟练掌握几何画板的各种技巧.但如果使用超级画板,就只要运行简单的函数命令.下面我们就来介绍具体作法.1　探索两圆的位置关系和公切线条数两圆的位置关系有5种情况,通常是通过测量圆心距,计算半径之和与之差来判断.那么我们该如何动态地演示两圆位置的变化过程,以及不同位置关系时,公切线的条数呢?这两个问题可以用一个课件来解决.作法如下:1)作以A为圆心过点B的圆;连线段AB,在线段AB上取点C;2)选定点B,C,点击【变换】|【选定平移向量】,选中点C,点击【变换】|【平移几何对象】,平移复制得点D;3)在平面上任作点E,自E向AB的延长线上引垂足F;4)仿照(2),选定向量DF,将点C平移复制得点G;5)作以G为心过点F的圆;在圆A内, BD的延长线上作点H;在圆A外,AB的延长线上作点I(图1);6)右键单击点C,在右键菜单中单击“属性”打开点C的属性对话框,删去x-拖动参数u000;对点H,I作同样的操作.这样,这几个点就拖不动了(要调整位置时,可修改属性恢复拖动参数);7)打开【对象】|【文本作图】,弹出【文本命令作图对话框】,输入函数命令“Common2 Tangent(7,15,0,);Common Tangent(7,15, 1,);Common Tangent(7,15,2,);Common2 Tangent(7,15,3,);”,点击运行;其中7和15是两个圆的编号;8)依次选择点E和H,在右键菜单中单击动画,作出点E运动到H的动画按钮,将按钮文本改为“无公切线”;同法作出E到D, E到C,E到B和E到I的动画按钮并将文本改为“1条公切线”,“2条公切线”,等;9)单击某个按钮,右边那个圆就会运动,使得公切线条数变成我们所需要的.譬如我们点击按钮“3条公切线”,即可得到图2.这个例子的制作,主要体现用平移安排点的位置的方法,以及用自由点的运动带动收稿日期:2007-02-10垂足和用点带动圆的方法.附带介绍了在属性对话框里去掉拖动参数使对象上的点位置相对固定的小窍门.图　1图　22　探索圆的一般方程中参数对圆的影响圆的一般方程x 2+y 2+Dx +Ey +F =0中有三个参数.我们通过超级画板探索,就能清楚地看出这三个参数对圆的影响.1)在文本作图框输入“ConicOf Equation (x^2+y^2+D 3x +E 3y +F =0,);”,点击运行;此命令是为了作出圆,但此时屏幕上并没出现圆,这与D ,E ,F 当前取值有关.2)在文本作图框输入“Variable (D ,);Variable (E ,);Variable (F ,);”,点击运行;此命令是作出控制圆的3把变量尺;3)打开【测量】|【测量表达式】,弹出【文本命令作图】对话框,计算D 2+E 2-4F ,得到的结果是-1115;4)拖动3把变量尺,改变D ,E ,F 三个参数的值,使得D 2+E 2-4F 的值大于0;在文本作图框输入“ConicCentre (5,);”,点击运行;5)选择点A ,在右键菜单中选择跟踪;选择圆,在右键菜单中选择跟踪;6)在文本作图框输入“MeasureCentre 2OfCircle (5);MeasureNormalOfCircle (5);Measure G eneralOfCircle (5);”,点击运行;此时屏幕如图3所示;7)拖动变量尺D ,可得图4;拖动变量尺E ,可得图5;拖动变量尺F ,可得图6;图　3图　43　探索圆锥曲线的一般方程与圆的一般方程相比,圆锥曲线的一般方程要多几个参数,因此变化也复杂得多,但通过超级画板,也能简单、直观地得到很多我们需要的信息,而且探索方法和圆基本类似,图　5图　6只不过需要多加几个参数.下面就介绍设置控制参数的另一种方法,以及探索过程中需要注意的事项.1)在文本作图框输入“ConicOf Equation (A 3x^2+B 3x 3y +C 3y^2+D 3x +E 3y +F ,);”,点击运行;此时屏幕上没出现任何图象,这说明6个参数的当前取值使得二元二次方程不能表示任何图形.2)在文本作图框输入“Variable (A ,);Variable (B ,);Variable (C ,);Variable (D ,);Variable (E ,);Variable (F ,);”,点击运行;此命令是为了作出控制圆锥曲线的6把变量尺;拖动变量尺,使得屏幕上有图象出现;3)在文本作图框输入“Mea 2sureNormalOfConic (5);”,点击运行;4)拖动变量尺A ,C 使之同号,此时屏幕如图7所示,图象为椭圆;图　75)拖动变量尺A ,C 使之异号,此时屏幕如图8所示,图象为双曲线;图　86)在右键菜单中单击参数A 的动画,参数范围从1到B^2Π(43C ),类型改为一次运动;点击动画按钮,此时屏幕如图9所示,图象为抛物线;图　9如果我们计算出B 2-4AC 的值,可以看出此值的正或负分别对应于双曲线或椭圆;如果我们作出参数B 的动画,使之变为0,曲线的对称轴会变得平行或垂直于x 轴.我们还可以作出更多的尝试.4　圆锥曲线随离心率而变化圆锥曲线有一个统一的定义,就是到一个定点的距离和到一条定直线的距离的比值为定值的点的轨迹.定点叫做该轨迹曲线的焦点,定直线叫做该轨迹曲线的准线,定值叫做该轨迹曲线的离心率.离心率通常用e 表示,e <1时为椭圆,e =1时为抛物线,e >1时为双曲线.这条随离心率变化的曲线是如何画出来的呢?最简单的方法是使用极坐标下圆锥曲线的统一方程:ρ=ep1-e cosθ.需要注意的是,希腊字母ρ和θ分别用rho 和thet 来表示,而离心率不能用e 来表示,因为在超级画板中把e 保留用于自然对数的底,即e =2.71828....不过,虽然内部用b 表示离心率,这并不妨碍我们在显示出来的文本中仍然用e 表示离心率.1)在文本作图框输入“Function (rho =a 3p Π(1-a 3cos (thet ),0,23pi ,500);”,点击运行生成双曲线;2)在文本作图框输入“Variable (a ,);Variable (p ,);”,点击运行作出控制圆锥曲线的2把变量尺;3)拖动变量尺a ,p ,观察两个参数对圆锥曲线的影响,尤其是a 在大于1和小于1时两者之间的不同;4)作出参数a 的动画,参数范围从1到1,类型改为一次运动;点击动画按钮,此时屏幕如图10所示,图象为抛物线;图　105　过五点的圆锥曲线与其切线给了不共线的3个点,可以确定一个圆.类似地,给了5个点,如果其中任意3点都不共线,就可以确定一条圆锥曲线.超级画板有一条文本图命令可以让我们体验这个有趣的事实.1)用智能画笔作5个点,其中任意3点都不共线;2)在文本作图框输入“ConicOf FivePoint (5,6,7,8,9,);MeasureNormalOfConic (10);”,点击运行;此命令作出了过5点的圆锥曲线,以及测量出该圆锥曲线的标准方程;3)用智能画笔作出圆锥曲线上的一点F ,并在文本作图框输入“Tangent (12,10,0,);”,点击运行作出过点F 的切线;其中12是点F 的编号,10是圆锥曲线的编号;4)用智能画笔作出圆锥曲线外的一点G ,并在文本作图框输入“Tangent (14,10,0,);Tangent (14,10,1,);”,点击运行作出过点G 的两条切线(图11);我们可以改变5个点的位置,得到更多的变化;图　11(注:科学出版社2006年出版的《超级画板自由行》(张景中著),该书详细讲述了《超级画板》免费版本的用法和技巧,附赠的光盘中有即插即用并且可以复制的《超级画板》的免费版本和作者制作的200多个范例.书的定价45.00元(邮购另加5.00元邮挂费).需要者可直接汇款到《数学通讯》编辑部购买.)。

专题14 圆锥曲线的切线问题一、结论圆锥曲线的切线问题常用方法有几何法，代数法：比如求圆的切线，常用圆心到直线的距离等于半径来解决切线问题，也可以联立直线与圆的方程根据0∆=来求解；比如涉及到椭圆的切线问题，也常常联立直线与椭圆的方程根据0∆=来求解； 对于抛物线的切线问题，可以联立，有时也可以通过求导来求解. 而对于这些圆锥曲线也常常存在一些特殊的求切线公式：1.过圆C :222()()x a y b R -+-=上一点00(,)P x y 的切线方程为200()()()()x a x a y b y b R --+--=.2.过椭圆22221x y a b +=上一点00(,)P x y 的切线方程为00221x x y ya b +=.3.已知点,抛物线:和直线: (1)当点00(,)M x y 在抛物线C 上时,直线l 与抛物线C 相切,其中M 为切点,l 为切线.当点在抛物线外时,直线与抛物线相交,其中两交点与点的连线分别是抛物线的切线,即直线为切点弦所在的直线.当点在抛物线内时,直线与抛物线相离.二、典型例题1．（2021·安徽·六安一中高二期末（文））已知椭圆具有如下性质：若椭圆的方程为()222210x y a b a b +=>>，则椭圆在其上一点()00,A x y 处的切线方程为00221x x y y a b +=，试运用该性质解决以下问题；椭圆221:12x C y +=，点B 为1C 在第一象限中的任意一点，过B 作1C 的切线l ，l 分别与x 轴和y 轴的正半轴交于,C D 两点，则OCD 面积的最小值为（ ） A ．1 BCD ．2【答案】C 【详解】设，由题意得，过点B 的切线l 的方程为： 令0y =，可得12(,0)C x ，令0x =，可得11(0,)D y ，所以OCD 面积111112112S x y x y =⨯⨯=，又点B 在椭圆上，所以221112x y +=，所以121111121111122x y S x y x y x x y y +===+≥当且仅当11112x yy x =，即111,x y ==时等号成立，所以OCD. 故选：C【反思】过椭圆上一点作切线，切线方程为：该结论可以在小题中直接使用，但是在解答题中，需先证后用，所以在解答题中不建议直接使用该公式.2．（2020·江西吉安·高二期末（文））已知过圆锥曲线221x y m n+=上一点()00,P x y 的切线方程为001x x y y m n +=.过椭圆221124x y +=上的点()3,1A -作椭圆的切线l ，则过A 点且与直线l 垂直的直线方程为（ ） A ．30x y --= B ．-20x y += C ．2330x y +-= D ．3100x y --=【答案】B 【详解】过椭圆221124x y +=上的点()3, 1A -的切线l 的方程为()31124y x -+=，即40x y --=，切线l 的斜率为1.与直线l 垂直的直线的斜率为-1，过A 点且与直线l 垂直的直线方程为()13y x +=--，即20x y +-=.故选：B【反思】根据题中信息，直接代入公式，但是在代入切线方程为注意不要带错，通过对比本题信息，将这些数字代入公式，可求出切线，再利用直线垂直的性质求解. 3．（2022·江苏南通·一模）过点作圆的切线交坐标轴于点、则_________. 【答案】2- 【详解】 圆的圆心为，因为，则点在圆上，所以，所以，直线AB 的斜率为1AB k =-，故直线AB 的方程为()11y x -=--，即20x y +-=， 直线20x y +-=交x 轴于点()2,0A ，交y 轴于点()0,2B ， 所以，因此，故答案为：另解：过圆:上一点的切线方程为.可知，代入计算得到过点作圆的切线为：整理得：直线交轴于点，交轴于点， 所以，因此， 故答案为：【反思】本题中提供了常规方法和使用二级结论的解法，特别提醒同学们，二级结论的公式代入数字时，最忌讳代入错误，所以需要特别仔细。