人教版初三数学一元二次方程最全面最经典
- 格式:pptx
- 大小:350.15 KB
- 文档页数:19

一元二次方程知识点及考点精析一、知识结构: 一元二次方程⎪⎩⎪⎨⎧*⇒韦达定理根的判别解与解法二、考点精析考点一、概念(1)定义:只含有一个未知数........,并且②未知数的最高次数是.........2.,这样的③整式方程....就是一元二次方程。
(2)一般表达式:)0(02≠=++a c bx ax 其中2ax 是二次项,a 叫二次项系数;bx 是一次项,b 叫一次项系数,c 是常数项。
二次项系数、一次项系数及常数项都是方程在一般形式下定义的,所以求一元二次方程的各项系数时,必须先将方程化为一般形式。
⑶难点:如何理解 “未知数的最高次数是2”:①该项系数不为“0”; ②未知数指数为“2”;③若存在某项指数为待定系数,或系数也有待定,则需建立方程或不等式加以讨论。
典型例题: 例1、下列方程中是关于x 的一元二次方程的是( )A ()()12132+=+x xB 02112=-+x xC 02=++c bx axD 1222+=+x x x 变式:当k 时,关于x 的方程3222+=+x x kx 是一元二次方程。
例2、方程()0132=+++mx x m m 是关于x 的一元二次方程,则m 的值为 。
针对练习:★1、方程782=x 的一次项系数是 ,常数项是 。
★2、若方程()021=--m xm 是关于x 的一元一次方程,⑴求m 的值;⑵写出关于x 的一元一次方程。
★★3、若方程()112=•+-x m x m 是关于x 的一元二次方程,则m 的取值范围是 。
★★★4、若方程nx m +x n -2x 2=0是一元二次方程,则下列不可能的是( )B.m=2,n=1C.n=2,m=1D.m=n=1考点二、方程的解⑴概念:使方程两边相等的未知数的值,就是方程的解。
⑵应用:利用根的概念求代数式的值; 例1、已知322-+y y 的值为2,则1242++y y 的值为 。
例2、关于x 的一元二次方程()04222=-++-a x x a 的一个根为0,则a 的值为 。

21章 一元二次方程知识点一、一元二次方程1、一元二次方程概念:等号两边是整式,含有一个未知数,并且未知数的最高次数是2的方程叫做一元二次方程。
注意:(1)一元二次方程必须是一个整式方程;(2)只含有一个未知数;(3)未知数的最高次数是2 ;(4)二次项系数不能等于02、一元二次方程的一般形式:)0(02≠=++a c bx ax ,它的特征是:等式左边是一个关于未知数x 的二次三项式,等式右边是零,其中2ax 叫做二次项,a 叫做二次项系数;bx 叫做一次项,b 叫做一次项系数;c 叫做常数项。
注意:(1)二次项、二次项系数、一次项、一次项系数,常数项都包括它前面的符号。
(2)要准确找出一个一元二次方程的二次项系数、一次项系数和常数项,必须把它先化为一般形式。
(3)形如02=++c bx ax 不一定是一元二次方程,当且仅当0≠a 时是一元二次方程。
二、 一元二次方程的解使方程左、右两边相等的未知数的值叫做方程的解,如:当2=x 时,0232=+-x x 所以2=x 是0232=+-x x 方程的解。
一元二次方程的解也叫一元二次方程的根。
一元二次方程有两个根(相等或不等)三、一元二次方程的解法1、直接开平方法:直接开平方法理论依据:平方根的定义。
利用平方根的定义直接开平方求一元二次方程的解的方法叫做直接开平方法。
根据平方根的定义可知,a x +是b 的平方根,当0≥b 时,b a x ±=+,b a x ±-=,当b<0时,方程没有实数根。
三种类型:(1)()02≥=a a x 的解是a x ±=;(2)()()02≥=+n n m x 的解是m n x -±=;(3)()()0,02≥≠=+c m c n mx 且的解是mn c x -±=。
2、配方法:配方法的理论根据是完全平方公式222)(2b a b ab a +=+±,把公式中的a 看做未知数x ,并用x 代替,则有222)(2b x b bx x ±=+±。


一元二次方程一、知识要点一元二次方程1.一元二次方程的有关概念:只含 个未知数,并且未知数的最高次数是 的整式方程叫做一元二次方程,一元二次方程的一般形式是 ,其中二次项系数是 ,一次项系数是 ,常数项是 。
2.一元二次方程的解法:(1)一元二次方程的解法有 、 、 、 。
(2)一元二次方程)0(02≠=++a c bx ax 的求根公式是 ,运用求根公式解一元二次方程的前提是 。
3、一元二次方程的根的判别式:对于一元二次方程)0(02≠=++a c bx ax ,ac b 42-=∆称为一元二次方程的根的判别式。
4.一元二次方程的根与系数的关系:设21,x x 分别是一元二次方程()002≠=++a c bx ax 的两根,则有=+21x x ,=21x x 。
二、知识运用典型例题例1.(1)(武汉) 2310x x --=. (2)(仙桃)2420x x ++=.例2.m 取什么值时,关于x 的方程22(1)0mx m x m -++=,(1)有两个相等的实数根,(2) 有两个不相等的实数根,(3)有实数根,(4)没有实数根,(5)有且只有一个实数根。
例3.已知1x 2x 是关于x 的一元二次方程062=+-k x x 的两个实数根,且21x 22x —1x —2x =115 (1)求k 的值;(2)求21x +22x +8的值。
例4.(淮安)小丽为校合唱队购买某种服装时,商店经理给出了如下优惠条件:如果一次性购买不超过10件,单价为80元;如果一次性购买多于10件,那么每增加1件,购买的所有服装的单价降低2元,但单价不得低于50元.按此优惠条件,小丽一次性购买这种服装付了1200元.请问她购买了多少件这种服装?三、知识运用课堂训练1. (河南)方程2x =x 的解是 ( )A .x =1 B.x =0 C.x 1=1 x 2=0 D. x 1=﹣1 x 2=0 2.(山西省太原市)用配方法解方程2250x x --=时,原方程应变形为( ) A .()216x += B .()216x -= C .()229x += D .()229x -= 3.(无锡)方程2310x x -+=的解是.4.(威海)若关于x 的一元二次方程2(3)0x k x k +++=的一个根是2-,则另一个根是______.5.(兰州)已知关于x 的一元二次方程01)12=++-x x m (有实数根,则m 的取值范围是 .6.(安徽芜湖)已知x 1、x 2是方程x 2+3x +1=0的两实数根,则x 13+8x 2+20=________.7.(成都)设1x ,2x 是一元二次方程2320x x --=的两个实数根,则2211223x x x x ++的值为__________________.8.(昆明)如图,在长为100米,宽为80米的矩形场地上修建两条宽度相等且互相垂直的道路,剩余部分进行绿化,要使绿化面积为7644米2,则道路的宽应为多少米?设道路的宽为x米,则可列方程为()A.100×80-100x-80x=7644B.(100-x)(80-x)+x 2=7644C.(100-x)(80-x)=7644D.100 x+80 x =3569.(荆州)已知:关于x的方程kx2-(3k-1)x+2(k-1)=0(1)求证:无论k为何实数,方程总有实数根;(2)若此方程有两个实数根x1,x2,且│x1-x2│=2,求k的值.10.(长沙)长沙市某楼盘准备以每平方米5000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望.为了加快资金周转,房地产开发商对价格经过两次下调后,决定以每平方米4050元的均价开盘销售.(1)求平均每次下调的百分率;(2)某人准备以开盘均价购买一套100平方米的房子.开发商还给予以下两种优惠方案以供选择:①打9.8折销售;②不打折,送两年物业管理费.物业管理费是每平方米每月1.5元.请问哪种方案更优惠?课后训练1.(河南)方程032=-x 的根是( )(A )3=x (B )3,321-==x x (C )3=x (D )3,321-==x x 2.(荆门)如果方程ax 2+2x +1=0有两个不等实根,则实数a 的取值范围是___ ___. 3.(玉溪市)一元二次方程x 2-5x +6=0 的两根分别是x 1,x 2,则x 1+x 2等于 ( ) A. 5 B. 6C. -5D. -64.(烟台市)设a b ,是方程220090x x +-=的两个实数根,则22a a b ++的值为( )A .2006B .2007C .2008D .20095.(包头)关于x 的一元二次方程2210x mx m -+-=的两个实数根分别是12x x 、,且22127x x +=,则212()x x -的值是( )A .1B .12C .13D .25。




一元二次方程的解法一元二次方程解法:⎧⎪⎪⎨⎪⎪⎩直接开方法配方法因式分解法公式法知识点一、直接开方法例1、用直接开方法解下列方程(1)x2=16 (2)2x2=16 (3)3x2+1=28 (4)(x-1)2=16 (5)2(x-1)2+2=100直接开方法步骤总结:①常数移去右边②二次项系数化为1③用“整体法”直接开方④解出来答案通常都有两个,别漏了哟~思考:是不是所有一元二次方程都有解呢?方程x2+1=0或(x+3)2+1=0该怎么解呢?1、用直接开方法解下列方程(1)(1+x)2=81 (2)2(1-x)2=162 (3)100(1+x)2=144 (4)3(x+9)2-81=02、当a________时,方程(x-1)2-a=0有实根,这时实根是________________;当a____________时,方程无实根直接开方法不是万能的,例如x2+2x=3就不能单独依赖它解出来,那么还有什么其他解法呢?知识点二、配方法后来人们发现,“直接开方法”并不能解决所有的一元二次方程。
例如x2+2x=3就不能直接开方于是到了大约公元前480年,我们中国人就开始使用另一种方法“配方法”来解一元二次方程,连《九章算术》中都有记载。
配成“完全平方公式”的方法叫做配方法,而且它是一元二次方程单元测验的重点,同学们一定要打起十二分精神听讲!例1、解方程:x2+2x=3 例2、解方程:x2-6x+2=0 例3、解方程:2x2+8x=24例4、解方程:3x2-6x-5=0 例5、2x2+3x-6=0配方法步骤总结:①常数移去右边②二次项系数化为1③配成完全平方公式(核心步骤:加上一次项系数一半的平方)④用“整体法”直接开方⑤求解思考:上述配方的题目都是“方程”,如果不是方程,有可能配方吗?例6、求证:无论k取何值,式子248k k++恒大于0例7、已知代数式2++,求证:不论m为任何实数,该代数式一定大于0 2m8m501、用配方法解下列方程:(1)025122=++x x (2)1042=+x x (3)1162=-x x(4)0422=--x x (5)01762=+-x x (6)0152=+-x x(7)52342=-x x (8)x x 2452-= (9)x x 91852=-2、配方法解方程x 2-2x -5=0时,原方程应变形为( )_______,21==x x A .(x +1)2=6 B .(x -1)2=6 C .(x +2)2=9 D .(x -2)2=93、用配方法解方程x 2+4x =3,配方正确的是( )A .(x +2)2=3B .(x +2)2=4C .(x +2)2=7D .(x +1)2=44、用配方法解方程0642=--x x ,则___6___42+=+-x x ,所以5、如果()4122++-x m x 是一个完全平方式,则=m 。

第2讲 一元二次方程的解法(二)----配方法配方法:利用完全平方公式把一元二次方程转化成的形式,再利用直接开平方法解一元二次方程的方法叫做配方法.①当p >0时,方程有两个不等的实数根,;②当p=0时,方程有两个相等的实数根=-n ;③当p <0时,因为对任意实数x ,都有,所以方程无实数根. 知识要点梳理:完全平方公式:222)(2b a b ab a +=++ 222)(2b a b ab a -=+-尝试解方程:x 2-4x +3=0我们把方程x 2-4x +3=0变形为(x -2)2=1,它的左边是一个含有未知数的完全平方式,右边是一个非负常数.这样,就能应用直接开平方的方法求解.这种解一元二次方程的方法叫做配方法.练一练 :配方.填空:(1)x 2+6x +( )=(x + )2;(2)x 2-8x +( )=(x - )2;(3)x 2+23x +( )=(x + )2; 从这些练习中你发现了什么特点?(1)________________________________________________(2)________________________________________________经典例题例1. 用配方法解下列方程:(1)x 2-6x -7=0; (2)x 2+3x -1=0. 解(1)移项,得x 2-6x =____.方程左边配方,得x 2-2·x ·3+_ _2=7+___,即(____ __)2=__ __.所以 x -3=_______.原方程的解是x 1=_____,x 2=_____.(2)移项,得x 2+3x =1.方程左边配方,得x 2+3x +( )2=1+____,即 ____________________所以___________________原方程的解是: x 1=______________x 2=___________总结规律用配方法解二次项系数是1的一元二次方程?有哪些步骤?例2.用配方法解下列方程:(1)011242=--x x (2)03232=-+x x(3)03422=+-x x例3.当x 为何值时,代数式5x 2 +7x +1和代数式x 2 -9x +15的值相等?例4.求证:不论a 、b 取何实数,多项式a 2b 2 +b 2 -6ab -4b +14的值都不小于1.例5. 试证:不论k 取何实数,关于x 的方程 (k 2 -6k +12)x 2 = 3 - (k 2 -9)x 必是一元二次方程.经典练习一、选择题1.若x 2+6x+m 2是一个完全平方式,则m 的值是( )A .3B .-3C .±3D .以上都不对2. 若9x 2 -ax +4是一个完全平方式,则a 等于( );A. 12B. -12C. 12或-12D. 6或-63.用配方法将二次三项式a 2-4a+5变形,结果是( )A .(a-2)2+1B .(a+2)2-1C .(a+2)2+1D .(a-2)2-14.把方程x x 432=+,得( )A .(x-2)2=7B .(x+2)2=21C .(x-2)2=1D .(x+2)2=25.用配方法解方程x 2+4x=10的根为( )A .2±B .-2C .D .6.不论x 、y 为什么实数,代数式x 2+y 2+2x-4y+7的值( )A .总不小于2B .总不小于7C .可为任何实数D .可能为负数二、填空1.用适当的数填空:①、x 2+6x+ =(x+ )2; ②、x 2-5x+ =(x - )2; ③、x 2+ x+ =(x+ )2; ④、x 2-9x+ =(x - )2⑤ (x - )2 = x 2 - 32x + ;2.将二次三项式2x 2-3x-5进行配方,其结果为_________.3.已知4x 2-ax+1可变为(2x-b )2的形式,则ab=_______.4.将一元二次方程x 2-2x-4=0用配方法化成(x+a )2=b 的形式为_______,所以方程的根为_________.三.用配方法解方程:(1)x2+8x-2=0 (2)x2-5x-6=0.(3)2x2-x=6 (4)4x2-6x+()=4(x-)2=(2x-)2(5)x2+px+q=0(p2-4q≥0).四、用配方法求解下列问题(1)求2x2-7x+2的最小值;(2)求-3x2+5x+1的最大值。


一元二次方程应用题总结分类及经典例题1、列一元二次方程解应用题的特点列一元二次方程解应用题是列一元一次方程解应用题的继续和发展,从列方程解应用题的方法来讲,列出一元二次方程解应用题与列出一元一次方程解应用题是非常相似的,由于一元一次方程未知数是一次,因此这类问题大部分都可通过算术方法来解决.如果未知数出现二次,用算术方法就很困难了,正由于未知数是二次的,所以可以用一元二次方程解决有关面积问题,经过两次增长的平均增长率问题,数学问题中涉及积的一些问题,经营决策问题等等.2、列一元二次方程解应用题的一般步骤和列一元一次方程解应用题一样,列一元二次方程解应用题的一般步骤是:“审、设、列、解、答”.(1)“审”指读懂题目、审清题意,明确已知和未知,以及它们之间的数量关系.这一步是解决问题的基础;(2)“设”是指设元,设元分直接设元和间接设元,所谓直接设元就是问什么设什么,间接设元虽然所设未知数不是我们所要求的,但由于对列方程有利,因此间接设元也十分重要.恰当灵活设元直接影响着列方程与解方程的难易;(3)“列”是列方程,这是非常重要的步骤,列方程就是找出题目中的等量关系,再根据这个相等关系列出含有未知数的等式,即方程.找出相等关系列方程是解决问题的关键;(4)“解”就是求出所列方程的解;(5)“答”就是书写答案,应注意的是一元二次方程的解,有可能不符合题意,如线段的长度不能为负数,降低率不能大于100%等等.因此,解出方程的根后,一定要进行检验.3、数与数字的关系两位数=(十位数字)×10+个位数字三位数=(百位数字)×100+(十位数字)×10+个位数字4、翻一番翻一番即表示为原量的2倍,翻两番即表示为原量的4倍.5、增长率问题(1)增长率问题的有关公式:增长数=基数×增长率实际数=基数+增长数(2)两次增长,且增长率相等的问题的基本等量关系式为:原来的×(1+增长率)增长期数=后来的说明:(1)上述相等关系仅适用增长率相同的情形;(2)如果是下降率,则上述关系式为:原来的×(1-增长率)下降期数=后来的6、利用一元二次方程解几何图形中的有关计算问题的一般步骤(1)整体地、系统地审读题意;(2)寻求问题中的等量关系(依据几何图形的性质);(3)设未知数,并依据等量关系列出方程;(4)正确地求解方程并检验解的合理性;(5)写出答案.7、列方程解应用题的关键(1)审题是设未知数、列方程的基础,所谓审题,就是要善于理解题意,弄清题中的已知量和未知数,分清它们之间的数量关系,寻求隐含的相等关系;(2)设未知数分直接设未知数和间接设未知数,这就需根据题目中的数量关系正确选择设未知数的方法和正确地设出未知数.8、列方程解应用题应注意:(1)要充分利用题设中的已知条件,善于分析题中隐含的条件,挖掘其隐含关系;(2)由于一元二次方程通常有两个根,为此要根据题意对两根加以检验.即判断或确定方程的根与实际背景和题意是否相符,并将不符合题意和实际意义的(一)传播问题1.市政府为了解决市民看病难的问题,决定下调药品的价格。


新人教版九年级数学(上)一元二次方程的解法——配方法、求根公式法知识点一、配方法解一元二次方程()002≠=++a c bx ax 222442a ac b a b x -=??? ??+? ※在解方程中,多不用配方法;但常利用配方思想求解代数式的值或极值之类的问题。
典型例题:例1、试用配方法说明322+-x x 的值恒大于0。
例2、已知x 、y 为实数,求代数式74222+-++y x y x 的最小值。
例3、已知,x、y y x y x 0136422=+-++为实数,求yx 的值。
例4、分解因式:31242++x x一元二次方程的解法(二)针对练习:★★1、试用配方法说明47102-+-x x 的值恒小于0。
★★2、已知041122=---+x x x x ,则=+x x 1 .★★★3、若912322-+--=x x t ,则t 的最大值为,最小值为。
★★★4、如果4122411-++-=--++b a c b a ,那么c b a 32-+的值为。
知识点二、根的判别式从配方法那里我们知道不是所有的一元二次方程都是有实数解的,原因在于配方得到的右边的项为2244a ac b - ;而当04422<-a ac b ,是不能开方的,所以方程无实数解。
而2244aac b -与0的大小关系又取决于ac b 42-;所以:当042>-ac b 时,方程有两个不相等的实数根;当042=-ac b 时,方程有两个相等的实数根;当042<-ac b 时,方程没有实数根。
由此可知ac b 42-的取值决定了一元二次方程根的情况,我们把ac b 42-称作根的判别式,用符号“Δ”表示;即:ac b 42-=? 根的判别式的作用:①定根的个数;②求待定系数的值;③应用于其它。
典型例题:例1、若关于x 的方程0122=-+x k x 有两个不相等的实数根,则k 的取值范围是。
例2、关于x 的方程()0212=++-m mx x m 有实数根,则m 的取值范围是( ) A.10≠≥且m m B.0≥m C.1≠m D.1>m例3、已知关于x 的方程()0222=++-k x k x (1)求证:无论k 取何值时,方程总有实数根;(2)若等腰?ABC 的一边长为1,另两边长恰好是方程的两个根,求?ABC 的周长。

解一元二次方程(公式法4种题型)【知识梳理】一、公式引入一元二次方程20ax bx c ++=(0a ≠),可用配方法进行求解:得:2224()24b b acx a a −+=.对上面这个方程进行讨论:因为0a ≠,所以240a >①当240b ac −≥时,22404b aca −≥利用开平方法,得:2b x a += 即:x = ②当240b ac −<时,22404b aca −< 这时,在实数范围内,x 取任何值都不能使方程2224()24b b acx a a−+=左右两边的值相等,所以原方程没有实数根. 二、求根公式一元二次方程20ax bx c ++=(0a ≠),当240b ac −≥时,有两个实数根:1x 2x =20ax bx c ++=(0a ≠)的求根公式. 三、用公式法解一元二次方程一般步骤①把一元二次方程化成一般形式20ax bx c ++=(0a ≠); ②确定a 、b 、c 的值;③求出24b ac −的值(或代数式);④若240b ac −≥,则把a 、b 、c 及24b ac −的值代入求根公式,求出1x 、2x ;若240b ac −<,则方程无解.四、 根的判别式1.一元二次方程根的判别式:我们把24b ac −叫做一元二次方程20(0)ax bx c a ++=≠的根的判别式,通常用符号“∆”表示,记作2=4b ac ∆−.2.一元二次方程20(0)ax bx c a ++=≠,当2=40b ac ∆−>时,方程有两个不相等的实数根; 当2=40b ac ∆−=时,方程有两个相等的实数根;当2=40b ac ∆−<时,方程没有实数根.五、根的判别式的应用(1)不解方程判定方程根的情况; (2)根据参数系数的性质确定根的范围; (3)解与根有关的证明题.【考点剖析】题型1用公式法解一元二次方程例1.用公式法解下列方程: (1)2270x x −+=;(2)211042x x −=.【答案】(1)27,021==x x ;(2)2,021==x x .【解析】(1)0,7,2==−=c b a ,则4942=−ac b ,则477−±−=x ,∴27,021==x x ;(2)0,21,41=−==c b a ,则4142=ac b ,则212121±=x ,∴2,021==x x .【总结】本题主要考查一元二次方程求根公式x 的运用.例2.用公式法解下列方程:(1)2320x x +−=;(2)25610x x −++=.【答案】(1)12x x ==;(2)12x x ==.【解析】(1)132a b c ===−,,,则1742=−ac b ,则2173±−=x ,∴12x x ==;(2)561a b c =−==,,,则5642=−ac b ,则101426−±−=x ,∴12x x ==.【总结】本题主要考查一元二次方程求根公式x 的运用.例3.用公式法解下列方程:(1)(24)58x x x −=−;(2)2(53)(1)(1)5x x x −+=++.【答案】(1)122222x x −+−==;(2)123322x x ==−,. 【解析】(1)方程可化为:05422=−+x x ,245a b c ===−,,,则5642=−ac b ,则41424±−=x ,∴122222x x −−==;(2)方程可化为:2490x −=,则123322x x ==−,.【总结】本题主要考查一元二次方程求根公式的运用,(2)也可以用直接开平方法求解. 例4.用公式法解下列方程:(1)20.2 2.5 1.30.1x x x +−=;(2)22(3)(31)(23)1552x x x x +−−+−=.【答案】(1)12x x ==;(2)12122x x ==−,. 【解析】(1)方程可化为2224130x x +−=,13,24,2−===c b a ,则68042=−ac b ,则4170224±−=x ,∴12x x =(2)两边同时乘以10,方程可化为02322=−−x x ,2,3,2−=−==c b a ,则2542=−ac b , 则453±=x ,∴12122x x ==−,.【总结】本题主要考查一元二次方程求根公式的运用,(2)也可以用因式分解法求解. 例5.用公式法解下列方程:(1)291x +=;(220+−=.【答案】(1)12x x =;(2)12x x ==【解析】(1)1,66,9=−==c b a ,则18042=−ac b ,则185666±=x ,∴原方程的解为:12x x =;(2)22,34,2−===c b a ,则6442=−ac b ,则22834±−=x ,∴原方程的解为:12x x ==【总结】本题主要考查一元二次方程求根公式的运用.题型2解系数中有字母的一元二次方程例6.用配方法解下列关于x 的方程:220ax x ++=(0a ≠).【解析】220ax x ++=(0a ≠),则22−=+x ax ,整理得:a x a x 212−=+,配方可得:22248141221a a a a a x −=+−=⎪⎭⎫ ⎝⎛+, 当81≤a 时,a a x 21811−−=,a a x 21812−−−=,当81>a 时,方程无实数根.【总结】注意配方时方程两边同加一次项系数一半的平方,另此题系数中含有字母,要注意分类讨论. 例7.用公式法解下列关于x 的方程:(1)20x bx c −−=;(2)2100.1ax a −−=. 【解析】(1)∵c b 42+=∆,∴当042≥+c b 时,2421c b b x ++=,2422c b b x +−=;当042<+c b 时,原方程无实数根;原方程可化为:22100x a −=,∵2222400a b a ∆=+≥,∴原方程的解为:12x +=,22x a=.【总结】本题主要考查利用公式法求解一元二次方程的根,注意分类讨论.题型3根的判别式例8.选择:(1) 下列关于的一元二次方程中,有两个不.相等的实数根的方程是( )(A )(B ) (C )(D )(2) 不解方程,判别方程25750x x −+=的根的情况是()(A )有两个相等的实数根 (B )有两个不相等的实数根 (C )只有一个实数根(D )没有实数根(3)方程2510x x −−=的根的情况是()(A )有两个相等实根 (B )有两个不等实根 (C )没有实根(D )无法确定(4)一元二次方程2310x x +−=的根的情况为()(A )有两个不相等的实数根 (B )有两个相等的实数根 (C )只有一个实数根(D )没有实数根【答案】(1)D ;(2)D ;(3)B ;(4)A .【答案】【答案】【解析】(1)A :1a =,0b =,1c =,2440b ac ∆=−=−<,方程无实根; B :1a =,2b =,1c =,240b ac ∆=−=,方程有两个相等实根; C :1a =,2b =,3c =,2480b ac ∆=−=−<,方程无实根;D :1a =,2b =,3c =−,24160b ac ∆=−=>,方程有两不等实根实根,故选D ; (2)5a =,7b =−,5c =,24510b ac ∆=−=−<,方程无实根,故选D ; (3)1a =,5b =−,1c =−,24290b ac ∆=−=>,方程有两不等实根,故选B ; (4)1a =,3b =,1c =−,24130b ac ∆=−=>,方程有两个相等实根,故选A .【总结】考查一元二次方程根的判别式判定方程根的情况,先列出方程中的a 、b 、c ,再代值计算∆,根据∆与0的大小关系确定方程根的情况,注意a 、c 异号时则必有两不等实根. 例9.不解方程,判别下列方程的根的情况: (1)24530x x −−=;(2)22430x x ++=;x 012=+x 0122=++x x 0322=++x x0322=−+x x(3)223x +=; (4)22340x x +−=.【答案】(1)方程有两不等实根;(2)方程无实数根;(3)方程有两相等实根; (4)方程有两不等实根.【解析】(1)4a =,5b =−,3c =−,24730b ac ∆=−=>,方程有两不等实根; (2)2a =,4b =,3c =,2480b ac ∆=−=−<,方程无实数根;(3)2a =,b =−,3c =,240b ac ∆=−=,方程有两相等实根; (4)2a =,3b =,4c =−,24410b ac ∆=−=>,方程有两不等实根.【总结】考查一元二次方程根的判别式判定方程根的情况,先将方程整理成一般形式,列出方程中的a 、b 、c ,再代值计算∆,根据∆与0的大小关系确定方程根的情况,注意a 、c 异号时则必有两不等实根.例10.关于x 的方程2(1)0x m x m +−−=(其中m 是实数)一定有实数根吗?为什么? 【答案】一定有.【解析】∵1a =,1b m =−,c m =−,∴()()()22241410b ac m m m ∆=−=−−⨯−=+≥恒成立,可知方程一定有实数根.【总结】考查一元二次方程根的判别式判定方程根的情况,对于含有字母系数的一元二次方程,只需要对最终的∆的值与0的大小关系,进而确定方程根的情况. 例11.已知关于x 的一元二次方程2(1)210m x mx −++=根的判别式的值为4,求m 的值. 【答案】0.【解析】∵1a m =−,2b m =,1c =,∴()()()2224241414b ac m m m m ∆=−=−⨯−=−+=,整理即得20m m −=,解得:11m =,20m =,同时方程是一元二次方程,知10a m =−≠,故1m ≠, 由此得0m =.【总结】考查一元二次方程根的判别式判定方程根的情况,对于含有字母系数的一元二次方程,尤其是二次项系数中含有字母的情况,一定要注意字母所隐含的取值范围,即二次项系数不能为0. 例12.已知方程组18ax y x by −=⎧⎨+=⎩的解是23x y =⎧⎨=⎩,试判断关于x 的方程20x ax b ++=的根的情况.【答案】方程无实数根.【解析】方程组18ax y x by −=⎧⎨+=⎩的解是23x y =⎧⎨=⎩,代入即得:231238a b −=⎧⎨+=⎩,可解得:22a b =⎧⎨=⎩,此时方程即为2220x x ++=,其中1a =,2b =,2c =,2480b ac ∆=−=−<,可知方程无实数根.【总结】考查一元二次方程根的判别式判定方程根的情况,对于系数含有字母的情况,根据题目条件确定字母取值,再确定其∆值,判定方程解的情况.例13.当m 取何值时,关于x 的方程221(2)104x m x m +−+−=,(1)有两个不相等的实数根? (2)有两个相等的实数根?(3)没有实数根? 【答案】(1)2m <;(2)2m =;(3)2m >. 【解析】对此方程,1a =,2b m =−,2114c m =−,则()22214241484b ac m m m ⎛⎫∆=−=−−−=−+ ⎪⎝⎭,由此可知,(1)当480m ∆=−+>,即2m <时,方程有两个不相等的实数根; (2)当480m ∆=−+=,即2m =时,方程有两两个相等的实数根; (3)当480m ∆=−+<,即2m >时,方程无实数根.∆值,方程可由∆值判定其根的情况,同样地,可由方程根的情况确定其∆值与0的大小关系,可在此基础上进行分类讨论.例14.当k 为何值时,关于x 的方程224(21)0x kx k −+−=有实数根?并求出这时方程的根(用含k 的代数式表示).【答案】14k ≥时,方程有实数根;方程的根为2x k =± 【解析】对此方程,1a =,4b k =−,()221c k =−,则()()22244421164b ac k k k ∆=−=−−−=−,因为方程有实数根,则有1640k ∆=−≥,即14k ≥时,方程有实数根;根据一元二次方程求根公式,可知方程解为()4222k b x k a −−−===【总结】考查一元二次方程根的判别式判定方程根的情况,对于系数含有字母的情况,先确定其∆值,方程可由∆值判定其根的情况,同样地,可由方程根的情况确定其∆值与0的大题型5根的判别式的应用例15.证明:方程()()212x x k −−=有两个不相等的实数根. 【解析】证明:对原方程进行整理,即为:22320x x k −+−= 其中1a =,3b =−,22c k =−,则()()22224342410b ac k k ∆=−=−−−=+>恒成立, 由此可证得方程有两个不相等的实数根.【总结】将方程整理成一元二次方程的一般形式,方程的根的情况,只需要根据方程的∆值即可以确定下来.例16.当k 为何值时,方程()()222210kx k x x k k −−=−−≠,(1)有两个不相等的实数根;(2)有两个相等的实数根;(3)没有实数根. 【答案】(1)54k <且1k ≠;(2)54k =;(3)54k >. 【解析】将方程整理成关于x 的一元二次方程的一般形式,即得:()()()212210k x k x k −−−++=,此时,1a k =−,()22b k =−−,1c k =+,由方程为一元二次方程,可知10a k =−≠,故1k ≠;()()()224424111620b ac k k k k ∆=−=−−−+=−+,由此可知,(1)当16200k ∆=−+>,即54k <且1k ≠时,方程有两不等实根; (2)当16200k ∆=−+=,即54k =时,方程有两相等实根;(3)当16200k ∆=−+<,即54k >时,方程无实根.【总结】考查一元二次方程根的判别式判定方程根的情况,首先将方程整理成一元二次方程的一般形式,然后确定二次项系数不能为0的情况,然后确定其∆值,可由方程根的情况确定其∆值与0的大小关系,可在此基础上进行分类讨论.例17.已知关于x 的一元二次方程()21230m x mx m +++−=有实数根,求m 的取值范围. 【答案】32m ≥−且1m ≠−.【解析】由原方程是一元二次方程,可知10m +≠,即1m ≠−;对此方程, 其中1a m =+,2b m =,3c m =−,方程有实根,则必有:()()()22424138120b ac m m m m ∆=−=−+−=+≥,可解得32m ≥−;即m 的取值范围为32m ≥−且1m ≠−.【总结】对于形如20ax bx c ++=的方程,首先要根据题意确定相关隐含条件,既要保证一元二次方程的二次项系数不能为0,然后在此基础上进行解题和计算.例18.如果m 是实数,且不等式(1)1m x m +>+的解集是1x <,那么关于x 的一元二次方程21(1)04mx m x m −++=的根的情况如何?【答案】方程无实根.【解析】由(1)1m x m +>+的解集是1x <,可知10m +<,即1m <−,对一元二次方程21(1)04mx m x m −++=而言,其中a m =,()1b m =−+,14c m =,则()221414214b ac m m m m ∆=−=+−⋅=+,1m <−时,0∆<恒成立, 由此可知方程无实数根.【总结】探求含有字母的一元二次方程根的情况,需要根据题目条件确定相关字母取值范围,再根据其∆值确定相关方程根的情况.例19.已知关于x 的方程()21230m x mx m +++−=总有实数根,求m 的取值范围. 【答案】32m ≥−. 【解析】(1)当10m +=,即1m =−时,方程为一元一次方程240x −−=,方程有实根; (2)当10m +≠,即1m ≠−时,方程为一元二次方程, 其中1a m =+,2b m =,3c m =−,方程有实根,则必有:()()()22424138120b ac m m m m ∆=−=−+−=+≥,可解得32m ≥−且1m ≠−;综上所述,m 的取值范围为32m ≥−.【总结】对于形如20ax bx c ++=的方程,首先要根据题意确定二次项系数能否为0,在此基础上进行相关分类讨论和计算.【过关检测】一、单选题【答案】B【分析】根据关于x 的一元二次方程20x x k −−=有实数根得到140k ∆=+≥,解不等式即可得到答案.【详解】解:∵关于x 的一元二次方程20x x k −−=有实数根,∴()()2141140k k ∆=−−⨯⨯−=+≥,解得14k ≥−,故选:B【点睛】此题考查了一元二次方程根的判别式,熟练掌握一元二次方程0∆≥时有实数根是解题的关键. 2.(2023春·广东潮州·九年级潮州市金山实验学校校考期末)如果关于x 的一元二次方程2(5)410a x x −−−=有两个不相等的实数根,则a 满足条件是( )A .5a ≠B .1a >且5a ≠C .1a ≥且5a ≠D .1a ≥【答案】B【分析】由二次项系数非零及根的判别式0∆>,即可得出关于a 的一元一次不等式组,解之即可得出a 的取值范围.【详解】解:∵关于x 的一元二次方程2(5)410a x x −−−=有两个不相等的实数根,∴()()()25044510a a −≠⎧⎪⎨−−⨯−⨯−>⎪⎩,解得:1a >且5a ≠, 故选B .【点睛】本题考查了一元二次方程的定义以及根的判别式,牢记“当0∆>时,方程有两个不相等的实数根”是解题的关键.3.(2023·浙江温州·统考三模)若关于x 的一元二次方程2160x bx ++=,有两个相等的实数根,则正数b 的值是( ) A .8B .8−C .4D .4−【答案】A【分析】根据一元二次方程有两个相等的实数根,运用根的判别式进行解答即可.【详解】解:∵关于x 的一元二次方程2160x bx ++=,有两个相等的实数根,∴22441160b ac b ∆=−=−⨯⨯=,∴264b =,∴8b =±, ∵b 是正数, ∴8b =, 故选:A .【点睛】本题考查了一元二次方程根的判别式,熟知关于x 的一元二次方程20(0)ax bx c a ++=≠,若240b ac ∆=−>,则原方程有两个不相等的实数根;若240b ac ∆=−=,则原方程有两个相等的实数根;若240b ac ∆=−<,则原方程没有实数根.【答案】C【分析】分别代入数值解方程,逐一判断即可解题.【详解】解:当12a =时,方程为28120x x −−=,解得4x =±A 选项不符合题意;当16a =时,方程为28160x x −−=,解得4x =±B 选项不符合题意;当20a =时,方程为28200x x −−=,解得10x =或2x =−是整数,故C 选项符合题意;当24a =时,方程为28240x x −−=,解得4x =±D 选项不符合题意;故选:C【点睛】本题考查一元二次方程的解法,掌握公式法解一元二次方程是解题的关键.5.(2023·安徽安庆·校考三模)如果关于x 的一元二次方程260x x a −+=无实数根,那么a 的值可以为( )A .10B .9C .8D .7【答案】A【分析】由一元二次方程根与系数的关键可得:Δ0<, 从而列不等式可得答案.【详解】解:∵一元二次方程260x x a −+=无实数根,∴()2246410b ac a ∆−−−⨯⨯==<,解得:>9a ,只有选项A 符合题意,故选:A .【点睛】本题考查的是一元二次方程根的判别式,掌握一元二次方程根的判别式是解题的关键. 6.(2023·河南商丘·统考三模)方程229x x −=的根的情况是( ) A .有两个相等的实数根 B .没有实数根 C .有一个实数根 D .有两个不相等的实数根 【答案】D【分析】根据一元二次方程根的判别式进行判断即可求解.【详解】解:∵229x x −=,即2290x x −−=,1,2,9a b c ==−=−,∴24436400b ac ∆=−=+=>,∴方程229x x −=有两个不相等的实数根,故选:D .【点睛】本题考查了一元二次方程20ax bx c ++= (0a a b c ≠,,,为常数)的根的判别式24b ac ∆=−,理解根的判别式对应的根的三种情况是解题的关键.当0∆>时,方程有两个不相等的实数根;当Δ0=时,方程有两个相等的实数根;当Δ0<时,方程没有实数根.7.(2022秋·江苏镇江·九年级校考阶段练习)已知关于x 的一元二次方程210x bx +−=的较大的一根小于1,则实数b 的取值范围是( ) A .一切实数 B .2b >C .1b >D .0b >【答案】D【分析】用公式法求出方程的解,根据题意得出关于b 的不等式,解不等式可得答案.【详解】解:解方程210x bx +−=得:x =,∵一元二次方程210x bx +−=的较大的一根小于1,∴1<,2b +,两边平方得:2244b b b +<+4+,∴0b >, 故选:D .【点睛】本题考查了公式法解一元二次方程,能够根据题意得出关于b 的不等式是解题的关键. 8.(2022·浙江·九年级自主招生)满足方程22419151x xy y −+=的整数对(),x y 有( ) A .0对 B .2对 C .4对 D .6对【答案】C【分析】利用一元二次方程有解判断出y 的范围,根据y 是整数求出y 的值,进而求出x 的值,利用x 也是整数判断即可得出结论. 【详解】解:原方程可化为()224191510x yx y −+−=,∵方程22419151x xy y −+=有实数根,∴()222164191516041510y y y ∆=−−=−+⨯≥,∴21511101515y ≤=,∵y 是整数,∴=3y −,2−,1−,0,1,2,3,当0y =时,原方程可化为2151x =,∴x =x 为整数,所以舍去),当1y =时,原方程可化为241320x x −−=,∴2x =±(由于x 为整数,所以舍去),当1y =−时,原方程可化为241320x x +−=,∴2x =−±x 为整数,所以舍去),当2y =时,原方程可化为28750x x −−=,∴4x =x 为整数,所以舍去),当=2y −时,原方程可化为28750x x +−=,∴4x =−x 为整数,所以舍去),当3y =时,原方程可化为212200x x −+=,∴2x =或10x =,当=3y −时,原方程可化为212200x x ++=,∴2x =−或10x =−,∴原方程的整数解为:23x y =⎧⎨=⎩或103x y =⎧⎨=⎩或23x y =−⎧⎨=−⎩或103x y =−⎧⎨=−⎩,即:方程22419151x xy y −+=的整数对(),x y 为()2,3、()10,3、()2,3−−,()10,3−−共四对,故选:C .【点睛】此题是非一次不定方程,主要考查了一元二次方程的有整数根问题.解题的关键是将原方程变形,利用判别式求解.二、填空题9.(2023·上海杨浦·统考三模)如果关于x 的方程220x x m −+=有两个相等的实数根,那么m 的值是________. 【答案】1【分析】利用一元二次方程根的判别式求解即可.【详解】解:∵关于x 的一元二次方程220x x m −+=有两个相等的实数根,∴()2240m ∆=−−=,解得1m = 故答案为:1.【点睛】本题主要考查了一元二次方程根的判别式,对于一元二次方程()200ax bx c a ++=≠,若240b ac ∆=−>,则方程有两个不相等的实数根,若240b ac ∆=−=,则方程有两个相等的实数根,若24<0b ac ∆=−,则方程没有实数根.10.(2023·浙江嘉兴·统考二模)在()240x −+=的括号中添加一个关于x 的一次项,使方程有两个相等的实数根,这个一次项可以是______. 【答案】4x ±【分析】设方程为240x kx −+=,根据方程有两个相等的实数根可知0∆=,据此列式求解即可.【详解】设方程为240x kx −+=,由题意得2160k −=,∴4k =±, ∴一次项为4x ±. 故答案为4x ±.【点睛】本题考查了一元二次方程的根的判别式,熟练掌握根的判别式与根的关系式解答本题的关键.11.(2023·江苏苏州·苏州市第十六中学校考二模)关于x 的一元二次方程()21210m x x −−−=有两个实数根,则实数m 的取值范围是________. 【答案】0m ≥且1m ≠【分析】根据一元二次方程根的判别式0∆≥以及一元二次方程的定义得出10m −≠,即可求解. 【详解】解:依题意()244410b ac m ∆=−=+−≥,且10m −≠,解得:0m ≥且1m ≠, 故答案为:0m ≥且1m ≠.【点睛】本题考查了一元二次方程的定义,一元二次方程根的判别式的意义,熟练掌握一元二次方程根的判别式的定义是解题的关键.12.(2023·山东东营·校考二模)如果关于x 的一元二次方程234x x m ++=有两个不相等的实数根,那么m 的取值范围是________. 【答案】254m <【分析】先把这个一元二次方程变成一般式,再根据一元二次方程根的判别式计算即可.【详解】234x x m ++=,∴2340x x m ++−=.关于x 的一元二次方程234x x m ++=有两个不相等的实数根,∴()2243440b ac m ∆=−=−−>∴4250m −+> ∴254m <.故答案为:254m <.【点睛】本题主要考查了一元二次方程根的判别式,熟练掌握根的判别式性质,准确计算是解本题的关键.13.(2023·四川巴中·校考二模)已知关于x 的一元二次方程()222210x m x m +++−=.两实数根分别为12x x 、,且满足221258x x +=,则实数m 的值为_____________.【答案】2【分析】先由一元二次方程根的判别式得到关于m 的不等式,解不等式即可得到m 的取值范围,再根据根与系数的关系可得:()1222x x m +=−+,2121x x m =−,代入()2221212122x x x x x x +=+−得到关于m 的一元二次方程,解方程并根据(1)中的m 的取值范围即可得到答案.【详解】解:∵关于x 的一元二次方程()222210x m x m +++−=有实数根, ∴()()22242241b ac m m ⎡⎤∆=−=+−−⎣⎦16200m =+≥,解得:54m ≥−,即m 的取值范围是54m ≥−;∵由根与系数的关系可得:()21212221x x m x x m +=−+=−,,∴()2221212122x x x x x x +=+−()()222221m m ⎡⎤=−+−−⎣⎦221618m m =++,∵221258x x +=,∴22161858m m ++=,即28200m m +−=,∴()()2100m m −+=,解得110m =−或22m =,∵54m ≥−,∴2m =, 故答案为:2.【点睛】此题考查一元二次方程根的判别式和根与系数关系,准确计算是解题的关键.三、解答题【答案】1x =,2x =【分析】用公式法解此方程即可.250x −+=a ==5b −,c =()224=540b ac −−−>x此方程的解为:1x =,2x =【点睛】此题考查的是用公式法解一元二次方程,解题的关键是掌握公式法解方程的步骤. 15.(2022秋·青海西宁·九年级校考期中)解方程:27180x x −−=(公式法) 【答案】129,2x x ==−【分析】利用公式法解答,即可求解.【详解】解:27180x x −−=,∵1,7,18a b c ==−=−, ∴()()2741181210∆=−−⨯⨯−=>,∴7711212x ±==⨯,∴129,2x x ==−.【点睛】本题主要考查解一元二次方程,熟练掌握解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,是解题的关键.16.(2023春·北京西城·九年级北师大实验中学校考阶段练习)已知关于x 的一元二次方程2(4)(21)0m x m x m ---+=有两个不相等的实数根.(1)求m 的取值范围;(2)当m 取满足要求的最小正整数时,求方程的解. 【答案】(1)112m >−且4m ≠(2)1x ,2x【分析】(1)根据方程有两个不相等的实数根,则根的判别式()()22421440b ac m m m ∆=−=−−−−>⎡⎤⎣⎦,且40m −≠,求出m(2)得到m 的最小整数,利用公式法解一元二次方程即可.【详解】(1)一元二次方程2(4)(21)0m x m x m ---+=有两个不相等的实数根,∴()()22421440b ac m m m ∆=−=−−−−=>⎡⎤⎣⎦,且40m −≠,即224414160m m m m +−−+>,且40m −≠,解得:112m >−且4m ≠;(2)m 满足条件的最小正整数是1m =,此时方程为2310x x −−+=,x ==解得:1x ,2x =【点睛】本题考查了一元二次方程根的判别式,公式法解一元二次方程,熟练掌握一元二次方程()200ax bx c a ++=≠的根与判别式24b ac ∆=−的关系是解答本题的关键.17.(2023·北京西城·校考模拟预测)关于x 的一元二次方程()2320x m x m −+++=.(1)求证:方程总有两个实数根;(2)若方程的两个实数根都是正整数,求m 的最小值. 【答案】(1)见解析 (2)1−【分析】(1)先求出一元二次方程根的判别式为()21m ∆=+,即可证明结论;(2)根据题意得到1212x x m ==+,是原方程的根,根据方程两个根均为正整数,可求m 的最小值. 【详解】(1)证明:由()2320x m x m −+++=得,()()()222342211m m m m m ∆=−+−+=++=+⎡⎤⎣⎦,∵()210m +≥,∴方程总有两个实数根; (2)∵()2320x m x m −+++=,∴()()120x x m −−+=⎡⎤⎣⎦,∴1212x x m ==+,,∵方程的两个实数根都是正整数, ∴21m +≥. ∴1m ≥−.∴m 的最小值为1−.【点睛】本题考查的是根的判别式及解一元二次方程,在解答(2)时得到方程的两个根是解题的关键. 18.(2018秋·广东清远·九年级统考期末)不解方程,判断方程22410x x −−=的根的情况. 【答案】有两个不相等的实数根【分析】先求一元二次方程的判别式,由∆与0的大小关系来判断方程根的情况. 【详解】解:∵2a =,4b =−,1c =− ∴()()2244421240b ac ∆=−=−−⨯⨯−=>∴原方程有两个不相等的实数根.【点睛】此题考查一元二次方程根的情况与判别式∆的关系:(1)0∆>,方程有两个不相等的实数根;(2)Δ0=方程有两个相等的实数根;(3)Δ0<方程没有实数根.19.(2023春·河南三门峡·九年级统考阶段练习)已知关于x 的方程2210x x a +−+=没有实数根,试判断关于y 的方程21y ay a ++=实数根的情况,并说明理由. 【答案】一定有两个不相等的实数根.理由见解析.【分析】根据关于x 的方程2210x x a +−+=没有实数根,求出a 的求值范围;再表示关于y 的方程21y ay a ++=,()()222412a a a ∆=−−=−,即可判断该方程根的情况.【详解】解:∵方程2210x x a +−+=没有实数根,()144140a a ∴∆=−−+=<,<0a ∴,对于关于y 的方程21y ay a ++=,()()222412a a a ∆=−−=−,0a <,()220a ∴−>,即20∆>,∴方程21y ay a ++=一定有两个不相等的实数根.【点睛】本题考查一元二次方程根的判别式,熟练掌握一元二次方程根的判别式与根的情况之间的关系是解题关键.20.(2022秋·四川遂宁·九年级校考期中)对于任意一个三位数k ,如果k 满足各个数位上的数字都不为零,且十位上的数字的平方等于百位上的数字与个位上的数字之积的4倍,那么称这个数为“喜鹊数”.例如:k =169,因为62=4×1×9,所以169是“喜鹊数”.(1)已知一个“喜鹊数”k =100a +10b +c (1≤a 、b 、c ≤9,其中a ,b ,c 为正整数),请直接写出a ,b ,c 所满足的关系式 ;判断241 “喜鹊数”(填“是”或“不是”),并写出一个“喜鹊数” ;(2)利用(1)中“喜鹊数”k 中的a ,b ,c 构造两个一元二次方程ax 2+bx +c =0①与cx 2+bx +a =0②,若x =m是方程①的一个根,x=n是方程②的一个根,求m与n满足的关系式;(3)在(2)中条件下,且m+n=﹣2,请直接写出满足条件的所有k的值.【答案】(1)b2﹣4ac=0;不是;121(2)mn=1(3)121,242,363,484【分析】(1)根据喜鹊数的定义解答即可;(2)根据一元二次方程的定义和根的判别式解答即可;(3)求出m与n互为倒数,又m+n=﹣2,得出m=﹣1,n=﹣1,求出b=a+c,a=c,结合喜鹊数的定义即可得出答案.【详解】(1)∵k=100a+10b+c是喜鹊数,∴b2=4ac,即b2﹣4ac=0;∵42=16,4×2×1=8,16≠8,∴241不是喜鹊数;∵各个数位上的数字都不为零,百位上的数字与个位上的数字之积的4倍,∴十位上的数字的平方最小为4,∵22=4,4×1×1=4,∴最小的“喜鹊数”是121.故答案为:b2﹣4ac=0;不是;121.(2)∵x=m是一元二次方程ax2+bx+c=0的一个根,x=n是一元二次方程cx2+bx+a=0的一个根,∴am2+bm+c=0,cn2+bn+a=0,将cn2+bn+a=0两边同除以n2得:a(1n)2+b(1n)+c=0,∴将m、1n看成是方程ax2+bx+c的两个根,∵b2﹣4ac=0,∴方程ax2+bx+c有两个相等的实数根,∴m=1n,即mn=1;故答案为:mn=1.(3)∵m+n=﹣2,mn=1,∴m =﹣1,n =﹣1,∴a ﹣b+c =0,∴b =a+c ,∵b2=4ac ,∴(a+c )2=4ac ,解得:a =c ,∴满足条件的所有k 的值为121,242,363,484.故答案为:121,242,363,484.【点睛】此题考查了一元二次方程的应用,解题关键是弄清喜鹊数的定义.【答案】(1)m=0或m=1(2)m=0或m=1【分析】(1)把x=2代入方程22(23)320x m x m m −++++=得到关于m 的一元二次方程,然后解关于m 的方程即可;(2)先计算出判别式,再利用求根公式得到12x m =+,21x m =+,则AC=m+2,AB=m+1.因为△ABC 是直角三角形,所以当BC 或AC 为斜边时根据勾股定理分别解关于m 的一元二次方程即可.【详解】(1)解:∵x=2是方程的一个根,∴242(23)320m m m −++++=,∴m=0或m=1;(2)解:∵△=22[(23)]4(32)1m m m −+−++=, ∴x=2312m +±∴12x m =+,21x m =+,∴AB 、AC (AB <AC )的长是这个方程的两个实数根,∴AC=m+2>0,AB=m+1>0.∴m>-1.∵△ABC 是直角三角形,∴当BC 为斜边时,有222(2)(1)m m +++=,解这个方程,得13m =−(不符合题意,舍去),20m =;当AC 为斜边时,有222(1)(2)m m ++=+,解这个方程,得1m =.综上所述,当m=0或m=1时,△ABC 是直角三角形.【点睛】此题考查了解一元二次方程和直角三角形的判定,解题的关键是掌握公式法解一元二次方程,熟练运用勾股定理进行分类讨论.【答案】(1)241不是“快乐数”;最大的“快乐数”为999(2)333【分析】(1)根据“快乐数”的定义解答即可;(2)根据“快乐数”可得出2a cb +=,根据一元二次方程根的情况可得2b ac =,再结合710a b c ≤++≤及1a ≤、b 、9c ≤,a 、b 、c 为自然数可得出a 、b 、c 的值,最后结合“快乐数”的定义即可得出答案.【详解】(1)解:∵2142+≠,∴241不是“快乐数”,∵各个数位上的数字都不为零,且十位上的数字等于百位上的数字与个位上的数字的平均数,各个数位上的数字最大为9,又∵9992+=,∴最大的“快乐数”为999.(2)∵10010k a b c =++为“快乐数”, ∴2a cb +=,∵关于x 的一元二次方程220ax bx c ++=有两个相等的实数根,∴()2240b ac −=,即2b ac =, ∴2271019a c b b ac a b c a b c +⎧=⎪⎪⎪=⎨⎪≤++≤⎪≤≤⎪⎩、、,解得:3a =,3b =,3c =,∴1001010031033333k a b c =++=⨯+⨯+=,综上所述,满足条件的所有k 的值为333.∴满足条件的所有k 的值为333.“快乐数”的定义. )已知在ABC 中,问题探究:(2)如图,将正方形CDEF问题拓展:(3)将正方形CDEF 绕点C 旋转一周,当=45ADC ∠︒时,若3AC =,1CD =,请直接写出线段AH 的长.【答案】(1)BF AD =,BF AD ⊥,理由见解析;(2)见解析;(3)2或【分析】(1)根据正方形的性质和全等三角形的判定证明()SAS BCF ACD ≌△△,得出BF AD =,FBC DAC ∠=∠,再利用角的代换得到90AHF ∠=︒,即可得到结论;(2)先证明()SAS BCF ACD ≌△△,得出CBK CAH ∠=∠,进而证明()SAS BCK ACH ≌△△,得到CK CH =,BCK ACH ∠=∠,进一步即可证明KCH 是等腰直角三角形,于是可得HK =,然后利用线段间的代换即可证得结论;(3)分两种情况:①当A ,()H F ,D 三点共线时,=45ADC ∠︒;②当B ,()D H ,F 三点共线时,=45ADC ∠︒;设AH x =,在Rt ABH △中根据勾股定理列出关于x 的方程,解方程即可求出结果.【详解】解:(1)BF AD =,BF AD ⊥;理由如下:∵四边形CDEF 是正方形,∴CF CD =,90FCD ∠=︒,在BCF △和ACD 中,,90,,BC AC BCF ACD CF CD =⎧⎪∠=∠=︒⎨⎪=⎩∴()SAS BCF ACD ≌△△, ∴BF AD =,FBC DAC ∠=∠,∵90BFC FBC ∠+∠=︒,BFC AFH ∠=∠,∴90AFH DAC ∠+∠=︒,∴90AHF ∠=︒,∴BF AD ⊥;(2)证明:如图,在线段BF 上截取BK AH =,连接CK ,∵四边形CDEF 是正方形,∴CF CD =,90FCD ACB ∠=︒=∠,∴ACD BCF ∠=∠,∴()SAS BCF ACD ≌△△,∴CBK CAH ∠=∠,在BCK 和ACH 中,,,,BC AC CBK CAH BK AH =⎧⎪∠=∠⎨⎪=⎩∴()SAS BCK ACH ≌△△, ∴CK CH =,BCK ACH ∠=∠,∴90KCH BCA ∠=∠=︒,∴KCH 是等腰直角三角形,∴HK ,∴BH AH BH BK KH −=−=;(3)分两种情况:①如图,当A ,()H F ,D 三点共线时,=45ADC ∠︒;同理可证明:BH AD =,BH AD ⊥,且1CD CF ==,FD =∵3BC =,∴AB =设AH x =,则BH AD x ==在Rt BAH 中,∵222BH AH AB +=,∴((222x x +=,解得x =或x =(舍去);②如图,当B ,()D H ,F 三点共线时,=45ADC ∠︒,设AH x =,∵BF AH =,∴BH AH HF x =−=在Rt ABH △中,∵222BH AH AB +=,∴((222x x +=,解得x =或x =(舍去);综上所述,线段AH 的长为2或.【点睛】本题考查了正方形的性质、全等三角形的判定和性质、勾股定理以及一元二次方程的求解等知识,属于常考题型,正确添加辅助线、证明三角形全等是解题的关键.。
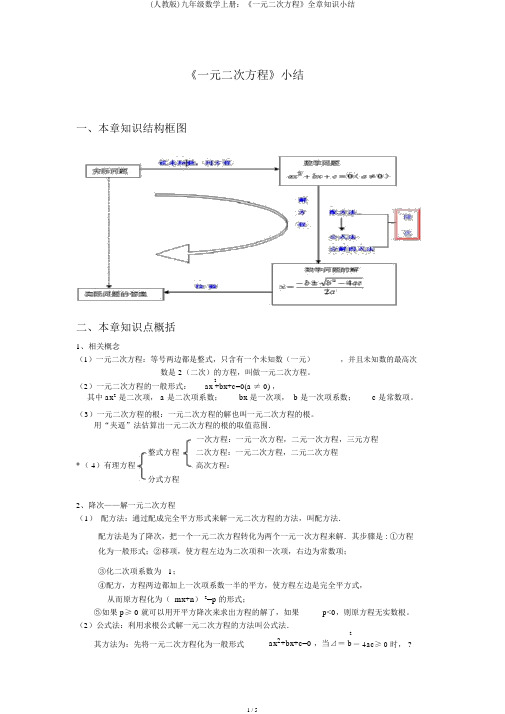
《一元二次方程》小结一、本章知识结构框图二、本章知识点概括1、相关概念(1)一元二次方程:等号两边都是整式,只含有一个未知数(一元)数是 2(二次)的方程,叫做一元二次方程。
2(2)一元二次方程的一般形式:ax +bx+c=0(a ≠ 0) ,,并且未知数的最高次其中 ax2是二次项, a 是二次项系数;bx 是一次项, b 是一次项系数; c 是常数项。
(3)一元二次方程的根:一元二次方程的解也叫一元二次方程的根。
用“夹逼”法估算出一元二次方程的根的取值范围.一次方程:一元一次方程,二元一次方程,三元方程整式方程二次方程:一元二次方程,二元二次方程* ( 4)有理方程高次方程:分式方程2、降次——解一元二次方程(1)配方法:通过配成完全平方形式来解一元二次方程的方法,叫配方法.配方法是为了降次,把一个一元二次方程转化为两个一元一次方程来解.其步骤是 : ①方程化为一般形式;②移项,使方程左边为二次项和一次项,右边为常数项;③化二次项系数为 1;④配方,方程两边都加上一次项系数一半的平方,使方程左边是完全平方式,从而原方程化为( mx+n)2=p 的形式;⑤如果 p≥ 0 就可以用开平方降次来求出方程的解了,如果p<0,则原方程无实数根。
(2)公式法:利用求根公式解一元二次方程的方法叫公式法.其方法为:先将一元二次方程化为一般形式2- 4ac≥ 0时, ? ax2+bx+c=0 ,当⊿= b将 a、 b、 c 代入求根公式x=bb2 4ac2≥ 0)就得到方程的根.2a( b -4ac(3)分解因式法:先因式分解使方程化为两个一次式的乘积等于0 的形式,再使这两个一次式分别等于 0, 从而降次.这种解法叫做因式分解法.步骤是:①通过移项将方程右边化为0;②通过因式分解将方程左边化为两个一次因式乘积;③令每个因式等于 0,得到两个一元一次方程;④解这两个一元一次方程,得一元二次方程的解。
3、一元二次方程根的判别式22(1)⊿= b -4ac 叫一元二次方程ax +bx+c=0(a ≠ 0) 的根的判别式。