2016年湖南省普通高等学校对口招生考试数学试卷

湖南省2016年普通高等学校对口招生考试数学(对口)试题一. 选择题(本大题共10小题, 每小题4分, 共40分, 在每小题给出的四个选项中, 只有一项是符合题目要求的)1. 设全集U ＝{1, 2, 3, 4, 5}, A ＝{1, 2}, B ＝{5}, 则( U A)∪B ＝( )A. {5}B. {3, 4, 5}C. {3, 4}D. {1, 2, 5} 2. 函数f (x )＝⎝⎛⎭⎫12x＋2, x ∈[－1, 2]的最大值为( )A. 4B. 3C. 52D. 943. “x ＜－1或x ＞2”是“x ＜－1”的( )A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件 4. 不等式|2x ＋1|＞5的解集为( )A. {x |x ＞2}B. {x |x ＜－3}C. {x |－3＜x ＜2}D. {x |x ＜－3或x ＞2} 5. 已知向量→a ＝(2, 3), →b ＝(1, m ), 且→a ∥→b , 则m ＝( )A. 3B. －32C.32D. – 36. 已知cos α＝45, α∈(－π2, 0), 则tan α＝( )A. 35B. －43C. －34D. 437. 已知定义在R 上的奇函数f (x ), 当x ＞0时, f (x )＝x 2＋2x , 则f (－1)＝( )A. 3B. 1C. －1D. －3 8. 设a ＝1. 70. 3, b ＝log 30. 2, c ＝0. 25, 则( )A. a ＜b ＜cB. b ＜a ＜cC. c ＜b ＜aD. b ＜c ＜a9. 已知点P (4, 5), 点Q 在圆C ：(x －1)2＋(y －1)2＝4上运动, 则|PQ |的取值范围为( )A. [1, 7]B. [1, 9]C. [3, 7]D. [3, 9] 10. 已知a , b , c 为三条不重合的直线, 给出下面三个命题：①若a ⊥b , a ⊥c 则b ∥c ；②若a ⊥b , a ⊥c 则b ⊥c ；③若a ∥b , b ⊥c , 则a ⊥c , 其中正确的命题为( )A. ③B. ①②C. ①③D. ②③ 二. 填空题：(本大题共5小题, 每小题4分, 共20分)11. 袋中有6个红色球, 3个黄色球, 4个黑色球, 从袋中任取一个球, 则取到的球不是．．黑色球的概率为____________12. 已知数列{a n }的前n 项和S n ＝n 2＋2n , 则a 2＝___________13. 若不等式x 2＋x －c ≤0的解集为{x |－2≤x ≤1}, 则c ＝________14. 6位同学站成一排照相, 其中甲, 乙两人必须相邻, 共有__________种不同的排法(用数字作答) 15. 已知A, B 为圆x 2＋y 2＝1上的两点, |AB|＝3, O 为坐标原点, 则→AB ⋅→O A ＝_____________三. 解答题：(本大题共7小题, 其中第21, 22小题为选做题. 满分60分, 解答应写出文字说明, 证明过程或演算步骤)16. (本小题满分10分) 已知函数f (x )＝log 2(x －2). (I )求f (x )的定义域；(II )若f (m )＋f (m －1)＝1, 求m 的值. 17. (本小题满分10分)在△ABC 中, 内角A, B, C 的对边分别为a , b , c , 已知a ＝3, b ＝23, A ＝π3.(I )求sinB 的值； (II )求sin ⎝⎛⎭⎫π2＋B 的值.18. (本小题满分10分)已知各项均为正数的等比数列{a n }中, a 1＝1, a 3＝3. (I )求{a n }的通项公式；(II )设{a n }的前n 项为S n , 且S n ＝13(3＋1), 求n 的值. 19. (本小题满分10分)如图, 在三棱柱ABC －A 1B 1C 1中, AA 1⊥底面ABC, AA 1＝3, AB ＝AC ＝1, AB ⊥AC. (I )证明：BA ⊥平面ACC 1A 1；(II )求直线B 1C 与平面ACC 1A 1所成的角的正弦值.20. (本小题满分10分)已知椭圆C ：x 2a 2＋y 24＝1(a ＞2)的离心率e ＝53.(I )求椭圆C 的方程；(II )设直线l ：y ＝kx －53与椭圆C 相交于A, B 两点, 且AB 中点的横坐标为1, 求k 的值. 选做题：请考生在第21, 22题中行选择一题作答. 如果两题都做, 则按所做的第21题计分. 作答时, 请写清题号. 21. (本小题满分10分)已知复数Z ＝1＋a i (a ∈R ), 且|Z |＝2. (I )求a 的值；(II )若a ＞0且Z n ∈R (n ∈N ＋且n ≤12), 求n 的所有值. 22. (本小题满分10分)某厂生产甲, 乙两种产品, 每件甲产品的销售收入为1500元, 每件乙产品的销售收入为1000元, 这两种产品都需要经过A, B 两种设备加工, 在A, B 设备上加工1件甲产品所需工作时数分别为2h , 4h , 加工1件乙产品所需工作时数分别为4h , 2h . 若A, B 两种设备每月工作时数分别不超过200h , 250h , 则每月生产甲, 乙两种产品各多少件, 才能使销售收入最大.参考答案： 1. B 2. A 3. BC 1A 1B 1B AC4. D5. C6. C7. D8. D9. C 10. A 11.91312. 5 13. 2 14. 240 15. －3216. 解：(I ) 由题意知：x －2＞0 解得：x ＞2∴ f (x )的定义域为(2, ＋∞)(II ) 首先由f (m )与f (m －1)有意义，则：m ＞3又∵ f (m )＋f (m －1)＝1, ∴ log 2(m －2)＋log 2(m －3)＝1 即：log 2[(m －2)(m －3)]＝1得：(m －2)(m －3)＝2, 即：m 2－5m ＋4＝0 解得：m ＝1或m ＝4综上所述知：m 的值为4.17. 解：(I ) 由正弦定理知：sinB ＝b sinA a ＝23sinπ33＝13.(II ) ∵ sinB ＝13, 又由b ＜a 知B ＜A, ∴ B 是锐角∴ cosB ＝1－sin 2B ＝1－(13)2＝223∴ sin ⎝⎛⎭⎫π2＋B ＝cosB ＝22318. 解：(I ) ∵ a 3＝a 1q 2, ∴ q 2＝3,又因为此等比数列各项都为正，∴ q ＝3,∴ a n＝a 1q n －1＝(3)n －1＝3n －12即数列{a n}的通项公式为a n＝3n －12.(II ) ∵ S n＝a 1(1－q n)1－q ＝1－(3)n1－3＝13(3＋1)∴ 1－(3)n＝－26, 即：3n2＝27＝33,∴ n ＝619. 解：(I ) ∵ A 1A ⊥底面ABC, ∴ A 1A ⊥AB,又AB ⊥AC 且AC ∩AA 1＝A ∴ AB ⊥平面ACC 1A 1.(II ) ∵ AB ⊥平面ACC 1A 1, BA ∥B 1A 1,∴ B 1A 1⊥平面ACC 1A 1, 连结A 1C, 则A 1C 是B 1C 在平面ACC 1A 1内的射影 ∴ ∠B 1C A 1是直线B 1C 与平面ACC 1A 1所成的角由AB ＝AC ＝1, AB ⊥AC 得BC ＝2, 又BB 1＝AA 1＝3, ∴ B 1C ＝5, 由AC ＝1, AA 1＝3得A 1C ＝2∴ 在△B 1C A 1中，由余弦定理得：cos ∠B 1C A 1＝B 1C 2＋A 1C 2－A 1B 212B 1C ⋅A 1C ＝5＋4－12×5×2＝25＞0∴ ∠B 1C A 1是锐角，∴ sin ∠B 1C A 1＝1－cos 2∠B 1CA 1＝55. 故直线B 1C 与平面ACC 1A 1所成的角的正弦值为55. 20. 解：(I ) 由题意知：⎩⎪⎨⎪⎧c a ＝53a 2－4＝c2，解之得：⎩⎨⎧a ＝3c ＝5∴ 椭圆C 的方程为x 29＋y24＝1.(II ) 设A(x 1,y 1),B(x 1,y 1),由⎩⎨⎧y ＝kx －53x 29＋ y 24＝1消去y 得：(4＋9k 2)x 2－30kx －11＝0,则由韦达定理知：x 1＋x 2＝30k4＋9k2, 又由题意知：x 1＋x 2＝2 ∴30k 4＋9k2＝2, 解之得：k ＝13或k ＝43.即所求的k 的值为13或43.21. 解：(I ) 由题意知：1＋a 2＝2, 解之得：a ＝± 3. ∴ a 的值为3或－ 3.(II ) 若a ＞0,则Z ＝1＋3i ＝2(12＋32i )＝2(cos π3＋i sin π3)∴ Z n＝2n(cos n π3＋i sin n π3), 由Z n∈R 知：sinn π3＝0, ∴ n π3＝k π，即：n ＝3k (k ∈Z ,n ∈N ＋且n ≤12) ∴ n 的所有值分别为3,6,9,12.22. 解：设每月生产甲、乙两种产品各为x 件、y 件，销售收入为Z则目标函数Z ＝1500x ＋1000y , 其满足的约束条件为：⎩⎨⎧2x ＋4y ≤2004x ＋2y ≤250x ≥0y ≥0画出其可行域及目标函数的0等值线如右图：由⎩⎨⎧2x ＋4y ＝1004x ＋2y ＝250解得图中M 点的坐标为M (50,25) 由图可知在x ＝50,y ＝25时， 目标函数有最大值Z max ＝1500×50＋1000×25＝100000(元)答：每月生产甲、乙两种产品各为50件、25件，销售收最大为100000元.。

湖南省2012年普通高等学校对口招生考试数学试题时量120分钟 总分：120分、选择题（本大题共10小题，每小题4分，共40分.在每小题给出的四个选项中，只 有一项是符合题目要求的)1. ...................................................................................................................... 设集合 A=(x | x >1},B={ x |0< x <1}, WJ AU B 等丁 ............................... () A.( x | x >0} B.{ x | x 丰 1} C.{ x | x >0 或x 丰 1}D.{ x | x >0且 x 丰 1}2. “ x 3 ” 是” x 2 9 ” 的 ............................................. ()A.充分不必要条件 D.既不充分也不必要条件3. .................................................................................................................... 不等式|2 x -3|>1的解集为 ..................................................... () A.(1,2)B.(- 8,1)U (2,+ 8)C.(- 8,1)D.(2,+ 8)4. ................................................................................ 已知 tan a =-2,贝U ^^~~22a)=cos aA. 4B. 2C. -2 抛掷一枚骰子，朝上的一面的点数大丁 3的概率为A. 1B. 1C.-6326. 若直线x y k 0过加圆x 2 y 2 2x 4y 7 0的圆心，则实数k 的值为........................................................................................................... () A. -1 B. -2 C. 1 D. 2 7. 已知函数f(x) =sinx, ............................................... 若e m =2,则f(m)的值为 () A. sin2B. sineC. sin(ln2)D. ln(sin2)8. 设a ,b,c 为三条直线，a , 6为两个平■面，则下列结论中正确的是• • •（） A.若 a ± b, b ± c ,则 a II c B.若 a ?也,b?6, a II b, WJ a // p C.若 a // b, b? a ，则 a //a D.若 aLa, b // a,则 b ± a9. 将5个培训指标全部分配给三所学校，每所学校至少有一个指标，则不同的分配方、填空题（本大题共5个小题,每小题4分,共20分.将答案填在答题卡中对应题号 后机密★启用前B.必要不充分条件C.充分必要条件D. -45. 案有（） A. 5种2210.双曲线L J916B. 6种C. 10 种 1的一个焦点到其渐近线的距离为A, 16 B. 9 C. 4D. 12 种 .............. ()D. 3的横线上）11. 已知向量a =(1,-1), b=(2,y).若a // b ,则y= .12. 某校高一年级有男生480人，女生360人，若用分层抽样的方法从中抽取一个容量为21的样本，则抽取的男生人数应为.13. 已知球的体积为七，则其表面积为^314. (x+ M)9的二项式展开式中的常数项为.( 用数字作答)x15. 函数f(x)=4 x-2x+1的值域为.三、解答题(本大题共7小题，其中第21,22小题为选做题,共60分.解答应写出文字说明或演算步骤))16. (本小题满分8分)已知函数f(x)=lg(1 - x2).(1)求函数f(x)的定义域；(2)判断f(x)的奇偶性，并说明理由.17. (本小题满分10分)uuu uuu已知a, b是不共线的两个向量.设AB =2a+b , BC =- a-2b .uuur uuu uuu(1)用a, b 表示AC ；(2)若|a|=|b|=1,< a , b >=60o,求AB BC .18. (本小题满分10分)设( a n｝是首项a〔=2,公差不为0的等差数歹U ,且a〔, a3, a、成等比数歹U ,(1) 求数列｛a n｝的通项公式；(2) 若数列｛b n｝为等比数列，且bi =a〔, a2 = b3,求数列｛b n｝的前n项和S n.19. (本小题满分10分)某射手每次射击命中目标的概率为2,且各次射击的结果互不影响.假设3该射手射击3次，每次命中目标得2分,未命中目标得-1分.记X为该射手射击3 次的总得分数.求(1) X的分布列；(2) 该射手射击3次的总得分数大丁0的概率.20. (本小题满分10分)x2 V2 6 4 , 一，已知点A 2,0是椭圆C:-y & 1(a b 0)的一个顶点，点B(—,—)在C上. a2 b2 5 5(1) 求C的方程；(2) 设直线l与AB平行，且l与C相交丁P,Q两点.若AP垂直AQ,求直线l的方程.四、选做题(注意：第21题(工科类),22题(财经，商贸与服务类)为选做题，请考生选择其中一题作答.)21. (本小题满分12分)已知函数 f (x) sin x , 3 cos x⑴ 将函数V f ( x)(0 3)图象上所有点向右平■移；个单位长度，得到函数g(x)的图象，若g(x)的图象经过坐标原点，求①的值.⑵ 在/\ ABCfr,角A,B,C 所对的边分别为a,b,c,若 f (A) V3 , a =2, b+c=3,求/\ ABC的面积.湖南省2013年普通高等学校对口招生考试数学试卷一、选择题（本大题共10小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合要求的）1.已知集合A= {3,4,5 } , B= {4,5,6 }，贝U A B 等丁A. (3,4,5,6} B{4,5} C. {3,6} D .2.凶数y=x2在其定义域内是A.增函数 B .减函数C.奇函数D.偶函数3. “x=2” 是“（x-1 ）A.充分不必要条件(x-2 ) =0” 的B.必要/、充分条件C.充分必要条件D.既小充分乂不必要条件4.已知点A (m^ -1 )关丁y轴的对称点为1B (3, n),则m n的值分别为A. m=3 n=-1B.m=3 n=1C.m=-3, n=-1D.m=-3, n=15.圆(x+2) 2+ (y-1 )2=9的圆心到直线3x+4y-5=0的距离为A. -B.3C.3D.15__ 4 一6.已知sin = —，且5是第二象限的角，则tan 的值为5 A 34 八43A. —B C D. —43347.不等式x2-2x-3>0的解集为A. (-3 , 1)B.(-,-3) U (1, +)C. (-1 , 3)D.(-，-1) U (3, +)8.在100件产品中有3件次品，其余的为正品。

1湖南省2016年高考理科数学试题（附答案）（满分150分，时间120分）分）第Ⅰ卷一. 选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的.（1）设集合2{|430}A x x x =-+<，{|230}B x x =->，则AB =（A ）3(3,)2-- （B ）3(3,)2- （C ）3(1,)2 （D ）3(,3)2 （2）设(1i)1i x y +=+，其中x ，y 是实数，则i =x y +（A ）1 （B ）2 （C ）3 （D ）2 （3）已知等差数列{}na 前9项的和为2727，，10=8a ，则100=a （A ）98 （B ）99 （C ）100 （D ）97（4）某公司的班车在7:007:00，，8:008:00，，8:30发车，小明在7:50至8:30之间到达发车站乘坐班车，且到达发车站的时刻是随机的，则他等车时间不超过10分钟的概率是分钟的概率是 （A ）31 （B ）21 （C ）32 （D ）43（5）已知方程表示双曲线，且该双曲线两焦点间的距离为4，则n 的取值范围是的取值范围是（A ）(0,3) （B ）(–1,3) （C ）(–1,3) （D ）(0,3) （6）如图，某几何体的三视图是三个半径相等的）如图，某几何体的三视图是三个半径相等的圆及圆及 每个圆中两条相互垂直的半径每个圆中两条相互垂直的半径每个圆中两条相互垂直的半径..若该几若该几 何体的体积是，则它的表面积是何体的体积是，则它的表面积是 （A ）20π （B ）18π （C ）17π （D ）28π（7）函数y =2x 2–e |x |在[–2,2]2,2]的图像大致为的图像大致为的图像大致为（A ） （B ）（C ） （D ）（8）若101a b c >><<，，则，则（A ）log log b a a c b c < （B ）c cab ba <（C ）c ca b < （D ）log log a b c c <（9）执行右面的程序框图，如果输入的0,1,x y ==n =1,则输出则输出,x y 的值满足的值满足（A ）4y x = （B ）3y x = （C ）2y x = （D ）5y x =(10)以抛物线以抛物线C 的顶点为圆心的圆交C 于A 、B 两点，交C 的标准线于D 、E 两点两点..已知|AB |=42，|DE|=25，则C 的焦点到准线的距离为的焦点到准线的距离为(A)2 (B)4 (C)6 (D)8 (11)(11)平面平面a 过正方体ABCD -A 1B 1C 1D 1的顶点A ，a ////平面平面CB 1D 1，a Ç平面ABCD =m ，a Ç平面ABA 1B 1=n ，则m 、n 所成角的正弦值为所成角的正弦值为(A) 33 (B )22 (C) 32 (D)1312.已知函数()sin()(0),24f x x+x ppw j w j =>£=-，为()f x 的零点，4x p=为()y f x =图像的对称轴，且()f x 在51836p p æöç÷èø，单调，则w 的最大值为的最大值为 （A ）11 11 （B ）9 9 （C ）7 7 （D ）5第II 卷本卷包括必考题和选考题两部分.第(13)题~第(21)题为必考题，每个试题考生都必须作答.第(22)题~第(24)题为选考题，考生根据要求作答. 二、填空题：本大题共4小题，每小题5分 (13) 设向量a=(m a=(m，，1)1)，，b=(1b=(1，，2)2)，且，且，且|a+b||a+b|2=|a|2+|b|2，则m=______.(14) 5(2)x x +的展开式中，的展开式中，x x 3的系数是的系数是__________.__________.__________.（用数字填写答案）（用数字填写答案）（用数字填写答案） （1515）设等比数列）设等比数列满足a 1+a 3=10=10，，a 2+a 4=5=5，则，则a 1a 2…a n 的最大值为的最大值为_________________________________。

湖南省2017年普通高等学校对口招生考试数学试题(附答案)本试题卷包括选择题、填空题和解答题三部分.时量120分钟.满分120分一、选择题（每小题4分，共40分．每小题只有一项是符合题目要求的）1.已知集合{},2,1=A ,{}4,32，=B ,则B A 等于 【答案】DA.{}2 B. {}4,32， C. {}4,3,1 D. {}4,3,2,12.已知32-=a，212=b ，2)21(=c ,则c b a ,,的大小关系为 【答案】BA ．c b a <<B ． b c a <<C ．c a b <<D ． a b c <<3.已知()παα,0,21cos ∈= ，则=αsin 【答案】A A ．23 B ． 23- C ．21 D ．21-4.已知两条直线1)2(2++=-=x a y ax y和互相垂直，则=a 【答案】DA ．2B ． 1C ．0D ．1-5.下列函数中，在区间()+∞,0上单调递增的是 【答案】C A.x ysin = B. x y 1=C. 2x y = D. x y 31log = 6.已知函数)(x f 的定义域为R ，则“)(x f 为偶函数” 是“)1()1(f f =-”的【答案】CA ． 充分必要条件B ． 必要不充分条件C ． 充分不必要条件D ． 既不充分也不必要条件 7.不等式0652<+-x x 的解集是 【答案】DA ．{}2<x x B ．{}3>x x C ．{}32><x x x 或 D ．{}32<<x x8.设m l 、 是两条不同的直线，α是平面，则下列命题正确的是 【答案】B A ．若α⊂⊥m m l,，则α⊥l B ．若l m l //,α⊥，则α⊥mC ．若αα⊂m l ,//，则l m //D ．若αα//,//m l ，则l m //9. 从1,2,3,4,5,6,7,8,9这9个数中取2个不同的数，使其和为偶数，则不同的取法共有A. 72种B. 36种C. 32种D. 16种 【答案】D10．在三棱锥ABC P - 中，PA ，PB ，PC 两两互相垂直，且PA=PB=PC=1 ，则该三棱锥的体积为 【答案】A A ．61 B ．31 C ．21D ．1 二、填空题（本大题共5小题，每小题4分，共20分）11、在一次中学生田径运动会上，参加男子跳高的10名运动员的成绩如下表所示：成绩/m 人数2242则这些运动员成绩的平均数是__________（m ）． 【答案】 12．若直线06=+-y kx 经过圆4)2()122=-+-y x （的圆心，则=k ______． 【答案】4-13．函数()x x f cos 21-=的最小值为 ． 【答案】1-14.若关于x 的不等式32<+b x 的解集为{}03<<-x x ，则=b ．【答案】3 15.若双曲线)0,0(12222>>=-b a by a x 上存在四点A ，B ，C ，D ，使四边形ABCD 为正方形，则此双曲线的离心率的取值范围为 ．【答案】()∞+，2三、解答题（本大题共7小题，其中第21，22题为选做题．满分60分．解答题应写出文字说明、证明过程或演算步骤）16. （本小题满分10分） 已知函数()1)1(),1,0(1)5(log 2=-≠>-+=f a a x x f a 且.（I ）求a 的值，并写出()x f 的定义域；（II ）当[]11,4-∈x 时，求()x f 的取值范围．解：（I ）依题意，有：()11)51(log 21=-+-=-a f ，解得：4=a ，由505->>+x x 得∴4=a ，()x f 的定义域为），（∞+-5（II ）由（1）得：()1)5(log 24-+=x x f ∵4>1,∴()1)5(log 24-+=x x f 为增函数，而314116log 2)11(,111log 2)4(44=-=-=-=-=-f f∴当[]11,4-∈x 时，()x f 的取值范围为[]3,1-．17. （本小题满分10分）某射击运动员射击3次，每次射击击中目标的概率为32，求： （I ）3次射击都击中目标的概率； （II ）击中次数ξ的分布列．解：（I ）278323)3(==）（P（II ）随机变量ξ的分布列为：18. （本小题满分10分）已知数列{}n a 为等差数列，若1231,1a a a a +==，求： （I ）求数列{}n a 的通项公式；（II ）设na nn a b )21(+=，求数列{}n b 的前n 项和n S ． 解：（I ）设数列{}n a 的首项为1a ，公差为d ，依题意，有：⎩⎨⎧==⇒⎩⎨⎧++=+=,1,12111111d a a d a d a a ∴n d n a a n =-+=)1(1∴数列{}n a 的通项公式为n a n =；（II ）n an n a b )21(+==nn ）（21+∴n nn n n n n ⎪⎭⎫ ⎝⎛-++=-⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-++=21221211211212)1(S 2）（19. （本小题满分10分）ξ 0 1 2 3P271 92 94 278已知向量),1(m a =，向量)3,2(=b（I ）若b a //，求m 的值； （II ）若b a ⊥，求)3()3a b a-⋅（的值．解：（1）由b a //得：32=m ，23=∴m（2）由b a⊥得023=+m 32-=∴m∴ ），（（3213)3-=a =），（23- ）（），（）（5,1233,2)3(-=--=-a b ∴135213)3()3-=⨯-+-⨯=-⋅）（）（（a b a20. （本小题满分10分）已知抛物线px y C 2:2=的焦点为().0,2F（I ）求抛物线C 的方程；（II ）过点M （1,2）的直线l 与C 相交于B A ,两点，且M 为AB 的中点，求直线l 的方程． 解：（I ）∵抛物线px y C 2:2=的焦点为()0,2F ，∴22=p，解得4=p ， 故抛物线C 的方程为：x y82=；（2）设)A 11y x ，（、)B 22y x ，（ ，则依题意有422121=+=+y y x x ，易知若直线l 的斜率不存在，则直线方程为1=x ，此时4021≠=+y y ，不合题意，由⎪⎩⎪⎨⎧==22212188x y x y 得：)(8212221x x y y -=- 即2121218y y x x y y +=-- ∴2488212121==+=--==y y x x y y k k AB l∴ 直线l 的方程为02=-y x注意：第21题，22题为选做题，请考生选择其中一题作答． 21．（本小题满分10分）已知c b a ,,，分别为△ABC 内角A ，B ，C 的对边，已知ab c22=，（I ）若 90=C ，且1=a ，求ABC ∆的面积； （II ）若C A sin sin =，求C cos 的值解：（I ）由 90=C，且1=a ，则222c b a =+，又ab c 22=∴0122=+-b b ，解得1=b ∴2121S ==∆ab ABC （II ）由正弦定理caC A C c A a =⇒=sin sin sin sin ， 又C A sin sin =， ∴c a =，又ab c22= ∴b c a 2==4122cos 2222==-+=ab b ab c b a C 由余弦定理得：22．某公司有40万元资金，计划投资甲、乙两个项目，按要求对项目甲的投资不小于对乙项目投资的31倍，且对每个项目的投资都不能低于5万元。

（完整）湖南省2016年普通⾼等学校对⼝招⽣考试计算机应⽤类专业综合知识试题湖南省2016年普通⾼等学校对⼝招⽣考试科⽬：计算机应⽤类综合（试题卷）注意事项：1.答题前，考⽣务必将⾃⼰的姓名、准考证号写在答题卡和本试题卷的封⾯上，并认真核对答题卡条形码上的姓名、准考证号和科⽬。

2.选择题和⾮选择题均须在答题卡上作答，在本试题卷和草稿纸上作答⽆效。

考⽣在答题卡上按如下要求答题：(1)选择题部分，⽤2B铅笔将答案填涂在题号下选项所对应的⽅框内，修改时⽤橡⽪摖⼲净，不留痕迹。

(2)⾮选择题部分，按题号⽤0.5毫⽶⿊⾊墨⽔签字笔书写，否则作答⽆效。

(3)请勿折叠答题卡，并保持字体⼯整、笔迹清晰、卡⾯清洁。

3.本试题卷共18页，如缺页，考⽣须及时报告监考⽼师，否则后果⾃负。

4.考试结束时，将本试题卷和答题卡⼀并交回。

机密★启⽤前湖南省2016年普通⾼等学校招⽣考试计算机应⽤类专业综合知识试题本试题卷共六⼤题，39⼩题，共18页。

时量150分钟，满分390分。

⼀、单选题（在本题的每⼀⼩题的备选答案中，只有⼀个答案是正确的，本⼤题共22⼩题，每⼩题5分，共110分）1.为了在资源管理器中快速浏览.DOC类⽂件，最快速的显⽰⽅式是A.按名称B.按类型C.按⼤⼩D.按⽇期2.下列各种进制的数中，最⼩的数是A.⼗进制数44B.⼋进制数52C.⼗六进制数2BD.⼆进制数1010013.为解决各类应⽤问题⽽编写的程序，例如学⽣档案管理系统，称为A.系统软件B.⽀撑软件4.在Windows系统中，当程序长时间⽆响应时，能较好地结束该程序的⽅法是A.按“Ctrl+Alt+Del”键，然后选择该程序，执⾏“结束任务”B.按“Shift+Alt+Del”键，然后选择该程序，执⾏“结束任务”C.按“Shift+Ctrl+Backspace”键，然后选择该程序，执⾏“结束任务”D.按“Alt+Shift+Backspace”键，然后选择该程序，执⾏“结束任务”5.在Windows回收站中，可以恢复A.从硬盘中删除的⽂件或⽂件夹B.从U盘中删除的⽂件或⽂件夹C.剪切掉的⽂档D.从光盘中删除的⽂件或⽂件夹6.在Word菜单右边有“…”符号，表⽰A.该命令不能执⾏B.单击该命令后，会弹出⼀个对话框C.该命令⼰执⾏D.该命令后有下⼀级⼦菜单7.当⽤户输⼊的⽂字中出现拼写错误时，Word会在⽂字下⾯标注A.红⾊直线B.红⾊波浪线C.绿⾊直线D.绿⾊波浪线8.在Excel中，利⽤填充柄可以将数据复制到相邻单元格中，若选择含有数值的左右相邻的两个单元格，左键拖动填充柄，则数据将以填充。

湖南省2016年普通高等学校对口招生考试科目：计算机应用类综合（试题卷）注意事项：1.答题前，考生务必将自己的姓名、准考证号写在答题卡和本试题卷的封面上，并认真核对答题卡条形码上的姓名、准考证号和科目。

2.选择题和非选择题均须在答题卡上作答，在本试题卷和草稿纸上作答无效。

考生在答题卡上按如下要求答题：（1）选择题部分，用2B铅笔将答案填涂在题号下选项所对应的方框内，修改时用橡皮擦干净，不留痕迹。

（2）非选择题部分，按题号用0.5毫米黑色墨水签字笔书写，否则作答无效。

（3）请勿折叠答题卡，并保持字体工整、笔迹清晰、卡面清洁。

3.本试题卷共18页，如缺页，考生须及时报告监考老师，否则后果自负。

4.考试结束时，将本试题卷和答题卡一并交回。

姓名准考证号祝你考试顺利！机密★启用前湖南省2016年普通高等学校对口招生考试机电类专业综合知识试题本试题卷共六大题，共11页。

时量150分钟，满分90分。

一、单选题（在本题的每一小题的备选答案中，只有一个答案是正确的，多选不给分。

本大共22小题，每小题5分，共110分）1.不可见轮廓线的线型是A.粗实线B.虚线C.细实线D.点划线2.20±0.025的公差范围为A.+0.025B.-0.025C.0.05D.03.在AutoCAD中，CIRCLE命令中的TTR选项表示的画圆弧方式是A.端点，端点，直径B.端点、端点、半径C.切点、切点、直径D.切点、切点、半径4.在AutoCAD中不能应用修剪命令TRIM进行修时的对象是A.圆弧B.圆C.直线D.文字5.对于平面力系，设F为合力，M为合力距，下列表示力偶系的是A.F=0，M=0B.F≠0，M=0C.F=0，M≠0D.F≠0，M≠06.自行车处于静止状态时，其车轮轴主要承受的载荷类型是A.拉压力B.剪切力C.力偶D.转距7.AC杆受力如图1所示，分别在截面B和载面C上施加30KN和80KN的轴向力后，其横截面上的最大轴力为A.30kNB.80kNC.110kND.50KN8.如图2所示，矩形截面梁高宽比为1:2，竖直放置时的承载能力是扁平放置时的A.2倍B.4倍C.6倍D.8倍9.轴承外圈和箱体配合时，优先采用的配合形式是A.基孔制B.基轴制C.模数制D.参数制10.不锈钢与普通碳素钢相比，主要是其含有较多的A.碳元素B.铅元素C.铬元素D.铜元素11.液压系统的表压力指的是A.绝对压力B.相对压力C.大气压D.真空度12.机床液压驱动系统中，要求液流压力中等，流量和压力脉动小，输送均匀，工作平稳可靠，则应选择的泵是A.齿轮泵B.叶片泵C.柱塞泵D.螺杆泵13.錾削加工低碳钢时，应将錾子的模角β刃磨为A.60°～70°B.15°～20°C.30°～50°D.80°～90°14.外径千分尺测量结果如图3所示，则其正确的读数是A.32.350mmB.35.000mmC.35.320mmD.32.850mm15.一个电热器，接在12V的直流电源上，产生的功率为P，把它改接在正弦交流电源上，使其产生的功率为P/2，则正弦交流电源电压的最大值为A.7.07VB.6VC.18VD.12V16.已知电源的外特性如图4所示，则该电源的电压等效模型为A.4Ω，4VB.4Ω，5VC.025Ω，4VD.025Ω，5V17.关于提高供电电路的功率因数，下列说法正确的是A.可以减少电路中的无功功率B.可以减少电路中的有功功率C.可以提高电源设备的容重D.可以提高电源设备的利用率并减小输电线路中的功率损耗18.如图5所示电路中，V D是硅二极管，电压源U=6V、输入电压Ui=4V，则输出电压U。

湖南省2024年一般高等学校对口招生考试数 学 试 题一、选择题（在本题的每一小题的备选答案中，只有一个答案是正确的，请把你认为正确的选项填入题后的括号内。

多选不给分。

本大题共10小题，每小题5分，共50分）1、已知全集{,,,,,,}U a b c d e f g =，集合{,,}U a e f =，集合{,,,}U b d e f =，则()U M N =（ ）。

（A ）{,}e f （B ）{,}c g （C ）{,,}a b d （D ）{,,,,}a b c d g2、不等式250x ->的解集是（ ）。

（A ）( （B ）(,(5,)-∞+∞（B ）(5,5)- （D ）(,5)(5,)-∞-+∞3、已知cos 0.618α=，(0180)α<<，则α的近似值是（ ）。

（A ）28.86 （B ）38.17 （C ）51.83 （D ）63.144、下列命题错误的是（ ）。

（A ）在复平面上，表示两个共轭复数的点关于实轴对称。

（B ）复数1的三角形式是2(sin cos )33i ππ+。

（C ）方程2160x +=在复数集内有两个根。

（D ）复数1的模是2。

5、已知33212n n C C =，则n =（ ）。

（A ）5 （B ）6 （C ）7 （D ）86、已知向量(2,3),(1,5)a b =-=，则下列命题错误的是（ ）。

（A ）2(0,3)a b += （B ）3(7,4)a b -=-（C ）||13a b += （D ）13a b ⋅=7、过点(3,2),(4,5)P Q -的直线方程是（ ）。

（A ）73230x y -+= （B ）37230x y -+=（C ）7370x y --= （D ）3770x y --=8、已知椭圆2216251600x y +=上一点P 到椭圆一个焦点的距离为8，则P 到另一个焦点的距离为（ ）。

（A ）6 （B ）10 （C ）12 （D ）149、甲、乙、丙3同学投篮命中的概率依次为0.6,0.5,0.4，3人各投1次，则其中恰有2人投中的概率是（ ）。

2016上期永州市中职一年级期末统一检测试卷数 学注意：（1）本试卷满分100分。

考试时量90分钟。

（2）在密封线内填写好相应项目。

1、下列各项中能构成集合的是A ．红星职业中专个子高的全体男生 B. 红星职业中专优秀的女学生 C. 红星职业中专模具专业全体学生 D. 红星职业中专篮球打得好的学生 2、“内错角相等”是“两直线平行”的A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件 3、下列命题为假命题的是A ．37是质数B ．66≤C ．293<D ．434≥ 4、不等式1<x 的解集是A ． RB ．Q C.()),1(1,+∞⋃-∞- D ．)1,1(-5、下列函数是奇函数的是A ．3)(+=x x fB ．x x f cos )(=C ．x x f sin )(=D ．x x f 2)(= 6、下列等式成立的是 A ．()26lg 36lg = B ．3lg 8lg 38lg-= C ．()4log 2log 42log 666+=+ D ．()e e ln 22ln = 7、函数x y 5=的图象过点A ．()0,1MB ．()1,0MC ．()0,0MD ．()1,1M 8、3π弧度用角度制表示为 A.30 B.45 C.60 D.120 9.()=-o 30cosA.21 B. 21- C. 23 D. 23- 10、已知角α的终边经过点()4,3P ,则αsin 的值为 A ．43 B ．34 C ．53D ．54二、填空题（本大题共20分，每小题4分，共5小题，请将正确答案填在空格内）11、集合}50,{≤<∈x z x x 用列举法表示为_______________ 12、不等式()()021≤--x x 的解集是_______________13、已知函数0)2(,2)(=-+-=f b x x f 且，则=b14、式子=3log 2215、已知54cos =α，则()=+απcos三、解答题:要求写出必要的解答过程，5道小题，每小题8分，共40 分.(请注意：第20、21题为选做题，若两道题都做了，只给第20题的得分)16、已知集合A=｛0，2，4，6｝，B=｛1，2，4，5｝求BA⋃、BA⋂.17、解不等式：0652<-+-xx18、计算：3227―3log22―81log219、已知()πα,0∈，且54cos-=α.求αsin及αtan的值.请注意：第20、21题为选做题，若两道题都做了，只给第20题的得分20、已知0cos3sin=+αα.(1)求αtan的值. (2)求ααααcossincos3sin2+-的值.21、已知函数()()53lg-=xxf.(1)求函数()x f的定义域; (2)求()()25ff-的值.2016上期永州市中职一年级期末统一检测试卷参考答案一、 C CCDCBBCCD二、 {}5,4,3,2,1，[]2,1，4-，3，54-三、16题解：{}6,5,4,2,1,0=⋃B A 4分 {}2=⋂B A 8分 17题、解：0652<-+-x x 0652>+-x x ()()032>--x x 2<x 或3>x原不等式的解集是()()+∞⋃∞-,32,18题： 解：原式()323232log 33--= 2分333323--=⨯ 4分632-= 6分 69-=3= 8分19题：解：∵()πα,0∈，54cos -=α ∴53541c o s 1s i n22=⎪⎭⎫⎝⎛--=-=αα 4分 435453c o s s i n t a n -=-==ααα 8分。

湖南省近七年(2011-2017)对口高考数学试题分类近七年湖南省普通高等学校对口招生考试的数学试题中，填空和选择题占据了很大比例。

以下是一些题目和解答：1.（2011.1）不等式(x-2)(x+1)≤0的解集是（）A.(-1,2)B.(-∞,2) ∪ (2,+∞)C.[-1,2]D.(-∞,-1) ∪ [2,+∞]2.（2012.3）不等式2x-3>1的解集为（）A.(1,2)B.(-∞,1) ∪ (2,+∞)C.(-∞,1)D.(2,+∞)3.（2013.7）不等式x^2-2x-3>0的解集为（）A.(-3,1)B.(-∞,-3) ∪ (1,+∞)C.(-1,3)D.(-∞,-1) ∪ (3,+∞)4.（2014.7）若a<0，则关于x的不等式(x-3a)(x+2a)<0的解集为（）A.{x|3a-2a} C.{x|-2a3a}5.（2015.8）不等式1-2x<3的解集为（）A.{x|x-1} C.{x|-2<x<4} D.{x|-1<x<2}6.（2016.4）不等式2x+1>5的解集为（）A.{x|x>2}B.{x|x2}7.（2016.13）若不等式x^2+x-c≤0的解集为{x-2≤x≤1}，则c=5.8.（2017.7）不等式x-5x+6<0的解集为（）A.{x|x3} C.{x|x3} D.{x|2<x<3}9.（2017.14）若关于x的不等式2x+b<3的解集为{x-3<x<5}，则b=-1.1.（2011.2）方程x^2-px+q=0有解的充分必要条件是p^2-4q≥0.2.（2012.2）"x>3"是"x^2>9"的充分必要条件。

3.（2013.3）"x=2"是"(x-1)(x-2)=0"的充要条件。

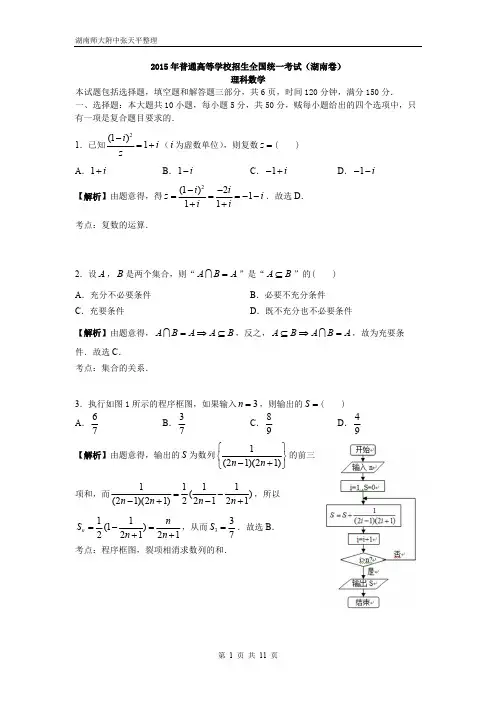
第 1 页 共 11页2015年普通高等学校招生全国统一考试（湖南卷）理科数学本试题包括选择题，填空题和解答题三部分，共6页，时间120分钟，满分150分．一、选择题：本大题共10小题，每小题5分，共50分，贼每小题给出的四个选项中，只有一项是复合题目要求的．1．已知（为虚数单位），则复数( )2(1)1i i z-=+i z =A ．B ．C ．D ．1i +1i-1i-+1i--【解析】由题意得，得．故选D ．2(1)2111i iz i i i--===--++考点：复数的运算．2．设，是两个集合，则“”是“”的( )A B A B A = A B ⊆A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件【解析】由题意得，A B A A B =⇒⊆ ，反之，A B A B A =⇒⊆ ，故为充要条件．故选C ．考点：集合的关系．3．执行如图1所示的程序框图，如果输入3n =，则输出的S =( )A ．B ．C ．D ．76739894【解析】由题意得，输出的为数列的前三S 1(21)(21)n n ⎧⎫⎨⎬-+⎩⎭项和，而，所以1111()(21)(21)22121n n n n =--+-+，从而．故选B ．11(122121n n S n n =-=++337S =考点：程序框图，裂项相消求数列的和．1第 2 页 共 11 页4．若变量，满足约束条件，则的最小值为( )x y ⎪⎩⎪⎨⎧≤≤--≥+1121y y x y x y x z -=3A ． B ．C ．1D ．27-1-【解析】如图所示，画出线性约束条件所表示的区域，即可行域，从而可知当，时，y x z -=3的最小值是7-．故选2x =-1y =A ．考点：线性规划．5． 设函数，则是( ))1ln()1ln()(x x x f --+=)(x f A ． 奇函数，且在是增函数B ． 奇函数，且在是减函数)1,0()1,0(C ． 偶函数，且在是增函数D ． 偶函数，且在是减函数)1,0()1,0(【解析】试题分析：显然，定义域为，关于原点对称，()f x (1,1)-又∵，∴为奇函数，显然在上单调()ln(1)ln(1)()f x x x f x -=--+=-()f x ()f x (0,1)递增．故选A ．考点：函数的性质．6．已知的展开式中含的项的系数为30，则( )5(xax -23x =a A ．B ．C ．6D ．33-6-【解析】，令，可得，从而．故选D ．5215(1)r r r rr T C a x-+=-1r =530a -=6a =-考点：二项式定理．7． 在如图2所示的正方形中随机投掷10000个点，则落入阴影部分（曲线为正态分布C 的密度曲线）的点的个数的估计值为( ))1,0(N A ．2386B ．2718C ．3413D ．4772附：若，则),(~2σμN X ,6826.0)(=+≤<-σμσμX P ．9544.0)22(=+≤<-σμσμX P 【解析】根据正态分布的性质，．故选．1(01)(11)0.34132P x P x <<=-<<=C 考点：正态分布．8． 已知点，，在圆上运动，且 ． 若点的坐标为,A B C 122=+y x BC AB ⊥P )0,2(第 3 页 共 11 页则的最大值为( )||PC PB PA ++A ．6 B ．7C ．8D ．9【解析】由题意得为圆的直径，故可设，，，AC (,)A m n (,)B m n --(,)C x y ∴，而，∴的(6,)PA PB PC x y ++=- 22(6)371249x y x -+=-≤||PC PB PA ++最大值为7．故选．B 考点：圆的性质，平面向量数量积．9． 将函数的图象向右平移个单位后得到函数的图象，x x f 2sin )(=ϕ)20(πϕ<<)(x g 若对满足的，，有，则( )2|)()(|21=-x g x f 1x 2x 3||min 21π=-x x =ϕA ．B ．C ．D ．125π3π4π6π【解析】向右平移ϕ个单位后，得到)22sin()(ϕ-=x x g ，又∵2|)()(|21=-x g x f ，∴不妨设ππk x 2221+=，ππϕm x 22222+-=-，∴πϕπ)(221m k x x -+-=-，又∵12min 3x x π-=，∴632πϕπϕπ=⇒=-．故选D ．考点：三角函数的图象和性质．10． 某工件的三视图如图所示，现将该工件通过切削，加工成体积尽可能大的长方体新工件，并使新工件的一个面落在原工件的一个面内，则原工件材料的利用率为（材料的利用率）( )原工件的体积新工件的体积=A ．B ．C ．D ．π98π916π2124）－（π21212）－（【解析】问题等价于圆锥的内接长方体的体积，如下图所示，则有，∴，212x h -=22h x =-∴长方体的体积为22(2)(22)x h x x =-，当且仅当4(22)x x x =-A A 3224()3x x x ++-≤3227=时，等号成立，2223x x x =-=即∴利用率为．故选A ．232162719123ππ=A A考点：圆锥内接长方体，基本不等式求最值．侧侧侧侧侧侧1育（列讲话，员中开我第 4 页 共 11 页二、填空题：本大题共5小题，每小题5分，共25分．11．__________．⎰=-2)1(dx x 【解析】．⎰=-2)1(dx x 2201|02x x -=考点：定积分的计算．12．在一次马拉松比赛中，35名运动员的成绩（单位：分钟）茎叶图如图所示．若将运动员按成绩由好到差编为1－35号，再用系统抽样的方法从中抽取7人，则其中成绩在区间上的运动员的人数是_________．]151,139[【解析】由茎叶图可知，在区间]151,139[的人数为20，再由系统抽样的性质可知人数为435720=⨯人．考点：系统抽样，茎叶图．13．设是双曲线的一个焦点，若上存在点，使线段的中点恰F C 1:2222=-by a x C P PF 为其虚轴的一个端点，则的离心率为________．C 【解析】根据对称性，不妨设，短轴端点为，从而可知点在双曲线(,0)F c (0,)b (,2)c b -上，∴，从而．222241c b a b -=ce a==考点：双曲线的标准方程及其性质．14．设为等比数列的前项和，若，且成等差数列，则n S }{n a n 11=a 321,2,3S S S ___________．=n a 【解析】等比数列中，，∴}{n a 2111S a a q q =+=+231S q q =++，24(1)31q q q +=+++解得，∴．3q =13n n a -=考点：等比、等比数列的通项公式及其前n 项和．的意业。

湖南省2015年普通高等学校对口招生考试数学试题（附答案）本试题卷包括选择题、填空题和解答题三部分。

时量120分钟.满分120分一、选择题（每小题4分，共40分．每小题只有一项是符合题目要求的）1.已知集合，，则等于【答案】BA. B。

C。

D。

2。

“”是“”的【答案】AA．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件3.函数的定义域为【答案】DA. B。

C. D。

4.点到直线的距离为【答案】CA．5B．C．1 D．5.已知，则【答案】BA．B．C．D．6。

的二项展开式中含的系数为，则【答案】CA．B．C．D．27。

下列函数中，既是奇函数又是增函数的是【答案】AA．B．C．D．8。

不等式的解集为【答案】DA。

B。

C。

D.9．已知向量，则【答案】BA．∥B．⊥C．D．10．若过点（0,2）的直线与圆有公共点,则直线的倾斜角的取值范围是【答案】C A．B．C．D．二、填空题(本大题共5小题,每小题4分,共20分）11、甲、乙两人独立地解答同一个问题，若他们解答正确的概率分别为0。

8和0。

6，则两人都解答正确的概率为__________．【答案】0。

4812．某公司现有员工500人，为了调查员工的健康状况,拟采用分层抽样的方法从中抽取一个容量为100的样本，若将所有员工分为A,B ，C 三个年龄组,各组人数依次为125,280，95，则在B 组中抽取的人数应为_________．【答案】56 13．若函数在上单调递增，则的取值范围是． 【答案】[—3,+∞) 提示:由14.已知点,且，则点的坐标为．【答案】(1，-1) 15已知等比数列的前项和，则．【答案】-3三、解答题（本大题共7小题，其中第21，22题为选做题．满分60分．解答题应写出文字说明、证明过程或演算步骤）16。

（本小题满分10分） 已知函数的图象过点。

(I)求的解析式；（II)当时，求的取值范围．解:(I ）依题意，有：,解得：,∴函数的解析式为； (II ）∵2>1，∴为增函数，而 ∴当时,的取值范围为． 17. （本小题满分10分）从装有5个红球和3个白球的箱子中,随机取出2个球，用表示取出的2个球中白球的个数．(I)求随机变量的分布列;（II)求事件“取出的2个球中至少有一个白球"的概率． 解：（I ）∴随机变量的分布列为:（II ）至少有1个白球的概率．18。

机密★启用前湖南省2016年普通高等学校对口招生考试计算机应用类专业综合知识试题本试题卷共六大题，39小题，共18页。

时量150分钟，满分390分。

一、单选题（在本题的每一小题的备选答案中，只有一个答案是正确的，本大题共22小题，每小题5分，共110分）1. 为了在资源管理器中快速浏览.DOC类文件，最快速的显示方式是A.按名称B按类型 C.按大小 D.按日期2. 下列各种进制的数中，最小的数是A.十进制数44B.八进制数52C.十六进制数2BD. 二进制数1010013. 为解决各类应用问题而编写的程序，例如学生档案管理系统，称为A.系统软件B.支撑软件C应用软件 D.服务性程序4. 在Windows系统中，当程序长时间无响应时，能较好地结束该程序的方法是A按“Ctrl+Alt+Del”键,然后选择该程序，执行“结束任务”B.按“Shift+Alt+Del”键，然后选择该程序，执行“结束任务”C.按“Shift+ Ctrl + Backspace”键，然后选择该程序，执行“结束任务”D.按“Alt+Shift+Backspace”键，然后选择该程序，执行“结束任务”5. 在Windows回收站中，可以恢复A.从硬盘中删除的文件或文件夹B.从U盘中删除的文件或文件夹C.剪切掉的文档D:从光盘中删除的文件或文件夹6. 在Word菜单右边有“…”符号，表示A.该命令不能执行B.单击该命令后，会弹出一个对话框C.该命令已执行D.该命令后有下一级子菜单7. 当用户输入的文字中出现拼写错误时，Word会在文字下面标注A.红色直线B.红色波浪线C.绿色直线D.绿色波浪线8. 在Excel中，利用填充柄可以将数据复制到相邻单元格中，若选择含有数位的左右相邻的两个单元格，左键拖动填充柄，则数据将以___________填充。

A.左单元格数值B.等比数列C.等差数列D.右单元格数值9. 要使幻灯片在放映时能够自动播放，需要为其设置A. 超链接B.动作按钮C.排练计时D.录制旁白10.微型计算机的各种接口中，经常在机箱正面和背面同时存在的是A. HDMI 接口B. VGA 接口C. USB 接口D. PS/2 接口11. 下列各种存储设备或介质中，读取数据速度最快的是A. SSD固态硬盘B. IDE硬盘C. SATA硬盘D. CD-ROM光盘12. 一般情况下，关于鼠标和键盘的PS/2接口颜色，下列说法中正确的是A.鼠标接口为白色，键盘接口为黑色B. 鼠标接口为绿色，键盘接口为紫色C.鼠标接口为绿色，键盘接口为红色D.鼠标接口为黄色，键盘接口为紫色13. 下列关于BIOS和CMOS中说法错误的是A. BIOS是一组固化到主板ROM芯片上的程序B. CMOS是主板上一种用电池供电的可读/写RAM芯片C. 当进入BIOS对硬盘参数或其它BIOS参数进行设置并保存时，这些设置被存储到CMOS RAM芯片的存储器区域中D. BIOS 就是 CMOS14. 作为互联网的前身，最早出现的计算机网络是A. ARPAnetB. IntranetC. ExtranetD. Ethernet15. 某计算机的IP地址为192.168.10.25,子网掩码为255.255.255.240,则该计算机所在子网的网络地址是A. 192.168.10.0B. 192.168.10.16C. 192.168.10.32D. 192.168.10.4816. 下列选项中，属于无线局域网标准的是A. IEEE802.2B. IEEE802.3C. 1EEE802.10D. IEEE802.1117. 在互联网中快速查找自己需要的信息，最合适的方式是使用A. DNS服务B.电子邮件C.搜索引擎D. DHCP服务18. 下列数据交换技术中，需要建立实际的物理连接的是A.报文交换B.电路交换C.数据报交换D.信元交换19. 在HTML中，用来定义一个段落的标记是A. <a>...</a>B. <b>...</b>C. <i>...</i>D. <p>...</p>20. 在C语言中，函数值类型在定义时可以缺省，缺省时函数值的隐含类型是A. voidB. intC. floatD. double21. 用scanf函数输入一个字符串到数组str中，以下选项中正确的语句是A. scanf("%s",&str);B. scanf("%c",&str[10]);C. scanf("%s",str[10]);D. scanf("%s",str);22. 设有定义语句:int m[ ]={2，4，6，8}，*k=m;以下选项中表达式的值为6的是A. *(k+2)B. k+2C. *k+2D. *k+=2二、基本操作题（本大题共5小题，每空4分，共60分）23. 组装微型计算机时，安装主板的正确步骤是：(1)___①____________________。

湖南省2017年普通高等学校对口招生考试数学试题(附答案)本试题卷包括选择题、填空题和解答题三部分.时量120分钟.满分120分一、选择题（每小题4分，共40分．每小题只有一项是符合题目要求的）1.已知集合{},2,1=A ,{}4,32，=B ,则B A 等于 【答案】DA. {}2B. {}4,32，C. {}4,3,1D. {}4,3,2,1 2.已知32-=a，212=b ，2)21(=c ,则c b a ,,的大小关系为 【答案】BA ．c b a <<B ． b c a <<C ．c a b <<D ． a b c <<3.已知()παα,0,21cos ∈= ，则=αsin 【答案】A A ．23B ． 23-C ．21D ．21-4.已知两条直线1)2(2++=-=x a y ax y和互相垂直，则=a 【答案】DA ．2B ． 1C ．0D ．1-5.下列函数中，在区间()+∞,0上单调递增的是 【答案】C A.x ysin = B. x y 1=C. 2x y = D. x y 31log = 6.已知函数)(x f 的定义域为R ，则“)(x f 为偶函数” 是“)1()1(f f =-”的【答案】CA ． 充分必要条件B ． 必要不充分条件C ． 充分不必要条件D ． 既不充分也不必要条件 7.不等式0652<+-x x 的解集是 【答案】DA ．{}2<x x B ．{}3>x x C ．{}32><x x x 或 D ．{}32<<x x8.设m l 、 是两条不同的直线，α是平面，则下列命题正确的是 【答案】B A ．若α⊂⊥m m l,，则α⊥l B ．若l m l //,α⊥，则α⊥mC ．若αα⊂m l ,//，则l m //D ．若αα//,//m l ，则l m //9. 从1,2,3,4,5,6,7,8,9这9个数中取2个不同的数，使其和为偶数，则不同的取法共有A. 72种B. 36种C. 32种D. 16种 【答案】D10．在三棱锥ABC P - 中，PA ，PB ，PC 两两互相垂直，且PA=PB=PC=1 ，则该三棱锥的体积为【答案】A A ．61 B ．31 C ．21D ．1二、填空题（本大题共5小题，每小题4分，共20分）11、在一次中学生田径运动会上，参加男子跳高的10名运动员的成绩如下表所示：则这些运动员成绩的平均数是__________（m ）． 【答案】1.62 12．若直线06=+-y kx 经过圆4)2()122=-+-y x （的圆心，则=k ______． 【答案】4-13．函数()x x f cos 21-=的最小值为 ． 【答案】1-14.若关于x 的不等式32<+b x 的解集为{}03<<-x x ，则=b ．【答案】3 15.若双曲线)0,0(12222>>=-b a by a x 上存在四点A ，B ，C ，D ，使四边形ABCD 为正方形，则此双曲线的离心率的取值范围为 ．【答案】()∞+，2三、解答题（本大题共7小题，其中第21，22题为选做题．满分60分．解答题应写出文字说明、证明过程或演算步骤）16. （本小题满分10分） 已知函数()1)1(),1,0(1)5(log 2=-≠>-+=f a a x x f a 且.（I ）求a 的值，并写出()x f 的定义域；（II ）当[]11,4-∈x 时，求()x f 的取值范围．解：（I ）依题意，有：()11)51(log 21=-+-=-a f ，解得：4=a ，由505->>+x x 得∴4=a ，()x f 的定义域为），（∞+-5 （II ）由（1）得：()1)5(l o g 24-+=x x f ∵4>1,∴()1)5(log 24-+=x x f 为增函数，而314116log 2)11(,111log 2)4(44=-=-=-=-=-f f∴当[]11,4-∈x 时，()x f 的取值范围为[]3,1-．17. （本小题满分10分）某射击运动员射击3次，每次射击击中目标的概率为32，求： （I ）3次射击都击中目标的概率； （II ）击中次数ξ的分布列．解：（I ）278323)3(==）（P（II ）随机变量ξ的分布列为：18. （本小题满分10分）已知数列{}n a 为等差数列，若1231,1a a a a +==，求： （I ）求数列{}n a 的通项公式；（II ）设na n n ab )21(+=，求数列{}n b 的前n 项和n S ．解：（I ）设数列{}n a 的首项为1a ，公差为d ，依题意，有：⎩⎨⎧==⇒⎩⎨⎧++=+=,1,12111111d a a d a d a a ∴n d n a a n =-+=)1(1∴数列{}n a 的通项公式为n a n =；（II ）n an n a b )21(+==nn ）（21+∴n nn n n n n ⎪⎭⎫ ⎝⎛-++=-⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-++=21221211211212)1(S 2）（19. （本小题满分10分）已知向量),1(m a =，向量)3,2(=b（I ）若b a //，求m 的值； （II ）若b a ⊥，求)3()3a b a-⋅（的值．解：（1）由b a //得：32=m ，23=∴m（2）由b a⊥得023=+m 32-=∴m∴ ），（（3213)3-=a =），（23- ）（），（）（5,1233,2)3(-=--=-a b 20. （本小题满分10分）已知抛物线px y C 2:2=的焦点为().0,2F（I ）求抛物线C 的方程；（II ）过点M （1,2）的直线l 与C 相交于B A ,两点，且M 为AB 的中点，求直线l 的方程． 解：（I ）∵抛物线px y C 2:2=的焦点为()0,2F ，∴22=p，解得4=p ， 故抛物线C 的方程为：x y82=；（2）设)A 11y x ，（、)B 22y x ，（ ，则依题意有422121=+=+y y x x ，易知若直线l 的斜率不存在，则直线方程为1=x ，此时4021≠=+y y ，不合题意，由⎪⎩⎪⎨⎧==22212188x y x y 得：)(8212221x x y y -=- 即2121218y y x x y y +=-- ∴2488212121==+=--==y y x x y y k k AB l∴ 直线l 的方程为02=-y x注意：第21题，22题为选做题，请考生选择其中一题作答． 21．（本小题满分10分） 已知c b a ,,，分别为△ABC 内角A ，B ，C 的对边，已知ab c22=，（I ）若 90=C ，且1=a ，求ABC ∆的面积； （II ）若C A sin sin =，求C cos 的值解：（I ）由 90=C，且1=a ，则222c b a =+，又ab c 22=∴0122=+-b b ，解得1=b （II ）由正弦定理caC A C c A a =⇒=sin sin sin sin ， 又C A sin sin =， ∴c a =，又ab c22= ∴b c a 2==22．某公司有40万元资金，计划投资甲、乙两个项目，按要求对项目甲的投资不小于对乙项目投资的31倍，且对每个项目的投资都不能低于5万元。

2008——2017年湖南省普通高等学校对口招生考试数学试题湖南省2008年普通高等学校对口招生考试数 学 试 题一、选择题（在本题的每一小题的备选答案中，只有一个答案是正确的，请把你认为正确的选项填入题后的括号内。

多选不给分。

本大题共10小题，每小题5分，共50分）1、已知全集{,,,,,,}U a b c d e f g =，集合{,,}U a e f =，集合{,,,}U b d e f =，则()U M N =（ ）。

（A ）{,}e f （B ）{,}c g （C ）{,,}a b d （D ）{,,,,}a b c d g2、不等式250x ->的解集是（ ）。

（A ）( （B ）(,(5,)-∞+∞（B ）(5,5)- （D ）(,5)(5,)-∞-+∞ 3、已知cos 0.618α=，(0180)α<<，则α的近似值是（ ）。

（A ）28.86 （B ）38.17 （C ）51.83 （D ）63.144、下列命题错误的是（ ）。

（A ）在复平面上，表示两个共轭复数的点关于实轴对称。

（B ）复数1+的三角形式是2(sin cos )33i ππ+。

（C ）方程2160x +=在复数集内有两个根。

（D ）复数1的模是2。

5、已知33212n n C C =，则n =（ ）。

（A ）5 （B ）6 （C ）7 （D ）86、已知向量(2,3),(1,5)a b =-=，则下列命题错误的是（ ）。

（A ）2(0,3)a b += （B ）3(7,4)a b -=-（C ）||13a b += （D ）13a b ⋅=7、过点(3,2),(4,5)P Q -的直线方程是（ ）。

（A ）73230x y -+= （B ）37230x y -+=（C ）7370x y --= （D ）3770x y --=8、已知椭圆2216251600x y +=上一点P 到椭圆一个焦点的距离为8，则P 到另一个焦点的距离为（ ）。

绝密★启封并使用完毕前试题类型：A2016年普通高等学校招生全国统一考试(湖南卷）理科数学注意事项： 1.本试卷分第Ⅰ卷(选择题）和第Ⅱ卷(非选择题）两部分.第Ⅰ卷1至3页，第Ⅱ卷3至5页。

2.答题前,考生务必将自己的姓名、准考证号填写在本试题相应的位置. 3。

全部答案在答题卡上完成，答在本试题上无效. 4。

考试结束后，将本试题和答题卡一并交回。

第Ⅰ卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中,只有一项是符合题目要求的。

（1）设集合A ＝{x |x 2－4x ＋3＜0},B ＝{x ｜2x －3＞0}，则A ∩B ＝（A)（－3，－23） （B)(－3,23） (C ）（1，23） （D ）（23，3）解：∵A ＝（1,3), B ＝),(+∞23,∴A ∩B ＝（23，3），选D(2)设（1＋i ）x ＝1＋y i ，其中x ,y 是实数，则|x ＋yi ｜＝ （A)1（B ）2(C ）3(D)2解：∵(1＋i ）x ＝1＋y i,∴x ＝y ＝1,故｜x ＋yi |＝2,选B (3）已知等差数列｛a n }前9项的和为27，a 10＝8,则a 100＝ (A)100 (B ）99 (C)98 （D ）97 解：∵S 9＝27,∴a 5＝3,又a 10＝8，∴d ＝1,因此a 100＝a 10＋90d ＝98,选C（4)某公司的班车在7∶00，8∶00，8∶30发车，小明在7∶50至8∶30之间到达发车站乘坐班车,且到达发车站的时刻是随机的，则他等车时间不超过10分钟的概率是(A ）31 (B)21 (C ）32 （D)43解：几何概型（长度比），选B（5)已知方程132222=--+nm y n m x 表示双曲线,且该双曲线两焦点间的距离为4，则n 的取值范围是（A)（–1，3) （B)（–1,错误!） （C)(0，3） （D)(0，错误!）解：依题意，m 2＋n ＋3m 2－n ＝4⇒m 2＝1,（m 2＋n ）(3m 2－n ）＝(1＋n )（3－n )＞0⇒－1＜n ＜3，选A 。

精品文档湖南省2018年普通高等学校对口招生考试数学本试题卷包括选择题、填空题和解答题三部分,共4页,时量120分钟,满分120分一、选择题(本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知集合A={1,2,3,4},B={3,4,5,6},则A∩B=（）A.{1,2,3,4,5,6}B.{2,3,4}C.{3,4}D.{1,2,5,6}23?x9x?”是“2. “）”的（ B.必要不充分条件A.充分必要条件D.既不充分也不必要条件C.充分不必要条件2x2?x?y）3.函数的单调增区间是（)∞,2] D.[0,+∞) C.(-A.(-∞,1] B. [1,+∞3???cos??=（）为第三象限角4.已知,则tan且, 54433?? D. A. B.C.44332x?1?1的解集是（不等式）5.x|x?0x|x?1} A.{} B.{x|x?0或x?11x?x?|0} C.{} D.{精品文档．精品文档0?4y?123x?OMO M长度的最小值6.点为坐标原点在直线,上，则线段）是（1212 D. A. 3 B. 4 C. 52512b?7a?b??42ba?baa的夹角为,满足,,，7.已知向量则向量，（）?30D. 150° B. 60° C. 120°A.）8.下列命题中,错误的是（．． A. 平行于同一个平面的两个平面平行 B.平行于同一条直线的两个平面平行 ,交线平行C. 一个平面与两个平行平面相交则必与另一个相交,D. 一条直线与两个平行平面中的一个相交c,a,b?sin100?sin200c?15a?sin?b?的大小关系为已知9.，,，则）（ba?b?ac??aa?b?c?c?bc C. A. B. D.224x??yO BA则相交于为坐标原点，两点过点10.(1,1)的直线与圆,,OAB?面积的最大值为（）33 A. 2 B. 4 C. D. 2二、填空题(本大题共5小题,每小题4分,共20分)11.某学校有900名学生,其中女生400名.按男女比例用分层抽样的方法,从该学校学生中抽取一个容量为45的样本,则应抽取男生的人数为 .精品文档．精品文档f(x)?cosx?bbb= . 则的部分图像如图所示(12.函,为常数)6)?1(x13.展开式中的5x的系数为用数字作() 答已知向量14. by?yx?bacaxc .则=(1,2),,=(3,4),+=(11,16),且=个2的正方形,再将这个正方形各边的中点相连得到第15.如图,画一个边长为4 .个正方形的面积为则第10,这样一共画了10个正方形.正方形,依次类推60满分，22小题为选做题.本大题共三、解答题(7小题,其中第21解答应写出文字说明、证明过程或演算步骤）分,)本小题满分10分16.(aaa为等差数列,，=1,=5已知数列{}3n1a {}的通项公式；（Ⅰ）求数列n SaS nn. 若的前{（Ⅱ）设数列}项和为 . =100，求nnn精品文档．精品文档17.(本小题满分10分）某种饮料共6瓶，其中有2瓶不合格,从中随机抽取2瓶检测.用表示取出?饮料中不合格的瓶数.求(Ⅰ)随机变量的分布列；?(Ⅱ)检测出有不合格饮料的概率.18.(本小题满分10分)f(x)?log(x?3)(a?0,且a?1)的图像过点已知函数(5，1) a f(x)f(x)的定义域；的解析式，并写出(Ⅰ)求1)?(fm m (Ⅱ)若的取值范围,求)10分19.(本小题满分AABCABC?A⊥底面如图在三棱柱中，,1111BC?AA?AB?ABCABC?D,，90，°1AC.为的中点CCAA BD⊥平面证明:；(I)11CAACBA. 所成的角与平面)(Ⅱ求直线111)10分20.(本小题满分22yx1??FF0a?b?:C A点(1,0),)的焦点为(-1,0)已知椭圆、(2122ba. 上在椭圆(0,1)C C的方程；(I)求椭圆精品文档．精品文档FAFCNll M两点,直线Ⅱ)与椭圆过点，且与相交于垂直,(II)(11MN的长求.选做题:请考生在第21，22题中选择一题作答.如果两题都做,则按所做的第21题计分,作答时,请写清题号.21.(本小题满分10分)ABCD,在四边形如图,中?BCD?6?BC?CD4?AB, ，°120,ABCD??ABC.求四边形的面积75°,)10分22.(本小题满分BA吨每种产品已知生产1两种原料.某公司生产甲、乙两种产品均需用，万4如果生产1吨甲产品可获利润.所需原料及每天原料的可用限额如表所示才能使公司每该公司如何规划生产:,吨乙产品可获利润5万元.问生产元,1?精品文档．精品文档参考答案一、选择题：1. C2. B3. B4. A5. D6. D7. C8. B9.D 10. A二、填空题：1 14.5 15. 25 12.2 13. 6 11.32三、解答题15?aaa（Ⅰ）数列{公差}为等差数列,d==1,=5 16.解：?2?3n113?1?2n1?a1?2(n?)?故n aSS n等差数列{}的前项和为=100nnn，（Ⅱ）∵nS?(a?a)n1n2n(1?2n?1)?100∴2n?10∴解：（Ⅰ）?的可能取值有0，1，17.22011CC?CC?822244????1?0?）（ P=）（ P=22155CC66精品文档．精品文档02C?C124??2? = P（）215C6?的分布列是：故随机变量0 1 2AA表示有不合格饮料（Ⅱ）设事件表示检测出的全是合格饮料，则?)P(A24?检测出的全是全格饮料的概率25C623?1?P(A)?20C?C2故检测出有不合格饮料的概率55f(x)?log(x?3)(a?0,且a?1)的图像过点(5，1)18.（Ⅰ）函数a∵解：log2?1a∴a?2∴f(x)?log(x?3)x?3?02有意义，则x?3∴(3,??))3)(x?log(x?f2函数的定义域是f(x)?log(x?3)f(m)?1)(Ⅱ2∵，log(m?3)?1?log222∴精品文档．精品文档2?3?m∴5m?∴),??(3)x?3f(x)?log(3m?2，即又的定义域是5m?3?∴m5）的取值范围是（3，ABC C?ABCAB AA⊥底面中，（Ⅰ）证明：在三棱柱19.1111∵AA BD⊥∴1AC?BC?ABCAB?D. 为的中点90°,，又AC BD⊥∴A AC?AA而1CAAC BD⊥平面11∴CCAA BD⊥平面由（Ⅰ）可知：Ⅱ()11CAACBA DA?BAD所成的角与平面是直线，则11111连结12AC?BD?ABAB?2ABBD?ARt在，中，1122 精品文档．精品文档BD1?BAD?sin?1∴2BA130?BAD?1∴BACAAC 30所成的角是与平面即直线.11122yx?1?FF0?b?a:C(1,0)的焦点为、(-1,0))(椭圆（20.Ⅰ）解：2122∵ba1?c∴A(0,1)在椭圆C上又点21?b∴22221?c?1?a?b?∴2x2?y?1C椭圆的方程是∴2k?1AFⅡ)的斜率直线(AF11FAFl过点而直线且与垂直11l1?k?的斜率是∴直线精品文档．精品文档1?y??x l直线的方程是1?y??x??2y0?4x?x32?x消去由得：21y???2?)y(x,)M(x,yN2112，则设，4?x??x0?x?x2121，342?)x?xx?4x?x?x(221211 3442?22x?x??MN?k?1213342MN的长是即3BD解：如图，连结21.6CD??BC BCD?中，在，?BCD?°，由余弦定理得：120222BCDcos?BC?CD?BD?BC?CD2?1226?6?2?6?6??(?)2精品文档．精品文档236??3?6BDSSS?ABCD四边形=的面积ABDBCD??ABCD四边形11ABD?sin??BC?CD?sin?BCDBA?BD =2211 45sin120??4?63sin6??6? =222113?34?6?6?6???=222293?66 =y x z最吨，乙产品吨，才能使公司获得的利润22.解：设公司每天生产甲产品y x y?5z?4x满足下列约束条件：大，则、，x?0??y?0??8?2x?y??3x?2y?12?作出约束条件所表示的平面区域，即可行域，如图中的阴影部分，四边形ABOC4x?y?及其平行线作直线5z4表示斜率直线ll??y?x，：55精品文档．精品文档4z过由图可知，直线为，纵截距为的平行直线系，当它在可行域内滑动时，l? 55时，取得最大值，点z A8?x?2y?由?)3,A(2得12??2y3x?23??3??z4?25万元∴max吨时，公司获得的利润最大，最3即当公司每天生产甲产品2吨，乙产品. 万元23大利润为精品文档．。

1 9、函数 y x 3 2 x 2 3 x 5 的单调递减区间为 3
A、 (,1)
B、 (1,3)
C、 (3, )
D
(,1) (3, )
、
10、某班级要从 4 名男生和 2 名女生中选派 4 人参加某次社区服务，如果要求至少 有 1 名女生，则选派方案种数有 A、14 B、24 C、28 D、48
科目：数学（对口）
（试 题 卷）
注意事项： 1．答题前，考生先将自己的姓名、准考证号、座位号等填写清楚， 并认真核对。 2．选择题和非选择题均须在答题卡上作答，在本试题卷和草稿纸上 作答无效，考生在答题卡上按如下要求答题： （1）选择题部分请按题号用 2B 铅笔填涂方框，修改时用橡皮擦干 净，不留痕迹； （2）非选择题部分请按照题号用 0.5 毫米黑色墨水签字笔书写，否 则作答无效； （3）请勿折叠答题卡．保持字体工整，笔迹清楚、卡面清洁。 3．本试卷共 4 页。如有缺页，考生须及时报告监考老师，否则后果 自负。 4．考试结束后，将本答题卷和答题卡一并交回。
2、函数 f x 3 x x 0,2 的值域为 A、 0,9 3、 a 2 是 | a | 2 的 A、充分不必要条件 C、充分必要条件 B、必要不充分条件 D、既不充分也不必要条件 B、 0,6 C、 1,6 D、 1,9
1 4、曲线 y sin 2 x , x 0, 与直线 y 1 的交点个数为 2
x2 y 2 1 的左右两个焦点， 设 F1 , F2 分别是椭圆 P 为椭圆上的一点， 已知 PF1 PF2 且 16 6 | PF1 || PF2 | .
（I）求 P 的坐标； （II ）求中心在原点，一个焦点为 (2 5, 0) ，一条渐近线的斜率为 标准方程。