运筹学
- 格式:docx
- 大小:51.61 KB
- 文档页数:6


运筹学的定义
运筹学是一门研究决策的学科,它综合了数学、统计学、信息学、经济学、管理学等多个领域的知识和技术,旨在通过科学的方法来解决实际问题。
运筹学在现代社会中拥有广泛的应用,涉及到许多领域,如物流、交通、金融、医疗、能源等。
运筹学的主要目标在于找到最优解决方案。
例如,在物流领域,如何在有限的时间内将货物运输到目的地,同时降低运输成本;在金融领域,如何通过科学的投资策略来最大化收益,同时降低风险。
这些问题都可以通过运筹学的方法来解决。
为了实现这些目标,运筹学应用了许多技术和方法。
其中最常用的是线性规划,即在一组约束条件下最小化或最大化一个线性函数。
除此之外,运筹学还包括非线性规划、整数规划、动态规划、图论、排队论、模拟等等方法。
这些方法都有不同的应用场景,可以根据具体问题的特点选择最合适的方法。
运筹学的应用不仅限于商业领域,也可以用于解决社会问题。
例如,在医疗领域,如何最大化患者的生存率,同时降低医疗成本;在能源领域,如何通过科学的能源规划来提高能源利用效率,降低污染和排放。
这些问题都需要运筹学的方法来提供解决方案。
运筹学是一门非常实用的学科,它可以为我们提供科学的决策方法,解决实际问题。
随着科技的发展和社会的进步,运筹学的应用范围
也将更加广泛。
我们应该深入学习和应用运筹学的知识和方法,为实现更高效、更节约、更可持续的社会发展做出贡献。

第一讲 运筹学概述一、运筹学是什么?----------------------晕愁学其实,这绝对一种误解,事实上运筹学方法及应用早在中小学就比较系统地学过,并且在我们每时每刻的生活过程中都在利用。
北师大版小学语文第六册教材中就有一篇课文《田忌赛马》,在座的各位应该都不陌生。
这是战国时期运筹学思想成功应用的典型实例。
孙膑同志合理地利用当时的现有资源、条件和比赛规则,只建议田忌调换了赛马的出场顺序,就使得原来屡战屡败的战局得到了彻底的扭转,以获胜而告终。
形成了本文主题中“初战失败”、“孙膑献计”、“再赛获胜”的三部分内容。
运筹学思想体现的是,将现有资源的作用得到充分发挥,以获得最优的结果。
运筹让生活得更有条理的艺术。
谈起运筹学,是否会想到很通俗的例子——沏茶水。
沏茶,看起来是一件日常生活中再小不过的事情,却包含着运筹学的道理。
让我们来看一看,沏茶的过程可以分为烧开水、洗茶壶、放茶叶多道“工序”。
其中,烧开水所需的时间最长,洗茶壶、放茶叶的时间则较短。
善于运筹的人,应该是先将水烧上,在烧水的过程中,从从容容地把茶壶洗净,把茶叶放好。
而不善运筹的人,可能会先把茶壶洗净,把茶叶放好,才想起来水还没有烧;或者先把水烧开了,才急急忙忙去洗茶壶、放茶叶,搞得手忙脚乱。
另外还有一个例子我们外地生到上海的路线选择,虽然条条大路都能通到上海,但我们都有一个明确的目标,有些人的目标是准备用最短的时间到达,有些人的目标是用最少费用到达,这样基于不同的目标,就会选择不同的最佳路线。
这两个生活中的运筹学实例说明了运筹学应用的思想并不神秘,而现实的生活中,从沏茶、选择路线这样一件小事,到规模宏大的建设项目,都能运用运筹学的原理。
在人生大事的安排上,也同样需要下功夫好好运筹一番。
从技术是,也就是运筹学解决决策问题的工具方面,在初中的数学教材中有一个重要的内容是《线性规划》,其中比较详细地讲述了线性规划的数学表述形式和求解方法。



![运筹学综述[全文]](https://uimg.taocdn.com/1e57e09c690203d8ce2f0066f5335a8102d26694.webp)
运筹学综述运筹学的简介一:什么是运筹学?运筹学是Operations Research的英文单词缩写。
运筹学界的元老说运筹学是执行部门对所控制的业务做出决策提供数量上的依据的科学或利用所有应用科学执行部门对其所属业务作出决策提供数量上依据的一门科学;世界上最早的运筹学协会说运筹学是运用科学方法来解决工业、商业、政府、国防等部门里有关人力、机器、物资、金钱等大型系统的指挥或管理中所出现的复杂问题的一门学科,其目的是“帮助管理者以科学方法确定其方针和行动”。
二:运筹学的三个来源1、军事二战期间例一:在第二次世界大战期间,鲍德西雷达站的研究——“布莱克特马戏团”的出色工作,Bawdsey雷达站—Blackett杂技班专门就改进空防系统进行研究。
成员组成:心理学家3,数学家2,数学物理学家2,天文物理学家1,普通物理学家1,陆军军官1,测量员1。
研究的问题是设计将雷达信息传送给指挥系统及武器系统的最佳方式;雷达与防空武器的最佳配置;对探测、信息传递、作战指挥、战斗机与防空火力协调等获得成功,大大提高了英国本土的防空能力,不久以后在对抗德国对英伦三岛的狂轰滥炸中发挥了极大的作用,堪称运筹学的发祥与典范,展示了运筹学的本色与特色。
二战期间例二:大西洋反潜战——Morse小组的重要工作。
1942年麻省Morse教授应美国大西洋舰队反潜战官员Baker舰长的请求担任反潜战运筹组的计划与监督工作,其最出色的工作之一是协助英国打破了德国对英吉利海峡的海上封锁,研究所提出的两条重要建议是:将反潜攻击由反潜舰艇投掷水雷改为飞机投掷深水炸弹,起爆深度由100米改为25米左右,即当德方潜艇刚下潜时攻击效果最佳;运送物资的船队及护航舰艇的编队由小规模、多批次改为大规模、少批次,从而减少了损失率丘吉尔采纳Morse的建议,从而打破德国封锁;重创德国潜艇部队;Morse同时获得英国及美国战时最高勋章二战期间例三:英国战斗机中队援法决策。


运筹学的概念运筹学是一种综合性学科,它在现代管理中起着至关重要的作用。
运筹学是一种运用数学、统计学、计算机科学以及其他相关领域的方法和理论来帮助制定最优决策的学科。
它的主要目标是通过通过信息分析和决策模型来使决策者在制定决策时更加合理、科学和精准。
下面是对运筹学概念的详细介绍。
一、运筹学的基本定义运筹学(Operations Research,简称OR)是一门科学,通过使用计算机和数学模型,研究如何最好地利用有限资源来达到预期目标,主要研究方法包括优化、数理统计、决策分析、模拟等。
二、运筹学的发展历程运筹学是在二战期间发展出来的,主要应用于军事后勤问题的解决。
之后,运筹学学科马不停蹄地在各个领域快速发展,至今已经成为了一门广泛的学科。
三、运筹学的应用范围运筹学在各个领域都有广泛的应用,例如生产制造、物流管理、金融风险管理、医疗管理、资源分配等。
它在实践中的应用能够使企业和组织在有限的资源下获得最大收益。
例如,电商企业可以利用运筹学和网络优化技术来解决配送问题。
医院可以利用运筹学与供应链的整合优化来提高采购成本的效率。
银行等金融机构则可以利用运筹学来建立风险管理模型,减轻市场波动造成的经济损失。
四、运筹学的关键技术该学科主要基于优化、数学建模、统计推断和计算机仿真等关键技术。
对于不同的问题,会采用不同的技术手段。
例如,对于线性规划问题,使用线性规划算法进行求解;对于决策树问题,可以使用决策树算法进行求解;对于复杂的大规模问题,可以使用数学建模与计算机仿真技术进行求解。
总之,运筹学是为了解决实际问题而产生的一种学科,它在生产、经济、政策等许多领域有广泛应用,发展迅速,使得成本降低、管理规范化、业务流程优化等问题得到了解决。

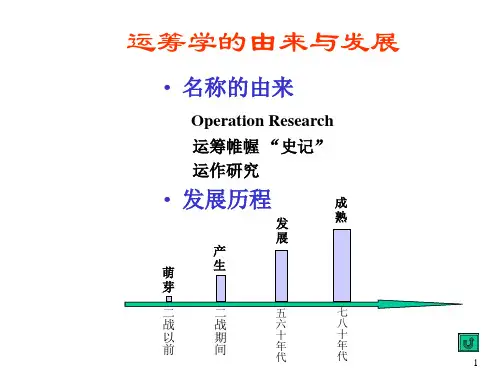
运筹学的起源与发展运筹学是一门研究优化资源配置、提高系统效率的学科。
从古代的军事思想和管理哲学中起源,运筹学经过多个阶段的发展,已成为解决现实问题不可或缺的工具。
1、运筹学的起源运筹学的思想可以追溯到古代。
例如,古代的军事家在策划战役时,会考虑兵力、战略和战术等因素,力求以最小的代价取得最大的胜利。
这种对资源优化配置的追求,正是运筹学的核心思想。
在管理哲学中,运筹学也得到了应用,如古代的皇帝在治理国家时,会考虑各种资源、政策和社会稳定等因素,以制定出最优的政策。
2、运筹学的发展运筹学真正的发展是在20世纪初。
当时,由于工业革命的出现,人们开始面对更加复杂的大规模问题,如生产计划、物资管理和交通运输等。
这些问题的出现促进了运筹学的诞生。
2.1产生阶段20世纪初,一些科学家开始运用数学和统计学方法来解决实际问题。
例如,亨利·福特在生产线上采用流水线生产方式,大大提高了汽车的生产效率。
这个阶段的主要成果是确定了运筹学的基本研究方法和应用领域。
2.2发展阶段在20世纪中叶,运筹学得到了进一步发展。
随着计算机技术的进步,运筹学开始采用更加高效的算法和优化技术,以解决更加复杂的问题。
例如,兰德公司在这个时期为美国军方提供了一系列重要的优化方案,为美国在冷战中的胜利做出了贡献。
2.3成熟阶段进入21世纪,运筹学已经发展成为一门成熟的学科。
随着大数据和人工智能等新技术的出现,运筹学开始与这些领域深度融合,形成了诸多新的研究方向和应用领域。
例如,机器学习和人工智能技术在运筹学中的应用,为解决实际问题提供了更加强大的支持。
3、运筹学的应用运筹学在各个领域都有广泛的应用。
在商业领域,运筹学被用来制定供应链管理、生产计划和库存管理等策略,以提高企业的效率和竞争力。
例如,亚马逊通过运用运筹学算法来优化其物流和仓储系统,从而实现了高效的商品配送和服务。
在工业领域,运筹学被应用于生产过程优化、设备维护和能源管理等方面。
运筹学的名词解释运筹学(Operations Research),又被称为运筹学、管理科学或决策科学,是一门综合运用数学、经济学和工程学等多学科的方法和技术,解决复杂问题的学科。
运筹学的主要目标是通过最优化方法和决策分析,提高系统的效率、效果和可行性。
运筹学的应用范围非常广泛,几乎涉及到各个领域,包括工业制造、物流管理、交通运输、金融投资、医疗卫生、军事战略、环境保护等等。
无论是企业的生产调度、供应链管理,还是城市交通的拥堵优化、航空航线的规划,运筹学都能发挥重要作用。
在运筹学的分析中,最为常见的方法之一是最优化。
最优化在数学中是一个非常重要的概念,它可以帮助我们找到一个系统或者问题的最佳解决方案。
最优化方法可以通过建立数学模型和运用优化算法来实现。
在实际应用中,最优化方法可以用来解决资源利用、成本控制、风险管理等问题,从而提高整个系统的效率和竞争力。
除了最优化方法,运筹学还涉及到决策分析。
决策分析是通过建立决策模型,分析不同决策方案的优劣,并选择最佳的决策方案。
决策分析可以帮助管理者在不确定性和风险下作出明智的决策。
在现实生活中,决策分析可以应用于项目管理、投资决策、市场营销、风险评估等方面,对于优化资源配置和风险控制起到关键作用。
运筹学的研究方法可以分为定量研究和定性研究两大类。
定量研究是基于数学、统计和计算机等工具,通过数据分析和模型建立,进行量化分析的研究方法。
定量研究可以提供精确的数据和结果,有助于准确判断问题的本质和解决方案的有效性。
而定性研究则更注重于描述性和解释性的研究方法,通过文字叙述、案例分析等方式,挖掘问题背后的隐含规律和原因。
定性研究可以帮助我们深入理解问题的本质,从而更好地制定解决方案。
运筹学的发展离不开计算机的支持。
随着计算机技术的进步,运筹学得以快速发展并取得了重大的突破。
计算机可以进行大规模的数据分析和模型求解,提高运筹学的效率和精确度。
同时,计算机还可以完成复杂的运算和优化算法,为决策提供多种方案,并通过模拟实验进行验证。
日常生活当中去了。
运筹学可以根据问题的要求,通过数学上的分析、运算,得出各种各样的结果,最后提出综合性的合理安排,以达到最好的效果。
运筹学作为一门用来解决实际问题的学科,在处理千差万别的各种问题时,一般有以下几个步骤:确定目标、制定方案、建立模型、制定解法。
虽然不大可能存在能处理极其广泛对象的运筹学,但是在运筹学的发展过程中还是形成了某些抽象模型,并能应用解决较广泛的实际问题。
随着科学技术和生产的发展,运筹学已渗入很多领域里,发挥了越来越重要的作用。
运筹学本身也在不断发展,规划论(包括线性规划、非线性规划、整数规划和动态规划)、图论、网络流、决策分析、排队论、可靠性数学理论、库存论、博弈论、搜索论、模拟等等。
运筹学有广阔的应用领域,它已渗透到诸如服务、搜索、人口、对抗、控制、时间表、资源分配、厂址定位、能源、设计、生产、可靠性等各个方面。
运筹学是软科学中"硬度"较大的一门学科,是系统工程学和现代管理科学中的一种基础理论和不可缺少的方法、手段和工具。
运筹学已被应用到各种管理工程中,在现代化建设中发挥着重要作用。
历史起源运筹学作为一门现代科学,是在第二次世界大战期间首先在英美两国发展起来的,有的学者把运筹学描述为就组织系统的各种经营作出决策的科学手段。
P.M.Morse与G.E.Kimball在他们的奠基作中给运筹学下的定义是:"运筹学是在实行管理的领域,运用数学方法,对需要进行管理的问题统筹规划,作出决策的一门应用科学。
"运筹学的另一位创始人定义运筹学是:"管理系统的人为了获得关于系统运行的最优解而必须使用的一种科学方法。
"它使用许多数学工具(包括概率统计、数理分析、线性代数等)和逻辑判断方法,来研究系统中人、财、物的组织管理、筹划调度等问题,以期发挥最大效益。
现代运筹学的起源可以追溯到几十年前,在某些组织的管理中最先试用科学手段的时候。
可是,普遍认为,运筹学的活动是从二次世界大战初期的军事任务开始的。
当时迫切需要把各项稀少的资源以有效的方式分配给各种不同的军事经营及在每一经营内的各项活动,所以美国及随后美国的军事管理当局都号召大批科学家运用科学手段来处理战略与战术问题,实际上这便是要求他们对种种(军事)经营进行研究,这些科学家小组正是最早的运筹小组。
第二次世界大战期间,"OR"成功地解决了许多重要作战问题,为"OR"后来的发展铺平了道路。
当战后的工业恢复繁荣时,由于组织内与日俱增的复杂性和专门化所产生的问题,使人们认识到这些问题基本上与战争中所曾面临的问题类似,只是具有不同的现实环境而已,运筹学就这样潜入工商企业和其它部门,在50年代以后得到了广泛的应用。
对于系统配置、聚散、竞争的运用机理深入的研究和应用,形成了比较完备的一套理论,如规划论、排队论、存贮论、决策论等等,由于其理论上的成熟,电子计算机的问世,又大大促进了运筹学的发展,世界上不少国家已成立了致力于该领域及相关活动的专门学会,美国于1952年成立了运筹学会,并出版期刊《运筹学》,世界其它国家也先后创办了运筹学会与期刊,1959年成立了国际运筹学协会(International Federation of Operations ResearchSocieties ,IFORS)。
运筹学展望运筹学正朝着3个领域发展:运筹学应用、运筹科学和运筹数学。
现代运筹学面临的新对象是经济、技术、社会、生态和政治等因素交叉在一起的复杂系统,因此必须注意大系统、注意与系统分析相结合,与未来学相结合,引入一些非数学的方法和理论,采用软系统的思考方法。
总之,运筹学还在不断发展中,新的思想、观点和方法不断出现。
应用重点1.市场销售:在广告预算和媒体的选择、竞争性定价、新产品开发、销售计划的制定等方面。
如美国杜邦公司在五十年代起就非常重视将作业研究用于研究如何做好广告工作、产品定价和新产品的引入。
通用电力公司对某些市场进行模拟研究。
2.生产计划:在总体计划方面主要是从总体确定生产、储存和劳动力的配合等计划以适应变动的需求计划,主要用线性规划和仿真方法等。
此外,还可用于生产作业计划、日程表的编排等。
还有在合理下料、配料问题、物料管理等方面的应用。
3.库存管理:存货模型将库存理论与计算器的物料管理信息系统相结合,主要应用于多种物料库存量的管理,确定某些设备的能力或容量,如工厂的库存、停车厂的大小、新增发电设备容量大小、计算机的主存储器容量、合理的水库容量等。
4.运输问题:这里涉及空运、水运、公路运输、铁路运输、捷运、管道运输和厂内运输等。
包括班次调度计划及人员服务时间安排等问题。
5.财政和会计:这里涉及预算、贷款、成本分析、定价、投资、证券管理、现金管理等。
用得较多的方法是:统计分析、数学规划、决策分析。
此外,还有盈亏点分析法、价值分析法等。
6.人事管理:这里涉及六方面。
(1)人员的获得和需求估计;(2)人才的开发,即进行教育和训练;(3)人员的分配,主要是各种指派问题;(4)各类人员的合理利用问题;(5)人才的评价,其中有如何测定一个人对组织、社会的贡献;(6)薪资和津贴的确定等。
7.设备维修、更新和可靠度、项目选择和评价:如电力系统的可靠度分析、核能电厂的可靠度以及风险评估等。
8.工程的最佳化设计:在土木、建筑、水利、信息、电子、电机、光学、机械、环境和化工等领域皆有作业研究的应用。
9.计算器和讯息系统:可将作业研究应用于计算机的主存储器配置,研究等候理论在不同排队规则对磁盘、磁鼓和光盘工作性能的影响。
有人利用整数规划寻找满足一组需求档案的寻找次序,利用图论、数学规划等方法研究计算器讯息系统的自动设计。
10.城市管理:包括各种紧急服务救难系统的设计和运用。
如消防队救火站、救护车、警车等分布点的设立。
美国曾用等候理论方法来确定纽约市紧急电话站的值班人数。
加拿大亦曾研究一城市警车的配置和负责范围,事故发生后警车应走的路线等。
此外,诸如城市垃圾的清扫、搬运和处理;城市供水和污水处理系统的规划等等。
具体内容运筹学的具体内容包括:规划论(包括线性规划、非线性规划、整数规划和动态规划)、库存论、图论、决策论、对策论、排队论、可靠性理论等。
数学规划即上面所说的规划论,是运筹学的一个重要分支,早在1939年苏联的康托洛维奇(H.B.Kahtopob )和美国的希奇柯克(F.L.Hitchcock)等人就在生产组织管理和制定交通运输方案方面首先研究和应用一线性规划方法。
1947年旦茨格等人提出了求解线性规划问题的单纯形方法,为线性规划的理论与计算奠定了基础,特别是电子计算机的出现和日益完善,更使规划论得到迅速的发展,可用电子计算机来处理成千上万个约束条件和变量的大规模线性规划问题,从解决技术问题的最优化,到工业、农业、商业、交通运输业以及决策分析部门都可以发挥作用。
从范围来看,小到一个班组的计划安排,大至整个部门,以至国民经济计划的最优化方案分析,它都有用武之地,具有适应性强,应用面广,计算技术比较简便的特点。
非线性规划的基础性工作则是在1951年由库恩(H.W.Kuhn)和塔克(A.W.Tucker)等人完成的,到了70年代,数学规划无论是在理论上和方法上,还是在应用的深度和广度上都得到了进一步的发展。
数学规划的研究对象是计划管理工作中有关安排和估值的问题,解决的主要问题是在给定条件下,按某一衡量指标来寻找安排的最优方案。
它可以表示成求函数在满足约束条件下的极大极小值问题。
数学规划和古典的求极值的问题有本质上的不同,古典方法只能处理具有简单表达式,和简单约束条件的情况。
而现代的数学规划中的问题目标函数和约束条件都很复杂,而且要求给出某种精确度的数字解答,因此算法的研究特别受到重视。
这里最简单的一种问题就是线性规划。
如果约束条件和目标函数都是呈线性关系的就叫线性规划。
要解决线性规划问题,从理论上讲都要解线性方程组,因此解线性方程组的方法,以及关于行列式、矩阵的知识,就是线性规划中非常必要的工具。
线性规划及其解法-单纯形法的出现,对运筹学的发展起了重大的推动作用。
许多实际问题都可以化成线性规划来解决,而单纯形法有是一个行之有效的算法,加上计算机的出现,使一些大型复杂的实际问题的解决成为现实。
非线性规划是线性规划的进一步发展和继续。
许多实际问题如设计问题、经济平衡问题都属于非线性规划的范畴。
非线性规划扩大了数学规划的应用范围,同时也给数学工作者提出了许多基本理论问题,使数学中的如凸分析、数值分析等也得到了发展。
还有一种规划问题和时间有关,叫做"动态规划"。
近年来在工程控制、技术物理和通讯中的最佳控制问题中,已经成为经常使用的重要工具。
库存论是一种研究物质最优存储及存储控制的理论,物质存储时工业生产和经济运转的必然现象。
如果物质存储过多,则会占用大量仓储空间,增加保管费用,使物质过时报废从而造成经济损失;如果存储过少,则会因失去销售时机而减少利润,或因原料短缺而造成停产。
因而如何寻求一个恰当的采购,存储方案就成为库存论研究的对象。
图论是一个古老的但又十分活跃的分支,它是网络技术的基础。
图论的创始人是数学家欧拉。
1736年他发表了图论方面的第一篇论文,解决了著名的哥尼斯堡七桥难题,相隔一百年后,在1847年基尔霍夫第一次应用图论的原理分析电网,从而把图论引进到工程技术领域。
20世纪50年代以来,图论的理论得到了进一步发展,将复杂庞大的工程系统和管理问题用图描述,可以解决很多工程设计和管理决策的最优化问题,例如,完成工程任务的时间最少,距离最短,费用最省等等。
图论受到数学、工程技术及经营管理等各方面越来越广泛的重视。
排队论又叫随机服务系统理论。
最初是在二十世纪初由丹麦工程师艾尔郎关于电话交换机的效率研究开始的,在第二次世界大战中为了对飞机场跑道的容纳量进行估算,它得到了进一步的发展,其相应的学科更新论、可靠性理论等也都发展起来。
1909年丹麦的电话工程师爱尔朗(A.K.Erlang)排队问题,1930年以后,开始了更为一般情况的研究,取得了一些重要成果。
1949年前后,开始了对机器管理、陆空交通等方面的研究,1951年以后,理论工作有了新的进展,逐渐奠定了现代随机服务系统的理论基础。
排队论主要研究各种系统的排队队长,排队的等待时间及所提供的服务等各种参数,以便求得更好的服务。
它是研究系统随机聚散现象的理论。
排队论又叫做随机服务系统理论。
它的研究目的是要回答如何改进服务机构或组织被服务的对象,使得某种指标达到最优的问题。
比如一个港口应该有多少个码头,一个工厂应该有多少维修人员等。
因为排队现象是一个随机现象,因此在研究排队现象的时候,主要采用的是研究随机现象的概率论作为主要工具。