当前位置：文档之家 › 第2章：正弦交流电

第2章：正弦交流电

  • 格式：doc
  • 大小：1.62 MB
  • 文档页数：19

下载文档原格式

  / 19

合集下载

电工电子技术-第2章 正弦交流电路

电工电子技术-第2章 正弦交流电路
区别与一般复数，相量的头顶上一般加符号“·”。 例：正弦量i=14.1sin(ωt+36.9°)A的最大值相量表示为：
•
I m = 14.1∠36.9°A
其有效值相量为：I• = 10∠36.9°A
由于一个电路中各正弦量都是同频率的，所以相量只需 对应正弦量的两要素即可。即模值对应正弦量的最大值或 有效值，幅角对应正弦量的初相。
i u u、i 即时对应！ R
电流、电压的瞬时值表达式
设 i Im sin t u、i 同相！
则 u ImR sin t Um sin t
u、i最大值或有效值之间符
合欧姆定律的数量关系。
Um ImR
或
U IR
•
相量关系式
•
I
U
U0
U
0 I0
RRR
相量图
U
I
（2）电阻元件上的功率关系
3
C -4
D
D 3 j4 第四象限 D 5 arctan 4
3
上式中的j 称为旋转因子，一个复数乘以j相当于在复
平面上逆时针旋转90°；除以j相当于在复平面上顺时针
旋转90°。
※数学课程中旋转因子是用i表示的，电学中为了区别 于电流而改为j。
正弦量的相量表示法
与正弦量相对应的复数形式的电压和电流称为相量。为
乘、除时用极坐标形式比较方便。
在复数运算当中，一定要根据复数所在象
限正确写出幅角的值。如：
+j
B4
A
A 3 j4 第一象限 A 553.1arctan 4 3
B 3 j4 第二象限 B 5180 arctan 4
-3 0
3
+1
3

电工电子技术第2章

电工电子技术第2章

第2章 正弦交流电路
在交流电路中，因各电流和电压多 +j A 为同一频率的正弦量，故可用有向线段 b r 来表示正弦量的最大值(有效值) Im 、 ψ Um(I、U)和初相ψ ，称为正弦量的相量。 O a +1 在正弦量的大写字母上打“•”表示，如 图2-5 有向线段的表示正弦量 幅值电流、电压相量用 I m、 m表示，有 U • U 效值电流、电压相量用 I 、 表示。将电 U • 路中各电压、电流的相量画在同一坐标 φ I ψ 中，这样的图形称为相量图。 ψ 同频率的u和i可用图2-6相量图表示。 图2-6 u和i的相量图 即 超前 Iφ°，I或 U滞后φ°。 U
第2章 正弦交流电路
2.1
正弦交流电的基本概念
正弦交流电压和电流的大小和方向都按正弦规律 作周期性变化，波形如图2-1a。
u U m s in ( t u ) i I m s in ( t i )
(2-1)
为便于分析，在电路中电压参考方向用“+”、“–” 标出，电流参考方向用实线箭头表示；电压、电流实 际方向用虚线箭头表示如图2-1b、c所示
第2章 正弦交流电路
u Im O φ Ψu Ψi i Um
u
i
t
T
图2-2 u和i相位不等的正弦量波形图
当φ=0º 时，称u、I同相；当φ=180º 时，称u比i反相； 当φ=±90º 时，称u与i正交 。 u i u i
u i
ui
u
i
t
u
i
O a) 同相
t O
b) 反相
O c)正交
t
图2-3 正弦量的同相、反相和正交
第2章 正弦交流电路

正弦交流电

正弦交流电

同频正弦信号的相位关系
同
相 位
2
1
相
i2
位

i1
t
i1 1 2 0
t
i i 领先于
1
2
相
i1
位
落 后
2 1
i2
1 2 0
t i i1 落后于 2
例 已知： i sin1000 t 30
幅度： 频率：
Im 1A
I 1 0.707 A 2
1000 rad/s f 1000 159 Hz
解：
3
I 141 .4 30 100 30 86.6 j50 A 2
U 311.1 60 220 60 110 j190.5 V 2
I
100 / 6
/3
220
U
例2：已知相量，求瞬时值。
已知两个频率都为 1000 Hz 的正弦电流其相量形
式为： I1 100 60 A
I2 10 e j30 A
ω
Um
t
矢量长度 = U m
矢量与横轴夹角 = 初相位
矢量以角速度ω 按逆时针方向旋转
相量的书写方式
旋转矢量
最大值 Um
有效值 U
1. 描述正弦量的有向线段称为相量 (phasor )。若其
幅度用最大值表示 ，则用符号： Um、Im
2. 在实际应用中，幅度更多采用有效值，则用符号：
3. 相量符号 U、I包含幅度与相位信息 U、I
则： U U1 U2 U1 U 2 e j(12 )
3. 除法运算
设： U1 U1e j1 U2 U 2e j 2
则：
U1 U2
U1 U2
e j12

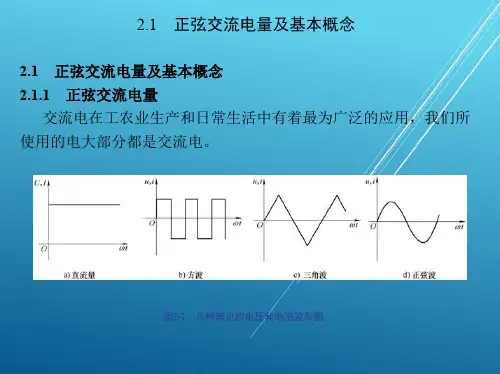
电工第2章 正弦交流电路

电工第2章 正弦交流电路
函数(cos)。 1.正弦量数学表达式
图2-2 正弦交流电波形图
2.1 正弦交流电量及基本概念
(1)最大值 又称为幅值，是正弦量的最大值，用带右下标m的大写 字母表示，如Im、Um、Em分别表示正弦电流、正弦电压、正弦电动 势的最大值。 (2)角频率ω 在单位时间内正弦量所经历的电角度，用ω表示，其单 位为弧度每秒(rad/s)。正弦交流电变化一次所需的时间，称为周期T， 其单位为秒（s），正弦量在单位时间内变化的次数，称为频率f， 其单位为赫[兹](Hz)。
图2-9 纯电阻电路
2.3 单一参数元件的正弦交流电路
(2) 有效值关系 由电流与电压的幅值关系Im= Um /R，两端同除 以 ，可得它们的有效值关系为U=IR (3) 相量关系 因为电流i和电压u均为同频率的正弦量。 相量形式为 2.电阻元件的功率 (1) 瞬时功率 在关联参考方向下，电阻元件的 瞬时功率(用小写字母p表示)：
图2-4 两正弦量的同相与反相
2.1 正弦交流电量及基本概念
例2.1 已知正弦量u=220sin(314t + 30°)V， 试求正弦量的三要素、有效值及变化周期。 解：对照式(2-1)，可知三要素：
2.1 正弦交流电量及基本概念
例2.2 已知正弦电压u和正弦电流i1、i2的瞬时表达式为u = 310sin(ωt -45°)V，，i2=28.2sin(ωt +45°)A，试以电压u为参考量重新写出u和 电流i1、i2的瞬时值表达式。 解：以电压u为参考量， 则电压u的表达式为 由于i1、i2与u的相位差为
2.2 正弦交流电的相量表示方法
2.2.2 正弦量的相量表示法 正弦量和相量是一一对应关系（注意：正弦量和相量不是相等
关系！）。在复平面中，例如相量可用长度为 ，与实轴正向的夹 角为ψ的矢量表示。这种表示相量的图形称为相量图。如图2-7所示

第二章 正弦交流电习题集

第二章 正弦交流电习题集

第二章正弦交流电一、填空1、已知u = 102sin（3140 t －240º）V ，则U m = V，U= V，ω=rad/s，f = Hz，T = s, Φ= 。

2、有一正弦交流电流：i(t)=5×1.414sin(1000t＋300o)A，那么它的有效值为I= ，角频率ω= ，初相角Φi= 。

3、周期T=0.02s，振幅为50V、初相角为60º的正弦交流电压u的解析式为，其有效值。

4、用电流表测得一正弦交流电路中的电流为10A ，则其最大值为A。

5、在正弦交流电中完成一次周期性变化所用的时间叫。

6、正弦交流电1s内变化的次数叫做正弦交流电的。

7、周期、频率和角频率三者间满足的关系是。

8、描述正弦量的三要素是。

9、电容器的容抗与自身电容量之间是（正比或反比）关系，与信号频率之间是（正比或反比）关系。

10、下列属于直流电压范围的有（），属于交流电压范围的是（）。

11、线圈的感抗与自身电感值之间是（正比或反比）关系，与信号频率之间是（正比或反比）关系。

12、在纯电阻电路中，功率因数为，感性负载电路中，功率因数介于与之间。

13、在R-L-C串联电路中，当X L>X C时，电路呈_ _性；当X L<X C时，电路呈_ 性；当X L=X C时，电路呈_ _性。

14、三相交流电相序正序为。

15、三相电源的连接方式有与两种，常采用方式供电。

16、根据电流对人体的伤害程度，触电可分为与两种。

18、当三相交流发电机作星形连接时，线路中存在着两种电压，一种是，它是与之间的电压。

另一种是,它是之间的电压。

这两种电压有效值之间的关系是。

19、对称三相电源星形连接时,U L= U P,线电压的相位超前于它所对应相电压的相位。

20、正序对称三相星形连接电源,若U VW,则U UV= V,U U= V,U W= V。

二、选择填空1、交流电流表在交流电路中的读数为（）A、瞬时值B、平均值C、最大值D、有效值2、正弦交流电压u=100Sin(628t+60°)V，它的频率为（）A、100HZB、50 HZC、60 HZD、628 HZ3、已知正弦交流电流i= 10T2sin（314t+25o）则频率为（）A、50H ZB、220H ZC、314H ZD、1000H Z4、已知正弦交流电压u=220sin(314t-30o)则其角频率为（）A、30B、220C、50D、100π5 、正弦交流电的有效值为10A，频率为50H Z，初相位为-30°，它的解析式为（）A、i=10sin（314t+30°）AB、i=10sin（314t30°）AC、i=10sin（314t-30°）AD、i=10sin（50t+30°）A6、相量U=100e-j60°V的解析式为（）A、u=100 2 sin(ωt-60°)VB、u=100sin(ωt-60°)VC、u=100sin(ωt+60°)VD、u=100 2 sin(ωt+60°)V7、关于正弦交流电相量的叙述中，（）的说法不正确的。

第二章正弦交流电的表示方法

第二章正弦交流电的表示方法
R R R
I
U
电工电子技术
（2）电阻元件上的功率关系
1)瞬时功率 p
瞬时功率用小写！
i I m sin ( t )
uip
则 p u i U m sin t I m sin t u U m sin ( t ) U m I m sin 2 t
p
u
0
i
ωt
结论：1. p随时间变化 2. p≥0；耗能元件,吸收电能，转换为热能
最大值 频率 初相角
第一篇
电工电子技术
一、解析式表示法
例1：已知某正弦交流电流的最大值是 2 A，频率为 50 Hz，初 相位为 60 ，写出该电流的解析式，并求t=0时的瞬时值。 Im=2A ；
ω 2πf 2 50π 100π rad / s
60
i0

则它的解析式是： i = Imsin( t i0) = 2sin(100π t 60) A t=0s时的电流瞬时值是： i = 2sin(100π ×0 60°) = 2sin(60) =2× 3 = 3 A
答：初相位是2π /3 rad，t=0.5s时的瞬时值是1.59A。
电工电子技术 五、正弦交流电的表示方法
前提： 在分析正弦交流电路时，同一电路中的 所有电压、电流都是同频率的正弦量， 且频率与电源的频率相同。 因此： 一个正弦量由最大值（或有效值）和初 相位两个要素也能确定。 描述正弦交流电的有向线段称为相量。
电工电子技术
参数
见书32页
2、电容
（1）电容是表征电容器容纳电荷本领的物 理量，用字母C表示，单位是F（法拉）。 1F=106μF=1012pF （2）电容的大小与极板间的介电常数ε， 电容极板的正对面积S，电容极板的距离d有 关。

电路 第二章 正弦交流电路(1)

11
所以交流电的有效值就是与它热效应相等的直流电的数值， 它们之间的关系由焦耳－楞次定律确定。为了区别，交流电 流、电压和电动势的有效值分别用大写字母I、U、E表示。 设正弦电流i＝Imsin(ωt+ψ)，通过计算可知，正弦电流的有 效值是其最大值的1/√2倍，如图2—9(c)所示，即 I＝Im/√2 ＝0.707Im (2—9) 同理，正弦电压和电动势的有效值分别为 U＝Um/√2 ; E＝Um/√2 在工程上，主要使用有效值，今后不加特别声明，交流电 的大小均指有效值。从交流电流表和电压表上读取的数值也 是有效值。电气设备所标明的交流电压、电流数值也都是有 效值。可以证明有效值为正弦量在一个周期内的方均根值， 即它不随时间变化，因此，和最大值比较，有效值更为实用。
15
相量也可以用复平面上的有向线段来表示。如图所示。这种 用来表示相量的图形，叫相量图，相量图与力学和物理学中 的向量图相似。但是，相量表示的是随时间作正弦变动的函 数，而向量指的是力、电 场强度等空间向量。 2 因为实际工程中，常采用正弦量的有效值，而且最大值与 有效值之间有着固定的 2关系，所以有效值相量应用较多。 它等于最大值相量除以 2 ，即 U=Um/ 2 同理 I＝Im/ 2
上式表明，为了保证电动势的频率稳定，必须保 持发电机转速稳定。 周期T、频率f及角频率ω反映了正弦量随时间作 ω 周期性交变的快慢。各国在电力工业上所用交流 电的频率都规定了各自的标准。我国和有些国家 电力工业的标准频率为50Hz，称为工频。一般我 们讲交流电时，如果不加说明，指的就是50Hz的 工频。还有一些国家工频采用60Hz。
采用适当的磁极形状，使电枢表面的磁感应强度B 沿圆周按正弦规律分布，如图 (a)所示。由于铁芯 的磁导率远大于空气的磁导率，故磁力线的方向 与铁芯表面垂直。在磁极之间的分界面O～O',B＝ 0，称为磁中性面。在磁极的轴线上，磁感应强度 具有最大值Bm 。设线圈的一条有效边AA'(切割磁 力线的部分)和转轴所组成的平面，与磁中性面的 夹角为α，则AA'边所处位置的磁感应强度为(见图 2—2) B＝Bmsinα 当电枢被原动机拖动，在磁场中以逆时 针方向作 等速旋转时，电枢线圈有效 边因切 割磁力线而产生感 应电动势。其表达式为 e＝Emsinωt (2—1)

2015第2章电工电子学

知识点及重点
1、正弦交流电的三要素、相位差、有效值和相量表示 法。 2、掌握用相量法计算简单正弦交流电路的方法
3、掌握有功功率、功率因数、无功功率和视在功率的 概念和计算方法。
4、提高功率因数的方法及意义 5、正弦交流电路串联谐振和并联谐振的条件。
2
第2章 正弦交流电路 2.1 正弦交流电的基本概念
15
2.2.2 正弦量的相量表示
对于任意一个正弦时间函数都有唯一与其对应的复数函数
i 2I sin (t )
相量为有 效值相量
2Ie
jt
j(t )
2 Ie e
复常数
j
jt

2 Ie
I I i
相量的模表示正弦量的有效值 相量的幅角表示正弦量的初相位
i(t ) 包含了三要素：I、 、 ，相量包含了I ,
第2章 正弦交流电路
2.1 正弦交流电的基本概念
2.2 正弦交流电的相量表示法 2.3 单一参数的正弦交流电路
2.4 正弦交流电路的分析 2.4.1基尔霍夫定律的相量形式 2.4.2正弦交流电路的串联电路 2.4.3正弦交流电路的电压、电流分析 2.5 正弦交流电路的功率
2.6 电路的谐振
1
第2章 正弦交流电路
24
2.3.2 电感元件的正弦交流电路
（2）.波形图及相量图：
uL O
pL i
2
UL
t
电压超前电 流900
I
i
电感电压与电流波形为同频率，电感的电压相 位要比电流的相位超前。
25 返回 上一节 下一节 上一页 下一页
2.3.2 电感元件的正弦交流电路
2.功率关系 u i (1) 瞬时功率 p=ui = Umcosωt Im sinωt O ωt = U I sin 2ωt 2 3 2 (2) 平均功率 ( 有功功率) 2 p 1 T P = T ∫ p0 dt = 0 (3) 无功功率 O ωt Q = U I = XLI2 3 2 2 2 2 = U (var) 发出 XL 发出 结论：纯电感不消耗能量， 取用 取用 只和电源进行能量交换（能量的吞吐）。26

电工学第二章

当电容两端的电压增大时，电场能量增大，在 此过程中，电容从电源取用电能转换为电场能量； 当电容两端的电压减小时，电场能量减小，电容释 放能量，电场能量转换为电能。可见电容器是一种 储能元件。
4.电容器的主要参数
（1）标称电容量 电容器的外壳上标出的电容量值称为标称电容量。
（2）允许偏差 电容器的允许偏差常用的有±2%、±5%、±10%、
用介电常数较大的物质作为电容器的电介质 可显著增大电容，而且能做成很小的极板间隔，因 而应用很广。
任何两个导体之间都存在着电容。
3. 电容器的充电和放电
（1）电容器的充电 当开关S置于A端，电源E通过电阻R 对电容器C开始充电。起初，充电电流 较大，但随着电容器C 两端电荷的不断积累，形成的电压 越来越高，它阻碍了电源 对电容器的充电，使充电电流越来越小，当电容器两端电压 达到了最大值E时，则不再变化，电流为零。故在直流稳态电 路中，电容相当于开路，这就是电容的隔直作用。
检测电感器
电感器的直流电阻很小，通常只有几欧或 几十欧，线径越细，圈数越多，电阻值越大。 一般情况下用万用表R×1电阻挡测量，只要能 测出电阻值，即可认为电感器是正常的；如果 测量结果为无穷大，说明电感器已经开路。
§2-3纯电阻、纯电感、纯电容交流电路
一、纯电阻交流电路
交流电路中如果只考虑电阻的作用，这种电 路称为纯电阻电路。
电容量也简称电容。
它只与电容器的极板正对面积、极板间距离 以及极板间电介质的特性有关；而与外加电压的 大小，电容器带电多少等外部条件无关。
C S
d
式中S、d、C的单位分别是m2、m、F，介电常 数ε的单位是F/m。
真空中的介电常数ε0≈8.86×10-12F/m ，某种介 质的介电常数ε与ε0之比，称该介质的相对介电常 数，用εr表示 。

第2章 正弦交流电路


eU Em sin t eV Em sin(t 120 ) eW Em sin(t 120 )
（2-31）
相应的波形图、相量图如图2-16（a）、 （b）所示。
图2-16 三相对称电动势
2．三相电源的星形联结
（1）星形联结
把上述三相绕组的末端U2、V2和W2连在一 起，就构成星形联结，如图2-17所示。
UR U 311 2 V 220V
【例2-4】
根据式（2-10），电流有效值为
P 100W IR 0.455A U R 220V
2.2.2 纯电感电路
1．电压和电流的关系
纯电感电路如图2-10（a）所示，电感电
流与电压参考方向一致，设电感电流为
iL 2 I L sin t
2.3.1 电压和电流关系 2.3.2 电路的功率和能量转换
2.3.1 电压和电流关系
RLC串联电路如图2-12所示，取电压和电 流的参考方向一致。 为便于分析，电路中各量均采用相量表 示，各元件也采用相量化模型。
图2-12 RLC串联电路
用相量法分析电路如下。
（1）作相量图
图2-13 相量图
（2）求相量和
IL IP
【例2-8】三相电源作星形联结，线电压是 380V，负载是额定电压为220V的电灯组，问： （1）三相负载采用什么联结方式； （2）若三相负载的等效电阻 R1=R2=R3=510 ， 求相电流、线电流和中线电流； （3）若三相负载的等效电阻分别为 R1=510 ， R2=510，R3=2k，求中线电流。
QC UC IC 50 0.157 var 7.85var
当 f 5 000Hz 时，
XC IC 1 1 3.19 2π fC 2 3.14 5 000 10 106
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第2章正弦交流电路第1 次课正弦量及其相量表示法一、学时：2学时二、目的与要求：1、交流电路不仅是交流电机和变压器的理论基础，而且要为电子电路作好理论基础，故这章是本课程的重要内容之一。

2、深刻理解正弦交流电的三要素、相位差及有效值概念。

3、熟悉正弦量的各种表示方法及相互间的关系。

三、重点：1、正弦量的特征及各种表示法。

2、 R、L、C的相量图和相位关系。

四、难点：相量计算中的相量图、相位关系。

五、教学方式：多媒体或胶片投影或传统方法。

六、习题安排：2.2.1、2.2.2七、教学内容：2.1 正弦电流与电压1、正弦量三要素i=I m sin(ωt+ψ) (下图是ψ=0时波形图)（1）I m：幅值（最大值）等于有效值I的根号2倍；有效值I等于发热效应等价的直流电流数值。

（2）角频率ω：等于2πf(频率)=2π/T（周期）；单位时间转过的弧度数（3）初相位ψ：t=0时，正弦量的起始相位角度；相位(ωt+ψ)：反映正弦量的变化进程。

2.相位差ϕ=ψ1-ψ2不随计时起点而变，反映同频率正弦量相位差，有超前、滞后等问题。

两个同频率正弦量的相位之差, 称为相位差, 用字母“φ”表示。

设两正弦量：（1）φ12=θ1-θ2>0且|φ12|≤π弧度U1达到振幅值后，U2需经过一段时间才能到达，U1越前于U2（2）φ12=θ1-θ2<0且|φ12|≤π弧度U1滞后U2 （3）φ12=θ1-θ2=0,称这两个正弦量同相 （4）φ12=θ1-θ2=π, 称这两个正弦量反相（5）φ12=θ1-θ2= , 称这两个正弦量正交2.2 相量表示法1、相量（1）定义： 正弦量除了用波形图及瞬时表达式表示外，还可用一个与之时应的复数表示，这个表示正弦量的复数称为相量。

即I=I ∠ψ按复数的运算法则计算加减用直角坐标或三角函数形式，乘除用指数形式或极坐标形式。

I =I ∠ψ=Ie j ψ=I(cos ψ+jsin ψ)212112222111)()()sin()sin(θθθωθωϕθωθω-=+-+=+=+=t t t U u t U u m m 2π(a )(b )(c )(d )2、相量图：（1）画法：把正弦量用一有向线段表示，同一量纲的相量采用相同的比例尺寸。

（2）加法减法运算：按平行四边形法则计算例题讨论✧ 已知工频正弦量为50Hz ，试求其周期T 和角频率。

【解】 T ＝f1＝Hz501＝0.02s ，ω＝2πf ＝2×3.14×50rad/s ，即工频正弦量的周期为0.02s ，角频率为314rad/s 。

✧ 已知两个正弦电流i 1＝4sin(ωt +30°)A ，i 2＝5sin(ωt -60°)A 。

试求i =i 1+i 2。

✧ 已知u A =2202sin314t V ，u B =2202sin(314t －120˚)V 和u C =2202sin(314t ＋120˚)V ，试用相量法表示正弦量，并画出相量图。

✧ 已知i 1＝100 2sin(ωt ＋45˚)A ，i 2＝602sin(ωt －30˚)A 。

试求总电流i ＝i １＋i ２，并做出相量图。

【解】由正弦电流i 1和 i 2的频率相同，可用相量求得 （1）先作最大值相量1mI =1002mI （2）用相量法求和电流的最大值相量mI ＝1m I +2m I ＝60129（A ）（3）将和电流的最大值相量变换成电流的瞬时值表达式i ＝1292sin(ωt ＋18.4˚) (A)（4）做出相量图，如右图所示。

也可以用有效值相量进行计算，方法如下 （1）先作有效值相量1I =100/45˚AI =60/－30˚ A2（2）用相量法求和电流的有效值相量，相量图如图2.2.５所示。

I ＝1I +2I ＝100/45˚＋60/－30˚＝129/18.4˚（A）（3）将和电流的有效值相量变换成电流的瞬时值表达式i＝129 2sin(ωt＋18.4˚) (A)由此可见，无论用最大值相量还是用有效值相量进行求和运算，其计算结果是一样的。

第 2 次课单一参数的交流电路一、学时：2学时二、目的和要求：1、掌握电阻、电感、电容等元件电路中电压电流之间各种关系。

2、理解瞬时功率、平均功率、无功功率的概念。

3、掌握感抗、容抗的概念。

三、重点：元件电压电流有效值、相量、相位关系。

四、难点：无功功率的概念。

五、教学方式：多媒体或胶片投影或传统方法。

六、习题安排：2.4.3、2.4.4七、教学内容：2.3单一参数的交流电路1、电阻元件及其交流电路（1）电压电流关系① 瞬时关系：u =iR②相量关系：令)sin(i m t I i ψω+= 即im mI I ψ∠=∙)sin(i m t RI u ψω+=um im mmU RI IR U ψψ∠=∠==∙∙mm RI U = 即R IU I U mm ==i u ψψ=u 、i 波形与相量如图（b ）（c ）所示。

（2）功率①瞬时功率)cos 1(sin 22t UI t I U ui p m m ωω-=== ②平均功率⎰===-=TRURIUI dt t UI TP 0222)cos 1(1ω（3）结论在电阻元件的交流电路中，电流和电压是同相的；电压的幅值（或有效值）与电流的幅值（或有效值）的比值，就是电阻R 。

（１） P>0 （耗能元件） （２） Ｐ随时间变化tt（３） Ｐ与Ｕ的平方Ｉ的平方成正比．2、电感元件的交流电路 （1）电压电流关系① 瞬时关系：dtdi Lu = ② 相量关系： 令)sin(i m t I i ψω+=即i m m I I ψ∠=∙如图（c ）i u mm LI U ψπψω+==2fL XL IU I U Lmm πω2====（称L X 为感抗）u 、I 的波形图与相量图，如图（b ）、(c)所示。

（2） 功率①瞬时功率为p =ui=U m I m sin ωt .sin(ωt+90º)=U m I m sin ωt .cos ωt=2m m I U sin2ωt ＝UI sin2ωt②平均功率为P ＝⎰Ttp T 0d 1＝⎰Ttt UIT 0d 2sin 1ω＝0im um m i mi mti m LI U U t LIt LI d t dI L u ψπωψψωπωψωωψω+∠=∠=⎪⎭⎫ ⎝⎛++=+=+=∙22sin )cos()sin(（3）结论电感元件交流电路中， u 比i 超前2；电压有效值等于电流有效值与感抗的乘积；平均功率为零，但存在着电源与电感元件之间的能量交换，所以瞬时功率不为零。

为了衡量这种能量交换的规模，取瞬时功率的最大值，即电压和电流有效值的乘积，称为无功功率用大写字母Q 表示，即 Q=UI=I 2X L =U 2/ X L (VAR)44443、电容元件交流电路（1）电压电流关系①瞬时关系： 如图（a ）所示i=C tu d d② 相量关系：在正弦交流电路中令u=U m sin （ωt +u ψ ）即 mU = u m U ψ∠ 则i = C tu d d =C tt U u d )sin(d m ψω+=ωCU m cos （ωt+u ψ）= ωCU m sin(ωt+u ψ+90º)=I m sin(ωt+u ψ+90º)I m =I m ∠ψi =ωCU m ∠900+u ψ可见，I m =ωCU m =U m /X C （X C =1/ωC 称为电容的容抗）ϕ=ψu -ψi = --900u 、i 的波形图和相量图，如图（b ）（c ） 。

（1）功率①瞬时功率p =u i =U m I m sin ωt.sin(ωt+90º) = U m I m sin ωt.cos ωt = 2m m I U sin2ωt＝ UIsin2ωt② 平均功率P ＝⎰Ttp T 0d 1＝⎰Ttt UIT 0d 2sin 1ω＝0（3）结论在电容元件电路中，在相位上电流比电压超前900；电压的幅值（或有效值）与电流的幅值（或有效值）的比值为容抗X C ；电容元件是储能元件，瞬时功率的最大值（即电压和电流有效值的乘积），称为无功功率，为了与电感元件的区别，电容的无功功率取负值，用大写字母Q 表示，即Q=－UI=－I 2X C =－U 2/ X C注： 1、 X C 、X L 与R 一样，有阻碍电流的作用。

2、适用欧姆定律，等于电压、电流有效值之比。

3、 X L 与 f 成正比，X C 与 f 成反比，R 与f 无关。

对直流电f =0，L 可视为短路，X C =∞，可视为开路。

对交流电f 愈高，X L 愈大，X C 愈小。

例题讨论✧ 把一个100Ω的电阻元件接到频率为50Hz ，电压有效值为10V 的正弦电源上，问电流是多少？如保持电压值不变，而电源频率改变为5000 Hz ，这时电流将为多少？解： 因为电阻与频率无关，所以电压有效值保持不变时，频率虽然改变但电流有效值不变。

即 I=U/R=（10/100）A=0.1=100mA若把上题中的，100Ω的电阻元件改为25μF 的电容元件，这时电流又将如何变化？【解】当f =50Hz 时X C ＝fCπ21＝)1025(5014.3216-⨯⨯⨯⨯＝127.4（Ω）I=CX U =4.12710=0.078（A ）=78（mA ）当f=5000Hz 时X C ＝)1025(500014.3216-⨯⨯⨯⨯＝1.274（Ω）I=274.110=7.8（A ）可见，在电压有效值一定时，频率越高，则通过电容元件的电流有效值越大。

第 3 次课 R 、L 、C 电路、电路中的谐振、功率因数的提高 一、学时：2学时 二、目的和要求：1、理解电路基本定律的相量形式和阻抗，并掌握用相量法计算简单正弦交流电路的方法；2、掌握有功功率和功率因数的计算，了解瞬时功率、无功功率、视在功率的概念和提高功率因数的经济意义；3、了解谐振的条件、特点及应用。

三、重点：相量计算中的相量图、相量关系的建立。

四、难点：单相交流电路的分析、计算方法。

五、教学方式：多媒体或胶片投影或传统方法。

六、习题安排：2.4.5、2.6.1、2.7.1 七、教学内容：2.4电阻、电感、电容元件串联的交流电路1.电路分析(1) 电压与电流的关系 u R =RI m sin ωt=U Rm sin ωt ①瞬时值计算：设i=I m sin ωt则 u = u R + u L + u C= RI m sin ωt+X L I m sin(ωt + 90º)+X C I m sin(ωt － 90º)=U m sin(ωt+φ)其幅值为U m ，与电流的相位差为φ。