Role of Parallel Tempering Monte Carlo Simulation in 2D Ising Spin Glass System with Distance De
- 格式:pdf
- 大小:393.51 KB
- 文档页数:8

A PROPOSAL FOR A BENCHMARK TO MONITOR THEPERFORMANCE OF DETAILED MONTE CARLO CALCULATIONOF POWER DENSITIES IN A FULL SIZE REACTOR CORE Current computers and Monte Carlo codes are not yet able to calculate the power density map in a full size reactor core with sufficient statistical accuracy.现有电脑以及蒙特卡罗代码不能以足够的令人满意的精度计算全堆芯的功率密度分布. The main aim of the benchmark is to determine the execution time for a Monte Carlo calculation of the power density with sufficient statistical accuracy in as many regions as possible and to monitor the efficiency of the calculation over the years considering improvements in Monte Carlo codes and computers.这次基准测试的主要目的是决定未得到足够精度的功率密度的蒙特卡罗计算所用的执行时间和监测计算的效率考虑到蒙特卡罗和计算技术的进度.Preliminary results with the MCNP5 code indicate that for a 1 % statistical uncertainty in the local power density more than 1010neutron hi stories must be simulated. 初步的结果表明为了得到1%一下的功率密度的统计学上的不准确,超过10^10=(10^7, 10 m illion ,1000)的中子历史记录必须被统计。

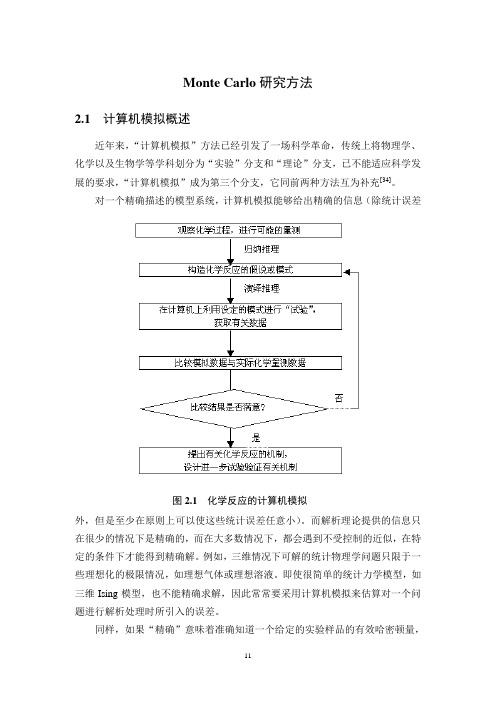
Monte Carlo研究方法2.1计算机模拟概述近年来,“计算机模拟”方法已经引发了一场科学革命,传统上将物理学、化学以及生物学等学科划分为“实验”分支和“理论”分支,已不能适应科学发展的要求,“计算机模拟”成为第三个分支,它同前两种方法互为补充[34]。
对一个精确描述的模型系统,计算机模拟能够给出精确的信息(除统计误差图2.1化学反应的计算机模拟外,但是至少在原则上可以使这些统计误差任意小)。
而解析理论提供的信息只在很少的情况下是精确的,而在大多数情况下,都会遇到不受控制的近似,在特定的条件下才能得到精确解。
例如,三维情况下可解的统计物理学问题只限于一些理想化的极限情况,如理想气体或理想溶液。
即使很简单的统计力学模型,如三维Ising模型,也不能精确求解,因此常常要采用计算机模拟来估算对一个问题进行解析处理时所引入的误差。
同样,如果“精确”意味着准确知道一个给定的实验样品的有效哈密顿量,那么由实验得到的数据也不是绝对准确的。
有时甚至不清楚实验观察到的某些现象究竟是固有的还是由未知杂质引起的。
由此可知,解析理论和实验结果之间的比较,并不总是导致确定无疑的结论,有时还需要用模拟来沟通理论和实验之间的隔阂。
模拟结果与实验结果相比,不受不精确的近似(它们通常是解析理论中不可避免的)的影响,可以检验模型是否忠实地代表实际系统。
通过模拟可以得到很多信息,不管什么物理量,只要研究者认为有用,就可以设法从模型中对其进行“抽样”。
此外,实验工作者虽然可以改变样品的温度和压力以探讨其影响,可是要估计原子间势能变化的影响,就比较困难了,而对计算机模拟来说,任意改变原子间作用力并不是什么大困难。
计算机模拟是用计算机方法研究化学反应及误差的重要手段之一,它构成化学计量学一个颇为独特的分支。
用计算机可模拟某些很难实际试验的化学反应,可用于研究化学量测方法,包括化学计量学数据解析方法的特性与误差,还可探讨有关化学反应的机理。

蒙特·卡罗方法(MonteCarlomethod)--也称统计模拟方法,是二十世纪四十年代中期由于科学技术的发展和电子计算机的发明,而被提出的一种以概率统计理论为指导的一类非常重要的数值计算方法。
是指使用随机数(或更常见的伪随机数)来解决很多计算问题的方法。
蒙特·卡罗方法(MonteCarlomethod),也称统计模拟方法,是二十世纪四十年代中期由于科学技术的发展和电子计算机的发明,而被提出的一种以概率统计理论为指导的一类非常重要的数值计算方法。
是指使用随机数(或更常见的伪随机数)来解决很多计算问题的方法。
蒙特·卡罗方法的名字来源于摩纳哥的一个城市蒙地卡罗,该城市以赌博业闻名,而蒙特·卡罗方法正是以概率为基础的方法。
与它对应的是确定性算法。
蒙特·卡罗方法在金融工程学,宏观经济学,计算物理学(如粒子输运计算、量子热力学计算、空气动力学计算)等领域应用广泛。
蒙特卡罗方法- 基本思想当所求解问题是某种随机事件出现的概率,或者是某个随机变量的期望值时,通过某种“实验”的方法,以这种事件出现的频率估计这一随机事件的概率,或者得到这个随机变量的某些数字特征,并将其作为问题的解。
有一个例子可以使你比较直观地了解蒙特卡罗方法:假设我们要计算一个不规则图形的面积,那么图形的不规则程度和分析性计算(比如,积分)的复杂程度是成正比的。
蒙特卡罗方法是怎么计算的呢?假想你有一袋豆子,把豆子均匀地朝这个图形上撒,然后数这个图形之中有多少颗豆子,这个豆子的数目就是图形的面积。
当你的豆子越小,撒的越多的时候,结果就越精确。
蒙特卡罗方法- 基本原理由概率定义知,某事件的概率可以用大量试验中该事件发生的频率来估算,当样本容量足够大时,可以认为该事件的发生频率即为其概率。
因此,可以先对影响其可靠度的随机变量进行大量的随机抽样,然后把这些抽样值一组一组地代入功能函数式,确定结构是否失效,最后从中求得结构的失效概率。


Nuclear Mathematical and Computational Sciences:A Century in Review,A Century AnewGatlinburg,Tennessee,April6-11,2003,on CD-ROM,American Nuclear Society,LaGrange Park,IL(2003) PARALLELIZATION OF THE PENELOPE MONTE CARLO PARTICLETRANSPORT SIMULATION PACKAGER.B.Cruise and R.W.SheppardUniversity Information Technology ServicesIndiana University2711E.Street,Bloomington,IN47408rcruise@;rsheppar@V.P.MoskvinDepartment of Radiation OncologyIndiana University School of Medicine535Barnhill Drive,RT-041,Indianapolis,IN46202vmoskvin@ABSTRACTWe have parallelized the PENELOPE Monte Carlo particle transport simulation package[1].Themotivation is to increase efficiency of Monte Carlo simulations for medical applications.Ourparallelization is based on the standard MPI message passing interface.The parallel code is especiallysuitable for a distributed memory environment,and has been run on up to256processors on the IndianaUniversity IBM Teraflop SP.Parallel speedup is nearly linear.Fortran90features have beenincorporated in the parallelized PENELOPE code.The code utilizes the parallel random numbergenerator(p.r.n.g.)developed by the MILC lattice-QCD collaboration[2].We have tested theparallelized PENELOPE in an application of calibration dosimetry of the Leksell Gamma Knife R[3].The parallel results of the test correspond with the serial results,which in turn have been empiricallyverified in[3].The parallelized PENELOPE Fortran90code,along with a simple example mainprogram,will be available from the Radiation Safety Information Computational Center(RSICC)atOak Ridge National Laboratory[4]upon completion of benchmark testing.Key Words:Monte Carlo simulation,MPI,parallel,PENELOPE,radiation transport1.INTRODUCTIONThe use of Monte Carlo(MC)methods for dose computation in radiation oncology applications has been limited by inadequate performance,even with continuing advances in computer architecture and clock speed.Clinical radiotherapy treatment planning systems should provide dose distributions with accuracy of 2–3%of the dose maximum,within an acceptable time limit(less than5minutes).Though most MC programs are quite fast for simulating dose deposition in homogeneous media and simple geometries, radiotherapy applications involve numerous variations of material and density over small distances.Patient geometry is usually simulated by a map of densities over a large number of parallelepipeds(voxels).The voxel size ranges from0.5to5.0mm,and the number of voxels may be512512200,which is partitioned into200512512slices obtained from CT scans.Currently,Monte Carlo simulation of the absorbed dose for such large-scale problems requires high-performance computational resources,including parallel programming and computers.R.B.Cruise,V.P.Moskvin,and R.W.SheppardThefirst parallelization of PENELOPE was implemented by J.Sempau et al.[5].The code was run on eight processors of an SGI Origin2000,a shared-memory parallel machine located at the Centre de Supercomputaci´o de Catalunya(CESCA).The parallelization was carried out with the aid of the MPI distributed-memory message passing library,version1.2,which is discussed below.The authors used the same random number generator(r.n.g.)employed in the serial version of PENELOPE.This bines two different pseudo-random sequences according to the scheme proposed by l’Ecuyer;see[1]for a detailed description.It is a congruential type with period of order.The authors assume one may safely use this approach provided different seeds are introduced in the various processors.The lack of correlation is reasonably guaranteed by the fact that the simulation of each particle involves a random number of calls to the r.n.g.The authors show that results obtained in these studies corroborate the validity of this assumption.The primary challenge of this work was to ensure the validity of the implementation of the parallel random number generator(p.r.n.g.).Our choice of p.r.n.g.was dictated by this need for validation and is discussed in Section2.1.A typical PENELOPE run generates showers with each averaging calls to the random number generator.Errors in the implementation could easily be hidden by the mass of data.The validity was verified in two ways,first by examining the step-by-step evolution of the ing a parallel debugger,and second by comparingfinal results with those of the serial PENELOPE program and with experimental results.Further tests of the statistical validity of the p.r.n.g.are forthcoming in a separate article.2.DETAILED STRUCTURE OF PARALLELIZED PENELOPEThe generation of the trajectory ensemble is an“embarrassingly”parallelizable computational task.Each parallel processor may read the same geometry and materialfiles specifying the target,and each may generate its own set of particle trajectories.No inter-processor communication is necessary while the trajectory ensemble is being developed.Each processor accumulates relevant raw data from its own trajectory set.Once all processors have completed,a single processor collects the raw data from the others, sums the data into grand totals,and computes ensemble averages and variances.This same processor produces the output,and the program terminates on all processors.The computational model employed in the parallelization of PENELOPE is the very convenient SPMD (single program,multiple data)model.In this model the distribution of work among the parallel processors is effected not by each performing a unique task or program.Rather,each processor performs a common task,but on a unique input data set.Only one program exists.Each processor executes this same program. However,each processor uses a unique sequence of random numbers,the unique input data set,from which to build its own unique set of trajectories.The critical aspect in the parallelization of PENELOPE, therefore,is the replacement of PENELOPE’s original serial random number generator RAND with a proven parallel random number generator.This parallel random number generator must be capable of producing a sequence of independent,uniformly distributed random numbers on each processor such that the processors’sequences are mutually uncorrelated.The current standard API(application programming interface)for implementing a SPMD program is MPI, the Message Passing Interfacefirst released in June1994[6].Our parallelization of PENELOPE is accomplished with the IBM MPI version3.2.MPI provides the parallel programmer a library of convenient subroutines for managing interprocessor communication.MPI also assigns each processor a unique identification number.This ID may serve as initialization for a parallel random number generator,Parallelization of PENELOPE Monte Carlo transport coderesulting in a unique random number sequence for each processor.2.1.Parallelization of the PENELOPE SubroutinesThe key to parallelizing the PENELOPE Fortran77subroutines is the replacement of subroutine RAND,the serial random number generator supplied with the PENELOPE package,with a proven parallel random number generator(p.r.n.g.).We have chosen the highly successful p.r.n.g.developed and used by the MILC lattice-QCD collaboration[2].We considered employing a SPRNG p.r.n.g.[7]but opted instead for the MILC p.r.n.g.in anticipation of our need to perform detailed verification of its implementation.The advantage of the MILC p.r.n.g.is its ease of implementation and easy-to-understand open-source code. Each processor needs only to instantiate a structure with its processor rank,then pass this structure as the argument in calls to the p.r.n.g.It was easy to track the detailed evolution of these structures using a parallel debugger,enabling us to verify the implementation of the MILC p.r.n.g.For instance,thisstep-by-step tracking revealed the MILC p.r.n.g.has a nonzero probability of returning zero,which is unacceptable to some of the Penelope subroutines,and we were able to easily discover and correct for the problem.We have,on the other hand,no evidence that actual use of the MILC p.r.n.g.is better than some other parallel generator.However,extensive testing of the MILC p.r.n.g.has shown its statistical performance is as good as the original r.n.g.of the serial Penelope distribution.Details of these statistical tests are forthcoming in a separate article.The MILC p.r.n.g.employs a Marsaglia-like127bit feedback shift register.The advantages of a shift register approach compared to a linear congruential or lagged Fibonacci approach are(i)the speed of logical operations compared to arithmetical operations,and(ii)the pseudo-random characteristics ofbit-mixing compared to purely arithmetical operations[8].The period of the127bit feedback shift register is;if used serially a gigaflop machine would not repeat its random sequence untilyears have elapsed.Going one step further,the combination of a shift register with another algorithmically different generator is a very effective means of suppressing any residual correlations in the shift register [8].The MILC bines its127bit feedback shift register with a32bit integer congruence generator.Parallelization is effected in the MILC p.r.n.g.by each processor using a different multiplier in the congruence generator and a different initial state in the shift register,so that each processor’s random sequence is uncorrelated with the others’sequences.The input to this unique initialization is the individual MPI processor ID mentioned above.The MILC p.r.n.g.has served the eight-member MILC collaboration for more than a decade in thousands of Monte Carlo lattice-QCD computations,resulting in well over a hundred publications verifying the theoretical predictions of QCD.Throughout this research programme no deficiencies in the MILC p.r.n.g.have been detected.However,it is known that a r.n.g.performing well in one application may when employed in another application introduce artifacts into the latter’s simulation results.Therefore,according to Ferrenberg et al.[9],“a specific algorithm must be tested together with the random number generator being used regardless of the tests which the generator passed.”We are currently testing the MILC p.r.n.g.alone and together with parallelized PENELOPE.The test system is based on the classical Sobol scheme[10].With various seeds the p.r.n.g.is tested alone and together with parallelized PENELOPE based on Pearson’s chi-squared criteria.Tests include:i)one-dimensional uniformity test(hypothesis H1)ii)frequency and pair test(bivariate uniformity test H2)iii)serial and poker test(H3)R.B.Cruise,V.P.Moskvin,and R.W.Sheppardiv)gap test(H4).Tests(i)and(ii)are classical r.n.g.tests.However,they are not sufficient.Tests(iii)and(iv)are performed on sampled random number subsets used in actual PENELOPE simulations.The subset length for tests(ii) and(iii)will be typical for generating one trajectory.Test(iv)applies to both a subset used for generating a single trajectory,and to the entire set used in the complete simulation.At present the stand-alone tests of the MILC p.r.n.g.are completed.The results are no worse than for l’Ecuyer’s generator used in the serial version of plete test results will be presented later.The MILC p.r.n.g.subroutine is named myrand.The C code for myrand may be obtained from the MILC collaboration web site[2].The use of the term“myrand”indicates that if I am one of the parallel processors,my calls to function myrand return a random number sequence unique to me.We slightly modified the MILC p.r.n.g.to eliminate the possibility of returning zero;several PENELOPE subroutines fail for a random variable of zero.In the SPMD parallelization model each processor calls the same function myrand but with a unique data set passed as the argument.These unique parameters are contained inside a structure.A structure is auser-defined type(derived type)that contains a set of elements that themselves may be of various types.It is a programming device ideal for containing the parameters of the random sequence.Each processor is programmed with such a structure,but the parameter values contained in each processor’s structure are unique to that processor.Fortran77,the programming language in which the PENELOPE subroutines are written,does not support derived types or structures.Fortran77recognizes only implicitly defined types(INTEGER,REAL,etc), while its only container is the array in which all elements must be of the same implicit type.On the other hand,Fortran90does support structures,and a Fortran90compiler will compile Fortran77code.By compiling PENELOPE with the IBM AIX xlf90Fortran90compiler,we are able to insert structures containing the parameters of the random sequence into the PENELOPE subroutines.The myrand function takes a single argument which is this structure.Throughout the PENELOPE subroutine code,calls to RAND are replaced with calls to myrand with this structure as argument.The derived type of this structure is termed PRNDATA.The definition of this type is housed in a Fortran90module named PRNDATA TYPE,which may be placed in thefile containing the main program:This module is shared among both the main program and all subroutines calling myrand by the initial line in the main program or subroutine:which is followed by the declaration of the structure itself:Parallelization of PENELOPE Monte Carlo transport codewhere MYNODE PRNDATA is the unique structure containing the parameters of the random sequence for each processor.Recall that in the SPMD parallelization model used here,each processor executes the same program.Each processor reads and executes the above lines of code.What distinguishes one processor from another is the unique initialization of the parameter values in each processor’s MYNODE PRNDATA structure.This initialization must take place in the user’s main program,discussed below.Note that any PENELOPE subroutine calling myrand is modified to take an additional argument which is the MYNODE PRNDATA structure.For instance,PENELOPE’s KNOCK subroutine is modified to:2.2.Parallelization of the User’s Main ProgramThe PENELOPE package consists only of subroutines.The user must write the main program which repeatedly calls PENELOPE’s subroutines to generate an ensemble of trajectories,then computes statistical averages.For parallelizing main programs the user need have only a rudimentary knowledge of parallel programming and MPI.In distributed parallel programming,each processor is assigned a unique identification number called MYRANK.Thefirst task of the parallelized main program is to initialize the MPI API and assign each processor its unique ID:The second task is for each processor to obtain the total number of processors NPROCS working in parallel: Each processor’s MYNODE PRNDATA structure is initialized with MYRANK via a call to the MILC p.r.n.g.’s initializing C-code function:Calls to the p.r.n.g.from within the main program are accomplished simply withmyrand(MYNODE PRNDATA),and as mentioned above,calls to PENELOPE subroutines that require random number generation must include the MYNODE PRNDATA structure,such asJUMP(DSMAX(MAT),DS,MYNODE PRNDATA).The main program divides the workload among the parallel processors.The user is free to decide this partitioning of trajectories.We have chosen an equal partitioning.If NTOT is the total number of primary trajectories to be generated,and MYNTOT is the number for each processor,then the following code performs an equal partitioning:R.B.Cruise,V.P.Moskvin,and R.W.SheppardThe shower simulation now loops over a counter N ranging from1to MYNTOT.The PENELOPE timer must be replaced with a parallel wall-clock timer.The MPI wall-clock timer is convenient.At the beginning of the shower simulation loop code:and later at the end of the shower simulation code:A processor’s completion of its portion of trajectories is tested by:where ITIME is the maximum wall-clock time allowed for the simulation,and where line101increments the shower counter N=N+1and initiates the generation of another primary trajectory.During the simulation each processor tracks its own trajectory data.For every datum of a serial main program,the corresponding parallel main program requires two data.For instance,the parallel main requires not only the usual declaration for the total number of secondary particles:but also a declaration for the number of secondary particles generated by each processor:At the conclusion of the shower simulations on all the parallel processors,the processor with MYRANK equaling0collects and sums the processors’values for MYSEC into the grand total SEC.This collection and amalgamation is very easily programmed with one single MPI function call:At this point all processors but processor0are done.Processor0computes the desired statistics and variances,and produces the output.This is easily programmed by nesting all this activity inside the if statement:Finally,all processors terminate with the conclusion of the main program:See Figure1for a simplifiedflow chart of parallelized PENELOPE.It is very important to recognize that each parallel processor executes this sameflow chart.See[6]for a detailed description of the above MPI function calls.The parallelized PENELOPE Fortran90code,along with a simple example main program, will be available from the Radiation Safety Information Computational Center(RSICC)at Oak Ridge National Laboratory[4]upon completion of benchmark testing.Parallelization of PENELOPE Monte Carlo transportcode3.APPLICATION OF PARALLELIZED PENELOPEOur motivation in parallelizing PENELOPE is to increase efficiency of Monte Carlo simulations and reduce run-time for medical physics applications.We have applied our parallelized PENELOPE to the simulation of photon beams from the Leksell Gamma Knife R,a precision method for treating intracranial lesions.The Gamma Knife R concentrates radiation from201Co sources partially arrayed about the exterior of a spherical helmet.Each source includes a primary andfinal collimator system creating beam diameters of approximately4,8,14,and18mm at the common isocenter of the beams.Individual sources may be plugged to create an optimal configuration.Modeling of the Gamma Knife R using the serial version of PENELOPE is detailed in[3].The parallelized main program used in testing parallelized PENELOPE is based on this same model.R.B.Cruise,V.P.Moskvin,and R.W.SheppardTable I.Parallel Performance for Gamma Knife R Simulation with ShowersNumber of Wall-Clock Speedup EfficiencyProcessors()Time(sec)(/)(%)165109——416378 3.9899.5881627.9899.816407815.9799.832205931.6298.864102863.3499.0128518125.6998.2256271240.2593.8The parallelized PENELOPE code has been compiled and tested on the Aries Complex of the Indiana University IBM Teraflop SP System.The Aries Complex includes eight frames of4-cpu Power3+Thin nodes,providing a homogeneous parallel processing environment with a total of508processors.The nodes within the Aries Complex are interconnected via a low-latency high-speed(150megabytes/second) network using crossbar switch technology.Each node runs its own copy of IBM’s Unix operating system, AIX5.1.0.The parallelized PENELOPE code has been compiled and linked with the IBM XL Fortran90 compiler,version7.1.1.The C code module containing the MILC p.r.n.g.has been compiled with the IBM C6.0compiler.Parallelization is managed by the IBM Parallel Environment3.2,which includes the IBM MPI libraries.For additional details of the Indiana University IBM Teraflop SP System,including both the Aries and Orion Complexes,see[11].The run-time test results for primary particle trajectories are listed in Table I and plotted in Figure2. The parallel speedup resulting from processors is defined by the formula:serial run time-processor run time(1) where times are wall-clock time,not CPU time.The parallel efficiency is defined:(2)The speedup is nearly linear while the parallel efficiency approaches as expected for embarrassingly parallelizable Monte Carlo algorithms.Efficiency decreases a bit for the256-processor run; communication overhead,as a fraction of run time,starts taking its toll as the number of processors increases while the number of showers per processor decreases.The parallel code is validated by comparison of output averages to those of the serial code,which in turn is empirically validated in[3].Because the parallel code uses a different random number generator than the serial code,its output averages are not numerically identical to those of the serial code,but are statistically identical.The parallel code’s output averages fall well within the range of estimated statistical error,Parallelization of PENELOPE Monte Carlo transport code050100150200250050100150200250300S p e e d u p (T _1/T _N )Number of Processors (N)Figure 2.Speedup vs.Number of Processors for Gamma Knife R Simulation with Showers thereby validating the output of the parallel code.Figures 3and 4areisodose plots of a sphericalpolystyrene phantom of radius 16cm centered at (100,100,100)which corresponds to the isocenter of the Gamma Knife.The plots compare outputs of the serial (dash-dot line)and parallel (solid line)versions ofFigure parison of dose calculations for Gamma Knife inplaneR.B.Cruise,V.P.Moskvin,and R.W.Sheppardparison of dose calculations for Gamma Knife in plane PENELOPE.The smooth dashed line represents GammaPlan R output.Details of the computational model are presented in[3].The plots show perfect agreement between parallel and serial versions of PENELOPE.Calculations for parallel and serial cases were done with primary photon trajectories corresponding to a statistical error of3%in dose calculations at the isocenter.The collimator for an18mm final beam size was used in the simulation.4.CONCLUSIONSOur Fortran90parallelization of PENELOPE for execution on distributed-memory machines running MPI exhibits near perfect efficiency.The use of parallelized PENELOPE is completely justified from a resource-utilization standpoint.The output is statistically close to the serial output,which in turn is empirically validated in[3].The code is presently running on the Aries Complex of the Indiana University IBM Teraflop SP System.However,the Fortran90features and MPI function calls in the parallel code are standard,and porting to other parallel Unix platforms should present no difficulties.The parallelized PENELOPE Fortran90code,along with a simple example main program,will be available from the Radiation Safety Information Computational Center(RSICC)at Oak Ridge National Laboratory[4]upon completion of benchmark testing.Parallelization of PENELOPE Monte Carlo transport codeACKNOWLEDGEMENTSThis research has been funded in part by the Shared University Research Grants[SUR]from International Business Machines Inc.,and the Indiana Genomics Initiative[INGEN].The Indiana Genomics Initiative of Indiana University is supported in part by Lilly Endowment Inc.Monte Carlo simulation of the Leksell Gamma Knife R is an internal project of the Department of Radiation Oncology,Indiana University.REFERENCES[1]F.Salvat,J.M.Fern´a ndez-Varea,J.Bar´o,J.Sempau,“PENELOPE,an algorithm and computer codefor Monte Carlo simulation of electron-photon showers,”Informes T´e cnicos Ciemat,799,CIEMAT, Madrid,Spain1996.[2]“The MIMD Lattice Computation(MILC)Collaboration,”C.Bernard,T.DeGrand,C.DeTar,S.Gottlieb,U.M.Heller,J.Hetrick,R.L.Sugar,D.Toussaint;the MILC code is available at/detar/milc/(2002).[3]V.Moskvin,C.DesRosiers,L.Papiez,R.Timmerman,M.Randall,P.DesRosiers,“Monte Carlosimulation of the Leksell Gamma Knife R:I.Source modelling and calculations in homogeneous media,”Physics in Medicine and Biology,47,pp.1995-2011(2002).[4]“Radiation Safety Information Computational Center,”Oak Ridge National Laboratory,/rsic.html(2002).[5]J.Sempau,A.Sanchez-Reyes,F.Salvat,H.Oulad ben Tahar,S.B.Jiang,and J.M.Fernandez-Varea,“Monte Carlo simulation of electron beams from an accelerator head usingPENELOPE,”Phys.Med.Biol.,46,pp.1163–1186(2001).[6]W.Gropp,E.Lusk,A.Skjellum,Using MPI,2nd ed.,Massachusetts Institute of Technology(1999).[7]M.Mascagni,”SPRNG:A Scalable Library for Pseudorandom Number Generation,”Proceedings ofthe4th International Conference on Numerical Methods and Applications,Sofia,Bulgaria19-23 August1998,O.P.Iliev,M.S.Kaschiev,S.D.Margenov,B.H.Sendov,P.S.Vassilevski,editors, World Scientific,1999.[8]W.H.Press,S.A.Teukolsky,W.T.Vetterling,B.P.Flannery,Numerical Recipes in Fortran90–The Art of Parallel Scientific Computing,2nd ed.,Cambridge University Press(1996).[9]A.M.Ferrenberg,ndau,and Y.J.Wong,“Monte Carlo simulations:hidden errors from’good’random number generators,”Phys.Rev.Letters,69,pp.3382–3384(1992).[10]I.M.Sobol,Numerical Monte Carlo Methods,NAUKA,Moscow(1973)(in Russian).[11]“The UITS Research SP System,”Indiana University,/(2002). American Nuclear Society Topical Meeting in Mathematics&Computations,Gatlinburg,TN,200311/11。
pt演算法PT演算法是一种用于分布式计算的算法,它可以有效地解决大规模数据处理和计算的问题。
本文将从以下几个方面详细介绍PT演算法的原理、应用场景、实现方法等相关内容。
一、PT演算法的原理1.1 PT演算法的概念PT演算法是Parallel Tempering Algorithm(并行淬火算法)的缩写,也称为Parallel Replica Exchange Monte Carlo(并行重复交换蒙特卡罗)算法。
它是一种基于马尔可夫链蒙特卡罗方法(MCMC)的分布式计算方法,主要用于求解高维复杂系统中的平衡态性质。
1.2 PT演算法的基本思想PT演算法通过在不同温度下对系统进行模拟,从而实现对平衡态性质的求解。
具体来说,它将待求解系统分成多个副本,并在每个副本中采用不同温度进行模拟。
这样做有两个好处:一方面可以避免陷入局部极小值;另一方面可以加快收敛速度。
1.3 PT演算法的流程PT演算法主要包括以下几个步骤:(1)初始化:随机生成多个温度,并在每个温度下随机生成一个初始状态。
(2)模拟:在每个温度下进行MCMC模拟,得到一系列状态序列。
(3)交换:定期对不同温度下的状态进行交换,以增加状态的多样性和避免陷入局部极小值。
(4)统计:根据得到的状态序列计算系统的平衡态性质,如自由能、热力学平均值等。
(5)终止条件:当系统达到平衡态时,停止模拟并输出结果。
二、PT演算法的应用场景2.1 分子模拟PT演算法在分子模拟中有广泛应用。
由于分子系统通常具有高度复杂性和多样性,因此传统的单一温度模拟方法很难得到准确的结果。
而PT演算法可以通过不同温度下的交换来增加状态空间覆盖率和避免局部极小值问题,从而提高了求解精度和效率。
2.2 优化问题PT演算法也可以用于求解优化问题。
例如,在图像处理中,可以将待求解图像分成多个副本,并在每个副本中采用不同参数进行处理。
通过对不同副本之间进行交换,可以有效地避免陷入局部极小值,提高求解精度和效率。
第八章 Monte Carlo 法§8.1 概述Monte Carlo 法不同于前面几章所介绍的确定性数值方法,它是用来解决数学和物理问题的非确定性的(概率统计的或随机的)数值方法。
Monte Carlo 方法(MCM ),也称为统计试验方法,是理论物理学两大主要学科的合并:即随机过程的概率统计理论(用于处理布朗运动或随机游动实验)和位势理论,主要是研究均匀介质的稳定状态[1]。
它是用一系列随机数来近似解决问题的一种方法,是通过寻找一个概率统计的相似体并用实验取样过程来获得该相似体的近似解的处理数学问题的一种手段。
运用该近似方法所获得的问题的解in spirit 更接近于物理实验结果,而不是经典数值计算结果。
普遍认为我们当前所应用的MC 技术,其发展约可追溯至1944年,尽管在早些时候仍有许多未解决的实例。
MCM 的发展归功于核武器早期工作期间Los Alamos (美国国家实验室中子散射研究中心)的一批科学家。
Los Alamos 小组的基础工作刺激了一次巨大的学科文化的迸发,并鼓励了MCM 在各种问题中的应用[2]-[4]。
“Monte Carlo ”的名称取自于Monaco (摩纳哥)内以赌博娱乐而闻名的一座城市。
Monte Carlo 方法的应用有两种途径:仿真和取样。
仿真是指提供实际随机现象的数学上的模仿的方法。
一个典型的例子就是对中子进入反应堆屏障的运动进行仿真,用随机游动来模仿中子的锯齿形路径。
取样是指通过研究少量的随机的子集来演绎大量元素的特性的方法。
例如,)(x f 在b x a <<上的平均值可以通过间歇性随机选取的有限个数的点的平均值来进行估计。
这就是数值积分的Monte Carlo 方法。
MCM 已被成功地用于求解微分方程和积分方程,求解本征值,矩阵转置,以及尤其用于计算多重积分。
任何本质上属随机组员的过程或系统的仿真都需要一种产生或获得随机数的方法。