2019届人教A版 算法初步 单元测试

第一章算法初步检测试题(时间:120分钟满分:150分)选题明细表一、选择题(每小题5分,共60分)1.下列语句表达中是算法的个数为( B )①从广州到东京可以先乘火车到北京再坐飞机抵达;②利用公式S=4πR2计算半径R=2球的表面积;③4x>2x+4;④f(x)=x2+2x+3.(A)1个(B)2个(C)3个(D)4个解析:①②是算法,③④不是算法.故选B.2.下列各进制中,最大的值是( D )(A)85(9) (B)111 111(2)(C)1 000(4)(D)210(6)解析:因为85(9)=8×9+5=77,111 111(2)=26-1=63,1 000(4)=43=64,210(6)=2×62+1×6+0=78,故选D.3.如图程序的输出结果为( C )(A)(4,3) (B)(7,7) (C)(7,10) (D)(7,11)解析:程序在运行过程中各变量的结果如下表示:X=4,Y=3,X=X+Y=7,Y=X+Y=10,故程序的输出结果为(7,10).故选C.4.如图所示的程序框图,如果输入三个实数a,b,c,要求输出这三个数中最大的数,那么在空白的判断框中,应该填入下面四个选项中的( A )(A)c>x (B)x>c (C)c>b (D)b>c解析:在第一个判断结束后,已经把a,b两个数中的大者赋给了x,因此只要在第二个判断中把x,c中的大者找出来即可,应填c>x.故选A.5.某程序框图如图所示,该程序运行后输出的k的值是( A )(A)4 (B)5(C)6 (D)7解析:程序执行第一次,S=0+20=1,k=1,第二次,S=1+21=3,k=2,第三次,S=3+23=11,k=3,第四次,S=11+211>100,k=4,跳出循环,输出k=4, 故选A.6.图象不间断函数f(x)在区间[a,b]上是单调函数,在区间(a,b)上存在零点,如图是用二分法求f(x)=0近似解的程序框图,判断框中可以填写( B )①f(a)f(m)<0;②f(b)f(m)>0;③f(b)f(m)<0;④f(a)f(m)>0.(A)①或④(B)①或②(C)①或③(D)②或④解析:由二分法求方程f(x)=0近似解的流程知:当满足f(a)f(m)<0时,令b=m;否则令a=m;故①正确,④错误;当满足f(m)f(b)>0时,令a=m;否则令b=m;故②正确,③错误.故选B.7.利用秦九韶算法求f(x)=x5+x3+x2+x+1当x=3时的值为( C )(A)121 (B)321 (C)283 (D)239解析:将函数式变形成一次式的形式可得f(x)=((((x+0)x+1)x+1)x+1)x+1. 当x=3时,f(3)=((((3+0)×3+1)×3+1)×3+1)×3+1=283.故选C.8.阅读下面的程序:S=1i=1WHILE i<=10S=3*Si=i+1WENDPRINT “S=”;SEND上述程序的功能是( C )(A)计算3×10的值(B)计算39的值(C)计算310的值(D)计算1×2×3×…×10的值解析:由程序知,当i>10时,退出循环.i=1,S=3;i=2,S=32;i=3,S=33;…;i=10,S=310;i=11时退出循环,故输出S的值为310的值.9.将2 012(3)化为六进制数为abc(6),则a+b+c等于( D )(A)6 (B)7 (C)8 (D)9解析:“三进制”数为2 012(3)转化为“十进制”数为2×33+0×32+1×31+2 =59,将59转化为六进制数:将59化为六进制数是135(6),从而可求a+b+c=1+3+5=9,故选D.10.执行如图所示的程序框图,输出的s值为( B )(A)(B)(C)(D)解析:k=1,s=1,s=1-=,k=2;s=+=,k=3,因为3≥3成立,所以输出s=.所以选B.11.五进制是以5为底的进位制,主因乃人类的一只手有五根手指.中国古代的五行学说也是采用的五进制,0代表土,1代表水,2代表火,3代表木,4代表金,依此类推,5又属土,6属水,……,减去5即得.如图,这是一个把k进制数a(共有n位)化为十进制数b的程序框图,执行该程序框图,若输入的k,a,n分别为5,324,3,则输出的b等于( B )(A)45 (B)89 (C)113 (D)445解析:模拟执行程序框图,a=324,k=5,n=3,b=0,i=1.进入循环t=4,b=0+4·50=4,i=2<3;t=2,b=4+2×5=14,i=3;t=3,b=14+3×52=89,i=4>3.输出b=89.故选B.12.某数学爱好者编制了如图的程序框图,其中mod(m,n)表示m除以n的余数,例如mod(7,3)=1.若输入m的值为8,则输出i的值为( B )(A)2 (B)3 (C)4 (D)5解析:输入m后,n=2<8;mod(m,n)=0,i=1,n=3<8;mod(m,n)≠0,n=4<8;mod(m,n)=0,i=2,n=5<8;mod(m,n)≠0,n=6<8;mod(m,n)≠0,n=7<8;mod(m,n)≠0,n=8;mod(m,n)=0,i=3,n=9>8,输出i=3,故选B.二、填空题(每小题5分,共20分)13.运行如图所示的程序,若输入的是-2 018,则输出的值是.INPUT xIF x<0 THENx=-xEND IFPRINT xEND解析:因为-2 018<0,所以x=-(-2 018)=2 018,故输出的值为2018. 答案:2 01814.执行如图所示的程序框图,若输入n=10,m=4,则输出的p= .解析:输入n=10,m=4,k=1,p=1进入循环,p=7;k=2,n=10,m=4,p=56;k=3,n=10,m=4,p=504;k=4,n=10,m=4,p=5 040;输出5 040.答案:5 04015.执行如图所示的程序框图,输出值a= .解析:模拟程序的运行,a=2,i=1<2 019,a=1-=;i=2<2 019,a=1-2=-1;i=3<2 019,a=1-(-1)=2;i=4<2 019,a=1-=;……i=2 018<2 019,a=-1;i=2 019,输出a=-1.答案:-116.已知程序:INPUT xIF x>0 THENy=3*x/2+3ELSEIF x<0 THENy=-3*x/2+5ELSEy=0END IFEND IFPRINT y若输出y的值为6,则输入x的值为. 解析:由题意得,当x>0时,令3×+3=6,解得x=2;当x<0时,令-3×+5=6,解得x=-,当x=0时,y=0不成立,综上可知x=2或x=-.答案:2或-三、解答题(共70分)17.(本小题满分10分)画出求p=1×3×5×7×…×31的值的算法流程图.解:算法流程图如图所示:18.(本小题满分12分)读下列程序,写出此程序表示的函数,并求当输出的y=4时,输入的x的值. INPUT xIF x<0 THENy=x∧2ELSEIF x>0 THENy=2*xELSEy=-1END IFEND IFPRINT yEND解:此程序表示的函数为y=当x<0时,x2=4得x=-2.当x>0时,2x=4得x=2.故当输出的y=4时,输入的x=±2.19.(本小题满分12分)分别用辗转相除法和更相减损术求81和135的最大公约数.解:辗转相除法:135=81×1+5481=54×1+27,54=27×2+0,则81与135的最大公约数为27.更相减损术法:135-81=54;81-54=27;54-27=27.所以81和135的最大公约数为27.20.(本小题满分12分)阅读如图所示的程序框图,解答下列问题:(1)求输入的x的值分别为-1,2时,输出的f(x)的值;(2)根据程序框图,写出函数f(x)(x∈R)的解析式;并求当关于x的方程f(x)-k=0有三个互不相等的实数解时,实数k的取值范围.解:(1)当输入的x的值为-1时,输出的f(x)=2-1=.当输入的x的值为2时,输出的f(x)=22-2×2+1=1.(2)根据程序框图,可得f(x)=当x<0时,f(x)=2x,此时f(x)单调递增,且0<f(x)<1;当x=0时,f(x)=2;当x>0时,f(x)=x2-2x+1=(x-1)2在(0,1)上单调递减,在(1,+∞)上单调递增,且f(x)≥0.结合图象,知当关于x的方程f(x)-k=0有三个不同的实数解时,实数k的取值范围为(0,1).21.(本小题满分12分)乘坐火车时,可以托运货物.从甲地到乙地,规定每张火车票托运费用计算方法是:当行李质量不超过50 kg时按0.25元/kg;超过50 kg而不超过100 kg时,其超过部分按0.35元/kg;超过100 kg时,其超过部分按0.45元/kg.请设计一个输入行李质量ω kg(ω≥0),计算出托运的费用x元的算法,画出算法框图并用基本语句描述该算法.解:设行李重量为ω kg,应付托运费为x元,则x=则x=程序框图如图所示:程序如下:INPUT “行李重量=”;ωIF ω<=50 THENx=0.25*ωELSEIF ω<=100 THENx=0.35*ω-5ELSEx=0.45*ω-15END IFEND IFPRINT x22.(本小题满分12分)设计算法求+++…+的值.要求画出程序框图,写出用基本语句编写的程序.解:这是一个累加求和问题,共99项相加,可设计一个计数变量,一个累加变量,用循环结构实现这一算法.程序及程序框图如图所示.S=0k=1DoS=S+1/k(k+1)k=k+1LOOP UNTIL k>99PRINT SEND。

2019-2020年秋季学期人教A 版高中数学必修三《算法初步》单元测试卷《算法初步》单元测试卷一、选择题(共12小题) 1.关于进位制说法错误的是( )A ． 进位制是人们为了计数和运算方便而约定的记数系统B ． 二进制就是满二进一，十进制就是满十进一C ． 满几进一，就是几进制，几进制的基数就是几D ． 为了区分不同的进位制，必须在数的右下角标明基数2.根据指定条件决定是否重复执行一条或多条指令的控制结构称为( ) A ． 条件结构 B ． 循环结构C ． 递归结构D ． 顺序结构3.执行如图所示的程序框图，若输入n 的值为6，则输出s 的值为( )A ． 105B ． 16C ． 15D ． 14.已知a ＝，b ＝，运算原理如图所示，则输出的值为( )A ．√22B ．√2C ．√2−12D ．√2+125.当a ＝1，b ＝3时，执行完下面一段程序后，x 的值是( )A ． 1B ． 3C ． 4D ． －26.阅读下面的程序框图，则输出的S 等于( )A ． 14B ． 20C ． 30D ． 557.一个算法步骤如下： S1 S 取值0，i 取值2；S2 如果i ≤10，则执行S3，否则执行S6； S3 计算S ＋i 并将结果代替S ； S4 用i ＋2的值代替i ； S5 转去执行S2； S6 输出S .运行以上步骤输出的结果为( ) A ． 25 B ． 30C ． 35D ． 408.二进制数11 011(2)化为十进制数是( ) A ． 27B ． 26C ． 25D ． 249.下面的程序运行后第3个输出的数是( )A ． 1B ．32C ． 2D ．5210.给出以下四个问题， ①输入x ，输出它的相反数； ①求面积为6的正方形的周长； ①求三个数a ，b ，c 中的最大数； ①求函数f (x )＝{x −1,x ≥0x +2,x <0的函数值.其中不需要用条件语句来描述其算法的有( ) A ． 1个 B ． 2个C ． 3个D ． 4个11.下列语句中，正确表示输出语句的是( ) A ． INPUT“提示内容”；变量 B ． PRINT“提示内容”；表达式C ． INPUT“变量”；提示内容D ． PRINT“表达式”；提示内容12.下面为一个求20个数的平均数的程序，在横线上应填充的语句为( )A ． i>20B ． i<20C ． i>＝20D ． i<＝20二、填空题(共5小题) 13.下列程序的运行结果为________．14.完成下列进位制之间的转化：1 101(2)＝____.15.计算图中空白部分面积的一个流程图如下，则①中应填________.16.根据下面的程序，可知输出的结果i 为________．17.如图所示的流程图的输出结果为sum＝132，判断框中条件为“i≥n？”(n①N)，则n＝________.三、解答题(共6小题)18.用辗转相除法求108与45的最大公约数，再用更相减损术验证．19.已知f(x)＝x3－1，设计一个程序，求f[f(13)]．20.“鸡兔同笼”问题是我国古代著名的趣题之一．大约在1 500年前，《孙子算经》中就记载了这个有趣的问题．书中这样描述：今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔几何？试设计一个算法，输入鸡兔的总数和鸡兔的脚的总数，分别输出鸡、兔的数量．21.画出程序框图并编写程序：任意输入三个实数，输出最小的数．22.分别用辗转相除法和更相减损术求261,319的最大公约数．23.判断所给程序的功能．答案解析1.【答案】D【解析】也可以不标明基数，用文字表述也可． 2.【答案】B【解析】根据循环结构的定义可知. 3.【答案】C【解析】按照程序过程，通过反复判断循环条件执行程序.执行过程为s ＝1×1＝1，i ＝3；s ＝1×3＝3，i ＝5；s ＝3×5＝15，i ＝7≥6，跳出循环.故输出s 的值为15. 4.【答案】D【解析】由a ＝√2<b ＝=lg3lg √3＝2，知a >b 不成立，故输出a+1b＝√2+12.5.【答案】C【解析】由a ＝1，b ＝3，a<b ，得x ＝1＋3＝4. 6.【答案】C【解析】由题意知：S ＝12＋22＋…＋i 2， 当i ＝4时循环程序终止， 故S ＝12＋22＋32＋42＝30. 7.【答案】B【解析】按算法步骤一步一步地循环计算替换，该算法作用为求和S ＝2＋4＋6＋8＋10＝30. 8.【答案】A【解析】由题意知11 011(2)＝1×20＋1×21＋1×23＋1×24计算出结果即可选出正确选项． 11 011(2)＝1×20＋1×21＋1×23＋1×24＝27. 9.【答案】C【解析】该程序中关键是循环语句， 第一次输出的数是1，第二次输出的数是x ＝1＋12＝32， 第三次输出的数是x ＝1＋12＋12＝2. 10.【答案】A【解析】①、①、①需要用条件语句，①不需用条件语句，故选A. 11.【答案】B【解析】由输出语句的格式可知． 12.【答案】A【解析】程序的功能是求20个数的平均数，则循环体需要执行20次，由循环变量的初值为1，增加量为1，直到循环20次时，此时循环变量的值为21，应退出循环．又因直到型循环是满足条件退出循环，即i>20时退出循环．故选A. 13.【答案】1,1,1【解析】此程序主要以赋值语句来设计，其作用是首先对变量m ，n ，p 分别赋值1,2,3，然后将变量m 的值赋给p ，再将变量p 的值赋给n ，最后将变量n 的值赋给m ，所以最后变量m ，n ，p 的值都等于1，运行结果输出1,1,1. 14.【答案】13【解析】1 101(2)＝1×23＋1×22＋0×21＋1×20＝13. 15.【答案】S ＝a 2－π16a 2【解析】本题即找出表示空白区域面积的公式. 16.【答案】5【解析】S ＝1×21×32×43×54，故i ＝5. 17.【答案】11【解析】① 132＝11×12，而sum ＝sum×i ，输出结果sum ＝(12－1)×12＝11×12，① 条件应为“i ≥11？”.18.【答案】①108＝2×45＋18， 45＝2×18＋9， 18＝2×9，①108与45的最大公约数为9. 检验：108－45＝63， 63－45＝18， 45－18＝27， 27－18＝9， 18－9＝9.经检验：108与45的最大公约数为9. 【解析】19.【答案】程序如下：【解析】20.【答案】算法步骤如下：第一步，输入鸡和兔的总数量M.第二步，输入鸡和兔的脚的总数量N..第三步，鸡的数量为A＝4M−N2第四步，兔的数量为B＝M－A.第五步，输出A，B，得出结果．程序如下：【解析】21.【答案】程序：【解析】22.【答案】辗转相除法：319＝261×1＋58，261＝58×4＋29，58＝29×2.①319与261的最大公约数是29.更相减损术：319－261＝58，261－58＝203，203－58＝145，145－58＝87，87－58＝29，58－29＝29，①319与261的最大公约数是29.【解析】2019-2020年秋季学期人教A版高中数学必修三《算法初步》单元测试卷23.【答案】由循环语句知：共输入10个x.由条件语句及计数变量n的变化可知：n记录的是满足x<0的x的个数．故本程序的功能是：统计10个数中负数的个数．【解析】11 / 11。

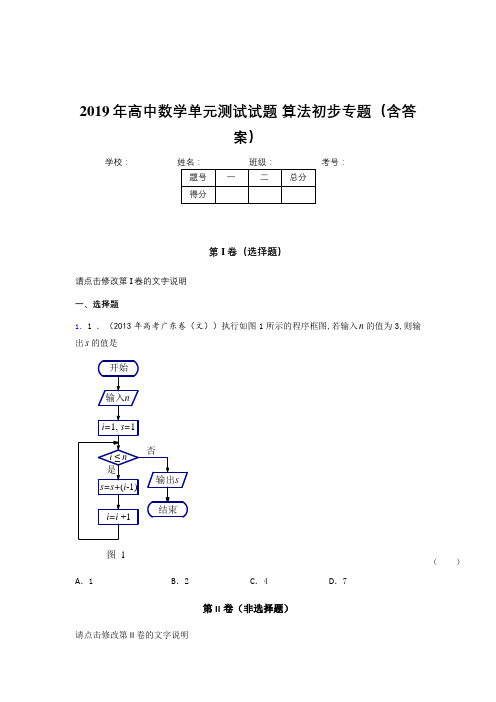
2019年高中数学单元测试试题 算法初步专题（含答案）学校：__________考号：__________第I 卷（选择题）请点击修改第I 卷的文字说明 一、选择题1．1 ．（2013年高考广东卷（文））执行如图1所示的程序框图,若输入n 的值为3,则输出s 的值是图 1（ ）A ．1B ．2C ．4D ．7第II 卷（非选择题）请点击修改第II 卷的文字说明二、填空题2．下图是一个算法的流程图，则输出的e 值是_________。

（第6题）3．某程序的伪代码如图所示，则程序运行后的输出结果为 ▲ ．4．观察下列程序，该循环变量I 共循环了 ▲ 次5．按下列流程图运算：规定：程序运行 到“判断结果是否大于244”为1次运算.若x =5，则运算进行______次才停止．6．如图，程序执行后输出的结果为_________ （2009上海九校联考） 答案 64S ←0For I From 1 To 7 Step 2 S ←S+I End For第9题图S ✐0 I ✐1 While S<60S ✐S+I I ✐ I+1 End While第7题7．阅读如图所示的程序框，若输入的n 是100，则输出的变量S 的值是 .8．如图所示的流程图，输出的结果S 是 ．9．补全求45和75的最大公约数的算法过程： S1 将45 因数分10．某程序框图如图所示，若输出的S=57，则判断框内位 （A ） k ＞4? （B ）k ＞5?（C ） k ＞6? （D ）k ＞7? （2010浙江理）（2）11．图1是求实数x 的绝对值的算法程序框图，则判断框①中可填 （2010湖南文）12.12．执行右图所示的程序框图，若输入10x =，则输出y 的值为 ．.（2010山东理）（13）13．如图所示的程序框图，若输入5n =，则输出的n 值为 （三明市三校联考） 答案-1第6题图14．在如图2的程序框图中，该程序运行后输出的结果为 . （2009厦门市高中毕业班质量检查）答案 15 215．以下伪代码： Read x If x ≤2 Then y←2x －3 Elsey←log 2x End If Print y表示的函数表达式是 ▲ ．16．某算法的程序框图如图，若输入4,2,6a b c ===，则输出的结果为 ．17．如图是一个求50名学生数学平均分的程序，在横线上应填的语句为 ▲ .第7题图 第8题图18．执行右边的程序框图,若15p =，则输出的n = .19．如图示的程序框图，若输入的n 是100，则(文科)S=_____. (理科)T=________.20．如果执行右面的程序框图，那么输出的S = ▲ ．(第4题)Read x If x >0 Then1y x ←+Else1y x ←-End IfPrint y21．下图是根据所输入的x 值计算y 值的一个算法程序，若x 依次取数1100n ⎧⎫-⎨⎬⎩⎭()n N +∈ 中的前200项，则所得y 值中的最小值为 ▲ ．22．右图是求样本x 1，x 2，…x 10平均数x 的程序框图，图中空白框中应填入的内容为（ ）(A) S =S +x n (B) S =S +n x n (C) S =S + n (D) S =S +1n（2010陕西理） 23．执行如图所示的程序框图,则输出的S 的值是: （ ）A ． 4B ．32C ．23D ．-1（2012辽宁文）24．在下面的程序框图中，输出的y 是x 的函数，记为)(x f y =，则=-)21(1f ．25．对于下列的伪代码（n ∈N *），给出如下判断： ①当输入n =2时，输出结果为1； ②当输入n =3时，输出结果为1；③当输入n =99时，输出结果一定是非负的． 其中所有正确命题的序号为 ．图，则输出的I26．运行如（右上）图所示的程序流程值为 ▲ ．27．根据如图所示的伪代码，可知输出S 的值为 ▲ .第6题图Print SEnd While 2i+3Si+2i<8While i 1i第7题28．一个用流程图表示的算法如图所示，则其 运行后输出的结果为 .29．某程序框图如图所示，该程序运行后输出的i30．如图是一个算法的流程图，若输出的结果是31中的整数M 的值是 ▲ ．i =i -1结束(第7题图)（第7题）。

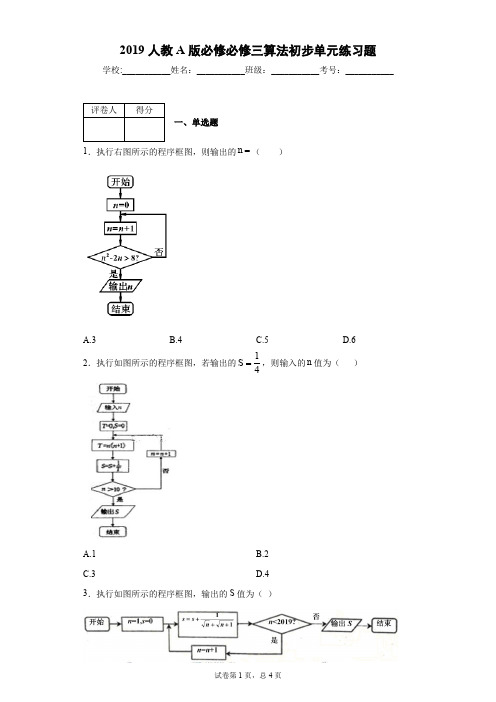
2019人教A版必修必修三算法初步单元练习题学校:___________姓名：___________班级：___________考号：___________一、单选题1．执行右图所示的程序框图，则输出的n=（）A.3B.4C.5D.62．执行如图所示的程序框图，若输出的14S=，则输入的n值为（）A.1B.2C.3D.4 3．执行如图所示的程序框图，输出的S值为（）1 1 1 1 4．如图给出的是计算1111124640324034+++++的值的程序框图，其中判断框内应填入的是（ ）A.4032i ≤B.4032i ≥C.4034i ≤D.4034i ≥5．如图所给的程序运行结果为41S =，那么判断框中应填入的关于k 的条件是()A.7k ≥？B.6k ≥？C.5k ≥？D.6k >？二、填空题6．某程序框图如图所示,则执行该程序后输出的结果是_______.7．下图所示的算法流程图中，输出的S表达式为__________．8．执行下面的程序框图，若输入的a，b，k分别为1，2，3，则输出的M _____三、解答题9．设计一个算法，判断25是否为质数.10．某函数的解析式由如图所示的程序框图给出.（1）写出该函数的解析式；（2）执行该程序框图，若输出的结果为4，求输入的实数x的值.参考答案1．C【解析】【分析】由已知中的程序语句可知：该程序的功能是利用循环结构计算并输出变量n的值，模拟程序的运行过程，分析循环中各变量值的变化情况，可得答案．【详解】第一次执行循环体后，n＝1，不满足退出循环的条件，第二次执行循环体后，n＝2，不满足退出循环的条件，第三次执行循环体后，n＝3，不满足退出循环的条件，第四次执行循环体后，n＝4，不满足退出循环的条件，第四次执行循环体后，n＝5，满足退出循环的条件，故输出的n值为5，故选：C．【点睛】本题考查了程序框图的应用问题，解题时应模拟程序框图的运行过程，以便得出正确的结论，是基础题．2．C【解析】【分析】设数列111(1)1nan n n n==-++，则程序框图表示的是从n项到11项之和，利用裂项相消法得到答案. 【详解】设数列111(1)1 nan n n n==-++则程序框图表示的是数列从n项到11项之和即111111111...1121112124 Sn n n n n=-+-++-=-= +++3n=故选：C【点睛】本题考查了程序框图，确定程序框图所表示的数列关系是解题的关键.3．D【解析】【分析】 程序框图表示的是数列n a =2019项和，利用裂项相消法得到答案. 【详解】 设数列n a =2019项和n a ==即2019122019......1S S a a a ==+++= 故选：D【点睛】 本题考查了程序框图，确定程序框图表示的是数列n a =2019项和是解题的关键.4．C【解析】【分析】按照程序框图运行程序，可知最后输出时，4036i =，从而确定判断框内容.【详解】根据程序框图运行程序 第一次循环：12S =，4i =；第二次循环：1124S =+，6i =；…… 直至1111124640324034S =+++⋅⋅⋅++，4036i =时结束循环，可填入4034i ≤ 本题正确选项：C【点睛】本题考查根据程序框图循环结构输出结果补全判断框的问题，关键是确定最终输出时i 的取值，属于常考题型.5．B【解析】【分析】程序运行结果为41S =,执行程序,当6k =时,判断条件成立,当5k =时,判断条件不成立,输出41S =,即可选出答案.【详解】根据程序框图,运行如下:初始10,1k S ==,判断条件成立,得到11011S =+=,1019k =-=;判断条件成立,得到11920S =+=,918k =-=;判断条件成立,得到20828S =+=,817k =-=;判断条件成立,得到28735S =+=,716k =-=;判断条件成立,得到35641S =+=,615k =-=;判断条件不成立,输出41S =,退出循环,即6k ≥符合题意.故选:B.【点睛】本题考查了程序框图的识别与判断,弄清进入循环体和跳出循环体的条件是解决本题的关键,考查了学生的推理能力,属于基础题.6．2047【解析】【分析】由该程序框图的功能可得121n n a a +=+，再结合递推公式可得{}1n a +是以2为首项，2为公比的等比数列，再利用通项公式求解即可.【详解】解：设2019n a ≤，则121n n a a +=+，且11a =，则112(1)n n a a ++=+，又112a +=，即{}1n a +是以2为首项，2为公比的等比数列，则12n n a +=，即21n n a =-，设212019n n a =-≤，则满足题意的n 的最大值为10，即1010211023a =-=，则112102312047a =⨯+=，故答案为：2047.【点睛】本题考查了程序框图的功能，主要考查了数列递推式求通项公式，重点考查了运算能力，属基础题.7．112399++++【解析】【分析】根据流程图知当1i =，满足条件100i <，执行循环体，1S =，依此类推，当100i =，不满足条件100i <，退出循环体，从而得到结论．【详解】1i =，满足条件100i <，执行循环体，1S =2i =，满足条件100i <，执行循环体，12S =+3i =，满足条件100i <，执行循环体，123S =++…依此类推99i =，满足条件100i <，执行循环体，1299S =++⋯+，100i =，不满足条件100i <，退出循环体， 输出1112399S S ==+++⋯+，故答案为112399++++．【点睛】本题主要考查了循环结构应用问题，此循环是先判断后循环，属于中档题．8．12【解析】【分析】由题意可知，从1n =开始，判断框条件成立，执行第一次循环，得到一组新的,,M a b 的值，再从2n =开始，判断框条件成立，执行第一次循环，得到一组新的,,M a b 的值，当3n =时，判断条件框不成立，输出此时M 的值，即可得出答案。

第一章算法初步章末检测时间：120分钟满分：150分一、选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．下面对算法描述正确的一项是( )A．算法只能用自然语言来描述B．算法只能用图形方式来表示C．同一问题可以有不同的算法D．同一问题的算法不同，结果必然不同解析：算法的特征有：有限性、确定性、逻辑性、不唯一性、普遍性，故C项正确，选C.答案：C2．如图，是某算法流程图的一部分，其算法的逻辑结构为( )A．顺序结构B．判断结构C．条件结构D．循环结构解析：条件结构是处理逻辑判断并根据判断结果进行不同处理的结构，由算法流程图知，该算法的逻辑结构为条件结构，故选C.答案：C3．下面的程序：a＝1WHILE a＜100a＝a＋1WEND执行完毕后a的值为( )A．99 B．100C．101 D．102解析：a＝99＋1＝100.答案：B4．下列语句中：①m＝x3－x2②T＝T×I③32＝A④A＝A＋2 ⑤a＝b＝4，其中是赋值语句的个数为( ) A．5 B．4解析：①m ＝x 3－x 2为赋值语句；②T ＝T ×I 为赋值语句；③32＝A ，因为左侧为数字，故不是赋值语句；④A ＝A ＋2为赋值语句；⑤a ＝b ＝4，因为是连等，故不是赋值语句．故赋值语句个数为3，故选C. 答案：C5．阅读下列程序：INPUT “A＝”；A A ＝A*2A ＝A*3A ＝A*4A ＝A*5PRINT A END若输入的A 的值为1，则输出的结果A 的值为( ) A ．5 B ．6 C．15D ．120解析：执行赋值语句后A 的值依次为2,6,24,120，故最后A 的值为120. 答案：D6．阅读下面的程序框图，运行相应的程序，则输出i 的值为( )A ．2B ．3C ．4D ．5解析：S ＝10，i ＝0，i ＝i ＋1＝1，S ＝S －i ＝10－1＝9，不满足S ≤1； i ＝i ＋1＝2，S ＝S －i ＝9－2＝7，不满足S ≤1； i ＝i ＋1＝3，S ＝S －i ＝7－3＝4，不满足S ≤1； i ＝i ＋1＝4，S ＝S －i ＝4－4＝0，满足S ≤1；输出i ＝47．用“辗转相除法”求得459和357的最大公约数是( )A．3 B．9C．17 D．51解析：∵459÷357＝1……102，357÷102＝3……51，102÷51＝2，∴459和357的最大公约数是51，故答案为D.答案：D8．下面进位制之间转化错误的是( )A．101(2)＝5(10)B．27(8)＝212(3)C．119(10)＝315(6)D．31(4)＝24(5)解析：101(2)＝1×22＋0×2＋1＝5，故A对；27(8)＝2×8＋7＝23,212(3)＝2×32＋1×3＋2＝23，故B对；315(6)＝3×62＋1×6＋5＝119，故C对；31(4)＝3×4＋1＝13,24(5)＝2×5＋4＝14，故D错．答案：D9．下面一段程序的目的是( )INPUT m，nWHILE m＜＞nIF m＞n THENm＝m－nELSEn＝n－mEND IFWENDPRINT mENDA．求m，n的最小公倍数B．求m，n的最大公约数C．求m被n除的商D．求n除以m的余数解析：本程序当m，n不相等时，总是用较大的数减去较小的数，直到相等时跳出循环，显然是“更相减损术”．故选B.答案：B10．用秦九韶算法计算多项式f(x)＝12＋35x－8x2＋79x3＋6x4＋5x5＋3x6，当x＝－4的值时，v4的值为( ) A．－57 B．220C．－845 D．3 392解析：∵f(x)＝3x6＋5x5＋6x4＋79x3－8x2＋35x＋12＝(((((3x＋5)x＋6)x＋79)x－8)x＋35)x＋12，v1＝3×(－4)＋5＝－7，v2＝－7×(－4)＋6＝34，v3＝34×(－4)＋79＝－57，v4＝－57×(－4)－8＝220.∴v4的值为220.答案：B11．执行下面的程序框图，如果输入的依次是1,2,4,8，则输出的S为( )A．2 B．2 2C．4 D．6解析：由程序框图可知，S＝1，i＝1；S＝1，i＝2，S＝2，i＝3；S＝2，i＝4；S＝22，i＝5，此时跳出循环，输出 S＝22，故选B.答案：B12．执行如图所示的程序框图，若输出的i的值为2，则输入的x的最大值是( )A．5 B．6C ．11D ．22解析：分析该程序框图可知⎩⎪⎨⎪⎧x 2－1＞3，12⎝ ⎛⎭⎪⎫x 2－1－2≤3，解得8＜x ≤22，所以输入的x 的最大值是22，故选D.答案：D二、填空题(本大题共4小题，每小题4分，共16分，把答案填在题中的横线上) 13．840和1 764的最大公约数是________． 解析：1 764＝2×840＋84,840＝84×10＋0， 所以84就是840和1 764的最大公约数． 答案：8414．已知多项式p (x )＝3x 5＋9x 4＋x 3＋kx 2＋4x ＋11，当x ＝3时值为1 616，则k ＝________. 解析：由秦九韶算法，得p (x )＝((((3x ＋9)x ＋1)x ＋k )x ＋4)x ＋11. 则当x ＝3时，p (3)＝(((54＋1)×3＋k )×3＋4)×3＋11.＝(495＋3k ＋4)×3＋11 ＝9k ＋1 508 ＝1 616， 所以k ＝12. 答案：1215．对任意非零实数a ，b ，若a ⊗b 的运算原理如图所示，则log 28⊗(12)－2＝________.解析：log 28＜(12)－2，由题图，知log 28⊗(12)－2＝3⊗4＝4－13＝1.答案：116. 阅读程序框图，该程序运行后输出的S 的值为________．解析：由程序框图可知，该程序运行的是1＋2＋3＋…＋10＝55，所以输出的S的值为55. 答案：55三、解答题(本大题共有6小题，共74分，解答应写出文字说明、证明过程或演算步骤) 17．(12分)下面给出一个用循环语句编写的程序：k＝1sum＝0WHILE k<10sum＝sum＋k^2k＝k＋1WENDPRINT sumEND(1)指出程序所用的是何种循环语句，并指出该程序的算法功能；(2)请用另一种循环语句的形式把该程序写出来．解析：(1)本程序所用的循环语句是WHILE循环语句，其功能是计算12＋22＋32＋…＋92的值．(2)用UNTIL语句改写程序如下：k＝1sum＝0DOsum＝sum＋k^2k＝k＋1LOOP UNTIL k>＝10PRINT sum18．(12分)画出求y＝|x－2|的值的算法结构框图．解析：结构框图如图所示．19．(12分)根据给出的程序，计算程序运行后的结果．j＝1n＝0WHILE j<＝11IF j MOD 4＝0 THENn＝n＋1END IFj＝j＋1WENDPRINT nEND解析：程序运行的结果是输出2.20．(12分)输入10个数，找出其中最大的数并输出，画出程序框图，并写出程序．解析：解析：程序框图如图：指出错误的地方，并说明修改方法．解析：图①有两处错误．第一处错误是：第三个框中p＝p＋i错，应改为p＝p＋i2.第二处错误是：在第三个框和判断框中漏掉了在循环体中起重要作用的框图，即i＝i＋2.图②有一处错误．即判断框中的内容错误．应将框内的内容“i＜100？”改为“i≤100？”或改为“i＞100？”，且判断框下面的流程线上的“是”和“否”互换．。

单元质量评估(120分钟150分)一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.下列说法正确的是 ( B )A.算法就是某个问题的解题过程B.算法执行后可以产生不同的结果C.解决某一个具体问题算法不同,则结果不同D.算法执行步骤的次数不可以很大,否则无法实施2.在程序框图中,算法中间要处理数据或计算,可以分别写在不同的 ( A )A.处理框内B.判断框内C.输入、输出框内D.起、止框内3.早上从起床到出门需要洗脸刷牙(5 min)、刷水壶(2 min)、烧水(8 min)、泡面(3 min)、吃饭(10 min)、听广播(8 min)几个过程.从下列选项中选出最好的一种算法( C )A.第一步,洗脸刷牙.第二步,刷水壶.第三步,烧水.第四步,泡面.第五步,吃饭.第六步,听广播B.第一步,刷水壶.第二步,烧水同时洗脸刷牙.第三步,泡面.第四步,吃饭.第五步,听广播C.第一步,刷水壶.第二步,烧水同时洗脸刷牙.第三步,泡面.第四步,吃饭同时听广播D.第一步,吃饭同时听广播.第二步,泡面.第三步,烧水同时洗脸刷牙.第四步,刷水壶4.将51化为二进制数得 ( C )A.11001(2) B.101001(2)C.110011(2)D.10111(2)5.下列是流程图中的一部分,表示恰当的是( A )6.如图所示的程序框图,下列说法正确的是( D )A.该框图只含有顺序结构、条件结构B.该框图只含有顺序结构、循环结构C.该框图只含有条件结构、循环结构D.该框图包含顺序结构、条件结构、循环结构7.如图所示的程序框图,其功能是( C )A.输入a,b的值,按从小到大的顺序输出它们的值B.输入a,b的值,按从大到小的顺序输出它们的值C.求a,b的最大值D.求a,b的最小值8.(2018·哈尔滨高二检测)程序框图如图所示,若输入p=200,则输出结果是( B )A.9B.8C.7D.69.如图所示的程序框图的算法思路;于世界数学名题“3+1问题”.执行该程序框图,若输入的N=3,则输出的i= ( C )A.6B.7C.8D.910.下面的程序运行后的输出结果为( C )A.17B.19C.21D.2311.我国古代数学典籍《九章算术》“盈不足”中有一道两鼠穿墙问题;“今有垣厚十尺,两鼠对穿,初日各一尺,大鼠日自倍,小鼠日自半,问几何日相逢?”现用程序框图描述,如图所示,则输出结果n= ( A )A.4B.5C.2D.312.执行如图所示的程序框图,若输出的结果为43,则判断框内应填入的条件是( A )A.≤42?B.≤20?C.≤50?D.≤52?二、填空题(本大题共4小题,每小题5分,共20分,将答案填在题中的横线上)13.程序框图如图所示.若输出结果为15,则①处的执行框内应填的是=3.14.如图所示的程序框图所表示的算法,输出的结果是2.15.如图程序执行后输出的结果是990.16.用秦九韶算法求多项式f()=6+25+34+43+52+6,当=2时f()的值为240.三、解答题(本大题共6小题,共70分.解答时应写出文字说明,证明过程或演算步骤)17.(10分)101(2)=y02(3),求数字,y的值.【解析】因为101(2)=1×20+×21+0×22+1×23=9+2,y02(3)=2×30+y×32=9y+2,所以9+2=9y+2且∈{0,1},y∈{0,1,2},所以=1,y=1.18.(12分)分别用辗转相除法和更相减损术求779与209的最大公约数. 【解析】(1)辗转相除法;779=209×3+152,209=152×1+57,152=57×2+38,57=38×1+19, 38=19×2.所以779与209的最大公约数为19. (2)更相减损术; 779-209=570, 570-209=361, 361-209=152, 209-152=57, 152-57=95, 95-57=38, 57-38=19, 38-19=19.所以779和209的最大公约数为19.19.(12分)有一堆桃子不知数目,猴子第一天吃掉一半,觉得不过瘾,又多吃了一个.第二天照此办法,吃掉剩下桃子的一半另加一个.天天如此,到第十天早上,猴子发现只剩一个桃子了.问这堆桃子原;有多少个?请写出算法步骤、程序框图和程序. 【解析】算法如下;第一步,a 1=1. 第二步,i=9. 第三步,a 0=2×(a 1+1). 第四步,a 1=a 0. 第五步,i=i-1.第六步,若i=0,执行第七步,否则执行第三步. 第七步,输出a 0的值. 程序框图和程序如图所示;20.(12分)设计程序框图,求出××××…×的值.【解析】程序框图如图所示;21.(12分)给出30个数;1,2,4,7,11,…,其规律是;第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3……以此类推,要计算这30个数的和,现在已知该问题的算法的程序框图如图所示.(1)请在图中判断框和处理框内填上合适的语句,使之能实现该题的算法功能.(2)根据程序框图写出程序.【解析】(1)该算法使用了当型循环结构,因为是求30个数的和,所以循环体应执行30次,其中i 是计数变量,因此判断框内的条件就是限制计数变量i 的,故应为“i ≤30?”.算法中的变量p 实质是表示参与求和的数,由于它也是变化的,且满足第i 个数比其前一个数大i-1,第i+1个数比其前一个数大i, 故处理框内应为p=p+i.故①处应填i ≤30?;②处应填p=p+i. (2)根据程序框图,可设计如下程序;22.(12分)已知某算法的程序框图如图所示,若将输出的(,y)值依次记为(1,y 1),(2,y 2),…,(n ,y n ),…(1)若程序运行中输出的一个数组是(9,t),求t 的值.(2)程序结束时,共输出(,y)的组数为多少?(3)写出程序框图的程序语句.【解析】(1)由程序框图知,当=1时,y=0;当=3时,y=-2;当=9时,y=-4,所以t=-4.(2)当n=1时,输出一对,当n=3时,又输出一对,…,当n=2 017时,输出最后一对,共输出(,y)的组数为1 009.(3)程序框图的程序语句如下;。

1.2.3循环语句课时过关·能力提升一、基础巩固1.下列说法正确的是()A.当型(WHILE)循环结构不能转化为直到型(UNTIL)循环结构B.当型(WHILE)循环结构先执行循环体,后判断条件C.当型(WHILE)循环结构先判断条件,后执行循环体D.以上说法都不正确,直到型循环是先执行循环体,后判断条件,它们之间可以进行转化,故选C.2.要使下面的程序能运算出“1+2+…+100”的结果,需将语句“i=i+1”加在()A.①处B.②处C.③处D.④处i=i+1”应在循环体中,并且先执行“S=S+i”后执行“i=i+1”,故应加在③处,故选C.3.下面为一个求10个数的平均数的程序,在横线上应填充的语句为()A.i>10B.i<10C.i>=10D.i<=10,在程序一开始,即当i=1时,开始执行循环体,当i=10时,继续执行循环体,题目中求10个数的平均数,所以当i>10时应终止循环.4.下列程序中循环体运行次数是()A.4B.5C.6D.601次运行后,i=50,第2次运行后,i=60,第3次运行后,i=70,第4次运行后,i=80,第5次运行后,i=90,第6次运行后,i=100>90开始成立,循环终止,则共运行了6次.5.下列程序的功能是()A.计算1+3+5+…+2 016B.计算1×3×5×…×2 016C.求方程1×3×5×…×i=2 016中的i值D.求满足1×3×5×…×i>2 016的最小整数iS=1×3×5×…×i,当S≤2016开始不成立,即S>2016开始成立时,输出i,则求满足1×3×5×…×i>2016的最小整数i.6.如图所示的程序运行后输出的第3个数是.:第一次输出的数是1,第二次输出的数是x=1第三次输出的数是x7.下列程序输出的结果是.a=1b=1b=1<5成立c=1+1=2a=1b=2b=2<5成立c=1+2=3a=2b=3b=3<5成立c=2+3=5a=3b=5b=5<5不成立输出b=5.8.下面程序是求1+3+5+…+99的值,阅读程序完成问题.问题:(1)程序中的循环语句是型循环语句;(2)将此程序用另一类型的循环语句来实现.当(WHILE)(2)改成直到型循环语句如下:9.写出求满足1+2+3+…+n>10 000的最小整数n的程序.二、能力提升1.下面的程序运行后,输出的i值等于()A.6B.7C.8D.9,S=0+0=0,i=0+1;第二次循环,S=0+1=1,i=1+1=2;第三次循环,S=1+2=3,i=2+1=3;第四次循环,S=3+3=6,i=3+1=4;第五次循环,S=6+4=10,i=4+1=5;第六次循环,S=10+5=15,i=5+1=6;第七次循环,S=15+6=21,i=6+1=7,因为S=21>20,所以输出i=7.2.下面两个程序最后输出的“S”分别等于()i=1WHILE i<8i=i+2S=2 i+3WENDPRINT SEND i=1WHILE i<8S=2 i+3i=i+2WENDPRINT SENDA.17,17B.21,21C.21,17D.14,21,i=7时执行循环体i=i+2,此时i为9,S=2×9+3=21,结束循环.第二个程序中,i=7时,S=2×7+3=17,然后执行i=i+2,此时i=9,结束循环.3.下面程序运行后输出的结果为()A.0B.1C.2D.4j=1时,余数a=1;当j=2时,余数a=3;当j=3时,余数a=1;当j=4时,余数a=0;当j=5时,余数a=0;当j=6时,不满足条件,此时退出循环.4.根据下列程序框图,把对应的程序中所缺少的语句补充完整.,对应的语句为直到型循环语句,DO后面执行的语句为循环体,故①②处应分别为S=S+i^2,i=i+1,直到满足条件i>100为止,所以③处应为i>100.S=S+i^2②i=i+1③i>100★5.下列循环体执行的次数是.6.根据下列程序,画出相应的程序框图.DOS=S+1/(k (k+1)):★7.下面程序的功能是输出1~100之间的所有偶数.程序:(1)试将上面的程序补充完整;(2)改写为含WHILE型循环语句的程序.①m=0②i=i+1(2)改写为含WHILE型循环语句的程序如下:。

算法初步注意事项：1．答题前，先将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。

2．选择题的作答：每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，写在试题卷、草稿纸和答题卡上的非答题区域均无效。

3．非选择题的作答：用签字笔直接答在答题卡上对应的答题区域内。

写在试题卷、草稿纸和答题卡上的非答题区域均无效。

4．考试结束后，请将本试题卷和答题卡一并上交。

一、选择题（本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）1．计算机执行如图的程序段后，输出的结果是（）A．2，3 B．2，2 C．0，0 D．3，2 2．如图所示的程序框图中，要想使输入的值与输出的值相等，输入的a值应为（）A．1 B．3 C．1或3 D．0或3 3．执行下图程序框图，若输出2y=，则输入的x为（）A．1-或B．1±C．1D．1-或4，则输入的x可能为（）A．1-B．1 C．1或5 D．1-或1 5．阅读下边的程序框图，运行相应的程序，则输出s的值为（）12A ．－1B ．0C ．1D ．36．计算机执行下面的程序段后，输出的结果是（ ）A ．1，3B ．4，1 0，0 D ．6，07．给出30个数：1，2，4，7，11，…，其规律是第一个数是1，第二个数比第一个数大1，第三个数比第二个数大2，第四个数比第三个数大3，……依此类推，要计算这30个数的和，现已知给出了该问题的程序框图如图所示．那么框图中判断框①处和执行框②处应分别填入（ ）A ．30?i ≤；p ＝p ＋i －1B ．29?i ≤；p ＝p ＋i －1C ．31?i ≤；p ＝p ＋iD ．30?i ≤；p＝p ＋i8．当x ＝5，y ＝－20时，下面程序运行后输出的结果为（ ）A ．22，－22 B．22，22 C ．12，－12 D ．－12，12 9．阅读如图所示的程序框图，运行相应的程序，输出的结果是（ ） A ．2 B ．4 C ．8 D ．16 10．读程序当输出的y 的范围大于1 ）A ．(－∞，－1)B ．(1，＋∞)3C ．(－∞，－1)∪(1，＋∞)D ．(－∞，0)∪(0，＋∞)11．用“辗转相除法”求得459和357的最大公约数是（ ）A ．3B ．9C ．17D ．5112．以下给出了一个程序框图，其作用是输入x 的值，输出相应的y 的值，若要使输入的x 的值与输出的y 的值相等，则这样的x 的值有（ ）A ．1个B ．2个C ．3个D ．4个二、填空题（本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上）13．读程序本程序输出的结果是________．14．人怕机械重复，如计算1＋2＋3＋…＋100，十岁的高斯就想到类似于梯形面积的求法：其和S ＝1＋1002×100＝5050，而不是算99次加法，但计算机不怕重复，使用________来做完99步计算，也是瞬间的事，编写这个程序可用________，______两种语句结构．15．某工厂2010年的年生产总值为200万元，技术革新后预计以后每年的年生产总值都比上一年增长5%．为了求年生产总值超过300万元的最早年份，有人设计了解决此问题的程序框图（如图），请在空白判断框内填上一个适当的式子应为________________．16．如图是一个程序框图，则输出的S 的值是_____．三、解答题（本大题共6个小题，共70分，解答应写出文字说明，证明过程或演算步骤） 17．（10分）把“五进制”数1234(5)转化为“十进制”数，再把它转化为“八进制”18．（12分）设计一个可以输入圆柱的底面半径r和高h，再计算出圆柱的体积和表面积的算法，画出程序框图．19．（12分）某公司为激励广大员工的积极性，规定：若推销产品价值在10000元之内的年终提成5%；若推销产品价值在10000元以上（包括10000元），则年终提成10%，设计一个求公司员工年终提成f(x)的算法的程序框图．20．（12分）如图所示，利用所学过的算法语句编写相应的程序．4521．（12分）编写程序，对于函数()()333010030x x y x x x ⎧+<⎪⎪==⎨⎪->⎪⎩要求输入x 值，输出相应的y 值．22．（12分）在边长为4的正方形ABCD 的边上有一点P ，在折线BCDA 中，由点B （起点）向A （终点）运动，设点P 运动的路程为x ，△APB 的面积为y ，求y 与x 之间的函数关系式，画出程序框图，写出程序．12018-2019学年必修三第一章训练卷算法初步（二）答 案一、选择题（本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）1．【答案】A【解析】运行程序可得312a =-=，213b =+=，所以输出的结果为2，3．选A ．2．【答案】D【解析】根据程序框图，知本题实质是解方程a ＝－a 2＋4a ，解得a ＝0或a ＝3， 故答案为D ．3．【答案】D【解析】程序框图实现的功能是计算分段函数220 0x x y x x -⎧≤⎪=⎨>⎪⎩，若2y=， 则1x =-或D ．4．【答案】B【解析】1x =1x =-，不满足2x ≤故错误．故选B ．5．【答案】B【解析】当i ＝1时，s ＝1×(3－1)＋1＝3；当i ＝2时，s ＝3×(3－2)＋1＝4；当i ＝3时，s ＝4×(3－3)＋1＝1；当i ＝4时，s ＝1×(3－4)＋1＝0；紧接着i ＝5，满足条件i>4，跳出循环，输出s 的值为0．故选B ．6．【答案】B【解析】把1赋给变量a ，把3赋给变量b ，把4赋给变量a ，把1赋给变量b ， 输出a ，b ．故选B ．7．【答案】D8．【答案】A【解析】具体运行如下：(x ，y)→(5，－20)→(5，－17)，∴x －y ＝22，y －x ＝－22．故选A ．9．【答案】C【解析】本小题考查的是程序框图中的循环结构，循环体中两个变量S 、n 其值对应变化，执行时，S 与n 对应变化情况如下表：S ＝2时，输出n ＝8．故选10．【答案】C 【解析】由程序可得01102x x y x >=⎨⎛⎫-≤⎪ ⎪⎝⎭⎩， ∵1y >，∴①当0x ≤时，1112x ⎛⎫-> ⎪⎝⎭，即22x >－，∴1x ->， ∴1x <-．②当0x >，即1x >， 故输入的x 值的范围为()()11∞∞-，-，+．故选C． 11．【答案】D 【解析】459＝357×1＋102，357＝102×3＋51，102＝51×2， 51是102和51的最大公约数，也就是459和357的最大公约数．故选D ． 12．【答案】C 二、填空题（本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上） 13．【答案】【解析】由题意知V 14．【答案】循环语句，WHILE 型，UNTIL 型 15．【答案】300?a > 16．【答案】63 【解析】当n ＝1时，S ＝1＋21＝3； 当n ＝2时，S ＝3＋22＝7； 当n ＝3时，S ＝7＋23＝15； 当n ＝4时，S ＝15＋24＝31；2 当n ＝5时，S ＝31＋25＝63>33．故S ＝63．三、解答题（本大题共6个小题，共70分，解答应写出文字说明，证明过程或演算步骤）17．【答案】见解析．【解析】1234(5)＝1×53＋2×52＋3×51＋4×50＝194，∴194＝302(8)18．【答案】见解析．【解析】算法如下：第一步：输入半径r 和高h第二步：计算底面积2S r =π第三步：计算体积V hs =第四步：计算侧面积2C rh =π第五步：计算表面积2B S C =+第六步：输出V 和B程序框图如右图，19．【答案】见解析．【解析】程序框图如下图所示：20．【答案】见解析．【解析】程序如下：INPUT ,0N =00WHILE N *10^N N 1WEND PRINT END x n m i i n x i m m i i m ==<=+=+=+ 21．【答案】见解析． 【解析】程序如下： ()()INPUT IF 0THEN 10ELSE IF 0THEN 3^3ELSE 3^3END IF END IF PRINT END x x y x y x y x y ==>=-=+ 22．【答案】见解析． 【解析】()204848212812x x y x x x ⎧≤≤⎪=<≤⎨⎪-<≤⎩程序框图如下图．3 程序如下：。

2019年高中数学单元测试试题 算法初步专题（含答案）学校：__________考号：__________第I 卷（选择题）请点击修改第I 卷的文字说明 一、选择题1．1 ．（2013年高考江西卷（文））阅读如下程序框图,如果输出i=4,那么空白的判断框中应填入的条件是（ ）A ．S<8B ．S<9C ．S<10D ．S<11第II 卷（非选择题）请点击修改第II 卷的文字说明 二、填空题2． 阅读如图所示的程序框，若输入的n 是100，则输出的变量S 的值是 ．3．计算机执行如图所示程序后,输出的结果是 ▲ .4．程序框图（即算法流程图）如图所示，其输出结果是_______.5．右图是一个算法的流程图，最后输出的S ▲ .a ← 1b ← 3 While a<8 a ← a ＋b b ← a －b End whilePrint b6．根据如图所示的算法语句，可得输出的结果是7．根据如图所示的算法流程图，可知输出的结果i 为_______________．8．一个用流程图表示的算法如图所示，则其 运行后输出的结果为 1320 .9．阅读下面流程图（2），该程序输出的结果是__________；10．方程3310x x --=在(0,2)内_______根。

（填“有”或“没有”）11．如图所示的流程图，输出的结果S是________；（第6题）12．左面伪代码的输出结果为．第8题13．某程序框图所示，若输出的S=57，则判断框内为(A) k>4? (B) k>5?(C) k>6? (D) k>7? （2010浙江文）4.14．下列伪代码输出的结果是．（2009金陵中学三模）答案1715．如图示程序运行后的输出结果为．16． 在如图所示的算法流程图中，若输入m = 4，n = 3，则输出的 a = ▲ ． 1217．执行图中程序框图表示的算法，若输入m ＝5533，n ＝2012，则输出d ＝ ▲ . （注：框图中的赋值符号“＝”也可以写成“←”或“：＝”）18．执行下列伪代码，输出的结果为 ▲．1A ← 2B ← 3C ←S A B C ←++Print S19．右边的程序框图（假设函数random ()0,1是产生随机数的函数，它能随机产生区间()0,1内的任何一个实数），随着输入N 的不断增大，输入的值q 会在某个常数p 附近摆动并趋于稳定，则常数p =20．随机抽取某产品n 件，测得其长度分别为1a ，2a ，⋅⋅⋅，n a ，若4=n ，1951=a ，1972=a ，1933=a ，1994=a ，则如右图所示的程序框图输出的=S ．输入n a a a n ,,,,21⋅⋅⋅1,0←←i s1+←i in i ≤ia s i s i+⨯-←)1(输出s结束（第5题图）21．如图，运行伪代码所示的程序，则输出的结果是 .否第7题22．若某程序流程图如图所示，则该程序运行后输出的y 等于 ．23．如图所示,程序框图(算法流程图)的输出结果是A ．3B ．4C ．5D ．8（2012安徽文）24．根据右图的伪代码，输出的结果T 为 ▲ ．25．执行如图算法框图，若输入10=a ，3=b 则输出的值为 ▲ ;26．右图是一个算法的流程图，则输出S 的值是______ _______[解析]考查流程图理解。

(四十八)算法与程序框图(对应学生用书第298页)A组基础达标(建议用时：30分钟)一、选择题1．(2017·北京高考)执行如图9-1-13所示的程序框图，输出的s值为()图9-1-13A．2B．3 2C．53 D.85C[开始：k＝0，s＝1；第一次循环：k＝1，s＝2；第二次循环：k＝2，s＝3 2；第三次循环：k＝3，s＝53，此时不满足循环条件，输出s，故输出的s值为5 3.故选C．]2．(2018·榆林模拟)执行如图9-1-14所示的程序框图，输出S 的值为( )图9-1-14A ．－3115B ．－75C ．－3117D ．－2117C [由程序框图可知i ＝1，S ＝13；i ＝2，S ＝－17；i ＝3，S ＝－913；i ＝4，S ＝－3117，此时不满足条件，退出循环，输出S ＝－3117.]3．(2016·四川高考)秦九韶是我国南宋时期的数学家，普州(现四川省安岳县)人，他在所著的《数书九章》中提出的多项式求值的秦九韶算法，至今仍是比较先进的算法．如图9-1-15所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例，若输入n ，x 的值分别为3,2，则输出v 的值为( )图9-1-15A．35 B．20C．18 D．9C[由程序框图知，初始值：n＝3，x＝2，v＝1，i＝2，第一次：v＝4，i＝1；第二次：v＝9，i＝0；第三次：v＝18，i＝－1.i＝－1<0，结束循环，输出v＝18，故选C．]4．(2018·黄山模拟)随机抽取某产品n件，测得其长度分别是a1，a2，…，a n，如图9-1-16所示的程序框图输出样本的平均值为s，则在处理框①中应填入的式子是()图9-1-16A．s＝s＋a ii B．s＝is＋a ii＋1C ．s ＝s ＋a iD ．s ＝(i －1)s ＋a i iD [设a 1＋a 2＋…＋a i ＝S i ，则在第i －1次时S i －1＝(i －1)s ，在第i 次时S i ＝S i －1＋a i ，∴s ＝S i i ＝S i －1＋a i i ＝(i －1)s ＋a i i，故选D.] 5．(2016·天津高考)阅读下边的程序框图，运行相应的程序，则输出S 的值为( )图9-1-17A ．2B ．4C ．6D ．8B [S ＝4不满足S ≥6，S ＝2S ＝2×4＝8，n ＝1＋1＝2；n ＝2不满足n >3，S ＝8满足S ≥6，则S ＝8－6＝2，n ＝2＋1＝3；n ＝3不满足n >3，S ＝2不满足S ≥6，则S ＝2S ＝2×2＝4，n ＝3＋1＝4； n ＝4满足n >3，输出S ＝4.故选B ．]6．(2018·河南百校联盟模拟)《九章算术》是中国古代数学名著，体现了古代劳动人民数学的智慧，其中第六章“均输”中，有一竹节容量问题，某教师根据这一问题的思想设计了如图9-1-18所示的程序框图，若输出的m 的值为35，则输入的a 的值为( )图9-1-18A ．4B ．5C ．7D ．11A [由程序框图知m ＝2(2a －3)－3＝4a －9，i ＝2；m ＝2(4a －9)－3＝8a －21，i ＝3；m ＝2(8a －21)－3＝16a －45，i ＝4，接着计算m ＝2(16a －45)－3＝32a －93，跳出循环，输出m ＝32a －93，令32a －93＝35，得a ＝4.]二、填空题7．(2017·江南名校联考)某程序框图如图9-1-19所示，判断框内为“k ≥n ？”，n 为正整数，若输出的S ＝26，则判断框内的n ＝________.4 [依题意，执行题中的程序框图，进行第一次循环时，k ＝1＋1＝2，S ＝2×1＋2＝4；进行第二次循环时，k ＝2＋1＝3，S ＝2×4＋3＝11；进行第三次循环时，k ＝3＋1＝4，S ＝2×11＋4＝26.因此当输出的S ＝26时，判断框内的条件n ＝4.]图9-1-19 图9-1-20 8．执行如图9-1-20所示的程序框图(算法流程图)，输出的n 为________．4 [执行第一次判断：|a －1.414|＝0.414＞0.005，a ＝32，n ＝2；执行第二次判断：|a －1.414|＝0.086＞0.005，a ＝75，n ＝3；执行第三次判断：|a －1.414|＝0.014＞0.005，a ＝1712，n ＝4；执行第四次判断：|a －1.414|＜0.005，输出n ＝4.]9．执行下边的程序，输出的结果是________．S ＝1i ＝3WHILE S ＜＝200S ＝S*i i ＝i ＋2WENDPRINT iEND11 [根据循环结构可得：第一次，S ＝1×3＝3，i ＝3＋2＝5，由于3≤200，则循环；第二次：S ＝3×5＝15，i ＝5＋2＝7，由于15≤200，则循环；第三次：S ＝15×7＝105，i ＝7＋2＝9，由于105≤200，则循环；第四次：S ＝105×9＝945，i ＝9＋2＝11，由于945＞200，则循环结束，故此时输出i ＝11.]10．(2018·资阳模拟)MOD(m ，n )表示m 除以n 的余数，例如MOD(8,3)＝2.如图9-1-21是某个算法的程序框图，若输入m 的值为48，则输出i 的值为________．图9-1-219 [由程序框图可知，该程序框图计算输入值m 除去自身的约数的个数.48的非自身的约数有1,2,3,4,6,8,12,16,24，共9个，易知输出i 的值为9.]B组能力提升(建议用时：15分钟)1．(2016·全国卷Ⅲ)执行下面的程序框图，如果输入的a＝4，b＝6，那么输出的n＝()图9-1-22A．3B．4C．5D．6B[开始a＝4，b＝6，n＝0，s＝0.第1次循环：a＝2，b＝4，a＝6，s＝6，n＝1；第2次循环：a＝－2，b＝6，a＝4，s＝10，n＝2；第3次循环：a＝2，b＝4，a＝6，s＝16，n＝3；第4次循环：a＝－2，b＝6，a＝4，s＝20，n＝4.此时，满足条件s>16，退出循环，输出n＝4.故选B．]2．(2018·长沙模拟)给出30个数：1,2,4,7,11，…，要计算这30个数的和，现已给出了该问题的程序框图如图9-1-23所示，那么判断框①处和执行框②处应分别填入()图9-1-23A．i≤30？；p＝p＋i－1 B．i≤31？；p＝p＋i＋1C．i≤31？；p＝p＋i D．i≤30？；p＝p＋iD[由于要计算30个数的和，故循环要执行30次，由于循环变量的初始值为1，步长为1，故终值应为30，即①中应填写i≤30；第1个数是1；第2个数比第1个数大1，即为1＋1＝2；第3个数比第2个数大2，即为2＋2＝4；第4个数比第3个数大3，即为4＋3＝7；……故②中应填写p＝p＋i.故选D.]3．(2018·江西宜春模拟)若开始输入x的值为3，则输出的x的值是()图9-1-24A．6 B．21C．156 D．231D[∵x＝3，∴x(x＋1)2＝6，∵6＜100，∴当x＝6时，x(x＋1)2＝21＜100，∴当x＝21时，x(x＋1)2＝231＞100，停止循环，则最后输出的x的值是231，故选D.]4．(2018·石家庄模拟)如图9-1-25所示的程序框图，程序运行时，若输入的S＝－12，则输出的S的值为________．图9-1-258[由程序框图知，初始值：S＝－12，n＝1；第一次循环，S＝－10，n＝2；第二次循环，S＝－6，n＝3；第三次循环，S＝0，n＝4；第四次循环，S＝8，n＝5，此时S＞n，退出循环，输出S＝8.]。