1999～2000年北大附中初二年级下学期期中数学试卷(几何)

一、选择题1．在ABCD 中AB BC ≠．F 是BC 上一点，AE 平分FAD ∠，且E 是CD 的中点，则下列结论：①AB BF =；②AF CF CD =+；③AF CF AD =+；④AE EF ⊥，其中正确的是（ ）A ．①②B ．②④C ．③④D ．①②④ 2．下列二次根式的运算：①2623⨯=，②1882-=，③255=，④()222-=-；其中运算正确的有（ ）．A ．1个B ．2个C ．3个D ．4个 3．下列计算正确的是（ ） A ．42=±B ．22423x x x +=C ．()326328a b a b -=-D ．()235x x x -=÷ 4．已知三个数2，2，4如果再添加一个数，使这四个数成比例，则添加的数是（ ）．A ．22B ．22或22C ．22，42或82D ．22，22或425．下列四个式子中，与1(2021)2021a a --的值相等的是（ ） A ．2021a - B ．2021a --C ．2021a -D ．2021a -- 6．如图，在平行四边形ABCD 中，90B ∠<︒，BC AB >．作AE BC ⊥于点E ，AF CD ⊥于点F ，记EAF ∠的度数为α，AE a =，AF b =．则以下选项错误的是（ ）A ．::a b CD BC =B ．D ∠的度数为αC ．若60α=︒，则四边形AECF 的面积为平行四边形ABCD 面积的一半D ．若60α=︒，则平行四边形ABCD 的周长为()433a b + 7．如图，已知ABC ∆的面积为24,点D 在线段AC 上，点F 在线段BC 的延长线上，且4,BC CF =四边形DCFE 是平行四边形，则图中阴影部分的面积为（ ）A ．6B ．8C ．3D ．48．如图，在平行四边形ABCD 中，点F 是AB 的中点，连接DF 并延长，交CB 的延长线于点E ，连接AE ．添加一个条件，使四边形AEBD 是菱形，这个条件是（ ）A ．BAD BDA ∠=∠B ．AB DE =C ．DF EF =D ．DE 平分ADB ∠9．如图，在ABC 中，AB AC =，8BC cm =，AE 平分BAC ∠，交BC 于点E ，D 为AE 上一点，且ACD CAD ∠=∠，3DE cm =，连接CD ．过点作DF AB ⊥，垂足为点F ．则下列结论正确的有（ ）①5CD cm =；②10AC cm =；③3DF cm =；④ACD △的面积为210cmA ．1B ．2C ．3D ．410．在ABC 中，10AB =，40AC =，BC 边上的高6AD =，则另一边BC 等于（ ）A ．10B ．8C ．6或10D ．8或10 11．勾股定理是人类最伟大的科学发现之一，在我国古代《周髀算经》中早有记载．如图①，以直角三角形的各边为边分别向外作正方形，再把较小的两张正方形纸片按图②的方式放置在最大正方形内．若图中阴影部分图形的面积为3，则较小两个正方形重叠部分图形的面积为（ ）A ．2B ．3C ．5D ．612．下图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案，已知大正方形面积为49，小正方形面积为4，若用x ，y 表示直角三角形的两直角边()x y >，下列四个说法：①2249x y +=，②2x y -=，③2449xy +=，④9x y +=．其中说法正确的是（ ）．A ．①③B ．①②③C ．②④D ．①②③④二、填空题13．如图，四边形ABCD 为菱形，以AD 为斜边的Rt AED △的面积为3，2DE =，点E ，C 在BD 的同侧，点P 是BD 上的一动点，则PE PC +的最小值是_____________．14．如图，AC 是ABCD 的对角线，点E 在AC 上，AD AE BE ==，102D =︒，则BAC ∠的度数是______．15．已知335x x y -+-=+，则3x y +的值为_________． 16．已知5ab =，则b a a b a b+=__． 17．若220x y -+=，则x y +=________．18．“东方之门”座落于美丽的金鸡湖畔，高度约为301.8米，是苏州的地标建筑，被评为“中国最高的空中苏式园林”．现以现代大道所在的直线为x 轴，星海街所在的直线为y 轴，建立如图所示的平面直角坐标系（1个单位长度表示的实际距离为100米），东方之门的坐标为4(6,)A -，小明所在位置的坐标为(2,2)B -，则小明与东方之门的实际距离为___________米．19．如图，点P 是等边ABC 内的一点，6PA =，8PB =，10PC =.若点P '是ABC 外的一点，且P AB PAC '≌△△，则APB ∠的度数为_____．20．如图，∠AOD =90°，OA =OB =BC =CD ，若AC =3，则AD =_______．三、解答题21．如图，在▱ABCD 中，AB =12cm ，BC =6cm ，∠A =60°，点P 沿AB 边从点A 开始以2cm/秒的速度向点B 移动，同时点Q 沿DA 边从点D 开始以1cm/秒的速度向点A 移动，用t 表示移动的时间（0≤t ≤6）．（1）当t 为何值时，△PAQ 是等边三角形？（2）当t 为何值时，△PAQ 为直角三角形？22．如图，在四边形ABCD 中，90B D ∠=∠=︒，60C ∠=°，5AB =．2AD =．（1）求CD 的长；（2）求四边形ABCD 的面积．23．计算：（1231(12)272224--- （2） 248(31)(31)(31)(31)1++++- 24．观察，计算，判断：（只填写符号：＞，＜，=）（1）①当2a =，2b =时，2a b +ab ②当3a =，3b =时，2a b +ab ； ③当4a =，1b =时，2a b +ab ④当5a =，3b =时，2a b +ab （2）写出关于2a b +ab ______探究证明：（提示：20a b ≥）（3）实践应用：要制作面积为1平方米的长方形镜框，直接利用探究得出的结论，写出镜框周长的最小值为______．25．如图，在Rt △ABC 中，∠C ＝90°，AC ＝8，AB ＝10，AB 的垂直平分线分别交AB 、AC 于点D 、E ．求AE 的长．26．本题分为A，B两题，可以自由选择一题，你选择题A：如图，小明想知道学校旗杆的高度，他将升旗的绳子拉到旗杆底端，并在绳子上打了一个结，然后将绳子拉到离旗杆底端6m处，发现此时绳子底端距离打结处2m，则旗杆的高度为多少米？B：如图，AB为一棵大树，在树上距地面10m的D处有两只猴子，它们同时发现地面上的C处有一筐水果，一只猴子从D处爬到树顶A处，利用拉在A处的滑绳AC，滑到C处，另一只猴子从D处滑到地面B，再由B跑到C，已知两只猴子所经路程都是16m，求树高AB．【参考答案】***试卷处理标记，请不要删除一、选择题1．C解析：C【分析】首先延长AD，交FE的延长线于点M，易证得△DEM≌△CEF，即可得EM＝EF，又由AE平分∠FAD ，即可判定△AEM 是等腰三角形，由三线合一的知识，可得AE ⊥EF ，进而可对各选项进行判断．【详解】解：延长AD ，交FE 的延长线于点M ，∵四边形ABCD 是平行四边形，∴AD ∥BC ，∴∠M ＝∠EFC ，∵E 是CD 的中点，∴DE ＝CE ，在△DEM 和△CEF 中，M EFC DEM CEF DE CE ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△DEM ≌△CEF （AAS ），∴EM ＝EF ，∵AE 平分∠FAD ，∴AM ＝AF ，AE ⊥EF ．即AF ＝AD +DM ＝CF +AD ；故③，④正确，②错误．∵AF 不一定是∠BAD 的角平分线，∴AB 不一定等于BF ，故①错误．故选：C ．【点睛】此题考查了平行四边形的性质、等腰三角形的判定与性质以及全等三角形的判定与性质．此题难度适中，注意掌握辅助线的作法，注意掌握数形结合思想的应用． 2．C解析：C【分析】由二次根式的性质、二次根式的混合运算进行计算，再进行判断，即可得到答案．【详解】 2623=，故①正确；18832222==②正确；255=，故③正确；2，故④错误；∴正确的3个；故选：C ．【点睛】本题考查了二次根式的性质、二次根式的混合运算，解题的关键是熟练掌握运算法则进行计算．3．C解析：C【分析】A 选项利用二次根式的化简判断即可；B 利用合并同类项的运算判断即可；C 利用积的乘方判断即可；D 利用同底数幂的除法判断即可；【详解】A 2= ，不符合二次根式的化简，故该选项错误；B 、22223x x x += ，不符合合并同类项的运算，故该选项错误；C 、()326328a ba b -=-，故该选项正确； D 、()523x x x -÷=- ，不符合同底数幂的除法，故该选项错误；故选：C ．【点睛】本题考查了二次根式的化简，合并同类项，整数指数幂，正确掌握公式是解题的关键； 4．D解析：D【分析】运用比例的基本性质，将所添的数当作比例式a ：b =c ：d 中的任何一项，进行计算即可，【详解】设添加的这个数是x当24:x =时，2x =x =当2:4x =时，2x =x =当2:4x =时，4x =2x =，当2:4x =8=， 解得x =故选D ．【点睛】本题考查比例的基本性质，注意写比例式的时候，一定要按照顺序写，顺序不同，结果不同.5．D解析：D【分析】根据二次根式有意义的条件可得出20210a ->，可得20210a -<，由此可将2021a -变形得出答案．【详解】由题意得：20210a ->，可得20210a -<，∴((2021a a ---== 故选：D ．【点睛】本题考查了二次根式的性质与化简，关键是由等式可确定出20210a ->． 6．C解析：C【分析】由平行四边形的性质得出//AD BC ，AD BC =，AB CD =，B D ∠=∠，得出180D C ∠+∠=︒，求出180EAF C ∠+∠=︒，得出B D EAF α∠=∠=∠=；由平行四边形ABCD 的面积得出::a b CD BC =；若60α=︒，则60B D ∠=∠=︒，求出30BAE DAF ∠=∠=︒，由直角三角形的性质得出BE AE ==，DF ，得出2AB BE =，2AD DF ==，求出平行四边形ABCD 的周长2())AB AD a b =+=+；求出ABE ∆的面积212BE AE =⨯=，ADF ∆的面积2=，平行四边形ABCD 的面积BC AE a =⨯=⨯=，得出四边形AECF 的面积=平行四边形ABCD 的面积ABE -∆的面积ADF -∆的面积22)a b =+≠平行四边形ABCD 面积的一半；即可得出结论． 【详解】 解：四边形ABCD 是平行四边形，//AD BC ∴，AD BC =，AB CD =，B D ∠=∠，180D C ∴∠+∠=︒，AE BC ⊥于点E ，AF CD ⊥于点F ，360290180EAF C ∴∠+∠=︒-⨯︒=︒，B D EAF α∴∠=∠=∠=；平行四边形ABCD 的面积BC AE CD AF =⨯=⨯，AE a =，AF b =，BC a CD b ∴⨯=⨯，::a b CD BC ∴=；若60α=︒，则60B D ∠=∠=︒，30BAE DAF ∴∠=∠=︒，33BE AE a ∴==，33DF AF b ==， 232AB BE a ∴==，232AD DF b ==， ∴平行四边形ABCD 的周长42()3()3AB AD a b =+=+； ABE ∆的面积2113322BE AE a a a =⨯=⨯⨯=，ADF ∆的面积2113322DF AF b b b =⨯=⨯⨯=，平行四边形ABCD 的面积2323BC AE b a ab =⨯=⨯=， ∴四边形AECF 的面积=平行四边形ABCD 的面积ABE -∆的面积ADF -∆的面积22233()ab a b =-+≠平行四边形ABCD 面积的一半； 综上所述，选项A 、B 、D 不符合题意，选项C 符合题意；故选：C ．【点睛】本题考查了平行四边形的性质、直角三角形的性质、三角形面积等知识；熟练掌握平行四边形的性质和直角三角形的性质是解题的关键．7．A解析：A【分析】想办法证明S 阴=S △ADE +S △DEC =S △AEC ，再由EF ∥AC ，可得S △AEC =S △ACF 解决问题；【详解】解：如图连接AF 、EC ．∵BC=4CF ，S △ABC =24，∴S △ACF = 14×24=6， ∵四边形CDEF 是平行四边形，∴DE ∥CF ，EF ∥AC ，∴S △DEB =S △DEC ，∴S 阴=S △ADE +S △DEC =S △AEC ，∵EF ∥AC ，∴S △AEC =S △ACF =6，∴S 阴=6．故选：A ．【点睛】本题考查平行四边形的性质、三角形的面积、等高模型等知识，解题的关键是熟练掌握等高模型解决问题，学会用转化的思想思考问题，属于中考常考题型．8．D解析：D【分析】先证明△ADF ≌△BEF ，得到AD=BE ，推出四边形AEBD 是平行四边形，再逐项依次分析即可．【详解】解：在平行四边形ABCD 中，AD ∥BC ，∴∠DAB=∠EBA ，∵点F 是AB 的中点，∴AF=BF ，∵∠AFD=∠BFE ，∴△ADF ≌△BEF ，∴AD=BE ，∵AD ∥BE ，∴四边形AEBD 是平行四边形，A 、当BAD BDA ∠=∠时，得到AB=BD ，无法判定四边形AEBD 是菱形，故该选项不符合题意；B 、AB=BE 时，无法判定四边形AEBD 是菱形，故该选项不符合题意；C 、DF=EF 时，无法判定四边形AEBD 是菱形，故该选项不符合题意；D 、当DE 平分ADB ∠时，四边形AEBD 是菱形，故该选项符合题意；故选：D ．【点睛】此题考查平行四边形的性质，全等三角形的判定及性质，菱形的判定，熟记平行四边形的性质是解题的关键．9．B解析：B【分析】根据AB AC =，AE 平分BAC ∠，得AE BC ⊥，12BE EC BC ==，从而得CD ，结合ACD CAD ∠=∠，得AD CD =，从而计算得AE ；连接BD ，通过证明BED CED △≌△，得BD CD AD ==，通过勾股定理得DF ，即可完成求解．【详解】∵AB AC =，AE 平分BAC ∠∴AE BC ⊥，142BE EC BC === ∴2222345CD DE EC =+=+=∵ACD CAD ∠=∠∴5AD CD ==cm ，故①正确；∴8AE AD DE =+= ∴22224845AC EC AE =+=+=cm ，故②错误； ∴45AB AC ==如图，连接BD∵90DE DE DEB DEF BE EC =⎧⎪∠=∠=⎨⎪=⎩∴BED CED △≌△∴BD CD =∴5BD CD AD ===∵DF AB ⊥∴1252AF BF AB === ∴()22225255DF AD AF =-=-=cm ，故③错误； ∴11541022ACD S AD EC =⨯=⨯⨯=△cm ，故④正确； 故选：B ．【点睛】本题考查了等腰三角形、勾股定理、全等三角形的知识；解题的关键是熟练掌握等腰三角形三线合一、勾股定理、全等三角形的性质，从而完成求解． 10．C解析：C【分析】分两种情况分类讨论，如图所示，分别在Rt ABD △与Rt ACD △中，利用勾股定理求出BD 与CD 的长，即可求出BC 的长．【详解】根据题意画出图形，如图所示，AD 是ABC 的高，∴90ADB ADC ∠=∠=︒，如图1，10AB =，40AC ，6AD =，在Rt ABD △中，由勾股定理得：222AD BD AB +=， ∴22221068BD AB AD =--=，在Rt ACD △中，由勾股定理得：222AD CD AC +=， ∴()22224062CD AC AD =-=-=，∴10BC BD CD =+=；如图2，10AB =，40AC 6AD =，在Rt ABD △中，由勾股定理得：222AD BD AB +=， ∴22221068BD AB AD =--=，在Rt ACD △中，由勾股定理得：222AD CD AC +=，∴()22224062CD AC AD =-=-=，∴6BC BD CD =-=，∴BC 的长度为：6或10．故选：C ．【点睛】本题考查了勾股定理，熟练掌握勾股定理是解题的关键．11．B解析：B【分析】由图①结合勾股定理可得三个正方形面积之间的关系，在图②中，可知两个小正方形的面积与阴影部分面积之和减去大正方形的面积即可得到重叠部分的面积．【详解】设以直角三角形三边为边长的正方形面积分别为S 1，S 2，S 3，大小正方形重叠部分的面积为S ，则由勾股定理可得：S 1+S 2=S 3，在图②中，S 1+S 2+3-S=S 3，∴S=3，故选：B ．【点睛】本题主要考查勾股定理与图形面积，灵活运用勾股定理处理图形面积之间的转化是解题关键．12．B解析：B【分析】根据直角三角形的性质，直角三角形面积的计算公式及勾股定理解答即可．【详解】解：如图所示，∵△ABC 是直角三角形，∴根据勾股定理：22249x y AB +==，故①正确； 由图可知42x y CE -===，故②正确；由图可知，四个直角三角形的面积与小正方形的面积之和为大正方形的面积， 列出等式为144492xy ⨯+=， 即2449xy +=，故③正确； 由2449xy +=可得245xy =，又∵2249x y +=，两式相加得：2224945x xy y ++=+，整理得：()294x y +=，9x y +=≠，故④错误； 故正确的是①②③．故选：B ．【点睛】 本题主要考查了勾股定理的应用，掌握勾股定理、直角三角形的面积公式和完全平方公式是解题的关键．二、填空题13．3【分析】根据菱形的轴对称性可得AC 关于BD 对称当APE 三点共线时的值最小为AE 再根据三角形的面积即可得出答案【详解】解：∵四边形菱形∴AC 关于BD 对称∵点EC 在BD 的同侧∴当APE 三点共线时的值最 解析：3【分析】根据菱形的轴对称性可得A 、C 关于BD 对称，当A 、P 、E 三点共线时，PE PC +的值最小为AE ，再根据三角形的面积即可得出答案．【详解】解：∵四边形ABCD 菱形，∴A 、C 关于BD 对称，∵点E ，C 在BD 的同侧，∴当A 、P 、E 三点共线时，PE PC +的值最小，且最小值为AE ；∵以AD 为斜边的Rt AED △的面积为3， 2DE =， ∴112322⨯=⨯=AE DE AE ， ∴AE=3， ∴PE PC +的最小值是3故答案为：3．【点睛】本题考查了菱形的性质、最短问题、面积法等知识，解题的关键是利用轴对称解决最值问题，是中考常考题型．14．【分析】由四边形ABCD 是平行四边形得到∠ABC=∠D=102°再AD=AE=BE 得出∠EAB=∠EBA ∠BEC=∠BCA 继而得到∠ACB=2∠BAC 再根据∠BAC+∠ACB=3∠BAC=180°-解析：26︒【分析】由四边形ABCD 是平行四边形，得到∠ABC=∠D=102°，再AD=AE=BE ，得出∠EAB=∠EBA ，∠BEC=∠BCA ，继而得到∠ACB=2∠BAC ，再根据∠BAC+∠ACB=3∠BAC=180°-∠ABC 求解即可．【详解】解：∵四边形ABCD 是平行四边形，∴AD=BC ， ∠ABC=∠D=102°，∵AD=AE=BE ，∴BC=AE=BE ，∴∠EAB=∠EBA ，∠BEC=∠BCA ，∵∠BEC=∠EAB ＋∠EBA=2∠EAB ，∴∠ACB=2∠BAC ，∴∠BAC+∠ACB=3∠BAC=180°-∠ABC=180°-102°=78°，∴3∠BAC=78°，即∠BAC=26°，故答案为：26°．【点睛】本题考查平行四边形的性质、三角形外角的性质、等腰三角形的性质，解题的关键是综合运用相关知识．15．2【分析】依据二次根式有意义的条件可求得x 的值然后可得到y 的值最后代入计算即可【详解】∵∴∴故答案为：2【点睛】本题主要考查了二次根式有意义的条件依据二次根式有意义的条件得到xy 的值是解题的关键解析：2【分析】依据二次根式有意义的条件可求得x 的值，然后可得到y 的值，最后代入计算即可．【详解】∵5y =， ∴3x =，5y =．∴2==．故答案为：2．【点睛】本题主要考查了二次根式有意义的条件，依据二次根式有意义的条件得到x 、y 的值是解题的关键．16．【分析】先利用二次根式化简然后分和两种情况解答即可【详解】解：原式当时原式；当时原式；即故答案为【点睛】本题主要考查了二次根式的性质和绝对值的性质根据二次根式的性质化简所给的二次根式是解答本题的关键解析：±【分析】先利用二次根式化简，然后分0a >、0b >和0a <，0b <两种情况解答即可．【详解】解：原式=+a b =+，=5ab =，∴当0a >，0b >时，原式==当0a <，0b <时，原式=-=-即=±故答案为±【点睛】本题主要考查了二次根式的性质和绝对值的性质，根据二次根式的性质化简所给的二次根式是解答本题的关键．17．2【分析】先根据非负数的性质得出关于xy 的方程求出xy 的值代入x+y 进行计算即可【详解】解得故答案为：2【点睛】本题考查的是非负数的性质解题的关键是掌握非负数的性质即几个非负数的和为0时这几个非负数解析：2【分析】先根据非负数的性质得出关于x 、y 的方程，求出x 、y 的值，代入x+y 进行计算即可．【详解】220x y -+=，20x ∴-=，0y =，解得2x =，202x y +=+=．故答案为：2．【点睛】本题考查的是非负数的性质．解题的关键是掌握非负数的性质，即几个非负数的和为0时，这几个非负数都为0．18．【分析】运用勾股定理可求出平面直角坐标系中AB 的长度再根据个单位长度表示的实际距离为米求出结果即可【详解】解：如图AC=6-（-2）=8BC=2-（-4）=6∴∴小明与东方之门的实际距离为10×10解析：1000【分析】运用勾股定理可求出平面直角坐标系中AB 的长度，再根据1个单位长度表示的实际距离为100米求出结果即可．【详解】解：如图，AC=6-（-2）=8，BC=2-（-4）=6 ∴2222=6+8=10AB BC AC +∴小明与东方之门的实际距离为10×100=1000（米）故答案为：1000．【点睛】此题主要考查了勾股定理的应用，构造直角三角形运用勾股定理是解答此题的关键． 19．150°【分析】由可知：PA ＝P′A ∠P′AB ＝∠PACBP′=CP 然后依据等式的性质可得到∠P′AP ＝∠BAC ＝60°从而可得到△APP′为等边三角形可求得PP′由△APP′为等边三角形得∠APP解析：150°【分析】由P AB PAC '≌△△可知：PA ＝P′A ，∠P′AB ＝∠PAC ，BP′=CP ，然后依据等式的性质可得到∠P′AP ＝∠BAC ＝60°，从而可得到△APP′为等边三角形，可求得PP′，由△APP′为等边三角形，得∠APP′＝60°，在△PP′B 中，用勾股定理逆定理证出直角三角形，得出∠P′PB ＝90°，进而可求∠APB 的度数．【详解】连接PP′，∵P AB PAC '≌△△，∴PA ＝P′A=6，∠P ′AB ＝∠PAC ，BP′=CP=10，∴∠P′AP ＝∠BAC ＝60°，∴△APP′为等边三角形，∴PP′＝AP ＝AP′＝6，又∵8PB =，∴PP′2＋BP 2＝BP′2，∴△BPP′为直角三角形，且∠BPP′＝90°∴∠APB ＝90°＋60°＝150°，故答案是：150°【点睛】本题主要考查的是全等三角形的性质、等边三角形的判定、勾股定理的逆定理的应用，证得△APP′为等边三角形、△BPP′为直角三角形是解题的关键．20．【分析】设OA=OB=BC=CD=a 可知AB=AC=AD=由题意知AC=3即可求出AD 的长；【详解】∵OA=OB=BC=CD ∴设OA=OB=BC=CD=a ∵∠AOD=90°∴AC===∴∵AC==3 解析：32【分析】设OA=OB=BC=CD=a ，可知2a ，5a ，10a ,由题意知AC=3，即可求出AD 的长；【详解】∵ OA=OB=BC=CD ，∴ 设OA=OB=BC=CD=a ，∵∠AOD=90°，∴22AO OC +()222a a +5a ， ∴2222(3)10AD OD OA a a a =+=+=，∵5a =3， ∴35∴5=故答案为：【点睛】本意考查了等腰直角三角形的性质，勾股定理，正确掌握等腰直角三角形的性质和勾股定理是解题的关键；三、解答题21．（1）t=2；（2）t=3或65t=．【分析】（1）根据等边三角形的性质，列出关于t的方程，进而即可求解．（2）根据△PAQ是直角三角形，分两类讨论，分别列出方程，进而即可求解．【详解】解：（1）由题意得：AP=2t（米），AQ=6-t（米）．∵∠A=60°，∴当△PAQ是等边三角形时，AQ=AP，即2t=6-t，解得：t=2，∴当t=2时，△PAQ是等边三角形．（2）∵△PAQ是直角三角形，∴当∠AQP=90°时，有∠APQ=30°，即AP=2AQ，∴2t=2（6-t），解得：t=3（秒），当∠APQ=90°时，有∠AQP=30°，即AQ=2AP，∴6-t=2·2t，解得65t=（秒），∴当t=3或65t=时，△PAQ是直角三角形．【定睛】本题主要考查等边三角形的性质，直角三角形的定义以及平行四边形的定义，熟练掌握等边三角形的性质，直角三角形的定义，列出方程，是解题的关键．22．（1）2）2【分析】（1）作DM⊥BC，AN⊥DM垂足分别为M、N，易知四边形MNAB是矩形，分别在Rt△ADN中求出DN，利用含60°的直角三角形求CD即可；（2）由（1）可知，四边形ABCD的面积就是△DCM与梯形ADMB的面积和．【详解】解：（1）如图作DM⊥BC，AN⊥DM垂足分别为M、N．∵∠B＝∠NMB＝∠MNA＝90°，∴四边形MNAB是矩形，∴MN＝AB＝5，AN＝BM，∠BAN＝90°，∵∠C +∠B +∠ADC +∠BAD ＝360°，∠C ＝60°，∠B ＝∠ADC ＝90°，∴∠DAN ＝∠BAD ﹣∠BAN ＝30°，在RT △AND 中，∵AD ＝2，∠DAN ＝30°，∴DN ＝12AD ＝1，AN ＝2222213AD DN -=-=， 在RT △DMC 中，∵DM ＝DN +MN ＝6，∠C ＝60°，∴∠CDM ＝30°，∴CD ＝2MC ，设MC ＝x ，则CD ＝2x ，∵CD 2＝DM 2+CM 2，∴4x 2＝x 2+62，∵x ＞0∴x ＝23，∴CD ＝43．（2）由（1）得，112366322DCM S CM DM =⨯⨯=⨯⨯=， 1111()3113222ADMB S AN DM AB =⨯⨯+=⨯⨯=梯形， 1123633322DCM ABCD ADMB S S S =+=+=四边形梯形．【点睛】本题考查了勾股定理和含有30°角的直角三角形的性质，通过作辅助线，构建特殊的直角三角形是解题关键．23．（1）52；（2）16332- 【分析】（1）先由二次根式的性质、立方根、绝对值的意义进行化简，然后进行计算，即可得到答案；（2）由平方差公式进行化简，然后得到答案．【详解】解：（1）原式3213222=++52=；（2）原式248(31)(31)(31)(31)(31)12-++++=-16163133122--=-=． 【点睛】本题考查了平方差公式，实数的混合运算，二次根式的性质，以及绝对值的化简，解题的关键是熟练掌握运算法则进行计算．24．（1）①＝；②＝；③>；④>；（2）2a b +≥，证明见解析；（3）4． 【分析】（1）①、②、③、④直接将a 、b 的值代入计算即可；（2）由20≥可得0a b -≥，最后移项即可说明；（3）当镜框为正方形时，周长最小，即然后根据正方形的面积求出边长即可解答．【详解】（1）①当2a =，2b =时，2a b +=2，则2a b +②当3a =，3b =时，2a b +=3，则2a b +③当4a =，1b =时，2a b +=2.5，则2a b +④当5a =，3b =时，2a b +=42a b + 故：①＝，②＝，③>，④>；（2）2a b +≥ 20≥，∴0a b -≥，整理得，2a b +≥； （3）当镜框为正方形时，周长最小∵镜框的面积为1∴镜框的边长为1，即周长为4．【点睛】 本题主要考查了二次根式的应用，确定出两个算式的大小关系并灵活运用这种关系成为解答本题的关键．25．254【分析】连接BE ，先利用勾股定理求出BC 的长，根据线段垂直平分线的性质可得AE ＝BE ，然后设AE ＝BE ＝x ，再由勾股定理可得方程（8−x ）2＋62＝x 2，求解后即可得出答案．【详解】解：连接BE ，在Rt △ABC 中，∵∠C ＝90°，AC ＝8，AB ＝10，∴AC 2＋BC 2＝AB 2．即82＋BC 2＝102，解得：BC ＝6．∵DE 是AB 的垂直平分线，∴AE ＝BE ．设AE ＝BE ＝x ，则EC ＝8−x ，∵Rt △BCE 中，EC 2＋BC 2＝BE 2，∴（8−x ）2＋62＝x 2，解得：x ＝254， ∴AE ＝254． 【点睛】此题考查了线段垂直平分线的性质以及勾股定理，掌握线段垂直平分线的性质并结合勾股定理求解线段的长度是解题的关键，且要注意数形结合思想应用．26．A 题：8米；B 题：41213m 【分析】A 题：设出旗杆的高度，利用勾股定理解答即可；B 题：根据题意表示出AD 、AC 、BC 的长，进而利用勾股定理求出AD 的长，即可得出答案．【详解】解：A 题：设旗杆的高度为x 米，则绳子长为（x+2）米，由勾股定理得：()22226x x +=+，解得：8x =，答：旗杆的高度为8米；B 题：由题意可得：BD=10m ，BC=6m ，设AD=xm ，则有：AC=()16x -m ，在Rt △ABC 中，222AB BC AC +=， 即()()22210616x x ++=-， 解得：3013x =， 故AB=30410121313+=m ， 答：树高AB 为41213m ． 【点睛】本题考察勾股定理的应用，善于观察题目的信息是解题的关键．。

初中数学试卷桑水出品北京教育学院附属中学2014-2015学年度 第二学期期中八年级数学试卷 2015.4考生须知1. 本试卷共4页.正卷满分100分，附加题5分，考试时间100分钟.2. 在试卷的密封线内准确填写班级、姓名、学号.3. 在试卷上按要求作答.4. 考试结束，请将试卷按页码顺序整理好交回.一．选择题（每小题3分，共30分）在下列各题的四个备选答案中，只有一个是正确的，请把正确结论的代号写在题后的括号内. 1. 在△ABC 中，∠C ＝90°，若AC=3，BC=5，则AB 等于（ ）. A ．34 B ．4 C ．20 D ．都不对 2. 下列各组数中，以a 、b 、c 为边长的三角形不是．．直角三角形的是（ ）. A ．a =3， b =4， c =5， B ．a =5， b =12， c =13 C ．a =23， b =2， c =3 D ．a =1， b =2， c =5 3. 顺次连结对角线垂直的四边形各边中点，所得四边形是（ ）. A.平行四边形 B.矩形 C.菱形 D.任意四边形 4. 对于反比例函数2y x=，下列说法不正确．．．的是 （ ）. A 、点(21)--，在它的图象上 B 、它的图象在第一、三象限C 、当0x >时，y 随x 的增大而增大D 、当0x <时，y 随x 的增大而减小 5.用配方法解一元二次方程0542=--x x 的过程中，配方正确的是（ ）． A ． 1)2(2=+x B ． 1)2(2=-x C ． 9)2(2=+x D ． 9)2(2=-x6. 如图，A 为反比例函数xky =图象上一点，AB ⊥x 轴与点B ， 若3=∆AOB S ，则k 的值为（ ）. A ．3 B ．6 C ．23D ．无法确定 7. 在下列方程中，没有实数根的是（ ）．A ．0122=-+x x B ．02222=++x xC ．0122=++x xD ．022=++-x x 8. 在函数xy 3-=的图象上有三个点)4(1y ，-，)1(2y ，-， )3(3y ，，则函数值 1y 、2y 、3y 的大小关系是（ ）． A.2y <3y <1y B.3y <2y <1y C.1y <2y <3y D.3y <1y <2y9. 如图，四边形ABCD 的对角线AC 、BD 互相平分，要使它成为正方形，需要添加的条件（ ）.A ．AB=CDB ．AC=BDC ．AC ⊥BD D ．AC=BD 且AC ⊥BD10. 将矩形纸片ABCD 按如图所示的方式折叠，恰好得到菱形AECF ．若AD ＝3，则菱形AECF的面积为（ ）.A ．23B ．34C ．4D ．8 二．填空题（11--19每小题2分，20题3分，共21分）11. 已知双曲线7m y x+=在第二、四象限内，则m 的取值范围是 . 12. 如图，在△ABC 中，∠ACB=90︒，∠B =40︒，D 为线段AB 的中点，则∠ACD = .13.一元二次方程052=-x x 的根是 .14.如图，在△ABC 中，D 、E 分别是AB 、AC 的中点，若DE ＝6㎝，则BC ＝ cm ．15. 如图，菱形ABCD 中，若BD=24，AC=10，则AB 的长等于 ． 16. 如图，矩形ABCD 中，对角线AC 和BD 交于点O ，过O 的直线分别交AD 和BC 于点E 、F ，已知AD=4 cm ，图中阴影部分的面积总和为6 cm 2，则矩形的对 角线AC 长为 cm ．第14题 第15题第16题 17. 平行四边形ABCD 的周长为20cm ，对角线AC 、BD 相交于点O ，若△BOC 的周长比 A D CBOB CDA A ED EO△AOB 的周长大2cm ，则CD ＝ cm .18. 如图 ，正方形ABCD 的边长为4，M 在DC 上，且DM=1，N 是AC 上一动点，则DN+MN 的最小值为 ．第18题 第20题19. 平行四边形的一个角的平分线分对边为3和4两部分，则平行四边形的周长为 .20. 已知，如图，在平面直角坐标系中，O 为坐标原点，四边形OABC 是矩形，点A 、C 的坐标分别为A （10，0）、C （0，4），点D 是OA 的中点，点P 在BC 边上运动，当△ODP 是腰长为5的等腰三角形时，点P 的坐标为 ．三．解答题（第21题10分，第22-24题6分，共28分） 21. 解一元二次方程：49)52)(1(2=-x 084)2(2=-+x x.22. 已知： 如图，在□ABCD 中，E 、F 分别是BC 、AD 上的点，BE=DF 。

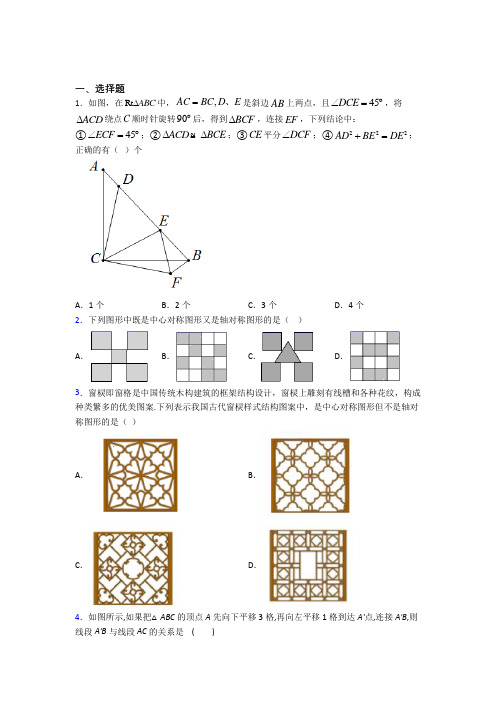
一、选择题1．如图，在Rt ABC ∆中，,AC BC D E =、是斜边AB 上两点，且45DCE ∠=︒，将ACD ∆绕点C 顺时针旋转90︒后，得到BCF ∆，连接EF ，下列结论中：①45ECF ∠=︒；②ACD ∆≌BCE ∆；③CE 平分DCF ∠；④222AD BE DE +=；正确的有（ ）个A ．1个B ．2个C ．3个D ．4个2．下列图形中既是中心对称图形又是轴对称图形的是（ ）A ．B ．C ．D ．3．窗棂即窗格是中国传统木构建筑的框架结构设计，窗棂上雕刻有线槽和各种花纹，构成种类繁多的优美图案.下列表示我国古代窗棂样式结构图案中，是中心对称图形但不是轴对称图形的是（ ）A ．B ．C ．D ．4．如图所示,如果把△ABC 的顶点A 先向下平移3格,再向左平移1格到达A'点,连接A'B ,则线段A'B 与线段AC 的关系是 ( )A ．垂直B ．相等C ．平分D ．平分且垂直5．若0m n <<，则下列结论中错误的是（ ） A ．99m n -<- B ．m n ->-C ．11n m> D ．1m n> 6．不等式组211x x ≥-⎧⎨>-⎩的解集是（ ）A ．1x >-B ．12x >-C ．21x ≥-D ．112x -<≤-7．不等式-3＜a≤1的解集在数轴上表示正确的是（ ）A ．B ．C ．D ．8．如图是一次函数1y kx b =+与2y x a =+的图象，则不等式kx b x a ++＜的解集是（ ）A ．0x >B ．0x <C ．3x >D ．3x <9．如图，30MON ∠=︒点1A ，2A ，3A ，…在射线ON 上，点1B ，2B ，3B ，…在射线OM 上，112A B A ，223A B A ，334A B A ，…均为等边三角形，若11OA =，则边67B B 的长为（ ）A ．63B ．123C ．3D ．64310．如图，在ABC 中，以点A 为圆心，AC 的长为半径作弧，与BC 交于点E ，分别以点E 和点C 为圆心、大于12EC 的长为半径作弧，两弧相交于点P ，作射线AP 交BC 于点D ．若45B ∠=︒，2C CAD ∠=∠，则BAE ∠的度数为（ ）A ．15︒B ．25︒C ．30D ．35︒11．如图，ABC 中，AB AC =，BD DC =，若80BAC ∠=︒，AD AE =，则CDE ∠的度数为（ ）A ．40°B ．30°C ．20°D ．10°12．如图，ABC 中，AB 的垂直平分线分别交AB 、BC 于点D 、E ，AC 的垂直平分线分别交AC 、BC 于点F 、G ，若100BAC ∠=︒，则EAG ∠的度数是（ ）A ．10°B ．20°C ．30°D ．40°二、填空题13．如图，将△ABC 沿BC 方向平移到△DEF ，若A 、D 间的距离为1，CE ＝2，则BF ＝_____．14．如图，在ABC 中，AB AC =，3BC cm =，将ABC 沿BC 方向平移得到DEF ，若5DE cm =，EC 1.5cm =，则四边形ABFD 的周长为_____cm ．15．如图，函数y x =和4y ax =+的图象交于点()2,2,A 则不等式4x ax <+的解集为_____________________．16．定义一种法则“⊗”如下：()()a a b a b b a b >⎧⊗=⎨≤⎩，如：122⊗=，若(25)33m -⊗=，则m 的取值范围是_______．17．不等式2(53)3(12)x x x +≤--的解集为_____．18．已知C ，D 两点在线段AB 的垂直平分线上，且∠ACB ＝50°，∠ADB ＝86°，则∠CAD 的度数是_____．19．如图，在ABC ∆中，AB AC =，36BAC ∠=︒，BD 是ABC ∠的平分线，交AC 于点D ，E 是AB 的中点．连接ED 并延长，交BC 的延长线于点F ，连接AF ．写出图中三角形中所有的等腰三角形______．20．如图，在ABC 中，AB BC =，30C ∠=︒，过点B 作BD BC ⊥，交AC 于点D ，若2CD =，则AD 的长为__________．三、解答题21．ABC 在平面直角坐标系中的位置如图所示，其中每个小正方形的边长为1个单位长度．（1）ABC 关于x 轴对称图形为111A B C △，画出111A B C △的图形；（2）将ABC 向右平移4个单位，再向下平移3个单位，得到图形为222A B C △，画出222A B C △的图形；（3）求ABC 的面积．22．在平面直角坐标系中，△ABC 的三个顶点坐标分别为A （-2，1），B （-4，5），C （-5，2）．（1）画出△ABC 关于y 轴对称的△A 1B 1C 1； （2）画出△ABC 关于原点O 成中心对称的△A 2B 2C 2； （3）求△A 2B 2C 2的面积．23．如图，ABC 中，8,6AC BC AB ===，现有两点,M N 分别从点A 点B 同时出发，沿三角形的边运动，已知点M 的速度为每秒1个单位长度，点N 的运度为每秒2个单位长度，当点M 到达B 点时，,M N 同时停止运动，设运动时间为t 秒． （1）当03t ≤≤时，AM = ，AN= ；(用含t 的代数式表示)（2）当点,M N在边BC上运动时，是否存在某个时刻，使得12 AMNABCS S=△△成立，若成立，请求出此时点M运动的时间；若不成立请说明理由．（3）当点,M N在同一直线上运动时，求运动时间t的取值范围．24．解不等式组32,121.25x xx x<+⎧⎪⎨++≥⎪⎩①②并把解集在数轴上表示出来．25．如图，已知：AD是∠BAC的平分线，AB＝BD，过点B作BE⊥AC，与AD交于点F．（1）求证：AC∥BD；（2）若AE＝2，AB＝3，BF＝355，求△ABF中AB边上的高．26．实践与探究如图1，三角尺ABC和三角尺DEF是两个全等的直角三角尺，其中，∠A=∠D=60°，∠B=∠E=30°，∠C=∠F=90°．操作发现（1）如图2，将三角尺ABC和三角尺DEF如图摆放，连接CF，交AB于点G，请你证明CG= FG；（2）在图2的基础上，将三角尺DEF沿BA方向平移至图3的位置，兴趣小组发现CG仍然与FG相等，请你证明CG= FG；（3）在图3的基础上，将三角尺DEF沿BA方向继续平移，使CF经过点A，如图4所示，兴趣小组测得BD=20.4cm，则三角尺DEF由图2所示位置平移至图4 的位置，平移的距离为_______cm （直接写出答案，不写过程）．【参考答案】***试卷处理标记，请不要删除一、选择题 1．C 解析：C 【分析】①根据旋转的性质可得出∠BCF=∠ACD ，由∠ACB=90°，∠DCE=45°，可得出∠BCF+∠BCE=∠ECF=45°，即可判断①；②根据旋转的性质可得出△ACD ≌△BCF ，不能推出ACD ∆≌BCE ∆，即可判断②； ③根据∠DCE=∠ECF=45°，根据角平分线定义即可判断③；④根据全等三角形的判定求出△AED ≌△AFD ，推出DE=EF ，求出∠EBF=90°，根据勾股定理推出即可． 【详解】解：∵在Rt △ABC 中，BC=AC ， ∴∠A=∠CBA=45°，①由旋转，可知：∠BCF=∠ACD ， ∵∠ACB=90°，∠DCE=45°， ∴∠ACD+∠BCE=45°，∴∠BCF+∠BCE=∠ECF=45°，故①正确；②由旋转，可知：△ACD ≌△BCF ，不能推出ACD ∆≌BCE ∆，故②错误； ③∵∠DCE=∠ECF=45°， ∴CE 平分∠DCF ，故③正确；④由旋转可知：AD=BF ，∠CBF=∠A=45°， ∵∠CBA=45°， ∴∠EBF=90°，由勾股定理得：BF 2+BE 2=EF 2， 即AD 2+BE 2=EF 2， 在△CDE 和△CFE 中，CE CE DCE ECF CD CF =⎧⎪∠=∠⎨⎪=⎩， ∴△CDE ≌△CFE （SAS ）， ∴DE=EF ， ∴AD 2+BE 2=DE 2， 故选：C ．【点睛】本题考查了全等三角形的判定、相似三角形的判定、勾股定理、等腰直角三角形以及旋转的性质，逐一分析四条结论的正误是解题的关键．2．A解析：A【分析】本题利用轴对称图形和中心对称图形的概念求解即可，轴对称图形：沿某一直线折叠后直线两旁的部分互相重合；中心对称图形：将一个图形绕着中心点旋转180°后能与自身重合的图形叫做中心对称图形；【详解】A、此图形既是中心对称图形，也是轴对称图形故此选项正确；B、此图形是中心对称图形，但不是轴对称图形故此选项不正确；C、此图形是轴对称图形，但不是中心对称图形故此选项不正确；D、此图形是轴对称图形，但不是中心对称图形故此选项不正确；故选：A．【点睛】本题考查了轴对称图形和中心对称图形的概念，正确理解它们的概念是解题的关键；3．C解析：C【分析】根据中心对称图形和轴对称图形的概念对各选项分析判断即可．【详解】选项A既是中心对称图形，也是轴对称图形；选项B既是中心对称图形，也是轴对称图形；选项C是中心对称图形，但不是轴对称图形；选项D既是中心对称图形，也是轴对称图形．故选：C．【点睛】本题考查中心对称图形与轴对称图形的概念.判定轴对称图形的关键是寻找对称轴,图形沿对称轴折叠后,对称轴两旁的部分可重合;判定中心对称图形的关键是寻找对称中心,图形绕对称中心旋转180°后,与原图形重合．4．D解析：D【分析】先根据题意画出图形，再利用勾股定理结合网格结构即可判断线段A′B与线段AC的关系．【详解】解：如图，将点A 先向下平移3格，再向左平移1格到达A′点，连接A′B ，与线段AC 交于点O ．∵2，2， ∴线段A′B 与线段AC 互相平分， 又∵∠AOA′=45°+45°=90°， ∴A′B ⊥AC ，∴线段A′B 与线段AC 互相垂直平分． 故选D ． 【点睛】本题考查了平移的性质，勾股定理，正确利用网格求边长长度及角度是解题的关键．5．C解析：C 【分析】分析各个选项是由m ＜n<0如何变化得到的，根据不等式的性质即可进行判断． 【详解】A 、由m ＜n ，根据不等式的两边都加上（或减去）同一个数，所得到的不等式仍成立．两边减去9，得到：m-9＜n-9；成立；B 、两边同时乘以不等式的两边都乘（或都除以）同一个负数，必须把不等号的方向改变，所得到的不等式成立．两边同时乘以-1得到-m ＞-n ；成立；C 、m ＜n ＜0，若设m=-2 n=-1验证11n m>不成立． D 、由m ＜n ，根据两边同时乘以不等式的两边都乘（或都除以）同一个负数，必须把不等号的方向改变，所得到的不等式成立．两边同时除以负数n 得到1mn>，成立； 故选：C ． 【点睛】利用特殊值法验证一些式子错误是有效的方法．不等式的性质运用时注意：必须是加上，减去或乘以或除以同一个数或式子；另外要注意不等号的方向是否变化．6．C解析：C 【分析】先求出2x≥-1的解集，再确定不等式组的解集即可．【详解】解：211x x ≥-⎧⎨>-⎩①②解不等式①得，21x ≥-， 解不等式②得，x>-1，∴不等式组的解集为：21x ≥- 故选：C ． 【点睛】本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．7．A解析：A 【分析】根据在数轴上表示不等式解集的方法求解即可． 【详解】 解：∵-3＜a≤1，∴1处是实心原点，且折线向左． 故选：A ． 【点睛】本题考查了在数轴上表示不等式的解集，掌握“小于向左，大于向右”是解题的关键．8．C解析：C 【分析】根据函数图象可以直接判断本题的答案． 【详解】解：结合图象，当3x >时，函数1y kx b =+在函数2y x a =+的下方， 即不等式kx b x a ++＜的解集是3x >； 故选：C ． 【点睛】本题考查了一次函数与一元一次不等式：从函数图象的角度看，一元一次不等式的解集就是确定直线=+y kx b 在另一条直线（或者x 轴）上（或下）方部分所有点的横坐标的集合；这是数形结合的典型考查．9．C解析：C 【分析】根据等腰三角形的性质以及平行线的性质得出A1B1∥A2B2∥A3B3，以及A2B2=2B1A2，得出B1B2=3，B2B3=23，B3B4=43，以此类推，B n B n+1的长为 2n-13，进而得出答案．【详解】解：∵△A1B1A2是等边三角形，∴A1B1=A2B1，∠3=∠4=∠12=60°，∴∠2=120°，∵∠MON=30°，∴∠1=180°-120°-30°=30°，又∵∠3=60°，∴∠5=180°-60°-30°=90°，∵∠MON=∠1=30°，∴OA1=A1B1=1，∴A2B1=1，∵△A2B2A3、△A3B3A4是等边三角形，∴∠11=∠10=60°，∠13=60°，∵∠4=∠12=60°，∴A1B1∥A2B2∥A3B3，B1A2∥B2A3，∴∠1=∠6=∠7=30°，∠5=∠8=90°，∴A2B2=2B1A2=2，∴B1B2=3，∵B3A3=2B2A3，∴A3B3=4B1A2=4，∴B2B3=23，∵A4B4=8B1A2=8，∴B3B4=43，以此类推，B n B n+1的长为2n-13，∴B6B7的长为323，故选：C．【点睛】本题考查了等边三角形的性质以及等腰三角形的性质，根据已知得出A3B3=4B1A2，A4B4=8B1A2，A5B5=16B1A2进而发现规律是解题的关键．10．A解析：A【分析】根据作图过程可得，AP是EC的垂直平分线，可得AE＝AC，∠ADB＝∠ADC＝90°，再根据∠B＝45°，∠C＝2∠CAD，即可求出∠CAD的度数，进而即可求解．【详解】解：由作图过程可知：AP是EC的垂直平分线，也是∠CAE的角平分线，∴AE＝AC，∠ADB＝∠ADC＝90°，∵∠B＝45°，∴∠BAD＝45°，∵∠C＝2∠CAD，∴3∠CAD＝90°，∴∠CAD＝30°，∴∠EAD＝30°，=45°-30°=15°．∴BAE故选：A．【点睛】本题考查了作图−基本作图，直角三角形的性质，解决本题的关键是掌握基本作图方法．11．C解析：C【分析】根据已知可求得∠DAC及∠ADE的度数，根据∠CDE=90°-∠ADE即可得到答案．【详解】解：∵AB＝AC，BD=DC∴ AD⊥BC（等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合）∴∠ADC=90°，∵∠BAC＝80°，∴∠BAD＝∠DAC＝ 80°÷2=40°（等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合），∵AD＝AE，∴∠ADE＝（180°−40°）÷2=70°，∴∠CDE＝∠ADC-∠ADE=90°-70°=20°，故答案为：C.【点睛】本题主要考查了等腰三角形的性质，三角形内角和定理，掌握等腰三角形的性质，三角形内角和定理是解题的关键.12．B解析：B【分析】根据三角形内角和定理求出∠C＋∠B，根据线段的垂直平分线的性质得到EA＝EB，根据等腰三角形的性质得到∠EAB＝∠B，同理，∠GAC＝∠C，计算即可．【详解】解：∵∠BAC＝100°，∴∠C＋∠B＝180°−100°＝80°，∵DE是AB的垂直平分线，∴EA＝EB，∴∠EAB＝∠B，同理：∠GAC＝∠C，∴∠EAB＋∠GAC＝∠C＋∠B＝80°，∴∠EAG＝100°−80°＝20°，故选B．【点睛】本题考查的是线段的垂直平分线的性质和等腰三角形的性质，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键．二、填空题13．4【分析】根据平移的性质由AD=1得到BE=1CF=1再根据BF=BE+EC+CF计算即可得到答案；【详解】解：根据平移的性质由AD=1得：BE=1CF=1由∵BF=BE+EC+CF∴BF=1+2+解析：4【分析】根据平移的性质，由AD=1得到BE=1，CF=1，再根据BF= BE+EC+CF，计算即可得到答案；【详解】解：根据平移的性质，由AD=1得：BE=1，CF=1，由∵BF= BE+EC+CF，∴BF= 1+2+1=4，故答案为：4；【点睛】本题主要考查了平移的性质，能根据AD=1得到BE=1，CF=1是解题的关键．14．16【分析】根据平移的基本性质得出四边形ABFD的周长＝AD＋AB＋BF＋DF＝15＋5＋45＋5即可得出答案【详解】根据题意将△ABC沿BC方向平移得到△DEF∴AD＝CF＝BEBF＝BC＋CFD解析：16【分析】根据平移的基本性质，得出四边形ABFD 的周长＝AD ＋AB ＋BF ＋DF ＝1.5＋5＋4.5＋5，即可得出答案．【详解】根据题意，将△ABC 沿BC 方向平移得到△DEF ，∴AD ＝CF ＝BE ，BF ＝BC ＋CF ，DE ＝AB ＝AC ＝DF ＝5cm ；又∵BC ＝3cm ，EC ＝1.5cm ，∴BE ＝BC−EC ＝1.5cm ，∴AD ＝CF ＝BE ＝1.5cm ，BF ＝BC ＋CF ＝4.5cm ，∴四边形ABFD 的周长＝AD ＋AB ＋BF ＋DF ＝1.5＋5＋4.5＋5＝16cm ．故答案为：16．【点睛】本题考查平移的基本性质：①平移不改变图形的形状和大小；②经过平移，对应点所连的线段平行且相等，对应线段平行且相等，对应角相等．得到DE ＝AB ＝AC ＝DF ＝5cm ，AD ＝CF ＝BE ＝1.5cm ，BF ＝BC ＋CF ＝4.5cm 是解题的关键．15．【分析】先利用A 点坐标然后观察函数图得到当x ＜2时y=x 的图象都在直线的下方由此得到不等式x ＜ax+4的解集【详解】解：A （23）观察函数图得到：当x ＜2时y=x 的图象都在直线的下方不等式x ＜ax+解析：2x <【分析】先利用A 点坐标，然后观察函数图得到当x ＜2 时，y=x 的图象都在直线4y ax =+的下方，由此得到不等式x ＜ax+4的解集．【详解】 解： A （2，3），观察函数图得到：当x ＜2 时，y=x 的图象都在直线4y ax =+的下方，∴ 不等式x ＜ax+4的解集x ＜2．故答案为：2x <．【点睛】本题考查了一次函数与一元一次不等式：从函数的角度看，就是寻求使一次函数y=ax+b 的值大于（或小于）0的自变量x 的取值范围；从函数图象的角度看，就是确定直线y=kx+b 在x 轴上（或下）方部分所有的点的横坐标所构成的集合．理解好上面原理是解题的关键．16．【分析】根据题意可得2m ﹣5≤3然后求解不等式即可【详解】根据题意可得∵(2m －5)⊕3＝3∴2m ﹣5≤3解得：m≤4故答案为【点睛】本题主要考查解一元一次不等式解此题的关键在于准确理解题中新定义法解析：4m ≤【分析】根据题意可得2m ﹣5≤3，然后求解不等式即可．【详解】根据题意可得，∵(2m－5)⊕3＝3，∴2m﹣5≤3，解得：m≤4m≤．故答案为4【点睛】本题主要考查解一元一次不等式，解此题的关键在于准确理解题中新定义法则的运算规律，得到一元一次不等式．17．【分析】利用不等式的基本性质先将不等式去括号然后移项合并同类项把系数化为1得到x的取值范围【详解】去括号得10x＋6≤x−3＋6x移项合并同类项得3x≤−9解得x≤−3故答案为：x≤−3【点睛】解不x≤-解析：3【分析】利用不等式的基本性质，先将不等式去括号，然后移项合并同类项，把系数化为1，得到x 的取值范围．【详解】去括号得，10x＋6≤x−3＋6x，移项合并同类项得，3x≤−9，解得，x≤−3．故答案为：x≤−3【点睛】解不等式应依据不等式的基本性质，在不等式的两边同时加上或减去同一个数或整式不等号的方向不变；在不等式的两边同时乘以或除以同一个正数不等号的方向不变；在不等式的两边同时乘以或除以同一个负数不等号的方向改变．特别是在系数化为1这一个过程中要注意不等号的方向的变化．18．18°或112°【分析】分点C与点D在线段AB两侧点C与点D在线段AB同侧两种情况根据线段垂直平分线的性质等腰三角形的性质解答【详解】解：如图∵CD两点在线段AB的中垂线上∴CA＝CBDA＝DB∵C解析：18°或112°【分析】分点C与点D在线段AB两侧、点C与点D在线段AB同侧两种情况，根据线段垂直平分线的性质、等腰三角形的性质解答．【详解】解：如图，∵C、D两点在线段AB的中垂线上，∴CA＝CB，DA＝DB，∵CD⊥AB，∴∠ACD＝12∠ACB＝12×50°＝25°，∠ADC＝12∠ADB＝12×86°＝43°，当点C与点D在线段AB两侧时，∠CAD＝180°﹣∠ACD﹣∠ADC＝180°﹣25°﹣43°＝112°，当点C与点D′在线段AB同侧时，∠CAD′＝∠AD′C﹣∠ACD′＝43°﹣25°＝18°，故答案为：18°或112°．【点睛】本题考查的是线段垂直平分线的性质、等腰三角形的性质，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键．19．△ABD△BCD△ABC△ACF△ABF【分析】分别求出所有的角度即可求解【详解】解：∵AB=AC∠BAC=36°∴∠ABC=∠ACB=72°△ABC是等腰三角形∵BD是∠ABC的平分线∴∠ABD=解析：△ABD，△BCD，△ABC，△ACF，△ABF【分析】分别求出所有的角度，即可求解．【详解】解：∵AB=AC，∠BAC=36°，∴∠ABC=∠ACB=72°，△ABC是等腰三角形，∵BD是∠ABC的平分线，∴∠ABD=∠CBD=36°=∠BAC，∴AD=BD，∠BDC=∠BAC+∠ABD=72°=∠ACB，∴△ABD是等腰三角形，BD=BC，∴△BDC是等腰三角形，∵AD=BD，E是AB的中点，∴DE是AB的中垂线，∴AF=BF，∴∠ABF=∠BAF=72°，△ABF是等腰三角形，∴∠CAF=36°=∠AFB ，∴AC=CF ，∴△ACF 是等腰三角形，故答案为：△ABD ，△BCD ，△ABC ，△ACF ，△ABF ．【点睛】本题考查了等腰三角形的判定和性质，掌握等腰三角形的性质是本题的关键．20．【分析】利用等腰三角形的性质判定证明BD=AD 利用直角三角形中30°角的性质计算BD 即可得解【详解】∵∴∠A=30°∠ABC=120°∵∴∠CBD=90°BD=1∴∠DBA=30°∴∠DBA=∠A ∴ 解析：1.【分析】利用等腰三角形的性质，判定，证明BD=AD ，利用直角三角形中30°角的性质计算BD 即可得解.【详解】∵AB BC =，30C ∠=︒，∴∠A=30°，∠ABC=120°，∵BD BC ⊥，2CD =，∴∠CBD=90°，BD=1，∴∠DBA=30°，∴∠DBA=∠A ，∴BD=AD ，∴AD=1.【点睛】本题考查了等腰三角形的判定和性质，直角三角形的性质，熟练掌握性质，并灵活运用性质是解题的关键.三、解答题21．（1）详见解析；（2）详见解析；（3）2．【分析】（1）分别作出A 、B 、C 关于对称轴x 的对应点A 1、B 1、C 1，再顺次连接即可得所求图形；（2）分别将A 、B 、C 三点向右平移4个单位，再向下平移3个单位，得到对应点A 2、B 2、C 2，再顺次连接即可得所求图形为222A B C △；（3）利用构图法即可求解；【详解】（1） ；（2） ；（3）ABC S =2×3-1112⨯⨯-1222⨯⨯-1132⨯⨯ 136222=--- 64=-2=．【点睛】本题考查作图—轴对称及平移变换，还涉及到三角形面积公式，解题的关键是熟练掌握轴对称的性质及平移的性质．22．（1）见解析；（2）见解析；（3）5【分析】（1）根据轴对称的性质确定点A 1、B 1、C 1的位置，顺次连线即可；（2）根据中心对称的性质确定点A 1、B 1、C 1的位置，顺次连线即可；（3）利用割补法计算【详解】（1）如图：△A 1B 1C 1即为所求；（2）如图：△A 2B 2C 2即为所求；（3）△A 2B 2C 2的面积=11134131324222⨯-⨯⨯-⨯⨯-⨯⨯=5 【点睛】此题考查轴对称的性质，中心对称的性质，割补法求网格中图形的面积，熟记轴对称的性质及中心对称的性质作出图形是解题的关键．23．（1）t ，62t -；（2）存在，10秒；（3）37t ≤≤或811t ≤≤【分析】（1）先由运动得出AM=t ，BN=2t ，继而得出AN ，即可得出结论；（2）当点M ，N 在边BC 上运动时，AM=t-8，CN=2t-6-8，即可得到MN=t-6，根据题意知12MN BC =，列出方程即可求解； （3）根据运动的时间、速度和距离即可求得运动时间t 的取值范围．【详解】（1）∵6÷2=3，∴当 0≤t≤3 时，点N 在AB 上运动（包括端点），∵运动时间为t 秒．∴AM=t ，BN=2t ，∴AN=6-2t ，故答案为：t ，6-2t ；（2）存在．理由如下：当M N 、在边BC 上运动时，8672t +>=，点N 在边BC 上， 881t >=，点M 在边BC 上， ∴点N 在点M 前面，此时，CM=t-8，CN=2t-14， ∵12AMN ABC S S ∆∆=，∴12MN BC =， 则1(214)(8)82t t ---=⨯， 解得：10t = 所以，当点M N 、在边BC 上运动，10t =秒时，12AMN ABCS S ∆∆=； （3）①当点M N 、同在AC 上时，∵68AB AC ==，，点N 的速度为2， ∴当66822t +≤≤即37t ≤≤时，点N 在AC 上， 又∵点M 的速度为1，∴当18t ≤≤时，点M 在AC 上， ∴当37t ≤≤时，点M N 、同在AC 上；②当点M N 、同在BC 上时，∵68AB AC ==，，点N 的速度为2，∴当6868822t +++≤≤即711t ≤≤时，点N 在BC 上， 又∵点M 的速度为1． ∴当88811t +≤≤即816t ≤≤时，点M 在BC 上， ∴当811t ≤≤时，点M N 、同在AC 上；综上所述，当37t ≤≤与811t ≤≤时，点M N 、在同一直线上运动．【点睛】本题考查了一元一次方程在几何中的应用，一元一次不等式在几何中的应用等，解题的关键是理解题意，学会用方程的思想思考问题．24．解集为：31x -<．在数轴上表示见解析．【分析】分别求出不等式组中两不等式的解集，找出两解集的公共部分确定出不等式组的解集，表示在数轴上即可．【详解】 解：32,12125x x x x <+⎧⎪⎨++≥⎪⎩①②，由①得：1x <；由②得：3x ≥-，∴不等式组的解集为31x -≤<，表示在数轴上，如图所示：．【点睛】本题考查了解一元一次不等式组，以及在数轴上表示不等式的解集，熟练掌握不等式组的解法是解本题的关键．25．（1）见解析；（2）△ABF 中AB 边上的高为255 【分析】 （1）根据角平分线的定义、等腰三角形的性质得到∠CAD ＝∠BDA ，根据平行线的判定定理证明即可；（2）作FG ⊥AB 于G ，根据勾股定理求出BE ，进而求出FE ，根据角平分线的性质定理解答即可．【详解】（1）证明：∵AD 是∠BAC 的平分线，∴∠CAD ＝∠BAD ，∵AB ＝BD ，∴∠BDA ＝∠BAD ，∴∠CAD ＝∠BDA ，∴AC ∥BD ；（2）解：作FG ⊥AB 于G ，在Rt △ABE 中，AE ＝2，AB ＝3，∴BE 2222325AB AE =-=-=，∴FE ＝BE ﹣BF 3255555=-=， ∵AD 是∠BAC 的平分线，BE ⊥AC ，FG ⊥AB ，∴FG ＝FE 255=，即△ABF 中AB 边上的高为255．【点睛】本题考查的是角平分线的性质、等腰三角形的性质，勾股定理,掌握角的平分线上的点到角的两边的距离相等是解题的关键．26．（1）见解析；（2）见解析；（3）6.8cm【分析】（1）由题意易得AC=AF ，进而可证△ACG ≌△AFG ，然后问题可证；（2）分别过点C ，F 作BD 的垂线，垂足为M ，N ，由题意易得AC=DF ，∠FDE=∠CAB ，进而可得∠AMC=∠BMC=∠DNF=∠FNE=90°，然后可证△AMC ≌△DNF ，则CM=FN ，最后根据△CMG ≌△FNG 可求证；（3）由（1）（2）易得AF=AC ，进而可证AD=AE ，然后可得AE=BE ，最后问题可求解．【详解】（1）证明：三角尺ABC 和三角尺DEF 全等，∴AC=AF ，∵在△ACG 和△AFG 中，AC AF CAB FAB AG AG =⎧⎪∠=∠⎨⎪=⎩，∴△ACG ≌△AFG （SAS ），∴CG= FG ；（2）证明：分别过点C ，F 作BD 的垂线，垂足为M ，N ，∵△ABC ≌△DEF ，∴AC=DF ，∠FDE=∠CAB ，∵CM ⊥BD ，FN ⊥BD ，∴∠AMC=∠BMC=∠DNF=∠FNE=90°，在△AMC 和△DNF 中，AMC DNE CAM FDN AC DE ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△AMC ≌△DNF ，∴CM=FN ，在△CMG 和△FNG 中，CGM FGN CMG FNG CM FN ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△CMG ≌△FNG ，∴CG=FG ；（3）解：由（1）（2）易证AF=AC ，∵△DFE ≌△ACB ，∴AC=DF ，∴AF=DF，∵∠D=60°，∠FED=30°，∴AD=AF=DF=AE，∵AB=DE，∴AD=AE=BE，∵BD=20.4cm，∴AD=AE=BE=6.8cm，∴平移的距离为6.8cm；故答案为6.8．【点睛】本题主要考查三角形全等性质与判定及等边三角形的性质与判定，熟练掌握三角形全等性质与判定及等边三角形的性质与判定是解题的关键．。

精选资料-3.判断正误：（2 分10=20 分） .请你将每道小题正确判断（对用“T”，错用“F”）的答案填北大附中初二几何期中试题在下表相应的地点。

...初二北大附中初二几何期中试题-3判断正误：（ 2 分10=20 分）请你将每道小题正确判断（对用“T”，错用“ F”）的答案填在下表相应的地点。

题号12345678910答案F F F F F F F T T T01．三角形内角和大于其外角和。

02． n 边形对角线共有n(n-3) 条。

03．当多边形的边数增添 1 时，它的外角和增添。

04．不存在既是菱形又是矩形的平行四边形。

05．对于中心对称的两个图形的对应线段平行且相等。

06．对角线相互垂直且有一组邻边相等的四边形是菱形。

07．不存在外角都是钝角的多边形。

09．有一组对边相等、一组对角是直角的四边形是矩形。

08．对角线和一边夹角为的菱形是正方形。

10．平行四边形各内角均分线围成的四边形其对角线相等。

二、选择题：（ 3 分10=30 分）在以下各题的四个被选答案中，只有一个是正确的，请你将每道小题正确的答案对应的字母填在下表相应的地点。

题号111213 1415 1617181920答案D C D D B C B C A C 11．下边性质中矩形不必定拥有的是（）。

（A）对角线相等（C）是轴对称图形（B）四个角都相等（D）对角线垂直12．菱形边长为2，一条对角线长是，另一条对角线长为（）。

(A)4（B）（C）2（D）13．平行四边形 ABCD一条对角线与一边垂直，且此对角线为另一边的一半，则此平行四边形两邻角之比为（）。

（A） 1 ：2（B）1：3（C）1：4（D）1：514．若一个四边形即是轴对称图形也是中心对称图形，则这个四边形能够是（）。

（A）等腰三角形（B）等边三角形（C）平行四边形（D）对角线相互垂直且均分的四边形15．下边命题中： ? 平行四边形两组对边分别平行；平行四边形两组对边分别相等； ? 平行四边形两组对角相等；ˉ 平行四边形一组邻角互补；° 平行四边形的对角线相互均分，抗命题为假命题的个数为（）个。

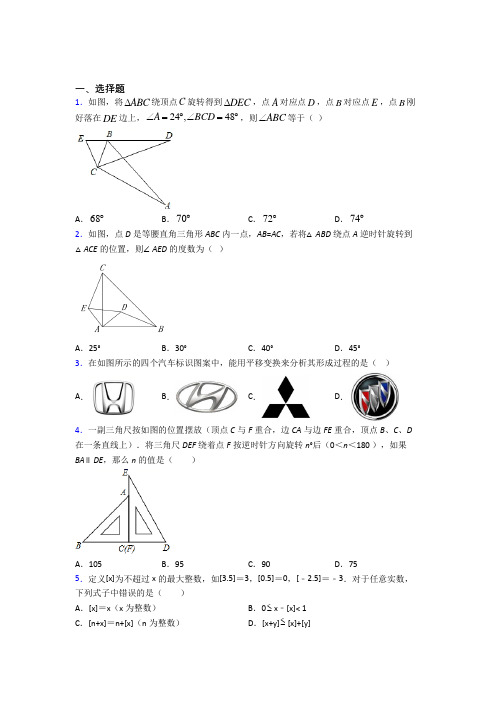
一、选择题1．如图，将ABC ∆绕顶点C 旋转得到DEC ∆，点A 对应点D ，点B 对应点E ，点B 刚好落在DE 边上，24,48A BCD ∠=︒∠=︒，则ABC ∠等于（ ）A ．68︒B ．70︒C ．72︒D ．74︒2．如图，点D 是等腰直角三角形ABC 内一点，AB =AC ，若将△ABD 绕点A 逆时针旋转到△ACE 的位置，则∠AED 的度数为（ ）A ．25°B ．30°C ．40°D ．45°3．在如图所示的四个汽车标识图案中，能用平移变换来分析其形成过程的是（ ） A ． B ． C ． D ． 4．一副三角尺按如图的位置摆放（顶点C 与F 重合，边CA 与边FE 重合，顶点B 、C 、D 在一条直线上）．将三角尺DEF 绕着点F 按逆时针方向旋转n °后（0＜n ＜180 ），如果BA ∥DE ，那么n 的值是（ ）A ．105B ．95C ．90D ．755．定义[x]为不超过x 的最大整数，如[3.5]＝3，[0.5]＝0，[﹣2.5]＝﹣3．对于任意实数，下列式子中错误的是（ ）A ．[x]＝x （x 为整数）B ．0≤x ﹣[x]< 1C ．[n+x]＝n+[x]（n 为整数）D ．[x+y]≤[x]+[y]6．估算192+的结果在（ ）A ．4和5之间B ．5和6之间C ．6和7之间D ．7和8之间 7．在平面直角坐标系中，将点A (m －1，n ＋2)先向右平移3个单位，再向上平移2个单位，得到点A ′．若点A ′位于第二象限，则m 、n 的取值范围分别是（ ）A ．m ＜0，n ＞0B ．m ＜0，n ＜－2C ．m ＜－2，n ＞－4D ．m ＜1，n ＞－2 8．不等式2﹣3x≥2x ﹣8的非负整数解有（ ）A ．1个B ．2个C ．3个D ．4个 9．如图，在等腰△ABC 中，5AB AC ==，6BC =，O 是△ABC 外一点，O 到三边的垂线段分别为OD ，OE ，OF ，且::1:4:4OD OE OF =，则AO 的长度为（ ）A ．5B ．6C ．407D ．801710．下列各组数分别为一个三角形三边的长，其中不能构成直角三角形的一组是（ ） A ．8，10，12 B ．3，4，5 C ．5，12，13 D ．7，24，25 11．如图AD 是ABC 的角平分线，DE AB ⊥于E ，点F ，G 分别是AB ，AC 上的点，且DF DG =，ADG 与DEF 的面积分别是10和3，则ADF 的面积是（ ）A ．4B ．5C ．6D ．712．如图，在ABC 中，ED //BC ，ABC ∠和ACB ∠的平分线分别交ED 于点F 、G ，若2FG =，6ED =，则DB EC +的值为（ ）A ．3B ．4C ．5D ．913．在平面直角坐标系中，点(,5)a 关于原点对称的点的坐标是(1,1)b +，则a b +=__________．14．如图，已知Rt △ABC ，∠ACB ＝90°，∠B ＝60°，AB ＝8，将△ABC 沿BC 方向平移7个单位长度得到△DEF ，则图中四边形ACED 的面积为_____．15．方程组24x y k x y +=⎧⎨-=⎩的解满足1x >，1y <，k 的取值范围是：__________. 16．若不等式12x x -<的解都能使关于x 的一次不等式()11a x a -<+成立，则a 的取值范围是________． 17．已知331n n <-<+，则整数n =________．18．如图，在三角形ABC 中，∠C ＝90°，BD 平分∠ABC 交AC 于点D ，且AD ＝2CD ，AC ＝6，点E 是AB 上一点，连接DE ，则DE 的最小值为____．19．如图，已知点D 为△ABC 内一点，AD 平分∠CAB ，BD ⊥AD ，∠C ＝∠CBD ．若AC ＝10，AB ＝6，则AD 的长为_____．20．如图，在ABC 中，AB AC =，38A ∠=︒，AB 的垂直平分线交AC 点E ，垂足为点D ，连接BE ，则EBC ∠的度数为________．21．矩形ABCD中，AB=4，AD=8，将矩形ABCD绕点C顺时针旋转，AD交CBʹ于点E.（1）如图1，当∠BCE=60°，△CDDʹ的形状是；（2）如图2，当AE=CE时，求阴影部分的面积.22．如图，已知直线y＝kx＋2与直线y＝3x交于点A（1，m），与y轴交于点B．（1）求k和m的值；（2）求△AOB的周长；（3）设直线y＝n与直线y＝kx＋2，y＝3x及y轴有三个不同的交点，且其中两点关于第三点对称，求出n的值．23．解不等式组68491153x xxx+>+⎧⎪+⎨≤-⎪⎩，并把不等式组的解在数轴上表示出来．24．一辆汽车在普通公路上行驶35km后，驶入高速公路，并以90km/h的速度匀速行驶了xh，设汽车行驶的总路程为ykm．（1）直接写出y与x的函数关系；（2）若汽车在高速公路上行驶了2小时，求此时汽车行驶的总路程；（3）若汽车在高速公路上行驶的路程不超过675km，求汽车在高速公路上行驶时间的取值范围．25．用圆规、直尺作图，不写作法，但要保留作图痕迹，并写出结论．如图，现要在ABC内建一中心医院，使医院到,A B两个居民小区的距离相等，并且到公路AB和AC的距离也相等，请确定这个中心医院的位置．26．如图，已知AB ＝AC ，E 为AB 上一点，ED ∥AC ，BD ＝CD ，求证：ED ＝AE ．【参考答案】***试卷处理标记，请不要删除一、选择题1．C解析：C【分析】先通过旋转得到24，ABC=DEC,∠=∠=︒∠∠=D A CE CB ，再通过等边对等角以及三角形外角的性质得到∠=∠=∠+∠E CBE BCD D ，最后代入已知的数据即可求解本题．【详解】解：由ABC ∆绕顶点C 旋转得到DEC ∆可知：24，ABC=DEC,∠=∠=︒∠∠=D A CE CB ，∴∠=∠=∠+∠E CBE BCD D ，∵48∠=︒BCD ，∴244872∠=︒+︒=︒CBE ，故ABC=DEC=72∠∠︒；故选：C ．【点睛】本题考查了旋转的性质、等腰三角形的性质、三角形的外角，熟练掌握旋转的性质即可得到结论．2．D解析：D【分析】由题意可以判断△ADE为等腰直角三角形，即可解决问题．【详解】解：如图，由旋转变换的性质知：∠EAD=∠CAB，AE=AD；∵△ABC为直角三角形，∴∠CAB=90°，△ADE为等腰直角三角形，∴∠AED=45°，故选：D．【点睛】该题考查了旋转变换的性质及其应用问题；应牢固掌握旋转变换的性质．3．D解析：D【分析】根据平移作图是一个基本图案按照一定的方向平移一定的距离，连续作图设计出的图案进行分析即可．【详解】解：A、不能用平移变换来分析其形成过程，故此选项错误；B、不能用平移变换来分析其形成过程，故此选项错误；C、不能用平移变换来分析其形成过程，故此选项正确；D、能用平移变换来分析其形成过程，故此选项错误；故选：D．【点睛】本题考查利用平移设计图案，解题关键是掌握图形的平移只改变图形的位置，而不改变图形的形状、大小和方向．4．A解析：A【分析】画出图形求解即可．【详解】解：∵三角尺DEF 绕着点F 按逆时针方向旋转n °后（0＜n ＜180 ），BA ∥DE ，∴旋转角＝90°+45°﹣30°＝105°，故选：A ．【点睛】本题考查了旋转变换，平行线的性质等知识，解题的关键是学会用分类讨论的思想思考问题，属于中考常考题型.5．D解析：D【分析】根据“定义[x]为不超过x 的最大整数”进行计算．【详解】解：A 、∵[x]为不超过x 的最大整数，∴当x 是整数时，[x]=x ，成立；B 、∵[x]为不超过x 的最大整数，∴0≤x -[x]＜1，成立；C 、[n+x]=n+[x]（n 为整数），成立；D 、例如，[-5.4-3.2]=[-8.6]=-9，[-5.4]+[-3.2]=-6+（-4）=-10，∵-9＞-10，∴[-5.4-3.2]＞[-5.4]+[-3.2]，∴[x+y]≤[x]+[y]不成立，故选：D ．【点睛】本题考查了一元一次不等式组的应用，解决本题的关键是理解新定义，新定义解题是近几年高考常考的题型．6．C解析：C【分析】 先确定4195<<，再根据不等式的性质得到61927<即可得到答案．【详解】∵16<19<25， ∴4195<<， ∴61927<<．故选：C ．【点睛】此题考查算术平方根的取值范围，不等式的性质，正确掌握算术平方根的取值范围的计算方法是解题的关键．7．C解析：C【分析】根据点的平移规律可得向右平移3个单位，再向上平移2个单位得到（m-1+3，n+2+2），再根据第二象限内点的坐标符号可得．【详解】点A （m-1，n+2）先向右平移3个单位，再向上平移2个单位得到点A′（m+2，n+4）， ∵点A′位于第二象限，∴2040m n +<⎧⎨+>⎩ 解得：m ＜-2，n ＞-4，故选C ．【点睛】此题主要考查了坐标与图形变化-平移，关键是横坐标，右移加，左移减；纵坐标，上移加，下移减．8．C解析：C【解析】试题分析：首先移项，合并同类项，然后系数化成1，即可求得不等式的解集，然后确定非负整数解即可．解：移项，得：﹣3x ﹣2x≥﹣8﹣2，合并同类项，得：﹣5x≥﹣10，则x≤2．故非负整数解是：0，1，2共有3个．故选C ．点评：本题考查了一元一次不等式的解法，理解解不等式的基本依据是不等式的基本性质是关键．9．D解析：D【分析】连接OA,OB,OC ，由OD:OE:OF=1:4:4，设OD=x ，OE=4x ，OF=4x ，根据OE=OF ，得到AO 为∠BAC 的角平分线，再根据AB=AC ，得到AO ⊥BC ，根据三线合一及勾股定理求出AD=4，再根据ABC ABO ACO BCO S S S S =+-△△△△，得到方程求解即可．【详解】解：连接OA,OB,OC, 由OD:OE:OF=1:4:4，设OD=x,OE=4x,OF=4x ，∵OE=OF ，∴AO 为∠BAC 的角平分线，又∵AB=AC ，∴AO ⊥BC ，∴AD 为△ABC 的中线，∴A 、D 、O 三点共线，∴BD=3，在Rt △ABD 中， AD=222253AB BD -=-=4，∴ABC ABO ACO BCO S S S S =+-△△△△∴12=10x+10x−3x ，∴x=1217∴AO=4+1217=8017. 故选：D ．【点睛】本题考查了角平分线的判定及性质，熟知等腰三角形的三线合一、角平分线的判定及三角形的面积公式是解题的关键．10．A解析：A【分析】利用勾股定理的逆定理：如果三角形两条边的平方和等于第三边的平方，那么这个三角形就是直角三角形，最长边所对的角为直角来判定即可．【详解】解：A 、∵82＋102≠122，∴三条线段不能组成直角三角形，故A 选项符合题意；B 、∵32＋42＝52，∴三条线段能组成直角三角形，故B 选项不符合题意；C 、∵52＋122＝132，∴三条线段能组成直角三角形，故C 选项不符合题意；D 、∵72＋242＝252，∴三条线段能组成直角三角形，故D 选项不符合题意；故选：A ．【点睛】本题考查的是勾股定理逆定理，解题的关键是掌握勾股定理逆定理以及准确计算． 11．A解析：A【分析】过点D 作DH ⊥AC 于H ，根据角平分线上的点到角的两边距离相等可得DF=DH ，然后利用“HL”证明Rt △DEF 和Rt △DGH 全等，根据全等三角形的面积相等可得S △EDF =S △GDH ，然后根据S △ADF =S △ADH 列出方程求解即可．【详解】解：如图，过点D 作DH ⊥AC 于H ，∵AD 是△ABC 的角平分线，DF ⊥AB ，DH ⊥AC∴DF=DH ，在Rt △DEF 和Rt △DGH 中，DE DG DF DH ⎧⎨⎩＝＝ ， ∴Rt △DEF ≌Rt △DGH （HL ），∴S △EDF =S △GDH =3，同理Rt △ADF ≌Rt △ADH ，∴S △ADF =S △ADH =ADG GDH △△S -S =10-3=7∴S △AED = =7-3=4ADF EDF SS -，故选：A ．【点睛】本题考查了角平分线上的点到角的两边距离相等的性质，全等三角形的判定与性质，作辅助线构造出全等三角形并利用角平分线的性质是解题的关键． 12．B解析：B【分析】根据平行线的性质和等腰三角形的判定证得EG ＝EB ，DF ＝DC 即可求得结果．解：∵ED∥BC，∴∠DFB＝∠FBC，∠EGC＝∠GCB，∵∠DBF＝∠FBC，∠ECG＝∠GCB，∴∠DFB＝∠DBF，∠ECG＝∠EGC，∴BD＝DF，CE＝GE，∵FG＝2，ED＝6，∴DB＋EC＝DF＋GE＝ED−FG＝6−2＝4，故选：B．【点睛】本题考查等腰三角形的判定和性质、角平分线的定义，平行线的性质等知识，解题的关键是等腰三角形的证明．二、填空题13．【分析】根据关于原点对称的点的坐标关系求解【详解】解：由关于原点对称的点坐标关系可得：a=-1b+1=-5∴b=-6∴a+b=-1-6=-7故答案为-7【点睛】本题考查关于原点对称的点的坐标熟练掌握解析：7-【分析】根据关于原点对称的点的坐标关系求解．【详解】解：由关于原点对称的点坐标关系可得：a=-1，b+1=-5，∴b=-6，∴a+b=-1-6=-7，故答案为-7．【点睛】本题考查关于原点对称的点的坐标，熟练掌握关于原点对称的点的坐标关系是解题关键．14．【分析】根据三角形的内角和得到∠BAC＝30°根据直角三角形的性质得到BC＝AB＝4根据勾股定理得到AC＝根据平移的性质得到AD＝BE＝7AD∥BE求得CE＝3根据梯形的面积公式即可得到结论【详解】【分析】根据三角形的内角和得到∠BAC＝30°，根据直角三角形的性质得到BC＝12AB＝4，根据勾股定理得到AC=AD＝BE＝7，AD∥BE，求得CE＝3，根据梯形的面积公式即可得到结论．∵∠ACB ＝90°，∠B ＝60°，∴∠BAC ＝30°，∵AB ＝8，∴BC ＝12AB ＝4， ∴AC=∵将△ABC 沿BC 方向平移7个单位长度得到△DEF ，∴AD ＝BE ＝7，AD ∥BE ，∴CE ＝3，∴图中四边形ACED 的面积＝12×（7+3）＝， 故答案为：【点睛】本题考查了含30°角的直角三角形，三角形的面积，平移的性质，熟练掌握平移的性质是解题的关键． 15．【分析】先求出方程组的解再得出关于k 的不等式组求出不等式组的解集即可【详解】解：解方程组得：∵关于xy 的方程组的解满足∴解得：-1＜k ＜3故答案为-1＜k ＜3【点睛】本题考查了解二元一次方程组和解一解析：13k -<<【分析】先求出方程组的解，再得出关于k 的不等式组，求出不等式组的解集即可．【详解】解：解方程组得：22x k y k +⎧⎨-⎩＝＝， ∵关于xy 的方程组24x y k x y +⎧⎨-⎩＝＝的解满足1x >，1y <， ∴2121k k +⎧⎨-⎩＞＜， 解得：-1＜k ＜3，故答案为-1＜k ＜3．【点睛】本题考查了解二元一次方程组和解一元一次不等式组，能得出关于k 的不等式组是解此题的关键．16．【分析】求出不等式的解求出不等式的解集得出关于a 的不等式求出a 即可【详解】解：解不等式可得∵不等式的解都能使不等式成立∴∴解得故答案为：【点睛】本题考查解一元一次不等式不等式的性质等知识点能根据已知 解析：113a ≤< 【分析】 求出不等式12x x -<的解，求出不等式()11a x a -<+的解集，得出关于a 的不等式，求出a 即可．【详解】 解：解不等式12x x -<可得2x >-， ∵不等式12x x -<的解都能使不等式()11a x a -<+成立， ∴10a -<，11a x a +>-， ∴121a a +≤--， 解得113a ≤<， 故答案为：113a ≤<． 【点睛】本题考查解一元一次不等式，不等式的性质等知识点，能根据已知得到关于a 的不等式是解此题的关键．．17．1【分析】估计在哪两个连续整数之间再根据不等式的性质求3-的范围即可【详解】解：∵即∵∴n=1故答案为：1【点睛】本题考查了算术平方根的估算解题关键是确定在哪两个连续整数之间再确定整数n 值解析：1【分析】【详解】解：∵<，即12<<，12---＞，21＞3， ∵31n n <<+∴n=1．故答案为：1【点睛】本题考查了算术平方根的估算，解题关键是确定3在哪两个连续整数之间，再确定整数n 值．18．2【分析】根据题意当时DE 的值最小根据已知条件求解即可；【详解】如图所示当时DE 的值最小如图所示∵BD 平分∠ABC ∠C ＝90°∴∵∴∴∴∵∴即整理得：∴又∵∴即整理得：解得：∴故答案是2【点睛】本题解析：2【分析】根据题意，当DE AB ⊥时，DE 的值最小，根据已知条件求解即可；【详解】如图所示，当DE AB ⊥时，DE 的值最小，如图所示，∵BD 平分∠ABC ，DE AB ⊥，∠C ＝90°，∴CD DE =，∵2AD CD =，∴2AD DE =， ∴30A ∠=︒，∴30CBD ABD ∠=∠=︒，2AB CB =，∵6AC =，∴222AB AC BC =+，即22246CB CB =+， 整理得：2336CB =， ∴3CB =又∵2BD CD =，∴222BD CD BC =+，即22412CD CD =+，整理得：2312CD =，解得：2CD =，∴2DE =．故答案是2．【点睛】本题主要考查了角平分线的性质、直角三角形的性质和勾股定理，准确分析计算是解题的关键．19．4【分析】延长BD交AC于E证明△ABE是等腰三角形利用等腰三角形三线合一得BD＝DE再由等角对等边得CE＝BE＝4最后由勾股定理可得答案【详解】解：如图延长BD交AC于E∵BD⊥AD∴∠ADE＝∠解析：42【分析】延长BD交AC于E，证明△ABE是等腰三角形，利用等腰三角形三线合一得BD＝DE，再由等角对等边得CE＝BE＝4，最后由勾股定理可得答案．【详解】解：如图，延长BD交AC于E，∵BD⊥AD，∴∠ADE＝∠ADB＝90°，∵AD平分∠CAB，∴∠EAD＝∠BAD，∴∠AED＝∠ABD，∴AE＝AB＝6，∴DE＝BD，∵AC＝10，∴CE＝10﹣6＝4，∵∠C＝∠CBD，∴BE＝CE＝4，∴BD1=BE＝2，2由勾股定理得：AD2222AB BD=--=2．62故答案为：2【点睛】本题考查的是勾股定理，等腰三角形的性质和判定，熟练掌握等腰三角形的性质和判定是关键．20．33°【分析】先根据等腰三角形的性质求出再根据垂直平分线的性质求解即可；【详解】∵在中∴∵的垂直平分线交点垂足为点∴AE=BE∴∴；故答案是【点睛】本题主要考查了等腰三角形的判定与性质垂直平分线的性解析：33°【分析】先根据等腰三角形的性质求出71ABC C ∠=∠=︒，再根据垂直平分线的性质求解即可；【详解】∵在ABC 中，AB AC =，38A ∠=︒，∴71ABC C ∠=∠=︒，∵AB 的垂直平分线交AC 点E ，垂足为点D ，∴AE=BE ，∴38A ABE ∠=∠=︒，∴713833EBC ∠=︒-︒=︒；故答案是33︒．【点睛】本题主要考查了等腰三角形的判定与性质、垂直平分线的性质，准确计算是解题的关键．三、解答题21．（1）等边三角形；（2）6【分析】（1）根据旋转的性质和等边三角形的判定方法，∠BCE=60°=∠DCD′，DC=D′C 可得△CDD′为等边三角形.（2）由勾股定理得，CD 2+DE 2=CE 2，假设CE 为x ，DE=8-x ，列方程，求出DE 的长度，再根据三角形的面积公式，得出阴影面积.【详解】（1）△CDD′的形状是等边三角形，∵矩形ABCD 绕点C 顺时针旋转，∴∠BCE=60°=∠DCD′DC=D′C∴△CDD′为等边三角形（2）在△CDE 中，由勾股定理得，CD 2+DE 2=CE 2设CE 为x ，则DE=8-x∴42+（8-x ）2=x 2解得，x =5，∴DE=8-5=3S 阴影=12DE CD ⋅=1342⨯⨯=6. 【点睛】 本题考查了旋转的性质，和勾股定理的应用，解题的关键是掌握旋转的性质，会利用勾股定理求线段的长度．22．（1）m=3，k=1；（2）C △AOB ；（3）n 的值为32或125或6． 【分析】（1）由直线y ＝3x 交于点A （1，m ），可得m=3，A(1，3)，由直线y ＝kx ＋2与直线y ＝3x 交于点A （1，3），代入得3=k+2，解得k=1；（2）求出直线y ＝x ＋2与y 轴交于点B （0，2）利用勾股定理两点距离公式AB ，OA ，OB ，可求周长C △AOB（3）先求出直线y ＝n 与直线y ＝x ＋2，y ＝3x 及y 轴有三个不同的交点，E （n-2，n ）,D （3n ，n ），C （0，n ），其中两点关于第三点对称，共有三种情况，①E （n-2，n ）,D （3n ，n ），关于C （0，n ）对称；②E （n-2，n ）, C （0，n ），关于D （3n ，n ）对称；③D （3n ，n ），C （0，n ）,关于E （n-2，n ）对称,列出两点距离等式，即可求出n 的值． 【详解】解：（1）直线y ＝3x 交于点A （1，m ），∴m=3，A(1，3)直线y ＝kx ＋2与直线y ＝3x 交于点A （1，3），∴3=k+2，∴k=1；（2）直线y ＝x ＋2与y 轴交于点B ．则x=0，y=2，B （0，2），，C △AOB ；（3）直线y ＝n 与直线y ＝x ＋2，y ＝3x 及y 轴有三个不同的交点，E （n-2，n ）,D （3n ，n ），C （0，n ）， 其中两点关于第三点对称，共有三种情况，①E （n-2，n ）,D （3n ，n ），关于C （0，n ）对称， 则n-2+3n =0， 32n =， ②E （n-2，n ）, C （0，n ），关于D （3n ，n ）对称， 则3n = 23n n --，23n n --=3n ±， 23n n --=3n 或23n n --=3n -， n=6或n=2舍去，③D （3n ，n ），C （0，n ）,关于E （n-2，n ）对称,， 则()2=23n n n ---， ()()2=23n n n ±---， 2=23n n n --+或2=23n n n -+-+， 125n =或n=0(舍去)， 综合以上三种情况n 的值为32或125或6．【点睛】本题考查待定系数法求点坐标与解析式，勾股定理两点距离公式，中心对称的性质，掌握待定系数法求点坐标与解析式，勾股定理两点距离公式，中心对称的性质，会利用分类思想解决中心对称是关键．23．12＜x≤1，数轴见详解【分析】首先解每个不等式，然后在数轴上表示出来，两个不等式的解集的公共部分就是不等式组的解集．【详解】6849 (115)...3x x x x +>+⎧⎪⎨+≤-⎪⎩①②， 解①得：x ＞12， 解②得：x≤1，数轴上表示如下：∴不等式组的解是：12＜x≤1． 【点睛】 本题考查了不等式组的解法，用数轴表示不等式的解集时，要注意“两定”：一是定界点，一般在数轴上只标出原点和界点即可．定边界点时要注意，点是实心还是空心，若边界点含于解集为实心点，不含于解集即为空心点；二是定方向，定方向的原则是：“小于向左，大于向右”．24．（1）y ＝90x ＋35；（2）2小时后汽车行驶215km ；（3）0 ≤ x ≤7.5．【分析】（1）根据y 与x 的意义及路程=速度×时间可以得到解答；（2）根据（1）即可得到解答；（3）由题意列出关于时间的不等式可以得到解答．【详解】解：（1）y ＝90x ＋35．（2）当x ＝2时，y ＝90×2＋35＝215；答：2小时后汽车行驶215km ．（3）由题意得：90x≤675，∴x≤7.5∵x≥0∴0≤x ≤7.5答：汽车在高速公路上行驶时间的取值范围是0≤x≤7.5．【点睛】本题考查一次函数与一元一次不等式的综合应用，熟练掌握一次函数表达式的求解与应用、一元一次不等式的求解与应用是解题关键．25．见解析【分析】根据线段垂直平分线性质作出AB 的垂直平分线，根据角平分线性质作出∠BAC 的角平分线，即可得出答案．【详解】解：作AB 的垂直平分线EF ，作∠BAC 的角平分线AM ，两线交于P ，则P 为这个中心医院的位置．【点睛】本题考查了线段垂直平分线性质，角平分线性质的应用，主要考查学生的理解能力和动手操作能力．26．见解析【分析】利用SSS 证△A DB ≌△ADC 可得∠D AB =∠DAC ，根据平行线性质得∠EDA =∠DAC ，再根据等量代换得到∠EAD=∠EDA ，从而得到ED=AE ．【详解】证明：在△ADB 和△ADC 中，,,,AB AC DB DC AD AD =⎧⎪=⎨⎪=⎩∴△ADB ≌△ADC （SSS ）．∴∠D AB =∠DAC ．∵ED ∥AC ，∴∠EDA =∠DAC ，∴∠EAD=∠EDA∴E D=AE ．【点睛】考核知识点：全等三角形判定，等边对等角的性质．判定三角形全等是关键．。

八年级下册数学期中考试试题(答案)一、选择题(每小题3分，共30分) 1．化简16的值为( A ) A ．4 B ．－4 C ．±4 D ．22．要使二次根式4＋x 有意义，x 的取值范围是( D ) A ．x ≠－4 B ．x ≥4 C ．x ≤－4 D ．x ≥－43．下列各组数中，以a ，b ，c 为边的三角形不是直角三角形的是( C ) A ．a ＝2 2，b ＝2 3，c ＝2 5 B ．a ＝32，b ＝2，c ＝52C ．a ＝6，b ＝8，c ＝10D ．a ＝5，b ＝12，c ＝13 4．下列二次根式中，化简后不能与3进行合并的是( C ) A.13B.27C.32D.12 5．顺次连接四边形ABCD 各边的中点，若得到的四边形EFGH 为菱形，则四边形ABCD 一定满足( A )A ．对角线AC ＝BDB ．四边形ABCD 是平行四边形C ．对角线AC ⊥BD D ．AD ∥BC 6．下列各式计算正确的是( B ) A ．3 3－3＝3 B.8×2＝8×2 C.323×4 3＝6 3 D ．215＋2 3＝ 5 7．如图，在△ABC 中，D 为AB 中点，E 在AC 上，且BE ⊥AC.若DE ＝5，AE ＝8，则BE 的长度是( C )A ．5B ．5.5C ．6D ．6.5,第7题图),第9题图),第10题图)8．已知菱形的周长为20，一条对角线长为6，则菱形的面积为(B)A．48 B．24 C．18 D．129．如图，把菱形ABCD沿AH折叠，点B落在BC边上的点E处．若∠BAE＝40°，则∠EDC的大小为(B)A．10°B．15°C．18°D．20°10．如图，点E，G分别是正方形ABCD的边CD，BC上的点，连接AE，AG，分别交对角线BD于点P，Q.若∠EAG＝45°，BQ＝4，PD＝3，则正方形ABCD的边长为(A)A．6 2 B．7 C．7 2 D．5二、填空题(每小题3分，共18分)11．化简：50－72＝．12．在Rt△ABC中，∠C＝90°，AC＝4 cm，BC＝3 cm，AB边上的高是______cm.13．计算：(6－2 3)2＝．14．如图，点E，F是正方形ABCD内两点，且BE＝AB，BF＝DF，∠EBF＝∠CBF，则∠BEF的度数为__45°__．,第14题图),第15题图),第16题图)15．如图，在矩形ABCD中，AB＝3，BC＝4，点E是BC边上一点，连接AE，把∠B沿AE折叠，使点B落在点B′处．当△CEB′为直角三角形时，CB′的长为．16．如图，在菱形ABCD中，对角线AC＝6，BD＝8，点E是边AB的中点，点F，P 分别是BC，AC上的动点，则PE＋PF的最小值是______．三、解答题(共72分)17．(8分)计算：4 12－1318.【解析】原式＝22－2＝ 2.18．(8分)如图，在▱ABCD中，对角线AC与BD交于点O，经过点O的直线交AB于点E，交CD于点F，连接DE，BF.(1)求证：四边形DEBF是平行四边形；(2)当EF与BD满足条件__EF⊥BD__时，四边形DEBF是菱形．【解析】(1)∵四边形ABCD是平行四边形，∴OD＝OB，DC∥AB，∴∠FDO＝∠EBO，∠DFO＝∠OEB，在△DOF和△BOE中．∠FDO＝∠EBO，∠DFO＝∠BEO，OD＝OB，∴△DOF≌△BOE(AAS)．∴OE＝OF.又∵OD＝OB，∴四边形DEBF是平行四边形．19．(8分)计算(7＋4 3)(2－3)2－(2＋3)(2－3)＋3的值． 【解析】原式＝1－1＋3＝ 3.20．(8分)如图，在▱ABCD 中，点E 是BC 的中点．连接AE 并延长，交DC 的延长线于点F ，且AF ＝AD ，连接BF.求证：四边形ABFC 是矩形．最新八年级下册数学期中考试题及答案人教版八年级下学期期中数学试卷八年级数学一、选择题 1、若二次根式5-x 有意义，则x 的取值范围是（ a ）A 、5≥xB 、5≤xC 、5 xD 、5 x2、下面各式是最简二次根式的是（ d ）A 、8B 、21C 、9D 、2 3、下列各组数中不能作为直角三角形的三边长的是（ c ）A 、6,8,10B 、5,12,13C 、1.5,2,3D 、9,12,15 4、下列计算正确的是（ c ） A 、532=+ B 、3223=- C 、632=⨯ D 、322324= 5、在平面直角坐标系中，点P （1，-3）到原点的距离是（ b ）A 、4B 、10C 、22D 、无法确定 6、如图所示，在平行四边形ABCD 中，已知AC=3cm ，若△ABC 的周长为9cm ， 则平行四边形的周长为（ b ）A 、6cmB 、12cmC 、16cmD 、11cm 7、下列命题是真命题的是（ c ）A 、一组对边平行，另一组对边相等的四边形是平行四边形B 、对角线互相垂直的平行四边形是矩形C 、四条边相等的四边形是菱形D 、对角线相等的矩形是正方形8、甲、乙两同学骑自行车从A 地沿同一条路到B 地，已知乙比甲先出发， 他们离出发地的距离s （km ）和骑行时间t （h ）之间的函数关系如图所示， 根据图像信息，以上说法正确的是（ d ）A 、甲和乙两人同时到达目的地；B 、甲在途中停留了0.5h;C 、相遇后，甲的速度小于乙的速度；D 、他们都骑了20km9、已知菱形的面积为24cm ²，一条对角线长为6cm ，则这个菱形的边长是（ b ）cm A 、8 B 、5 C 、10 D 、410如图，点P 是正方形ABCD 的对角线BD 上一点，PE ⊥BC 于E ，PF ⊥CD 于 F ，连接EF ，给出下列四个结论：①AP=EF,②△APD 一定是等腰三角形，G ，③∠PFE=∠BAP,④PD=2EC.其中正确结论的序号是（ d ） A 、①②④ B 、②④ C 、①②③ D 、①③④ 二、填空题11、=÷218__3_____12、在实数范围内因式分解：32-x =__)3)(3(-+x x _13、如图，在直角三角形ABC 中，点D 为AC 的中点，BC=3，AB=4，则BD=____2.5______ 14、“全等三角形的对应角相等”的逆命题 对应角相等的三角形是全等三角形 ,这个命题是__假__命题。

【若缺失公式、图片现象属于系统读取不成功，文档内容齐全完整，请放心下载。

】八年级（下）期中数学试卷一、选择题（本大题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的）1．（4分）若等腰三角形的顶角为40︒，则它的底角度数为( ) A ．40︒B ．50︒C ．60︒D ．70︒2．（4分）下列图形中，既是轴对称图形又是中心对称图形的是( )A ．B ．C ．D ．3．（4分）不等式121x x +-的解集在数轴上表示为( ) A ． B ． C ．D ．4．（4分）如图，已知AB AD =，那么添加下列一个条件后，仍无法判定ABC ADC ∆≅∆的是( )A ．CB CD =B ．BAC DAC ∠=∠C ．BCA DCA ∠=∠D ．90B D ∠=∠=︒5．（4分）如图，将“笑脸”图标向右平移4个单位，再向下平移2个单位，点P 的对应点P '的坐标是( )A ．(1,6)-B ．(9,6)-C ．(1,2)-D ．(9,2)-6．（4分）如图所示，在ABC ∆中，AB AC =，50A ∠=︒，AB 的垂直平分线交AB 于D ，交AC 于E ，连接BE ，则EBC ∠的度数是( )A ．15︒B ．20︒C ．65︒D ．100︒7．（4分）下列说法中，错误的是( ) A ．不等式26x ->的解集是3x <-B ．不等于3x >-的正数解有有限个C ．3-不是不等式39x ->的解D ．若a b >，则22c a c b -<-8．（4分）为有效开展“阳光体育”活动，某校计划购买篮球和足球共50个，购买资金不超过3000元．若每个篮球80元，每个足球50元，则篮球最多可购买( ) A ．16个B ．17个C ．33个D ．34个9．（4分）如图，直线y kx b =+经过点(1,2)A --和点(2,0)B -，直线2y x =过点A ，则不等式20x kx b <+<的解集为( )A ．2x <-B ．21x -<<-C ．20x -<<D ．10x -<<10．（4分）如图，Rt ABC ∆中，90ACB ∠=︒，30B ∠=︒，1AC =，且AC 在直线l 上，将ABC ∆绕点A 顺时针旋转到B 位置①，可得到点1P ，此时12AP =；将位置①的三角形绕点1P 顺时针旋转到位置②，可得到点2P ，此时223AP =+②的三角形绕点2P 顺时针旋转到位置③，可得到点3P ，此时333AP =+⋯按此规律继续旋转，直到点2018P 为止，则2018AP等于( )A ．20166733+B ．20176733+C ．20186733+D ．20196733+二、填空题（本大题共6小题，每小题4分，共24分．） 11．（4分）x 与3的和是负数，用不等式表示为 ．12．（4分）用反证法证明“三角形中至少有一个角不小于60︒时，假设“ ”，则与“ ”矛盾，所以原命题正确．13．（4分）如图，O 是BAC ∠内一点，且点O 到AB ，AC 的距离OE ，OF 相等，则AEO AFO ∆≅∆的依据是 ．14．（4分）如图，在ABC ∆中，60B C ∠=∠=︒，点D 为AB 边的中点，DE BC ⊥于E ，若1BE =，则AC 的长为 ．15．（4分）如图所示，在ABC ∆中，70CAB ∠=︒，在同一平面内，将ABC ∆绕A 点逆时针旋转到△AB C ''的位置，使//CC AB '，则BAB ∠'= ．16．（4分）若关于x 的不等式组324x a x a <+⎧⎨>+⎩无解，则a 的取值范围是 ．三、解答题（共86分）17．（12分）解不等式：（1）5113xx-<+，并把它的解集在数轴上表示出来．（2）求不等式3(1)53x x+-的正整数解．18．（8分）解不等式组：21512x xxx+>⎧⎪⎨+-⎪⎩，并把解集在数轴上表示出来．19．（8分）如图，已知ABC∆中，AB AC=，D为AC上一点，12DBC BAC∠=∠求证：AC BD⊥．请将下面的证明过程补充完整，并在相应的括号内注明理由．证明：如图，过点A作AE BC⊥于点E，交BD于点F．AB AC=，AE BC⊥．12CAE∴∠=12DBC BAC∠=∠，（已知）CAE DBC∴∠=∠()又12∠=∠，1802ADF∠=︒-∠-，1801BEF∠=︒-∠-AC BD∴⊥()．20．（6分）如图，在钝角ABC∆中，过钝角顶点B作BD BC⊥交AC于点D．请用尺规作图法在BC边上求作一点P，使得点P到AC的距离等于BP的长．（保留作图痕迹，不写作法）21．（8分）ABC ∆在平面直角坐标系xOy 中的位置如图所示． （1）作ABC ∆关于点C 成中心对称的△111A B C ．（2）将△111A B C 向右平移4个单位，作出平移后的△222A B C ．（3）在x 轴上求作一点P ，使12PA PC +的值最小，并写出点P 的坐标（不写解答过程，直接写出结果）22．（10分）如图 1 、图 2 ，AOB ∆，COD ∆均是等腰直角三角形，90AOB COD ∠=∠=︒，（1） 在图 1 中，AC 与BD 相等吗？请说明理由；（2） 若COD ∆绕点O 顺时针旋转一定角度后， 到达图 2 的位置， 请问AC 与BD 还相等吗？为什么？23．（10分）定义运算{min a ，}b ：当a b 时，{min a ，}b b =；当a b <时，{min a ，}b a =；如：{4min ，0}0=；{2min ，2}2=；{3min -，1}3-=-．根据该定义运算完成下列问题：（1）{3min -，2}= ，当2x 时，{min x ，2}= ； （2）若{31min x -，3}31x x -+=-，求x 的取值范围；（3）如图，已知直线1y x m =+与22y kx =-相交于点(2,1)P -，若{min x m +，2}2kx kx -=-，结合图象，直接写出x 的取值范围是 ．24．（12分）市园林处为了对一段公路进行绿化，计划购买A ，B 两种风景树共900棵．A ，B 两种树的相关信息如下表：品种 项目 单价（元/棵） 成活率A 80 92% B10098%若购买A 种树x 棵，购树所需的总费用为y 元． （1）求y 与x 之间的函数关系式；（2）若购树的总费用不超过82 000元，则购A 种树不少于多少棵？（3）若希望这批树的成活率不低于94%，且使购树的总费用最低，应选购A ，B 两种树各多少棵？此时最低费用为多少？25．（12分）如图，在ABC ∆中，2AB AC ==，40B C ∠=∠=︒，点D 在线段BC 上运动(D 不与B 、C 重合），连接AD ，作40ADE ∠=︒，DE 交线段AC 于E ．（1）当115BDA ∠=︒时，EDC ∠= ︒，DEC ∠= ︒；点D 从B 向C 运动时，BDA ∠逐渐变 （填“大”或“小” )；（2）当DC 等于多少时，ABD DCE ∆≅∆，请说明理由；（3）在点D 的运动过程中，ADE ∆的形状可以是等腰三角形吗？若可以，请直接写出BDA ∠的度数．若不可以，请说明理由．2018-2019学年福建省漳州市台商投资区八年级（下）期中数学试卷参考答案与试题解析一、选择题（本大题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的）1．（4分）若等腰三角形的顶角为40︒，则它的底角度数为()A．40︒B．50︒C．60︒D．70︒【考点】KH：等腰三角形的性质【分析】根据等腰三角形的性质和三角形内角和定理可直接求出其底角的度数．【解答】解：因为等腰三角形的两个底角相等，又因为顶角是40︒，所以其底角为18040702-=︒．故选：D．【点评】此题考查学生对等腰三角形的性质的理解和掌握，解答此题的关键是知道等腰三角形的两个底角相等．2．（4分）下列图形中，既是轴对称图形又是中心对称图形的是()A．B．C．D．【考点】3P：轴对称图形；5R：中心对称图形【分析】根据把一个图形绕某一点旋转180︒，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形；如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴进行分析即可．【解答】解：A、是轴对称图形，不是中心对称图形，故此选项错误；B、是轴对称图形，是中心对称图形，故此选项正确；C、不是轴对称图形，是中心对称图形，故此选项错误；D、是轴对称图形，不是中心对称图形，故此选项错误；故选：B．【点评】此题主要考查了轴对称图形和中心对称图形，关键是掌握轴对称和中心对称图形的概念．3．（4分）不等式121x x +-的解集在数轴上表示为( ) A ． B ． C ．D ．【考点】4C ：在数轴上表示不等式的解集；6C ：解一元一次不等式 【分析】根据不等式解集的表示方法，可得答案． 【解答】解：移项，得：211x x ---， 合并同类项，得：2x --， 系数化为1，得：2x ，将不等式的解集表示在数轴上如下：，故选：B ．【点评】本题考查了在数轴上表示不等式的解集，不等式的解集在数轴上表示出来(>，向右画；<，向左画），注意在表示解集时“”，“”要用实心圆点表示；“<”，“ >”要用空心圆点表示．4．（4分）如图，已知AB AD =，那么添加下列一个条件后，仍无法判定ABC ADC ∆≅∆的是( )A ．CB CD =B ．BAC DAC ∠=∠C ．BCA DCA ∠=∠D ．90B D ∠=∠=︒【考点】KB ：全等三角形的判定【分析】要判定ABC ADC ∆≅∆，已知AB AD =，AC 是公共边，具备了两组边对应相等，故添加CB CD =、BAC DAC ∠=∠、90B D ∠=∠=︒后可分别根据SSS 、SAS 、HL 能判定ABC ADC ∆≅∆，而添加BCA DCA ∠=∠后则不能．【解答】解：A、添加CB CD=，根据SSS，能判定ABC ADC∆≅∆，故A选项不符合题意；B、添加BAC DAC∆≅∆，故B选项不符合题意；∠=∠，根据SAS，能判定ABC ADC∠=∠时，不能判定ABC ADCC、添加BCA DCA∆≅∆，故C选项符合题意；D、添加90∆≅∆，故D选项不符合题意；∠=∠=︒，根据HL，能判定ABC ADCB D故选：C．【点评】本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．5．（4分）如图，将“笑脸”图标向右平移4个单位，再向下平移2个单位，点P的对应点P'的坐标是()A．(1,6)--D．(9,2) -B．(9,6)-C．(1,2)【考点】3Q：坐标与图形变化-平移【分析】根据平移规律：横坐标，右移加，左移减；纵坐标，上移加，下移减即可解决问题；【解答】解：由题意(5,4)P-，向右平移4个单位，再向下平移2个单位，点P的对应点P'的坐标是(1,2)-，故选：C．【点评】本题考查坐标与平移，解题的关键是记住平移规律：横坐标，右移加，左移减；纵坐标，上移加，属于中考常考题型．6．（4分）如图所示，在ABC∆中，AB AC∠=︒，AB的垂直平分线交AB于D，A=，50交AC于E，连接BE，则EBC∠的度数是()A．15︒B．20︒C．65︒D．100︒【考点】KH ：等腰三角形的性质；KG ：线段垂直平分线的性质【分析】先根据ABC ∆中，AB AC =，50A ∠=︒求出ABC ∠的度数，再根据线段垂直平分线的性质可求出AE BE =，即50A ABE ∠=∠=︒即可解答． 【解答】解：等腰ABC ∆中，AB AC =，50A ∠=︒， 18050652ABC ︒-︒∴∠==︒， DE 是线段AB 垂直平分线的交点， AE BE ∴=，50A ABE ∠=∠=︒，655015CBE ABC ABE ∴∠=∠-∠=︒-︒=︒．故选：A ．【点评】此题主要考查线段的垂直平分线及等腰三角形的性质等几何知识．线段的垂直平分线上的点到线段的两个端点的距离相等． 7．（4分）下列说法中，错误的是( ) A ．不等式26x ->的解集是3x <-B ．不等于3x >-的正数解有有限个C ．3-不是不等式39x ->的解D ．若a b >，则22c a c b -<-【考点】2C ：不等式的性质；3C ：不等式的解集【分析】根据不等式的解集，不等式的解的定义可判断出A 、B 、C 的正误，根据不等式的性质可得到D 的正误．【解答】解：A 、不等式26x ->的解集是3x <-正确；B 、不等式3x >-的正数解有有限个错误，应为无限个；C 、不等式39x ->的解集为3x <-，故3-不是不等式39x ->的解正确；D 、若a b >，则22a b -<-，所以22a c b c -+<-+，即22c a c b -<-正确；故选：B ．【点评】此题主要考查了不等式的解集，和解的定义i ，以及不等式的性质，题目比较基础，关键是熟记不等式的性质，注意在不等式两边同时除以或乘以同一个负数时要改变不等号的方向．8．（4分）为有效开展“阳光体育”活动，某校计划购买篮球和足球共50个，购买资金不超过3000元．若每个篮球80元，每个足球50元，则篮球最多可购买( )A ．16个B ．17个C ．33个D ．34个【考点】9C ：一元一次不等式的应用【分析】设买篮球m 个，则买足球(50)m -个，根据购买足球和篮球的总费用不超过3000元建立不等式求出其解即可．【解答】解：设买篮球m 个，则买足球(50)m -个，根据题意得： 8050(50)3000m m +-， 解得：2163m ，m 为整数，m ∴最大取16，∴最多可以买16个篮球．故选：A ．【点评】本题考查了列一元一次不等式解实际问题的运用，解答本题时找到建立不等式的不等关系是解答本题的关键．9．（4分）如图，直线y kx b =+经过点(1,2)A --和点(2,0)B -，直线2y x =过点A ，则不等式20x kx b <+<的解集为( )A ．2x <-B ．21x -<<-C ．20x -<<D ．10x -<<【考点】FD ：一次函数与一元一次不等式【分析】根据不等式20x kx b <+<体现的几何意义得到：直线y kx b =+上，点在点A 与点B 之间的横坐标的范围．【解答】解：不等式20x kx b <+<体现的几何意义就是直线y kx b =+上，位于直线2y x =上方，x 轴下方的那部分点， 显然，这些点在点A 与点B 之间． 故选：B ．【点评】本题考查了一次函数与不等式（组)的关系及数形结合思想的应用．解决此类问题关键是仔细观察图形，注意几个关键点（交点、原点等），做到数形结合．10．（4分）如图，Rt ABC ∆中，90ACB ∠=︒，30B ∠=︒，1AC =，且AC 在直线l 上，将ABC ∆绕点A 顺时针旋转到B 位置①，可得到点1P ，此时12AP =；将位置①的三角形绕点1P 顺时针旋转到位置②，可得到点2P ，此时223AP =+；将位置②的三角形绕点2P 顺时针旋转到位置③，可得到点3P ，此时333AP =+；⋯按此规律继续旋转，直到点2018P 为止，则2018AP 等于( )A ．20166733+B ．20176733+C ．20186733+D ．20196733+【考点】KO ：含30度角的直角三角形；38：规律型：图形的变化类；2R ：旋转的性质 【分析】仔细审题，发现将Rt ABC ∆绕点A 顺时针旋转，每旋转一次，AP 的长度依次增加231，且三次一循环，按此规律即可求解． 【解答】解：90ACB ∠=︒，30B ∠=︒，1AC =，2AB ∴=，3BC =∴将ABC ∆绕点A 顺时针旋转到①，可得到点1P ，此时12AP =，将位置①的三角形绕点1P 顺时针旋转到位置②可得到点2P ，此时223AP =+ 将位置②的三角形绕点2P 顺时针旋转到位置③，可得到点3P ，此时333AP =⋯ 201836722÷=⋯，2018672(33)2320186733AP ∴=+++故选：C ．【点评】本题考查了旋转的性质及直角三角形的性质，得到AP 的长度依次增加231，且三次一循环是解题的关键．二、填空题（本大题共6小题，每小题4分，共24分．） 11．（4分）x 与3的和是负数，用不等式表示为 30x +< ．【考点】8C：由实际问题抽象出一元一次不等式【分析】理解：x与3的和，即3x+；负数，即小于0．【解答】解：根据题意，得30x+<．故答案是：30x+<．【点评】考查了由实际问题抽象出一元一次不等式，找准关键字，把文字语言转换为数学语言．12．（4分）用反证法证明“三角形中至少有一个角不小于60︒时，假设“三角形的三个内角都小于60︒”，则与“”矛盾，所以原命题正确．【考点】3O：反证法【分析】熟记反证法的步骤，直接填空即可．【解答】解：用反证法证明“三角形中至少有一个角不小于60︒时，假设“三角形的三个内角都小于60︒”，则与“三角形的内角和是180︒”矛盾，所以原命题正确．【点评】本题结合角的比较考查反证法，解此题关键要懂得反证法的意义及步骤．反证法的步骤是：（1）假设结论不成立；（2）从假设出发推出矛盾；（3）假设不成立，则结论成立．在假设结论不成立时要注意考虑结论的反面所有可能的情况，如果只有一种，那么否定一种就可以了，如果有多种情况，则必须一一否定．13．（4分）如图，O是BAC∠内一点，且点O到AB，AC的距离OE，OF相等，则AEO AFO∆≅∆的依据是HL．【考点】KB：全等三角形的判定；KF：角平分线的性质【分析】根据HL证明Rt AOE Rt AOF∆≅∆即可．【解答】解：OE AB⊥，⊥，OF AC∴∠=∠=︒，90AEO AFO在Rt AOE∆和Rt AOF∆中，OE OFAO AO =⎧⎨=⎩， Rt AOE Rt AOF(HL)∴∆≅∆．故答案为HL ．【点评】本题考查全等三角形的判定，解题的关键是熟练掌握基本知识，属于中考常考题型． 14．（4分）如图，在ABC ∆中，60B C ∠=∠=︒，点D 为AB 边的中点，DE BC ⊥于E ，若1BE =，则AC 的长为 4 ．【考点】KK ：等边三角形的性质；KO ：含30度角的直角三角形【分析】根据直角三角形的性质得到22BD BE ==，求出AB ，根据等边三角形的判定定理和性质定理解答即可． 【解答】解：DE BC ⊥，60B C ∠=∠=︒，30BDE ∴∠=︒，22BD BE ∴==，点D 为AB 边的中点，24AB BD ∴==，60B C ∠=∠=︒， ABC ∴∆为等边三角形， 4AC AB ∴==，故答案为：4．【点评】本题考查的是直角三角形的性质、等边三角形的性质，掌握在直角三角形中，30︒角所对的直角边等于斜边的一半是解题的关键．15．（4分）如图所示，在ABC ∆中，70CAB ∠=︒，在同一平面内，将ABC ∆绕A 点逆时针旋转到△AB C ''的位置，使//CC AB '，则BAB ∠'= 40︒ ．【考点】JA ：平行线的性质；2R ：旋转的性质【分析】由旋转性质可知AC AC ='，C AB CAB ∠''=∠，从而可得出ACC ∆'为等腰三角形，且CAC BA B ∠'=∠'和已知//CC AB '，得出ACC ∠'的度数．则可得出答案．【解答】解：ABC ∆绕A 点逆时针旋转到△AB C ''的位置AC AC C AB CAB ∴='∠''=∠ AC C ACC C AC B AB ∴∠'=∠'∠'=∠' //CC AB '70C CA CAB ∴∠'=∠=︒ 18070240CAC ∴∠'=︒-︒⨯=︒ 40BAB ∠'=︒【点评】本题考查了旋转的性质：对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．解题的关键是抓住旋转变换过程中不变量，判断出ACC ∆'是等腰三角形．16．（4分）若关于x 的不等式组324x a x a <+⎧⎨>+⎩无解，则a 的取值范围是 1a ．【考点】CB ：解一元一次不等式组【分析】先把a 当作已知条件求出各不等式的解集，再根据不等式组无解求出a 的取值范围即可．【解答】解：324x a x a <+⎧⎨>+⎩①②，不等式组无解，432a a ∴++．解得：1a 故答案为：1a ．【点评】本题考查的是解一元一次不等式组，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的法则是解答此题的关键．三、解答题（共86分）17．（12分）解不等式：（1）5113xx-<+，并把它的解集在数轴上表示出来．（2）求不等式3(1)53x x+-的正整数解．【考点】7C：一元一次不等式的整数解；4C：在数轴上表示不等式的解集；6C：解一元一次不等式【分析】（1）不等式去分母，去括号，移项合并，把x系数化为1，求出解集，表示在数轴上即可；（2）求出不等式的解集，找出正整数解即可．【解答】解：（1）去分母得：5133x x-<+，移项合并得：24x<，解得：2x<，（2）去括号得：3353x x+-，移项合并得：26x，解得：3x，则不等式的正整数解为1，2，3．【点评】此题考查了一元一次不等式的整数解，以及在数轴上表示不等式的解集，熟练掌握运算法则是解本题的关键．18．（8分）解不等式组：21512x xxx+>⎧⎪⎨+-⎪⎩，并把解集在数轴上表示出来．【考点】4C：在数轴上表示不等式的解集；CB：解一元一次不等式组【分析】先求出不等式组中每一个不等式的解集，再求出它们的公共部分就是不等式组的解集．【解答】解：2151 2x xxx+>⎧⎪⎨+-⎪⎩①②解不等式①得：1x>-，解不等式②得：3x，则不等式组的解集是：13x-<，不等式组的解集在数轴上表示为：【点评】本题考查了不等式组的解法，把每个不等式的解集在数轴上表示出来(>，向右画；<，向左画），数轴上的点把数轴分成若干段，如果数轴的某一段上面表示解集的线的条数与不等式的个数一样，那么这段就是不等式组的解集．有几个就要几个．在表示解集时“”，“”要用实心圆点表示；“<”，“>”要用空心圆点表示．19．（8分）如图，已知ABC∆中，AB AC=，D为AC上一点，12DBC BAC∠=∠求证：AC BD⊥．请将下面的证明过程补充完整，并在相应的括号内注明理由．证明：如图，过点A作AE BC⊥于点E，交BD于点F．AB AC=，AE BC⊥．12CAE∴∠=BAC∠12DBC BAC∠=∠，（已知）CAE DBC∴∠=∠()又12∠=∠，1802ADF∠=︒-∠-，1801BEF∠=︒-∠-AC BD∴⊥()．【考点】KH：等腰三角形的性质【分析】根据等腰三角形的性质、三角形的内角和定理及垂直定义可得结论．【解答】证明：如图，过点A 作AE BC ⊥于点E ，交BD 于点F ． AB AC =，AE BC ⊥． 12CAE BAC ∴∠=∠12DBC BAC ∠=∠，（已知） CAE DBC ∴∠=∠( 等量代换）又12∠=∠，1802ADF CAE ∠=︒-∠-∠， 1801BEF DBC ∠=︒-∠-∠，AC BD ∴⊥( 垂直定义）． 故答案为：BAC ∠，等量代换，CAE ∠，DBC ∠，垂直定义．【点评】本题考查等腰三角形的性质、三角形的内角和定理及垂直定义等知识，解题的关键是熟练掌握基本知识解决问题，属于中考常考题型．20．（6分）如图，在钝角ABC ∆中，过钝角顶点B 作BD BC ⊥交AC 于点D ．请用尺规作图法在BC 边上求作一点P ，使得点P 到AC 的距离等于BP 的长．（保留作图痕迹，不写作法）【考点】KF ：角平分线的性质；2N ：作图-基本作图 【分析】根据题意可知，作BDC ∠的平分线交BC 于点P 即可． 【解答】解：如图，点P 即为所求．【点评】本题考查的是作图-基本作图，熟知角平分线的作法和性质是解答此题的关键．21．（8分）ABC ∆在平面直角坐标系xOy 中的位置如图所示． （1）作ABC ∆关于点C 成中心对称的△111A B C ．（2）将△111A B C 向右平移4个单位，作出平移后的△222A B C ．（3）在x 轴上求作一点P ，使12PA PC +的值最小，并写出点P 的坐标（不写解答过程，直接写出结果）【考点】PA ：轴对称-最短路线问题；4Q ：作图-平移变换；8R ：作图-旋转变换【分析】（1）延长AC 到1A ，使得11AC A C =，延长BC 到1B ，使得11BC B C =，即可得出图象；（2）根据△111A B C 将各顶点向右平移4个单位，得出△222A B C ；（3）作出1A 关于x 轴的对称点A '，连接2A C '，交x 轴于点P ，再利用相似三角形的性质求出P 点坐标即可． 【解答】解；（1）如图所示：（2）如图所示：（3）如图所示：作出1A 关于x 轴的对称点A '，连接2A C '，交x 轴于点P ，可得P 点坐标为：8(3，0)．【点评】此题主要考查了图形的平移与旋转和相似三角形的性质等知识，利用轴对称求最小值问题是考试重点，同学们应重点掌握．22．（10分）如图 1 、图 2 ，AOB ∆，COD ∆均是等腰直角三角形，90AOB COD ∠=∠=︒，（1） 在图 1 中，AC 与BD 相等吗？请说明理由；（2） 若COD ∆绕点O 顺时针旋转一定角度后， 到达图 2 的位置， 请问AC 与BD 还相等吗？为什么？【考点】KD ：全等三角形的判定与性质；KW ：等腰直角三角形；2R ：旋转的性质【分析】（1） 根据等腰三角形的两腰相等进行解答 ．（2） 证明DOB COA ∆≅∆，根据全等三角形的对应边相等进行说明 ． 【解答】解： （1） 相等 ．在图 1 中，AOB ∆，COD ∆均是等腰直角三角形，90AOB COD ∠=∠=︒，OA OB ∴=，OC OD =， 000A C B OD ∴-=-， AC BD ∴=；（2） 相等 ．在图 2 中，90AOB COD ∠=∠=︒，DOB COD COB ∠=∠-∠，COA AOB COB ∠=∠-∠， DOB COA ∴∠=∠ 在DOB ∆和COA ∆中，OD OC DOB COA OB OA =⎧⎪∠=∠⎨⎪=⎩， ()DOB COA SAS ∴∆≅∆，BD AC ∴=．【点评】本题考查了等腰三角形的性质、 全等三角形的性质以及旋转问题， 在旋转的过程中要注意哪些量是不变的， 找出图形中的对应边与对应角 ．23．（10分）定义运算{min a ，}b ：当a b 时，{min a ，}b b =；当a b <时，{min a ，}b a =；如：{4min ，0}0=；{2min ，2}2=；{3min -，1}3-=-．根据该定义运算完成下列问题：（1）{3min -，2}= 3- ，当2x 时，{min x ，2}= ； （2）若{31min x -，3}31x x -+=-，求x 的取值范围；（3）如图，已知直线1y x m =+与22y kx =-相交于点(2,1)P -，若{min x m +，2}2kx kx -=-，结合图象，直接写出x 的取值范围是 ．【考点】FD ：一次函数与一元一次不等式【分析】（1）由定理可知：{3min -，2}的值就是取3-和2的最小值，即3-；同理可得另一个式子的结果；（2）由定义列不等式解出即可；（3）根据图象可知：当2x -，12y y ．【解答】解：（1）{3min -，2}3=-，当2x 时，{min x ，2}x =； 故答案为：3-，x ；（2）由题意得：313x x --+，44x ， 1x ；（3）{min x m +，2}2kx kx -=-， 12y y ∴，由图象得：2x -， 故答案为：2x -．【点评】本题考查了一次函数与不等式以及新定义的理解，此类题目要认真阅读并理解新定义的内含：结果取最小值，第三问利用数形结合的思想求解更简便．24．（12分）市园林处为了对一段公路进行绿化，计划购买A ，B 两种风景树共900棵．A ，B 两种树的相关信息如下表：品种 项目 单价（元/棵） 成活率A 80 92% B10098%若购买A 种树x 棵，购树所需的总费用为y 元． （1）求y 与x 之间的函数关系式；（2）若购树的总费用不超过82 000元，则购A 种树不少于多少棵？（3）若希望这批树的成活率不低于94%，且使购树的总费用最低，应选购A ，B 两种树各多少棵？此时最低费用为多少？ 【考点】FH ：一次函数的应用【分析】（1）根据购树的总费用=买A 种树的费用+买B 种树的费用，化简后便可得出y 与x 的函数关系式；（2）根据（1）得到的关系式，然后将所求的条件代入其中，然后判断出购买A 种树的数量；（3）先用A 种树的成活的数量B +种树的成活的数量树的总量⨯平均成活率来判断出x 的取值，然后根据函数的性质判断出最佳的方案． 【解答】解：（1）80100(900)y x x =+- 2090000(0900x x =-+且为整数）；（2）由题意得：209000082000x -+， 解得：400x ，又因为计划购买A ，B 两种风景树共900棵， 所以900x ，即购A 种树为：400900x 且为整数．（3）92%98%(900)94%900x x +-⨯92989009894900x x +⨯-⨯ 64900x --⨯ 600x2090000y x =-+随x 的增大而减小．∴当600x =时，购树费用最低为206009000078000y =-⨯+=（元)．当600x =时，900300x -=，∴此时应购A 种树600棵，B 种树300棵．【点评】本题主要考查用待定系数法求一次函数关系式，并会用一次函数研究实际问题．注意根据自变量的取值范围来判断所要求的解．25．（12分）如图，在ABC ∆中，2AB AC ==，40B C ∠=∠=︒，点D 在线段BC 上运动(D 不与B 、C 重合），连接AD ，作40ADE ∠=︒，DE 交线段AC 于E ．（1）当115BDA ∠=︒时，EDC ∠= 25 ︒，DEC ∠= ︒；点D 从B 向C 运动时，BDA ∠逐渐变 （填“大”或“小” )；（2）当DC 等于多少时，ABD DCE ∆≅∆，请说明理由；（3）在点D 的运动过程中，ADE ∆的形状可以是等腰三角形吗？若可以，请直接写出BDA ∠的度数．若不可以，请说明理由．【考点】KB ：全等三角形的判定；KJ ：等腰三角形的判定与性质【分析】（1）根据115BDA ∠=︒以及40ADE ∠=︒，即可得出180EDC ADB ADE ∠=︒-∠-∠，进而求出DEC ∠的度数，（2）当2DC =时，利用140DEC EDC ∠+∠=︒，140ADB EDC ∠+∠=︒，求出ADB DEC ∠=∠，再利用2AB DC ==，即可得出ABD DCE ∆≅∆，（3）当BDA ∠的度数为110︒或80︒时，ADE ∆的形状是等腰三角形． 【解答】解：（1）1801801154025EDC ADB ADE ∠=︒-∠-∠=︒-︒-︒=︒， 1801804025115DEC EDC C ∠=︒-∠-∠=︒-︒-︒=︒，BDA ∠逐渐变小；故答案为：25︒，115︒，小；（2）当2DC =时，ABD DCE ∆≅∆， 理由：40C ∠=︒， 140DEC EDC ∴∠+∠=︒，又40ADE ∠=︒， 140ADB EDC ∴∠+∠=︒， ADB DEC ∴∠=∠，又2AB DC ==，()ABD DCE AAS ∴∆≅∆，（3）当BDA ∠的度数为110︒或80︒时，ADE ∆的形状是等腰三角形， 理由：110BDA ∠=︒时， 70ADC ∴∠=︒， 40C ∠=︒，70DAC ∴∠=︒，304070AED C EDC ∠=∠+∠=︒+︒=︒， DAC AED ∴∠=∠，ADE ∴∆的形状是等腰三角形；当BDA ∠的度数为80︒时， 100ADC ∴∠=︒，40C ∠=︒， 40DAC ∴∠=︒， DAC ADE ∴∠=∠，ADE ∴∆的形状是等腰三角形．【点评】此题主要考查了等腰三角形的性质以及全等三角形的判定等知识，熟练地应用等腰三角形的性质是解决问题的关键．初中奥数题试题一一、选择题（每题1分，共10分）1．如果a ，b 都代表有理数，并且a ＋b=0，那么 ( ) A ．a ，b 都是0 B ．a ，b 之一是0 C ．a ，b 互为相反数 D ．a ，b 互为倒数 2．下面的说法中正确的是 ( ) A ．单项式与单项式的和是单项式 B ．单项式与单项式的和是多项式 C ．多项式与多项式的和是多项式 D ．整式与整式的和是整式3．下面说法中不正确的是 ( )A. 有最小的自然数 B ．没有最小的正有理数 C ．没有最大的负整数 D ．没有最大的非负数4．如果a ，b 代表有理数，并且a ＋b 的值大于a －b 的值，那么 ( ) A ．a ，b 同号 B ．a ，b 异号 C ．a ＞0 D ．b ＞0 5．大于－π并且不是自然数的整数有 ( ) A ．2个 B ．3个 C ．4个 D ．无数个 6．有四种说法：甲．正数的平方不一定大于它本身； 乙．正数的立方不一定大于它本身；丙．负数的平方不一定大于它本身；丁．负数的立方不一定大于它本身。

2023北京北大附中初二（下）期中数 学班级__________ 数学教室号__________ 姓名__________ 考号__________第1—8题均有四个选项，符合题意的选项只有．．一个． 1. 计算2的结果为（ ）A. 2B. 4D. 2. 以下列各组数为边长，可以构成直角三角形的是（ ）A. 5，12，13 B. 1，2，3 C. 4，4，4 D. 4，5，6 3. 下列二次根式中，最简二次根式是（ ）4.在平面直角坐标系中，点()1,2P −到原点的距离是（ ）A. 1B. 25. 下列计算正确的是（ ）=B. 3= =2÷= 6. 如图，已知平行四边形ABCD ，BAD∠的角平分线交边BC 于点E ．交DC 延长线于点F ，如果70F ∠=︒，那么B ∠的度数是（ ）A. 30︒B. 40︒C. 50︒D. 70︒ 7. 如图，在实践活动课上，小华打算测量学校旗杆的高度，她发现旗杆顶端的绳子垂到地面后还多出1m ，当她把绳子斜拉直，且使绳子的底端刚好接触地面时，测得绳子底端距离旗杆底部5m ，由此可计算出学校旗杆的高度是（ ）A. 8mB. 10mC. 12mD. 15m⨯的正方形网格中的两个格点，称四个顶点都是格点的矩形为格点矩形，在此图中以8. 如图，A，B为55A，B为顶点的格点矩形共可以画出（）A. 1个B. 2个C. 3个D. 4个二、填空题（本题共24分，每小题3分）9. x的取值范围是______．10. 在平行四边形ABCD中，∠A+∠C＝100°，则∠A＝__．11. 在四边形ABCD中，如果AB CD，请你添加一个条件，使得四边形ABCD成为平行四边形，这个条件可以是______．（写出一种情况即可）12. “”的逆命题是：___________________________DE=，则BC的长为______．13. 如图，在ABC中，D，E分别为AB，AC边的中点，若314. 如图所示的正方形网格中，每一个小正方形的面积均为1，正方形ABCM，CDEN，MNPQ的顶点都在格点上，则正方形MNPQ的面积为__________．15. 如图，在ABCD 中，对角线AC BD ﹑相交于点O ，过点O 作OE AC ⊥交AD 于E ，如果4,,2AE DE DC ===AC 长为_________．16. 在Rt △ABC 中，∠ACB =90°，AC =BC =1． 点Q 在直线BC 上，且AQ =2，则线段BQ 的长为___________．三、解答题（本题共52分，第17题6分，第18—21题每小题4分，第22—24题每小题5分，第25题7分，第26题8分）17.计算（1+（2）+18. 如图，点E 、F 是平行四边形ABCD 的对角线AC 上的两点．AE CF =．求证：DF BE =．19. 下面是小明设计的“过直线外一点作已知直线的平行线”的尺规作图过程．已知：如图1，直线l 及直线l 外一点A ．求作：直线AD ，使得AD // l ．作法：如图2，①在直线l 上任取两点B ，C ，连接AB ；②分别以点A ，C 为圆心，线段BC ，AB 长为半径画弧，两弧在直线l 上方相交于点D ；③作直线AD ．直线AD 就是所求作的直线．根据小明设计的尺规作图过程，（1）使用直尺和圆规，补全图形（保留作图痕迹）；（2）完成下面的证明．证明：连接CD ．∵ AB ＝________，BC ＝________，∴ 四边形ABCD 为平行四边形（_________）（填推理的依据）．∴ AD // l ．20. 在解决问题“已知a =，求2281a a −+的值”时，小明是这样分析与解答的：∵2a ===−∴2a −=∴()223a −=，即2443a a −+=∴241a a −=−∴()()222812412111a a a a −+=−+=⨯−+=−. 请你根据小明的分析过程，解决如下问题：(1)(2)若121a ，求2361a a −−的值. 21. 如图，在ABC 中，90ABC ∠=︒，在边AC 上截取AD AB =，连接BD ，过点A 作AE BD ⊥于点E ．已知6AB =，8BC =，如果F 是边BC 的中点，连接EF ，求EF 的长．22. 如图，Rt ABC △中，90C ∠=︒，AD 平分BAC ∠，交BC 于点D ，4BC =， 2.5BD =．（1）则点D 到直线AB 的距离为______．（2）求线段AC 的长．23. 如图，每个小正方形的边长都是1，A ，B ，C ，D 均在网格的格点上．（1）判断BCD ∠是否为直角：______．（填写“是”或“不是”）（2）直接写出四边形ABCD 的面积为______．（3）找到格点E ，并画出四边形ABED （一个即可），使得其面积与四边形ABCD 面积相等． 24. 已知：如图，四边形ABCD 中，AD ∥BC ，∠A ＝90°，BC ＝2，∠ABD ＝15°，∠C ＝60°．（1）求∠BDC 的度数；（2）求CD 的长．25. 如图，三角形ABC 中，AB BC ⊥，4AB BC ==，E 为线段AC 上任意一点，D 是BC 的中点，连接DE ，作DF 垂直于DE 且满足DF DE =（点F 与点B 在直线ED 同侧），连接EF ，直线EF 交AB于点G ．（1）根据题意补全图1；若AE =ED 的长为______；（2）若点G 恰好是线段EF 的中点，连接BF ，证明：4AC BF =且AC BF ⊥．（3）作点B 关于直线DF 的对称点Q ．连接AQ ，DQ ，当AQ DQ +取最小值时，直接写出此时ABQ 的面积．26. 对平面上的两个图形X ，Y ，若平移图形X 所得的图形X '与Y 相交，则称X '为X 关于Y 的“巡逻平移图形”，称X 关于Y 的所有巡逻平移图形所组成的整体，为X 关于Y 的“巡逻区域”，其面积为X 关于Y 的“巡逻面积”．示例：如下图，线段DG 是线段AB 关于线段CD 的一个巡逻平移图形；平行四边形EFGH 是线段AB 关于线段CD 的巡逻区域．注：图中每个小方格都是边长为1的正方形．（1）①请在图中画出线段CD 关于线段AB 的巡逻区域，其面积为______；②已知线段m 和线段n 的长度分别为1，x ，且m 关于n 的巡逻面积为1，则x 的取值范围是______； （2）图中三角形区域T 关于平行四边形区域P 的巡逻面积为______；注：此处所指的三角形区域，平行四边形区域，以及下文的正方形区域均包含内部的所有点． （3）①若线段k 关于某边长为1的正方形区域的巡逻面积为3，则线段k 长度的最小值为______； ②若正方形区域S 关于某长度为1的线段的巡逻面积为12，则S 边长的最小值为______．参考答案一、选择题（本题共24分，每小题3分）第1—8题均有四个选项，符合题意的选项只有．．一个． 1. 【答案】A【解析】【分析】直接根据二次根式的性质求解即可．【详解】解：2=2， 故选A ．【点睛】此题主要考查了二次根式的性质，熟练掌握2(0)a a =≥是解答此题的关键． 2. 【答案】A【解析】【分析】根据勾股定理的逆定理、三角形的三边关系逐项判断即可得．【详解】解：A 、22251216913+==，则此项可以构成直角三角形，符合题意；B 、123+=，则此项不能构成三角形，不符合题意；C 、222444+≠，则此项不可以构成直角三角形，不符合题意；D 、22245416+=≠，则此项不可以构成直角三角形，不符合题意；故选：A ．【点睛】本题考查了勾股定理的逆定理、三角形的三边关系，熟练掌握勾股定理的逆定理是解题关键． 3. 【答案】A【解析】【分析】检查最简二次根式的两个条件是否同时满足，同时满足的就是最简二次根式，否则就不是．【详解】A 、被开方数不含分母；被开方数不含能开得尽方的因数或因式是最简二次根式，故A 符合题意；B B 不符合题意；C 7，被开方数含分母，不是最简二次根式，故C 不符合题意；D m ，被开方数含能开得尽方的因数或因式，不是最简二次根式，故D 不符合题意； 故选A ．【点睛】本题考查最简二次根式的定义，最简二次根式必须满足两个条件：被开方数不含分母；被开方数不含能开得尽方的因数或因式．4. 【答案】D【解析】【分析】直接利用勾股定理求解即可．【详解】解：在平面直角坐标系中，点()1,2P −到原点的距离是=故选D 【点睛】本题考查的是勾股定理的应用，掌握“由两点的坐标求解两点之间的距离”是解本题的关键． 5. 【答案】C【解析】【分析】根据二次根式的加减乘除法法则逐项判断即可得．【详解】解：AB 、=C =D =故选：C ．【点睛】本题考查了二次根式的加减乘除法，熟练掌握运算法则是解题关键．6. 【答案】B 【解析】【分析】先根据平行四边形的性质可得,AB CD AD BC ，再根据平行线的性质可得70BAF F ∠=∠=︒，然后根据角平分线的定义可得2140B BAD AF ∠==∠︒，最后根据平行线的性质即可得．【详解】解：∵四边形ABCD 是平行四边形，,AB CD AD BC ∴∥∥，70BAF F ∴∠=∠=︒，AF 是BAD ∠的角平分线，2140BAF BAD ∴∠==∠︒，又AD BC ，18040B BAD ∴∠=︒−∠=︒，故选：B ．【点睛】本题考查了平行四边形的性质、平行线的性质等知识点，熟练掌握平行四边形的性质是解题关键．7. 【答案】C【解析】【分析】由题可知，旗杆，绳子与地面构成直角三角形，根据题中数据，用勾股定理即可解答．【详解】解：设旗杆的长度为x m ，则绳子的长度为：（x +1）m ，如图，在Rt△ABC中，由勾股定理得：x2+52=（x+1）2，解得：x=12，∴旗杆的高度为12m．故选：C．【点睛】本题考查的是勾股定理的应用，根据题意得出直角三角形是解答此题的关键．8. 【答案】D【解析】【分析】根据网格特点、矩形的判定画出相应的图形即可得．【详解】解：共可以画出以下4个格点矩形：故选：D．【点睛】本题考查了矩形与网格问题，熟练掌握矩形的判定是解题关键．二、填空题（本题共24分，每小题3分）x≥9. 【答案】1【解析】【分析】根据二次根式的被开方数是非负数即可得．x−≥，【详解】解：由题意得：10x≥，解得1x≥．故答案为：1【点睛】本题考查了二次根式有意义的条件，熟练掌握二次根式的被开方数是非负数是解题关键．10. 【答案】50°．【解析】【分析】根据平行四边形的性质即可求解.【详解】解：∵四边形ABCD 是平行四边形，∴∠A ＝∠C ，∵∠A +∠C ＝100°，∴∠A ＝50°，故答案为：50°．【点睛】本题主要考查了平行四边形的性质，解题的关键在于能够熟练掌握平行四边形的性质. 11. 【答案】AD BC ∥（答案不唯一）【解析】【分析】根据平行四边形的判定即可得．【详解】解：根据两组对边分别平行的四边形是平行四边形可知，这个条件可以是AD BC ∥， 故答案为：AD BC ∥（答案不唯一）．【点睛】本题考查了平行四边形的判定，熟练掌握平行四边形的判定是解题关键．12. 【答案】如果两个实数的绝对值相等，那么这两个实数相等【解析】【分析】把一个命题的条件和结论互换就得到它的逆命题．【详解】解：命题“如果两个实数相等，那么它们的绝对值相等”的题设是“如果两个实数相等”，结论是“那么它们的绝对值相等”，故其逆命题是“如果两个实数的绝对值相等，那么这两个实数相等”．故答案为：如果两个实数的绝对值相等，那么这两个实数相等.13. 【答案】6【解析】【分析】直接根据三角形中位线定理即可得． 【详解】解：在ABC 中，D ，E 分别为AB ，AC 边的中点，且3DE =，26BC DE ∴==故答案为：6．【点睛】本题考查了三角形中位线定理，熟练掌握三角形中位线定理是解题关键．14. 【答案】45【解析】【分析】根据勾股定理即可得到结论．【详解】解：∵CM=3，CN=6，∠MCN=90°，∴MN2=CM2+CN2=32+62=45，∴正方形MNPQ的面积=MN2=45，故答案为：45．【点睛】本题考查了勾股定理，熟练掌握勾股定理是解题的关键．15. 【答案】【解析】【分析】连接CE，根据平行四边形的性质可得AO=CO，CD=AB=OE垂直平分AC，再根据线段垂直平分线上的点到两端点的距离相等可得CE=AE=4，利用勾股定理的逆定理得到∠CED=90°，得到△AEC是等腰直角三角形，根据勾股定理即可求得结论．【详解】解：连接EC，如图四边形ABCD是平行四边形，∴=，AO OC⊥，OE AC∴是线段AC的垂直平分线，OEEC AE∴==，4在DEC中，2222+=+=，EC ED42202220DC==222∴+=，EC ED DCDEC∴∠=︒，90∴∠=︒90AEC222224432∴=+=+=，AC AE EC∴=（舍负）．AC【点睛】本题主要考查了平行四边形的性质，线段垂直平分线的性质，勾股定理及逆定理，正确作出辅助线证得∠CED=90°是解决问题的关键．16. 11【解析】【分析】分当Q在射线CB上和当Q在射线BC上两种情况利用勾股定理求解即可.【详解】解：如图所示，当Q在射线CB上时，∵AC =BC =1，AQ =2，∠ACB =90°，∴CQ ==∴1BQ CQ CB =−=；如图所示，当Q 在射线BC 上时，∵AC =BC =1，AQ =2，∠ACB =90°，∴∠ACQ =90°，∴CQ ==∴1BQ CQ CB =+=+，11.Q 的位置有两个.三、解答题（本题共52分，第17题6分，第18—21题每小题4分，第22—24题每小题5分，第25题7分，第26题8分）17. 【答案】（1）+（2）6【解析】【分析】（1）先化简各式，再合并同类二次根式；（2）先化简各式，再进行加减运算．【小问1详解】解：原式=；【小问2详解】原式523=−+6=． 【点睛】本题考查二次根式的性质，二次根式的运算．熟练掌握二次根式的性质，正确的计算，是解题的关键．18. 【答案】证明见解析【解析】【分析】先根据平行四边形的性质可得AB CD ，CD AB =，根据平行线的性质可得DCF BAE ∠=∠，再根据三角形全等的判定可得△△CDF ABE ≅，然后根据全等三角形的性质即可得证． 【详解】证明：四边形ABCD 是平行四边形，AB CD ∴∥，CD AB =，DCF BAE ∴∠=∠，在CDF 和ABE 中，CD AB DCF BAE CF AE =⎧⎪∠=∠⎨⎪=⎩，()SAS CDF ABE ∴≅，DF BE ∴=．【点睛】本题考查了平行四边形的性质、三角形全等的判定与性质等知识点，熟练掌握平行四边形的性质是解题关键．19. 【答案】（1）见解析；（2）DC ，AD ，两组对边分别相等的四边形是平行四边形【解析】【分析】（1）根据作法画出图形即可；（2）根据“两组对边分别相等的四边形是平行四边形”进行证明即可．【详解】（1）如图所示，（2）证明：连接CD ．∵ AB ＝CD ，BC ＝AD ，∴ 四边形ABCD 为平行四边形（两组对边分别相等的四边形是平行四边形）（填推理的依据）．∴ AD // l ．故答案为：DC ，AD ，两组对边分别相等的四边形是平行四边形．【点睛】本题考查了作图-复杂作图：复杂作图是在五种基本作图的基础上进行作图，一般是结合了几何图形的性质和基本作图方法．解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．也考查了平行四边形的判定．20. 【答案】（1+（2）2．【解析】【分析】（1）根据分母有理化的方法可以解答本题；（2）根据题目中的例子可以灵活变形解答本题．【详解】解：（12=2,2==+ （2）∵1.a ===+ ∴1a −=∴2212a a −+=，∴221a a −=∴2363,a a −=∴23612a a −−=． 【点睛】二次根式的化简求值，熟练掌握分母有理化的方法是解题的关键.21. 【答案】2【解析】【分析】先利用勾股定理可得10AC =，从而可得4CD =，再根据等腰三角形的三线合一可得点E 是BD 的中点，然后根据三角形中位线定理即可得．【详解】解：在ABC 中，90ABC ∠=︒，6AB =，8BC =，10AC ∴==，=AD AB ，4CD AC AD AC AB ∴=−=−=，又=AD AB ，AE BD ⊥，∴点E 是BD 的中点，F 是边BC的中点， 122EF CD ∴==． 【点睛】本题考查了勾股定理、等腰三角形的三线合一、三角形中位线定理，熟练掌握三角形中位线定理是解题关键．22. 【答案】（1）1.5（2）4【解析】【分析】（1）过点D 作DE AB ⊥于点E ，根据角平分线的性质，即可求解；（2）首先利用勾股定理，即可求得BE 的长，再利用相似三角形的判定与性质，即可求解．【小问1详解】解：4BC =， 2.5BD =，4 2.5 1.5CD BC BD ∴=−=−=，过点D 作DE AB ⊥于点E ，Rt ABC △中，90C ∠=︒，DC AC ∴⊥ AD 平分BAC ∠，1.5DE DC ∴==，∴D 到直线AB 的距离为1.5，故答案为：1.5；【小问2详解】解：在Rt BDE △中，2BE ===，90C DEB ∠=∠=︒，B B ∠=∠，ABC DBE ∴∽，AC BC DE BE∴=， 4 1.532BC DE AC BE ⋅⨯∴===． 【点睛】本题考查了角平分线的性质，勾股定理，相似三角形的判定与性质，熟练掌握和运用相似三角形的判定与性质是解决本题的关键．23. 【答案】（1）不是 （2）14（3）见解析（答案不唯一）【解析】【分析】（1）先利用勾股定理分别求出222,,BC CD BD 的长，再利用勾股定理的逆定理进行判断即可得； （2）利用分割法求解即可得；（3）先利用平行四边形的性质找到格点E ，再利用等高模型画出图形即可．【小问1详解】解：2222529BC =+=，222125CD =+=，2224432BD =+=，222BC CD BD ∴+≠，BCD ∴∠不是直角，故答案为：不是．【小问2详解】解：四边形ABCD 的面积为1111552521111315142222⨯−⨯⨯−⨯⨯−⨯−⨯⨯−⨯⨯=， 故答案为：14．【小问3详解】解：如图，点E 和四边形ABED 即为所求．【点睛】本题考查了勾股定理与网格问题、勾股定理的逆定理、平行四边形的性质，解题的关键是灵活运用所学知识解决问题，属于常考题型．24. 【答案】（1）45° （21【解析】【分析】（1）由AD ∥BC ，∠A ＝90°，∠C ＝60°，可求得∠ABC 与∠ADC 的度数，然后在Rt △ABD 中，利用直角三角形的性质，求得∠A DB 的度数，继而求得∠BDC 的度数；（2）过点B 作BE ⊥CD 于点E ，在Rt △BCE 中，由BC =2，∠C =60º，得∠EBC =30º，由此CE =112BC =，由勾股定理可求得BE =DE =BE ，即可求得CD 的值. 【小问1详解】解：∵AD ∥BC ，∠A ＝90°，∠C ＝60°，∴∠ABC ＝90°，∠ADC ＝180°−∠C ＝120°．在Rt △ABD 中，∵∠A ＝90°，∠ABD ＝15°，∴∠ADB ＝75°，∴∠BDC ＝∠ADC −∠ADB ＝45°；【小问2详解】解：过点B 作BE ⊥CD 于点E ，在Rt △BCE 中，∵BC =2，∠C =60º，∴∠EBC =30º，∴CE =112BC =，BE ==， ∵∠BDC =45º，∴DE =BE∴CD =DE +CE【点睛】此题考查了直角梯形的性质、直角三角形的性质以及勾股定理等知识，正确的作出辅助线构造直角三角形是解题的关键．25. 【答案】（1（2）见解析 （3）205− 【解析】【分析】（1）过点E 作EH BC ⊥于点H ，先后求得AC =，32CE ，3CH EH ==，1HD =，在Rt DHE △中，利用勾股定理即可求解；（2）过点E 作EM BF ∥交AB 于点M ，过点D 作ND BC ⊥交AC 于点N ，推出CDN △是等腰直角三角形，得到点N 是线段AC 的中点，证明()SAS BFD NED ≌△△，得到NE BF =，34∠∠=，再证明()ASA EMG FBG ≌△△，ME BF =，ME NE =，推出AEM △是等腰直角三角形，据此即可证明结论；（3）由于DQ DB DC ==，则点Q 的运动轨迹是以D 为圆心，BC 为直径的圆，则当A 、Q 、D 三点共线时，AQ DQ +的值最小，求得55AQ AD ==，142ABD S AB BD =⨯=△，利用等高的两个三角形的面积关系即可求解．【小问1详解】解：过点E 作EH BC ⊥于点H ，则90CHE ∠=︒，三角形ABC 中，AB BC ⊥，4AB BC ==，∴AC ==∵D 是BC 的中点， ∴122CD BD BC ===，∵AE =，∴CE AC AE =−=∵45C ∠=︒，∴CHE 是等腰直角三角形，∴32CH EH CE ===， ∴1HD CH CD =−=，在Rt DHE △中，由勾股定理得，ED ===；【小问2详解】证明：过点E 作EM BF ∥交AB 于点M ，过点D 作ND BC ⊥交AC 于点N ，∴CDN △是等腰直角三角形， ∴122CD ND BC ===，∴12CN AC ===，即点N 是线段AC 的中点， ∵BD CD =，∴BD ND =，∵5906BDE BDE ∠+∠=︒=∠+∠，∴56∠=∠，在BFD △和NED 中，56BD ND DF DE =⎧⎪∠=∠⎨⎪=⎩，∴()SAS BFD NED ≌△△，∴NE BF =，34∠∠=，∵点G 是线段EF 的中点，∴GE GF =，∵EM BF ∥，∴12∠=∠，在BFD △和NED 中，12GE GF MGE BGF ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴()ASA EMG FBG ≌△△，∴ME BF =，∴ME NE =，∵2345∠+∠=︒，∴1445∠+∠=︒，∴1490MEN FED ∠=∠+∠+∠=︒，∴90AEM ∠=︒，即ME AC ⊥，∴FB AC ⊥；∵45A ∠=︒，∴AEM △是等腰直角三角形， ∴1124AE ME BF EN AN AC =====， 即4AC BF =且AC BF ⊥；【小问3详解】解：由题意得DQ DB DC ==，∴点Q 的运动轨迹是以D 为圆心，BC 为直径的圆，∴当A 、Q 、D 三点共线时，AQ DQ +的值最小，如图，∵4AB =，2BD =，∴AD ==，2AQ AD QD =−=−，142ABD S AB BD =⨯=△，∴55AQ AD ===，∴55ABQABD S AQ S AD==△△， ∴ABQ的面积为12025AB QK −⨯⨯=． 【点睛】本题考查了等腰直角三角形的判定和性质，勾股定理，全等三角形的判定和性质，解答本题的关键是明确题意，找出所求问题需要的条件．26. 【答案】（1）①画图见解析，8；②12x ≥（2）50（3）①2【解析】【分析】（1）①先根据题意画出对应的图形，然后利用网格求出面积即可；②先画出线段m 关于线段n 的巡逻区域，过点G 作GM EF ⊥交EF 延长线于M ，由m 关于n 的巡逻面积为1，求出12GM =，由此即可得到答案；（2）如解析图，先画出三角形区域T 关于平行四边形区域P 的巡逻区域，然后利用网格求出面积即可； （3）①如图所示，ABCD 是边长为1的正方形，则由平行四边形ADEF ABGF BCHK CDHT ，，，和正方形ABCD 组成的区域即为线段k 关于正方形ABCD 区域的巡逻区域，其中AF BG BK CH DT DE =====，过点A 作AN FG ⊥于N ，过点K 作KM BC ⊥于M ，证明ANF BMK △≌△，得到FN MK =，设FN MK a AN b ===，，由线段k 关于正方形ABCD 区域的巡逻面积为3，推出1a b +=，再由勾股定理得到2211222AF a ⎛⎫=−+ ⎪⎝⎭，则2AF ≥，即可求出线段k 长度的最小值为2；②如图所示，线段1AB =，则由平行四边形ABCD ABEF EFMN CDKL ，，，和正方形BHGD BHNE ACLQ AQPF ，，，组成的区域即为区域S 关于线段AB 的巡逻区域，过点C 作CT DK ⊥于T ，CW BD ⊥于W ，证明四边形TCWD 是矩形，则TC DW =，设TC DW m CW n ===，，正方形区域S 的边长为x ，由正方形区域S 关于线段AB 的巡逻面积为12，推出262x m n x −+=，由勾股定理得221+=m n ，再证明m n +≤，得到262x x−≤进而求出x ≥或x ≤（舍去），则S ． 【小问1详解】解：①如图所示，平行四边形MNKL 即为线段CD 关于线段AB 的巡逻区域，其面积为248⨯=；②如图所示，设1AB CD x ==，，则平行四边形EFGH 是线段AB 关于线段CD 的巡逻区域，即平行四边形EFGH 是线段m 关于线段n 的巡逻区域，∴22EF AB ==，过点G 作GM EF ⊥交EF 延长线于M ，∵m 关于n 的巡逻面积为1，∴1EF GM ⋅=， ∴12GM =， ∴12CD GM ==最小， ∴12x ≥；【小问2详解】解：如图所示，即为三角形区域T 关于平行四边形区域P 的巡逻区域，∴三角形区域T 关于平行四边形区域P 的巡逻面积为162422242424222502⨯+⨯+⨯+⨯+⨯+⨯+⨯⨯=；【小问3详解】解：①如图所示，ABCD 是边长为1的正方形，则由平行四边形ADEF ABGF BCHK CDHT ，，，和正方形ABCD 组成的区域即为线段k 关于正方形ABCD 区域的巡逻区域，其中AF BG BK CH DT DE =====，过点A 作AN FG ⊥于N ，过点K 作KM BC ⊥于M ，∴90ANF BMK ==︒∠∠，∵18090ABC ABG CBK ABC ++=︒=︒∠∠∠，∠，∴90ABG CBK NFA NAF +=︒=+∠∠∠∠，又∵NFA ABG =∠∠，∴NAF MBK =∠∠，∴()AAS ANF BMK △≌△，∴FN MK =，设FN MK a AN b ===，，∵线段k 关于正方形ABCD 区域的巡逻面积为3，∴平行四边形ADEF ABGF BCHK CDHT ，，，和正方形ABCD 组成的区域的面积为3，∴2223AB AN BC KM AB ⋅+⋅+=，∴2213a b ++=，∴1a b +=，在Rt ANF △中，由勾股定理得222AF AN FN =+，∴()22222AF a b a b ab =+=+−， ()121a a =−−2221a a =−+212122a ⎛⎫− ⎪⎭+⎝=， ∵2012a ⎛⎫−⎪⎝⎭≥ ， ∴21112222a ⎛⎫−+≥ ⎪⎝⎭， ∴212AF ≥，∴2AF ≥，∴线段k 长度的最小值为2；②如图所示，线段1AB =，则由平行四边形ABCD ABEF EFMN CDKL ，，，和正方形BHGD BHNE ACLQ AQPF ，，，组成的区域即为区域S 关于线段AB 的巡逻区域，过点C 作CT DK ⊥于T ，CW BD ⊥于W ，∴90CTD CWD TCW ===︒∠∠，∴四边形TCWD 是矩形，∴TC DW =，设TC DW m CW n ===，，正方形区域S 的边长为x ，∵正方形区域S 关于线段AB 的巡逻面积为12，∴平行四边形ABCD ABEF EFMN CDKL ，，，和正方形BHGD BHNE ACLQ AQPF ，，，组成的区域的面积为12，∴242212BD AC BD AC CT +⋅+⋅=，∴242212x mx nx ++=， ∴262x m n x−+=， 在Rt CWD △中，由勾股定理得222CD DW CW =+，∴221+=m n ，∵()22220m n m mn n −=−+≥，∴222m n mn +≥，∴2222222m n m mn n +≥++，∴()22222m n m n +≥+，∴()2222m n m n ++≥， ∴()212m n +≤，即()22m n +≤， ∵m n 、都是非负数，∴m n +≤∴262x x−≤∴262x −≤，即2260x +−≥，∴)230−+≥，∴由乘法的性质可得2030−≥+≥或2030−≤+≤，∴x ≥x ≤（舍去）， ∴S．【点睛】本题主要考查了正方形的性质，平行四边形的性质，勾股定理，完全平方公式的变形求值，矩形的性质与判断，全等三角形的性质与判定等等，正确画出对应的巡逻区域示意图是解题的关键．。

一、选择题1．如图，△ABC 中，∠BAC ＝58°，∠C ＝82°，∠BAC 的平分线AD 交BC 于点D ，点E 是AC 上一点，且∠ADE ＝∠B ，则∠CDE 的度数是（ ）A ．29°B ．39°C ．42°D ．52° 2．一副透明的三角板，如图叠放，直角三角板的斜边AB 、CE 相交于点D ，则BDC∠的度数是（ ）A ．65︒B ．75︒C ．85︒D ．105︒ 3．如图，DE 经过点A ，DE ∥BC ，下列说法错误的是（ ）A ．∠DAB ＝∠EACB ．∠EAC ＝∠C C ．∠EAB+∠B ＝180°D ．∠DAB ＝∠B4．解关于,x y 的方程组()()()1328511m x n y n x my ①②⎧+-+=⎪⎨-+=⎪⎩可以用①2+⨯②，消去未知数x ，也可以用①+②5⨯消去未知数y ，则mn 、的值分别为（ ） A ．23,39-- B ．23,40-- C ．25,39-- D ．25,40-- 5．一次函数y =2x +1的图像，可由函数y =2x 的图像（ ）A ．向左平移1个单位长度而得到B ．向右平移1个单位长度而得到C ．向上平移1个单位长度而得到D ．向下平移1个单位长度而得到 6．两条直线y ax b =+与y bx a =+在同一直角坐标系中的图象位置可能为（ ）． A ． B ． C ． D ．7．如图，在平面直角坐标系中，ABC ∆的顶点坐标分别为(1,1)A ，(3,1)B ，(2,2)C ，当直线3y kx =+与ABC ∆有交点时，k 的取值范围是（ ）A ．2132k -≤≤-B ．223k -≤≤-C ．223k -<<-D ．122k -≤≤- 8．如图，在两个形状、大小完全相同的大长方形内，分别互不重叠地放入四个如图③的小长方形后得图①、图②，已知大长方形的长为2a ，两个大长方形未被覆盖部分分别用阴影表示，则图①阴影部分周长与图②阴影部分周长的差是（ ）（用a 的代数式表示）A ．﹣aB ．aC ．12aD ．﹣12a 9．已知代数式x a ﹣b y 2与xy 2a +b 是同类项，则a 与b 的值分别是（ ）A ．a ＝0，b ＝1B ．a ＝2，b ＝1C ．a ＝1，b ＝0D ．a ＝0，b ＝2 10．已知点P 在第三象限内，点P 到x 轴的距离是2，到y 轴的距离是1，那么点P 的坐标为（ ）A ．（﹣1，2）B ．（﹣2，1）C ．（﹣1，﹣2）D ．（﹣2，﹣1）11．对任意两个正实数a ，b ，定义新运算a ★b 为：若a b ≥，则a ★a bb ；若a b <，则a ★b b a．则下列说法中正确的有（ ） ①=a b b a ★★；②()()1a b b a =★★；③a ★b 12a b +<★ A ．① B ．② C ．①②D ．①②③ 12．如图，分别以Rt ABC 的三边为斜边向外作等腰直角三角形，若斜边6AB =，则图中阴影部分的面积为（ ）．A ．6B ．12C ．16D ．18二、填空题13．下列命题，①对顶角相等；②两直线平行，同位角相等；③全等三角形的对应角相等．其中逆命题是真命题的命题共有_________个．14．如图，在△ABC 中，点O 是△ABC 内一点，且点O 到△ABC 三边的距离相等，若∠A ＝70°，则∠BOC ＝________．15．若方程组ax y c x by d -=⎧⎨-=⎩的解为12x y =⎧⎨=-⎩，则方程组y ax c by x d -=⎧⎨-=⎩的解为______． 16．如图，1l 表示某机床公司一天的销售收入y （万元）与机床销售量x （件）的关系，2l 表示该公司一天的销售成本y （万元）与机床销售量x （件）的关系．有以下四个结论：①1l 对应的函数表达式是y x =；②2l 应的函数表达式是1y x =+；③当一天的销售量为2件时，销售收入等于销售成本；④一天的利润w （万元）与销售量x （件）之间的函数表达式是0.51w x =-．其中正确的结论为_______（请把所有正确的序号填写在横线上）．17．在一次函数28(2)1k y k x -=-+中，随y 的x 增大而增大，则k =________．18．如图，已知1(1,0)A ，2(1,1)A ，3(1,1)A -，4(1,1)A --，5(2,1)A -，则2020A 的坐标为_______．19．化简：()2223x x --=______20．已知：如图在△ABC ，△ADE 中，∠BAC=∠DAE=90°，AB=AC ，AD=AE ，点C ，D ，E 三点在同一条直线上，连接BD ，BE ，以下四个结论：①BD=CE ；②BD ⊥CE ；③∠ACE+∠DBC=45°；④BE 2=2（AD 2+AB 2），其中结论正确的是________________．三、解答题21．如图，已知：∠DGA=∠FHC ，∠A=∠F ．求证：DF ∥AC ．（注：证明时要求写出每一步的依据）22．已知0k ≠，将关于x 的方程0kx b +=记作方程☆．（1）当3k =，2b =-时，方程☆的解为______．（2）若方程☆的解为5x =-，写出一组满足条件的k ，b 值：k ＝______，b ＝______； （3）若方程☆的解为3x =，求关于y 的方程()250k y b --=的解．23．为了落实政府的“精准扶贫”政策，某县政府准备购买A 、B 两种类型的化肥，通过市场调研得知：购买2袋A 种化肥和3袋B 种化肥共需560元；购买3袋A 种化肥比购买2袋B 种化肥多用60元．（1）每袋A 种化肥和B 种化肥各多少元？（2）现某村组需要购买A ，B 两种类型的化肥共30袋，设购买A 种化肥a 袋，购买A 种化肥和B 种化肥的总费用为w 元，如果购买A 种化肥的数量不超过15袋，求购买这批化肥的最少费用．24．在如图所示的正方形网格中，每个小正方形的边长都是1，△ABC 的顶点都在正方形网格的格点（网格线的交点）上．（1）请在如图所示的网格平面内作出平面直角坐标系，使点A 坐标为(1，3)，点B 坐标为(2，1)，则C 点坐标为 ；（2）画出△ABC 关于y 轴对称的图形为△A 1B 1C 1，并写出点B 1的坐标为 ；写出△A 1B 1C 1的面积为 ；（3）在y 轴上画出P 点，使得PA+PC 的值最小，最小值为 ．25．已知；53a =+，53b =-．求值：（1）ab ；（2）223a ab b -+； 26．中国机器人创意大赛于2014年7月15日在哈尔滨开幕．如图是一参赛队员设计的机器人比赛时行走的路径，机器人从A 处先往东走4m ，又往北走1.5m ，遇到障碍后又往西走2m ，再转向北走4.5m 处往东一拐，仅走0.5m 就到达了B ．问机器人从点A 到点B 之间的距离是多少？【参考答案】***试卷处理标记，请不要删除一、选择题1．A解析：A【分析】根据三角形的内角和得到∠B ＝180︒-∠BAC -∠C ＝40︒，根据角平分线的定义得到∠BAD=12∠BAC=29︒，根据三角形的外角的性质即可得到结论． 【详解】解：∵在△ABC 中，∠BAC ＝58︒，∠C ＝82︒，∴∠B ＝180︒-∠BAC -∠C ＝180︒-58︒-82︒＝40︒，∵AD 平分∠BAC ，∴∠BAD ＝12∠BAC ＝29︒， ∴∠ADC ＝∠B +∠BAD ＝69︒，∵∠ADE＝∠B＝40︒，∴∠CDE＝29︒，故选：A．【点睛】本题考查了三角形的内角和定理，熟练掌握三角形的内角和定理是解题的关键．2．B解析：B【分析】根据三角板的性质以及三角形内角和定理计算即可．【详解】解：∵∠CEA=60︒，∠BAE=45︒，∴∠ADE= 180︒−∠CEA−∠BAE=75︒，∴∠BDC=∠ADE=75︒，故选：B【点睛】本题考查三角板的性质，三角形内角和定理等知识，对顶角相等，解题的关键是熟练掌握基本知识，属于中考基础题．3．A解析：A【分析】根据两直线平行，内错角相等、同旁内角互补逐一判断可得．【详解】解：∵DE∥BC，∴∠DAB＝∠ABC（两直线平行，内错角相等），A选项错误、D选项正确；∠EAC＝∠C（两直线平行，内错角相等），B选项正确；∠EAB+∠B＝180°（两直线平行，同旁内角互补），C选项正确；故选A．【点睛】本题考查平行线的性质，解题关键是掌握两直线平行，内错角相等、同旁内角互补．4．A解析：A【分析】根据已知得出关于m、n的方程组，求出方程组的解即可．【详解】解：∵解关于x，y方程组()()()m1x3n2y85n x my11⎧+-+=⎪⎨-+=⎪⎩①②可以用①×2+②，消去未知数x；也可以用①+②×5消去未知数y，2(1)(5)0(32)50m n n m ++-=⎧∴⎨-++=⎩∴27532m n m n -=-⎧⎨-=⎩解得：2339m n =-⎧⎨=-⎩， 故答案为：A ．【点睛】本题考查了解二元一次方程组，能得出关于m 、n 的方程组是解此题的关键． 5．C解析：C【分析】根据一次函数图象平移规律，直接判断即可．【详解】解：∵一次函数图象向上平移m （m>0）个单位，常数项增加m ，∴函数y =2x 的图像向上平移1个单位可以得到y =2x +1的图像，故选：C ．【点睛】本题考查了一次函数图象平移的规律，解题关键是掌握一次函数图象平移的规律：上加下减常数项，左加右减自变量．6．B解析：B【分析】由于a 、b 的符号均不确定，故应分四种情况讨论，找出合适的选项．【详解】解：分四种情况讨论：当a ＞0，b ＞0时，直线y ax b =+与y bx a =+的图象均经过一、二、三象限，4个选项均不符合；当a ＞0，b ＜0，直线y ax b =+图象经过一、三、四象限，y bx a =+的图象经过第一、二、四象限；选项B 符合此条件；当a ＜0，b ＞0，直线y ax b =+图象经过一、二、四象限，y bx a =+的图象经过第一、三、四象限，4个选项均不符合；当a ＜0，b ＜0，直线y ax b =+图象经过二、三、四象限，y bx a =+的图象经过第二、三、四象限，4个选项均不符合；故选：B.【点睛】此题主要考查了一次函数的图象性质，要掌握它的性质才能灵活解题．一次函数y ＝kx +b 的图象有四种情况：①当k ＞0，b ＞0，函数y ＝kx +b 的图象经过第一、二、三象限；②当k ＞0，b ＜0，函数y ＝kx +b 的图象经过第一、三、四象限；③当k ＜0，b ＞0时，函数y ＝kx +b 的图象经过第一、二、四象限；④当k ＜0，b ＜0时，函数y ＝kx +b 的图象经过第二、三、四象限．7．B解析：B【分析】把A 点和B 点坐标分别代入y=kx+3中求出对应的的值，即可求得直线y=kx+3与△ABC 有交点时k 的临界值，然后再确定k 的取值范围．【详解】解：把A （1,1）代入y=kx+3得1=k+3，解得k=-2把B （3,1）代入y=kx+3得1=3k+3，解得：k=23- 所以当直线y=kx+3与△ABC 有交点时，k 的取值范围是223k -≤≤-． 故答案为B ．【点睛】 本题考查了一次函数与系数的关系,将A 、B 点坐标代入解析式确定k 的边界点是解答本题的关键．8．A解析：A【分析】设图③小长方形的长为m ，宽为n ，则由已知可以求得m 、n 关于a 的表达式，从而可以用a 表示出图①阴影部分周长与图②阴影部分周长，然后即可算得二者之差．【详解】解：设图③小长方形的长为m ，宽为n ，则由图①得m=2n ，m+2n=2a ， ∴2a m a n ==，， ∴图①阴影部分周长=22245a n a a a ⨯+=+=，图②阴影部分周长=()2322126n n n n a ++==，∴图①阴影部分周长与图②阴影部分周长的差是：5a-6a=-a ，故选A ．【点睛】本题考查二元一次方程组的几何应用，设图③小长方形的长为m ，宽为n ，并用a 表示出m 和n 是解题关键．9．C解析：C【分析】根据同类项的定义可得关于a 、b 的方程组，解方程组即得答案．【详解】解：由同类项的定义，得122a b a b -=⎧⎨+=⎩，解得：10a b =⎧⎨=⎩． 故选：C ．【点睛】本题考查了同类项的定义和二元一次方程组的解法，属于基本题目，正确理解题意、掌握解答的方法是解题的关键．10．C解析：C【分析】根据第三象限点的横坐标与纵坐标都是负数，点到x 轴的距离等于纵坐标的长度，到y 轴的距离等于横坐标的长度解答即可．【详解】解：∵点P 在第三象限内，点P 到x 轴的距离是2，到y 轴的距离是1，∴点P 的横坐标为﹣1，纵坐标为﹣2，∴点P 的坐标为（﹣1，﹣2）．故选：C ．【点睛】本题考查了点的坐标，熟记点到x 轴的距离等于纵坐标的长度，到y 轴的距离等于横坐标的长度是解题的关键，也是最容易出错的地方．11．A解析：A【分析】①根据新运算a b ★的运算方法，分类讨论：a b ≥，a b <，判断出a b ★是否等于b a ★即可；②由①，推得=a b b a ★★，所以()()1a b b a =★★不一定成立；③应用放缩法，判断出1a b a b+★★与2的关系即可． 【详解】解：①a b ≥时，a a bb ★， b a a b ★， ∴=a b b a ★★；a b <时，a b ba ★，b b a a★， ∴=a b b a ★★；∴①符合题意．②由①，可得：=a b b a ★★，当a b ≥时，∴()()()()22a b b a a b a a a bb b ba b ====★★★★， ∴()()a b b a ★★不一定等于1， 当a b <时， ∴()()()()22a b b a a b b b b aa a aa b ====★★★★， ∴()()a b b a ★★不一定等于1，∴()()1a b b a =★★不一定成立， ∴②不符合题意． ③当a b ≥时，0a >，0b>，∴1a b≥，∴(12a b a b a b b a ab ab ++===+=≥≥★★，当a b <时，∴(12a b a b a b a b ab ab ++===+=≥≥★★，∴12a b a b+<★★不成立， ∴③不符合题意，∴说法中正确的有1个：①．故选：A ．【点评】此题主要考查了定义新运算，以及实数的运算，要熟练掌握，解答此题的关键是要明确：在进行实数运算时，和有理数运算一样，要从高级到低级，即先算乘方、开方，再算乘除，最后算加减，有括号的要先算括号里面的，同级运算要按照从左到右的顺序进行．另外，有理数的运算律在实数范围内仍然适用．12．D解析：D【分析】根据勾股定理和等腰直角三角形的面积公式，可以证明：以直角三角形的两条直角边为斜边的等腰直角三角形的面积和等于以斜边为斜边的等腰直角三角形的面积．则阴影部分的面积即为以斜边为斜边的等腰直角三角形的面积的2倍．【详解】解：在Rt △AHC 中，AC 2=AH 2+HC 2，AH=HC ，∴AC 2=2AH 2，∴2， 同理：22， 在Rt △ABC 中，AB 2=AC 2+BC 2，AB=6，S 阴影=S △AHC +S △BFC +S △AEB =12HC•AH+12CF•BF+12AE•BE ， 即22211112224222++=(AC 2+BC 2+AB 2) 14=(AB 2+AB 2) 12=AB 2 2162=⨯ 18=．故选：D ．【点睛】本题考查了勾股定理的知识，难度适中，解题关键是运用勾股定理证明三个等腰直角三角形的面积之间的关系．二、填空题13．1【分析】根据逆命题对顶角平行线全等三角形的性质对各个选项逐个分析即可得到答案【详解】对顶角相等的逆命题为：相等的角是对顶角故①错误；两直线平行同位角相等的逆命题为：同位角相等两直线平行故②正确；全解析：1【分析】根据逆命题、对顶角、平行线、全等三角形的性质，对各个选项逐个分析，即可得到答案．【详解】对顶角相等的逆命题为：相等的角是对顶角，故①错误；两直线平行，同位角相等的逆命题为：同位角相等，两直线平行，故②正确；全等三角形的对应角相等的逆命题为：对应角相等的三角形为全等三角形，故③错误；逆命题是真命题的命题共有：1个故答案为：1．【点睛】本题考查了逆命题、对顶角、平行线、全等三角形的知识；解题的关键是熟练掌握对顶角、平行线、全等三角形的性质，从而完成求解．14．125°【分析】求出O为△ABC的三条角平分线的交点求出∠OBC=∠ABC∠OCB=∠ACB根据三角形内角和定理求出∠ABC+∠ACB求出∠OBC+∠OCB再根据三角形内角和定理求出∠BOC的度数即解析：125°【分析】求出O为△ABC的三条角平分线的交点，求出∠OBC=12∠ABC，∠OCB=12∠ACB，根据三角形内角和定理求出∠ABC+∠ACB，求出∠OBC+∠OCB，再根据三角形内角和定理求出∠BOC的度数即可；【详解】∵在△ ABC中，点O是△ABC内的一点，且点O到△ ABC三边距离相等，∴ O为△ABC的三条角平分线的交点，∴∠OBC=12∠ABC，∠OCB=12∠ACB，∵∠A=70°，∴∠ABC+∠ACB=180°-∠A=110°，∴∠OBC+∠OCB=55°，∴∠BOC=180°-∠OBC-∠OCB=125°，故答案为：125°．【点睛】本题考查了角平分线的有关计算，三角形内角和定理的应用，能正确掌握与角平分线有关的三角形内角和问题是解题的关键；15．【分析】用换元法求解即可【详解】解：∵∴∵方程组的解为∴∴故答案为：【点睛】此题考查利用换元法解二元一次方程组注意要根据方程的特点灵活选用合适的方法解数学题时把某个式子看成一个整体用一个变量去代替它解析：12 xy=-⎧⎨=⎩【分析】用换元法求解即可．【详解】解：∵y ax c by x d-=⎧⎨-=⎩，∴()() ()()a x y cx b y d ⎧---=⎪⎨---=⎪⎩，∵方程组ax y cx by d-=⎧⎨-=⎩的解为12xy=⎧⎨=-⎩，∴12xy-=⎧⎨-=-⎩，∴12xy=-⎧⎨=⎩，故答案为：12xy=-⎧⎨=⎩．【点睛】此题考查利用换元法解二元一次方程组，注意要根据方程的特点灵活选用合适的方法．解数学题时，把某个式子看成一个整体，用一个变量去代替它，从而使问题得到简化，这叫换元法．16．①③④【分析】用待定系数法求出解析式可判断①和②根据图象可判断③根据利润=收入-成本可得利润与销售量之间的函数关系式可判断④【详解】解：①观察图象可知直线l1经过原点设l1的解析式为y1=kx将点（解析：①③④【分析】用待定系数法求出解析式可判断①和②，根据图象可判断③，根据“利润=收入-成本”可得利润与销售量之间的函数关系式，可判断④．【详解】解：①观察图象可知直线l1经过原点，设l 1的解析式为y 1=kx ，将点（2，2）代入解析式可得 2=2k ，解得k=1，所以l 1的解析式为y 1=x ，故①正确；②观察图象可知直线l 2不经过原点，设l 2的解析式为y 2=kx+b ，将点（0，1）、（2，2）代入解析式可得1=22b k b ⎧⎨=+⎩解得121k b ⎧=⎪⎨⎪=⎩， 所以l 2的解析式为2112y x =+， 故②错误；③观察图象可知，直线l 1与直线l 2交于点（2，2），所以，当销售量为2时，销售收入等于销售成本，故③正确；④利润1211(1)122wy y x x x ， 故④正确；故答案为①③④．【点睛】本题考查了一次函数的应用，考查了识别函数图象的能力，待定系数法求一次函数解析式，准确观察图象提供的信息是解题的关键． 17．-3【分析】根据一次函数图象的增减性来确定（2-k ）的符号从而求得k 的取值范围【详解】解：∵在一次函数y=（2-k ）x+1中y 随x 的增大而增大∴2-k ＞0∴k ＜2k=±3∴k=-3故答案是：-3【点解析：-3【分析】根据281k -=，一次函数图象的增减性来确定（2-k ）的符号，从而求得k 的取值范围．【详解】解：∵在一次函数y=（2-k ）x+1中，y 随x 的增大而增大，∴2-k ＞0，281k -=，∴k ＜2，k=±3，∴k=-3故答案是：-3．【点睛】本题考查了一次函数图象与系数的关系．关键是掌握在直线y=kx+b （k≠0）中，当k ＞0时，y 随x 的增大而增大；当k ＜0时，y 随x 的增大而减小．18．【分析】根据题意可得各个点分别位于象限的角平分线上（A1和第四象限的点除外）逐步探索出下标和各点坐标之间的关系总结出规律根据规律推理结果【详解】通过观察可得：下标数字是4的倍数的点在第三象限∵202 解析：()505,505--【分析】根据题意可得各个点分别位于象限的角平分线上（ A 1和第四象限的点除外），逐步探索出下标和各点坐标之间的关系，总结出规律，根据规律推理结果．【详解】通过观察可得：下标数字是4的倍数的点在第三象限，∵2020÷4=505，第一圈第三象限点的坐标是（-1，-1），第二圈第三象限点的坐标是（-2，-2），第三圈第三象限点的坐标是（-3，-3）……，∴点2020A 在第三象限，且转了505圈，即在第505圈上，∴2020A 的坐标为()505,505--．顾答案为：()505,505--．【点睛】本题考查平面直角坐标系中找点的坐标规律，结题关键是找出坐标系中点的位置和坐标之间的对应关系以及点所在象限和下角标的关系．19．-1【分析】根据二次根式有意义的条件求出的范围再根据二次根式的性质和绝对值的性质化简即可得到答案【详解】由可知故答案为：【点睛】本题考查了二次根式化简求值正确掌握二次根式有意义的条件二次根式的性质绝 解析：-1【分析】根据二次根式有意义的条件，求出x 的范围，再根据二次根式的性质和绝对值的性质化简，即可得到答案．【详解】20x -≥，∴2x ≤，30x ∴-<223x x -=---，∴()2323231x x x x x x ---=---=--+=-故答案为：1-．【点睛】本题考查了二次根式化简求值，正确掌握二次根式有意义的条件，二次根式的性质，绝对值的性质是解题关键．20．①②③【分析】①由条件证明△ABD ≌△ACE 就可以得到结论；②由△ABD ≌△ACE 就可以得出∠ABD=∠ACE 就可以得出∠BDC=90°而得出结论；③由条件知∠ABC=∠ABD+∠DBC=45°由∠解析：①②③【分析】①由条件证明△ABD ≌△ACE ，就可以得到结论；②由△ABD ≌△ACE 就可以得出∠ABD=∠ACE ，就可以得出∠BDC=90°而得出结论； ③由条件知∠ABC=∠ABD+∠DBC=45°，由∠DBC+∠ACE=90°，就可以得出结论； ④△BDE 为直角三角形就可以得出BE 2=BD 2+DE 2，由△DAE 和△BAC 是等腰直角三角形就有DE 2=2AD 2，BC 2=2AB 2，就有BC 2=BD 2+CD 2≠BD 2就可以得出结论．【详解】解：①∵∠BAC=∠DAE ，∴∠BAC+∠DAC=∠DAE+∠DAC ，即∠BAD=∠CAE ．在△ABD 和△ACE 中，AD AE BAD CAE AB AC ⎧⎪∠∠⎨⎪⎩＝＝＝，∴△ABD ≌△ACE （SAS ），∴BD=CE ．故①正确；∵△ABD ≌△ACE ，∴∠ABD=∠ACE ．∵∠CAB=90°，∴∠ABD+∠DBC+∠ACB=90°，∴∠DBC+∠ACE+∠ACB=90°，∴∠BDC=180°-90°=90°．∴BD ⊥CE ；故②正确；③∵∠BAC=90°，AB=AC ，∴∠ABC=45°，∴∠ABD+∠DBC=45°．∴∠ACE+∠DBC=45°，故③正确；④∵BD ⊥CE ，∴BE 2=BD 2+DE 2．∵∠BAC=∠DAE=90°，AB=AC ，AD=AE ，∴DE 2=2AD 2，BC 2=2AB 2．∵BC 2=BD 2+CD 2≠BD 2，∴2AB 2=BD 2+CD 2≠BD 2，∴BE 2≠2（AD 2+AB 2）．故④错误．故答案为：①②③．【点睛】本题考查了全等三角形的性质和判定的应用，垂直的性质和判定的应用，等腰直角三角形的性质的应用，勾股定理的应用，能利用全等三角形的性质和判定求解是解此题的关键．三、解答题21．见解析．【分析】先根据∠DGA=∠EGC 证出AE ∥BF ，再根据平行证明出∠F=∠FBC 即可求证出结论．【详解】证明：∵∠DGA=∠EGC(对顶角相等)又∵∠DGA=∠FHC （已知）∴∠EGC=∠FHC （等量代换）∴AE ∥BF (同位角相等，两直线平行）∴∠A=∠FBC (两直线平行，同位角相等)又∵∠A=∠F （已知）∴∠F=∠FBC (等量代换)∴DF ∥AC (内错角相等,两直线平行)．【点睛】此题考查平行线的判定与性质：同位角相等，两直线平行；两直线平行，同位角相等；内错角相等，两直线平行．22．（1）x=23；（2）1，5（答案不唯一）；（3）y=1 【分析】（1）将k 和b 代入后解方程即可；（2）将x=-5代入方程，得到k 和b 的关系，取一组特殊值即可；（3）将x=3代入方程☆：得3b k =-，从而得到关于y 的方程()220k y -=，结合k≠0求出y 值即可．【详解】解：（1）当k=3，b=-2时，方程☆为：3x-2=0，解得：x=23． 故答案为：x=23； （2）∵方程☆的解为x=-5，∴-5k+b=0，∴k=1，b=5，故答案为：1，5（答案不唯一）；（3）∵方程的解为x=3，代入方程☆，则30k b +=，∴3b k =-，解关于y 的方程：()250k y b --=，即()2530k y k -+=，得：()220k y -=，∵k≠0，∴2y-2=0．解得：y=1．【点睛】本题考查了一元一次方程的解，二元一次方程的解，熟练掌握解一元一次方程是关键． 23．（1）A 种化肥100元一袋，B 种化肥120元一袋；（2）3300元．【分析】（1）设A 种化肥x 元一袋，B 种化肥y 元一袋，根据“购买2袋A 种化肥和3袋B 种化肥共需560元；购买3袋A 种化肥比购买2袋B 种化肥多用60元”，即可得出关于x ，y 的二元一次方程组，解之即可得出结论；（2）购买A 种化肥a 袋，则购买B 种化肥（３0-ａ）袋，根据购买A 种化肥和B 种化肥的总费用为w 元，即可得出关一次函数解析式，再根据且购买A 种化肥的数量不超过15袋，即可得出函数值．【详解】解：（1）设A 种化肥x 元一袋，B 种化肥y 元一袋，依题意，得：235603260x y x y +=⎧⎨-=⎩， 解得：100120x y =⎧⎨=⎩． 答：A 种化肥100元一袋，B 种化肥120元一袋．（2）由题意得，w=100a+120(30-a)=-20a+3600，∵-20<0，∴w 随a 的增大而减小，又∵0<a≤15，∴当a=15时，w 最小，即w 最小= -20×15+3600=3300(元)，∴购买这批化肥的最少费用为3300元．【点睛】本题考查了二元一次方程组的应用以及一次函数的应用，解题的关键是：（1）找准等量关系，正确列出二元一次方程组；（2）根据各数量之间的关系，正确列出一次函数解析式．24．（1）见解析，（5，5）；（2）见解析，（-2，1），5；（3）见解析，210．【分析】（1）根据点A及点B的坐标，易得y轴在A的左边一个单位，x轴在B的下方1个单位，建立直角坐标系，即可得出C点坐标；（2）根据关于y轴对称的点的坐标特点可得各点的对称点，再顺次连接即可画出ABC关于y轴对称的图形为△A1B1C1，再利用△A1B1C1所在的正方形的面积减去三个直角三角形的面积即可求出△A1B1C1的面积；（3）直接利用轴对称求最短路线的方法，根据点C的对称点为C1，连接AC1与y轴相交，此交点即为点P．再利用勾股定理求出AC1，即可得出PA+PC的最小值．【详解】解：（1）如图所示：即为作出的平面直角坐标系，∴C点坐标为（5，5）；故答案为：（5，5）；（2）如图所示：△A1B1C1'即为所求，∵A(1，3)，B (2，1)，C（5，5），∴A1(-1，3)，B1(-2，1)，C1（-5，5），∴△A1B1C1的面积为：111441224345⨯-⨯⨯-⨯⨯-⨯⨯=；222故答案为：（-2，1），5；（3）如图所示：点P即为所求作的点．∵点C的对称点为C1，∴连接AC1与y轴相交于一点即为点P，此时PA+PC的值最小，由勾股定理得AC122+=26210∴PA+PC的最小值为10．故答案为：10【点睛】本题考查了轴对称与坐标变化和勾股定理，掌握轴对称的性质及轴对称与坐标的变化规律并利用其准确作图是解答本题的关键．25．（1）2；（2）10．【分析】（1）根据二次根式的乘法法则求出ab 即可；（2）根据二次根式的减法法则求出-a b ，根据二次根式的乘法法则求出ab ，把原式化简，把a b ab -、代入计算即可．【详解】 解：53a =+，53b =-，()()5353532ab ∴=+-=-=，535323a b -=+-+= ∴ （1）ab =2（2）()()2222323210a ab b a b ab -+=--=-=．【点睛】本题是一道求代数式值的问题，考查了的是二次根式的减法和乘法和整式的完全平方公式，掌握二次根式的减法法则、乘法法则是解题的关键． 26．132【解析】试题分析：过点B 作BC ⊥AD 于C ，可以计算出AC 、BC 的长度，在直角△ABC 中根据勾股定理即可计算AB ．试题过点B 作BC ⊥AD 于C ，所以AC=4﹣2+0．5=2．5m ，BC=4．5+1．5=6m ，在直角△ABC 中，AB 为斜边，则22225136()22AB BC AC =+=+=m, 答：机器人从点A 到点B 之间的距离是132m ． 考点：勾股定理．。

一、选择题1．如图，ABC 中，//DE BC ，//EF AB ，要判定四边形DBFE 是菱形，可添加的条件是（ ）A ．BD EF =B ．AD BD =C ．BE AC ⊥D ．BE 平分ABC ∠ 2．下列二次根式的运算：①2623⨯=，②1882-=，③2555=，④()222-=-；其中运算正确的有（ ）．A ．1个B ．2个C ．3个D ．4个 3．下列各式不是最简二次根式的是（ ）A ．21a +B ．21π+C ．2bD ．0.1y 4．如果n 与2是同类二次根式，那么下列各数中，n 可以取的数为（ ）． A ．4 B ．6 C ．8 D ．125．下列四个式子中，与1(2021)2021a a --的值相等的是（ ） A ．2021a - B ．2021a --C ．2021a -D ．2021a -- 6．如图，已知正方形ABCD 的边长为4，点Р是对角线BD 上一动点（不与D ，B 重合），PF CD ⊥于点F ，PE BC ⊥于点E ，连接AP ，EF ．则下列结论错误的是（ ）A ．2PD EC =B ．AP EF =，且AP EF ⊥C ．四边形PECF 的周长是8D ．12BD EF AB ≤< 7．下列命题中，正确的命题是（ ）A ．菱形的对角线互相平分且相等B ．顺次联结菱形各边的中点所得的四边形是矩形C ．矩形的对角线互相垂直平分D ．顺次连结矩形各边的中点所得的四边形是正方形 8．如图，把一张长方形纸片沿对角线折叠，若△EDF 是等腰三角形，则∠BDC （ ）A ．45ºB ．60ºC ．67.5ºD ．75º9．如图，在Rt △ABC 中，∠C ＝90°，AC ＝2，BC ＝1，在BA 上截取BD ＝BC ，再在AC 上截取AE ＝AD ，则AE AC 的值为（ ）A ．352 B ．51- C ．5﹣1 D ．51+ 10．2002年8月在北京召开的国际数学家大会会标如图所示，它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形．若大正方形的面积是13，小正方形的面积是1，直角三角形的较长直角边为a ，较短直角边为b ，则2()a b +的值为（ ）A ．25B ．19C ．13D ．16911．如图，是我国古代数学家赵爽的《勾股圆方图》，它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形．如果大正方形的面积是12，小正方形的面积是2，直角三角形的短直角边为a ，较长的直角边为b ，那么(a+b)2的值为（ ）A ．144B ．22C ．16D ．1312．如图，在Rt ABC 中，90ACB ∠=︒，3AC =，4BC =，AD 平分CAB ∠交BC于D 点，E ，F 分别是AD ，AC 上的动点，则CE EF +的最小值为（ ）A ．152B ．152C ．3D ．125二、填空题13．如图，EF 过ABCD 对角线的交点O ，交AD 于E ，交BC 于F ，若ABCD 的周长为19， 2.5OE =，则四边形EFCD 的周长为_____．14．己知菱形ABCD 的边长是3，点E 在直线AD 上，DE =1，联结BE 与对角线AC 相交于点M ，则AM MC 的值是______． 15．已知223y x x =-+-+，则xy 的值为__________．16．数轴上有A ，B ，C 三点，相邻两个点之间的距离相等，其中点A 表示2-，点B 表示1，那么点C 表示的数是________．17．若220x y -+=，则x y +=________．18．已知一个三角形三边的长分别为5,10,15，则这个三角形的面积是_________________．19．直角三角形两边长分别为3和4，则它的周长为__________．20．如图AD=4，CD=3，∠ADC=90°，AB=13，BC=12，则图形ABCD 的面积=______________．三、解答题21．如图，四边形ABCD 中，//AD BC ，90A D ∠=∠=︒，点E 是AD 的中点，连接BE ，将ABE △沿BE 折叠后得到GBE ，且点G 在四边形ABCD 内部，延长BG 交DC 于点F ，连接EF ．（1）求证：EGF EDF △△≌；（2）求证：BG CD =；（3）若点F 是CD 的中点，8BC =，求CD 的长．22．如图，在方格纸中，点A ，B ，P 都在格点上．请按要求画出以AB 为边的格点图形．（1）在图甲中画出一个三角形，使BP 平分该三角形的面积．（2）在图乙中画出一个至少有一组对边平行的四边形，使AP 平分该四边形的面积． 23．回答下列问题：（1）计算：221(3)|35|202-⎛⎫---++ ⎪⎝⎭； （2）计算：33(1)|12|8-+-+． 24．计算：()211824226⨯--． 25．如图，在Rt △ABC 中，∠C ＝90°，AC ＝8，AB ＝10，AB 的垂直平分线分别交AB 、AC 于点D 、E ．求AE 的长．26．《九章算术》中有一道“引葭赴岸”问题：“今有池一丈，葭生其中夹，出水一尺，引葭赴岸，适与岸齐，问水深，葭长各几何？”题意是：有一个池塘，其底面是边长是10尺的正方形，一根芦苇AB生长在它的中央，高出水面部分BC为1尺．如果把该芦苇沿与水池边垂直的方向拉向岸边，那么芦苇的顶部B恰好碰到岸边的B'（如图）．水深和芦苇长各多少尺？【参考答案】***试卷处理标记，请不要删除一、选择题1．D解析：D【分析】当BE平分∠ABC时，四边形DBFE是菱形，可知先证明四边形BDEF是平行四边形，再证明BD=DE即可解决问题．【详解】解：当BE平分∠ABC时，四边形DBFE是菱形，理由：∵DE∥BC，∴∠DEB=∠EBC，∵∠EBC=∠EBD，∴∠EBD=∠DEB，∴BD=DE，∵DE∥BC，EF∥AB，∴四边形DBFE是平行四边形，∵BD=DE，∴四边形DBFE是菱形．其余选项均无法判断四边形DBFE是菱形，故选：D．【点睛】本题考查菱形的判定、平行四边形的判定和性质等知识，解题的关键是灵活运用所学知识解决问题．2．C解析：C【分析】由二次根式的性质、二次根式的混合运算进行计算，再进行判断，即可得到答案．【详解】=，故①正确；==②正确；=，故③正确；2，故④错误；∴正确的3个；故选：C．【点睛】本题考查了二次根式的性质、二次根式的混合运算，解题的关键是熟练掌握运算法则进行计算．3．D解析：D【分析】满足下列条件的二次根式，叫做最简二次根式：（1）被开方数的因数是整数，因式是整式；（2）被开方数中不含能开得尽方的因数或因式，据此判断即可．【详解】A是最简二次根式，故本选项错误；B是最简二次根式，故本选项错误；C是最简二次根式，故本选项错误；D=，不是最简二次根式.故选：D．【点睛】本题考查了最简二次根式的定义，掌握最简二次根式条件，是解题的关键．4．C解析：C【分析】是同类二次根式．【详解】解：A2=不是同类二次根式；B不是同类二次根式；C ＝是同类二次根式，正确；D =不是同类二次根式；故选：C ．【点睛】本题考查了同类二次根式的定义．要化简为最简二次根式后再判断．5．D解析：D【分析】根据二次根式有意义的条件可得出20210a ->，可得20210a -<，由此可将2021a -变形得出答案．【详解】由题意得：20210a ->，可得20210a -<，∴((2021a a ---== 故选：D ．【点睛】本题考查了二次根式的性质与化简，关键是由等式可确定出20210a ->． 6．A解析：A【分析】由三个直角的四边形是矩形，由此判断四边形PECF 是矩形，得到EC PF =，再结合正方形的性质，解得PD =，由此判断A ；过点P 作PN AB ⊥垂足为N ，过P 作//PM EF 交DC 于点M ，连接AM ，由角平分线的性质得到PN PE =，继而结合勾股定理证明AP EF =、证明四边形PEFM 是平行四边形，即可得到EF PM AP ==，设BE x =，结合勾股定理证明222PM A M P A +=，即可判断B ；根据等腰直角三角形的性质计算四边形PECF 的周长即可判断C ；设BE x =，由勾股定理解得EF 的长，再结合04x ≤≤，解得EF 与BD AB 、的数量关系即可判断D ．【详解】解：A. ,PE BC PF CD ⊥⊥90PEC PFC ∴∠=∠=︒90C ∠=︒∴四边形PECF 是矩形EC PF ∴=正方形ABCD 中45PDF ∠=︒22PD PF EC ∴==故A 错误；B.过点P 作PN AB ⊥垂足为N ，过P 作//PM EF 交DC 于点M ，连接AM ，BD 平分ABC ∠，PN AB ⊥，PE BC ⊥PN PE ∴=222222,AP AN PN EF EC PE =+=+且,AN EC PN PE ==AP EF ∴=//,//PM EF PE CD∴四边形PEFM 是平行四边形EF PM AP ∴==设BE x =，则,42PE FC MF x DM x ====-，4EC PF x ==-22(4)AP EF PM x x ===+-222216(42)AD MD AM x +==+-222AP PM AM +=AP PM ∴⊥AP EF ∴⊥故B 正确；C.BPE 为等腰直角三角形PE BE ∴=4PE PF BE EC BC ∴+=+==故四边形PECF 的周长为2()8PE PF +=， 故C 正确；D.设BE x =EF ∴=2222(4)28+16=2(2)4x x x x x +-=--+04x ≤≤42EF ∴≥12EF BD ∴≥ 4EF <EF AB ∴<1 2BD EF AB∴≤<故D正确，故选：A．【点睛】本题考查四边形的综合题，涉及勾股定理、矩形的判定与性质、正方形的判定与性质、平行四边形的判定与性质等知识，是重要考点，难度一般，掌握相关知识是解题关键．7．B解析：B【分析】根据菱形的性质、矩形的性质、中点四边形的定义逐一判断即可．【详解】解：A. 菱形的对角线互相平分，但不相等，该命题错误；B. 顺次联结菱形各边的中点所得的四边形是矩形，该命题正确；C. 矩形的对角线互相平分，但是不垂直，该命题错误；D. 顺次连结矩形各边的中点所得的四边形是菱形，该命题错误；故选：B．【点睛】本题考查特殊四边形的判定和性质，掌握菱形的性质、矩形的性质、中点四边形的定义是解题的关键．8．C解析：C【分析】由翻折可知：△BDF≌△BCD，所以∠EBD=∠CBD，∠E=∠C=90°，由于△EDF是等腰三角形，易证∠ABF=45°，所以∠CBD=12∠CBE=22.5°，从而可求出∠BDC=67.5°．【详解】解：由翻折的性质得，∠DBC=∠EBD，∵矩形的对边AD∥BC，∠E=∠C=90°，∴∠DBC=∠ADB，∴∠EBD=∠ADB，∵△EDF是等腰三角形，∠E=90°，∴△EDF是等腰直角三角形，∴∠DFE=45°，∵∠EBD+∠ADB=∠DFE，∴∠DBF=12∠DFE=22.5°，∴∠CBD =22.5°，∴∠BDC=67.5°，故选：C ．【点睛】本题考查等腰三角形，涉及矩形的性质，全等三角形的判定与性质等知识，需要学生灵活运用所学知识．9．B解析：B【分析】先由勾股定理求出BD=BC=1，得1，即可得出结论．【详解】解：∵∠C=90°，AC=2，BC=1，∴==∵BD=BC=1，∴1-，∴12AE AC =， 故选B ．【点睛】本题考查了黄金分割以及勾股定理，熟练掌握黄金分割和勾股定理是解题的关键． 10．A解析：A【分析】根据正方形的面积及直角边的关系，列出方程组，然后求解．【详解】 解：由条件可得：22131131240a b ab a b ⎧+=⎪-⎪=⎨⎪>>⎪⎩， 解之得：32a b =⎧⎨=⎩． 所以2()25a b +=，故选A【点睛】本题考查了正方形、直角三角形的性质及分析问题的推理能力和运算能力．11．B解析：B【分析】先求出四个直角三角形的面积，再求出直角三角形的斜边的长即可求解．【详解】解：∵大正方形的面积12，小正方形的面积是2，∴四个直角三角形的面积和是12-2=10，即4×12ab =10 ∴2ab=10，∵直角三角形的短直角边为a ，较长的直角边为b∴a 2+b 2=12∴(a+b)2= a 2+b 2+2ab=22．故答案为B ．【点睛】本题主要考查了勾股定理、三角形的面积、完全平方公式等知识点，完全平方公式和勾股定理的灵活变形是解答本题的关键． 12．D解析：D【分析】利用角平分线构造全等，使两线段可以合二为一，则EC+EF 的最小值即为点C 到AB 的垂线段长度．【详解】在AB 上取一点G ，使AG ＝AF∵在Rt △ABC 中，∠ACB ＝90°，AC ＝3，BC ＝4∴AB=5，∵∠CAD ＝∠BAD ，AE ＝AE ，∴△AEF ≌△AEG （SAS ）∴FE ＝GE ，∴要求CE+EF 的最小值即为求CE+EG 的最小值，故当C 、E 、G 三点共线时，符合要求，此时，作CH ⊥AB 于H 点，则CH 的长即为CE+EG 的最小值，此时，AC BC AB CH ，∴CH=·AC AB BC =125， 即：CE+EF 的最小值为125，故选：D．【点睛】本题考查了角平分线构造全等以及线段和差极值问题，灵活构造辅助线是解题关键．二、填空题13．145【分析】根据平行四边形的性质易证三角形全等进而易得AE=CF故四边形的周长=AD+CD+EF根据已知求解即可【详解】解：在平行四边形ABCD中AD∥BCAC与BD互相平分∴AO=OC∠DAC=解析：14.5【分析】根据平行四边形的性质易证三角形全等，进而易得AE=CF，故四边形EFCD的周长=AD+CD+EF，根据已知求解即可．【详解】解：在平行四边形ABCD中，AD∥BC，AC与BD互相平分∴AO=OC，∠DAC=∠ACB，∠AOE=∠COF∴△AOE≌△COF∴AE=CF，OF=OE=2.5∴四边形EFCD的周长=CF+DE+CD+EF=AE+DE+CD+EF=AD+CD+EF=192.5 2×2=14.5．故答案为：14.5．【点睛】本题考查了平行四边形的性质以及三角形全等的证明，将所求线段转化为已知线段是解题的关键．14．或【分析】首先根据题意作图注意分为E在线段AD上与E在AD的延长线上然后由菱形的性质可得AD∥BC则可证得△MAE∽△MCB根据相似三角形的对应边成比例即可求得答案【详解】解：∵菱形ABCD的边长是解析：23或43 【分析】 首先根据题意作图，注意分为E 在线段AD 上与E 在AD 的延长线上，然后由菱形的性质可得AD ∥BC ，则可证得△MAE ∽△MCB ，根据相似三角形的对应边成比例即可求得答案．【详解】解：∵菱形ABCD 的边长是3，∴AD=BC=3，AD ∥BC ，如图①：当E 在线段AD 上时，∴AE=AD －DE=3－1=2，∴△MAE ∽△MCB ，∴23MA AE MC BC ==； 如图②，当E 在AD 的延长线上时，∴AE=AD+DE=3+1=4，∴△MAE ∽△MCB ，∴43MA AE MC BC ==． ∴MA MC的值是23或43． 故答案为23或43．【点睛】此题考查了菱形的性质，相似三角形的判定与性质等知识．解题的关键是注意此题分为E 在线段AD 上与E 在AD 的延长线上两种情况，小心不要漏解．15．6【分析】根据二次根式有意义的条件可得关于x 的不等式组进而可求出xy 然后把xy 的值代入所求式子计算即可【详解】由题意得：所以x=2当x=2时y=3所以故答案为：6【点睛】本题考查了二次根式有意义的条解析：6【分析】根据二次根式有意义的条件可得关于x 的不等式组，进而可求出x 、y ，然后把x 、y 的值代入所求式子计算即可．【详解】由题意得：2020x x -≥⎧⎨-≥⎩，所以x=2， 当x=2时，y=3，所以236xy =⨯=．故答案为：6．【点睛】本题考查了二次根式有意义的条件、代数式求值和一元一次不等式组，属于基础题目，熟练掌握基本知识是解题的关键．16．或或【分析】分点C 在点A 的左侧点C 在点AB 的中间点C 在点B 的右侧三种情况再分别利用数轴的定义建立方程解方程即可得【详解】设点C 表示的数是由题意分以下三种情况：（1）当点C 在点A 的左侧时则即解得；（2解析：1--或12或2+【分析】分点C 在点A 的左侧、点C 在点A 、B 的中间、点C 在点B 的右侧三种情况，再分别利用数轴的定义建立方程，解方程即可得．【详解】设点C 表示的数是x ，由题意，分以下三种情况：（1）当点C 在点A 的左侧时，则AC AB =，即1(x =-，解得1x =--（2）当点C 在点A 、B 的中间时，则AC BC =，即(1x x -=-，解得12x -=； （3）当点C 在点B 的右侧时，则AB BC =，即1(1x -=-，解得2x =综上，点C 表示的数是1--或12或2故答案为：1--12或2+ 【点睛】本题考查了实数与数轴、一元一次方程的应用，熟练掌握数轴的定义是解题关键． 17．2【分析】先根据非负数的性质得出关于xy 的方程求出xy 的值代入x+y 进行计算即可【详解】解得故答案为：2【点睛】本题考查的是非负数的性质解题的关键是掌握非负数的性质即几个非负数的和为0时这几个非负数解析：2【分析】先根据非负数的性质得出关于x 、y 的方程，求出x 、y 的值，代入x+y 进行计算即可．【详解】220x y -+=，20x ∴-=，0y =，解得2x =，202x y +=+=．故答案为：2．【点睛】本题考查的是非负数的性质．解题的关键是掌握非负数的性质，即几个非负数的和为0时，这几个非负数都为0．18．【分析】根据勾股定理的逆定理判断这是一个直角三角形再结合面积公式求解【详解】解：∵∴∴该三角形为直角三角形∴其面积为故答案为：【点睛】本题考查了勾股定理的逆定理以及二次根式的乘法法则熟练掌握勾股定理【分析】根据勾股定理的逆定理，判断这是一个直角三角形，再结合面积公式求解．【详解】解：∵2215+=，215=，∴222+=，∴该三角形为直角三角形，∴其面积为12=【点睛】本题考查了勾股定理的逆定理以及二次根式的乘法法则，熟练掌握勾股定理的逆定理是解决本题的关键． 19．12或7+【分析】分两种情况求出第三边即可求出周长【详解】分两种情况：①当3和4都是直角边时第三边长==5故三角形的周长=3+4+5=12；②当3是直角边4是斜边时第三边长故三角形的周长=3+4+=解析：12或7+7 【分析】 分两种情况求出第三边，即可求出周长． 【详解】分两种情况：①当3和4都是直角边时，第三边长=2234+=5，故三角形的周长=3+4+5=12； ②当3是直角边，4是斜边时，第三边长22437=-=，故三角形的周长=3+4+7=7+7，故答案为：12或7+7．【点睛】此题考查勾股定理的应用，题中不明确所给边长为直角三角形的直角边或是斜边时，应分情况讨论求解．20．24【分析】连接AC 在中根据勾股定理求得AC 的长度利用勾股定理逆定理可得为直角三角形根据即可求解【详解】解：连接AC 在中∴∵∴∴为直角三角形∴故答案为：24【点睛】本题考查勾股定理及其逆定理掌握勾股 解析：24【分析】连接AC ，在Rt ACD △中根据勾股定理求得AC 的长度，利用勾股定理逆定理可得ABC 为直角三角形，根据ABCD ABC ACD S SS =-即可求解．【详解】解：连接AC ， ，在Rt ACD △中，90ADC ∠=︒，4=AD ，3CD =，∴225AC AD CD =+=，∵13AB =，12BC =，∴222AC BC AB +=，∴ABC 为直角三角形，90ACB ∠=︒，∴112422ABCD ABC ACD S S S AC BC AD CD =-=⋅-⋅=， 故答案为：24．【点睛】本题考查勾股定理及其逆定理，掌握勾股定理的内容是解题的关键．三、解答题21．（1）见解析；（2）见解析；（3）【分析】（1）根据HL证明Rt△EGF≌Rt△EOF即可；（2）证明四边形ABCD为矩形，可得BG=CD；（3）设CD=x，分别表示出BE2，EF2，BF2，证明∠BEF=90°，利用勾股定理得到方程，解之即可．【详解】解：（1）∵E是AD中点，∴AE=DE，由折叠可知：AE=EG，∠EGB=∠EGF=∠D=∠A=90°，∴EG=ED，又EF=EF，∴Rt△EGF≌Rt△EOF（HL）；（2）△ABE折叠得到△GBE，∴AB=BG，∵AD∥BC，∠A=∠D=90°，∴∠ABC=90°，∠C=90°，∴四边形ABCD为矩形，∴AB=DC，∴BG=CD；（3）∵点E是AD中点，AD=BC=8，∴AE=DE=4，∵点F是CD中点，∴设CD=x，则DF=12x，则BE2=BG2+EG2，即BE2=CD2+AE2，即BE2=x2+42，且EF2=DE2+DF2，即EF2=42+（12x）2，且BF2=BC2+CF2，即BF2=82+（12x）2，∵∠AEB=∠GEB，∠DEF=∠GEF，∴∠BEF=∠GEB+∠GEF=90°，∴BF2=BE2+EF2，∴82+（12x）2= x2+42+42+（12x）2，解得：x=，即CD=【点睛】本题考查了矩形的判定和性质，勾股定理，折叠的性质，全等三角形的判定和性质，熟记性质，找出三角形全等的条件，合理利用勾股定理得到方程是解题的关键．22．（1）画图见解析；（2）画图见解析．【分析】△即为所求；（1）连接AP延长至D点，使AP=DP，再连接BD，ABD（2）作EP平行且相等于AB，连接AE，四边形ABPE即为所求．【详解】（1）作图如下，连接AP延长至D点，使AP=DP，再连接BD，△即为所求，ABD=，AP DP∴和BDPABP△是等底同高的两个三角形，∴BP平分ABD△三角形的面积；（2）作图如下，作EP平行且相等于AB，连接AE，四边形ABPE即为所求，AB平行且相等于EP，∴四边形ABPE为平行四边形，∴AP为ABCD的对角线，∴AP平分ABCD的面积．【点睛】本题考查学生的作图能力，涉及三角形面积以及平行四边形面积相关的知识，根据题意作出图像是解题的关键．23．（1）1035+；（22【分析】（1）根据乘方、负整数指数幂、二次根式的运算法则计算；（2）根据乘方、立方根的运算法则计算．【详解】解：（1）原式＝(493-+＝493-+＝10+；（2）原式＝)112-++＝112-++【点睛】本题考查实数的混合运算，涉及到乘方、负整数指数幂、二次根式的运算法则，熟练掌握各运算法则是关键．242．【分析】利用二次根式的乘除法则，再化为最简式并合并同类二次根式即可．【详解】原式2=，2=，2=，2=．【点睛】本题考查二次根式的混合运算．掌握二次根式的乘除法则是解答本题的关键． 25．254【分析】连接BE ，先利用勾股定理求出BC 的长，根据线段垂直平分线的性质可得AE ＝BE ，然后设AE ＝BE ＝x ，再由勾股定理可得方程（8−x ）2＋62＝x 2，求解后即可得出答案．【详解】解：连接BE ，在Rt△ABC中，∵∠C＝90°，AC＝8，AB＝10，∴AC2＋BC2＝AB2．即82＋BC2＝102，解得：BC＝6．∵DE是AB的垂直平分线，∴AE＝BE．设AE＝BE＝x，则EC＝8−x，∵Rt△BCE中，EC2＋BC2＝BE2，∴（8−x）2＋62＝x2，解得：x＝254，∴AE＝254．【点睛】此题考查了线段垂直平分线的性质以及勾股定理，掌握线段垂直平分线的性质并结合勾股定理求解线段的长度是解题的关键，且要注意数形结合思想应用．26．水深12尺，芦苇长13尺【分析】依题意画出图形，设芦苇长AB=AB'=x尺，则水深AC=（x-1）尺，因为B'E=10尺，所以B'C=5尺，利用勾股定理求出x的值即可得到答案．【详解】解：依题意画出图形，如下图，设芦苇长AB=AB'=x尺，则水深AC=（x-1）尺，因为B'E=10尺，所以B'C=5尺，在Rt△ACB'中，52+（x-1）2=x2，解得：x=13，即水深12尺，芦苇长13尺．【点睛】此题考查勾股定理的实际应用，正确理解题意，构建直角三角形利用勾股定理解决问题是解题的关键．。