回归分析的人工神经网络算法模型研究

人工神经网络的研究进展与应用人工神经网络是一种基于神经元模型的计算机模型，它能够通过学习和适应提高自己的性能，从而解决各种复杂的问题。

近年来，随着科学技术的不断进步，人工神经网络的研究和应用也越来越广泛，本文将以此为主题，探讨其研究进展和应用。

一、人工神经网络的发展历程人工神经网络的概念最早可以追溯到1943年，当时生物学家麦卡洛克和数学家皮茨在研究海马的神经元模型时，提出了“神经元网络”的概念。

然而，由于当时计算机技术的不发达，研究进展缓慢，直到20世纪80年代，人工神经网络才开始进入蓬勃发展期。

在接下来的几十年里，人工神经网络不断得到完善和改进。

1986年，加利福尼亚大学教授里夫金首次提出了反向传播算法，从理论上提高了神经网络的学习能力；1998年，Yan LeCun等人在训练卷积神经网络上取得了突破性的进展，为语音识别、图像识别等领域的应用奠定了基础；2006年，西谷和众人提出了深层神经网络，在语音识别、自然语言处理、图像处理等领域取得了重大突破。

二、人工神经网络的应用领域1. 图像识别人工神经网络在图像识别领域的应用非常广泛。

以2012年ImageNet大规模视觉识别挑战赛为例，该比赛采用卷积神经网络进行图像识别，识别准确率达到了85.4%，远高于传统算法。

2. 语音识别人工神经网络在语音识别领域也有广泛的应用。

在过去的十年里，深度神经网络被广泛用于语音识别，取得了显著的进展。

例如，微软研究院的DeepSpeech就是一种深度神经网络模型，能够通过学习进行语音识别并生成相应的文本。

3. 金融分析人工神经网络在金融领域也有广泛的应用。

例如，在股票交易中，人工神经网络能够通过学习历史股价数据，预测未来的股票价格走势。

此外，人工神经网络还可以用于信用评估、风险管理等方面，为金融决策提供有力的辅助。

4. 医学诊断人工神经网络在医学诊断领域也有广泛的应用。

例如，在疾病诊断方面，人工神经网络能够通过学习医学数据，对病情进行准确的判断和诊断。

研究不同变量之间影响关系的算法
研究不同变量之间影响关系的算法有很多种，以下是一些常用的算法：
1. 相关分析：通过计算变量之间的相关系数来衡量它们之间的线性关系。

常用的相关系数包括Pearson相关系数、Spearman相关系数和Kendall相关系数。

2. 回归分析：通过建立一个数学模型来描述变量之间的关系。

常用的回归分析方法包括线性回归、多元线性回归和逻辑回归。

3. 因子分析：将一组相关的变量转化为几个无关的因子，以减少变量的数量并揭示变量之间的潜在关系。

4. 聚类分析：将样本或变量分成互相相似的组，以揭示变量之间的相似性和差异性。

5. 结构方程模型：通过建立一个结构模型来描述变量之间的关系，并进行模型拟合和参数估计。

6. 神经网络：通过建立一个多层的人工神经网络模型，学习变量之间的复杂关系。

7. 决策树：通过构建一棵树形结构来描述变量之间的条件关系，用于分类和预测。

这些算法可以根据具体的研究问题和数据特点选择和应用。

同时，还可以结合统计方法和机器学习方法进行分析，以获取更准确和全面的结果。

神经网络在回归问题上的应用研究神经网络是一种模仿人脑神经网络结构和功能而设计的数学模型，用于处理复杂的输入输出关系，近年来在计算机科学领域得到了广泛的应用。

其中，神经网络在回归问题上的应用研究是一个非常重要的方向。

回归问题是指一类针对回归分析的问题，即寻找输入与输出之间的函数关系，通常是一个连续变量做因变量的问题。

为了解决回归问题，传统的方法包括线性回归、多项式回归、岭回归等，并且这些方法在实际应用中得到了广泛的应用。

不过，这些方法存在的限制是需要人为地选择特征和参数，并且不能发现非线性关系。

相比之下，神经网络的优势就在于它可以用于任何形式的输入输出，自动学习关系并发现非线性特征。

现在，神经网络在回归问题上的应用非常广泛。

首先，神经网络可以用于解决多变量的回归问题。

多变量回归是一种更复杂的回归问题，其中存在多个输入变量和一个输出变量。

这种问题通常需要对每个输入变量的影响进行分析，并找到它们与输出变量之间的最佳关系。

神经网络的多层结构可以很好地表示这种关系，并利用反向传播算法进行参数优化。

其次，神经网络也可以用于时间序列预测。

时间序列预测是预测一个连续变量在未来时间段内的走势。

这种问题通常与数据的趋势、周期和季节性有关，因此需要寻找隐藏在数据中的模式。

传统的统计方法往往过于简单，不能充分挖掘数据的信息，而神经网络可以通过窗口滑动来识别这些模式并进行预测。

此外，神经网络也可以用于非参数回归问题。

非参数回归是在没有假定一个具体形式的基函数或先验概率下，对样本空间的连续数据建立回归函数的一种方法。

一个典型的例子是核回归，其中一个核函数（如高斯核）用于评估每个样本与目标之间的距离。

神经网络可以用于非参数回归，通过运用自适应阶段和反向传播算法，可以发现数据中的非线性特征。

最后，神经网络也可以用于局部回归问题。

局部回归是一种回归方法，其中与查询点相邻的训练数据被用来生成局部线性模型，查询点的输出变量是根据这些局部模型的加权平均值生成的。

基于人工神经网络的预测算法研究人工神经网络（Artificial Neural Network）是一种模拟人脑神经系统工作原理的计算模型，它通过大量的神经元单元之间的连接和相应的加权值，模拟人脑神经元之间的信息传递和处理过程。

基于人工神经网络的预测算法利用这一模型，通过对已有数据进行学习和训练，来预测未来的数据走势和趋势。

本文将围绕基于人工神经网络的预测算法进行研究，讨论其原理、应用、优势和局限性。

首先，我们来介绍基于人工神经网络的预测算法的原理。

人工神经网络由输入层、隐藏层和输出层组成，其中隐藏层可以包含多层。

每个神经元接收来自上一层的输入，并通过加权值和激活函数对输入进行处理，然后将结果传递给下一层。

在预测问题中，输入层通常表示历史数据特征，而输出层表示预测结果。

通过在训练过程中调整神经网络的连接权重，以及选择合适的激活函数和网络结构，使网络能够对输入与输出之间的关系进行建模和预测。

基于人工神经网络的预测算法在多个领域都有广泛的应用。

例如，它可以应用于金融市场预测，通过学习历史行情数据，来预测未来股票价格的走势；它也可以应用于气象预测，通过学习气象观测数据，来预测未来天气的变化；此外，它还可以应用于交通流量预测、销售预测、疾病预测等领域。

基于人工神经网络的预测算法可以为决策提供参考和辅助，帮助人们做出更准确的预测和计划。

相比于传统的统计分析方法，基于人工神经网络的预测算法具有一些优势。

首先，它可以处理非线性关系，而传统方法通常只能处理线性关系；其次，它可以自动学习和提取特征，无需过多人工干预；此外，它对于噪声和缺失数据具有一定的容错性，能够处理部分数据缺失的情况。

因此，基于人工神经网络的预测算法在处理复杂、非线性的预测问题时表现出色。

然而，基于人工神经网络的预测算法也存在一些局限性。

首先，神经网络的训练过程较为耗时，特别是在大规模数据集上进行训练时；其次，网络结构和参数的选择对预测结果的影响较大，需要进行一定的调试和优化；此外，神经网络的黑盒特性使得其内部的判断过程难以解释和理解，缺乏可解释性。

习题2.1什么是感知机？感知机的基本结构是什么样的？解答：感知机是Frank Rosenblatt在1957年就职于Cornell航空实验室时发明的一种人工神经网络。

它可以被视为一种最简单形式的前馈人工神经网络，是一种二元线性分类器。

感知机结构：2.2单层感知机与多层感知机之间的差异是什么？请举例说明。

解答：单层感知机与多层感知机的区别：1. 单层感知机只有输入层和输出层，多层感知机在输入与输出层之间还有若干隐藏层；2. 单层感知机只能解决线性可分问题，多层感知机还可以解决非线性可分问题。

2.3证明定理：样本集线性可分的充分必要条件是正实例点集所构成的凸壳与负实例点集构成的凸壳互不相交.解答：首先给出凸壳与线性可分的定义凸壳定义1：设集合S⊂R n，是由R n中的k个点所组成的集合，即S={x1,x2,⋯,x k}。

定义S的凸壳为conv(S)为：conv(S)={x=∑λi x iki=1|∑λi=1,λi≥0,i=1,2,⋯,k ki=1}线性可分定义2：给定一个数据集T={(x1,y1),(x2,y2),⋯,(x n,y n)}其中x i∈X=R n , y i∈Y={+1,−1} , i=1,2,⋯,n ,如果存在在某个超平面S：w∙x+b=0能够将数据集的正实例点和负实例点完全正确地划分到超平面的两侧，即对所有的正例点即y i=+1的实例i，有w∙x+b>0，对所有负实例点即y i=−1的实例i，有w∙x+b<0，则称数据集T为线性可分数据集；否则，称数据集T线性不可分。

必要性：线性可分→凸壳不相交设数据集T中的正例点集为S+，S+的凸壳为conv(S+)，负实例点集为S−，S−的凸壳为conv(S−)，若T是线性可分的，则存在一个超平面：w ∙x +b =0能够将S +和S −完全分离。

假设对于所有的正例点x i ，有：w ∙x i +b =εi易知εi >0，i =1，2，⋯，|S +|。

供应链管理中的预测算法研究随着全球贸易的不断增加，供应链管理越来越成为企业经营和战略规划的重要方面。

在供应链管理中，预测算法被广泛应用于预测需求、库存管理、生产计划以及供应网络优化等方面。

本文将探讨供应链管理中常用的预测算法及其应用。

一、基于时间序列的预测算法基于时间序列的预测算法是目前供应链管理中最常用的预测方法之一。

它是一种通过分析历史数据，预测未来趋势的方法。

时间序列预测算法可以分为两种类型：平稳时间序列和非平稳时间序列。

对于平稳时间序列，最常用的预测方法是ARIMA模型。

ARIMA模型是一种基于差分和自回归移动平均模型的预测方法。

它通过对历史数据进行差分，使序列变为平稳时间序列，然后使用自回归移动平均模型对未来进行预测。

对于非平稳时间序列，最常用的预测方法是趋势指数法。

趋势指数法是一种通过幂函数拟合数据并预测未来趋势的方法。

它可以反映出未来趋势的增减速度和变动幅度，并对未来数据进行预测。

二、基于回归分析的预测算法基于回归分析的预测算法是一种通过分析变量之间的关系，预测未来趋势的方法。

在供应链管理中，基于回归分析的预测算法主要应用于需求预测和价格预测。

对于需求预测，最常用的方法是多元回归分析。

多元回归分析通过分析多个变量和需求之间的线性关系，预测未来需求。

在实际应用中，需求预测模型通常包括历史需求、价格、促销活动等变量。

对于价格预测，最常用的方法是回归分析。

回归分析通过分析价格和市场变量之间的线性关系，预测未来的价格。

在实际应用中，价格预测模型通常包括市场规模、品牌影响力、竞争力度等变量。

三、基于人工神经网络的预测算法基于人工神经网络的预测算法是目前较为热门的预测方法之一。

人工神经网络模型通过模拟人脑的神经网络系统，对数据进行分析和预测。

在供应链管理中，人工神经网络模型主要应用于需求预测和库存管理。

对于需求预测，人工神经网络模型最主要的优势是可以处理非线性关系。

与传统的基于线性回归的预测方法相比，人工神经网络模型不受变量之间的线性关系限制，并且可以处理复杂的非线性关系。

多元线性回归与BP神经网络预测模型对比与运用研究一、本文概述本文旨在探讨多元线性回归模型与BP（反向传播）神经网络预测模型在数据分析与预测任务中的对比与运用。

我们将首先概述这两种模型的基本原理和特性，然后分析它们在处理不同数据集时的性能表现。

通过实例研究，我们将详细比较这两种模型在预测准确性、稳健性、模型可解释性以及计算效率等方面的优缺点。

多元线性回归模型是一种基于最小二乘法的统计模型，通过构建自变量与因变量之间的线性关系进行预测。

它假设数据之间的关系是线性的，并且误差项独立同分布。

这种模型易于理解和解释，但其预测能力受限于线性假设的合理性。

BP神经网络预测模型则是一种基于神经网络的非线性预测模型，它通过模拟人脑神经元的连接方式构建复杂的网络结构，从而能够处理非线性关系。

BP神经网络在数据拟合和预测方面具有强大的能力，但模型的结构和参数设置通常需要更多的经验和调整。

本文将通过实际数据集的应用，展示这两种模型在不同场景下的表现，并探讨如何结合它们各自的优势来提高预测精度和模型的实用性。

我们还将讨论这两种模型在实际应用中可能遇到的挑战，包括数据预处理、模型选择、超参数调整以及模型评估等问题。

通过本文的研究，我们期望为数据分析和预测领域的实践者提供有关多元线性回归和BP神经网络预测模型选择和应用的有益参考。

二、多元线性回归模型多元线性回归模型是一种经典的统计预测方法，它通过构建自变量与因变量之间的线性关系，来预测因变量的取值。

在多元线性回归模型中，自变量通常表示为多个特征，每个特征都对因变量有一定的影响。

多元线性回归模型的基本原理是，通过最小化预测值与真实值之间的误差平方和，来求解模型中的参数。

这些参数代表了各自变量对因变量的影响程度。

在求解过程中，通常使用最小二乘法进行参数估计，这种方法可以确保预测误差的平方和最小。

多元线性回归模型的优点在于其简单易懂，参数估计方法成熟稳定，且易于实现。

多元线性回归还可以提供自变量对因变量的影响方向和大小，具有一定的解释性。

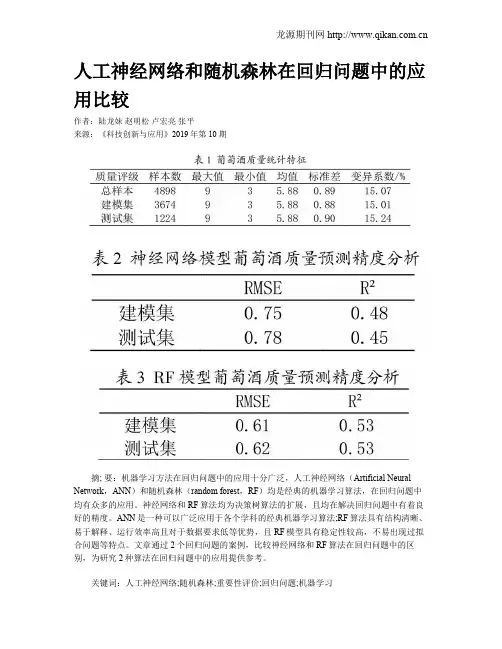
人工神经网络和随机森林在回归问题中的应用比较作者：陆龙妹赵明松卢宏亮张平来源：《科技创新与应用》2019年第10期摘; 要：机器学习方法在回归问题中的应用十分广泛，人工神经网络（Artificial Neural Network，ANN）和随机森林（random forest，RF）均是经典的机器学习算法，在回归问题中均有众多的应用。

神经网络和RF算法均为决策树算法的扩展，且均在解决回归问题中有着良好的精度。

ANN是一种可以广泛应用于各个学科的经典机器学习算法;RF算法具有结构清晰、易于解释、运行效率高且对于数据要求低等优势，且RF模型具有稳定性较高，不易出现过拟合问题等特点。

文章通过2个回归问题的案例，比较神经网络和RF算法在回归问题中的区别，为研究2种算法在回归问题中的应用提供参考。

关键词：人工神经网络;随机森林;重要性评价;回归问题;机器学习中图分类号：TP391.77; ; ; 文献标志码：A 文章编号：2095-2945（2019）10-0031-03Abstract： The machine learning method is widely used in regression. Artificial neural network （ANN） and random forest （RF） are classical machine learning algorithms widely applied in regression problems. Both neural network and RF algorithm are extensions of decision tree algorithm， and both of them have good accuracy in solving regression problems. ANN is a classical machine learning algorithm which can be widely used in various disciplines， RF algorithm has the advantages of clear structure， easy interpretation， high running efficiency and low data requirements， and the RF model has high stability. It is not easy to have the characteristics of over-fitting problem and so on. In this paper， two cases of regression problems are used to compare the difference between neural network and RF algorithm in regression problems， which provides a reference for the study of the application of the two algorithms in regression problems.Keywords： artificial neural network; stochastic forest; importance evaluation; regression problem; machine learning1 概述随着计算机和信息技术不断地发展，大数据的到来使机器学习算法成为解决实际问题的重要工具，对于机器学习算法的研究也成为了热门的研究方向。

逐步线性回归与神经网络预测的算法对比分析谭立云;刘海生;谭龙【摘要】逐步线性回归能较好地克服多重共线性现象的发生，因此逐步回归分析是探索多变量关系的最常用的分析方法，智能算法是现代数据分析的主要方法。

本文通过一个实例进行了对比研究，预测结果显示：在预测的精度上，在隐含层数目相同时，RBF径向神经网络＞BP神经网络＞逐步线性回归＞ELM极限学习机。

通过对比分析，发现神经网络方法较回归分析预测效果更好，误差相对较小。

%Gradient linear regression can well solve the occurrence of Multicollinearity , so the gradient regres-sion analysis is analytical method to research the correlation among multivariable.Intelligent algorithm is one of the dominant methods in modern data analysis.Both of the methods above are applied to one example and further to be compared.The forecasted result shows:for the accuracy of the forecasted results , when the num-ber of hidden layer is consistent ,RBF radial basis neural networks >BP neural networks >Gradient linear regression >ELM limit machine learning.Through the analysis of comparison , we infer that the accuracy and error of neural networks is smaller than the regression model.【期刊名称】《华北科技学院学报》【年(卷),期】2014(000)005【总页数】6页(P60-65)【关键词】逐步线性回归;BP神经网络;RBF径向神经网络;ELM极限学习机【作者】谭立云;刘海生;谭龙【作者单位】华北科技学院基础部，北京东燕郊 101601;华北科技学院基础部，北京东燕郊 101601;武汉大学经济与管理学院，湖北武汉 430072【正文语种】中文【中图分类】TP301.60 引言在计量经济学的学习中，探讨经济变量的关系常用回归分析方法，由于经济变量之间一般存在多重共线性，因此在建立多变量的回归方程的过程中，常需要进行各种检验，从理论上讲，只有通过了各种检验的方程才能得以使用。

基于人工神经网络模型的物理实验数据分析随着计算机技术的日益发展，人工智能技术在各个领域中得以应用，其中人工神经网络模型是一种被广泛研究和应用的算法。

在物理实验数据分析方面，人工神经网络模型也具有很大的潜力。

本文将探讨基于人工神经网络模型的物理实验数据分析方法，并着重介绍其在晶体生长和物理力学等领域中的应用。

一、人工神经网络模型简介人工神经网络模型是一种通过学习和仿真生物神经网络的行为和特性而设计的计算机算法。

它的结构类似于生物神经网络，由一组节点和连接它们的边组成，每个节点代表一个神经元，每个边代表神经元之间的连接。

人工神经网络利用反向传播算法不断调整节点之间连接的权值，从而实现模型的训练和学习。

在模型训练和学习完成后，人工神经网络可以应用于不同的领域，例如物理实验数据分析。

二、晶体生长领域中的人工神经网络模型应用晶体生长是一项重要的材料制备技术，在半导体、化学、生物等领域中都有着广泛的应用。

利用物理方法和化学方法可以获得不同形态和尺寸的晶体。

利用人工神经网络模型，可以对晶体生长过程中的数据进行分析和预测，从而提高晶体质量和生长效率。

晶体生长过程中，温度、浓度、污染物浓度等参数对晶体质量有着重要的影响。

用传统的统计方法分析这些影响因素往往不够准确，而人工神经网络模型能够通过对实验数据的学习和训练，找到其背后的规律和模式。

例如，研究人员通过将晶体生长过程中的影响因素输入神经网络模型，建立了预测晶体质量的模型。

该模型能够准确预测晶体质量，并可以通过动态调整生长参数来优化生长过程。

三、物理力学领域中的人工神经网络模型应用物理力学是研究物体受力、运动和变形等现象的学科。

在物理力学领域中，人工神经网络模型也具有着很大的潜力，可以应用于分析材料的力学性能、预测材料的断裂点等。

例如，研究人员通过将不同应变条件下材料的应力应变曲线输入神经网络模型，建立了材料力学性质的模型。

该模型能够利用已知的实验数据准确预测材料的力学性能，并可以通过改变输入的应变条件来进一步优化材料的力学性能。

基于时间序列分析的流量预测算法研究随着科技的不断发展，互联网的应用已经深入到我们的生活中的方方面面，特别是移动互联网的高速发展，使得人们更加依赖互联网。

任何一个应用都需要稳定的网络基础设施作为支撑，在这样的背景下，流量预测成为了网络规划和网络管理工程中的一个重要环节。

本文将介绍一些流量预测算法，其中时间序列分析是经典的算法之一。

一、流量预测的意义流量预测可以帮助网络规划师和网络管理员在对网络的设计和管理进行决策时提供有利的信息。

流量预测能够预测未来某个时间段内网络的流量情况，帮助其合理分配带宽，优化网络资源并提高用户体验。

二、流量预测算法1、回归分析法回归分析法是构建一个数学模型，通过历史数据、业务需求、网络拓扑结构等因素进行预测。

其基本思想是对网络流量进行分析，建立数学模型，再通过对于历史数据进行分析和拟合，来预测网络流量的未来走势。

但是，该方法不能适用于季节性较强的网络流量预测。

2、人工神经网络算法人工神经网络算法是一种模拟人脑神经系统进行计算的数学模型。

它通过学习样本数据的规律，自动对网络流量进行预测，具有很好的容错性。

但是，其计算时间复杂度过高，容易陷入局部最优解等问题。

3、时间序列分析算法时间序列分析算法是常用的一种方法，它将流量的变化理解为一个时间序列，再通过均值、方差和自相关函数等指标，构建AR、MA、ARIMA、ARCH、GARCH等时间序列模型从而进行预测。

这种算法具有不依赖事前知识，模拟时间变化的特性，适用性广，精度较高，是经典的流量预测算法之一。

三、时间序列分析算法的模型1、AR模型AR模型指的是容错自回归模型。

其基本思想是仅根据历史值预测未来值，即当前值取决于上一时刻的数据。

根据不同的数据特征，可以构建不同阶次的AR模型。

2、MA模型MA模型指的是移动平均模型。

其基本思想是根据过去若干个时间点的残差值，预测未来值。

通过设定不同的参数，可以构建不同阶次的MA模型。

3、ARMA模型ARMA模型指的是容错自回归移动平均模型，是AR模型和MA模型的混合。

时间序列回归分析方法的研究现状与应用时间序列回归分析方法是一种常用的数据分析方法，在金融、经济、自然科学等领域得到广泛应用。

本文旨在探讨时间序列回归分析方法的研究现状和应用。

一、时间序列回归分析方法的基本概念时间序列回归分析方法是通过对时间序列数据进行回归分析，预测未来的数值趋势。

时间序列数据是按照时间顺序排列的连续数据，因此具有时间相关性，可以用来研究时间趋势、季节变化以及周期性等问题。

回归分析是一种统计学方法，通过建立数学模型，探讨自变量和因变量之间的关系。

时间序列回归分析方法结合了时间序列数据和回归分析方法，可以提高数据分析的准确性和可靠性。

在进行时间序列回归分析时，需要根据数据的特点选择适当的模型和算法。

二、时间序列回归分析方法的研究现状随着数据分析技术的发展，时间序列回归分析方法的研究也得到了重视。

近年来，学者们对时间序列回归分析方法进行了广泛研究，提出了许多新的模型和算法。

1. 自回归滑动平均模型（ARIMA）ARIMA模型是一种广泛应用的时间序列模型，可以根据过去的序列值预测未来的值。

ARIMA模型包括三个主要部分：自回归（AR）、差分（I）、滑动平均（MA）。

其中自回归模型用来描述序列值之间的自相关性，差分模型用来消除序列的非平稳性，滑动平均模型用来消除序列的噪声。

2. 季节性自回归滑动平均模型（SARIMA）SARIMA模型是在ARIMA模型的基础上加入季节性成分的一种时间序列模型。

SARIMA模型包括四个主要部分：季节性自回归（SAR）、差分（I）、季节性滑动平均（SMA）、季节性周期（S）。

3. 神经网络时间序列模型（NN）神经网络时间序列模型是基于人工神经网络的一种时间序列分析方法。

NN模型通过学习时间序列数据的复杂关系，预测未来的趋势。

NN模型具有较强的自适应性和非线性拟合能力，可以处理高维度、非线性、非平稳的数据。

三、时间序列回归分析方法的应用时间序列回归分析方法可以应用于多个领域，如金融、经济、气象、环境等。

神经网络算法及模型思维学普遍认为，人类大脑的思维分为抽象（逻辑）思维、形象（直观）思维和灵感（顿悟）思维三种基本方式。

人工神经网络就是模拟人思维的第二种方式。

这是一个非线性动力学系统，其特色在于信息的分布式存储和并行协同处理。

虽然单个神经元的结构极其简单，功能有限，但大量神经元构成的网络系统所能实现的行为却是极其丰富多彩的。

神经网络的研究内容相当广泛，反映了多学科交叉技术领域的特点。

主要的研究工作集中在以下几个方面：（1）生物原型研究。

从生理学、心理学、解剖学、脑科学、病理学等生物科学方面研究神经细胞、神经网络、神经系统的生物原型结构及其功能机理。

（2）建立理论模型。

根据生物原型的研究，建立神经元、神经网络的理论模型。

其中包括概念模型、知识模型、物理化学模型、数学模型等。

（3）网络模型与算法研究。

在理论模型研究的基础上构作具体的神经网络模型，以实现计算机模拟或准备制作硬件，包括网络学习算法的研究。

这方面的工作也称为技术模型研究。

（4）人工神经网络应用系统。

在网络模型与算法研究的基础上，利用人工神经网络组成实际的应用系统，例如，完成某种信号处理或模式识别的功能、构作专家系统、制成机器人等等。

纵观当代新兴科学技术的发展历史，人类在征服宇宙空间、基本粒子，生命起源等科学技术领域的进程中历经了崎岖不平的道路。

我们也会看到，探索人脑功能和神经网络的研究将伴随着重重困难的克服而日新月异。

神经网络和粗集理论是智能信息处理的两种重要的方法,其任务是从大量观察和实验数据中获取知识、表达知识和推理决策规则。

粗集理论是基于不可分辩性思想和知识简化方法,从数据中推理逻辑规则,适合于数据简化、数据相关性查找、发现数据模式、从数据中提取规则等。

神经网络是利用非线性映射的思想和并行处理方法,用神经网络本身的结构表达输入与输出关联知识的隐函数编码,具有较强的并行处理、逼近和分类能力。

在处理不准确、不完整的知识方面,粗集理论和神经网络都显示出较强的适应能力,然而两者处理信息的方法是不同的,粗集方法模拟人类的抽象逻辑思维,神经网络方法模拟形象直觉思维,具有很强的互补性。

基于人工神经网络模型的机器学习算法研究机器学习是人工智能领域中的一个重要分支，它可以让计算机在不需要人类干预的情况下从数据中自动学习和改进。

其中最重要的算法就是人工神经网络模型，它是一种模拟人脑神经元工作方式的数学模型，可以用来解决特定的数据处理和分析问题。

本文将探讨基于人工神经网络模型的机器学习算法研究。

一、人工神经网络模型概述人工神经网络（Artificial Neural Network，ANN）是一种模拟生物神经网络的人工智能技术，它是由许多人工神经元相互连接而成的计算机系统。

每个神经元接收输入信息，进行处理后，传递给下一个神经元，最终得到网络的输出结果。

这个过程和人脑中神经元的工作方式非常相似。

人工神经网络模型的核心是神经元之间的连接，连接的权值决定了输入信号对输出信号的影响程度。

神经网络模型可以通过调整连接权值来学习输入和输出之间的关系，从而实现数据的分类、识别和预测等任务。

二、基于人工神经网络模型的机器学习算法基于人工神经网络模型的机器学习算法主要包括感知机、多层感知机、循环神经网络和卷积神经网络等。

感知机是最简单的神经网络模型，它只有一个神经元，可以用于二元分类。

多层感知机（Multilayer Perceptron，MLP）是一种含有多个隐层的神经网络模型，可以用于解决更加复杂的问题，如图像识别和语音识别等。

循环神经网络（Recurrent Neural Network，RNN）是一种前馈神经网络的扩展模型，可以处理时序数据和序列数据，如语言模型和音频处理等。

卷积神经网络（Convolutional Neural Network，CNN）是一种特殊的神经网络模型，可以通过卷积操作提取图像和视频中的特征，并用于图像识别、目标检测和视频分类等应用中。

三、研究应用基于人工神经网络模型的机器学习算法在实际应用中具有广泛的研究和应用价值。

以下是一些实际应用案例：1.图像识别基于卷积神经网络模型的机器学习算法可以用于图像识别，如人脸识别和汽车识别等。

神经网络算法在高斯过程回归中的应用研究随着科技的不断发展和计算机算力的提升，机器学习在各个领域越来越受到人们的关注和应用。

在机器学习中，神经网络算法作为一种重要的模型，在回归问题中的应用也越来越广泛。

本文将就神经网络算法在高斯过程回归中的应用进行研究和探讨。

1. 高斯过程回归高斯过程回归是一种用于回归分析的非参数贝叶斯模型。

其基本思想是将未知函数视为一组在各个输入点上的随机变量的高斯分布，从而通过观测数据推断出该函数的先验分布和后验分布，并根据后验分布进行预测。

高斯过程回归不仅可以用于单变量回归，还可以用于多变量回归和时间序列预测等问题。

2. 神经网络与高斯过程回归的结合神经网络是一种由多个节点组成的计算系统。

神经网络通过模拟人类神经系统的工作原理，实现对复杂输入数据的分类和预测等任务。

在高斯过程回归中，神经网络可以被用来模拟未知函数。

可以使用神经网络的隐含层来表示未知函数的非线性部分。

在将神经网络与高斯过程回归相结合时，可以使用神经网络来确定高斯过程回归的均值函数和方差函数。

均值函数通常是一个神经网络模型，其输入是观测数据的输入变量，输出是一个实数，该输出用于表示未知函数在该输入点的平均值。

方差函数也可以是一个神经网络模型，其输入与均值函数相同，输出是一个正值，该输出用于表示未知函数在该输入点的不确定度。

3. 高斯过程回归中的神经网络模型构建在实际应用中，构建一个可用于高斯过程回归的神经网络模型是非常重要的。

下面将介绍一些神经网络模型的构建方法。

（1）全连接网络全连接网络是指神经网络中，相邻两层的所有节点之间都有连接。

全连接网络通常用于解决简单的问题，例如分类器和状态估计器等问题。

在高斯过程回归中，可以使用全连接网络作为均值函数和方差函数。

（2）卷积网络卷积神经网络是一种深度学习模型，通常用于图像分类和语音识别等问题。

卷积神经网络可以编码输入数据中的局部模式，从而实现对输入数据的分析。

在高斯过程回归中，可以使用卷积神经网络作为均值函数和方差函数。

人工神经网络的数学模型建立及成矿预测BP网络的实现一、本文概述本文旨在探讨人工神经网络的数学模型建立及其在成矿预测中的应用，特别是使用反向传播（Backpropagation，简称BP）网络的具体实现。

我们将对人工神经网络的基本原理和数学模型进行概述，包括其结构、学习机制以及优化算法。

然后，我们将深入研究BP网络的设计和实现过程，包括网络层数、节点数、激活函数、学习率等关键参数的选择和优化。

在理解了BP网络的基本原理和实现方法后，我们将进一步探讨其在成矿预测中的应用。

成矿预测是一个复杂的地质问题，涉及到众多的影响因素和不确定性。

BP网络作为一种强大的非线性映射工具，能够有效地处理这类问题。

我们将详细介绍如何根据地质数据的特点，设计合适的BP网络模型，并通过实例验证其预测效果。

我们将对BP网络在成矿预测中的优势和局限性进行讨论，并展望未来的研究方向。

通过本文的研究，我们希望能够为地质领域的决策和预测提供一种新的、有效的工具和方法。

二、人工神经网络的数学模型建立人工神经网络（ANN）是一种模拟人脑神经元网络结构的计算模型，它通过学习大量的输入输出样本数据，自动调整网络权重和阈值，从而实现对新数据的分类、识别或预测。

在建立ANN的数学模型时，我们首先需要明确网络的拓扑结构、激活函数、学习算法等关键要素。

拓扑结构决定了神经网络的层次和连接方式。

在成矿预测中，我们通常采用前馈神经网络（Feedforward Neural Network），也称为多层感知器（MLP）。

这种网络结构包括输入层、隐藏层和输出层，每一层的神经元与下一层的神经元全连接，但同一层内的神经元之间不连接。

输入层负责接收原始数据，隐藏层负责提取数据的特征，输出层负责给出预测结果。

激活函数决定了神经元如何对输入信号进行非线性变换。

常用的激活函数包括Sigmoid函数、Tanh函数和ReLU函数等。

在成矿预测中，由于数据的复杂性和非线性特征，我们通常选择ReLU函数作为隐藏层的激活函数，因为它在负值区域为零，可以有效缓解梯度消失问题。