刘占国《利息理论》第二章习题详解及提示

第一章习题答案1. 设总量函数为A(t) = t2 + 2t + 3 。

试计算累积函数a(t) 和第n 个时段的利息In 。

解: 把t = 0 代入得A(0) = 3 于是:a(t) =A(t)/A(0)=（t2 + 2t + 3）/3 In = A(n) − A(n − 1)= (n2 + 2n + 3) − ((n − 1)2 + 2(n − 1) + 3))= 2n + 12. 对以下两种情况计算从t 时刻到n(t < n) 时刻的利息: (1)Ir(0 < r <n); (2)Ir = 2r(0 < r < n). 解:()n n-1t 11I A (n )A (t)I I I n (n 1)/2t(t 1)/2+=-=+++=+-+・・・(2)1t 11I A (n )A (t) 22nn k k t I ++=+=-==-∑3. 已知累积函数的形式为:2a (t) at b=+。

若0 时刻投入的100 元累积到3 时刻为172 元，试计算：5 时刻投入的100 元在10 时刻的终值。

解: 由题意得a(0) = 1, a(3) =A(3)/A(0)= 1.72⇒ a = 0.08, b = 1∴ A(5) = 100 A(10) = A(0) ・ a(10) = A(5) ・ a(10)/a(5)= 100 × 3 = 300. 4. 分别对以下两种总量函数计算i5 和i10 :(1) A(t) = 100 + 5t; (2)tA (t) 100(1 0.1)=+.解：(1)i5 =(A(5) − A(4))/A(4)=5120≈ 4.17% i10 =(A(10) − A(9))/A(9)=5145≈ 3.45% (2)i5 =(A(5) − A(4))/A(4)()()()544109109100(1 0.1)100(1 0.1)10%100(1 0.1)100(1 0.1)100(1 0.1)i (A 10A 9)/A 9 10%100(1 0.1)+-+==++-+=-==+5.设()n A 4 1000, i 0.01n==. 试计算A(7) 。

《利息理论》实验教学大纲课程代码：15340016 开课单位：保险系课程总学时：54 学分：3.0 实验学时：9 实验学分：3实验项目数：3课程类别：专业实验课程先修课程：微积分、概率论适用专业：保险（保险实务）一、教学目标金融、保险领域的许多计算问题具有共同的数学特征和模型，大量的计算和分析实践的基础是现金流分析和货币的时间价值（累积和贴现）计算。

本课程的目的是学习如何通过数学模型刻画许多金融领域中遇到的有关利息的计算以及与利息有关的金融产品的定量分析方法，掌握金融数学中以货币时间价值为基础的金融定量分析方法，并为今后对现代金融业务作进一步研究或实务打下坚实的基础。

开设实验课的目的在于将理论与实际相结合，即将保险理论与保险实务紧密地结合在一起，使学生学以致用。

由于许多课程只有通过实验、或通过上机操作才能真正弄清楚，所以说，实验课的开设对培养学生的动手操作能力是必不可少的内容，是保险理论与实务教学的重要组成部分。

本实验课程通过计算机中的Excel或专门的精算软件，解决有关利息的度量、单一支付现值与终值、年金现值与终值的计算、投资决策（NPV、IIR的计算）、摊还表及偿债基金的设计与计算、债券价格的确定及风险的度量等内容，具有综合性的特点。

这些实验课的开设是为了使同学在理论学习的基础上通过计算机实际操作，加深对所学内容的理解，为以后工作和科研提供可以借鉴的实际经验。

二、教学要求课堂讲授：采用多媒体课件，在讲授过程中尽量运用启发式、参与式、情境教学、案例教学等方法与学生形成良性互动。

学生能够了解相关的英语术语，能够学会使用excel进行相关计算。

实验：学生能够在理论学习的基础上，熟练使用计算机中的Excel或专门的精算软件，解决有关利息理论的计算问题。

作业：中国精算师资格考试用书——利息理论中的例题和习题。

三、学时分配四、教学方法采用多媒体课件，在讲授过程中尽量运用启发式、参与式、情境教学、案例教学等方法。

第二章 年金 部分习题参考答案证明：(1)(1)(1)(1)(1)(1)[]()m nn m m n m n m n v v v v v v i iv v i i a a i i⌝⌝----=---=⨯--=⨯-=⨯-证明：n n n-t t n t t n tttt nnnnn nn t t tt t t t t t t t n na S a a v a a v a =a S v a v a v a v a i v a ia 1111v =====1v v a viv a v v v--+=+----（1-）（1-）（1-）（1-）6. 解：由公式得：mn m+n mva =a a-71118777v a =a a 7.036=9.180 5.153i i=1=0.08299---也即：（1+）解得：7. 设X 可取得的存款额为S,根据题意：5712120.08 0.0818187121000(10.08)1000(10.08)100037.45024 1.0839169.84S S S -=+=+=⨯⨯=12. 解：根据题意，有1010301030101000a 1000a v =a a v K K +-又由于，则上式经整理得：10v =1/21030101030101030101030101111(1)a -a v 10001-v -v (1v )5822111a +a v 1-v +v (1v )91(1)8221800K K ----====--+-=解得：14. 设该永续年金每年支付R ，结合公式: nn a =a v a ∞∞+根据题意该永续年金为三人年金现值之和，即：n n n a a Ra =Rv a 22RR ∞∞++又由于三人所领取的年金现值相等，有:nnn n n 1v a v 2=v a R =R 2i i v =1/3R R ∞- 即，所以，19. 根据题意：22i i 2222222i i 222105105i i 22105i 2i 21051051000=1700011==171=t t t 17t 15=0f()t t 17t 15escart t=f =-0.00117fS S S S t D ⨯++++++-++-+（）（）（）（）（）（）（）（）（）（）-1+（）-1则：令，上式经过整理为：令=根据规则，上式最多有两个正根，而1显然不符合实际，故排除。

第一章 利息的基本概念1.)()0()(t a A t A =2.11)0(=∴=b a 180)5(100=a ，508)8()5(300=a a 3~5.用公式(1-4b)7~9.用公式（1-5）、（1-6）11.第三个月单利利息1%，复利利息23%)11(%)11(+-+12.1000)1)(1)(1(321=+++i i i k 14.n n n n i i i i --+⋅+>+++)1()1(2)1()1( 16.用p.6公式17.用P.7最后两个公式19.用公式（1-26）20.(1)用公式（1-20）; (2)用公式（1-23）22. 用公式（1-29）23.(1) 用公式（1-32）;(2) 用公式（1-34）及题6（2）结论24. 用公式（1-32） 25.44216%1(1)(110%)118%45%12i ⎛⎫+=++ ⎪-⎝⎭⎛⎫- ⎪⎝⎭ 26.对于c)及d)，δn e n a =)(，1111)1(-=-=+==∴v d i e a δ，∴c)中，v ln -=δ， d)中，δ--=e d 128.⎰=tdx x e t a 0)()(δ 29.4411⎪⎭⎫ ⎝⎛+=+j i ；h e j =+1 31.（1）902天39.t e t A dr +=⎰10δ )1ln(0t dr t A +=⎰∴δ，两边同时求导，t t A +=11)(δ，)(t B δ类似 46.10009200.081000d -==，920)2108.01(288)08.01(=⨯-+-x 第三章 收益率2.解：234000 1.120000.93382⨯-⨯=3.解：237000100040005500(0)v v v v v --++=110.090.11.09 1.1i v i v ====时，；时， 令(0)0v v i =⇒及7.解：81.516.510(1)11.995%x x i i ⋅⋅=+⇒=8.解：11100.250.751(1)1(1)1(1)100000150002000011000k k k dt dt dt t k t k t k ee e +-+-+-⎰⎰⎰+-= 解得：0.14117k = 10.解：560.0450.0461000 1.04550.04s i is -⎛⎫++ ⎪⎝⎭13.解：50000068000060000500055000A B I ===-=，，29.78%I i A B I=≈+- 14.解：()11144320000112%5000180001112%196104B i -⎛⎫⎡⎤⎛⎫=⨯++⨯+-⨯+-⨯= ⎪ ⎪⎢⎥⎝⎭⎣⎦⎝⎭15.解：1212121k t dt t e k ++⎰=⇒= 书后答案是1k =，不知我对它对。

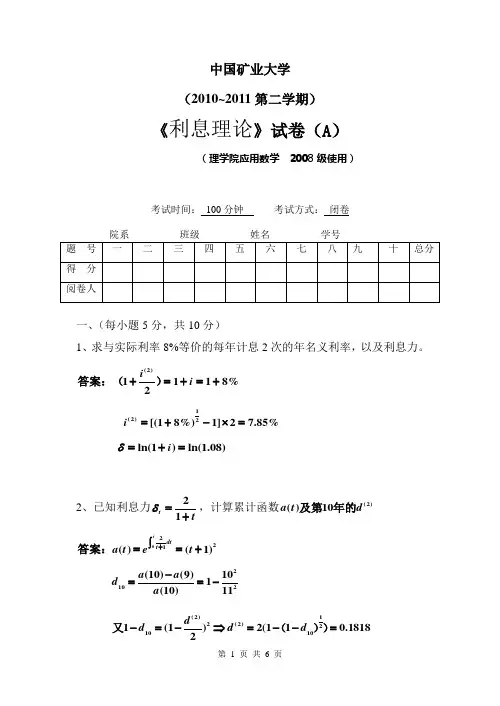
中国矿业大学 （2010~2011第二学期）《利息理论》试卷（A ）（理学院应用数学 2008级使用）考试时间： 100分钟 考试方式： 闭卷一、（每小题5分，共10分）1、求与实际利率8%等价的每年计息2次的年名义利率，以及利息力。

(2)1118%2i i +=+=+答案：（）1(2)2[(18%)1]27.85%i=+-⨯= l n (1)l n (1.0i δ=+=2、已知利息力21t tδ=+，计算累计函数(2)()10a t d 及第年的 0221()(1)tdtt a t et +⎰==+答案：2102(10)(9)101(10)11a a d a -==-1(2)2(2)210101(1)2(110.18182d d d d -=-⇒=--=又（））二（10分）、某期末付永续年金中，各次付款额为123 ，，，，证明该年金的现值为211i i +。

1p a pv pv i ∞=+=+答案：1(1)p v i⇒-= 211111i p d i i i i i+===+三、（10分）某永续年金在第一年末支付1，第二年末支付3，第三年末支付5， ，证明该年金的现值为：22(1)v v v +-。

2212(1)v v v p i i i v +=+=-答案： （证明方法很多种，仅列一种最简单的方法）四、（10分）现有两个n 年期年金,一个现值为100元,另一个终值为100元,计算年金差额, i=10%100*10i -==n n100100答案： 年金支付差额=a s五、（10分）某年金每年初付款1000元，共8年，各付款利率为8%，各付款所得利息的再投资利率为6 %，计算第8年末的年金积累值及该投资的实际收益率i '(写出算式及计算说明即可)。

0.060.068(.0)11321.730.06⨯-⨯=N-1n 答案：累积值=8000+10000.08(IS)s =10008+088100011321.73i a '= 解出i '即可六、（10分）某总额1000元的债务，原定将分10年于每年年末等额偿付，合同规定年利率为5%，当第4次偿付完成时，年利率上调为6%，如果余下6次等额还款，则每次还款额是多少？P 答案：设原还款额为100.051000pa =129.5p = 440.05100010.05129.5657.34s =+-=第四次还款后的余额（） 6R 余下的次还款 60.06657.34R =133.67Ra =⇒七、（10分）某人以半年度转换利率12%借款10000元，期限5年，他以偿债基金的方式偿还本金，在未来的5年内每年末向偿债基金等额存款，假设偿债基金的年利率为8%，则他总共支付的金额是多少？R 答案：设偿债基金的存款额为50.08Rs 10000=R=1704.56解得.50.061014523⨯⨯⨯=支出总额=170465+10000八、（10分）面值1000元的10年期债券，票息率为每年计息两次的年名义利率8.4%，赎回值为1050元。

第四章债务偿还1.解：5510000 1.1220004917.72s ⨯-=2.解：()10100.081.081468.0510x x x a -=+⋅-3.解：设共需还款n 次415001200n a -=最初贷款额1500n a =4.解： 100.0810000100001.5100002X i P Ps X i P =+⎧⎪=⎨⎪=⨯+⎩5.解：过去法：()()()()7251051510524000300020001400013000a a a a a i s i s ⎡⎤+-+-+-+-⎣⎦ 未来法：33530002000a a v +7.解：()11481211 1.5i i +=+=月 80120100000i i a a 月月8.解:由于不知利率上调后偿还期的变化，因此用过去法比较简便()()121212120.03120.0352311510.0310.0351000 1.0351000s s ++-- 9.解：2012011k k v v -+-+=-10.解：()()()6126100011366.87110001i i i ---+++=⇒+= ()31366.871i -∴+= 11.解：2016120171201812019120201vv v v v -+-+-+-+-+++++ 5543211v v v v v v i -=++++=； 2031100Pv P -+=⇒；51v P i- 12.解：20817720(1)k s v a i a -++=+- （k 为剩余还款数）解得：k =12原利息：2020a -； 现利息：207x k a ++-∴节省利息 131********x k v v --=--=-13.解：()()358113522114144113511080.25P P v P v v -+-+=⎧⎧-=⎪⎪⇒⎨⎨-=⎪⎪=⎩⎩ 第29次 ()35291172P v-+-= 14.解：L 每次还款额为030B a ， N 每次还款本金为030B ，第t 次还款额为000030(1)3030B B B B t i a ⎡⎤--+<⎢⎥⎣⎦ 15.解：30121121121.0021 1.051250001.0510.002P ⨯⎛⎫ ⎪- ⎪⎝⎭=-- 16.解：3108112i v --+⎛⎫=+ ⎪⎝⎭17.解：()31300012000n vn -+-=⇒613000n v -+ 18.解：418%(1i +=+季）()4050040i a -季19.解：每月还款额360100000i P a =月 120120325.40)(1)100000120i k i Pa P a i k -+++=⇒=月月月（∴利息支出为：120(325.40)12010000066261.2P P ⨯++⨯-=20.解：10444104410410 1.054 1.0520010 1.0520010 1.050.050.05a a B a a --⎛⎫⎛⎫-⨯-⨯=+⨯-+⨯ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭第5次还款中的利息为4iB21.解：10101010a v Pa P i P i ⎡⎤-+=⎢⎥⎢⎥⎣⎦22.解：1055510510510510(1)(1)10(1)(1)a v a v a i a i i i i ⎧⎫⎡⎤⎡⎤--⎪⎪+-+-+-+⎢⎥⎢⎥⎨⎬⎢⎥⎢⎥⎪⎪⎣⎦⎣⎦⎩⎭23.解：（1） 331.041 1.12000400 1.11287.760.06⎡⎤⎛⎫-⎢⎥ ⎪⎝⎭⎢⎥-=⎢⎥⎢⎥⎣⎦（2）第二年末贷款余额为： 221.041 1.12000400 1.115640.06⎡⎤⎛⎫-⎢⎥ ⎪⎝⎭⎢⎥-=⎢⎥⎢⎥⎣⎦∴第三次还款中本金为 1564-1287.76=276.2424.此题较麻烦25.解：10102555ln1.05 2.8658t t B dt a dt δ-==⎰⎰ 27.解：10.1t B t =-（1）510.150.5B =-⨯=前5年还款本金为：510.5B -=（2）55000.1(10.1)0.375t B dt t dt δ=-=⎰⎰28.解：120.04250.0410000100005%0.04355.69s s ⨯-= 第9年偿债基金增长额为80.04250.04250.0410000100000.04328.61s s s +=29.解：40.03100.0310******** 1.03100005%s s -+⨯ 30.解:(1)1000010%1000Li =⨯=(2)1500-1000=500(3)5000100050000.08600Li j -=-⨯=（4）5000(1)5005000900j ++-=（5）5000(1)5005900j ++=32.解：100.0710000Xs = 33．解: 100.04100.05220.0510002L Ds L xa L D x ⎧=⎪⎪⎪=⎨⎪⎪++=⎪⎩34.解：10100.04100.0412000(280 1.04400)s s -+ 35.解：310.0340000040000036000i s += 36.解：2020200.03200.0320 1.0350 1.031000000.03a Xa -⎡⎤-⨯+=⎢⎥⎢⎥⎣⎦。

利息理论智慧树知到课后章节答案2023年下云南财经大学云南财经大学绪论单元测试1.利息和利率存在于跨时期的资金借贷活动当中，是借贷双方发生了跨时期资金借贷的行为结果。

A:对 B:错答案:对2.利息和利率是最重要的经济变量。

它们在生产生活实践当中发挥着重要的杠杆作用，可以通过影响人们的投资和消费行为，进而强有效的影响资金的流动和国民经济的整体发展。

A:对 B:错答案:对3.《利息理论》是保险学、精算学、金融数学、金融工程等专业的核心课程，是参加精算师资格考试的必考内容，其提供的思维方式可以广泛的运用于保险产品定价，尤其是寿险产品定价、财务管理、投资决策、公司金融、金融工程等领域。

A:错 B:对答案:对1.以下关于利息的说法，错误的是（）。

A:利息是从属于信用的一个经济范畴B:利息是借款人支付给贷款人的代价 C:信用关系是利息产生的基础 D:利息是借款人由于借出货币使用权而从贷款人那里获得的报酬答案:利息是借款人由于借出货币使用权而从贷款人那里获得的报酬2.利息是资金的（）。

A:价格 B:价值 C:水平 D:指标答案:价格3.利率是衡量利息高低的（）。

A:指标 B:水平 C:价格 D:价值答案:指标4.利息是借款人为了获得一笔资金的使用权而向贷款人支付的款项。

（）A:错 B:对答案:对5.利息的存在是不合理的。

（）A:对 B:错答案:错1.以下说法正确的是（）。

A:实际贴现率等于实际利率的终值 B:实际贴现率等于实际利率的现值 C:当t>1时，复利的累计值小于单利的累积值 D:累积函数是贴现函数的倒数答案:实际贴现率等于实际利率的现值2.名义利率适应通货膨胀的变化而变化应（）。

A:不同向，但同步 B:同向，同步 C:同向，不同步 D:不同向，不同步答案:同向，同步3.投资者从银行借款20000元，4年后需要偿还本息25249.54元，请计算该笔贷款的年复利利率是多少（）。

A:7% B:6% C:5% D:4%答案:6%4.单利的计算不用把利息计入本金；而复利恰恰相反，它的利息要并入本金中重复计息。

第一章 利息的基本概念1.)()0()(t a A t A =2.11)0(=∴=b a 180)5(100=a ，508)8()5(300=a a3~5.用公式(1-4b)7~9.用公式（1-5）、（1-6）11.第三个月单利利息1%，复利利息23%)11(%)11(+-+ 12.1000)1)(1)(1(321=+++i i i k14.n n n n i i i i --+⋅+>+++)1()1(2)1()1( 16.用p.6公式17.用P .7最后两个公式19.用公式（1-26）20.(1)用公式（1-20）; (2)用公式（1-23） 22. 用公式（1-29）23.(1) 用公式（1-32）;(2) 用公式（1-34）及题6（2）结论 24. 用公式（1-32）25.44216%1(1)(110%)118%45%12i ⎛⎫+=++ ⎪-⎝⎭⎛⎫- ⎪⎝⎭ 26.对于c)及d)，δn e n a =)(，1111)1(-=-=+==∴vdi e a δ，∴c)中，v ln -=δ，d)中，δ--=e d 128.⎰=tdxx et a 0)()(δ29.4411⎪⎭⎫ ⎝⎛+=+j i ；he j =+131.（1）902天 39.tetA dr+=⎰10δ )1ln(0t dr tA +=⎰∴δ，两边同时求导，tt A +=11)(δ，)(t B δ类似46.10009200.081000d -==，920)2108.01(288)08.01(=⨯-+-x第二章 年金4.解：12010.087110.0870.08712160001000110.087121212A --⎛⎫-+ ⎪⎛⎫⎛⎫⎝⎭=+⋅++ ⎪ ⎪⎝⎭⎝⎭5.解：()()()()22211111111(*)nnn nn i a x i xiii xi a y ii----+==⇒+=--+--===将1d i d=-代入（*）7.解：()51218100010.0839169.84s -+=8.解：100.1100.15000s Ra = 9.解：100.1100.155000s Ra = 14.解：永续年金每年支付R112n n Ra R a i ⎛⎫=- ⎪⎝⎭17.解：0.0081500100000m a = 解得95.6m ≈ 即正常还款次数为95次 95950.0081500(10.008)100000a f -++= 解得965.74f =19.解：()()()(2)(2)(2)1055222105100020001700011171150i i i s s s i i i ⎛⎫-+= ⎪ ⎪⎝⎭∴+++-++= 令105()1715f t t t t =+-+0(1.03)(1.035)(1.03)1.031.0351.03f ff i --=--(1.032)0.003f =- 1000 1000 1000 011718…23.解：()4660.0411 1.04i a i---++，40.04114i ⎛⎫+=+ ⎪⎝⎭24.解：4321.05 1.1025 1.05 1.1025 1.05 1.205 1.0511000R R R R ⨯+++= 得2212.147R =25.解：()()()1211111nn nn n a i n i i i a iii----∂-++-++=∴=∂.1020.116.8670.10.002n n nn i a a a i==∂-∴==∂ 其中n 通过公式（2-76）得到29.解: 7777111v a v i a iK i-=∴=-=-类似地，111811181111via iL via iM =-=-=-=-，71118(1)(1)1v v vi K i L i M=∴--=- 从而L K Mi K L+-=31.解：(2)(12)(2)(12)(12)1112nnnnn v v i i a a a idi--⎛⎫===+ ⎪⎝⎭ ，32.解：()500lim 110000tn in a i -→∞+= 半半()()122111111i i id d-+==+⇒+=--半半，()1211i d -=--半()1120ti i -+∴=半半36.解：()()()2020201195.36n na nv a i n i Ia ii--+-+=∴=37.解：该永续年金现值为1i1 1 0123 … …R 1.1025R 1.205R 014231该永续年金现值为：()()24111(2)i i i i--++++=+∴所求年金现值为：113(2)(2)i i i i i i++=++ 39.解：()01nt kt v dt f g h -=--⎰11lim limnn n n vf a δδ→∞→∞-===1(1)ng k n v δ=-⋅40.解：011()1tdrr a t et +⎰==+11()ln(1)1n n n a a t dt dt n t-===++⎰⎰42.解：后五年等比()()()551051111000105011k i s s i i i k+⎛⎫- ⎪+⎝⎭-+⨯++-43.解：4684468111vv vva a a iiiiii i v d-+-+-+=+++=- 45.解：2300.015251.0215K s K a -=+46.解：1010120180180300300 1.031.03i iiiia a a a a --++=月月新月新月月11x 110000047.解：011()1tdrr a t e t +⎰==+1414212111(0)(1)()(1)84.51v t a t dt t dt t-=-=-=+⎰⎰48.解：11tnt n vva a δδ--==，1 2 0 5 67 … …10 9 8 3…4 111 0123... (6)5 41 2 3()01111144010%tnn n t nvv a dt dt n n a δδδδ⎛⎫--==-=-=⨯= ⎪⎝⎭⎰⎰49.解：1）()11t nnttt t a tv Ia i==-=∑∑第三章收益率2.解：234000 1.120000.93382⨯-⨯=3.解：237000100040005500(0)v v v v v --++= 110.090.11.091.1i v i v ====时，；时，令(0)0v v i =⇒及7.解：81.516.510(1)11.995%x x i i ⋅⋅=+⇒= 8.解：11100.250.751(1)1(1)1(1)100000150002000011000kkkdtdtdtt k t k t k eee+-+-+-⎰⎰⎰+-=解得：0.14117k =10.解：560.0450.04610001.04550.04s i i s -⎛⎫++⎪⎝⎭13.解：50000068000060000500055000A B I ===-=，， 29.78%I i A B I=≈+-14.解：()11144320000112%5000180001112%196104B i -⎛⎫⎡⎤⎛⎫=⨯++⨯+-⨯+-⨯= ⎪ ⎪⎢⎥⎝⎭⎣⎦⎝⎭15.解：1212121kt dtt ek ++⎰=⇒= 书后答案是1k =，不知我对它对。

第一章 利息的基本概念1.)()0()(t a A t A =2.11)0(=∴=b a 180)5(100=a ，508)8()5(300=a a 3~5.用公式(1-4b) 7~9.用公式（1-5）、（1-6）11.第三个月单利利息1%，复利利息23%)11(%)11(+-+ 12.1000)1)(1)(1(321=+++i i i k14.n n n n i i i i --+⋅+>+++)1()1(2)1()1(16.用p.6公式17.用P.7最后两个公式 19.用公式（1-26）20.(1)用公式（1-20）; (2)用公式（1-23） 22. 用公式（1-29）23.(1) 用公式（1-32）;(2) 用公式（1-34）及题6（2）结论 24. 用公式（1-32）25.44216%1(1)(110%)118%45%12i ⎛⎫+=++ ⎪-⎝⎭⎛⎫- ⎪⎝⎭ 26.对于c)及d)，δn e n a =)(，1111)1(-=-=+==∴v di e a δ，∴c)中，v ln -=δ， d)中，δ--=ed 128.⎰=tdxx e t a 0)()(δ29.4411⎪⎭⎫ ⎝⎛+=+j i ；he j =+131.（1）902天39.t etA dr +=⎰10δ )1ln(0t dr tA +=⎰∴δ，两边同时求导，tt A +=11)(δ，)(t B δ类似 46.10009200.081000d -==，920)2108.01(288)08.01(=⨯-+-x第二章 年金4.解：12010.087110.0870.08712160001000110.087121212A --⎛⎫-+ ⎪⎛⎫⎛⎫⎝⎭=+⋅++ ⎪⎪⎝⎭⎝⎭5.解：()()()()22211111111(*)nnn nn i a x i xiii xi a y ii----+==⇒+=--+--===将1di d=-代入（*）7.解：()51218100010.0839169.84s -+=8.解：100.1100.15000s Ra = 9.解：100.1100.155000s Ra = 14.解：永续年金每年支付R112n n Ra R a i ⎛⎫=- ⎪⎝⎭17.解：0.0081500100000m a = 解得95.6m ≈ 即正常还款次数为95次 95950.0081500(10.008)100000a f -++= 解得965.74f =19.解：()()()(2)(2)(2)1055222105100020001700011171150i i i s s s i i i ⎛⎫-+= ⎪ ⎪⎝⎭∴+++-++= 令105()1715f t t t t =+-+0(1.03)(1.035)(1.03)1.03 1.035 1.03f f f i --=-- (1.032)0.003186f =-1000 1000 1000 011718…23.解：()4660.0411 1.04i a i---++，40.04114i ⎛⎫+=+ ⎪⎝⎭24.解：修改于2009/11/4分解成两个数列：第一个数列：时刻0，2，4，…，20共付款11次，各期付款额成等比数列。

《利息理论》习题详解第一章 利息的基本概念1、解：（1）)()0()(t a A t A =又()25A t t =(0)5()2()1(0)55A A t a t t A ∴===++ （2）3(3)(2)11(92 2.318I A A =-===（3）4(4)(3)0.178(3)A A i A -=== 2、解：202()(0)(1)1(1-6)180=100(a 5+1)4a=125a t at ba b i =+∴==+=∴∴用公式(8)300(83)386.4A a ∴=-=12、解：设原始金额为(0)A 有(0)(10.1)(10.08)(10.06)1000A +++=解得(0)794.1A =15、解：3400300(1)i =+ 0.1006i ∴= 又11110.9085911 1.1006i v d i i =-=-===++ 246500()1034.7v v v ∴++=19、解：（1）430.06(3)10000(1)119564A ⨯=+= （2）1()1441(1)4d i -+=-1()14334(3)10000(1)10000(1)122854d A i -⨯∴=+=-=20、解：（1）()1(1)m m i i m +=+， 1()(1)1m m i i m ∴+=+11(6)(5)651(1),1(1)65i i i i ∴+=++=+ (5)11()530(6)161(1)5(1)11(1)6m i i i i i m i ++∴==+=+++所以m=30 （2）1()()1(1),1(1)m m m m d d d d m m-=-∴-=-，所以和（1）有类似的解答m=30。

24、解：0()t t dt a t e δ⎰=，1212000.01(12)100001000020544.332t dt tdt A e e δ⎰⎰∴===25、解：设常数实际利率为i 有41420.060.05(1)(10.1)(10.08)(1)(1)42i --+=+-+-解得 0.0749i = 33、解：27.722e δ= ln 227.72δ∴==0.025 又2(12)7.04n δ+=21.057.0449.5616n ∴== 49.56161.05log 80n ∴== 36、解：设第十年末未付金额为x ，有40.12(1)10.125514i =+-= 11(1) 1.12551v i --∴=+= 又51015101000400800400 1.12551800 1.12551 1.12551v v xv x ---=++=⨯+⨯+⨯解得x=657.8375 42、解：338104001100(3)0.8166865t dt ae e -⎰=== 44、解：0.510.3(10.25)v -=-，解得v=0.87111110.14796i v ∴=-= 51、解：46400(1)6404j ⨯+=，解得j=0.079106第二章 年金 4解：实际月利率为0.087/120.00725i ==，16000010001200.0072580037.04A a =-=7解：X 取得的存款为：11251000180.08(10.08)39169.84s -⨯⨯+= 8解：50001010s Ra =，500015.93742 6.14457R ∴⨯=⨯，解得R=12968.719解：5000100.1100.15s Ra =，解得R=15187.4814解：10.5an an i =-，111.5 1.5n v an i i -∴==，解得13n v = 17解：月利率为0.096/12=0.008，15000.008100000an ∴=，0.00866.66667an ∴=，解得n=95.6取整数n=95，又951500950.008(10.008)100000a f -++=，解得f=965.7528解：设3年的实际利率为j ，有31(1)j i +=+，又112991j =，3912301(1)129129i ∴+=+=，解得i=0.195。