SPSS多元线性回归分析报告报告材料实例操作步骤

在多重共线性。 第4-10列：各特征根解释各解释变量的方差比。 从方差比看，第5个特征根解释投入普通高校人数96%；发表科技论文数
49%；可以认为：这些变量存在多重共线性。需要建立回归方程。
2.重建回归方程
模型
输入／移去的变量b
输入的变量
移去的变量
方法
1
教职工总数(万
人), 专利申请授
权数(件), 研究
b. 预测变量: (常量), 教职工总数(万人), 专利申请授权数(件), 研究与试验发展机构数(个), 普通高校数(所), 发表 科技论文数量(篇)。 c. 预测变量: (常量), 教职工总数(万人), 专利申请授权数(件), 研究与试验发展机构数(个), 发表科技论文数量(篇)。 d. 预测变量: (常量), 教职工总数(万人), 专利申请授权数(件), 发表科技论文数量(篇)。 e. 预测变量: (常量), 教职工总数(万人), 发表科技论文数量(篇)。 f. 因变量: 毕业生数(万人)
. 输入
a. 已输入所有请求的变量。
模型汇总
模型
R
R 方 调整 R 方 标准 估计的误差
1
.999a
.998
.997
a. 预测变量: (常量), 教职工总数(万人), 专利申请授权数(件), 研究与试验发展机构数(个), 普通高校数(所), 发表科技论文数 量(篇), 在校学生数(万人)。
注解：模型的拟合优度检验：
第五列：回归方程的估计标准误差＝
Anovab
模型
平方和
df
均方
F
Sig.
1
回归
6
.000a
残差
7
总计
13
a. 预测变量: (常量), 教职工总数(万人), 专利申请授权数(件), 研究与试验发展机构 数(个), 普通高校数(所), 发表科技论文数量(篇), 在校学生数(万人)。 b. 因变量: 毕业生数(万人)

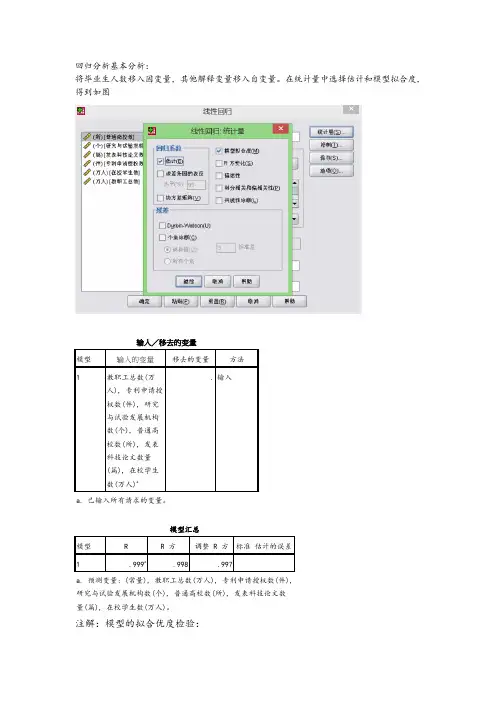
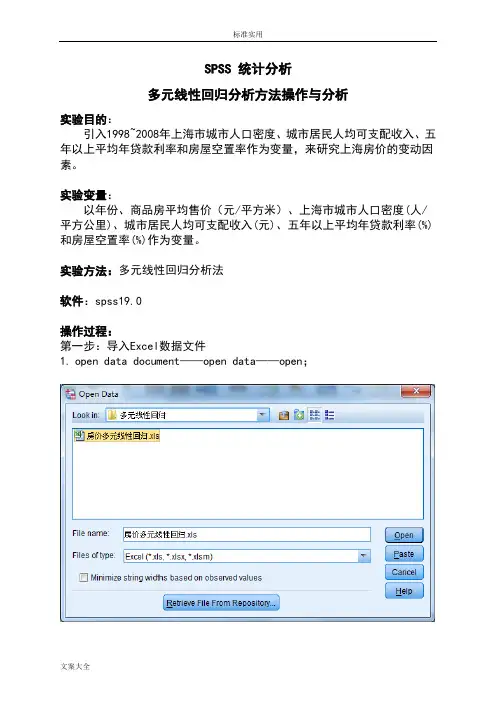
实验八报告一、数据来源Employee data. sav 二、基本结果（1）确定自变量、因变量：）确定自变量、因变量：一般而言，因变量y与各自变量xj(j=1,2,3,…,n)之间的多元线性回归模型：之间的多元线性回归模型：其中：b0是回归常数；b k (k=1,2,3,…,n)是回归参数；e是随机误差。

是随机误差。

根据employee data.sav的数据，其中Y是当前工资salary，X1是起始资金salbegin，X2是工作经验prevexp，X3是工作时间jobtime，X4是工作种类jobcat，X5是受教育年限edcau。

（2）做出因变量与自变量的散点图：）做出因变量与自变量的散点图：从散点图可以看出因变量与各自变量之间存在线性关系。

（3）检验因变量Y是否服从正态分布的模型假定——因变量Y并没有很好地服从正态分布。

地服从正态分布。

的残差图（4）线性回归Y的残差图此标准化残差图表明，此线性回归的标准化残差呈楔形分布而非带状分布，不满足回归模型同方差的假定。

布，不满足回归模型同方差的假定。

当前薪金多元线性回归分析的残差图图当前薪金多元线性回归分析的残差图（5）通过以上检验可以看出，当前薪金并不是好的变量，对当前薪金进行Ln变换（取对数）生成新的随进变量logsale，将logsale作为因变量Y用逐步回归的方法进行回归分析：的方法进行回归分析：1）p-p图：图：较好的服从了正态分布。

发现取对数后，logY较好的服从了正态分布。

2）logY的标准化残差图：的标准化残差图：上图表明因变量Y（logsale）的标准化残差近似呈带状分布，满足模型同方差的假定。

差的假定。

3）逐步回归的判定系数：）逐步回归的判定系数：通过逐步回归，得到方程的判定系数如下表。

R²越接近1，说明回归方程解释了因变量总变异量的绝大部分比例。

本估计的回归方程有一个好的拟合，，可以认为拟合度高。

在模型5中达到0.810，且调整后的R²达到0.808，可以认为拟合度高。

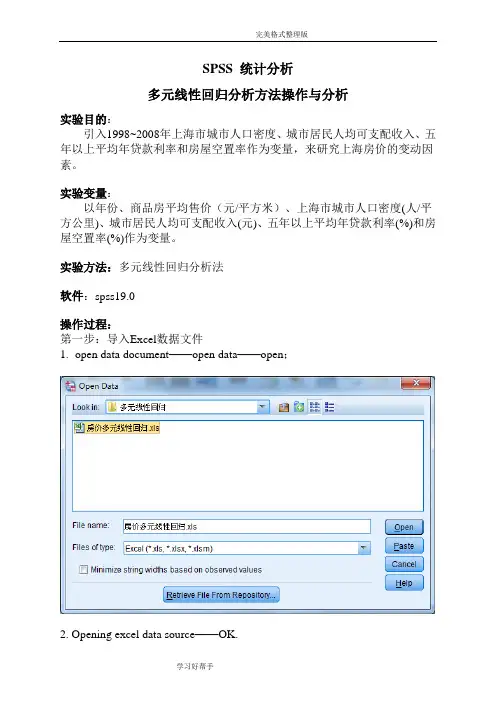
SPSS 统计分析多元线性回归分析方法操作与分析实验目的：引入1998~2008年上海市城市人口密度、城市居民人均可支配收入、五年以上平均年贷款利率和房屋空置率作为变量，来研究上海房价的变动因素。

实验变量：以年份、商品房平均售价（元/平方米）、上海市城市人口密度(人/平方公里)、城市居民人均可支配收入(元)、五年以上平均年贷款利率(%)和房屋空置率(%)作为变量。

实验方法：多元线性回归分析法软件：spss19.0操作过程：第一步：导入Excel数据文件1.open data document——open data——open；2. Opening excel data source——OK.第二步：1.在最上面菜单里面选中Analyze——Regression——Linear ，Dependent（因变量）选择商品房平均售价，Independents（自变量）选择城市人口密度、城市居民人均可支配收入、五年以上平均年贷款利率、房屋空置率；Method 选择Stepwise.进入如下界面：2.点击右侧Statistics，勾选Regression Coefficients（回归系数）选项组中的Estimates；勾选Residuals（残差）选项组中的Durbin-Watson、Casewise diagnostics默认；接着选择Model fit、Collinearity diagnotics；点击Continue.3.点击右侧Plots，选择*ZPRED（标准化预测值）作为纵轴变量，选择DEPENDNT（因变量）作为横轴变量；勾选选项组中的Standardized Residual Plots（标准化残差图）中的Histogram、Normal probability plot；点击Continue.4.点击右侧Save，勾选Predicted Vaniues（预测值）和Residuals（残差）选项组中的Unstandardized；点击Continue.5.点击右侧Options，默认，点击Continue.6.返回主对话框，单击OK.输出结果分析：1.引入/剔除变量表Variables Entered/Removed aModel Variables Entered Variables Removed Method1 城市人口密度(人/平方公里) . Stepwise (Criteria:Probability-of-F-to-enter<= .050,Probability-of-F-to-remove >=.100).2 城市居民人均可支配收入(元) . Stepwise (Criteria:Probability-of-F-to-enter<= .050,Probability-of-F-to-remove >=.100).a. Dependent Variable: 商品房平均售价（元/平方米）该表显示模型最先引入变量城市人口密度(人/平方公里)，第二个引入模型的是变量城市居民人均可支配收入(元)，没有变量被剔除。

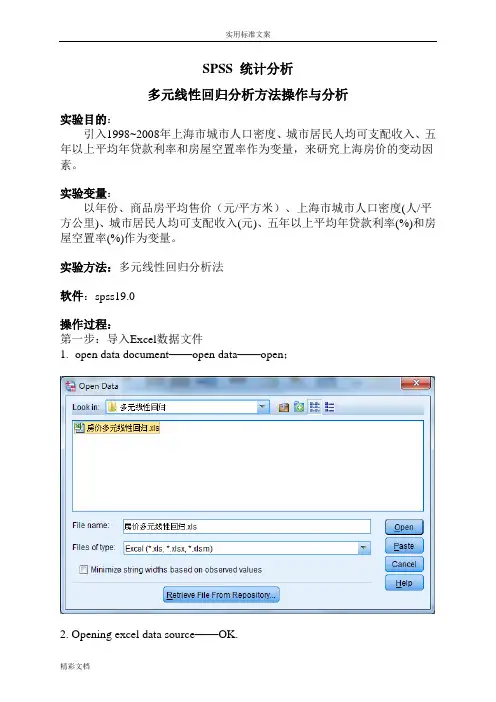
SPSS 统计分析多元线性回归分析方法操作与分析实验目的：引入1998~2008年上海市城市人口密度、城市居民人均可支配收入、五年以上平均年贷款利率和房屋空置率作为变量，来研究上海房价的变动因素。

实验变量：以年份、商品房平均售价（元/平方米）、上海市城市人口密度(人/平方公里)、城市居民人均可支配收入(元)、五年以上平均年贷款利率(%)和房屋空置率(%)作为变量。

实验方法：多元线性回归分析法软件：spss19.0操作过程：第一步：导入Excel数据文件1.open data document——open data——open；2. Opening excel data source——OK.第二步：1.在最上面菜单里面选中Analyze——Regression——Linear ，Dependent（因变量）选择商品房平均售价，Independents（自变量）选择城市人口密度、城市居民人均可支配收入、五年以上平均年贷款利率、房屋空置率；Method 选择Stepwise.进入如下界面：2.点击右侧Statistics，勾选Regression Coefficients（回归系数）选项组中的Estimates；勾选Residuals（残差）选项组中的Durbin-Watson、Casewise diagnostics默认；接着选择Model fit、Collinearity diagnotics；点击Continue.3.点击右侧Plots，选择*ZPRED（标准化预测值）作为纵轴变量，选择DEPENDNT（因变量）作为横轴变量；勾选选项组中的Standardized Residual Plots（标准化残差图）中的Histogram、Normal probability plot；点击Continue.4.点击右侧Save，勾选Predicted Vaniues（预测值）和Residuals（残差）选项组中的Unstandardized；点击Continue.5.点击右侧Options，默认，点击Continue.6.返回主对话框，单击OK.输出结果分析：1.引入/剔除变量表Variables Entered/Removed aModel Variables Entered Variables Removed Method1 城市人口密度(人/平方公里) . Stepwise (Criteria:Probability-of-F-to-enter<= .050,Probability-of-F-to-remove >=.100).2 城市居民人均可支配收入(元) . Stepwise (Criteria:Probability-of-F-to-enter<= .050,Probability-of-F-to-remove >=.100).a. Dependent Variable: 商品房平均售价（元/平方米）该表显示模型最先引入变量城市人口密度(人/平方公里)，第二个引入模型的是变量城市居民人均可支配收入(元)，没有变量被剔除。

SPSS多元线性回归分析实例操作步骤多元线性回归是一种常用的统计分析方法，用于探究多个自变量对因变量的影响程度。

SPSS（Statistical Package for the Social Sciences）是一款常用的统计软件，可以进行多元线性回归分析，并提供了简便易用的操作界面。

本文将介绍SPSS中进行多元线性回归分析的实例操作步骤，帮助您快速掌握该分析方法的使用。

步骤一：准备数据在进行多元线性回归分析之前，首先需要准备好相关的数据。

数据应包含一个或多个自变量和一个因变量，以便进行回归分析。

数据可以来自实验、调查或其他来源，但应确保数据的质量和可靠性。

步骤二：导入数据在SPSS软件中，打开或创建一个新的数据集，然后将准备好的数据导入到数据集中。

可以通过导入Excel、CSV等格式的文件或手动输入数据的方式进行数据导入。

确保数据被正确地导入到SPSS中，并正确地显示在数据集的各个变量列中。

步骤三：进行多元线性回归分析在SPSS软件中，通过依次点击"分析"-"回归"-"线性"，打开线性回归分析对话框。

在对话框中，将因变量和自变量移入相应的输入框中。

可以使用鼠标拖拽或双击变量名称来快速进行变量的移动。

步骤四：设置分析选项在线性回归分析对话框中，可以设置一些分析选项，以满足具体的分析需求。

例如，可以选择是否计算标准化回归权重、残差和预测值，并选择是否进行方差分析和共线性统计检验等。

根据需要，适当调整这些选项。

步骤五：获取多元线性回归分析结果点击对话框中的"确定"按钮后，SPSS将自动进行多元线性回归分析，并生成相应的分析结果。

结果包括回归系数、显著性检验、残差统计和模型拟合度等信息，这些信息可以帮助我们理解自变量对因变量的贡献情况和模型的拟合程度。

步骤六：解读多元线性回归分析结果在获取多元线性回归分析结果之后，需要对结果进行解读，以得出准确的结论。

1，确定因变量与自变量，初步设定回归方程。
这里我们以总成绩作为因变量Y，平时成绩和期中成绩分别作为自变量X1，X2，建立的多元回归模型为：
Байду номын сангаас2，估计参数，建立回归预测模型
利用SPSS可得一下结果：
Variables Entered/Removedb
Model
Variables Entered
Variables Removed
1183.800
19
a. Predictors: (Constant),期中成绩,平时成绩
b. Dependent Variable:总成绩
注释：从表中可得拟合方程的F统计量值为7.586，相应的P值为0.000说明，拟合方程是显著的。是具有统计意义的。
Coefficientsa
Model
Unstandardized Coefficients
Method
1
期中成绩,平时成绩a
.
Enter
a. All requested variables entered.
b. Dependent Variable:总成绩
注释：根据这个表的结果我们可以初步的知道，经过检验自变量X1，X2是可以加入到准备估计的回归方程中作为变量的。
Model Summaryb
Standardized Coefficients
t
Sig.
95% Confidence Interval for B
Correlations
Collinearity Statistics
B
Std. Error
Beta
Lower Bound
Upper Bound
Zero-order

SPSS 统计分析多元线性回归分析方法操作与分析实验目的：引入1998~2008年上海市城市人口密度、城市居民人均可支配收入、五年以上平均年贷款利率和房屋空置率作为变量，来研究上海房价的变动因素。

实验变量：以年份、商品房平均售价（元/平方米）、上海市城市人口密度(人/平方公里)、城市居民人均可支配收入(元)、五年以上平均年贷款利率(%)和房屋空置率(%)作为变量。

实验方法：多元线性回归分析法软件：spss19.0操作过程：第一步：导入Excel数据文件1.open data document——open data——open；2. Opening excel data source——OK.第二步：1.在最上面菜单里面选中Analyze——Regression——Linear ，Dependent（因变量）选择商品房平均售价，Independents（自变量）选择城市人口密度、城市居民人均可支配收入、五年以上平均年贷款利率、房屋空置率；Method选择Stepwise.进入如下界面：2.点击右侧Statistics，勾选Regression Coefficients（回归系数）选项组中的Estimates；勾选Residuals（残差）选项组中的Durbin-Watson、Casewise diagnostics默认；接着选择Model fit、Collinearity diagnotics；点击Continue.3.点击右侧Plots，选择*ZPRED（标准化预测值）作为纵轴变量，选择DEPENDNT（因变量）作为横轴变量；勾选选项组中的Standardized Residual Plots（标准化残差图）中的Histogram、Normal probability plot；点击Continue.4.点击右侧Save，勾选Predicted Vaniues（预测值）和Residuals（残差）选项组中的Unstandardized；点击Continue.5.点击右侧Options，默认，点击Continue.6.返回主对话框，单击OK.输出结果分析： 1.引入/剔除变量表该表显示模型最先引入变量城市人口密度 (人/平方公里)，第二个引入模型的是变量城市居民人均可支配收入(元)，没有变量被剔除。

线性回归分析的SPSS操作本节内容主要介绍如何确定并建立线性回归方程。

包括只有一个自变量的一元线性回归和和含有多个自变量的多元线性回归。

为了确保所建立的回归方程符合线性标准，在进行回归分析之前，我们往往需要对因变量与自变量进行线性检验。

也就是类似于相关分析一章中讲过的借助于散点图对变量间的关系进行粗略的线性检验，这里不再重复。

另外，通过散点图还可以发现数据中的奇异值，对散点图中表示的可能的奇异值需要认真检查这一数据的合理性。

一、一元线性回归分析1．数据以本章第三节例3的数据为例，简单介绍利用SPSS如何进行一元线性回归分析。

数据编辑窗口显示数据输入格式如下图7-8（文件7-6-1.sav）：图7-8：回归分析数据输入2．用SPSS进行回归分析，实例操作如下：2.1.回归方程的建立与检验（1）操作①单击主菜单Analyze / Regression / Linear…，进入设置对话框如图7-9所示。

从左边变量表列中把因变量y选入到因变量（Dependent）框中，把自变量x选入到自变量（Independent）框中。

在方法即Method一项上请注意保持系统默认的选项Enter，选择该项表示要求系统在建立回归方程时把所选中的全部自变量都保留在方程中。

所以该方法可命名为强制进入法（在多元回归分析中再具体介绍这一选项的应用）。

具体如下图所示：图7-9 线性回归分析主对话框②请单击Statistics…按钮，可以选择需要输出的一些统计量。

如Regression Coefficients(回归系数)中的Estimates，可以输出回归系数及相关统计量，包括回归系数B、标准误、标准化回归系数BETA、T值及显著性水平等。

Model fit项可输出相关系数R，测定系数R2，调整系数、估计标准误及方差分析表。

上述两项为默认选项，请注意保持选中。

设置如图7-10所示。

设置完成后点击Continue返回主对话框。

图7-10：线性回归分析的Statistics选项图7-11：线性回归分析的Options选项回归方程建立后，除了需要对方程的显著性进行检验外，还需要检验所建立的方程是否违反回归分析的假定，为此需进行多项残差分析。

计量经济学实验报告一.实验目的：1、学习和掌握用SPSS做变量间的相关系数矩阵；2、掌握运用SPSS做多元线性回归的估计；3、用残差分析检验是否存在异常值和强影响值4、看懂SPSS估计的多元线性回归方程结果；5、掌握逐步回归操作；6、掌握如何估计标准化回归方程7、根据输出结果书写方程、进行模型检验、解释系数意义和预测；二．实验步骤：1、根据所研究的问题提出因变量和自变量，搜集数据。

2、绘制散点图和样本相关阵，观察自变量和因变量间的大致关系。

3、如果为线性关系，则建立多元线性回归方程并估计方程。

4、运用残差分析检验是否存在异常值点和强影响值点。

5、通过t检验进行逐步回归。

6、根据spss输出结果写出方程，对方程进行检验（拟合优度检验、F检验和t检验）。

7、输出标准化回归结果，写出标准化回归方程。

8、如果通过检验，解释方程并应用（预测）。

三.实验要求：研究货运总量y与工业总产值x1,农业总产值x2，居民非商品支出x3,之间的关系。

详细数据见表：（1）计算出y,x1,x2,x3的相关系数矩阵。

（2）求y关于x1,x2,x3的三元线性回归方程（3）做残差分析看是否存在异常值。

（4）对所求方程拟合优度检验。

（5）对回归方程进行显著性检验。

（6）对每一个回归系数做显著性检验。

（7）如果有的回归系数没有通过显著性检验，将其剔除，重新建立回归方程，在做方程的显著性检验和回归系数的显著性检验。

（8）求标准化回归方程。

（9）求当x1=75,x2=42,x3=3.1时y。

并给出置性水平为99%的近似预测区间。

（10）结合回归方程对问题进行一些基本分析。

四.绘制散点图或样本相关阵相关性货运总量工业总产值农业总产值 居民非商品支出货运总量Pearson 相关性1.556 .731*.724*显著性（双侧）.095.016 .018 N10 10 10 10 工业总产值Pearson 相关性.556 1.155 .444 显著性（双侧） .095 .650.171 N10 11 11 11 农业总产值Pearson 相关性.731*.155 1.562 显著性（双侧） .016 .650 .072N10 11 11 11 居民非商品支出 Pearson 相关性.724* .444 .562 1显著性（双侧）.018 .171 .072 N10111111*. 在 0.05 水平（双侧）上显著相关。

3 利用SPSS10.0进行多元线性回归分析【例】同上例。

第一步，录入或调入数据。

完全类同于一元线性回归分析，不赘述（图1）。

图1 录入或调入的数据第二步，回归操作。

多元线性分析的详细步骤的基本进程与一元线性回归分析相似，稍有不同。

⑴打开线性回归对话框。

即沿着主菜单的Analyse→Regression→Linear…路径打开Linear Regression选项框（图2）。

⑵将“运输业产值”置于因变量（Dependent）的空白栏，将“工业产值”、“农业产值”和“固定资产投资”置于自变量（Independent(s)）的空白栏（图3）。

⑶在统计（Statistics）选项框中，除了选择“Durbin-Watson”外，还应该选择“Part and partial correlations”(部分与偏相关，给出零阶相关系数、偏相关系数和部分相关系数)以及“Collinearity diagnostics（共线性诊断）”。

然后继续。

⑷在Plot选项框中，除了可以选择“Histogram”（直方图）和“Normal probability plot”(正态概率图)外，还可选择“Produce all partial plot(s)”（给出所有自变量与因变量的残差散点图）。

然后继续。

⑸修改显著性水平或置信度，可以进入Save对话框，改变Prediction intervals的Confidence intervals（置信区间）；修改逐步回归的F临界值，可以进入Option选项框，改变Stepping method criteria中的F值或者F概率。

如果对此缺乏足够的知识，可由系统默认。

然后继续。

⑹在线性回归对话框中，Method一栏由系统默认为enter（让所有的自变量都参入回归）。

完成上述设置以后，点击“OK”确定（图3），立即可以得到回归结果（Output）。

图2 线性回归对话框图3 设置变量图4 统计选项框的设置图5 图形对话框的设置在Variables Entered/Removed （变量取舍即变量的输入或剔除）表中，给出的采用的变量、剔除的变量和回归方法（enter ）,此表中没有剔除变量。

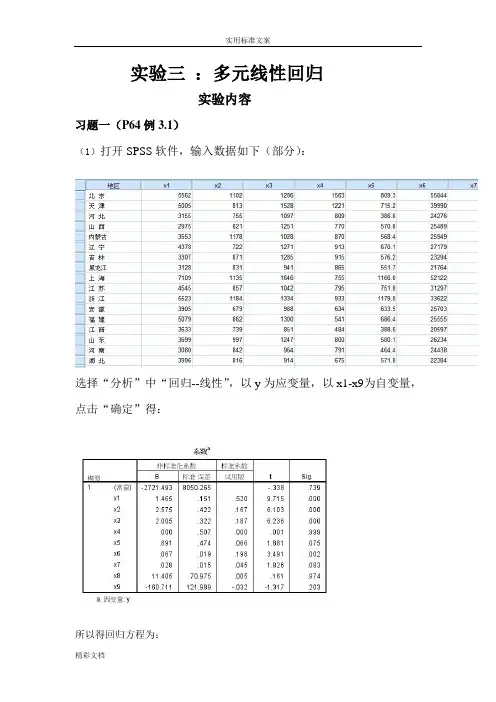
实验三：多元线性回归实验内容习题一（P64例3.1）（1）打开SPSS软件，输入数据如下（部分）：选择“分析”中“回归--线性”，以y为应变量，以x1-x9为自变量，点击“确定”得：所以得回归方程为：y=1.465x1+2.575x2+2.005x3+0.891x5+0.67x6+0.28x7+11.405x8-160.711x9-2721.493从回国方程可以看到，x1-x9对居民的消费支出起正影响，x9对居民的消费性支出起负影响。

（2）F检验。

用SPSS软件计算出的方差分析图如下：从输出结果可知，Sig即显著性P值，由P值为0.000可知，此回归方程高度显著。

t检验。

通过定性分析，先剔除x4，用y与其他8个变量做回归分析，计算结果如下图：剔除x4之后，仍然有不显著的自变量，此时最大的P值为p8=0.827，因此进一步剔除x8，用y与其余6个变量作回归，回归系数表如下图：T检验中，依次剔除P值最大的自变量，直到最后所有的自变量在显著性水平为0.05时都显著。

习题二（P93.例4.3）（1）打开SPSS软件，输入数据如下图：（2）建立y对x的普通最小二乘回归，决定系数R2=0.912，回归标准差为247.62.方差分析表和回归系数输出表如下：（3）在原始数据中增加一列变量RES_1，即残差值，如图：然后以x（居民收入）为x轴，残差值为y轴画散点图：从残差图看出，误差项具有明显的异方差性，误差随着x的增加而呈现出增加的趋势。

（4）计算等级相关系数。

先计算出残差的绝对值，如图：然后选择分析中的“相关--双变量”，选择x和e为变量，在相关系数一栏里选择Spearman 打钩，点击确定即得到等级相关系数，如下图所示：从上图可知，相关系数为0.686，P值=2.055E-5，即残差绝对值e与自变量x显著相关，存在异方差。

（5）用加权最小二乘法来消除异方差。

选择“分析”中“回归--权重估计”，以x为自变量，y为因变量，对x进行加权估计，得：然后画出加权最小二乘残差图，如下：比较前后两幅残差图，可以得出，加权最小二乘估计的效果好于普通最小二乘估计效果。

SPSS 统计分析多元线性回归分析方法操作与分析实验目的：引入1998~2008年上海市城市人口密度、城市居民人均可支配收入、五年以上平均年贷款利率和房屋空置率作为变量，来研究上海房价的变动因素。

实验变量：以年份、商品房平均售价（元/平方米）、上海市城市人口密度(人/平方公里)、城市居民人均可支配收入(元)、五年以上平均年贷款利率(%)和房屋空置率(%)作为变量。

实验方法：多元线性回归分析法软件：spss19.0操作过程：第一步：导入Excel数据文件1.open data document——open data——open；2. Opening excel data source——OK.第二步：1.在最上面菜单里面选中Analyze——Regression——Linear ，Dependent（因变量）选择商品房平均售价，Independents（自变量）选择城市人口密度、城市居民人均可支配收入、五年以上平均年贷款利率、房屋空置率；Method选择Stepwise.进入如下界面：2.点击右侧Statistics，勾选Regression Coefficients（回归系数）选项组中的Estimates；勾选Residuals（残差）选项组中的Durbin-Watson、Casewise diagnostics默认；接着选择Model fit、Collinearity diagnotics；点击Continue.3.点击右侧Plots，选择*ZPRED（标准化预测值）作为纵轴变量，选择DEPENDNT（因变量）作为横轴变量；勾选选项组中的Standardized Residual Plots（标准化残差图）中的Histogram、Normal probability plot；点击Continue.4.点击右侧Save，勾选Predicted Vaniues（预测值）和Residuals（残差）选项组中的Unstandardized；点击Continue.5.点击右侧Options，默认，点击Continue.6.返回主对话框，单击OK.输出结果分析： 1.引入/剔除变量表该表显示模型最先引入变量城市人口密度 (人/平方公里)，第二个引入模型的是变量城市居民人均可支配收入(元)，没有变量被剔除。

SPSS 统计分析多元线性回归分析方法操作与分析实验目的：引入1998~2008年上海市城市人口密度、城市居民人均可支配收入、五年以上平均年贷款利率和房屋空置率作为变量，来研究上海房价的变动因素。

实验变量：以年份、商品房平均售价（元/平方米）、上海市城市人口密度(人/平方公里)、城市居民人均可支配收入(元)、五年以上平均年贷款利率(%)和房屋空置率(%)作为变量。

实验方法：多元线性回归分析法软件：操作过程：第一步：导入Excel数据文件1.open data document——open data——open；2. Opening excel data source——OK.第二步：1.在最上面菜单里面选中Analyze——Regression——Linear ，Dependent（因变量）选择商品房平均售价，Independents（自变量）选择城市人口密度、城市居民人均可支配收入、五年以上平均年贷款利率、房屋空置率；Method选择Stepwise.进入如下界面：2.点击右侧Statistics，勾选Regression Coefficients（回归系数）选项组中的Estimates；勾选Residuals（残差）选项组中的Durbin-Watson、Casewise diagnostics默认；接着选择Model fit、Collinearity diagnotics；点击Continue.3.点击右侧Plots，选择*ZPRED（标准化预测值）作为纵轴变量，选择DEPENDNT（因变量）作为横轴变量；勾选选项组中的Standardized Residual Plots（标准化残差图）中的Histogram、Normal probability plot；点击Continue.4.点击右侧Save，勾选Predicted Vaniues（预测值）和Residuals（残差）选项组中的Unstandardized；点击Continue.5.点击右侧Options，默认，点击Continue.6.返回主对话框，单击OK.输出结果分析： 1.引入/剔除变量表该表显示模型最先引入变量城市人口密度 (人/平方公里)，第二个引Variables Entered/Removed aModel Variables Entered Variables RemovedMethod1城市人口密度 (人/平方公里). Stepwise (Criteria: Probability-of-F-to-enter <= .050,Probability-of-F-to-remove >= .100).2城市居民人均可支配收入(元). Stepwise (Criteria: Probability-of-F-to-enter <= .050,Probability-of-F-to-remove >= .100).a. Dependent Variable: 商品房平均售价（元/平方米）入模型的是变量城市居民人均可支配收入(元)，没有变量被剔除。

SPSS多元线性回归分析报告实例操作步骤步骤1：导入数据首先，打开SPSS软件，并导入准备进行多元线性回归分析的数据集。

在菜单栏中选择"File"，然后选择"Open"，在弹出的窗口中选择数据集的位置并点击"Open"按钮。

步骤2：选择变量在SPSS的数据视图中，选择需要用于分析的相关自变量和因变量。

选中的变量将会显示在变量视图中。

确保选择的变量是数值型的，因为多元线性回归只适用于数值型变量。

步骤3：进行多元线性回归分析在菜单栏中选择"Analyze"，然后选择"Regression"，再选择"Linear"。

这将打开多元线性回归的对话框。

将因变量移动到"Dependent"框中，将自变量移动到"Independent(s)"框中，并点击"OK"按钮。

步骤4：检查多元线性回归的假设在多元线性回归的结果中，需要检查多元线性回归的基本假设。

这些假设包括线性关系、多重共线性、正态分布、独立性和等方差性。

可以通过多元线性回归的结果来进行检查。

步骤5：解读多元线性回归结果多元线性回归的结果会显示在输出窗口的回归系数表中。

可以检查各个自变量的回归系数、标准误差、显著性水平和置信区间。

同时，还可以检查回归模型的显著性和解释力。

步骤6：完成多元线性回归分析报告根据多元线性回归的结果，可以编写一份完整的多元线性回归分析报告。

报告应包括简要介绍、研究问题、分析方法、回归模型的假设、回归结果的解释以及进一步分析的建议等。

下面是一个多元线性回归分析报告的示例：标题：多元线性回归分析报告介绍：本报告基于一份数据集，旨在探究x1、x2和x3对y的影响。

通过多元线性回归分析，我们可以确定各个自变量对因变量的贡献程度，并检验模型的显著性和准确性。

研究问题：本研究旨在探究x1、x2和x3对y的影响。

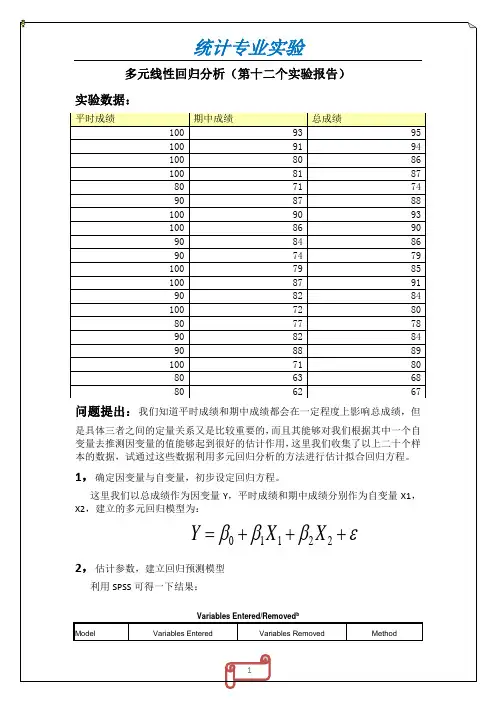
研究期末成绩受哪些因素影响？其影响程度的情况?班级半期成绩 期末成绩 每周学习时间 入学等级 教师等级1 85 87 42 2 1 1 98 96 45 1 1 1 74 80 35 2 1 1 87 90 40 2 1 1 86 88 38 1 2 1 75 70 353 2 1 65 67 28 3 2 1 78 72 30 2 2 1 64 70 30 3 2 1 82 75 34 1 2 1 89 86 38 1 2 2 73 77 38 2 3 2 72 68 32 2 3 2 60 65 20 3 3 2 66 61 30 3 3 2 89 93 39 2 1 2 88 88 43 1 1 2 82 80 41 1 3 2 80 85 39 2 3 2 83 85 45 2 3 2 77 80 40 3 3 297 96 50 1 1初步设定回归方程：0123y p i t ββββε=++++Descriptive StatisticsMean Std. DeviationN期末成绩 79.95 10.330 22 班级 1.50 .512 22 每周学习时间 36.91 6.768 22 半期成绩 79.55 10.294 22 入学等级 1.95 .785 22 教师等级2.05.84422表中为各因素的均值，标准差，和样本量。

表中为各因素的相关系数和P值，从表中可看出班级的相关性最低Variables Entered/Removed bModel VariablesEnteredVariablesRemoved Method1 教师等级, 入学等级, 班级, 每周学习时间, 半期成绩a . Enter采用向后剔除法，即每次剔除一个最不符合进入模型判断依据的变量，直到回归方程中不再含有不符合判断依据的自变量为止。

a. Predictors: (Constant), 教师等级, 入学等级, 班级,每周学习时间, 半期成绩b. Predictors: (Constant), 教师等级, 班级, 每周学习时间, 半期成绩c. Predictors: (Constant), 教师等级, 每周学习时间, 半期成绩d. Predictors: (Constant), 每周学习时间,半期成绩e. Predictors: (Constant), 半期成绩f. Dependent Variable: 期末成绩首先剔除了入学等级，然后剔除了班级，再次剔除了教师等级，再后剔除了每周学习时间，最后剔除半期成绩，剩下了期末成绩，从剔除顺序可知各因素对期末成绩的影响程度，入学等级最低，半期成绩最高。

SPSS多元线性回归分析实例操作步骤在数据分析领域，多元线性回归分析是一种非常实用且强大的工具，它可以帮助我们探究多个自变量与一个因变量之间的线性关系。

下面，我将为您详细介绍使用 SPSS 进行多元线性回归分析的实例操作步骤。

首先，打开 SPSS 软件，我们需要准备好数据。

假设我们有一组关于房屋价格的数据集，其中包含房屋面积、房间数量、地理位置等自变量，以及房屋的销售价格作为因变量。

在 SPSS 中，通过“文件”菜单中的“打开”选项，找到并导入我们的数据文件。

确保数据的格式正确，并且变量的名称和类型都符合我们的预期。

接下来，选择“分析”菜单中的“回归”，然后点击“线性”选项，这就开启了多元线性回归分析的设置窗口。

在“线性回归”窗口中，将我们的因变量（房屋销售价格）放入“因变量”框中，将自变量（房屋面积、房间数量、地理位置等）放入“自变量”框中。

然后，我们可以点击“统计”按钮，在弹出的“线性回归：统计”窗口中，根据我们的需求选择合适的统计量。

通常，我们会勾选“估计”“置信区间”“模型拟合度”等选项，以获取回归系数的估计值、置信区间以及模型的拟合优度等信息。

接着，点击“图”按钮，在“线性回归：图”窗口中，我们可以选择绘制一些有助于分析的图形，比如“标准化残差图”，用于检查残差的正态性；“残差与预测值”图，用于观察残差的分布是否均匀。

再点击“保存”按钮，在这里我们可以选择保存一些额外的变量，比如预测值、残差等，以便后续的进一步分析。

设置完成后，点击“确定”按钮，SPSS 就会开始进行多元线性回归分析，并输出相应的结果。

结果中首先会给出模型的汇总信息，包括 R 方（决定系数）、调整后的 R 方等。

R 方表示模型对因变量的解释程度，越接近 1 说明模型的拟合效果越好。

调整后的 R 方则考虑了自变量的个数，对模型的拟合优度进行了更合理的修正。

接着是方差分析表，用于检验整个回归模型是否显著。

如果 F 值对应的显著性水平小于设定的阈值（通常为 005），则说明回归模型是显著的，即自变量整体上对因变量有显著的影响。

SPSS多元线性回归分析实例操作步骤SPSS（Statistical Package for the Social Sciences）是一种统计分析软件，广泛应用于社会科学研究领域。

其中，多元线性回归分析是SPSS中常用的一种统计方法，用于探讨多个自变量与一个因变量之间的关系。

本文将演示SPSS中进行多元线性回归分析的操作步骤，帮助读者了解和掌握该方法。

一、数据准备在进行多元线性回归分析之前，首先需要准备好数据。

数据应包含一个或多个因变量和多个自变量，以及相应的观测值。

这些数据可以通过调查问卷、实验设计、观察等方式获得。

确保数据的准确性和完整性对于获得可靠的分析结果至关重要。

二、打开SPSS软件并导入数据1. 启动SPSS软件，点击菜单栏中的“文件（File）”选项；2. 在下拉菜单中选择“打开（Open）”选项；3. 导航到保存数据的文件位置，并选择要导入的数据文件；4. 确保所选的文件类型与数据文件的格式相匹配，点击“打开”按钮；5. 数据文件将被导入到SPSS软件中，显示在数据编辑器窗口中。

三、创建多元线性回归模型1. 点击菜单栏中的“分析（Analyse）”选项；2. 在下拉菜单中选择“回归（Regression）”选项；3. 在弹出的子菜单中选择“线性（Linear）”选项；4. 在“因变量”框中，选中要作为因变量的变量；5. 在“自变量”框中，选中要作为自变量的变量；6. 点击“添加（Add）”按钮，将自变量添加到回归模型中；7. 可以通过“移除（Remove）”按钮来删除已添加的自变量；8. 点击“确定（OK）”按钮，创建多元线性回归模型。

四、进行多元线性回归分析1. 多元线性回归模型创建完成后，SPSS将自动进行回归分析并生成结果；2. 回归结果将显示在“回归系数”、“模型总结”和“模型拟合优度”等不同的输出表中；3. “回归系数”表显示各个自变量的回归系数、标准误差、显著性水平等信息；4. “模型总结”表提供模型中方程的相关统计信息，包括R方值、F 统计量等；5. “模型拟合优度”表显示模型的拟合优度指标，如调整后R方、残差平方和等；6. 可以通过菜单栏中的“图形（Graphs）”选项，绘制回归模型的拟合曲线图、残差图等。