横截面数据分类：机器学习方法

计量知识：1、横截面数据、时间序列、面板数据：横截面数据是在同一时间，不同统计单位相同统计指标组成的数据列。

横截面数据是按照统计单位排列的。

因此，横截面数据不要求统计对象及其范围相同，但要求统计的时间相同。

也就是说必须是同一时间截面上的数据。

,Pr i t emium ,1Pr i t emiun -H A Turnover Tutnover A H Size +/H A H SO SO +22/A H σσDummy时间序列数据：在不同时间点上收集到的数据，这类数据反映了某一事物、现象等随时间的变化状态或程度。

面板数据：是截面数据与时间序列数据综合起来的一种数据类型。

其有时间序列和截面两个维度，当这类数据按两个维度排列时，是排在一个平面上，与只有一个维度的数据排在一条线上有着明显的不同，整个表格像是一个面板,所以把panel data 译作“面板数据”。

举例：如：城市名：北京、上海、重庆、天津的GDP 分别为10、11、9、8（单位亿元）。

这就是截面数据，在一个时间点处切开，看各个城市的不同就是截面数据。

如：2000、2001、2002、2003、2004各年的北京市GDP 分别为8、9、10、11、12（单位亿元）。

这就是时间序列，选一个城市，看各个样本时间点的不同就是时间序列。

如：2000、2001、2002、2003、2004各年中国所有直辖市的GDP 分别为： 北京市分别为8、9、10、11、12；上海市分别为9、10、11、12、13；天津市分别为5、6、7、8、9；重庆市分别为7、8、9、10、11（单位亿元）。

这就是面板数据。

*变量合并2、截面数据，多重共线性和异方差都需要考虑，截面数据不需要检测DW 值！你做出来R 方比较小，可能原因是你的回归方程中没有纳入关键变量，建议你采用逐步回归方法，以提高R 方！对于截面数据来说，R 方一般在0.7左右都能接受！相关分析不是必要做的，在模型中加入什么变量进行回归，主要是依据前期的理论分析和研究目的！仅就计量回归而言，这些步骤只是告诉你，自变量与因变量的相关性会影响变量在模型中的显著性，而自变量间的相关则会带来多重共线性！3、线性相关，也叫自相关：可以用来看x和y的相关性，常用来考察各个x 自变量之间是否存在相关关系。

第四部分：横截面数据分析(Cross Data)西安交大管理学院2011‐春2内容•判别分析(Discriminant analysis)•典型相关分析(Canonical correlation analysis ）•对应分析(Correspondence analysis)•联合分析（Conjoint analysis/measurement)•多维尺／标度分析(Multi-Dimentional Scaling)对应分析(Correspondence analysis)•也称关联分析、R ‐Q 型因子分析，是近年新发展起来的一种多元相依变量统计分析技术，通过分析由定性变量构成的交互汇总表来揭示变量间的联系。

可以揭示同一变量的各个类别之间的差异，以及不同变量各个类别之间的对应关系。

主要应用在市场细分、产品定位、地质研究以及计算机工程等领域中。

原因在于，它是一种视觉化的数据分析方法，它能够将几组看不出任何联系的数据，通过视觉上可以接受的定位图展现出来。

•由法国人Benzenci 于1970年提出的，起初在法国和日本最为流行，然后引入到美国。

由法国人Benzenci 于1970年提出的，起初在法国和日本最为流行，然后引入到美国。

•对应分析法是在R 型和Q 型因子分析的基础上发展起来的一种多元统计分析方法。

在因子分析中，如果研究的对象是样品，则需采用Q 型因子分析；如果研究的对象是变量，则需采用R 型因子分析。

但是，这两种分析方法往往是相互对立的，必须分别对样品和变量进行处理。

因此，因子分析对于分析样品的属性和样品之间的内在联系，就比较困难，因为样品的属性是变值，而样品却是固定的。

于是就产生了对应分析法。

它综合了R 型和Q 型因子分析的优点，并将它们统一起来使得由R 型的分析结果很容易得到Q 型的分析结果，这就克服了Q 型分析计算量大的困难；更重要的是可以把变量和样品的载荷反映在相同的公因子轴上，这样就把变量和样品联系起来便于解释和推断。

longitudinal和cross-sectional study-概述说明以及解释1.引言1.1 概述概述：在科学研究领域，研究者为了探究研究对象的某些特定方面或现象，使用各种研究设计方法进行数据收集和分析。

而在这些研究设计中，长期纵向研究（Longitudinal study）和横断面研究（Cross-sectional study）是两种常用的方法。

长期纵向研究即长期追踪同一组人或事物的发展变化情况。

研究者通过多次收集数据，观察研究对象在一段时间内的变化过程和发展趋势。

相反，横断面研究是在同一时间点上对不同个体或不同群体进行数据采集，并进行相应的研究分析。

这两种研究方法都有各自的优势和应用场景。

本文将着重介绍长期纵向研究和横断面研究的定义、特点、设计方法、应用和优势，并进行比较和对比。

同时，我们也将探讨如何选择合适的研究设计，并提供具体的实际应用建议。

通过对长期纵向研究和横断面研究的深入了解，研究者将有助于更好地设计和实施具有科学性和可靠性的研究项目，并为未来的研究方法和技术提供一定的参考和启示。

然而，任何研究方法都存在一定的局限性，因此我们也需要在结论部分对这些局限性进行讨论，并提出未来发展的方向和建议。

1.2文章结构文章结构部分的内容可以参考以下写法：1.2 文章结构本文将分为以下几个部分来探讨长期研究和横断面研究的特点、设计、方法、应用和优势，并进行比较和对比。

首先，在引言中概述了长期研究和横断面研究的背景和重要性，并明确了本文的目的。

接下来，正文部分将分为两个小节，分别介绍长期研究和横断面研究。

在长期研究部分，我们将定义和解释长期研究的特点，并详细介绍其设计和方法。

然后，我们将探讨长期研究在实际应用中的优势和应用领域。

在横断面研究部分，我们将同样定义和解释横断面研究的特点，并介绍其设计和方法。

随后，我们将讨论横断面研究在实际应用中的优势和应用领域。

最后，在比较和对比部分，我们将分析长期研究和横断面研究之间的相似之处和差异之处，并提供选择合适研究设计的建议。

计量经济学横截面数据模型: 理论基础与应用引言计量经济学是经济学领域中的重要分支，旨在通过利用数理统计方法来研究和解释经济现象。

计量经济学的数据来源多种多样，其中之一便是横截面数据。

横截面数据指的是在一定时间点上收集的多个经济单元的相关变量。

本文将重点讨论计量经济学中横截面数据模型的下标表示以及其应用。

横截面数据模型下标: 变量与经济单元在横截面数据模型中，我们通常用不同的下标来表示不同的变量和经济单元。

下面是一些常用的下标及其含义：•i: 表示第i个经济单元，通常是个体或者行为者。

•t: 表示在第t个时间点上采集的数据。

•y it: 表示第i个经济单元在t时间点上的被解释变量，也可以称为因变量或观测变量。

•x it: 表示第i个经济单元在t时间点上的解释变量，也可以称为自变量或控制变量。

在横截面数据模型中，我们通常考虑的是多个经济单元在同一时间点上的数据。

因此，对于变量的下标，我们通常会同时考虑到经济单元和时间点的信息。

横截面数据模型下标的应用在应用计量经济学中的横截面数据模型时，我们需要结合具体问题来选择和使用适当的下标。

下面将介绍一些常见的应用场景。

线性回归模型线性回归模型是计量经济学中应用最广泛的横截面数据模型之一，可以用来研究因变量和解释变量之间的关系。

在线性回归模型中，通常使用下面的下标表示：y it=β0+β1x it1+β2x it2+⋯+βk x itk+u it其中，y it表示第i个经济单元在t时间点上的被解释变量，x it1,x it2,…,x itk表示第i个经济单元在t时间点上的k个解释变量，β0,β1,…,βk表示模型的参数，u it表示误差项。

检验经济假设横截面数据模型还常常被用来检验经济理论和假设。

例如，我们想要检验收入对教育水平的影响。

在这种情况下，我们可以建立下面的模型：y it=β0+β1x it1+u it其中，y it表示第i个经济单元在t时间点上的教育水平，x it1表示第i个经济单元在t时间点上的收入，β0表示模型的截距，β1表示收入对教育的影响，u it表示误差项。

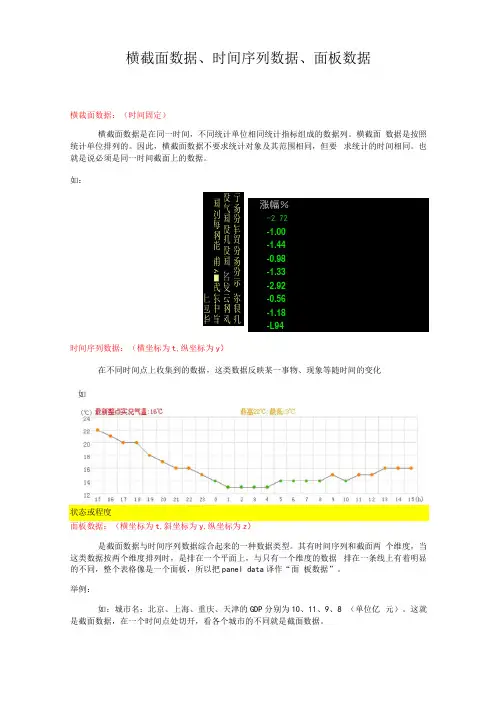
横截面数据、时间序列数据、面板数据横裁面数据：（时间固定）横截面数据是在同一时间，不同统计单位相同统计指标组成的数据列。

横截面 数据是按照统计单位排列的。

因此，横截面数据不要求统计对象及其范围相同，但要 求统计的时间相同。

也就是说必须是同一时间截面上的数据。

如：涨幅％-2.72 -1.00 -1.44 -0.98 -1.33 -2.92 -0.56 -1.18 -L94时间序列数据：（横坐标为t,纵坐标为y ）在不同时间点上收集到的数据，这类数据反映某一事物、现象等随时间的变化 状态或程度面板数据：（横坐标为t,斜坐标为y,纵坐标为z ）是截面数据与时间序列数据综合起来的一种数据类型。

其有时间序列和截面两 个维度，当这类数据按两个维度排列时，是排在一个平面上，与只有一个维度的数据 排在一条线上有着明显的不同，整个表格像是一个面板，所以把panel data 译作“面 板数据”。

举例：如：城市名：北京、上海、重庆、天津的GDP 分别为10、11、9、8 （单位亿 元）。

这就是截面数据，在一个时间点处切开，看各个城市的不同就是截面数据。

行场粉车贸粉场粉际称银机股汽国股机股国名发云钢风国创海钢能浦6■武东中首上包华如如：2000、2001、2002、2003、2004 各年的北京市GDP 分别为8、9、10、11、12 （单位亿元）。

这就是时间序列，选一个城市，看各个样本时间点的不同就是时间序列。

如：2000、2001、2002、2003、2004各年中国所有直辖市的GDP分别为：北京市分别为8、9、10、11、12；上海市分别为9、10、11、12、13；天津市分别为5、6、7、8、9；重庆市分别为7、8、9、10、11 （单位亿元）。

这就是面板数据。

城2000200120022003北京1453上海2436重庆2135天津4531关于面板数据的统计分析在写论文时经常碰见一些即是时间序列又是截面的数据，比如分析1999-2010的公司盈余管理影响因素，而影响盈余管理的因素有6个，那么会形成如下图的数据公司1公司2公司100因素1因素6盈余管理程度因素1因素6盈余管理程度因素1因素6盈余管理程度1999 20002010如上图所示的数据即为面板数据。

基于时间序列与横截面数据的吉林省水稻产量预测对比分析陈威;祁伟彦;袁福香;李哲敏【摘要】[目的]对比不同模型预测效果,分析各模型预测水稻产量的特点、不足及适用条件,为粮食产量预测问题模型选择提供依据.[方法]从时间序列预测和横截面数据预测两种角度,利用ARIMA、LSTM、SVR、MLP这4种模型,通过吉林省水稻产量、病虫害及其他特征历史数据对吉林省水稻产量进行预测,并对不同模型的预测结果进行了对比分析.[结果]基于ARIMA模型和LSTM模型的时间序列预测结果较好,横截面数据预测中,原始数据经主成分分析PCA降维处理后,可提高模型预测性能.[结论]对于水稻产量预测,应根据掌握的影响产量因素的数据以及趋势延续性情况合理选择预测模型,以达到较理想的预测效果.【期刊名称】《中国农业信息》【年(卷),期】2018(030)005【总页数】11页(P91-101)【关键词】水稻产量;ARIMA;LSTM;SVR;MLP;时间序列【作者】陈威;祁伟彦;袁福香;李哲敏【作者单位】中国农业科学院农业信息研究所,北京100081;中国农业科学院农业信息研究所,北京100081;吉林省气象科学研究所,长春130062;中国农业科学院农业信息研究所,北京100081【正文语种】中文0 引言水稻是世界三大粮食作物之一，是我国最主要的粮食作物，全国65%以上的人口以稻米为主食。

我国水稻播种面积占全国粮食播种面积的27%左右，产量占全国粮食总产量的37%左右［1］。

因此，水稻的稳产增产以及对水稻产量的准确预测对我国农业政策调整和保障我国粮食安全问题具有重要意义。

国内学者在粮食产量预测方面做了大量研究，有的利用粮食产量的时间序列数据进行预测，有的利用与粮食生产密切相关的多重参数的横截面数据进行预测。

时间序列数据预测常用的预测算法有自回归滑动平均、人工神经网络等。

由于时间序列预测只需变量本身的历史数据，不需要其他参数的数据，模型构建较为简单，因此在粮食产量预测中应用十分广泛。

stata截面数据定义Stata截面数据分析方法简介引言：截面数据（Cross-sectional data）是指在某一特定时点或一段时间内，对不同个体或单位进行的观察数据。

Stata作为一种统计软件，提供了丰富的功能来分析截面数据。

本文将介绍Stata中常用的截面数据分析方法，包括描述统计、回归分析、面板数据分析等。

一、描述统计描述统计是对截面数据进行基本的统计分析，以揭示数据的特征和分布情况。

Stata中常用的描述统计命令有：1. summarize：可计算变量的均值、标准差、最小值、最大值等统计量。

2. tabulate：可生成变量的频数表、列联表等。

3. histogram：可绘制变量的直方图，以直观展示数据分布情况。

二、回归分析回归分析是研究截面数据之间关系的重要方法。

Stata提供了多种回归分析方法，常用的有：1. 简单线性回归：使用regress命令可以进行简单线性回归分析，探究一个自变量对一个因变量的影响。

2. 多元线性回归：使用regress命令进行多元线性回归分析，探究多个自变量对一个因变量的影响。

3. 逻辑回归：使用logit命令可以进行逻辑回归分析，研究一个二分类因变量与多个自变量之间的关系。

4. 面板数据回归：使用xtreg命令可以进行面板数据回归分析，考虑了个体间和时间间的固定效应。

三、面板数据分析面板数据（Panel data）是一种特殊的截面数据，具有个体间和时间间的固定效应。

Stata提供了多种面板数据分析方法，常用的有：1. 固定效应模型：使用xtreg命令进行固定效应模型分析，探究个体间的差异对因变量的影响。

2. 随机效应模型：使用xtreg命令进行随机效应模型分析，考虑了个体间和时间间的随机变动。

3. 差分法：使用areg命令进行差分法分析，通过个体间或时间间的差异来研究因变量的影响。

四、数据可视化Stata提供了丰富的数据可视化功能，通过绘制图表可以更直观地展示截面数据的特征和关系。

横截面数据、时间序列数据、面板数据2篇横截面数据篇横截面数据是经济学和统计学中常用的一种数据类型。

横截面数据是在同一时期对多个个体进行观察和测量的数据。

它强调的是对不同个体在同一时间点上的状态或特征的描述。

横截面数据的应用广泛，特别是在市场调研、人口统计、社会调查、企业管理等领域。

例如，在市场调研中，研究人员可以通过对不同消费者群体进行调查和测量，得到他们在某一时间点上的购买行为、消费偏好等信息。

这些数据可以帮助企业制定市场营销策略，改进产品设计，提升客户满意度。

横截面数据的分析方法有很多种。

最常用的方法是描述统计分析，通过计算平均值、标准差、频数等统计量来摸索横截面数据的特征。

此外，还可以利用假设检验、回归分析等统计方法，揭示变量之间的关系以及对因变量的影响程度。

横截面数据的分析还可以辅助其他数据类型的研究。

例如，在宏观经济研究中，研究人员除了使用时间序列数据，还可以借助横截面数据来检验宏观经济模型的有效性和适用性。

另外，在金融领域，横截面数据可以用于评估股票的价值、预测市场走势等。

这些应用都需要将横截面数据和其他数据类型进行巧妙地结合和比较。

总之，横截面数据是一种非常重要的数据类型。

它可以用于描述不同个体之间的差异，揭示变量之间的关系，辅助其他数据类型的研究。

在使用横截面数据时，我们需要选择适当的分析方法，准确地描述和解释数据的特征，从而得出有关个体和变量的有意义的结论。

时间序列数据篇时间序列数据是研究某一现象随时间变化的变化规律的一种数据类型。

它是在一定时间间隔内对同一现象进行测量和观察的数据。

时间序列数据的分析可以帮助人们了解现象的长期走势、周期性、趋势性以及可能存在的突发事件。

时间序列数据广泛应用于经济学、金融学、气象学、环境科学等领域。

例如，在经济学中，国民经济的发展是一个动态过程，通过分析GDP、失业率、通货膨胀率等时间序列数据，可以了解经济的增长速度、经济周期以及经济政策的影响等。

计量经济学横截面数据举例子什么是计量经济学计量经济学是使用统计方法分析经济数据；通常分析非实验数据。

计量经济分析的典型目标L估计经济变量之间的关系；2.检验经济理论和假设；3.预测经济变量；4. 评估和执行政府和企业政策经济模型可能是微观或者宏观模型；时常使用优化行为，平衡建模；建立经济变量之间的关系例如：需求方程，定价方程…例1.1犯罪的经济模式在一篇开创性的文章中，诺贝尔奖获得者加里•贝克尔提出了一个效用最大化框架来描述个人参预犯罪。

某些犯罪有明确的经济回报，但大多数犯罪行为都有成本。

犯罪的机会成本妨碍了罪犯参预其他活动,如合法就业。

此夕卜,还有与被抓的可能性相关的成本，如果被定罪，还有与监禁相关的成本。

从贝克尔的观点来看，从事非法活动的决定是一种资源分配，考虑到竞争活动的利益和成本。

在普通假设下，我们可以推导出一个等式，描述犯罪活动中花费的时间是各种因素的函数。

我们可以表示这样一个函数y=f(x1,x2,x3,x4,x5,x6, x7),(L1)犯罪的经济模型(Becker (1968 ))基于效用最大化推导犯罪活动方程y=f(x1,x2,x3,x4,x5,x6,x7),(L1)y-在犯罪活动中花费的时间x1一犯罪活动的“工资”；x2一合法就业工资；x3一其他收入；x4一被抓住的概率；x5一如果被抓住，定罪的概率；x6一预期句子；x7一年龄未指定关系的功能形式；在没有经济模型的情况下，这个方程可以假设例1.2工作培训和工作效率考虑在第1.1节开头提出的问题。

一位劳动经济学家想研究工作培训对工人生产力的影响。

在这种情况下，形式理论几乎没有必要。

基本的经济学知识足以认识到教育、经验和培训等因素会影响工人的生产力。

此外，经济学家也很清晰, 工人的工资与彳他们的生产力相称。

这种简单的推理导致了一个模型，比如：工资=f （教育、经验、培训）（1.2）岗位培训模式与员工生产力额外培训对工人生产力有什么影响？正式经济理论并不需要推导方程式：工资=f（教育、经验、培训）工资一小时工资；教育一正规教育年限；经验丰富一多年的工作经验；培训一工作培训周其他因素也可能相关，但这些是最重要的犯罪活动的计量经济模型必须指定功能形式；变量可能必须用其他量来近似犯罪邛0+B1工资邛2其他收入邛3频率邛4频率转换邛5平均值邛6年龄+U犯罪一犯罪活动的量度工资一合法就业工资；其他收入一其他收入；频率一先前逮捕的频率；频率转换一定罪频率；犯罪活动的量度一定罪后的平均刑期；年龄一年龄；U一犯罪活动的不可观察的决定因素举例：道德品质，犯罪活动的工资，家庭背景…职业培训与工人生产率的计量经济学模型工资邛0+阿教育邛2经验邛3培训+ u工资一小时工资；教育一正规教育年限；经验丰富一多年的工作经验；u- 工作培训周；不可观察的工资决定因素举例：先天能力，教育质量，家庭背景…大多数计量经济学研究的是误差的说明经济计量模型可用于假设检验例如，参数B3表示培训对工资的影响这种影响有多大？它和零不同吗？经济计量分析需要数据不同类型的经济数据集截面数据；时间序列数据；合并横截面；面板/纵向数据计量经济学方法取决于所用数据的性质使用不适当的方法可能会导致误导性的结果横断面数据集在给定时间点/给定时期内的个人、家庭、公司、城市、州、国家或者其他利益单位的样本横断面观察或者多或者少是独立的例如，从总体中进行纯随机抽样有时，纯粹的随机抽样是违反的，例如单位拒绝在调查中作出答复，或者如果抽样的特点是聚类应用微观经济学中常见的横截面数据工资和其他特征的横截面数据集指标变量（I 二是，0二否）观察数；小时工资关于增长率和国家特征的横截面数据M J A scconddn人均实际国内生产总值增长率政府消费占国内生产总值的百分比；成人中 等教育率时间序列数据—个或者几个变量随时间的变化：比如股票价格，货币供应量，消费者价格指 数，国内生产总值，年谋杀率，汽车销售…时间序列观测值通常是串行相关的DwnaEcn oritirf HftrfpfiWGffwnmcrt drunixm SflNrth ntE ofrui M&lipoCW观察结果的顺序传达了重要信息数据频率：每日、每周、每月、每季度、每年…时间序列的典型特征:趋势与季节性典型应用：应用宏观经济学和金融学最低工资及相关变量的时间序列数据・Tlmw 质凶組data an MiHRiwiurvi and elated v^ir La M its给定年份的平均最低工资平均覆盖率；失业率；国民生产总值合并横截面两个或者多个横截面组合在一个数据集中横截面是相互独立绘制的通常用于评估政策变化的汇总横截面例子：•评估房产税变化对房价的影响•1993年房价随机抽样•1995年新的随机房价样本•先后比较（1993年：改革前，1995年：改革后）住宅价格综合截面图房产税；房屋面积（平方英尺）洗手间数量；改革前；改革后面板或者纵向数据相同的横截面单位会随着时间的推移而变化面板数据具有横截面和时间序列维度面板数据可以用来解释时不变的不可观测现象 面板数据可用于建模滞后响应 例子：•城市犯罪统计;每一个城市在两年内进行观察•可对不可观测的时不变城市特征进行建模•警察对犯罪率的影响可能表现出时滞城市犯罪统计两年小组数据每一个城市都有两个时间序列1986年警察人数；1990年警察人数 因果关系与平等概念X 对y 因果关系的定义:"如果变量x 改变了，变量y 如何变化但所有其他相关因素都保持不变。

计量经济学横截面数据模型下标横截面数据模型是计量经济学中的一种重要分析方法，用于研究不同个体之间的关系。

在横截面数据模型中，我们关注的是同一时间点上不同个体之间的差异，而不是随着时间变化的个体内部变化。

下标在横截面数据模型中起到了标识和描述变量的作用。

通过使用下标，我们可以对不同个体、不同变量以及不同时期进行区分和描述。

1. 个体下标：在横截面数据模型中，我们通常研究多个个体之间的关系。

为了区分这些个体，我们可以使用一个索引或编号来表示每个个体。

通常情况下，我们使用i来表示第i个个体，其中i可以是1、2、3等整数。

2. 变量下标：在横截面数据模型中，我们通常关注多个变量之间的关系。

为了区分这些变量，我们可以使用一个字母或符号来表示每个变量。

通常情况下，我们使用j来表示第j个变量，其中j可以是1、2、3等整数。

3. 时间下标：在横截面数据模型中，我们研究的是同一时间点上不同个体之间的差异，并不涉及随时间推移的个体内部变化。

时间下标在横截面数据模型中并不常用。

4. 横截面数据模型的表达式：在横截面数据模型中，我们通常使用方程来表示个体之间的关系。

这些方程可以是线性的或非线性的，可以包含单个变量或多个变量。

为了表示不同个体之间的差异，我们使用个体下标和变量下标来描述方程中的系数。

我们可以使用以下形式来表示一个简单的横截面数据模型：Yi = β0 + β1Xi + εi其中，Yi表示第i个个体的因变量，Xi表示第i个个体的自变量，β0和β1分别表示所有个体共享的常数项和斜率系数，εi表示随机误差项。

通过对多个个体进行观测，并利用最小二乘法等估计方法，我们可以得到每个变量下标对应的系数估计值。

这些系数估计值可以帮助我们理解不同变量对因变量的影响程度，并进行统计推断和经济政策分析。

总结：横截面数据模型是计量经济学中研究不同个体之间关系的重要方法。

通过使用下标来区分和描述不同个体、不同变量以及不同时期，我们可以建立横截面数据模型的表达式，并通过估计系数来分析个体之间的关系。

第四部分横截面数据分析第四部分：横截面数据分析(Cross Data)西安交大管理学院2011‐春2内容判别分析(Discriminant analysis)典型相关分析(Canonical correlation analysis ）?对应分析(Correspondence analysis)联合分析（Conjoint analysis/measurement)多维尺／标度分析(Multi-Dimentional Scaling)联合分析（Conjoint analysis/measurement)用于评估不同属对消费者的相对重要性，以及不同属性水平给消费者带来的效用的统计分析方法。

联合分析始于消费者对产品或服务（刺激物）的总体偏好判断（渴望程度评分，购买意向，偏好排序等），从消费者对不同属性及其水平组成的产品的总体评价（权衡），可以得到联合分析所需要的信息。

?联合分析法又称多属性组合模型，或状态优先分析，是一种多元的统计分析方法，它产生于1964年。

虽然最初不是为市场营销研究而设计的，但这种分析法在提出不久就被引入市场营销领域，被用来分析产品的多个特性如何影响消费者购买决策问题。

多重变量分析主要分析之一，在社会学、生物统计学、数量心理学、市场营销、产品管理、运筹学等领域的统计实证分析应用广泛。

?它产生于1964年。

虽然最初不是为市场营销研究而设计的，但这种分析法在提出不久就被引入市场营销领域，被用来分析产品的多个特性如何影响消费者购买决策问题。

联合分析（Conjoint analysis)西安交大管理学院2011‐春5基本原理联合分析是通过假定产品具有某些特征，对现实产品进行模拟，然后让消费者根据自己的喜好对这些虚拟产品进行评价，并采用数理统计方法将这些特性与特征水平的效用分离，从而对每一特征以及特征水平的重要程度作出量化评价的方法。

西安交大管理学院2011‐春6基本假定联合分析假定分析的对象如品牌、产品、商店等，是由一系列的基本特征（如：质量、方便程度、价格）以及产品的专有特征（如电脑的CPU 速度、硬盘容量等）所组成的；消费者的抉择过程是理性地考虑这些特征而进行的。

简述截面数据法和时间序列法
截面数据法（Cross-sectional data）是一种收集和分析多个个体（如不同人、不同地区、不同公司等）在同一时间点上的数据的方法。

该方法可以用于比较不同个体之间的差异和关系，例如比较不同地区的人均收入、不同公司的市值等。

截面数据法通常用于描述和分析横截面数据集。

时间序列法（Time series data）是一种收集和分析同一组个体在连续时间点上的数据的方法。

该方法可以用于观察和分析个体随时间变化的趋势和模式，例如观察某公司的销售额在过去几个季度的变化、某地区的人口数量在过去几年的变化等。

时间序列法通常用于描述和分析时间序列数据集。

第五章横截面数据分类：机器学习方法李世君2018年4月8日#p72 5.1.2setwd("D:/数据文件/FZdata")Fold=function(Z=10,w,D,seed=7777){n=nrow(w)d=1:n;dd=list()e=levels(w[,D])T=length(e);set.seed(seed)for(i in 1:T){d0=d[w[,D]==e[i]];j=length(d0)ZT=rep(1:Z,ceiling(j/Z))[1:j]id=cbind(sample(ZT,length(ZT)),d0);dd[[i]]=id}mm=list();for(i in 1:Z){u=NULL;for(j in 1:T)u=c(u,dd[[j]][dd[[j]][,1]==i,2])mm[[i]]=u}return(mm)}w=read.csv("CTG.NAOMIT.csv")F=21:23;for(i in F)w[,i]=factor(w[,i])D=23;Z=10;n=nrow(w);mm=Fold(Z,w,D,8888)#p74 5.2.1library(rpart.plot)## Loading required package: rpart(a=rpart(NSP~.,w))#用决策树拟合全部数据并打印输出## n= 2126#### node), split, n, loss, yval, (yprob)## * denotes terminal node#### 1) root 2126 471 1 (0.778457197 0.138758231 0.082784572)## 2) CLASS=1,2,3,4,6,7 1681 29 1 (0.982748364 0.017251636 0.000000000) *## 3) CLASS=5,8,9,10 445 179 2 (0.006741573 0.597752809 0.395505618)## 6) CLASS=5,10 269 4 2 (0.011152416 0.985130112 0.003717472) *## 7) CLASS=8,9 176 1 3 (0.000000000 0.005681818 0.994318182) *rpart.plot(a,type=2,extra=4)#画决策树#p75wp=predict(a,w,type="class")(z=table(w[,D],wp))## wp## 1 2 3## 1 1652 3 0## 2 29 265 1## 3 0 1 175sum(w[,D]!=wp)/nrow(w)## [1] 0.01599247#p76 5.2.2library(rpart)E=rep(0,Z)for(i in 1:Z){m=mm[[i]];n1=length(m);a=rpart(NSP~.,w[-m,])E[i]=sum(w[m,D]!=predict(a,w[m,],type="class"))/n1} mean(E)## [1] 0.01601179#p77 5.3.1library(adabag)## Loading required package: mlbench## Loading required package: caret## Loading required package: lattice## Loading required package: ggplot2set.seed(4410)a=boosting(NSP~.,w)wp=predict(a,w)$class(z=table(w[,D],wp))## wp## 1 2 3## 1 1654 1 0## 2 0 295 0## 3 0 0 176sum(w[,D]!=wp)/nrow(w)## [1] 0.0004703669barplot(a$importance,=.6)#画出变量重要性图#78newdata=w[11,]a=rpart(NSP~.,w)predict(a,newdata[-D],type="class")## 11## 2## Levels: 1 2 3b=boosting(NSP~.,w)predict(b,newdata)$class## [1] "2"predict(b,newdata[-D])$class## [1] "2"newdata[,D]=factor(3)predict(b,newdata)$class## [1] "2"#79levels(newdata[,D])## [1] "3"levels(newdata[,D])=levels(w[,D])levels(newdata[,D])## [1] "1" "2" "3"predict(b,newdata)$class## [1] "2"new.data=w[1:20,]new.data[,D]=factor(rep("1",20))levels(new.data[,D])=levels(w[,D])predict(b,new.data)$class## [1] "2" "1" "1" "1" "1" "3" "3" "3" "3" "3" "2" "2" "1" "1" "1" "1" "1" ## [18] "2" "1" "1"#p79 5.3.2set.seed(1010)E=rep(0,Z)for(i in 1:Z){m=mm[[i]]n1=length(m)a=boosting(NSP~.,w[-m,])E[i]=sum(as.character(w[m,D])!=predict(a,w[m,])$class)/n1}mean(E)## [1] 0.01129685#p80 5.4.1set.seed(1010);D=23a=bagging(NSP~.,w)#函数bagging（）的程序包为ipred。