1.3 截一个几何体 课件 北师大版七年级上 (7)

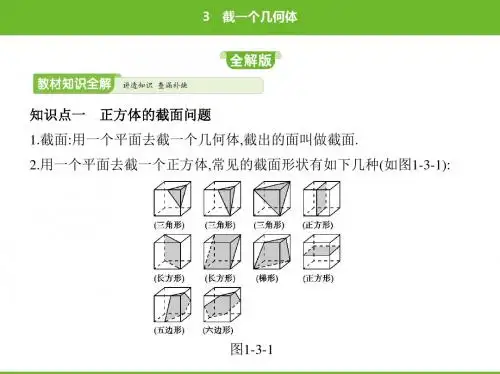
1.3 截一个几何体一、单选题1．如图，一个有盖．．的圆柱形玻璃杯中装有半杯水，若任意放置这个水杯，则水面的形状不可能是A．B．C．D．【答案】D【解析】【分析】根据圆柱体的截面图形可得．【详解】解：将这杯水斜着放可得到A选项的形状，将水杯倒着放可得到B选项的形状，将水杯正着放可得到C选项的形状，不能得到三角形的形状，故选D．【点睛】本题主要考查认识几何体，解题的关键是掌握圆柱体的截面形状．2．粉刷墙壁时，粉刷工人用滚筒在墙上刷过几次后，墙壁马上换上了“新装”，在这个过程中，你认为下列判断正确的是（）A．点动成线B．线动成面C．面动成体D．面与面相交得到线【答案】B【解析】【分析】点动线，线动成面，将滚筒看做线，在运动过程中形成面．【详解】解：滚筒看成是线，滚动的过程成形成面，故选：B．【点睛】本题考查点、线、面的关系；理解点动成线，线动成面的过程是解题的关键．3．用一个平面取截一个几何体，得到的截面是四边形，这个几何体可能是（）A．圆柱B．球体C．圆锥D．以上都有可能【答案】A【解析】【分析】根据圆柱、球体、圆锥的几何特征，分别分析出用一个平面去截该几何体时，可能得到的截面的形状，逐一比照后，即可得到答案．【详解】解：A、用一个平面去截一个圆柱，得到的图形可能是四边形，故A选项符合题意；B、用一个平面去截一个球体，得到的图形可能是圆，故B选项不合题意；C、用一个平面去截一个圆锥，得到的图形可能是圆、椭圆、抛物线、三角形，不可能是四边形，故C选项不符合题意；D、因为A选项符合题意，故D选项不合题意；故选A．【点睛】本题考查了截一个几何体，截面的形状随截法的不同而改变，一般为多边形或圆，也可能是不规则图形，一般的截面与几何体的几个面相交就得到几条交线，截面就是几边形，因此，若一个几何体有几个面，则截面最多为几边形．4．如图，在一密闭的圆柱形玻璃杯中装一半的水，水平放置时，水面的形状是（）A．圆B．长方形C．椭圆D．平行四边形【答案】B【解析】分析：此题实质是垂直圆柱底面的截面形状；解：水面的形状就是垂直圆柱底面的截面的形状，即为长方形；故选B．5．用一个平面去截几何体，截面不可能是三角形的是（）A．圆柱B．圆锥C．三棱柱D．正方体【答案】A【解析】【分析】根据正方体、球体、棱柱、圆柱的形状特点判断即可．【详解】A、圆柱的截面跟圆、四边形有关，截面不可能是三角形，符合题意；B、过圆锥的顶点和下底圆心的面得到的截面是三角形，不符合题意；C、过三棱柱的三个面得到的截面是三角形，不符合题意；D、过正方体的三个面得到的截面是三角形，不符合题意．故选：A．【点睛】截面的形状既与被截的几何体有关，还与截面的角度和方向有关．对于这类题，最好是动手动脑相结合，从中学会分析和归纳的思想方法．6．用一个平面去截一个几何体，其截面形状是圆，则原几何体可能为（）①圆柱①圆锥①球①正方体①长方体A．①①B．①①①C．①①①①D．①①①①①【答案】B【解析】【分析】根据圆柱、圆锥、球、正方体、长方体的形状进行判断即可，可用排除法．【详解】解：①圆柱的截面形状可能是圆，符合题意；①圆锥的截面形状可能是圆，符合题意；①球的截面形状一定是圆，符合题意；①正方体的截面形状不可能是圆，不符合题意；①长方体的截面形状不可能是圆，不符合题意；故选B．【点睛】本题考查了用平面去截一个几何体，截面的形状即与被截的几何体有关，还与截面的角度和方向有关．7．如图所示，用一个平面去截一个圆柱，则截得的形状应是（①A．B．C．D．【答案】B【解析】【分析】当截面的角度和方向不同时,圆柱体的截面不相同进行判断即可.【详解】解:平面平行圆柱底面截圆柱可以得到一个圆,而倾斜截得到椭圆,所以B选项是正确的.【点睛】本题考查的是截面位置与截面的关系, 解答的关键是知道截面位置不同所得截面可能不同;8．一个几何体的一个截面是三角形，则原几何体一定不是下列图形中的( )A．圆柱和圆锥B．球体和圆锥C．球体和圆柱D．正方体和圆锥【答案】C【解析】【分析】观察题目，每个选项中都有圆锥，而圆锥的截面可能是三角形，故可以判断A①B①D；根据圆柱的截面可能是圆，长方形，不会是三角形，球体的截面永远是圆对C选项进行判断.【详解】圆柱的截面可能是圆，长方形，不会是三角形，球体的截面永远是圆，也不会是三角形.故选C①【点睛】本题主要考查的是几何体的有关知识，熟练掌握常见几何体截面的形状是解答本题的关键.9．用一个平面去截圆锥，截面图形不可能是（）A．B．C．D．【答案】C【解析】试题分析：根据圆锥的形状特点判断即可，也可用排除法．解：如果用平面取截圆锥，平面过圆锥顶点时得到的截面图形是一个等腰三角形，如果不过顶点，且平面与底面平行，那么得到的截面就是一个圆，如果不与底面平行得到的就是一个椭圆或抛物线与线段组合体，所以不可能是直角形．故选；C．点评：此题主要考查了截一个几何体，截面的形状既与被截的几何体有关，还与截面的角度和方向有关．对于这类题，最好是动手动脑相结合，亲自动手做一做，从中学会分析和归纳的思想方法．10．一个正方体锯掉一个角后，顶点的个数是① ①A．7个或8个B．8个或9个C．7个或8个或9个D．7个或8个或9个或10个【答案】D【解析】如下图，一个正方体锯掉一个角，存在以下四种不同的情形，新的几何体的顶点个数分别为：7个、8个、9个或10个.故选D.二、填空题11．正方体的截面中，边数最多的是________边形．【答案】六【解析】解：①用平面去截正方体时最多与六个面相交得六边形，最少与三个面相交得三角形，①最多可以截出六边形．故答案为：六．12．在“长方体、圆柱、圆锥”三种几何体中，用一个平面分别去截三种几何体，则截面的形状可以截出长方形也可以截出圆形的几何体是_____．【答案】圆柱【解析】【分析】首先当截面的角度和方向不同时，长方体的截面始终不是圆，无论什么方向截取圆锥都不会截得长方形，从而可用排除法可得答案．【详解】解：用一个平面截长方体，不管角度与方向，始终截不到圆，所以排除长方体，用一个平面截圆锥，不管角度与方向，始终截不到长方形，所以排除圆锥，用一个平面截圆柱，可以截到长方形与圆．故答案为：圆柱．【点睛】本题考查的是对基本的几何立体图形的认识，掌握长方体，圆柱，圆锥的特点是解题的关键．13．用一个平面去截下列几何体，截面可能是圆的是__________．（填写序号）①三棱柱；①圆柱；①圆锥；①长方体；①球【答案】①①①【解析】【分析】根据一个几何体有几个面，则截面最多为几边形，由于棱柱没有曲边，所以用一个平面去截棱柱，截面不可能是圆．【详解】用一个平面去截球，截面是圆，用一个平面去截圆锥或圆柱，截面可能是圆，但用一个平面去截棱柱，截面不可能是圆．故答案为：①①①【点睛】本题考查了截一个几何体：用一个平面去截一个几何体，截出的面叫做截面．截面的形状随截法的不同而改变，一般为多边形或圆，也可能是不规则图形，一般的截面与几何体的几个面相交就得到几条交线，截面就是几边形，因此，若一个几何体有几个面，则截面最多为几边形．14．小华用一个平面去截圆柱体，所得到的截面形状可能是_______（写出一个即可）．【答案】长方形或梯形或椭圆或圆【解析】【分析】用平面取截一个圆柱体，横着截时截面是椭圆或圆（截面与上下底平行），竖着截时，截面是长方形（截面与两底面垂直）或梯形．【详解】用平面取截一个圆柱体，横着截时截面是椭圆或圆（截面与上下底平行）．竖着截时，截面是长方形（截面与两底面垂直）或梯形．故答案为：长方形或梯形或椭圆或圆．【点睛】截面的形状既与被截的几何体有关，还与截面的角度和方向有关．15．下列说法：①球的截面一定是圆；①正方体的截面可以是五边形；①棱柱的截面不可能是圆；①长方体的截面一定是长方形，其中正确的有___________个【答案】3【解析】【分析】根据用一个平面截几何体，从不同角度截取所得形状会不同，进而分析得出答案．【详解】解：：①球的截面一定是圆，说法正确；①正方体的截面可以是五边形，说法正确；①棱柱的截面不可能是圆，说法正确；①长方体的截面中，边数最多的多边形是六边形，也可以是三角形，故说法错误；故答案为：3．【点睛】本题考查了截面的形状．截面的形状既与被截的几何体有关，还与截面的角度和方向有关．主要考查学生的观察图形的能力、空间想象能力和动手操作能力．16．用一个平面分别截棱柱、圆锥，都能截出的一个图形是________.【答案】三角形【解析】【分析】分析用一个平面分别去截圆锥、棱柱，分别能够得到哪些截面图形，然后从分别得到的截面图形中找出都有的图形即可.【详解】用一个平面去截棱柱可以得到三角形、长方形；用一个平面去截圆锥可以得到圆、三角形等.故用一个平面分别去截分别截棱柱、圆锥，都能截出的一个截面是三角形.故答案为三角形.【点睛】此题考查几何体的截面图形，熟练掌握常见几何体的截面图形是解题的关键.17．用一个平面截三棱柱，最多可以截得________边形；用一个平面截四棱柱，最多可以截得________边形；用一个平面截五棱柱，最多可以截得________边形.试根据以上结论，猜测用一个平面去截n棱柱，最多可以截得________边形.n .【答案】五，六，七，2【解析】【分析】三棱柱有五个面，用平面去截三棱柱时最多与五个面相交得五边形．因此最多可以截得五边形;四棱柱有六个面，用平面去截三棱柱时最多与六个面相交得六边形．因此最多可以截得六边;五棱柱有七个面，用平面去截三棱柱时最多与七个面相交得七边形．因此最多可以截得七边形;n棱柱有n+2个面，用平面去截三棱柱时最多与n+2个面相交得n+2边形．因此最多可以截得n+2边形.【详解】用一个平面去截三棱柱最多可以截得5边形，用一个平面去截四棱柱最多可以截得6边形，用一个平面去截五棱柱最多可以截得7边形，试根据以上结论，用一个平面去截n棱柱，最多可以截得n+2边形.故答案为五;六;七; n+2.【点睛】此题考查截一个几何体，解题关键在于熟练掌握常见几何体的截面图形.18．一块方形蛋糕，一刀切成相等的两块，两刀最多切成4块，试问：五刀最多可切成__ 块相等体积的蛋糕，十刀最多可切成____块（要求：竖切，不移动蛋糕）．【答案】16 56【解析】当切1刀时，块数为1+1=2块；当切2刀时，块数为1+1+2=4块；当切3刀时，块数为1+1+2+3=7块；…当切n刀时，块数=1+①1+2+3…+n①=1+()12n n+.n=5代入公式得16,n=10,代入公式得56.点睛：找规律题需要记忆常见数列1①2①3①4……n.1①3①5①7……2n-1.2①4①6①8……2n.2①4①8①16①32……2n.1①4①9①16①25 (2)2①6①12①20……n(n+1).学会常见数列的变形，才能具体问题找到规律.三、解答题19．(1)用一个平面去截一个几何体，可以得到圆形的截面的几何体有？(2)用一个平面去截一个几何体，可以得到三角形的截面的几何体有？【答案】（1）球，圆柱，圆锥；（2）三棱柱，三棱锥，正方体.【解析】（1）根据截面是圆，可得几何体是旋转体，根据旋转得到的几何体，可得答案；（2）根据截面与几何体的三个面相交，可得截面是三角形．【详解】(1)用一个平面去截一个几何体，可以得到圆形的截面的几何体有球，圆柱，圆锥；(2)用一个平面去截一个几何体，可以得到三角形的截面的几何体有三棱柱，三棱锥，正方体，故答案为：（1）球，圆柱，圆锥；（2）三棱柱，三棱锥，正方体.【点睛】此题考查截一个几何体，解题关键在于掌握图形的形状结构.20．如图所示是一个圆柱体，它的底面半径为3cm ，高为6cm ．（1）请求出该圆柱体的表面积；（2）用一个平面去截该圆柱体，你能截出截面最大的长方形吗？截得的长方形面积的最大值为多少？【答案】（1）()254πcm ；（2）能截出截面最大的长方形，长方形面积的最大值为：()236cm 【解析】【分析】（1）用圆柱上下底面积加上侧面积即可；（2）当截得的面积最大时，长方形的长为底面直径，宽为6，可得面积最大值.解：（1）圆柱体的表面积为：232236ππ⨯⨯+⨯⨯1836ππ=+；()254π=cm ；（2）能截出截面最大的长方形．该长方形面积的最大值为：()2(32)636⨯⨯=cm ．【点睛】本题考查了圆柱表面积的求法和截几何体，根据截面的形状既与被截的几何体有关，还与截面的角度和方向有关，得出这个圆柱体的截面面积最大是长方形是本题的关键．21．如图，图①1①是正方体木块，把它切去一块，可能得到①2①①①3①①①4①①①5①所示的图形，问①2①①①3①①①4①①①5①图中切掉的部分可能是其他几块中的哪一块?【答案】①2①图切掉的部分可能是①3①图和①5①图，①3①图切掉的部分可能是①2①图，①5①图切掉的部分可能是①2①图．【解析】试题分析：如图所示，图（3）可能是通过如下图（6①方法切割得到的，切下去的就是图（2①①图（5）可通过如下图（7）方法切割得到的，切下的是图（2①.试题解析：（2）图切掉的部分可能是（3）图和（5）图，（3）图切掉的部分可能是（2）图，（5）图切掉的部分可能是（2）图．22．如图，用一个平面去截一个正方体，如果截去的几何体是一个三棱锥，请回答下列问题：(1)截面一定是什么图形？(2)剩下的几何体可能有几个顶点？【答案】(1)三角形；(2)剩下的几何体可能有7个顶点、或8个顶点、或9个顶点、或10个顶点.【解析】【分析】①1）如果截去的几何体是一个三棱锥，那么截面一定是一个三角形；①2）当截面截取由三个顶点组成的面时可以得到三角形，剩下的几何体有7个点，当截面截取一棱的一点和两底点组成的面时可剩下几何体有8个点，当截面截取由2条棱中点和一顶点组成的面时剩下几何体有9个顶点．当截面截取由三棱中点组成的面时，剩余几何体有10个顶点．【详解】①1）如果截去的几何体是一个三棱锥，那么截面一定是一个三角形；①2）剩下的几何体可能有7个顶点、或8个顶点、或9个顶点、或10个顶点，如图所示：【点睛】截面的形状既与被截的几何体有关，还与截面的角度和方向有关．23．一个表面涂满色的正方体，现将棱三等分，再把它切开变成若干个小正方体.问：其中三面都涂色的小正方体有多少个？两面都涂色的小正方体有多少个？只有一面涂色的小正方体有多少个？各面都没有涂色的小正方体有多少个？【答案】8,12,6,1【解析】试题分析：在大正方体的顶点处的小正方体的三面都有色；有一条棱在大正方体的棱上的小正方体的两面有色，与大正方体没有公共棱的小正方体有一面有色，在大正方体的中心的小正方体各面都无色.试题解析：解：由题意知,各顶点处的小正方体的三面都涂色，共有8个；有一条边在棱上的小正方体有12个，是两面涂色；每个面的正中间有一个只有一面涂色的，有6个；正方体正中心处有1个小正方体，它的各面都没有涂色．因此三面涂色的小正方体有8个，两面涂色的小正方体有12个，只有一面涂色的小正方体有6个，各面都没有涂色的小正方体有1个．24．如图①是一个正方体，不考虑边长的大小，它的平面展开图为图①，四边形APQC是截正方体的一个截面．问截面的四条线段AC，CQ，QP，PA分别在展开图的什么位置上？【答案】线段AC，CQ，QP，PA分别在展开图的面ABCD，BCGF，EFGH，EFBA上.【解析】【分析】把立体图形表面的线条画在平面展开图上，找到四边形APQC四个顶点所在的位置这个关，再进一步确定四边形的四条边所在的平面即可①【详解】根据四边形所在立体图形上的位置，确定其顶点所在的点和棱，以及四条边所在的平面：顶点：A−A①C−C①P在EF边上，Q在GF边上．边AC在ABCD面上，AP在ABFE面上，QC在BCGF面上，PQ在EFGH面上．如图：【点睛】此题考查正方体的展开图，解决此题的关键是抓住四边形APQC四个顶点所在的位置，再进一步确定四边形的四条边所在的平面就可容易地画出．。

北师大版七年级第一章第三节截一个几何体教案教学目标(一)知识与技能能够识别一些几何体截面的形状.(二)过程与方法经历切截几何体的活动过程，体会几何体在切截的过程中的变化，在面与体的转换中丰富数学活动经验，发展空间观念.(三)情感态度与价值观进一步丰富数学学习的成功体验，激发对空间与图形学习的好奇心，初步形成积极参与数学活动、主动与他人合作交流的意识.教学重点1.能够识别一些几何体截面的形状.2.经历切截一个几何体，培养学生的空间观念.教学难点体会几何体在切截过程中的变化，在面与体的转换中丰富数学活动经验，发展空间观念.教学过程一、引入新课［师］上一节课从展开与折叠研究了常见的几何体与平面图形的转换.同时我们又知道构成图形的最基本的元素是点、线、面，面与面相交可以得到线，线与线相交可得到点.如果用一个平面去截一个几何体，截面会是什么形状呢？这一节课我们就针对这个问题来作研究.二、讲授新课1.截一截问题1：用一个平面去截一个正方体，截出的面叫截面，那么截面可能是什么形状？［师］同学们手中都有橡皮泥及其小刀，以同桌为单位，先用橡皮泥捏一个正方体，小刀的刀面我们就可以将它当成截这个正方体的面，当我们用小刀截你手中的正方体时，便可得到一个截面.下面看我手中的这块正方体的橡皮泥，我用小刀去截这个正方体，截面可能是什么形状呢？(老师按下图的截法去演示)（1）（2）（3）（4）截面可能是正方形，也可能是长方形；截面的形状可能是三角形吗?可能是三条边都相等的三角形吗？先做一做，再想一想。

当我们用一个平面去截正方体的一个角时，截到了正方体的三个面，因为面与面相交可得到线，因此这个平面就与正方体的三个面相交从而交出三条线，得到的截面是三角形.截面是三条边都相等的三角形就此一种情况能截得吗？不是，过正方体的一个顶点有三条边，分别在此三条边上以此顶点为端点截取相同长度得到另外三个端点，只要一个平面过此三个端点，便可得到截面是三条边都相等的三角形.用一个平面去截正方体的三个面，得到的截面是三角形.如果用一个平面去截正方体的四个面就能得到四边形，除能得到正方形、长方形这样的四边形外，能否得到其他的四边形，如梯形，平行四边形等.截面是一个梯形. 截面是五边形和六边形的截法可如下图所示：2.做一做上面我们研究了用一个平面去截正方体可以截到的截面有三角形、四边形、五边形、六边形.如果用一个平面去截其他的几何体，得到的截面又如何呢？例如：用平面去截圆柱，截面会有哪些形状呢？先想一想，画出来，再试一试，做一做，看你自己想像的结果与实际结果有何差异.三、应用新知［例1］在下图中的截面的形状分别是什么？解：截面分别是长方形、长方形、长方形、三角形.四、课堂作业1.分别指出图中几何体截面形状的标号.分析：不要求学生实际操作，通过想像来完成.解：(1)②;(2)③;(3)②.2.下图中截面的形状是什么？解：(1)圆；(2)三角形；(3)梯形.五、课时小结这节课我们通过切截的方式进一步研究了几何体，体会到了几何体在切截过程中的变化，并且在面与体的转换中丰富了我们的数学活动经验，发展了空间观念.你有何收获呢？六、课后作业1.课本第十五页的习题2.你能把圆锥可能的截面图形找到吗？找到后，贴在墙上，展示给大家.教学反思为了增强学生的空间感，可以让学生准备一些橡皮泥，上课时自己亲自操作，并相互交流加深记忆。

1.3截一个几何体新知概览：知识要点课标要求中考考点节内对应例题节内对应习题用平面去截几何体所得截面的形状探索并理解几何体的截面形状。

截面的定义（掌握）试练例1；易错典例1；题型典例1，2，3；新题精炼1,6,7，10,12,13,15几种常见几何体的截面掌握几种常见几何体的截面。

判断一个几何体的截面(应用)试练例2；易错典例2；题型典例1,2,3，4,5，6,7，8；中考典例,1新题精炼3，4,5,8，9,10,11,13,14，本节重、难点1.重点：截面的定义和形状．2.难点：利用截面解决实际问题．知识全解知识点1截面（1）截面的概念：用一个平面去截几何体，截出的面叫做截面．（2）正方体的截面：根据面与面相交可以得到线可知用一个平面去截正方体的三个面，得到的截面是三角形.如果用一个平面去截正方体的四个面，就能得到四边形，除能得到正方形、长方形这样的四边形外，还能得到其他的四边形，如梯形、平行四边形等.知识警示：（1）正方体总共有六个面，用一个平面去截最多只能得到六条交线，从而截面的边数最多只能是六，还可以得到五，但不可能截得七边形.（2）一般地，截面与几何体的几个面相交就得到几条交线，截面就是几边形.因此，若一个几何体有n个面，则截面最多的边数是n．知识拓展正方体的截面主要有三角形、四边形、五边形和六边形，如图1-3-1所示.【试练例题1 】如图1-3-2所示的一块长方体木头，想象沿虚线所示位置截下去所得到的截面图形是（）思路导引：首先根据两组对边平行，可确定为平行四边形；又有一角为直角，故截面图形是长方形．答案：B.长方体的截面，经过长方体四个侧面，长方体中，对边平行，故可确定为平行四边形，交点垂直于底边，故为长方形．知识方法：截面的形状既与被截的几何体有关，还与截面的角度和方向有关．对于这类题，最好是动手动脑相结合，亲自动手做一做，从中学会分析和归纳的思想方法．知识点2几种常见几何体的截面图1-3-1A图1-3-2B C D（1）如图1-3-3所示，用平面截圆柱体，可能出现以下的几种情况．（2）如图1-3-4所示，用平面去截一个圆锥，能截出圆和三角形两种截面．（3）如图1-3-5所示,用平面去截球体，只能出现一种形状的截面---圆.知识警示：(1) 用一个平面去截一个圆柱所得到的截面有圆、长方形、椭圆、拱形形状和梯形. (2) 用一个平面去截圆锥，可得到圆、三角形、拱形形状和椭圆. 【试练例题2】如图1-3-6中几何体的斜截面形状是（ ）图1-3-4图1-3-5 图1-3-6思路导引：几何体是一个圆柱体，用一个平面斜截它，得到的截面应该是类似拱形的图形．答案C 用一个平面去截一个圆柱体，过平行于上下底面的面去截可得到圆；圆柱体的轴截面是矩形；过侧面且不平行于上下底面的面去截可得到椭圆；过一底面不平行于另一底面的面去截可得到类似拱形的截面．方法：平面与平面相交得直线，平面与曲面相交可能得到直线，也可能得到曲线．易错易混辨析易错点1：在切截的过程中，不注意切截方向，导致截面形状判断错误【易错典例1】如图1-3-7，用一个垂直于长方体底面的平面去截长方体，截面应为（ ）解：因为垂直于长方体底面的截面，经过长方体四个侧面，长方体中，对边平行，故可确定为平行四边形，交点垂直于底边，故为长方形．故选B ．易错总结：判断被截物体截面的形状，要特别注意切截的方向，不同的切截方向所产生的截面的形状有可能是不同的．易错点2：立体观念不强，用平面截一个几何体时，分类讨论不全面【易错典例2】用一个平面去截一个正方体，截得的多边形从边数来看，可能有哪些结果？请画出这些结果．解：如图1-3-8（注意：看不见的线要画成虚线）．图1-3-7B ADC图1-3-8易错总结：(1)用一个平面去截一个正方体，所得的多边形有多种情况，需分类讨论，且不可遗漏.(2)当平面截过同一顶点的三个面时，截得三角形，且这样的三角形肯定是锐角三角形.平面截正方体所得的四边形可能是平行四边形，也可能是梯形，但不可能是没有一对对边平行的四边形.平面截正方体所得的多边形至多为六边形，且每条边正好是平面与正方体的六个面相交所得.基础经典全析题型1截正方体问题【题型典例1】如图1-3-9，用一个平面去截一个正方体，截面相同的是（）①②③④图1-3-9A.①与②B.③与④C.①与③④D.①与②，③与④思路导引：据图形可知①②都是截面与正方体的面平行，而③④的截面都是长为正方体的一个面的对角线的长，宽为正方体的棱长的长方形．答案：由图形可知截面相同的是①与②，③与④．故选D．方法：正方体截面的形状与截面的角度和方向有关，要认真观察和思考，这里最好是动手切截．题型2截圆柱问题【题型典例2】如图1-3-10，圆柱体被一个平面所截，其截面的形状不可能的是（）思路导引：根据从不同角度截得几何体的形状判断出正确选项．答案：当截面与轴截面平行时，得到的形状为长方形；当截面与轴截面斜交时，得到的截面的形状是椭圆；当截面与轴截面垂直时，得到的截面形状是圆；所以截面的形状不可能是A ．故选A ．方法：可从截面与轴截面的不同位置关系得到截面的不同形状． 题型3截圆锥问题【题型典例3】如图1-3-11，一平面经过圆锥的顶点截圆锥所得到的截面形状是（ ）思路导引：经过圆锥顶点的平面与圆锥的侧面和底面截得的都是一条线，由图可知经过圆锥顶点的平面截圆锥所得的截面应该是个等腰三角形．答案：经过圆锥顶点的平面与圆锥的侧面和底面截得的都是一条线，由图可知经过圆锥顶点的平面截圆锥所得的截面应该是个等腰三角形，故选B ．方法：判断几何体的截面，关键要理解面与面相交得到线． 题型4由截面判断几何体的形状【题型典例4】用一个平面截一个几何体，所截出的面出现了如图1-3-12所示的四种形式，试猜想，该几何体可能是 .①② ③ ④图1-3-12AB DC 图1-3-10ABCD图1-3-11思路导引：根据当截面的角度和方向不同时，截面不相同可判断几何体的形状． 答案：圆柱．平面倾斜竖截圆柱侧面和底面截圆柱截得到图①；平面倾斜圆柱底面截圆柱截得到椭圆；平面竖截圆柱得到长方形；平面平行圆柱底面截圆柱可以得到一个圆．故该几何体可能是圆柱．方法：由截面①②④可以推断几何体不是多面体，可能是圆柱、圆锥或圆台，由截面③可以推断该几何体可能是圆柱．综合创新探究题型5判断截后剩余图形的顶点数、棱数、面数【题型典例5】如图1-3-13，一正方体截去一角后，剩下的几何体有____个面，____条棱（ ）A ．6，14 B.7，14 C.7，15 D.6，15思路导引：由图可知：截取一角后，剩下的几何体多了一个面，多了3条棱，即可求得． 答案：截取一角后，剩下的几何体多了一个面，多了3条棱，即剩下的几何体由7个面，15条棱，故选C ．方法：本题结合截面来判断多面体的顶点数、棱数、面数，这里一般可利用欧拉公式． 题型６复杂的正方体的切截问题【题型典例６】如图1-3-14，是正方体被分割后的一部分，它的另一部分是（ ）思路导引：解答此类问题要从正方体分割后的一部分入手来观察分析，我们会发现截口图1-3-13图1-3-14AB DC呈“F ”形，因此只要在四个选项中寻找相应的“F ”即可． 答案：B方法：解决正方体的切截问题，应利用认知的角度来感知三维世界的“空间”，最好是动手制作切截模型来验证.题型7截面知识在生产、生活中的应用【题型典例7】某车间要切割一些外形是长方体的物体，但该种物体的内部构造不详．于是工人师傅决定用一组水平的平面切截这个物体，得到了一组（自下而上）的截面，截面形状如图所示1-3-15，这个长方体的内部构造可能是什么？思路导引：通过观察可以发现：在正方体内部的圆自下而上由大圆逐渐变成小圆和点． 答案：这个长方体的内部构造为：长方体中间有一圆锥状空洞．方法：由截面形状去想象几何体与给一个几何体想象它的截面是一个互逆的思维过程，要根据所给截面形状仔细分析，展开想象．．备战中考用一个平面去截一个几何体后判断截面的形状是本节的考点，但中考中考查的量不大，主要目的是考查同学们的空间想象能力，题型一般以填空题、选择题为主，分值为3~6分，难度较小.考法1几何体的切截问题中考典例1用一个平面去截一个几何体，不能截得三角形截面的几何体是（ ） A.圆柱 B.圆锥 C.三棱柱 D.正方形(2010．宁夏中考．第4题．3分)思路导引：看所给选项的截面能否得到三角形即可．答案：A 选项中圆柱的截面可能是圆，长方形，符合题意；B 选项中圆锥的截面可① ②④图1-3-15能是圆，三角形，不符合题意；C选项中三棱柱的截面可能是三角形，长方形，不符合题意；D选项中正方体的截面可能是三角形，或四边形，或五边形，或六边形，不符合题意.故选A．点拨：本题考查常见几何体的截面的形状，注意正方体的截面经过几个面就可得到几边形．变式练习1用平面去截下列几何体，截面的形状不可能是圆的几何体是（）A．球 B.圆锥 C.圆柱 D.正方体思路导引：根据圆锥、圆柱、球、正方体的形状特点判断即可．答案:正方体有六个面，用平面去截正方体时最多与六个面相交得六边形，最少与三个面相交得三角形．故选D．(2008．广东茂名中考．第4题．3分)新题精炼基础巩固1．如图1-3-16是一个正方体，用一个平面去截这个正方体截面形状不可能为图中的（）2．用一平面截下面的几何体，无法得到长方形截面的是（）A.正方体B.长方体C.圆锥D.圆柱３．一个四棱柱被一刀切去一部分，剩下的部分可能是（）A.四棱柱B.三棱柱C.五棱柱D.以上都有可能４．如图1-3-17所示，用一个平面沿与棱平行的方向去截一个棱柱，则截面的形状应为（）A．梯形 B.正方形 C.平行四边形 D.长方形5．如图1-3-18所示，用平面去截下列几何体，能截得长方形、三角形、等腰梯形三种形状的截面，这个几何体是（）6.用一个平面截一个正方体，截面最多是____________边形．7.下列图形：①等腰三角形；②矩形；③正五边形；④正六边形中，只有三个是可以通过切正方体（如图1-3-19）面得到的切口平面图形，这三个图形的序号是_________．（请填序号）知识点1题型1知识点2题型4图1-3-19 图1-3-17图1-3-16A B C DA B C D图1-3-18知识点2题型4知识点1题型5知识点2题型4知识点1题型6知识点1题型18.如图1-3-20，下列正方体被一刀切入一部分，写出剩下部分几何体的名称．能力提升9. 如图1-3-21，一刀将藕切断，所得的截面开头像（）10. 把一个正方形的一个角切去，得到的图形可能是①一个三角形（1）（2）图1-3-20A B图1-3-21②一个四边形③一个五边形④一个六边形．其中正确的是（）A．①② B.③④ C.②③ D.①②③11.如图1-3-22，一个物体的外形是圆柱，但不清楚它的内部结构，为探明其内部结构，给其“做CT”，用一组水平的平面去截这个物体，从上至下的五个截面依次如图所示，则这个物体可能是下列选项中的哪一个？（）知识点2题型1、2知识点2题型2知识点1题型1知识点2题型712.如图1-3-23，，将正方A B C D图1-3-22体沿面AB′C剪下，则截下的几何体为．13.如图1-3-24，从边长为10的正方体的一顶点处挖去一个边长为1的小正方体，则剩下图形的表面积为．14.如图1-3-25，有一个外观为圆柱形的物体，它的内部构造面看不到，当分别用一组平面沿水平方向（自上而下）和竖直方向（自左而右）截这个物体时，得到了如图所示的（1）（2）两组形状不同的截面，请你试着说出这个物体的内部构造．15.如图1-3-26（1）的正方体，它的平面展开图为图1-3-26（2），四边形APQC是切正方体的一个截面.问截面的四条线段AC、CQ、QP、PA分别在展开图的什么位置上？知识点2知识点1题型6知识点1题型7知识点2题型7图1-3-24图1-3-25图1-3-23(1) (2)图1-3-26知识点1题型6、7新题精炼参考答案基础巩固：1.D思路导引：正方体有六个面，用平面去截正方体时最多与六个面相交得六边形，最少与三个面相交得三角形．无论如何去截，截面也不可能有弧度，因此截面不可能是圆．故选D．点拨：本题考查正方体的截面．正方体有六个面，截面与其六个面相交最多得六边形，不可能是七边形或多于七边的图形或其他的弧形．2．C思路导引：根据正方体、长方体、圆锥、圆柱的特点判断即可．圆锥的截面可以是椭圆，圆（截面与底面平行），三角形（截面经过圆锥的顶点）但是无法得到长方形的截面．故选C．3．D思路导引：三棱柱、四棱柱、五棱柱都有可能，关键是看切的位置．三棱柱、四棱柱、五棱柱都有可能．故选D．4．D思路导引：由图中棱柱的形状和截面的角度可知，两组对边平行，可先确定为平行四边形，交点垂直于底边，故为长方形．竖截棱柱，截面垂直于两底，那么截面就应该是个矩形．故选D．5．D思路导引：圆台的截面不能得到长方形；圆锥的截面不能得到长方形；圆柱的截面不能得到等腰梯形；当截面经过正方体的3个面时，得到三角形，当截面与正方体的一个面平行时得到长方形，当截面经过正方体的一个正方形的对角的顶点，经过4个面，又与对面斜交时，可得到等腰梯形，故选D．6．六思路导引：正方体有六个面，用平面去截正方体时最多与六个面相交得六边形，最少与三个面相交得三角形．因此最多可以截出六边形．∵用平面去截正方体时最多与六个面相交得六边形，最少与三个面相交得三角形，∴最多可以截出六边形．7. ①②③思路导引：根据正方体的特性即截面图的定义即可解．解答：解：正方体利用斜截面可以截得等腰三角形和正六边形，当截面与经过相对棱的面成45°时就可得到．当截面与棱平行时，得到的切口就是矩形．故答案为①②③．8．（1）三棱柱（2）圆柱（3）五棱柱．思路导引：先得到立体图形被一刀切入一部分的剩下部分几何体，再针对立体图形的特征，直接填写它们的名称即可．根据图示可知，剩下部分几何体的名称依次为：（1）三棱柱（2）圆柱（3）五棱柱．点拨：本题考查了截图和立体图形的认识，熟记常见立体图形的特征是解决此类问题的关键．9．B思路导引：根据藕的特点，考虑截面从不同角度和方向截取的情况作答．解答：解：一刀将藕切断，由藕的特点可知，横切就是椭圆和中间的小孔．故选D．10．D思路导引：根据截线经过的不同的位置可得剩余图形的相应的形状．当截线为经过正方形对角2个顶点的直线时，剩余图形为三角形；当截线为经过正方形一组对边的直线时，剩余图形是四边形；当截线为只经过正方形一组邻边的一条直线时，剩余图形是五边形；所以正确的是①②③，故选D．11．B思路导引：通过观察可以发现：在圆柱内部的圆自下而上由大圆逐渐变成小圆、再由小圆逐渐变成大圆．所以这个圆柱的内部构造为：圆柱中间有一双侧圆台状空洞．故选B．12．三棱锥思路导引：由图可以很明显的看出沿面AB′C剪下后，截面是三角形，截下的几何体为三棱锥．13．600思路导引：由图可知，挖去小正方体后，其实剩下的图形的表面积与原正方体的面表积是相等的．因此，剩下图形的表面积=10×10×6=600．故应填600．14.这个圆柱的内部构造为：圆柱中间有一球状空洞，即空心球．思路导引：通过观察可以发现：在圆柱内部的圆由上至下由点逐渐变成小圆、大圆，又逐渐变成小圆、点；从左往右由点逐渐变成小圆、大圆，又逐渐变成小圆、点．故其内部构造为空心球．15.截面的四条线段AC、CQ、QP、PA分别在展开图中的位置如图1-3-27.思路导引：将图1-3-26（2）中未标的顶点标上，分别在对应面上确定对应线段即可.点拨：解决本题关键是设法找准两图中的对应面.图1-3-27。