矩阵的运算实例程序

hlsl 矩阵乘法HLSL (High-Level Shading Language) 矩阵乘法是在图形编程中使用的重要计算技术之一。

HLSL矩阵乘法可以用来进行矩阵变换、坐标变换、向量旋转等操作。

矩阵乘法是一种性能较高，且具有广泛应用的算法，可以广泛应用于图形编程中的各种应用场景。

本文将介绍HLSL矩阵乘法的基础知识、常用技巧以及应用实例。

一、基础知识1.1 矩阵乘法定义矩阵乘法是指将两个矩阵相乘得到一个新的矩阵。

在有限维向量空间中，矩阵可以看作是一种线性映射，即通过矩阵乘法可以将一个向量映射到另一个向量。

1.2 矩阵乘法规则在HLSL程序中，矩阵乘法的运算符为“*”。

如果A 是m行n列的矩阵，B是n行p列的矩阵，则C=A*B是m行p列的矩阵。

C矩阵中每个元素C(i,j)由以下式子计算得到：C(i,j)=sum(A(i,k)*B(k,j)),其中k的取值范围为1~n。

1.3 矩阵乘法性质1）矩阵乘法不满足交换律，即A*B ≠ B*A 2）矩阵乘法满足结合律，即A*(B*C)=(A*B)*C 3）矩阵乘法中，单位矩阵I是一个特殊的矩阵，满足A*I=I*A=A，其中A为任意矩阵。

二、常用技巧2.1 矩阵转置在矩阵乘法中，A*B与B*A的结果相同，是由于B矩阵在乘法运算之前被转置了。

因此，在HLSL程序中，如果要使用矩阵乘法进行向量或坐标的变换，一般会先转置矩阵，然后再进行乘法运算。

例如，如果要进行向量变换，可以通过如下方式定义顶点着色器：struct VS_INPUT { float4 position : POSITION; float4 normal : NORMAL; };struct VS_OUTPUT { float4 position :SV_POSITION; float3 normal : NORMAL; };cbuffer ConstantBuffer : register(b0){ float4x4 world; float4x4 view;float4x4 projection; };VS_OUTPUT main(VS_INPUT input) { VS_OUTPUT output; output.position = mul(input.position, mul(world, mul(view, projection)));output.normal = mul(input.normal, world).xyz; return output; }其中，world、view和projection是三个矩阵，分别表示世界坐标系、观察坐标系和投影坐标系的变换矩阵。

B1=[b11 b12 b13 b14 ;b21 b22 b23 b24; b31 b32 b33 b34]
运行
17
矩阵的运算(矩阵的加减、数乘、乘积)
C=A1+B1 D=A1-B1 syms c, cA=c*A1 A2=A1(:,1:3), B1 G=A2*B1
18
矩阵的运算(矩阵的加减、数乘、乘积)
求解方程组Ax=b x=A\b 若A为可逆方阵, 输出原方程的解x; 若A为nxm(n>m)阵, 且A’A可逆,输出
原方程的最小二乘解x.
21
矩阵的运算(求解线性方程组)
求矩阵方程：
设A、B满足关系式：AB＝2B+A,求B。 其中A=[3 0 1; 1 1 0; 0 1 4]。
取出A的1、3行和1、3列的交叉处元素 构成新矩阵A1
程序
A=[1 0 1 1 2;0 1 -1 2 3;

3 0 5 1 0;2 3 1 2 1],
vr=[1, 3];vc=[1, 3];
A1=A(vr, vc)
观察结果
26
分块矩阵（矩阵的标识）
将A分为四块，并把它们赋值到矩阵B 中，观察运行后的结果。
3
2
2

35 20 60 45
, B 10
15
50
40

20 12 45 20
将 表 格 写 成 矩 阵 形 式
6
计算
输入下面Matlab指令 A=[4 2 3;1 3 2;1 3 3;3 2 2], B=[35 20 60 45;10 15 50 40;20

3 0 5 1 0;2 3 1 2 1]

col_1=1;
col_2=1;
col_3=1;
col_4=0;
keyfind(12);
col_1=0;
col_2=0;
col_3=0;
col_4=0;
//第一列输出'0'
//第二列输出'0'
//第三列输出'0'
//第四列输出'0'
//列线输出全为'0'
flag++; //每按一下标志位加 1
while(((P1&0x0f)!=0x0f)); //等待按键释放
break; case 2:
keynum=2+col_dat; break; case 4: keynum=3+col_dat; break; case 8: keynum=4+col_dat; break; }
} void keyprocess(void) {
switch(keynum) {
case 1:if(flag==1) //flag=1 表示是第一次按下，按得是被除数 num1=7; //第一个键按下对应是数字 7 if(flag==3) //flag=3 表示是第三次按下，按的是除数 num2=7; break;
计算器
1.程序要求：
用矩阵按键实现简单的加减乘除运算。
2.程序代码：
#include <reg51.h> #include <stdio.h> sbit col_1=P1^4; sbit col_2=P1^5; sbit col_3=P1^6; sbit col_4=P1^7;
unsigned char code table[]={0x3f,0x06,0x5b,0x4f,0x66,0x6d,0x7d,0x07,0x7f,0x6f};//共阴极数 码管 unsigned char keynum,flag; unsigned char num1,num2,flag1,flag2,flag3,flag4; void keyscan(void); void display(); void keyfind(unsigned char); void keyprocess(void);

矩阵的乘法运算矩阵是线性代数中重要的概念，乘法运算是矩阵操作中的核心。

本文将介绍矩阵的乘法运算并详细解析其计算方法。

一、基本概念矩阵是一个由数字构成的矩形阵列。

在描述矩阵时，我们用m行n列的格式表示，即一个m×n的矩阵。

其中，m代表矩阵的行数，n代表列数。

例如，一个2×3的矩阵由2行3列的数字构成，如下所示：```a b cd e f```在矩阵乘法运算中，我们需要注意两个矩阵的尺寸要满足乘法规则：第一个矩阵的列数必须等于第二个矩阵的行数。

二、乘法运算步骤矩阵乘法运算的结果是一个新的矩阵，其行数等于第一个矩阵的行数，列数等于第二个矩阵的列数。

具体的计算步骤如下所示：1. 确定结果矩阵的行数和列数：结果矩阵的行数等于第一个矩阵的行数，列数等于第二个矩阵的列数。

2. 计算元素的值：将第一个矩阵的第i行和第二个矩阵的第j列对应元素相乘，然后将结果累加，得到结果矩阵中的元素值。

通过以上步骤，我们可以进行矩阵的乘法运算。

下面通过一个实例进行具体讲解。

三、实例演示假设有两个矩阵A和B，分别为3×2和2×4的矩阵：```A = a1 a2a3 a4a5 a6B = b1 b2 b3 b4b5 b6 b7 b8```根据乘法规则，我们可以得到结果矩阵C，其尺寸为3×4：```C = c1 c2 c3 c4c5 c6 c7 c8c9 c10 c11 c12```根据乘法运算步骤，我们可以逐个元素地计算矩阵C的值。

C的第一个元素c1的值为a1×b1 + a2×b5，通过类似的计算，我们可以得到C的所有元素值。

通过以上实例演示，我们可以清晰地了解矩阵的乘法运算及其计算步骤。

四、乘法运算的性质矩阵的乘法运算具有一些重要的性质，包括结合律、分配律等。

这些性质使得矩阵乘法在实际中有广泛的应用。

1. 结合律：对于任意的三个矩阵A、B和C，满足(A×B)×C =A×(B×C)。

25 .0 40 .0 55 .0
25 .0 25 .0 47 .5
矩阵运算应用示例三
问题描述：
设我们要为一次聚会准备餐饮，需要10个大型
三明治（巨无霸）、6夸脱（每夸脱约1.14 升——译注）果汁饮料、3夸脱土豆沙拉及2盘 开胃菜。以下数据给出3家不同供货商提供这 些商品的单价：
问题分析一：
问题所要求的是对于题目中所给出的四种矩阵，
理解它们所代表的含义，并根据所提出的三个 问题，将对应的矩阵组合起来，以乘积形式表 述出来。由于各个矩阵代表的含义不同，所以 局阵乘积所代表的含义也尽不相同。
问题分析二：
对于第一个问题是要求出为建造每种类型住宅
需要各种物品的数量，由题意对于C矩阵的定 义我们得知矩阵C正是题目所要求的答案。 对于第二个问题是要求出在每个国家制造每种物
（b）哪个矩阵乘积给出了在每个国家制造 每种物品需要多少费用？ （c）哪个矩阵乘积给出了在每个国家建造 每种类型住宅需要多少费用？
预备知识：
两个矩阵乘积的定义： 矩阵A与B的乘积C的第i行第j列的元素等于第
一个矩阵A的第i行与第二个矩阵B的第j列的对 应元素乘积的和。当然，在矩真乘积定义中， 我要求第二个矩阵的行数与第一个矩阵的列数 相等。

A
机时
I/O 执行 系统
计时收费
B I/0 执行 系统
方式Ⅰ
方式Ⅱ
作业A 作业B
20 10 作业C 5 4 25 8 10 10 5
2 3 6 5 3 4

C 每种类型的作业数量 D 方式Ⅰ 方式Ⅱ 机时比
供货商A 供货商B 供货商C
巨无霸 $ 4.00 $ 6.00 $ 1.00 $ 0.85 $ 5.00 $ 5.00 $ 0.85 $ 1.00 $ 7.00

#include<stdio.h>#define M 20#define N 20float A[M][N];float B[M][N];float C[M][N];int i,j,m,n,p,q;float y=1.0;void main(){printf(" ###########################################\n");printf(" ##### 欢迎您使用矩阵函数包系统。

######\n");printf(" ##### 系统功能: ######\n");printf(" ##### 计算两个矩阵相加,相减; ######\n");printf(" ##### 数乘矩阵；矩阵转置;求逆 ######\n");printf(" ##### 矩阵 ######\n");printf(" ###########################################\n");printf("请选择您需要的运算，按回车键结束\n");printf("************************************************************* *****\n");printf("1，矩阵相加\n");printf("2，矩阵相减\n");printf("3，数乘矩阵\n");printf("4，矩阵转置\n");printf("5，逆矩阵 \n");printf("6，退出 \n");printf("************************************************************* *****\n");int x;scanf("%d",&x);switch (x){case 1:{printf("请输入矩阵A的行数和列数(用逗号隔开):");scanf("%d,%d",&i,&j);printf("请输入矩阵B的行数和列数(用逗号隔开):") ;scanf("%d,%d",&m,&n);if(i!=m||j!=n)printf("***对不起，您输入的两个矩阵不能相加，请重试.***\n");else printf("请输入矩阵A:\n");for(p=0;p<i;p++)for(q=0;q<j;q++)scanf("%f",&A[p][q]);printf("输出矩阵A：\n");for(p=0;p<i;p++)for(q=0;q<j;q++){printf("%10.2f",A[p][q]);if((q+1)%j==0)printf("\n");}printf("请输入矩阵B：\n");for(p=0;p<i;p++)for(q=0;q<j;q++)scanf("%f",&B[p][q]);printf("输出矩阵B：\n");for(p=0;p<i;p++)for(q=0;q<j;q++){printf("%10.2f",B[p][q]);if((q+1)%j==0)printf("\n");}printf("矩阵A+矩阵B为:\n"); //计算两个矩阵相加for(p=0;p<i;p++)for(q=0;q<j;q++)C[p][q]=A[p][q]+B[p][q];for(p=0;p<i;p++)for(q=0;q<j;q++){printf("%10.2f",C[p][q]);if((q+1)%j==0)printf("\n");}};break;case 2:{printf("请输入矩阵A的行数和列数(用逗号隔开):");scanf("%d,%d",&i,&j);printf("请输入矩阵B的行数和列数(用逗号隔开):") ;scanf("%d,%d",&m,&n);if(i!=m||j!=n)printf("***对不起，您输入的两个矩阵不能相减，请重试.***\n"); else printf("请输入矩阵A:\n");for(p=0;p<i;p++)for(q=0;q<j;q++)scanf("%f",&A[p][q]);printf("输出矩阵A:\n");for(p=0;p<i;p++)for(q=0;q<j;q++){printf("%10.2f",A[p][q]);if((q+1)%j==0)printf("\n");}printf("请输入矩阵B：\n");for(p=0;p<i;p++)for(q=0;q<j;q++)scanf("%f",&B[p][q]);printf("输出第矩阵B:\n");for(p=0;p<i;p++)for(q=0;q<j;q++){printf("%10.2f",B[p][q]);if((q+1)%j==0)printf("\n");}printf("矩阵A-矩阵B为：\n"); //计算两个矩阵相减for(p=0;p<i;p++)for(q=0;q<j;q++)C[p][q]=A[p][q]-B[p][q];for(p=0;p<i;p++)for(q=0;q<j;q++){printf("%10.2f",C[p][q]);if((q+1)%j==0)printf("\n");}};break;case 3:{float k;printf("请输入矩阵A的行数和列数(用逗号隔开):"); scanf("%d,%d",&i,&j);printf("请输入矩阵A\n");for(p=0;p<i;p++)for(q=0;q<j;q++)scanf("%f",&A[p][q]);printf("输出矩阵A\n");for(p=0;p<i;p++)for(q=0;q<j;q++){printf("%10.2f",A[p][q]);if((q+1)%j==0)printf("\n");}printf("请输入一个实数:\n");scanf("%f",&k);for(p=0;p<i;p++) //数乘矩阵for(q=0;q<j;q++)B[p][q]=k*A[p][q];printf("输出k乘矩阵A的结果\n");for(p=0;p<i;p++)for(q=0;q<j;q++){printf("%10.2f",B[p][q]);if((q+1)%j==0)printf("\n");}};break;case 4:{printf("请输入矩阵A的行数和列数(用逗号隔开):"); scanf("%d,%d",&i,&j);printf("请输入矩阵A:\n");for(p=0;p<i;p++)for(q=0;q<j;q++)scanf("%f",&A[p][q]);printf("输出矩阵A\n");for(p=0;p<i;p++)for(q=0;q<j;q++){printf("%10.2f",A[p][q]);if((q+1)%j==0)printf("\n");}for(p=0;p<i;p++) //转置for(q=0;q<j;q++)B[q][p]=A[p][q];printf("输出矩阵A的转置矩阵:\n");for(p=0;p<j;p++)for(q=0;q<i;q++){printf("%10.2f",B[p][q]);if((q+1)%i==0)printf("\n");}};break;case 5:float a[M][2*M];float b[N][2*N];float t,x;int k,T;printf("输入方阵的维数：\n"); //请输入方阵，即行和列相等的矩阵。

fortran77中矩阵的表示方法【原创版5篇】目录（篇1）1.Fortran77 简介2.Fortran77 中矩阵的表示方法2.1 矩阵的存储方式2.2 矩阵的访问方式2.3 矩阵的操作方法3.Fortran77 矩阵操作的实例4.总结正文（篇1）一、Fortran77 简介Fortran（Formula Translation，公式翻译）是一种编程语言，主要用于数值计算和科学计算领域。

Fortran77 是 Fortran 语言的一个版本，发布于 1977 年。

由于其在数值计算方面的优越性能，Fortran77 在科学研究和工程应用中得到了广泛应用。

二、Fortran77 中矩阵的表示方法在 Fortran77 中，矩阵是一种数组，可以用来存储和处理数据。

矩阵的表示方法包括以下几个方面：2.1 矩阵的存储方式Fortran77 中，矩阵采用行存储方式，即按行存储矩阵元素。

矩阵的下标从 1 开始，行下标和列下标都是从 1 开始的。

2.2 矩阵的访问方式在 Fortran77 中，可以通过以下方式访问矩阵元素：- 直接访问：使用数组下标，例如 A(i,j) 表示访问矩阵 A 中第 i 行第 j 列的元素。

- 间接访问：使用指向数组的指针，例如指针 P 指向矩阵 A 的首地址，那么 P(i,j) 表示访问矩阵 A 中第 i 行第 j 列的元素。

2.3 矩阵的操作方法Fortran77 提供了丰富的矩阵操作函数，包括矩阵加法、减法、乘法、转置等。

矩阵操作的方法如下：- 矩阵加法：使用函数 CALL "MXPLUS"，例如 CALL "MXPLUS"(A, B, C)，表示对矩阵 A 和矩阵 B 进行加法运算，并将结果存储在矩阵 C 中。

- 矩阵减法：使用函数 CALL "MXMINUS"，例如 CALL "MXMINUS"(A, B, C)，表示对矩阵 A 和矩阵 B 进行减法运算，并将结果存储在矩阵 C 中。

矩阵旋转90度的运算
摘要：
1.矩阵旋转90 度的概念
2.矩阵旋转90 度的运算方法
3.矩阵旋转90 度的应用实例
正文：
一、矩阵旋转90 度的概念
矩阵旋转是一种重要的矩阵变换方式，它可以将一个矩阵按照某个中心点进行旋转。

在二维空间中，矩阵旋转90 度指的是将矩阵沿y 轴进行旋转90 度。

具体来说，就是将矩阵中的每个元素按照其与y 轴的距离进行重新排列。

矩阵旋转90 度在数学、物理和工程领域中有着广泛的应用。

二、矩阵旋转90 度的运算方法
矩阵旋转90 度的运算方法可以通过以下步骤来完成：
1.确定旋转矩阵的大小。

根据旋转的角度和矩阵的尺寸，可以计算出旋转矩阵的大小。

2.计算旋转矩阵的元素。

根据旋转矩阵的大小，可以计算出旋转矩阵的每个元素。

3.对原矩阵进行矩阵乘法运算。

将原矩阵与旋转矩阵进行矩阵乘法运算，得到旋转后的矩阵。

三、矩阵旋转90 度的应用实例
矩阵旋转90 度在实际应用中有很多实例，下面举一个简单的例子来说
明。

P14-7
3. 矩阵的乘法
3) 矩阵乘法满足下列运算律: (1) 结合律 (AB)C=A(BC)
矩 阵
(2) 数乘结合律 k(AB)=(kA)B=A(kB), 其中k是实数
(3) 左分配律 A(B+C)=AB+AC 右分配律 (B+C)A=BA+CA 左提？右提？
(4) 设 A 是 m × n 矩阵，Em 是 m 阶的单位矩阵，
En 是 n 阶单位矩阵，则 Em A=AEn = A
单位阵相当于数1 P14-8
3. 矩阵的乘法
矩 阵
4) 方阵的幂 设A是 n 阶矩阵, k个A的连乘积称为A的 k 次幂,
记作 Ak ，即
A AA A
k k个
• 方阵的幂满足下列性质：（ m,k为正整数）
(1) AmAk=Am+k (2) (Am)k=Amk
b12 b1 n a22 b2 n as 2 bsn
s
• 则A与B之乘积AB，记作C=(cij )，是一个mn矩阵,
cij ai1b1 j ai 2b2 j aisbsj aikbkj
k 1
• 矩阵C的第 i 行第 j 列元素cij , 是A的第 i 行元素与B的 第 j 列元素对应相乘相加 两个矩阵能够进行乘法运算的条件是什么？ P14-6
1. 矩阵的加法 1) 设A=(aij)和B=(bij)是两个mn矩阵, 规定
Hale Waihona Puke 矩 阵 a11 b11 a b A B ( aij bij ) 21 21 am1 bm1
a12 b12 a22 b22 am 2 bm 2
a1n b1 n a2 n b2 n amn bmn

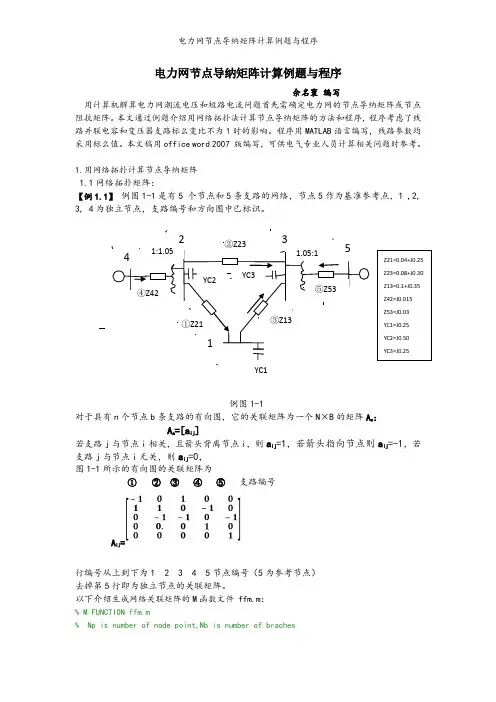
电力网节点导纳矩阵计算例题与程序佘名寰 编写用计算机解算电力网潮流电压和短路电流问题首先需确定电力网的节点导纳矩阵或节点阻抗矩阵。

本文通过例题介绍用网络拓扑法计算节点导纳矩阵的方法和程序，程序考虑了线路并联电容和变压器支路标么变比不为1时的影响。

程序用MATLAB 语言编写，线路参数均采用标么值。

本文稿用office word 2007 版编写，可供电气专业人员计算相关问题时参考。

1.用网络拓扑计算节点导纳矩阵 1.1网络拓扑矩阵：【例1.1】 例图1-1是有5 个节点和5条支路的网络，节点5作为基准参考点，1 ,2, 3, 4为独立节点，支路编号和方向图中已标识。

例图1-1对于具有n 个节点b 条支路的有向图，它的关联矩阵为一个N ×B 的矩阵A a ：A a =[a ij ]若支路j 与节点i 相关，且箭头背离节点i ，则a ij =1，若箭头指向节点则a ij =-1，若支路j 与节点i 无关，则a ij =0，图1-1所示的有向图的关联矩阵为① ② ③ ④ ⑤ 支路编号A ij =行编号从上到下为1 2 3 4 5节点编号（5为参考节点） 去掉第5行即为独立节点的关联矩阵。

以下介绍生成网络关联矩阵的M 函数文件 ffm.m ：% M FUNCTION ffm.m% Np is number of node point,Nb is number of braches ②Z23③Z13①Z21YC2YC3YC1④Z42⑤Z531:1.051.05:142315Z21=0.04+J0.25 Z23=0.08+J0.30 Z13=0.1+J0.35 Z42=J0.015 Z53=J0.03 YC1=J0.25 YC2=J0.50 YC3=J0.25% nstart--the start point of branches ,nend -- the end point,% A -- network incidence matrixfunction[A]=ffm(nstart,nend)global Np Nbn=length(nstart);A=zeros(Np,Nb);for i=1:nA(nstart(i),i)=1;A(nend(i),i)=-1;end以例图1-1网络为例调用ffm.m文件求其关联矩阵运算以上程序可得关联矩阵 mm ij如下：mm =-1 0 1 0 01 1 0 -1 00 -1 -1 0 -10 0 0 1 00 0 0 0 1Mm ij明显与A ij是相同的。

课程设计任务书目录PART I1 需求分析 (2)2 算法基本原理 (2)3 类设计 (3)4 详细设计 (4)4.1类的接口设计 (4)4.2类的实现 (5)4.3主函数设计 (11)5 运行结果与分析 (12)5.1程序运行结果 (12)5.2运行结果分析 (14)PART Ⅱ1 需求分析 (24)2 算法基本原理 (24)3 类设计 (14)4 详细设计 (15)4.1类的实现 (15)4.2主函数设计 (19)5 运行结果与分析 (27)5.1程序运行结果 (27)5.2运行结果分析 (27)6 参考文献 (15)PART I1 需求分析矩阵是线性代数里一个重要的概念，在这里采用C++语言实现一个简单的n ×n矩阵类，类中包括一些简单的运算等操作具体要求如下：（1）使用构造函数完成方阵的初始化赋值（动态内存分配）；（2）使用析构函数完成矩阵动态内存的释放；（3）重载加法运算符＋，实现两个矩阵的和；（4）重载加法运算符－，实现两个矩阵的差；（5）重载加法运算符*，实现两个矩阵的积；（6）重载加法运算符=，实现两个矩阵之间的赋值；（7）使用函数实现矩阵的转置；（8）使用函数求矩阵中的最大值；（9）使用函数求矩阵中的最小值；（10）添加函数Det以得到矩阵对应行列式的值；（11）重载加法运算符<<，实现矩阵按照行列的格式输出；（12）编写一个主函数测试上述功能。

2 算法基本原理矩阵进行加法，减法，乘法运算时，必须满足两个矩阵阶数相同的条件。

加法，减法计算是把矩阵对应的各行各列的每一对数值分别进行加减法运算，结果组成一个新的同阶矩阵。

矩阵乘法是这样定义的，只有当矩阵A的列数与矩阵B的行数相等时A×B才有意义。

一个m×n的矩阵a（m,n)左乘一个n×p的矩阵b（n,p)，会得到一个m×p的矩阵c（m,p)，满足矩阵乘法满足结合率，但不满足交换率3 类设计从上面的算法分析可以看到，本设计面临的计算问题的关键是矩阵运算。

二．概要设计：
1、抽象数据类型定义如下： ADT SparseMatrix{ 数据对象D：D=｛aij|i=1,2,3…,m;j=1,2,3…,n; ai ∈ElemSet,m和n分别称为矩阵的行数和列数｝ 数据关系R： R={Row,Col} Row={<ai,j,ai,j+1>|1≤i≤m, 1≤j≤n-1} Col={<ai,ai+1,j>|1≤i≤m-1, 1≤j≤n} 基本操作 本程序中，用三元组顺序表作为存储结构。 (1)、CreatSMatrix (TSMatrix &M) 操作结果：创建矩阵M。 (2)、AddSMatrix(TSMatrix A,TSMatrix B,TSMatrix &C,int n) 初始条件：矩阵A和B的行数和列数对应相等。 操作结果：求矩阵A、B的和C=A+B。 (3)、SubMatrix (TSMatrix *a,TSMatrix *b) 初始条件：矩阵A和B的行数和列数对应相等。 操作结果：求矩阵A、B的和C=A+B。 (4)、MultiplicationMatrixPow (TSMatrix *a,TSMatrix *b,TSMatrix *c) 初始条件：矩阵A和B的行数和列数匹配 操作结果：求矩阵A、B的和C=A*B。 (5) OutputSMatrix(TSMatrix M) 初始条件：矩阵M已存在 操作结果：输出矩阵M 2、 本程序包含5个模块
for(i=1;i<=M->mu;i++)//输出矩阵 { for(j=1;j<=M->nu;j++) printf("%5d",a[i][j]); printf("\n"); } } //*************矩阵的求和运算*****************// int AddSMatrix(TSMatrix *M,TSMatrix *N,TSMatrix *Q)//求 采用三元组顺序表存储表示的稀疏矩阵M和N的和,结果赋给矩阵Q { int i,j,p,q,x=0,y=0; if((M->mu<=0)||(M->nu<=0)||(M->tu<=0)||(N->mu<=0)||(N>nu<=0)||(N->tu<=0))//判断行数列数非零元素个数是否符合匹配 return ERROR; if(M->mu!=N->mu||M->nu!=N->nu)//判断A与B的行列数 是否相等的 return ERROR; Q->mu=M->mu;//矩阵Q的初始化 Q->nu=M->nu; Q->tu=0; for(i=1;i<=Q->mu;i++) { for(j=1;j<=Q->nu;j++)//寻找矩阵M,N中非零元素相等 的行列 { for(p=1;p<=M->tu;p++)//求矩阵M行列中所对应的 非零元素的值 赋值给X { if((i==M->data[p].row)&&(j==M->data[p].col))// 如果i是矩阵M中非零元素行，j是其列 { x=M->data[p].e;

matlab 矩阵运算程序MATLAB是一种强大的数学软件，主要用于数值计算、算法开发、数据可视化和数据分析等。

在MATLAB中，矩阵运算是非常常见的操作。

以下是一个简单的MATLAB矩阵运算程序示例：```matlab创建两个矩阵A和BA = [1, 2, 3;4, 5, 6;7, 8, 9];B = [9, 8, 7;6, 5, 4;3, 2, 1];矩阵加法C = A + B;disp('矩阵A和矩阵B的和：');disp(C);矩阵减法D = A - B;disp('矩阵A和矩阵B的差：'); disp(D);矩阵乘法E = A * B;disp('矩阵A和矩阵B的乘积：'); disp(E);矩阵转置T = transpose(A);disp('矩阵A的转置：');disp(T);求矩阵的行列式det_A = det(A);disp('矩阵A的行列式：');disp(det_A);求矩阵的逆矩阵inv_A = inv(A);disp('矩阵A的逆矩阵：');disp(inv_A);求矩阵的秩rank_A = rank(A);disp('矩阵A的秩：');disp(rank_A);求矩阵的特征值eig_A = eig(A);disp('矩阵A的特征值：');disp(eig_A);```以上程序演示了MATLAB中的一些基本矩阵运算，如加法、减法、乘法、转置、求行列式、求逆矩阵、求秩和求特征值等。

您可以根据实际需求修改矩阵A和B的值，然后运行该程序以观察结果。

需要注意的是，这里的矩阵运算都是在MATLAB环境下进行的。

如果要编写比MATLAB更快的矩阵运算程序，可以尝试使用如C、C++等编程语言，并链接到高性能的数学库，如Intel的Math Kernel Library（MKL）。

matlab 计算矩阵hurwitz的程序在Matlab中，你可以使用以下代码计算一个矩阵的Hurwitz矩阵。

Hurwitz矩阵是一个实对称矩阵，其主子式都是正的。

```matlabfunction isHurwitz = isHurwitzMatrix(A)% 输入参数A是待检测的矩阵% 获取矩阵A的大小[n, ~] = size(A);% 初始化Hurwitz矩阵标志isHurwitz = true;% 检查矩阵是否为实对称矩阵if ~isequal(A, A')disp('矩阵不是实对称矩阵，无法判断是否为Hurwitz矩阵。

');isHurwitz = false;return;end% 检查主子式是否都为正for k = 1:nsubmatrix = A(1:k, 1:k);if det(submatrix) <= 0isHurwitz = false;disp(['矩阵不是Hurwitz矩阵，因为第', num2str(k), ' 个主子式非正。

']);return;endenddisp('矩阵是Hurwitz矩阵。

');end```你可以将这个函数保存在一个名为`isHurwitzMatrix.m` 的文件中，然后在Matlab中调用它：```matlab% 定义一个实对称矩阵AA = [1, 2, 3; 2, 4, 5; 3, 5, 6];% 检测是否为Hurwitz矩阵isHurwitz = isHurwitzMatrix(A);```请注意，这个代码片段假设输入矩阵`A` 是实对称矩阵。

如果矩阵不是实对称的，它将输出相应的提示信息并返回`false`。

否则，它将检查矩阵的主子式是否都为正。

如果是，它将输出成功的消息并返回`true`。

如果有一个主子式非正，它将输出相应的提示信息并返回`false`。

矩阵的乘法运算及其计算器程序
马德胜;孔繁芸
【期刊名称】《中国校医》
【年(卷),期】1991(5)1
【摘要】随着卫生统计学的广泛应用及模糊数学的兴起和发展,儿少卫生学科中在处理调查和实验资料时采用矩阵运算法已逐渐增多。

本文把常用的矩阵乘法运算结合儿少实例作一简单介绍,并编制一份可由CASIOfx-180P(或3500P、3600P等)计算器完成其全部运算的计算程序,用以简化运算。

1
【总页数】5页(P61-64)
【关键词】矩阵;乘法运算;计算器程序
【作者】马德胜;孔繁芸
【作者单位】南通医学院
【正文语种】中文
【中图分类】R311
【相关文献】
1.S—W型二阶矩阵快速乘法的最少乘法运算次数 [J], 周德俊;邢永丽
2.MATLAB 程序对分块矩阵在矩阵乘法中算法的实现 [J], 樊馨蔓;梅玉
3.基于MATLAB矩阵运算的大整数乘法设计与实现 [J], 滕旭
4.基于TBL理念的线性代数课程教学设计——以“矩阵乘法及其运算规律”为例
[J], 涂正文;吴艳秋
5.卫星网络中的压缩编码分布式矩阵-向量乘法运算算法 [J], 赵家毅;张金钡;辛宁因版权原因，仅展示原文概要，查看原文内容请购买。

torch不同维矩阵相加运算摘要：1.引言2.torch 中矩阵的定义和操作3.不同维矩阵相加的规则4.实例解析5.结论正文：1.引言在深度学习框架PyTorch（简称torch）中，矩阵运算是非常常见的操作。

矩阵在torch 中被称为张量（tensor），它可以是多维的，即可以有不同的维度。

这就涉及到一个常见的问题，即如何对不同维度的矩阵进行相加操作。

本文将对此进行详细的解析。

2.torch 中矩阵的定义和操作在torch 中，矩阵实际上是一个多维数组，称为张量。

张量的每个元素都是一个标量。

张量可以进行各种数学运算，如加法、减法、乘法等。

torch 提供了丰富的操作函数来方便地进行这些运算。

3.不同维矩阵相加的规则在torch 中，对不同维度的矩阵进行相加操作，需要遵循以下规则：- 两个矩阵的维度必须相同，否则无法进行相加操作。

- 相加操作会自动将两个矩阵的对应元素进行相加，并返回一个新的矩阵。

4.实例解析下面通过一个实例来说明如何在torch 中对不同维度的矩阵进行相加操作：```pythonimport torch# 创建两个不同维度的张量a = torch.tensor([[1, 2], [3, 4]]) # 维度为2x2b = torch.tensor([1, 2, 3, 4]) # 维度为4# 对两个张量进行相加操作result = a + bprint(result)```运行上述代码，会输出如下结果：```tensor([[2, 4],[4, 6]])```从结果可以看出，两个不同维度的矩阵在torch 中进行了相加操作，并返回了一个新的矩阵。

5.结论在torch 中，对不同维度的矩阵进行相加操作，需要确保两个矩阵的维度相同。

相加操作会自动将两个矩阵的对应元素进行相加，并返回一个新的矩阵。