当前位置：文档之家 › 数学物理方法 第5章 傅里叶变换

数学物理方法 第5章 傅里叶变换

  • 格式：ppt
  • 大小：628.00 KB
  • 文档页数：52

下载文档原格式

  / 52

合集下载

数学物理方法 复变函数 第五章 傅立叶变换

数学物理方法 复变函数 第五章 傅立叶变换

从物理上看 , 显然有 ∞
∫
ρ (x) d x = m......(4)
ቤተ መጻሕፍቲ ባይዱ
也即
-∞
∫
∞
-∞
lim ρ l (x) d x = m
l→ 0
由 (3) 、（ 4）可以看出质点线密度
分布函数的直观图像。
它在
x ≠ 0时 , 为 0; 在 x = 0时，为 ∞ 。它的积分值为 m. 也即由 (3) 、 共 (4) 同来描述。
因此 , 在 Dirac 首次引入 δ 函数时，曾遭到许多数 学家的非难 但它在近代物理学中有 许多重要的应用 , 它可以用来描述物 理学中的一切点量 (点质量 \ 点电荷 \ 瞬时源 )且物理图象清 晰 .这样迫使数学家对 δ 函数的性质等进行研究 和解释 .
下一页 上一页 返回
第5章
傅里叶变换(Fourier transforms)
-∞
第5章
傅里叶变换(Fourier transforms)
第5节 δ函数
五 δ函数的性质
2 δ 函数具有挑选性
若 a = 0, 则有
这 一 性 质 表 明 , 虽 然 δ (x) 是 广 义 函 数 ， 但 它 和 任 何 连 续 函 数 的 乘 积 在 （ － ∞， ＋ ∞） 内 的 积 分 都 有 明 确 的 意 义 。 这 使 得 它在近代物理和工程技术中有广泛的应用。
..........
...(1)
下一页 上一页 返回
第5章
傅里叶变换(Fourier transforms)
第5节 δ函数
引入δ 一 引入δ函数的物理背景
注意 rect() 的写法 : 即保证 rect() 中的量的绝对值 >
数学物理方法 第五章 傅里叶变换

数学物理方法 第五章 傅里叶变换


将上式改写成

f (x) 0 C() cos[x ()]d
其中
1
C() [ A()]2 [B()]2 2
称为f (x)的振幅谱
() arctan[B() / A()] 称为f (x)的相位谱
与傅里叶级数的情形类似，奇函数f (x)的傅里叶积分
是傅里叶正弦积分。
A

2N
0 0
[cos( 0 )t cos( 0 )t]dt
N 2


A


sin( 0 0
)t

sin( 0 )t 0

0 0
A sin( N 2 )[ 1 1 ]
0
0 0
解：f (t)是偶函数，可按余弦展开。

f (t) 0 A() costd
其中：
A() 2

f ( ) cos d
0

2

T
0
h cos d

2h


sin T
例2 由2N个（N是正整数）正弦波组成的有限正弦波列：
f
(t
)


A
sin
0t


l
cos
l
k x
l
cos n x
l
dx
0
(k n)


l
sin
l
k x sin
l
n x
l
dx

0
(k n)


l
cos
l
k x sin
l
数学物理方程第五章 傅里叶变换

数学物理方程第五章 傅里叶变换


1 k
1 k
0 2E0 ] 1 k [1 ( 2 n ) 2 ] 1
k 2n 1 k 2 n.
2012-8-1
阜师院数科院
b1
E0 2
,
和
bk 0

E (t )
E0


E0 2
sin t
2E0

1 (2n)
n 1
1
2
cos 2 n t .


f ( ) sin d .
(5.2.4) 是 f(x) 的傅里叶积分，(5.2.5) 为它的傅里叶变换。
f ( x ) A ( ), B ( )
为某函数从时域到频域的变换。频域中的函数可能是连续的。
傅里叶积分定理：若函数 f(x) 在区间 ( , ) 上满足条件(1) 在任意有限区间满足狄 里希利条件；(2) 在区间 ( , ) 上绝对可积（即
2 2
0
( ) tg
1
[ B ( ) / A ( )].
C ( )
为振幅谱
3. 奇、偶函数 偶函数
2012-8-1
( )
为相位谱
A ( ) cos xd ,
f (x) A ( )


0
奇函数
f (x) B ( )


B ( ) sin xd ,
f (x)
k
c

k
e
ikx
,
ck
1 2



f ( )e ( 1 ik e
ikx
d
0
1 2 ( 1 ik
数学物理方法 5 傅里叶变换

数学物理方法 5 傅里叶变换


4
( t , t 0)
由上例可以推断：一个周期为2l的函数f(x+2l)= f(x) 可以 看作是许多不同频率的简谐函数的叠加.
6
2. 三角函数族及其正交性 引入三角函数族
①其中任意两个不同的函数之积在 [-l,l]上的积分等于 0 .
②两个相同的函数的乘积在[-l,l]
上的积分不等于 0 .
(2m ,(2m 1) ) ((2m 1) , 2m )
k
ce
k
ik

ikx
,

1
0
1


2
x
0



f ( )e
1 d 2


0
1 e

0
ik
1 d 2

1 e ik d
1 1 ik ( e ) 2 ik
ak cos
l
l
d
12
1 l k ak f ( )cos d ( k 1, 2 , ) l l l
类似地, 用 sin kπξ/l 乘 ① 式两边, 再逐项积分可得
1 l k bk f ( )sin d l l l
归纳:
(k 1, 2, )
变换 延拓
23
3. 傅里叶级数的复数形式
利用欧拉公式导出
• 1 • 2
24
5.2 傅里叶积分与傅里叶变换 （一） 傅里叶变换
周期函数的性质是f(x+2l)=f(x), x每增大2l，函数值就重复 一次，非周期函数没有这个性质，但可以认为它是周期2l∞ 的周期函数。所以，我们也可以把非周期函数展开为所谓“傅 里叶积分”。 考察复数形式的傅里叶级数:
数学物理方法梁昆淼答案

数学物理方法梁昆淼答案

数学物理方法梁昆淼答案【篇一：第五章傅里叶变换数学物理方法梁昆淼】>?t1.函数 f(t)???0?12. 函数 f(t)???03.设(|t|?1)(|t|?1)的傅里叶变换为2(?cos??sin?/?)/(??)(|t|?1)(|t|?1)的傅里叶变换为f(?)?2sin?/??。

的傅立叶变换像函数，的傅立叶变换像函数为 _______________________ 。

4.?2012?2011excosx??(x??) dx?[sinx??(x??e??。

5. ?12009?6 ?2008) ]dx? 6.?xsinx?(x? ?1?3) dx?。

7. ?xsinx?(x?) dx? ?128.?[(x2?1)tan(sinx)??(x?)] dx? 。

?201038?911??9.?x3 ?(x?3) dx?－27 。

?tf(t)?10.函数 ??0(|t|?1)(|t|?1)的傅里叶变换为2(?cos??sin?/?)/(??)。

(0?t?1)?1?(?1?t?0)的傅里叶变换为。

11. f(t)???1?0(|t|?1)?12. 在(??,?)这个周期上，f(x)?x。

其傅里叶级数展开为?k?1?2sinkx k13.当0?x?2时，f(x)??1；当?2?x?0时，f(x)?1；当|x|?2时，f(x)?0。

则函数的f(x)傅里叶变换为b(?)?2??(1?cos2?)1?14已知函数f(x)的傅里叶变换为f(?)，试证明f(ax)的傅里叶变换为f()。

af[f(ax)]?1?2????f(ax)e?i?xdx【令x?y/a】?1?2????f(y)e?i?aydya【令y?x】?1?f(x) ?i?ax2????aedx?1?af(a)a---(2分) ---(2分) ---(2分) ---(2分) 证明：【篇二：8000份课程课后习题答案与大家分享~~】> 还有很多，可以去课后答案网（/bbs）查找。

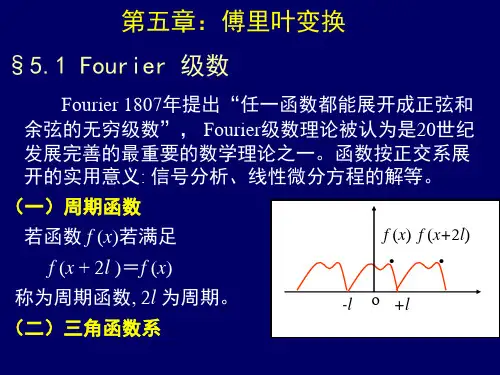
数学物理方法 第五章 傅里叶变换

数学物理方法 第五章 傅里叶变换


l
2
1 2 2 2 2 [ f ( x )] dx 2la0 l a k l bk 2l l k 1 k 1
l n n
n n 1 l k x 2 k x 2 2 l 2 l 2 [ f ( x )] dx a k [cos ] dx bk [ sin ] dx l l l 2l l l k 0 k 1 n n 1 l k x 2 k x 2 2 l 2 l 2 [ f ( x )] dx a k [cos ] dx bk [ sin 10 ] dx l l l 2l l l k 0 k 0
积化和差后容易证明其余三式， 例如：
cos( ) cos( ) 2 cos cos kx nx 1 ( k n )x ( k n )x cos cos cos cos l l 2 l l l l kx nx 1 l ( k n )x ( k n )x -l cos l cos l dx 2 -l cos l dx -l cos l dx
0πx πx 2πx kx 1 cos , cos , cos , , cos , l l l l 0πx πx 2πx kx sin 0, sin , sin , , sin , l l l l
k x -l 1 cos l dx 0 (k 0) 正交性 l k x -l 1 sin l dx 0 l k x n x -l cos l cos l dx 0 (k n) l k x n x -l sin l sin l dx 0 (k n) l k x n x -l cos l sin l dx 0
f (x) f (x+2l) • -l o +l •
傅里叶变换

傅里叶变换


线性性质
k f(x) → k F(ω); f(x)+g(x) → F(ω)+ G(ω)
分析性质
f '(x) → iωF(ω);
∫
x
∞
f ( x ) dx →
1 iω
F (ω )
傅里叶变换
位移性质
f(x-a) → exp(-iωa)F(ω) ; exp(iφx)f(x) → F(ω-φ)
相似性质
f(ax) → F(ω/a)/a; f(x/b)/b → F(bω) .
卷积性质
f(x)*g(x)≡∫f(ξ)g(x-ξ)dξ → 2πF(ω)G(ω); f(x)g(x) → F(ω)*G(ω)≡∫ F(φ)G(ω-φ)dφ
对称性质
正变换与逆变换具有某种对称性; 适当调整定义中的系数后,可以使对称性更加明显.
傅里叶变换
应用举例
rect( x) → sin 1 ω /(π ω) 2
S1 1
S3 0.75
0.5
0.5 0.25
-3
-2
-1 -0.5
1
2
3
-3
-2
-1 -0.25 -0.5 -0.75
1
2
3
-1
S6 0.75 0.5 0.25 -3 -2 -1 -0.25 -0.5 -0.75 1 2 3 -3 -2 -1
S24 0.75 0.5 0.25 1 -0.25 -0.5 -0.75 2 3
展开系数:
1 cn = 2L
∫
L
L
exp(i
nπ x ) f ( x)dx L
傅里叶生平
1768年生于法国 1807年提出"任何 周期信号都可用正 弦函数的级数表示" 1822年发表"热的 分析理论",首次 提出"任何非周期 信号都可用正弦函 数的积分表示" 返 回
数学物理方法第五章傅里叶变换

数学物理方法第五章傅里叶变换


l
l
l
l kx nx
sin cos dx0
l
l
l
l
1 2 dx 2 l
l
l
sin
2 k x dx
l
l
l
cos
2 k x dx
l
l
2、可以由函数的正交性求出傅立叶级数中的系数；
a f 1 l
0 2l l
xdx
a f 1l n l l
xconsxdx
l
(n1,2,3, )
b f 1l n l l
( a k cos
kπx l
b k sin
kπx )
l
k 1
2
2l l
说明 1、三角函数族是两两正交的
l kx
cos d x 0
l
l
(k 0),
l kx
sin d x 0
l
l
l kx nx
cos cos d x 0 (k n)
l
l
l
l kx nx
sin sin dx0 (kn),
f (x)
a
x
l
延拓到（- l，l）后再周期延拓，如图做偶延拓：
f (x)
a
l 0 l
x
所以
1l
x
a
a0
l
a(1
0
l
)dx 2
ak2 l0 la(1x l)co k lx sd x 2(2 4 n a 0 1 )2(k (k 2n )2n1 )
如图做奇延拓： f (x)
a
l
0l
x
2l x kx 2a
An 2cn
A n 称为f ( x)的振幅频谱（简称为频谱）.它描述了各次谐波 的振幅随频率变化的分布情况。它清楚地表明了一个非正旋 周期函数包含了哪些频率分量及各分量所占的比重（如振幅 的大小）。因此频谱图在工程技术中应用比较广泛.所谓频谱 图，通常是指频率和振幅的关系图。
数学物理方法5傅里叶变换

数学物理方法5傅里叶变换

图像压缩。
图像增强
通过改变图像的频率成分，傅里叶 变换可以帮助增强图像的某些特征， 如边缘和纹理。
图像去噪
傅里叶变换可以帮助识别和去除图 像中的噪声，从而提高图像的质量。
量子力学
波函数分析
在量子力学中，波函数是一个描述粒子状态的函数。傅里叶变换 可以用来分析波函数的性质和行为。
量子纠缠
傅里叶变换在量子纠缠的研究中也有应用，可以帮助我们更好地理 解这种神秘的现象。
时间-频率分析
傅里叶变换将时间域的信号转换 为频率域的信号，通过分析信号 在不同频率下的强度和相位，可 以揭示信号的频率结构和变化规
律。
周期信号分析
对于周期信号，傅里叶变换可以 将其表示为一系列正弦波和余弦 波的叠加，从而方便地分析其频
率成分和振幅。
非周期信号分析
对于非周期信号，傅里叶变换将 其表示为无穷多个不同频率的正 弦波和余弦波的叠加，可以揭示
振动系统分析
在振动系统的分析中，傅里叶变换可以用于将时间域的振动信号转换为角频率域的信号， 从而方便地计算系统的固有频率、阻尼比等参数。
热传导分析
在热传导现象的分析中，傅里叶变换可以用于将时间域的温度分布转换为角频率域的温度 分布，从而方便地分析热传导的频率特性和变化规律。
05结果 具有共轭对称性，即F(-ω)=F*(ω)。
傅里叶变换的应用
01
02
03
信号处理
傅里叶变换在信号处理中 应用广泛，如频谱分析、 滤波、调制解调等。
图像处理
傅里叶变换在图像处理中 用于图像的频域分析，如 图像增强、去噪、特征提 取等。
数值分析
傅里叶变换在数值分析中 用于求解偏微分方程、积 分方程等数学问题。
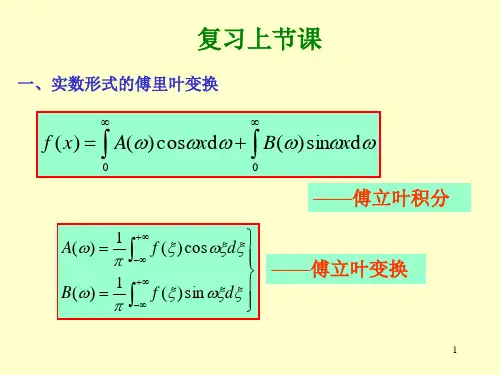
数学物理方法chp5-3 傅里叶变换delta函数

数学物理方法chp5-3 傅里叶变换delta函数


a
11
5.函数的
( x ) 0 的实根 xk (k 1,2,3,) 全为单根 ( ' ( x) 0) 有 ( x xk ) ( x ) k | ' ( xk ) |
0, ( x ) 0 ( x) , ( x ) 0
1/l -l/2
o
l/2
x
15
（2）sinc 函数序列：
1 sin Kx ( x ) lim K x
6 5 4 3
K=8
K=16
sinKt/(pi*t)
2 1 0 -1 -2 -2
K=4Leabharlann -1.5-1-0.5
0 t
0.5
1
1.5
2
16
（3） 函数序列： ( x )
60
lim
m x 0, ( x 0) ( x) lim l ( x) lim rect , ( x 0) l 0 l 0 l l



( x)dx lim l ( x)dx m
l 0

引入δ函数：
0, ( x 0) ( x) , ( x 0) 0, a ( x)dx 1
（一）δ函数概念
– 问题 • 质点的密度函数如何表示？ • 一般函数无法描写物理上的“点源”，如“点电荷”、 “质点”的密度，以及“瞬时力”等概念。 – 思路 • 质点是物体在尺度趋于零时的理想模型； • 一个位于原点、长度l、质量为m的线，线密度为 l(x)=m/l rect(x/l)的物体，当l->0时,可以看成质点；
( x ) C ( )eix d
傅里叶变换

傅里叶变换

傅立叶原理表明：任何连续测量的时序或信号，都可以表示为不同频率的正弦波信号的无限叠加。

而根据该原理创立的傅立叶变换算法利用直接测量到的原始信号，以累加方式来计算该信号中不同正弦波信号的频率、振幅和相位。

傅立叶变换要求连续信号在时间上必须可积这一充分非必要条件F(jw)是频谱密度函数或频谱函数傅立叶级数明确地表示了谐波频率与其幅值与相位的关系，根据频率就可以确定各次谐波的幅值。

那对非周期信号做傅立叶变换得到的是连续频谱密度函数，某一频率点的信号幅度是无穷小，没有意义，那这个频谱密度函数有什么用呢？前四种傅里叶变换都是针对正无穷大和负无穷大的信号，即信号的的长度是无穷大的，计算机无法处理。

针对长度有限的信号，解决方法有两种：（1）.长度有限的信号表示成长度无限的信号，可以把信号无限地从左右进行延伸，延伸的部分用零来表示，这样，这个信号就可以被看成是非周期性离散信号，我们就可以用到离散时域傅立叶变换的方法。

（2）.也可以把信号用复制的方法进行延伸，这样信号就变成了周期性离散信号，这时我们就可以用离散傅立叶变换方法进行变换。

但是对于非周期性的信号，我们需要用无穷多不同频率的正弦曲线来表示，这对于计算机来说是不可能实现的。

所以对于有限离散信号的变换只有方法（2）才可以。

当离散的信号为周期序列时，严格的讲，傅立叶变换是不存在的，因为它不满足信号序列绝对级数和收敛（绝对可和）这一傅立叶变换的充要条件，但是采用DFS（离散傅立叶级数）这一分析工具仍然可以对其进行傅立叶分析。

得出每个主值序列在各频率上的频谱分量，这样就表示出了周期序列的频谱特性。

时域上连续的信号在频域上都有非周期的特点，但对于周期信号和非周期信号又有在频域离散和连续之分。

DTFT：时域上是离散的，频域上是连续的DFT：时域上是离散的，频域上是离散的，就相当于DTFT变换成连续频谱后再对其采样，此时采样频率等于序列延拓后的周期N，即主值序列的个数。

数学物理方法1课件——第五章 傅里叶变换


∑ ∑ ∞ sin (2n −1) x
m sin (2n −1) x
f (x) =
= lim
n=1 2n −1
m→∞ n=1 2n −1
(−π < x < π )
m=1 1
0.5
-3 -2 -1 -0.5 -1
1
2
3
m=2 0.75
0.5 0.25
-3 -2 -1 -0.25 -0.5 -0.75
第五章傅里叶变换51傅里叶级数52傅里叶变换53傅里叶变换的性质54函数约瑟夫傅里叶傅立叶早在1807年就写成关于热传导的基本论文热的传播在论文中推导出著名的热传导方程并在求解该方程时发现函数可以由三角函数构成的级数形式表示从而提出任一函数都可以展成三角函数的无穷级数
第五章 傅里叶变换
§ 5.1 傅里叶级数 § 5.2 傅里叶变换 § 5.3 傅里叶变换的性质 § 5.4 δ函数
其中傅里叶变换系数为：
∫ A(k) = 1
∞
f (x) cos(kx)dx
π −∞
∫ B(k) = 1
∞
f (x) sin(kx)dx
π −∞
傅里叶变换存在的条件：
¾
函数
f (x) 在 (−∞, ∞) 区间内绝对可积，即积分
∞
∫−∞
f (x) dx 收敛
¾ 函数 f (x) 在任意有限区间内满足狄里希利条件，即 f (x) 分段
3. 展开式中的波数kn或频率ωn，取值是不连续的，
即 n = 0,1, 2,... (实数形式的展开) 或 n = 0, ±1, ±2,... (复数形式的展开)。
§ 5.2 傅里叶变换
1、实数形式的傅里叶积分变换
傅里叶积分定理：设函数f(x)是区间[-∞, ∞]上的非周期函数，

北京大学数学物理方法经典课件第五章-傅里叶变换


逆变换的概念
详细介绍傅里叶变换的逆变换 以及其作用。
逆变换公式
掌握逆变换的常用公式，理解 如何从频域还原原始信号。
信号重构
通过逆变换实现原始信号的还 原，并研究其重构误差。
时频分析和不确定性原理
时域分析 频域分析 不确定性原理
在时间域上分析信号的时变特性，研究信号的 时序行为。
将信号转换到频域，揭示信号的频谱分布和频 域行为。
学习如何使用傅里叶级数分析周期性信号， 揭示其频域特性。
实际案例
探索傅里叶级数在音频、图像和通信等实际 应用中的作用。
傅里叶变换的定义和性质
1
线性性质
2
学习傅里叶变换的线性性质及其意义。
3
定义
介绍傅里叶变换的基本定义和公式。
频域解释
了解傅里叶变换的频域解释，研究信 号的频谱特征。
傅里叶变换的逆变换
北京大学数学物理方法经 典课件第五章-傅里叶变 换 本课件是北京大学数学物理方法经典课件的第五章，深入讲解了傅里叶变换
的概念和性质，以及在不同领域中的广泛应用。
傅里叶级数
数学基础
了解傅里叶级数的定义和性质，掌握其在数 学领域中的应用。
信号重建
通过傅里叶级数的逆变换，实现信号的还原 和重建。
周期信号分析
探索时频分析中的不确定性原理，分析信号在 时频平面上的限制条件。
傅里叶变换的应用
信号滤波
利用傅里叶变换对信号进行滤波处理，去除 干扰或提取感兴趣的频率成分。
通信技术
研究傅里叶变换在调制、解调和频谱分析等 通信技术中的应用。
图像处理
探索傅里叶变换在图像处理中的应用，如图 像增强和去噪。
量子力学
了解傅里叶变换在量子力学研究中的重要作 用，如波函数的变换和量子力学运算符的表 示。

傅里叶变换超详细总结

“周期信号都可表示为谐波关系的正弦信号的加权”——傅里叶的第一个主要论点——“非周期信号都可用正弦信号的加权积分表示”——傅里叶的第二个主要论点——频域分析：傅里叶变换，自变量为 j Ω复频域分析：拉氏变换，自变量为 S = σ +j ΩZ域分析：Z 变换，自变量为z傅立叶级数是一种三角级数，它的一般形式是)sin cos (10t n b t n a A n n n ωω++∑∞=将周期性的(非正弦的)波,用一系列的正弦波的迭加来表示,然后对每一项正弦波进行分析,因此提出了把周期函数 f(x) 展开成三角级数01()sin()n n n f t A A n t ωϕ∞==++∑01(cos sin )n n n A a n t b n t ωω∞==++∑为了讨论如何把周期函数展开成三角级数，首先考虑三角函数系的正交性。

{}1,cos ,sin ,cos 2,sin 2,,cos ,sin ,t t t t n t n t ωωωωωω⋯⋯正交性:不同的基本单位向量的点积(内积)等于零,而相同的基本单位向量不等于零傅里叶变换•周期信号的傅里叶级数分析(FS)•非周期信号的傅里叶变换(FT)•周期序列的傅里叶级数（DFS）•非周期的离散时间信号的傅里叶变换（DTFT）•离散傅里叶变换（DFT）1 周期信号的傅里叶级数分析(FS)三角函数集是最重要的基本正交函数集，正、余弦函数都属是三角函数集。

优点：(1)三角函数是基本函数；(2)用三角函数表示信号，建立了时间与频率两个基本物理量之目的联系；(3)单频三角函数是简谐信号，简谐信号容易产生、传输、处理；(4)三角函数信号通过线性时不变系统后，仍为同频三角函数信号，仅幅度和相位有变化，计算方便。

由于三角函数的上述优点，周期信号通常被表示(分解)为无穷多个正弦信号之和。

利用欧拉公式还可以将三角函数表示为复指数函数，所以周期函数还可以展开成无穷多个复指数函数的之和，其优点是与三角函数级数相同。

数学物理方法傅里叶变换法


F()
1
2
f(x )e ixdx
f (x) F()eixd
F F （1）导数定理 f t i f t iF()
（2）积分定理
F F
t
f
t
dt
1
i
ft
（3）相似性定理
F
f(ax )
1 a
F( )
a
2
（4）延迟性定理
F f x x0 eix0F()
（5）位移性定理
则化为关于w的定解问题:
wt w |
a2 x0
wxx u |x
0
0 N0
0
w |t0 u |t0 N0 N0
这是第一类齐次边界条件,意味着奇延拓,即
wt a2wxx 0
w
|t 0
N0 N0
(x (x
0) 0)
引用例2结果可得
w(x,t)
0
N0
1
2a t
e d
(
x )2 4a2t
2
2a ik
故 U (t, k) 1 (k)eikat 1 1 (k)eikat
2
2a ik
1 (k )eikat 1 1 (k )eikat
2
2a ik
对U作逆傅里叶变换，可得最后的结果如下：
5
u( x, t) 1 [( x at) ( x at)] 1
x at
( )d
2dS 2d
at
a2t 2 (x x)2 ( y y)2
泊松公式在二维空间中为
u(x, y,t) 1
(x, y)
dxdy
2
a t
x, at
y
a2t 2 (x x)2 ( y y)2
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

0 xl l x 0 x l
-l 0

F(x)
l
x
图5.7(a)
1 l 1 l 1 l l a0 F ( x)dx f ( x) xdx l 0 l 0 l 0 2
2 l kx 2 l kx 2 l kx ak F ( x) cos dx f ( x) cos dx x cos dx 0 0 0 l l l l l l
k 1
a0 E (t )dt 2 2
1



0
E0 cost E 0 sin tdt 2


0
E0

E0 a k E0 sin t cos ktdt 0 2


0
[sin(k 1)t sin(k 1)t ]dt
解：
l 2 l kx 2 l kx l bk x sin dx x( ) cos 0 l l l k l 0 k
l 2 l l 2 kx 2l l ( )( 1) k ( ) sin (1) k 1 l k k l 0 k
f ( x)

0
A( ) cosxd

0
B( ) sin xd
（称为傅里叶积分式）
A( )
B( )

1
1


f ( x) cosxdx
f ( x) sin xdx

（称为傅里叶变换式）
在 f (x) 的间断点，傅里叶积分的值
1 [ f ( x 0) f ( x 0)] 2
例4：定义在区间 (0, l ) 上的函数 f ( x) x ，试把它 展开为傅里叶级数。 解:方法一：偶延拓法，所找的周期函数 F (x)为偶 函数,如图5.7(a)所示。
f ( x) F ( x) f ( x) 以2l为周期平移
kx F ( x) a 0 a k cos l k 1
a kx kx kx 2 f ( x) a0 (a k cos bk sin ) a0 a k bk2 sin[ tan 1 ( k )] l l l bk k 1 k 1
其中a0 称为直流分量，与原物理量同频的简谐分量称为基 波，频率是原物理量频率倍的简谐分量称为次谐波。
2．信号频谱
k 次谐波的频率 k k
谱，如图5.4所示。

l
与幅度
图5.4
2 Ak a k bk2 的关系称为信号的频
三、奇的和偶的周期函数
1．奇的周期函数 如果 f (x) 是以 2l 为周期的奇函数，满足狄里希 利条件，则 f (x) 可展开为正弦傅里叶级数。
kx f ( x) bk sin l k 1
( x )
(0 l x)
(1) k 1 kx f ( x) sin k 1 k l 2l

【几点结论】
1. 定义在有限区间上的函数的傅里叶级数展开有 无穷多种形式。 f (0) f (l ) 0 2. 偶延拓可使级数满足边界条件 奇延拓可使级数满足边界条件 f (0) f (l ) 0 。
E0 cos(k 1)t cos(k 1)t (k 1) 2 (k 1) 0 E0 cos 2t 2 2 0
k2 k 1
E 0 2
(c)
u 0 (t )
E 1 ( RC ) 2
sin[t tan 1 ( RC )]
ui
t (d) 图5.1
问题：如果网络的输入电压不是正弦电压，而是直流脉动电
压，例如图5.1(d)所示的半波整流电压，在这个周期内半波整流 电压可表示为：
E cost , 0 t ui 0 t 2

1 l 其中 a0 f ( x)dx l 0
2 l kx a k f ( x) cos dx 0 l l
特点：余弦傅里叶级数满足边界条件
f (0) f (l ) 0
例3：如图5.6所示，f (x) 是以 2l 为周期的周期函 数，在 [l , l ] 周期上 f ( x) x ，试求其傅里叶级数。
0 E0 2
k2 k 1
E0 2 E0 u i (t ) sin t cos 2nt 2 2 n 1 (1 4n )
E0
二、傅里叶级数的物理意义和信号频谱
1．傅里叶级数的物理意义
周期性的非简谐物理量可以分解为一系列简谐物 理量的叠加，简谐物理量的频率只能是原物理量 频率的整数倍。
R
3. 几个物理问题
例1. 非正弦交流电问题。
如图5.1(a)所示的低通滤波网络，如果输入电压为图 5.1(b)所示的正弦交流电 ui (t ) E sin t
ui
i
C
uo
(a) ui
t
(b)
由于电阻两端的电压降与电流同相，电容两端的 电压降滞后电流 90o 因此，电压、电流向量 如图5.1(c)所示，因此网络的输出电压为：

(0 x l )
方法二：奇延拓法，所找的周期 F (x) 函数为奇函 数，如图5.7(b)所示。
F(x)
f ( x) F ( x) f ( x) 以2l为周期平移

0 xl l x 0 x l
-l
0 l
x
图5.7(b)
(1) k 1 kx F ( x) sin k 1 k l 2l
第五章 傅里叶变换
引言——傅里叶级数和积分的意义
1. 一种重要的数学方法
把非简谐的函数分解为一系列简谐函数的叠加的方法。
2. 解决复杂物理问题的有效手段
正是由于有傅里叶级数和积分才使大量的物理现象 。应用物理学的基本原理结合该数学方法可以解决 许多重要的实际物理问题。如一般的振动、波动、 交流电等问题。
问题的提出：周期性的非简谐物理量可分 解为一系列简谐物理量的叠加。在物理学 中更广泛的是非周期性的物理量，如一段 歌曲的声波是非周期性。那么，非周期的 物理量能否也可分解为一系列简谐物理量 的叠加呢？
一、实数形式的傅里叶变换
f 傅里叶积分定理：(x) 如果是定义在 (,) 上的非周期函数，满足以下两个条件：⑴ 在 x 的任意有限的区间上满足狄里希利条 件，⑵在 (,) 上绝对可积，即 f ( x) dx 存在。则 f ( x) 可表示为：
kx 0 cos l dx
l
f(x)
(1) k 1 kx f ( x) sin k 1 k l 2l

0 -l l x
图5.6
四、定义在有限区间上的函数的傅里叶 级数
f (x) 是定义在区间 (0, l ) 上的函数，该函数一定 不是周期函数，将该函数展开为傅里叶级数的方 法如下： ⅰ）找一周期函数 F (x) ，满足条件：当 0 x l 时,有 F ( x) f ( x) 。 ⅱ）将 F (x) 展开为傅里叶级数，该级数在整个 实轴上成立。 ⅲ）把变量 x 限制在区间 (0, l ) ，得到 f (x) 的傅里叶级数。
f ( x) a0 (a k cos
k 1
kx kx bk sin ) l l
1 l 其中： a0 l f ( x)dx 2l
1 l kx ak f ( x) cos dx l l l
1 l kx bk f ( x) sin dx l l l

[ , ] 内： 在周期
ui
0
t
0 ui (t ) E0 sin t
t 0 0t
图5.2
ui (t ) a0 [ak cos
k 1


k t

bk sin
k t

]
a0 [a k cos kt bk sin kt ]
等号在 f (x) 的连续点成立， 在 f (x) 的间断点级数的收敛值等于
1 [ f ( x 0) f ( x 0)] 2
例1：交流电压 e(t ) E0 sin t ，经过半波整流， 负压被“削去”（如图5.2所示），试研究半波整 流电压的傅里叶级数。试研究半波整流电压 i (t ) u 的傅里叶级数。
(1) k 1 (1) k 1 (k 1) (k 1) 0
k2 k 1
2 E 0 2 [( 1) k 1] 2 (k 1) 0
2 E0 (1 4n 2 ) 0
k2 k 1
五、复数形式的傅里叶级数
如果 f (x) 是以 2l 为周期的周期函数，且满足狄里 希利条件，则可把 f (x) 展开为以下的复数形式的 傅里叶级数。
f ( x)
k
c e
k

i
kx l
其中
1 c k f ( x )e 2l l
l
i
kx l
dx
§5.2傅里叶积分与傅里叶变换
k 2n, n 1 k 2n 1, n 0
bk E0 sin t sin ktdt 0 E0 0 [cos(k 1)t cos(k 1)t ]dt 2
E sin(k 1)t sin(k 1)t 0 (k 1) (k 1) 2 0 E0 sin 2t t 2 2 0 k2 k 1
。
二、奇和偶函数的傅里叶变换
1.如果 f (x)是奇函数，则： f ( x) B() sin xd , B( ) 2 f ( x) sin xdx