最优化作业

1.用薄钢板制造一体积5m 3，长度不小于4m ，无上盖的货箱，要求钢板耗量最小。

确定货箱的长x 1、宽x 2和高x 3。

试列出问题的数学模型。

解：min 32312122x x x x x x z ++= s.t 5321=x x x 41≥x 0,,321≥x x x2.将下面的线性规划问题表示为标准型并用单纯形法求解max f=x 1+2x 2+x 3s ．t ．2x 1+x 2-x 3≤2 -2x 1+x 2-5x 3≥-6 4x 1+x 2+x 3≤6 x i ≥0 i=1，2，3 解：先化标准形：Min 321x x x z -+=224321=+-+x x x x 6525321=++-x x x x646321=+++x x x x列成表格：121610011460105122001112-----可见此表已具备1°，2°，3°三个特点，可采用单纯形法。

首先从底行中选元素-1，由2/2,6/2,6/4最小者决定选第一行第一列的元素2，标以记号，迭代一次得121210231040116201002121211--------再从底行中选元素-2/3，和第二列正元素1/2，迭代一次得12123230210231040116201002121211-------再从底行中选元素-3，和第二列正元素2，迭代一次得4233410120280114042001112---再迭代一次得1023021062210231010213000421021013--选取最优解：01=x 42=x 23=x3. 试用DFP 变尺度法求解下列无约束优化问题。

min f （X ）=4（x 1-5）2+（x 2-6）2取初始点X=（8，9）T ，梯度精度ε=0.01。

解：取IH=0,初始点()TX 9,8=2221)6()5(4)(-+-=x x x f⎥⎦⎤⎢⎣⎡--=∇122408)(21x x x f⎪⎪⎭⎫⎝⎛=∇624)()0(xfTx f d )6,24()()0()0(--=-∇=)0(0)0()1(dxxα+=T)69,248(00αα--=])669()5248(4min[)(min 2020)0(0)0(--+--⨯=+αααdxf 0)6()63(2)24()2458(8)(00)0(0)0(=-⨯-+-⨯--=+ααααd d xdf13077.0130170≈=α⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛--⨯+⎪⎪⎭⎫ ⎝⎛=21538.886153.462413077.098)1(x⎪⎪⎭⎫⎝⎛-=∇43077.410784.1)()1(xf进行第二次迭代：⎥⎦⎤⎢⎣⎡--=-=78463.013848.31)0()1(xxδ⎥⎦⎤⎢⎣⎡--=∇-∇=56924.110783.25)()(1)0()1(xf xf γ101011011101γγγγγδδδH HH H H TTTT-+=03172.8011=γδT86614.6321101==γγγγH T⎥⎦⎤⎢⎣⎡=61561.046249.246249.285005.911Tδδ⎥⎦⎤⎢⎣⎡==46249.240022.3940022.3940363.630110110TTHH γγγγ所以：⎪⎪⎭⎫⎝⎛--=0038.103149.003149.012695.01H⎪⎪⎭⎫⎝⎛-⨯⎪⎪⎭⎫⎝⎛---=∇-=43076.410784.10038.103149.003149.012695.0)()1(1)1(xf H d⎪⎪⎭⎫⎝⎛-=48248.428018.0令 )1(1)1()2(dx x α+=利用)()1()1(=+ααd dxdf ，求得49423.01=α，所以⎪⎪⎭⎫⎝⎛-+⎪⎪⎭⎫⎝⎛=+=21538.213848.021538.886152.449423.0)1()1()2(dxx⎪⎪⎭⎫ ⎝⎛=65因)()2(=∇xf ，于是停，)2(x 即为最优解。

最优化方法及其Matlab程序设计习题作业暨实验报告学院：数学与信息科学学院班级：12级信计一班姓名：李明学号：1201214049第三章 最速下降法和牛顿法一、上机问题与求解过程1、用最速下降法求212221216423),(x x x x x x f --+=的极小值。

解：仿照书上编写最速下降法程序如下：function [x,val,k]=grad(fun,gfun,x0) %功能：用最速下降法求解无约束化问题：min f(x) %输入：x0是初始点，fun,gfun 分别是目标函数和梯度 %输出：x,val 分别是近似嘴有点和最优值，k 是迭代次数 maxk=5000;rho=0.5;sigma=0.4;%一开始选择时选择的rho 和sibma 选择的数据不够合理，此处我参照书上的数据编写数据 k=0;epsilon=1e-5; while (k<maxk)g=feval(gfun,x0); %计算梯度 d=-g;%计算搜索方向if (norm(d)<epsilon),break ;end m=0;mk=0; while (m<20)%Armijo 搜索if (feval(fun,x0+rho^m*d)<feval(fun,x0)+sigma*rho^m*g'*d) mk=m;break ;%直接利用Armijo 搜索公式,一开始的时候没有记住公式编写出现错误 end m=m+1; endx0=x0+rho^mk*d; k=k+1; end x=x0;val=feval(fun,x0) %求得每一个的函数值然后仿照书上建立两个目标函数和梯度的M 文件：function f=fun(x)f=3*x(1)^2+2*x(2)^2-4*x(1)-6*x(2); function g=gfun(x) g=[6*x(1)-4,4*x(2)-6]';选取初始点为']0,0[，调用函数程序，得出最小极值点为']500.1,6667.0[，极小值为8333.5-，在界面框中输入的程序如下：[x,val,k]=grad('fun','gfun',x0) val = -5.8333 x =0.6667 1.5000 val =-5.8333 k = 10从结果可以看出迭代次数为10次，如果选取不同的初值点则迭代次数不一样，但是极小值相同。

最优化作业2Armijo准则Armijo准则（Armijo criterion）是最优化算法中一个重要的线准则，用于确定步长的大小。

它通过将目标函数在当前点处的函数值与它沿梯度方向的下降量进行比较，来判断是否接受或拒绝当前的步长。

Armijo准则的基本思想是选择一个小于1的常数幅度因子α（通常为0.1或0.5），并不断减小步长，直到目标函数值满足以下条件：f(x_k+α*d_k)<=f(x_k)+c*α*d_k^T*g_k其中，x_k是当前的位置，d_k是负梯度方向的单位向量，g_k是当前位置处的梯度，c是一个小于1的常数。

这个条件可以解释为，在当前位置沿着负梯度方向前进一段距离α之后，函数值应该下降的足够，大于等于在当前位置直接沿着梯度方向前进一段距离α*c带来的下降量。

如果当前步长满足Armijo准则，那么这个步长就被接受，更新位置为x_{k+1} = x_k + α*d_k。

否则，步长就会被减小，重新计算。

具体来说，根据Armijo准则，可以使用以下的步长算法来确定最优步长：1.设置初始步长α为12.计算f(x_k+α*d_k)。

3.如果f(x_k+α*d_k)<=f(x_k)+c*α*d_k^T*g_k，那么接受这个步长，更新位置为x_{k+1}=x_k+α*d_k。

算法结束。

4.否则，减小步长，重新计算。

一般可以将步长减小为α/2，重复步骤25. 重复步骤4，直到找到满足Armijo准则的步长。

Armijo准则的一个优点是它相对简单且易于实现。

然而，它也有一些缺点。

由于只要求函数值在当前位置沿着梯度方向前进一段距离后下降，所以可能会接受过大的步长，导致算法很难收敛。

此外，Armijo准则只考虑了一阶信息，没有考虑二阶信息，可能导致步长选择不够精确。

因此，在一些情况下，可以使用其他的步长控制准则，如Wolfe准则、Goldstein准则等，来进一步改进最优化算法的性能。

总之，Armijo准则是最优化算法中常用的线准则之一、它通过比较当前步长带来的下降量与在当前位置沿梯度方向前进一段距离带来的下降量，来决定是否接受当前步长。

无约束优化算法最优化课程作业（一）姓名：丁敏学号：31130510012014/6/24一、无约束优化算法无约束优化计算方法是数值计算领域中十分活跃的研究课题。

快速地求解无约束优化问题已经成为当今的焦点，除了其自身的重要性外，还由于目前求解约束优化问题的基本思想之一就是把约束问题变换为一系列无约束子问题进行求解。

因此，无约束优化算法的求解效率将直接影响到约束问题的求解，尤其是在大规模优化问题中。

所以，对无约束优化算法的研究具有重要的理论意义和实际价值。

无约束优化问题，是指优化问题的可行集为n R ，无约束的标准形式（1-1）为：R R f x f n→:)(m i n求解无约束优化问题时将会涉及到以下概念：(1) 驻点、鞍点：若f (x )在点x*处可微，并且0f (x*)∇=，则称x*为f (x )的一个驻点(或者平稳点)。

既不是极小点，也不是极大点的驻点称为鞍点。

(2) 全局最优解：若n x*Z,x R ∈∀∈均有f (x )f (x*)≥，则称x*为问题(1-1)的全局 最优解(3) 局部最优解：若*x D ∈且存在0δ>使得()()()**f x f x ,x DN x δ≥∀∈则称x*为问题(1-1)的一个局部最优解（极小点）；若*x D ∈且存在0δ>使得()()()**f x f x ,x DN x δ≤∀∈则称x*为问题(1-1)的一个局部最优解（极大点）；当目标函数 f ( x )为凸函数时，我们认为全局最优解即是局部最优解，然而，通常寻求全局最优解并不容易。

因此，在非线性优化中我们认为局部最优解即为所求。

无约束优化算法可以分为两大类: 一类是借助目标函数的导数信息来构造下降的搜索方向。

另一类是由目标函数值信息直接搜索求解的方法。

本文章重点介绍最速下降法，阻尼牛顿法以及共轭梯度法。

二、最速下降法1、最速下降法思想经典最速下降法是由 Cauchy 于 1847 年提出的，Forsythe 和 Motzkin 在 1951 年对它做了初步的分析。

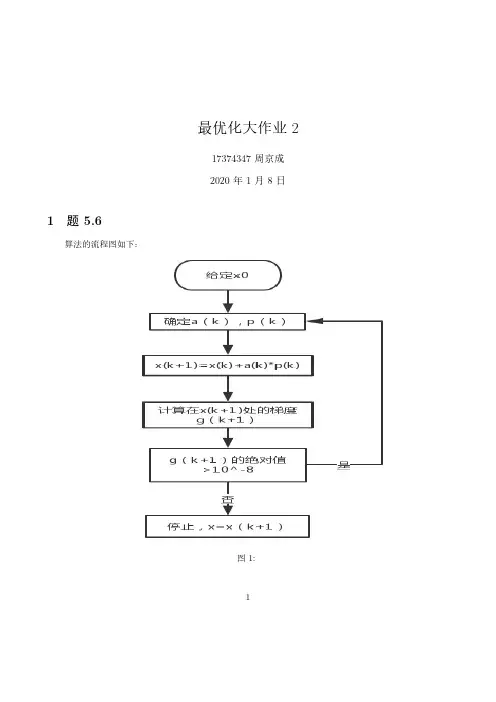
[键入公司名称]一题目要求：1.分别用①牛顿法和②变尺度法求解优化问题min f(x)=x^2-2*x*y+4*y^2+x-3*y2.利用①外点法和②内点法解下列约束问题 min f(x)=(x-3)^3+(y-2)^2 s.t. h(x)=x1+x2-4≤0二基本思想牛顿法：应用基本迭代公式X k+1=X k +t k P k 中，每轮迭代在迭代的起始点X K 处用一个适当的二次函数来近似该点处的目标函数，由此用点X K 指向近似二次函数极小点的方向来构造搜索方向Pk. 设()f x 是二次可微实函数，n k x R ∈，Hesse 矩阵()2k f x ∇正定。

在k x 附近用二次Taylor 展开近似f ，()()()()()()212TTk T k k k k f x s q s f x s f x s s f x s +≈=+∇+∇ k s x x =-，()()k q s 为()f x 的二次近似。

将上式右边极小化，便得： ()()121k k k k x x f x f x -+⎡⎤=-∇∇⎣⎦，这就是牛顿法的迭代公式。

在这个公式里，步长因子1k α=。

令()()2,k k k k G f x g f x =∇=∇，则上式也可写成：11k k k k x x G g -+=-显然，牛顿法也可以看成在椭球范数kG⋅下的最速下降法。

事实上，对于()()T k k k f x s f x g s +≈+，k s 是极小化问题minn Tk s R g ss∈的解。

该极小化问题依赖于所取的范数，当采取2l 范数时，k k s g =-，所得方法为最速下降法。

当采用椭球范数kG⋅时，1k k k s G g -=-，所得方法即为牛顿法。

对于正定二次函数，牛顿法一步即可达到最优解。

而对于非二次函数，牛顿法并不能保证有限次迭代求得最优解，但由于目标函数在极小点附近近似于二次函数，故当初始点靠近极小点时，牛顿法的收敛速度一般是快的。

命题人：审核人：大作业学期：至学年度第学期课程：最优化方法课程代号：签到序号：使用班级：姓名：学号：题号一二三四五六七八九十总分得分一、（目标1）请从以下6种算法中任选一种，说明算法的来源、定义、基本思想和优缺点，并给出算法步骤（包含算法流程图）和例子（包含程序与运算结果）。

①禁忌搜索算法；②模拟退火算法；③遗传算法；④神经网络算法；⑤粒子群算法；⑥蚁群算法。

二、（目标1）某工厂生产甲、乙两种产品，已知生产这两种产品需要消耗三种材料A 、B 和C ，其中生产过程中材料的单位产品消耗量和总量，以及单位产品的利润如下表所示。

该如何配置安排生产计划，使得工厂所获得的利润最大？材料甲乙资源总量材料A （Kg ）3265材料B （Kg ）2140材料C （Kg ）0375单位利润（元/件）15002500-（1）要保证工厂利润的最大化，写出相应的生产计划数学模型；（2）根据对偶理论，直接写出该线性规划的对偶问题；（3）采用单纯形表法对该该线性规划问题进行求解，写出详细的计算过程；（4）采用Matlab 软件对该线性规划问题进行求解，写出完整的源程序，并给出程序运行结果；（5）讨论当材料B 的资源总量发生变化时，该线性规划问题的最优解会如何变化？课程目标目标1……题号一、二、三、四、五……分值20、25、20、20、15……得分得分三、（目标1）求解下列无约束非线性规划问题（1）采用黄金分割法求解：min 4()24f x x x =++。

初始区间为[-1.0]，精度为ε=10-4。

（要求：采用黄金分割法进行Matlab 编程求解，写出源程序，并给出运行结果，列出迭代过程的数据表格）（2）采用阻尼牛顿法求解：222121212min (,)4f x x x x x x =+-。

分别取两个初始点：x A =(1,1)T ，x B =(3,4)T 。

（要求：采用阻尼牛顿法进行Matlab 编程求解，并给出运行结果，列出迭代过程的数据表格）四、（目标1）求解下列约束非线性规划问题：22112212121212min ()23532..00f x x x x x x x x x x x s t x x =-+--+≤⎧⎪-≤⎪⎨≥⎪⎪≥⎩（1）采用罚函数法进行求解，需写出具体计算过程；（2）采用二次规划方法进行求解，需写出具体计算过程，并进行MATLAB 编程，写出源程序和运算结果；五、（目标1）（1）某商店在未来的4个月里，准备利用它的一个仓库来专门经营某种商品，仓库的最大容量为1000单位，而且该商店每月只能出卖仓库现有的货。

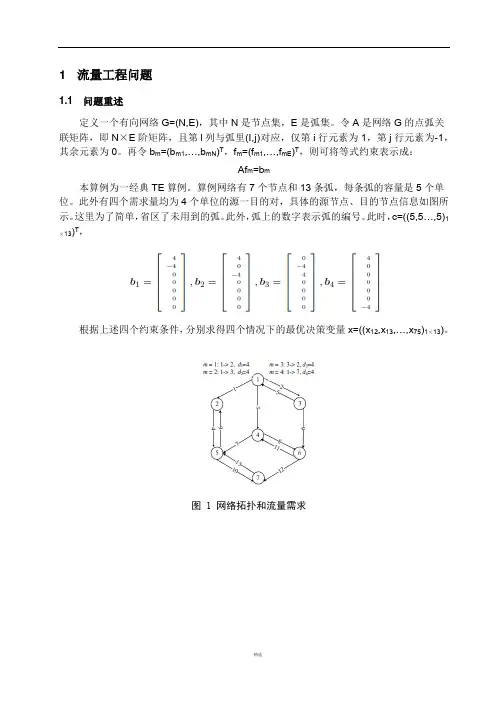
1 流量工程问题1.1 问题重述定义一个有向网络G=(N,E)，其中N是节点集，E是弧集。

令A是网络G的点弧关联矩阵，即N×E阶矩阵，且第l列与弧里(I,j)对应，仅第i行元素为1，第j行元素为-1，其余元素为0。

再令b m=(b m1,…,b mN)T，f m=(f m1,…,f mE)T，则可将等式约束表示成：Af m=b m本算例为一经典TE算例。

算例网络有7个节点和13条弧，每条弧的容量是5个单位。

此外有四个需求量均为4个单位的源一目的对，具体的源节点、目的节点信息如图所示。

这里为了简单，省区了未用到的弧。

此外，弧上的数字表示弧的编号。

此时，c=((5,5…,5)1 )T，×13)。

根据上述四个约束条件，分别求得四个情况下的最优决策变量x=((x12,x13,…,x75)1×13图 1 网络拓扑和流量需求1.2 7节点算例求解1.2.1 算例1（b1=[4;-4;0;0;0;0;0]T）转化为线性规划问题：Minimize c T x1Subject to Ax1=b1x1>=0利用Matlab编写对偶单纯形法程序，可求得:最优解为x1*=[4 0 0 0 0 0 0 0 0 0 0 0 0]T对应的最优值c T x1=201.2.2 算例2（b2=[4;0;-4;0;0;0;0]T）Minimize c T x2Subject to Ax2=b2X2>=0利用Matlab编写对偶单纯形法程序，可求得:最优解为x2*=[0 4 0 0 0 0 0 0 0 0 0 0 0]T对应的最优值c T x2=201.2.3 算例3（b3=[0;-4;4;0;0;0;0]T）Minimize c T x3Subject to Ax3=b3X3>=0利用Matlab编写对偶单纯形法程序，可求得:最优解为x3*=[4 0 0 0 4 0 0 0 0 0 0 0 0]T对应的最优值c T x3=401.2.4 算例4（b4=[4;0;0;0;0;0;-4]T）Minimize c T x4Subject to Ax4=b4X4>=0利用Matlab编写对偶单纯形法程序，可求得:最优解为x4*=[4 0 0 4 0 0 0 0 0 4 0 0 0]T对应的最优值c T x4=601.3 计算结果及结果说明1.3.1 算例1（b1=[4;-4;0;0;0;0;0]T）算例1中，由b1可知，节点2为需求节点，节点1为供给节点，由节点1将信息传输至节点2的最短路径为弧1。

第6-7次课作业-参考答案1. 用进退法确定函数f(x)=x 2-7x+16的一维优化初始区间[a,b ]，设初始点x 1=0，h 0=1。

解： f 1=f(x 1)=16,取x 2=x 1+ h 0=0+1=1, f 2=f(x 2)=10。

比较函数值：f 1>f 2。

则加大步长令h=2h 0=2。

取x 3=x 2+h=3, 则 f 3=4。

比较函数值：f 3<f 2。

令x 1= x 2=1, f 1=10; x 2= x 3=3, f 2=4;取x 3=x 2+h=5, f 3=6。

比较函数值：f 3>f 2, 这时满足：f 1>f 2 , f 2<f 3，故单峰区间为[1,5]。

2．用牛顿法求0()arctg xf x tdt =⎰的极小点，取11,0.01x ε==。

解：因为21'()arctg ,"()1f x x f x x ==+，取11x =，计算 '()0.7854,"()2f x f x ==故有 1211'()0.5708"()f x x x f x =-=- 同理有2322'()0.5708(0.5178) 1.32580.1169"()f x x x f x =-=---⨯= 3433'()0.11690.1163 1.01370.00106"()f x x x f x =-=-⨯=- 而4|'()|=0.001060.01f x <，故迭代停止，输出近似极小解：*0.00106x ≈-。

3. 用黄金分割法求函数f(x)=x3-2x+1在区间[0,3]上的极小点，ε=0.5。

解：根据(0.618)k≤εb−a =0.53,k≥4.可知需迭代4次，即可满足精度要求。

第一次缩小区间：x1=0+0.382· (3-0)=1.146, f1=0.213x2=0+0.618·(3-0)=1.854, f2=3.665由于f1<f2, 则新区间[a,b]=[a, x2]=[0, 1.854], b-a>0.5，应继续缩小区间。

仓库物品摆放十大原则一、作业最优化原则仓库作业优化是指提高作业的连续性，实现一次性作业，减少装卸次数，缩短搬运距离，最短的搬运距离；最少的搬运环节；使仓库完成既定的任务所发生的装卸搬运量最少。

同时还要注重各作业场所和科室之间的业务联系和信息传递。

保证仓库安全。

二、单一的物流流向原则保持直线作业，避免迂回逆向作业；强调唯一的物流出口和唯一的物流入口，便于监控和治理。

三、最大限度的利用原则提高仓储作业效率，仓储定位系统如果高效运作，能大大节约寻找、存放及取出时间，节约了不少物化劳动及活劳动，而且能防止差错，便于清点。

确定合理仓储量，资源从采购到生产再到客户之间的整个过程，需要经过数个阶段，几乎在每一个阶段都需要进行存储，通过分析从原材料、半成品、成品等每一个物流环节的最佳仓储量，分析补充库存的速度等，使存货水平最低、仓储浪费最小、空间占用最小。

四、节约原则仓库中的延伸型设施一一供电、供水、供暖、通讯等设施对基建投资和运行费用的影响都很大，所以应当尽可能集中布置。

五、易于储存原则仓库货物摆放应便于储存保管，提高物品保管质量。

六、隔离易混物料原则1、保管在同一区域的货物必须具有互容性，当货物的性质互相有影响或相互有抵触时，不能在相同的库房内保留。

2、灭火措施不同的货物不能混存。

灭火方法不同的货物放在一起，不仅会使安全隐患增加，也增加了火灾控制和扑救的难度和危险性。

3、作业手段不同的货物不能混存。

当在同一保管空间内，物体的体积和重量相差悬殊时，将严重影响该区域作业所配置的设备利用率，同时也增加了作业的复杂性和作业难度。

4、保管条件不同的货物不能混存。

如温湿度等保管条件不同，不宜将它们放在一起，因为在同一个保管空间内，同时满足两个或多个保管条件的成本是非常高的，是不实际的。

七、面对通道原则即把商品的标示面对通道，不仅是把外面的一层面对通道，而且要把所有的商品标示都要面对通道，面对同一方向，使分拣人员能够始终流畅地进行工作，不用中断工作去确认标示。

北航最优化方法大作业参考旅行商问题是一个经典的组合优化问题，目标是找到一条最短路径，使得旅行商能够在访问所有城市后回到起始城市。

在实际应用中，旅行商问题有着广泛的应用，例如物流配送、城市规划等领域。

为了解决旅行商问题，我们可以采用启发式算法，其中一个常用的方法是遗传算法。

遗传算法是一种模拟自然进化过程的优化算法，通过模拟生物遗传的选择、交叉和变异等操作，逐步优化问题的解。

首先，我们需要对问题进行建模。

假设有N个城市，我们可以通过一个N*N的距离矩阵来表示各个城市之间的距离。

同时，我们需要定义一个染色体表示一条路径，其中每个基因表示一个城市的编号。

接下来，我们可以采用遗传算法来求解最优解。

遗传算法一般包括以下几个步骤：1.初始化种群：随机生成初始的染色体种群，每个染色体都表示一条路径。

2.适应度评价：根据染色体的路径长度来评估每个染色体的适应度，路径越短适应度越高。

3.选择操作：选择适应度较高的染色体作为父代，采用轮盘赌选择算法确定父代。

4.交叉操作：采用部分映射交叉算子对父代进行交叉操作，生成新的子代。

5.变异操作：对子代进行变异操作，以增加种群的多样性。

6.环境选择：根据适应度选择下一代种群，同时保留精英个体，避免解的丢失。

7.终止条件：当达到预设的迭代次数或者达到最优解时，终止算法。

通过以上步骤的迭代，我们可以逐步优化路径的长度，最终得到一条最短路径。

除了遗传算法，我们还可以尝试其他的优化算法，例如模拟退火算法、蚁群算法等。

这些算法在求解旅行商问题时都有一定的优势和适用性。

总结起来，旅行商问题是一个经典的组合优化问题，在北航最优化方法大作业中可以选择使用启发式算法来解决。

我们可以尝试使用遗传算法来求解最优路径，并根据实际情况选择合适的算法参数和终止条件。

通过不断地迭代和优化，我们可以得到一条最短路径，满足旅行商的需求。

以上是关于北航最优化方法大作业的参考内容，希望对你的写作有所帮助。

如果有其他疑问，欢迎继续提问。

最优化方法及其Matlab程序设计习题作业暨实验报告学院：数学与信息科学学院班级：12级信计一班姓名：李明学号：1201214049第四章 共轭梯度法一、上机问题与求解过程1、用DFP 算法求解,3)(m in 2221x x x f +=取初始点和初始矩阵为 .1112,1100⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡-=H x 。

解：仿照书上编写DFP 程序，将程序HESS 矩阵变为0H 具体如下：function [x,val,k]=dfp(fun,gfun,x0)%功能：用DFP 算法求解吴宇舒问题：min f(x)%输入：x0是初始点，fun,gfun 分别是目标函数及其梯度%输出：x,val 分别是近似最优点和最优值，k 是迭代次数maxk=1e5;%给出最大迭代次数rho=0.55;sigma=0.4;epsilon=1e-5;k=0; n=length(x0);Hk=[2 1;1 1];while (k<maxk)gk=feval(gfun,x0);%计算梯度if (norm(gk)<epsilon),break ;enddk=-Hk*gk;%计算搜索方向m=0;mk=0;while (m<20)%用Armijo 搜索求步长if (feval(fun,x0+rho^m*dk)<feval(fun,x0)+sigma*rho^m*gk'*dk) mk=m;break ;endm=m+1;endx=x0+rho^mk*dk;sk=x-x0;yk=feval(gfun,x)-gk;if (sk'*yk>0)Hk=Hk-(Hk*yk*yk'*Hk)/(yk'*Hk*yk)+(sk*sk')/(sk'*yk);endk=k+1;x0=x;endval=feval(fun,x0);然后仿照书上建立两个目标函数和梯度的M 文件：function f=fun(x)f=x(1)^2+3*x(2)^2;function g=gfun(x)g=[2*x(1) 6*x(2)]'; 选取初始点为']1,1[-，调用函数程序，得出最小极值点为'66]101599.0,102203.0[--⨯-⨯-，极小值为13102527.1-⨯，在界面框中输入的程序如下：x0=[1 -1]';[x,val,k]=dfp('fun','gfun',x0)x =1.0e-06 *-0.2203-0.1599val =1.2527e-13k =4从结果可以看出迭代次数为4次，如果选取不同的初值点则迭代次数不一样，但是极小值相同。

最优化算法作业
1、某企业通过市场预测，了解到市场对企业所生产的主要产品在今后的四季度内的需求分别为2,3,2,4个单位。

假定该厂生产每批产品的固定成本为3千元，若不生产则固定成本为0；此外，每生产一个单位产品的成本为1千元，每个时期企业生产能力所允许的最大生产批量不超过6各单位。

若每个时期末未售出的产品的库存总费用为0.5千元。

还假定第一季度的初始库存量为0，第四季度末的库存量也为0。

现要为企业确定一个生产与库存方案，使企业既能满足市场需求，又使生产与库存总费用最低。

要求：①建立数学模型；
②用动态规划方法求解。

写出递推公式以及求解过程，并给出最有结果。

2..某农场有甲乙丙三块地，分别为200公顷、400公顷和600公顷，计划种植三种农作物A、B、C。

已知生产A、B、C的费用为3000、2250和1500（单位：元/公顷），种植各农作物的收成如下表（单位：吨/公顷）：
请制定种植计划，使得总收成最大，而总成本最小。

要求：
①建立数学模型
②分别用分层求解法和目标规划法求解该问题。

写出求解过程中所涉及的相关模型和程序，以及计算结果。

最优化方法及其Matlab程序设计习题作业暨实验报告学院：数学与信息科学学院班级：12级信计一班姓名：李明学号：1201214049第二章 线搜索技术一、上机问题与求解过程 1、用0.618法求解 .1)(min 2--=x x x f 初始区间]1,1[-，区间精度为50.=0δ. 解：当初始时不限制近似迭代函数值得大小，编写程序运行结果为：从结果可以看出迭代次数为9次，极小点为5016.0，极小点的函数值为2500.1-。

根据人工手算，极小值点应该为500.0，所以在设计程序的时候添加函数值误差范围，并取范围为10101-⨯。

编写的设计函数程序并调试改正如下：function [s,fs,k,G,FX,E]=gold(f,a,b,H,F) %输入：% f:目标函数，a ：搜索区间左侧端点；b:搜索区间右侧端点； % H ：搜索区间允许范围；F ：搜索区间函数值允许范围； %输出：% s:近似极小值点：fa ：近似极小点数值；k:迭代次数：% FX ：近似迭代函数值；E=[h,fh]，h 为近似区间误差，fh 为函数值误差 t=(sqrt(5)-1)/2;h=b-a; p=a+(1-t)*h;q=a+t*h;fa=feval(f,a);fb=feval(f,b); fp=feval(f,p);fq=feval(f,q); k=1;G(k,:)=[a,p,q,b];%初始时错误语句：G(1,:)=[a,p,q,b]; %初始调试的时候没有注意到后面需要开辟k 行空间 FX(k,:)=[fa,fp,fq,fb];while (abs(fa-fb)>F) ((b-a)>H) if (fp<fq)b=q;fb=fq;q=p;fq=fp;h=b-a;p=a+(1-t)*h;fp=feval(f,p); %初始时错误语句：b=q;fb=fq;h=b-a;q=a+t*h;fq=feval(f,q); %初始调试的时候对0.618方法没有充分理解所以出现错误 elsea=p;fa=fp;p=q;fp=fq;h=b-a;q=a+t*h;fq=feval(f,q);%初始时错误语句：a=p;fa=fp;h=b-a;p=a+(1-t)*h;fp=feval(f,p); %初始调试的时候对0.618方法没有充分理解所以出现错误 end极小点(s) 迭代次数搜索区间误差 函数值误差 0.501690.04260.0006k=k+1;G(k,:)=[a,p,q,b];%初始时错误语句：G(1,:)=[a,p,q,b]; %初始调试的时候没有注意到前面已经开辟k 行空间 FX(k,:)=[fa,fp,fq,fb]; end if (fp<fq) s=p;fs=fp; elses=q;fs=fq; endh=b-a;fh=abs(fb-fa);%选取试探点最小的数值为近似点，并且计算出以上为搜索区间的的最后误差以及函数值误差 E=[h,fh];在命令窗口内输入如下命令：[s,fs,k,G,FX,E]=gold(inline('s^2-s-1'),-1,1,0.05,1e-10) 回车之后得到如下数据结果：附：在窗口中输出的结果如下>> [s,fs,k,G,FX,E]=gold(inline('s^2-s-1'),-1,1,0.05,1e-10) s = 0.5000 fs = -1.2500 k = 24 G =-1.0000 -0.2361 0.2361 1.0000 -0.2361 0.2361 0.5279 1.0000 0.2361 0.5279 0.7082 1.0000极小点 极小点数值 迭代次数 搜索区间误差 函数值误差 0.500-1.250024410321.0-⨯0000.00.2361 0.4164 0.5279 0.70820.4164 0.5279 0.5967 0.70820.4164 0.4853 0.5279 0.59670.4164 0.4590 0.4853 0.52790.4590 0.4853 0.5016 0.52790.4853 0.5016 0.5116 0.52790.4853 0.4953 0.5016 0.51160.4953 0.5016 0.5054 0.51160.4953 0.4992 0.5016 0.50540.4953 0.4977 0.4992 0.50160.4977 0.4992 0.5001 0.50160.4992 0.5001 0.5006 0.50160.4992 0.4997 0.5001 0.50060.4997 0.5001 0.5003 0.50060.4997 0.5000 0.5001 0.50030.4997 0.4999 0.5000 0.50010.4999 0.5000 0.5000 0.50010.5000 0.5000 0.5000 0.50010.5000 0.5000 0.5000 0.50000.5000 0.5000 0.5000 0.50000.5000 0.5000 0.5000 0.5000 FX =1.0000 -0.7082 -1.1803 -1.0000 -0.7082 -1.1803 -1.2492 -1.0000 -1.1803 -1.2492 -1.2067 -1.0000 -1.1803 -1.2430 -1.2492 -1.2067 -1.2430 -1.2492 -1.2406 -1.2067 -1.2430 -1.2498 -1.2492 -1.2406 -1.2430 -1.2483 -1.2498 -1.2492 -1.2483 -1.2498 -1.2500 -1.2492 -1.2498 -1.2500 -1.2499 -1.2492 -1.2498 -1.2500 -1.2500 -1.2499 -1.2500 -1.2500 -1.2500 -1.2499 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.25001.0e-04*0.3121 0.00002、用0.618法求解.12)(min 3+-=x x x f的近似最优解，初始搜索区间为]3,0[，区间精度为50.=1δ. 解：当初始时不限制近似迭代函数值得大小，编写程序运行结果为：从结果可以看出迭代次数为8次，极小点为8115.0，极小点的函数值为0886.0-。