矢量分析

矢量分析与张量初步第一章矢量分析U STU STU ST标量（数量）：有大小，没方向的物理量。

矢量：既具有大小又具有方向的物理量，矢量又称为向量。

矢量与标量的根本区别是：有没有方向性。

如：温度、质量、角度、长度等。

如：力、速度、电场强度、力矩等。

矢量的模：矢量的大小。

矢量的模记为：或。

A K A ||A KU STU STU ST自由矢量：矢量平移后，其作用效果不变。

即自由矢量就是具有平移不变性的矢量。

FK 只考虑刚体的质心运动，作用力可以平移。

能不能平移？下面只讨论自由矢量。

如果要考虑刚体的转动，则作用力不能平移。

U STU STU ST始端在坐标原点的矢量常称为矢径，显然矢径的末端与直角坐标系中的三个坐标分量之间具有一一对应的关系，则矢径可用其末端的空间坐标来表示：①在直角坐标中的表示对矢量，始端平移到坐标原点，表示为：A Kr xi yj zk=++KK K K、、：单位矢量，分别指向三个坐标轴的正向。

i K j K k K x y z A A i A j A k=++K K K KU STU STU ST其中：为矢量的模，为指向矢量方向上的单位矢量。

R A A e A 三个：、和。

R βαcos cos cos A e i j kαβγ=++K K K KAKRxy zO因为222cos cos cos 1αβγ++=的直角坐标表示为A e K有几个独立坐标量？A Kr e =KU STU STU STOxe ρρK zA kK A K cos sin e i j ρϕϕ=+K K K三个：、和。

ρϕz 的直角坐标表示为e ρK在矢量的球坐标及柱坐标表示中，只要分别把单位矢量和的直角坐标表示代入，即得到矢量的直角坐标表示。

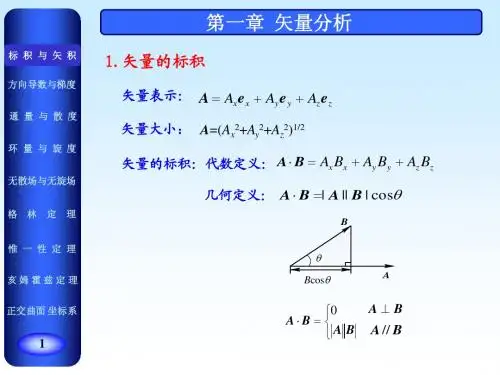
e ρKr e K 有几个独立坐标量？A K第一章矢量分析U STU ST U ST U STU STcos xA Aα=cos yA Aβ=cos zA A γ=(cos cos cos )A A i j k αβγ=++K K K K④方向余弦表示：设矢量与直角坐标三个坐标轴正向的夹角分别为、和，则：αγβA K用方向余弦（）表示矢量：A Kcos ,cos ,cos αβγcos x A A α=这实际上就是直角坐标表示，因为：cos y A A β=cos z A A γ=U STU STU ST不能按大小排列）。

性质
∇ × ∇ϕ = 0
梯度
三、矢量场的通量、散度
1、通量
r 定义：若矢量场 A 分布于空间中，在空间中存在任意曲面 S
r 上。定义 A 在曲面上的积分为通量。
r r Ψ = ∫ A ⋅ dS
s
曲面 S 的方向 开表面： 作一封闭线圈，选定绕行方向后，沿绕行方向 按右手螺旋法则，拇指方向为开表面方向 闭合面：外法线方向
s l
无旋场 性质
r ∇× A = 0
r ∇ ⋅ (∇ × A) = 0
旋度
例题讲解（课本） 例题1-8 例题1-9 例题1-10
例题
五、亥姆霍兹定理
内容：位于空间有限区域内的矢量场，当它的散度，旋度 以及它在区域边界上的场分布给定之后，该矢量场就被唯 一确定；对于无限大空间，如果矢量在无限远处减少至零 则该矢量由其散度和旋度唯一确定。
基础
矢量表示式
r r r r A = er Ar + eϕ Aϕ + e z Az
微分长度
r r r r dl = er dr + eϕ rdϕ + e z dz
微分面积
r r dS r = er rdϕdz r r dS ϕ = eϕ drdz r r dS z = e z rdrdϕ
微分体积
dV = rdrd ϕdz
只改变大小，不改变方向 矢量与矢量点乘
s r r r A ⋅ B = A B cosθ AB = Ax Bx + Ay B y + Az Bz
r r r r A⋅B = B⋅A
基础
说明： 1、两个矢量的标量积或点积，是一个标量 。 2、Θ是A、B之间较小的夹角，小于Π弧度。 3、其结果表示一个矢量的模和另一个矢量在该矢量 上的投影和乘积。 矢量与矢量叉乘

0
定理2 若有向曲线C上取 取定一点M0 作为计算弧长s的起点，并 C之正向作为 并以 s增大的方向；M为C上的 的一点，在点M处 沿C之正向作一与C相切的 的射线，则函数 l u在点M处沿l方向的方向导 导数等于u对s的 l 全导数： du(s) ∂u |M = |M （ ） 2.3 ds ∂l
数量场等值线
u( x, y) = c
M0 过数量场中每一点 （x0，y0，z0 都有 ） 唯一等值面 u( x, y, z) = u（x0，y0，z0 ）。
R −x − y −z
2 2 2 2 2
如数量场: u( x, y, z) =
2 2 2
等值面:
R −x − y −z =c
R 00 过（， ）的等值面: ， 2 R −x − y −z =
最大值，所以梯度向量的方向为±( 0，0，1)，
0， 0， grad u| = ±32 ( 0，0，1) = ± ( 0， 32) M
模为32，即 32，
∂u ∂u ∂u u u u 又 因 为 grad u|M = （ ， ， ） (4a + 3c,4a - b,2b - 2c ) == ∂x ∂y ∂z x y z 比较上两式得 4a + 3c = 0, 4a - b = 0, 2b - 2c = ±32
于是所求曲面方程为
7 ( x -1) - 3 ( y +1) +8(z - 2) = 0
第8.3节 节
矢量场
1. 矢量场的矢量线 r r
矢量 A = A M） 场 （
r r 在直 角坐标系下，A = A x y z ， （ ， ，） 它的坐标表示式为 为 r r r A = Ax x y z i + Ay x y z j （ ， ，） （ ， ，） r + Az x y z k。 （ ， ，）

格 林 定 理
立了面积分和线积分的关系。从物理角度可以理解为斯托克 立了面积分和线积分的关系。从物理角度可以理解为斯托克 斯定理建立了区域 S 中的场和包围区域 S 的闭合曲线 l 上的 场之间的关系。因此， 中的场， 场之间的关系。因此，如果已知区域 S 中的场，根据斯托克 上的场，反之亦然。 斯定理即可求出边界 l 上的场，反之亦然。
Ψ = ∫ A ⋅ dS
S
通量可为正、或为负、或为零 当矢量穿出某个闭合面时， 通量可为正、或为负、或为零。当矢量穿出某个闭合面时， 认为该闭合面中存在产生该矢量场的源 认为该闭合面中存在产生该矢量场的源；当矢量进入这个闭合 面时，认为该闭合面中存在汇聚该矢量场的洞 ）。闭合 面时，认为该闭合面中存在汇聚该矢量场的洞（或汇）。闭合
惟 一 性 定 理 亥姆霍兹定理 正交曲面 坐标系
10
第一章 矢量分析
标 积 与 矢 积 方向导数与梯度 通 量 与 散 度 环 量 与 旋 度 环 量 与 旋 度 无散场与无旋场 格 林 定 理
2. 旋度：旋度是一个矢量。若以符号 rot A 表示矢量 A 的旋 旋度：旋度是一个矢量。 具有最大环量强度的方向， 度, 则其方向是使矢量 A 具有最大环量强度的方向， 其大小等于对该矢量方向的最大环量强度， 其大小等于对该矢量方向的最大环量强度，即
惟 一 性 定 理 亥姆霍兹定理 正交曲面 坐标系
1
0 A⋅ B = A B
A⊥B
A // B
第一章 矢量分析
标 积 与 矢 积 方向导数与梯度
2.矢量的失积 2.矢量的失积
矢量的失积：代数定义： 矢量的失积：代数定义：
ex A × B = Ax Bx ey Ay By ez Az Bz

矢量分析报告简介矢量分析是地理信息系统（GIS）中常用的一种分析方法，通过对矢量数据进行处理和分析，从中提取有用的信息并得出结论。

本文档将介绍矢量分析的基本概念和方法，并以实际案例解释如何应用矢量分析来解决各种问题。

什么是矢量数据？在GIS中，矢量数据是用于表示现实世界中的地理对象的一种数据模型。

它利用矢量空间来描述和存储地理对象，在计算机中以点、线和面的形式表示。

矢量数据具有以下特点： - 离散性：矢量数据以离散的点、线和面对象形式存储。

- 拓扑性：矢量数据中的要素之间具有拓扑关系，可以通过空间关系进行分析。

- 位置和属性：矢量数据不仅包含地理位置信息，还包含与之相关的属性数据。

矢量数据的基本属性矢量数据包含两个基本属性：几何属性和属性数据。

几何属性几何属性描述了地理对象的位置和形状。

在矢量数据中，几何属性可以是点、线或面。

•点（Point）：在地理空间中的一个离散位置。

点没有长度或面积，仅有一个坐标位置。

•线（Line）：由一系列连接的点组成的几何对象。

线可以表示道路、河流或边界等。

•面（Polygon）：由一系列闭合的线组成的几何对象。

面可以表示土地使用类型、行政区划等。

属性数据属性数据是与几何对象相关联的数据。

它描述了地理对象的特征和属性。

属性数据可以是任何类型的信息，如名称、面积、人口数量等。

这些属性数据通常以表格的形式存储，其中每一行代表一个地理对象，每一列代表一个属性。

矢量分析方法矢量分析基于矢量数据进行，可以帮助我们理解和解释地理现象，从而做出决策。

以下是常用的矢量分析方法：缓冲区分析缓冲区分析用于确定距离某个地理对象一定范围内的其他地理对象。

它可以帮助我们分析空间关系、评估风险和规划用地。

缓冲区分析的步骤如下：1.选择要进行缓冲区分析的对象。

2.指定缓冲区的半径或距离单位。

3.进行缓冲区分析并可视化结果。

叠加分析叠加分析用于确定两个或多个矢量对象之间的空间关系。

通过叠加分析，我们可以识别出重叠、相交、包含和邻近等关系。

二、方向导数 在实际应用中，不仅需要宏观上了解场在空间的数值，还要知道在不同 方向上场变化的情况。方向导数表征标量场空间中，某点处场沿各个方向变 化的规律。
取等位面 u 1、定义：
x, y , z
增加的方向，相互垂直且满足右手螺旋法则
v ˆ ˆ ˆ 矢量表示： A = e x Ax + e y Ay + e z Az
v 位置矢量： r = e x x + e y y + e z z ˆ ˆ ˆ
v ˆ ˆ ˆ dr = e x dx + e y dy + e z dz 微分长度元：
（2）球面坐标系下矢量运算
v ˆ ˆ ˆ A = er Ar + eθ Aθ + eϕ Aϕ v ˆ ˆ ˆ B = er Br + eθ Bθ + eϕ Bϕ
v v ˆ ˆ ˆ A ± B = er ( Ar ± Br ) + eθ ( Aθ ± Bθ ) + eϕ ( Aϕ ± Bϕ )
v v A• B = Ar Br + Aθ Bθ + Aϕ Bϕ
e 单位矢量：ˆ ρ
ρ
,φ
ˆ , eφ
,z
ˆ , ez
0 ≤ ρ < ∞ , 0 ≤ φ ≤ 2π , − ∞ < z < ∞
ˆ ˆ ˆ e z = e ρ × eφ ˆ ˆ ˆ e ρ = eφ × e z ˆ ˆ ˆ eφ = e z × e ρ
ˆ ˆ ˆ ↑ e ρ 、eφ 、e z
分别代表ρ、φ、z 增加的方向，相互垂直且满足右手螺旋法则
ˆ 由于 θ、ϕ 不是常矢量，与 er
ˆ ∂er ˆ =eθ ∂θ ˆ ∂ eθ ˆ = −er ∂θ ˆ ∂ eϕ = 0 ∂θ

对于矢量也存在相应的函数，称为矢性函数
例如：卫星的速度是时间 t 的矢性函数
V V t
第一章
矢量分析
场的定义：
如果在某一空间区域内的每一点，都对应着某 个物理量的一个确定的值，则称在此区域内确定了 该物理量的一个场。
若该物理量为标量，则称标量场,
可用标量函数表示f(x,y,z)；
x
证明：M点的坐标为M(x0+Δx, y0+Δy, z0+Δz)，由于函数φ在 M0处可微，故
( M ) ( M 0 ) x y z x y z
第一章
矢量分析
z
两边除以ρ，可得

x y z x y z cos cos cos x y z
x 2 y 2 c2 解之即得矢量方程 z c1 x
c1和c2是积分常数。
第一章
矢量分析
1.2 标量场的方向导数和梯度
1.2.1 标量场的方向导数
方向导数表征标量 场空间中，某点处场值沿
各个方向变化的规律。
方向导数的定义：
图 1-2 方向导数的定义
第一章
矢量分析
设M0是标量场φ=φ(M)中的一个已知点，从M0出发沿某一方

A B
矢量的加法运算
A B B A
A B
A B

A B A ( B)
矢量的减法运算
A B
第一章
矢量分析
两个矢量的乘积
两个矢量的乘积有两个定义： 点积
运算结果 运算结果
标量 矢量
标积 矢积

F dS S
S1 F dS1
S2 F dS2
S3 F dS3
S4 F dS4
S5 F dS5
S6 F dS6
aˆx aˆz 0, aˆy aˆy 1,
aˆy aˆz 0 aˆz aˆz 1
A B (Axaˆx Ayaˆy Azaˆz ) (Bxaˆx Byaˆy Bzaˆz )
Ax Bx Ay By Az Bz
•结论: 两矢量点积等于对应分量的乘积之和。
电磁场与电磁波
第1章 矢量分析
其中：dl ,dS 和 dV 称为微分元。
dS
dl
1. 直角坐标系
在直角坐标系中，坐标变量为(x,y,z)，如图，做一微分体元。
线元：dlx dxaˆx
dly dyaˆy
面元： dSx dydzaˆx dSy dxdzaˆy
dlz dzaˆz dl dxaˆx dyaˆy dzaˆz
电磁场与电磁波
第1章 矢量分析
3.乘法：
（1）标量与矢量的乘积：
k 0 方向不变，大小为|k|倍
kA k | A | aˆ
k
0
k 0 方向相反，大小为|k|倍
（2）矢量与矢量乘积分两种定义
a. 标量积（点积）：
B
A B | A| | B | cos
A
两矢量的点积含义： 一矢量在另一矢量方向上的投影与另一矢量模的乘积，
定义： A BC | A|| B || C | sin cos
含义： 标量三重积结果为三矢量构成
的平行六面体的体积 。
h BC
A C
B
电磁场与电磁波
第1章 矢量分析
V A (BC) C (A B) B (C A)

矢量分析的知识点总结一、矢量的定义和表示1.1 矢量的定义矢量是指在空间中具有大小和方向的量，它可以用来表示物理量的大小和方向，如力、速度等。

矢量通常用箭头表示，箭头的长度表示矢量的大小，箭头的方向表示矢量的方向。

1.2 矢量的表示矢量可以用不同的方式表示，常见的表示方法有坐标表示和分量表示。

坐标表示是指用矢量所在空间的坐标系来表示矢量，分量表示是指将矢量在坐标系中的投影表示为一组数值。

1.3 矢量的运算矢量的运算包括加法、减法、数量乘法和点乘等。

加法和减法的运算结果是一个新的矢量，数量乘法是指将矢量的长度进行缩放，点乘是指将两个矢量的长度和夹角进行运算得到一个标量。

二、矢量的微积分2.1 矢量的导数矢量的导数是指对矢量的每个分量分别求导，得到的是一个新的矢量。

矢量的导数在物理学中有着广泛的应用，如速度、加速度等物理量都可以用矢量的导数来表示。

2.2 矢量场矢量场是指在空间中的每个点都有一个矢量与之对应的场，它可以用来描述流体的速度场、电场、磁场等。

矢量场的微积分可以用来研究矢量场的性质和行为。

2.3 曲线积分曲线积分是指对沿着曲线的矢量场进行积分，得到的是一个标量。

曲线积分在物理学中有着重要的应用，如对力沿着曲线的功的计算等。

2.4 曲面积分曲面积分是指对矢量场在曲面上的投影进行积分，得到的是一个标量。

曲面积分在物理学中也有着广泛的应用，如对电场在闭合曲面上的通量计算等。

三、矢量分析的应用3.1 物理学中的应用矢量分析在物理学中有着广泛的应用，如在力学中用于描述力、速度、加速度等物理量；在电磁学中用于描述电场、磁场等物理量。

3.2 工程学中的应用矢量分析在工程学中也有很多应用，如在流体力学中用于描述流体的速度场、压力场等；在航空航天工程中用于描述飞行器的运动状态、姿态等。

3.3 计算机科学中的应用矢量分析在计算机科学中也有着重要的应用，如在图形学中用于描述图像的旋转、平移等运动；在机器学习中用于描述数据的特征、相似度等。

例：已知一矢量场F=axxy-ayzx, 试求：
（1） 该矢量场的旋度;
（2） 该矢量沿半径为3的四分 之一圆盘的线积分， 如图所 示， 验证斯托克斯定理。
y B
r＝ 3
O
Ax
四分之一圆盘
第 7、8 学时 1.4 标量的方向导数和梯度
1.4.1标量的方向导数和梯度
一个标量场u可以用一个标量函数来表示。在直角坐标 系中， 可将u表示为
lim l A dl
SP S
称固定矢量R为矢量A的 旋度，记作
rotA=R
上式为旋度矢量在n方 向的投影，如图所示， 即
A dl
lim l
SP S
rotn A
ro tA
n
旋涡面
P l
旋度及其投影
矢量场的旋度仍为矢量。在直角坐标系中，旋度的表达式为
rotA
ax
Az y
Ay z
a
y
Ax z
Az x
z
l
式 中 ， 当 Δl→0 时 δ→0 。 将 上 式 两 边 同 除 以 Δl 并 取 极限得到方向导数的计算公式：
u u cos u cos u cos
l x
y
z
ห้องสมุดไป่ตู้
其中，cosα, cosβ, cosγ为l方向的方向余弦。
1.4.4 标量场的梯度
1. 梯度的定义
方向导数为我们解决了函数u(P)在给定点处沿某个方向的 变化率问题。然而从场中的给定点P出发，标量场u在不 同方向上的变化率一般说来是不同的，那么，可以设想，
▽ ·(▽ ×A)≡0
即如果有一个矢量场B的散度等于零，则该矢量B就可 以用另一个矢量A的旋度来表示，即当 ▽ ·B=0 则有

关于散度的一些计算
r r r r ∇ ⋅ ( A ± B) = ∇ ⋅ A ± ∇ ⋅ B r r r ∇ ⋅ (ϕ A) = ϕ∇ ⋅ A ± A ⋅∇ϕ
3)、散度定理（奥——高定理） 、散度定理（ 高定理） 高定理
∫
V
r r r ∇ ⋅ AdV = A ⋅ dS ∫
S
它将矢量散度的体积分变换成该矢量的面积分， 它将矢量散度的体积分变换成该矢量的面积分，或将矢量 的面积分转换为该矢量散度的体积分。 的面积分转换为该矢量散度的体积分。
第一章 矢量分析
场的几何描述 r 矢量场 A( x, y, z ) 的场线及场线方程
dx dy dz = = Ax Ay Az
标量场
ϕ (x, y, z) 的等值面方程为
ϕ ( x, y , z ) = const.
第一章 矢量分析
2 通过点M 的等值面方程。 例1、 求标量场 ϕ = ( x + y ) − z 通过点 (1, 0, 1)的等值面方程。 、 的等值面方程
第一章 矢量分析
4、 矢量场的环量和旋度
1）、环流（环量 ） 环流（
r r 沿曲线c关于 在矢量场 A 中，沿曲线 关于 的线积分称为该矢量场 A
的环流 。
∫
c
r r A ⋅ dl = A cos θ dl ∫
c
环流表示闭合曲线内存在另 一种源——涡旋源 一种源 涡旋源
第一章 矢量分析
2）、 矢量场的旋度 ）、
max
r ∂ϕ r ∂ϕ r ∂ϕ r = G =| ex + ey + ez | ∂x ∂y ∂z
第一章 矢量分析
中的一点M处有一矢量 处有一矢量， 定义：在标量场 ϕ ( x, y , z )中的一点 处有一矢量，其方向取函 r 点处变化率最大的方向， 数 ϕ 在M点处变化率最大的方向，其模等于 | G | ，该矢量称为标 点处变化率最大的方向 点处的梯度 表示。 量场 ϕ 在M点处的梯度，用grad ϕ 表示。 点处的梯度， 在直角坐标系中， 梯度的表达式为 直角坐标系中

第一章 矢量分析§1 场的概念 一. 矢量与标量1.概念标量 实数域内只有大小的量。

如：电压、温度、时间、电荷等。

矢量 实数域内既有大小又有方向的量，且加法运算遵循平行四边形法则。

如：力F 、电场强度E 、磁场强度H、速度等。

常矢：矢量的模和方向都不变。

如：x e 、y e 、z e。

变矢：模和方向或两者之一变化的矢量(在实际问题中遇到的更多)。

如：r e 、θe 、ϕe 、ρe。

物理量 标量或矢量被赋予物理单位，成为有物理意义的量。

2.矢量的表示印刷 黑体 A ；A(白体)表示A的模。

手写 模和方向均表示出。

表示A 的方向(模为1)。

A 表示矢量A 的模。

▪ 零矢（空矢）：模为零的矢量。

0▪单位矢量：模为1的矢量。

如直角坐标系坐标轴方向x e 、y e 、z e （参考书）。

也有用x a、y a 、z a或i 、j 、k 或 x ˆ、y ˆ、z ˆ 等表示。

若三个相互垂直的坐标轴上的分量已知，一个矢量就确定了。

如直角坐标系中，矢量A的三个分量模值分别是A x , A y , A z ，则直角坐标系： A的模为 A的单位矢量为判断以下手写表示是否正确：（矢量≠标量） （标量≠矢量） ☹ 常见手写表示错误： Aa A 0=A A a=0zz y y x x A e A e A e A ++=222z y x A A A A ++=γβcos cos cos ˆ0z y x zz y y x x A e e a e A A e A A e A A e A A a A++=++===5=E 5x e E=5x e E =765zy x e e e E ++= 765z y x e e e E++=二. 矢量的代数运算1.矢量的加减法2.矢量的乘法a.标量积(点乘) 结果为标量！b.矢量积(叉乘) 结果为矢量！直角坐标系：∙ 点乘 垂直 平行点乘符合交换律： ∙ 叉乘平行 垂直注意：z x y e e e-=⨯ 叉乘不符合交换律： 三.矢量场与标量场1.场在某一空间区域内的每一点，都对应着某个物理量的一个确定的值，则称在此区域内确定了该物理量的一个场。

矢量分析课件矢量分析课件矢量分析是现代数学中的重要分支，它在物理学、工程学、计算机图形学等领域发挥着重要的作用。

本文将对矢量分析课件进行探讨，从其定义、基本概念到应用实例，展示矢量分析的魅力与实用性。

一、矢量分析的定义与基本概念矢量分析是一种研究矢量和矢量场的数学方法。

矢量是具有大小和方向的量，常用箭头表示。

矢量分析的基本概念包括矢量的加法、减法、数乘、点乘和叉乘等运算。

这些运算使得矢量能够进行综合运算，方便描述和计算多种物理量。

在矢量分析中，矢量场是一个在空间中每个点上都有确定大小和方向的矢量的集合。

矢量场可以用来描述电场、磁场、速度场等物理现象。

通过对矢量场的分析，我们可以得到关于场的性质和变化规律的有用信息。

二、矢量分析的应用实例1. 物理学中的应用矢量分析在物理学中有广泛的应用。

以力学为例，通过对物体所受力的矢量分析，我们可以推导出牛顿第二定律，揭示物体运动的规律。

此外，矢量分析还可以用来描述电磁场、引力场等力学现象，为物理学的研究提供了强有力的工具。

2. 工程学中的应用在工程学中，矢量分析被广泛应用于结构力学、流体力学、电路分析等领域。

例如，在结构力学中，通过对受力构件的矢量分析，我们可以计算出构件的受力情况，从而评估结构的稳定性和安全性。

在流体力学中，矢量分析可以用来描述流体的速度场、压力场等，为工程设计和优化提供指导。

3. 计算机图形学中的应用计算机图形学是矢量分析的另一个重要应用领域。

通过对二维和三维图形的矢量分析，我们可以实现图像的绘制、变换和渲染等功能。

矢量分析在计算机图形学中的应用包括曲线绘制、图像变形、光线追踪等，为计算机生成的图像提供了基础。

三、矢量分析课件的设计与优化为了更好地教授和学习矢量分析，设计一份优质的矢量分析课件至关重要。

在设计过程中，需要考虑以下几个方面：1. 清晰的结构与逻辑矢量分析课件应该有清晰的结构和逻辑，便于学生理解和掌握。

可以按照矢量分析的基本概念、运算规则和应用实例等方面进行组织，使得知识点之间有明确的联系和衔接。

t → t0 → → → →
4°
lim
t → t0 →
[ A （t）× B （t）]=
→
lim A （t）× lim B （t）
t → t0 t → t0
5°若 A （t）= Ax（t）
→
i
+Ay（t）
j
→
+Az（t）
→
k ，则
→
lim A （t）= lim Ax（t） i + lim Ay（t）
t → t0 t → t0 t → t0
第一章 矢量分析
矢量分析，是矢量代数的继续，也是场论的基础知识，同时它还是研究其他许多学科的有用 工具。 本章主要介绍矢性函数及其微分，积分。
第一节 矢性函数
1 矢量函数的定义 常矢： 模和方向都保持不变的矢量。 局限性：不能刻划所有矢量 变矢：模和方向或其中之一会改变的矢量 例：质点 M 沿曲线 l 运动时，其速度矢量 V 在运动过程中就是一个变矢 V2
o
y
注： 矢径
→
r
= OM =x
i
+y
j
+z
k
， 因此， 若矢性函数 A（t） 的起点取在坐标原点， 则 A（t）
→
= OM ，而 A （t）={ Ax（t） ，Ay（t） ，Az（t）}， OM ={x，y，z}， 从而
⎧ x = Ax (t ) ⎪ ⎨ y = Ay(t) ……矢端曲线 L 的以 t 为参数的参数方程 ⎪ z = Az(t) ⎩
3 矢性函数的微分 ，称 △定义：设有矢性函数 A = A （t） 为矢性函数 A （t）在 t 处的微分
→ → → →
d A = A ˊ（t）dt

第二十章 矢量分析
第二十章 矢量分析 场是物理学中的重要概念。象温度场、引力场、流速场、电场， 磁场。场是对一种物理量在空间分布状况的描述。在数学上，场 就是空间点的函数。对场的微积分，人们广泛采用了矢量符号。 因此，场的微积分，又称为“矢量分析”。矢量分析的理论是流 体力学和电磁场理论的基本语言和工具。 本章介绍矢量分析的初步知识，内容包括七节。第一节主要介 绍矢量的三种乘法。第二节介绍曲线与曲面的矢量方程以及线矢 量微元和面矢量微元的表达式。第三节给出梯度、散度、旋度的 定义。第四节由功的计算引出曲线积分的概念，并介绍了曲线积 分的环量意义。第五节由通量引出曲面积分的概念。第六、七两 节分别给出高斯定理和斯托克斯定理。
r(t)在空间描绘出一条曲线，称为质点的运动路径。起点到终
第二十章 矢量分析
§ 20. 2
质点的运动路径也可表示为
x = x(t ) y = y (t ) z = z (t )
称为路径的参数方程。见图20.2-1。
Z p
(2)
r =xi + yj +zk
X
O
图 20.2-1
Y
第二十章 矢量分析
x = x(u , v) y = y (u , v) z = z (u , v)
(5)
(5) 称为曲面的参数方程。
第二十章 矢量分析
§ 20. 2
曲面的参数方程可以看做从UV空间到XYZ空间的一个映射，这 一映射把UV空间中的平面域映为XYZ空间中的一张曲面。
r (u, v)
∆v
∆δ
c a
b
u
图20.2-4
∆u
X
第二十章 矢量分析
§ 20. 2

运 算 规律： A B B A （交换律）
A (B C) A B AC （分配律）
AB
AB 0
A// B
A B AB
ex ey ey ez ez ex 0
ex ex ey ey ez ez 1
第一章 矢量分析
（4）矢量的矢量积（叉积）
A B
A B en ABsin
C=A+B
A
AB
B
C2 C C (A B) (A B)
A A B B 2A B
A2 B2 2 ABcosAB A2 B2 2 ABcos
第一章 矢量分析
1.2 三种常用的正交曲线坐标系
三维空间任一点的位置可通过三条相互正交曲线的交点来确定。 三条正交曲线组成的确定三维空间任意点位置且满足右手螺旋 规则的体系，称为正交曲线坐标系；三条正交曲线称为坐标轴； 描述坐标轴的量称为坐标变量。 在电磁场与波理论中，三种常用的正交曲线坐标系为：直角坐 标系、圆柱坐标系和球坐标系。
B
推论：任意多个矢量首尾相连组成闭合多边
矢量的减法
形，矢量和必为零。
第一章 矢量分析
（2）标量乘矢量（数乘）
kA exkAx eykAy ezkAz
（3）矢 量 的标量积（点积）
A B AB cos AxBx Ay By Az Bz
两矢量点积含义：矢量在另一矢量方向上的投影与另一
矢量模的乘积，其结果是一标量。
0
坐标变量
,, z 0 2
坐标单位矢量
e , e , ez
z
位置矢量
r e ez z
线元矢量
dl ed e d ezdz
面元矢量
dS
e dldlz

0
2 2 2 2
x2 y2 z2
1 .4 .2 格林定理
将散度定理中矢量A表示为某标量函数的梯度 ψ与另一标 量函数 φ的乘积, 则有
A ( ) 2
取上式在体积V内的积分, 并应用散度定理, 得
(2 )dv
V
s( ) nˆds
s
n
ds
(1 -49)
式中S是包围体积V的封闭面, nˆ 是封闭面S的外法线方向单位矢
量。此式对于在体积V内具有连续二阶偏导数的标量函数φ和ψ都 成立, 称为格林( G .Green)第一定理。
divA A
A
xˆ
x
yˆ
y
zˆ
z
(xˆAx
yˆAy
zˆAz
)
Ax Ay Az x y z
利用哈密顿算子, 读者可以证明, 散度运算符合下列规则:
(A B) A B
(A) A A
1 .2 .3 散度定理
既然矢量的散度代表的是其通量的体密度, 因此直观地可知, 矢量场散度的体积分等于该矢量穿过包围该体积的封闭面的总 通量, 即
ds nˆds
nˆ 是面元的法线方向单位矢量。nˆ 的取法(指向)有两种情形: 对
开曲面上的面元, 设这个开曲面是由封闭曲线l所围成的, 则当选
定绕行l的方向后, 沿绕行方向按右手螺旋的姆指方向就是 nˆ 的方 向, 如图1 -4所示; 对封闭曲面上的面元, nˆ 取为封闭面的外法线方
向。
图 1 -4 开曲面上的面元
为A , B崐所在平面的右手法向 n:ˆ
A B nˆAB sin aAB
它不符合交换律。 由定义知,
A B (B A)
并有
xˆ xˆ yˆ yˆ zˆ zˆ 0 xˆ yˆ zˆ, yˆ zˆ xˆ, zˆ xˆ yˆ