凸轮曲线sandex
- 格式:pdf
- 大小:230.37 KB
- 文档页数:28

巧借Excel在AutoCAD中设计凸轮轮廓曲线摘要:本文介绍一种借用EXCEL应用程序来计算并保存数据,并与CAD精确绘图巧妙地结合,设计凸轮轮廓曲线的方法,该方法也可用于其它二维或三维曲线的绘制中。
论文毕业论文关键词:凸轮轮廓曲线 AutoCAD 图解法1.问题的提出本文以设计二维凸轮轮廓曲线为例,介绍一种一般操作者就能方便做到的,借用EXCEL应用程序来计算并保存数据,并与AutoCAD精确绘图巧妙地结合,绘制二维或三维非规则曲线的方法,以供大家参考。
2.概述在凸轮机构中,最常用的就是平面凸轮机构,要设计平面凸轮的轮廓曲线。
设计方法通常有图解法和解析法两种。
作图法简便易行、直观,作图误差较大,精度较低,适用于低速对从动件运动规律要求不高的一般精度凸轮设计;对于精度要求高的高速凸轮、靠模凸轮等,必须用解析法列出凸轮的轮廓曲线方程,用计算机辅助设计精确地设计凸轮机构。
我们沿用原有的图解法思路,使用CAD作为工具,两者的联合运用,能产生意想不到的更简单、直接、方便的处理方法。
在这种基于AutoCAD的图解法基础上,利用AutoCAD与其它文档交换信息和数据的功能,对于一些计算量较大输入点较多的图形,与EXCEL应用程序相结合,使作图更加简便快捷。
如设计下面的偏置滚子从动件盘形凸轮轮廓曲线,已知偏距e=10㎜,基圆半径r0=40㎜,行程h=25㎜,滚子半径rT=10㎜。
凸轮以角速度ω顺时针转动,从动件的运动规律为:运动阶段1,推程Φ=180°、凸轮转角φ(°)为0~180,运动形式:等加速-等减速运动,运动方程方程:s=(2h/Φ2)φ2=(2*25/1802)φ(0≤φ≤90)或s=h-2h(Φ-φ)2/Φ2=25-2*25*(180-φ)2/1802(90≤φ≤180)运动阶段2,远休止ΦS=30°、凸轮转角φ(°)为180~210,运动形式:静止不动,运动方程方程: s=h=25(180≤φ≤210)运动阶段3,回程Φ=90°、凸轮转角φ(°)为210~300,运动形式:等加速-等减速运动,运动方程方程: s= h-(2h/Φ’2)/φ’2=25-(2*25/180)2/(φ-210)2(180≤φ≤210)或s=2h(Φ’-φ’)2/Φ’2=2*25*(90-(φ-210))2/902(180≤φ≤210)运动阶段4,远休止ΦS=60°、凸轮转角φ(°)为300~360,运动形式:静止不动,运动方程方程: s=0(300≤φ≤360)3、解题思路要使基于CAD技术的图解法充分发挥软件精确、高效绘图的作用,就要首先改进原来的作图方法。


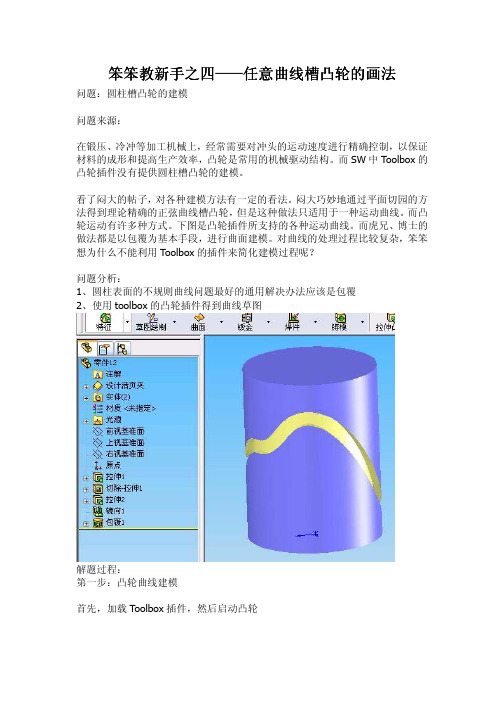
笨笨教新手之四——任意曲线槽凸轮的画法
问题:圆柱槽凸轮的建模
问题来源:
在锻压、冷冲等加工机械上,经常需要对冲头的运动速度进行精确控制,以保证材料的成形和提高生产效率,凸轮是常用的机械驱动结构。
而SW中Toolbox的凸轮插件没有提供圆柱槽凸轮的建模。
看了闷大的帖子,对各种建模方法有一定的看法。
闷大巧妙地通过平面切园的方法得到理论精确的正弦曲线槽凸轮,但是这种做法只适用于一种运动曲线。
而凸轮运动有许多种方式。
下图是凸轮插件所支持的各种运动曲线。
而虎兄、博士的做法都是以包覆为基本手段,进行曲面建模。
对曲线的处理过程比较复杂,笨笨想为什么不能利用Toolbox的插件来简化建模过程呢?
问题分析:
1、圆柱表面的不规则曲线问题最好的通用解决办法应该是包覆
2、使用toolbox的凸轮插件得到曲线草图
解题过程:
第一步:凸轮曲线建模
首先,加载Toolbox插件,然后启动凸轮
建立一个线性的凸轮,三个选项页参数设置如下图。
注意为方便起见,第三页的设置为不穿透的,使用圆弧拟和。
具体用法不难,参考帮助和凸轮的基本知识。
做完的平面凸轮
第二步:圆柱基体的建模,注意使用弧长来做半圆柱然后镜像完成。
这样才能尺寸精确
第三步:使用凸轮的两侧曲线包覆得到结果
最后的结果。

巧借Excel在AutoCAD中设计凸轮轮廓曲线摘要:本文介绍一种借用EXCEL应用程序来计算并保存数据,并与CAD精确绘图巧妙地结合,设计凸轮轮廓曲线的方法,该方法也可用于其它二维或三维曲线的绘制中。
论文毕业论文关键词:凸轮轮廓曲线 AutoCAD 图解法1.问题的提出本文以设计二维凸轮轮廓曲线为例,介绍一种一般操作者就能方便做到的,借用EXCEL应用程序来计算并保存数据,并与AutoCAD精确绘图巧妙地结合,绘制二维或三维非规则曲线的方法,以供大家参考。
2.概述在凸轮机构中,最常用的就是平面凸轮机构,要设计平面凸轮的轮廓曲线。
设计方法通常有图解法和解析法两种。
作图法简便易行、直观,作图误差较大,精度较低,适用于低速对从动件运动规律要求不高的一般精度凸轮设计;对于精度要求高的高速凸轮、靠模凸轮等,必须用解析法列出凸轮的轮廓曲线方程,用计算机辅助设计精确地设计凸轮机构。
我们沿用原有的图解法思路,使用CAD作为工具,两者的联合运用,能产生意想不到的更简单、直接、方便的处理方法。
在这种基于AutoCAD的图解法基础上,利用AutoCAD与其它文档交换信息和数据的功能,对于一些计算量较大输入点较多的图形,与EXCEL应用程序相结合,使作图更加简便快捷。
如设计下面的偏置滚子从动件盘形凸轮轮廓曲线,已知偏距e=10㎜,基圆半径r0=40㎜,行程h=25㎜,滚子半径rT=10㎜。
凸轮以角速度ω顺时针转动,从动件的运动规律为:运动阶段1,推程Φ=180°、凸轮转角φ(°)为0~180,运动形式:等加速-等减速运动,运动方程方程:s=(2h/Φ2)φ2=(2*25/1802)φ(0≤φ≤90)或s=h-2h(Φ-φ)2/Φ2=25-2*25*(180-φ)2/1802(90≤φ≤180)运动阶段2,远休止ΦS=30°、凸轮转角φ(°)为180~210,运动形式:静止不动,运动方程方程: s=h=25(180≤φ≤210)运动阶段3,回程Φ=90°、凸轮转角φ(°)为210~300,运动形式:等加速-等减速运动,运动方程方程: s= h-(2h/Φ’2)/φ’2=25-(2*25/180)2/(φ-210)2(180≤φ≤210)或s=2h(Φ’-φ’)2/Φ’2=2*25*(90-(φ-210))2/902(180≤φ≤210)运动阶段4,远休止ΦS=60°、凸轮转角φ(°)为300~360,运动形式:静止不动,运动方程方程: s=0(300≤φ≤360)3、解题思路要使基于CAD技术的图解法充分发挥软件精确、高效绘图的作用,就要首先改进原来的作图方法。

基于SolidWorks和Excel的凸轮设计与运动仿真肖思伟;张晋西;陈江洪;饶贝;陈奕婷;李洋;胡青松【摘要】采用Excel计算凸轮运动方程位移值,在SolidWorks环境中建立三维模型,运动仿真模块Motion添加直线马达和旋转马达,反转法获得凸轮轮廓曲线坐标点,得到盘形凸轮三维实体模型,并对该凸轮机构进行运动仿真,绘制出推杆运动规律曲线并加以验证。
【期刊名称】《重庆理工大学学报》【年(卷),期】2017(031)008【总页数】4页(P73-75,92)【关键词】凸轮反转法运动仿真 SolidWorks Excle【作者】肖思伟;张晋西;陈江洪;饶贝;陈奕婷;李洋;胡青松【作者单位】重庆理工大学机械工程学院,重庆400054【正文语种】中文【中图分类】TH13凸轮机构是由凸轮、从动件和机架组成的高副机构,广泛应用于各种机械特别是自动机械、自动控制装置等。
基于SolidWorks的盘形凸轮的建模方法很多,可“通过XYZ点的曲线”直接生成凸轮轮廓曲线[1],也可通过Toolbox中的“凸轮”插件生成凸轮模型。
但是这些都需要完全计算出凸轮的相关参数或点的坐标,人为计算有时难免会出现失误。
本文采用Excel工具生成推杆的位移运动规律,结合反转法、 SolidWorks运动仿真模块Motion分析直接生成凸轮轮廓曲线的点坐标[2],通过凸轮点坐标创建凸轮三维模型,最后运动仿真验证凸轮曲线的准确性。
1.1 设计实例凸轮设计的一般步骤是:根据工作要求合理地选择从动件运动规律,按照结构所允许的空间和具体要求,确定凸轮的基圆半径,根据计算公式分段列出从动件位移s 和凸轮角位移φ的函数关系[3],最后画出函数图像。
设计一直动对心凸轮机构,基圆半径80 mm,滚子半径15 mm,凸轮转动2π/3,推杆等加速等减速上升30 mm;凸轮转动π/3,推杆静止;最后等加速等减速各π/2回到最低位置。
1.2 Excel计算凸轮运动方程位移1.2.1 列出从动件方程根据已知条件列出从动件位移方程[3]:式中:δ0为推杆等加速等减速上升凸轮转过的角度,δ0 =2π/3; δ1为推杆等加速等减速下降凸轮转过的角度,δ1 =π; h 为推杆上升的高度,h=30 mm;δ为推杆上升或下降时凸轮转过的角度。
具体作图步骤如下:1.使用工具栏Circle(圆)命令,绘制直径为200的凸轮基圆。
2.使用工具栏Line(直线)命令,捕捉圆心作凸轮基圆铅垂方向的直线B1B7。
注意保持提示直线角度及其前的距离数值(定B1点时应为OB1的长度值,定B7点时应为OB7的长度值)。
3.重复使用Line命令,利用每隔30°呈现的角度提示,保证所绘制直线沿圆周分布每30°一条;利用提示中角度之前的距离数值分别确定样条拟合数据点:OB1、OB2、OB3……、OB11;B0和B12是凸轮轮廓的起讫,也是基圆上的同一点,提示中显示的“交点”即为B0/B12点。
4.使用工具栏中Spline(样条曲线绘制)命令。
系统提示输入初始点:用鼠标捕捉B0点;系统要求输入第二点:用鼠标捕捉B1点;如此,系统不停要求输入数据点,用鼠标依次捕捉B2、B3、…、B11、B12(B0)。
在完成最后一个数据点的输入时,单击鼠标右键确定即可。
5.使用工具栏中Circle命令,绘制凸轮内小圆,与基圆同心,半径为40。
该圆表示凸轮与轴配合的轮廓线。
6.使用工具栏橡皮擦命令,擦除基圆轮廓线和直线段。
7.使用工具栏中ARC(弧线绘制)命令。
圆整凸轮轮廓曲线。
系统提示弧线起点或中心,即:Specify start point of are or [Center]:c(表示给出圆心)。
Specify center point of are:用鼠标捕捉圆心。
Specify start point of are:鼠标捕捉样条曲线(凸轮轮廓曲线)的起点B0点。
Specify end point of are:鼠标捕捉样条曲线的终点B12点。
8.在下拉菜单中选择Modify→Properties(修改→对象特性)命令。
选择所绘制的全部图线,改线宽(Line weight)为0.70mm,打开命令下方开关LWT(打开显示线宽)。
9.凸轮平面绘制完毕。
其绘图速度快、图形效果好。
凸轮曲线三次多项式
凸轮曲线是机械工程中常用的曲线形状,用于控制机械运动。
一种常见的凸轮曲线形状是三次多项式。
下面我将从多个角度来解
释三次多项式凸轮曲线。
首先,三次多项式凸轮曲线是一个三次方程的图像。
三次多项
式的一般形式为y = ax^3 + bx^2 + cx + d,其中a、b、c、d为
常数,x为自变量,y为因变量。
这种曲线形状通常具有两个极值点,即曲线的凹凸性在这两个点发生变化,因此被称为凸轮曲线。
其次,三次多项式凸轮曲线可以通过调整系数a、b、c、d来控
制曲线的形状。
例如,系数a的正负决定了曲线的开口方向,正值
表示曲线向上开口,负值表示曲线向下开口;系数b的大小决定了
曲线的陡峭程度,较大的b值会使曲线更陡峭,较小的b值则会使
曲线更平缓;系数c决定了曲线的平移位置,正值表示曲线向右平移,负值表示曲线向左平移;系数d则是曲线的纵向平移。
此外,三次多项式凸轮曲线在机械工程中有广泛的应用。
凸轮
是一种用于控制运动的机械元件,通过凸轮曲线的形状可以实现不
同的运动轨迹。
例如,在内燃机中,凸轮曲线用于控制气门的开关
时间和行程,从而实现进气、排气和压缩等工作过程;在机床中,凸轮曲线用于控制刀具的运动轨迹,实现加工工件的形状和尺寸。
最后,三次多项式凸轮曲线的特点是光滑且可微。
由于三次多项式是连续可导的,因此凸轮曲线在运动过程中不会出现突变或者不连续的情况,保证了机械系统的稳定性和可靠性。
综上所述,三次多项式凸轮曲线是一种常见的机械工程曲线形状,通过调整多项式的系数可以控制曲线的形状,广泛应用于机械系统中的运动控制。
自动车床主要靠凸轮来控制加工过程,能否设计出一套好的凸轮,是体现自动车床师傅的技术高低的一个标准。
凸轮设计计算的资料不多,在此,我将一些基本的凸轮计算方法送给大家。
凸轮是由一组或多组螺旋线组成的,这是一种端面螺旋线,又称阿基米德螺线。
其形成的主要原理是:由A点作等速旋转运动,同时又使A点沿半径作等速移动,形成了一条复合运动轨迹的端面螺线。
这就是等速凸轮的曲线。
凸轮的计算有几个专用名称:1、上升曲线——凸轮上升的起点到最高点的弧线称为上升曲线2、下降曲线——凸轮下降的最高点到最低点的弧线称为下降曲线3、升角——从凸轮的上升起点到最高点的角度,即上升曲线的角度。
我们定个代号为φ。
4、降角——从凸轮的最高点到最低点的角度,即下降曲线的角度。
代号为φ1。
5、升距——凸轮上升曲线的最大半径与最小半径之差。
我们给定代号为h,单位是毫米。
6、降距——凸轮下降曲线的最大半径与最小半径之差。
代号为h1。
7、导程——即凸轮的曲线导程,就是假定凸轮曲线的升角(或降角)为360°时凸轮的升距(或降距)。
代号为L,单位是毫米。
8、常数——是凸轮计算的一个常数,它是通过计算得来的。
代号为K。
凸轮的升角与降角是给定的数值,根据加工零件尺寸计算得来的。
凸轮的常数等于凸轮的升距除以凸轮的升角,即K=h/φ。
由此得h=Kφ。
凸轮的导程等于360°乘以常数,即L=360°K。
由此得L=360°h/φ。
举个例子:一个凸轮曲线的升距为10毫米,升角为180°,求凸轮的曲线导程。
(见下图) 解:L=360°h/φ=360°×10÷180°=20毫米升角(或降角)是360°的凸轮,其升距(或降距)即等于导程。
这只是一般的凸轮基本计算方法,比较简单,而自动车床上的凸轮,有些比较简单,有些则比较复杂。
在实际运用中,许多人只是靠经验来设计,用手工制作,不需要计算,而要用机床加工凸轮,特别是用数控机床加工凸轮,却是需要先计算出凸轮的导程,才能进行电脑程序设计。