高中数学选修2-2 北师大版 导数的几何意义 作业(含答案)

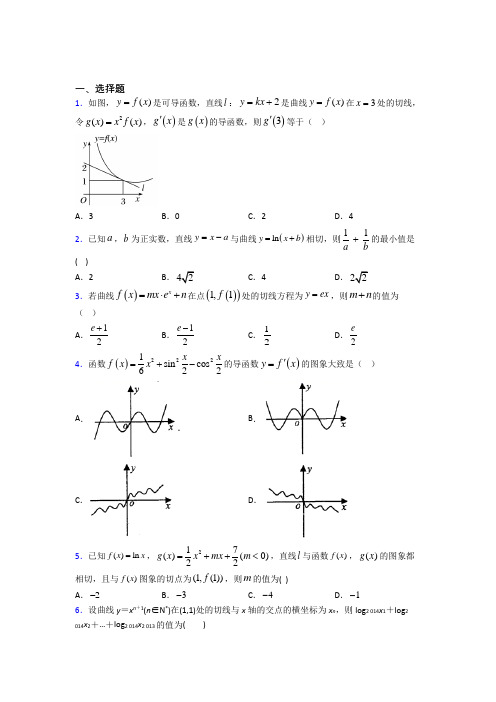
一、选择题1．如图，()y f x =是可导函数，直线l ：2y kx =+是曲线()y f x =在3x =处的切线，令2()()g x x f x =，()g x '是()g x 的导函数，则()3g '等于（ ）A ．3B ．0C ．2D ．42．已知a ，b 为正实数，直线y x a =-与曲线()ln y x b =+相切，则11ab+的最小值是( ) A ．2B ．42C ．4D ．223．若曲线()xf x mx e n =⋅+在点()()1,1f 处的切线方程为y ex =，则m n +的值为（ ） A ．12e + B ．12e - C ．12D ．2e 4．函数()2221sin cos 622x xf x x =+-的导函数()y f x '=的图象大致是（ ） A ． B ．C ．D ．5．已知()ln f x x =，217()(0)22g x x mx m =++<，直线l 与函数()f x ，()g x 的图象都相切，且与()f x 图象的切点为(1,(1))f ，则m 的值为( ) A ．2-B ．3-C ．4-D ．1-6．设曲线y ＝x n ＋1(n ∈N *)在(1,1)处的切线与x 轴的交点的横坐标为x n ，则log 2 014x 1＋log 2014x 2＋…＋log 2 014x 2 013的值为()A ．－log 2 0142 013B ．－1C ．(log 2 0142 013)－1D ．17．已知直线:l y m =，若l 与直线23y x =+和曲线ln(2)y x =分别交于A ，B 两点，则||AB 的最小值为A ．1B ．2C ．455D ．2558．设正弦曲线y ＝sin x 上一点P ，以点P 为切点的切线为直线l ，则直线l 的倾斜角的范围是( ) A ．30,,44πππ⎡⎤⎡⎫⋃⎪⎢⎥⎢⎣⎦⎣⎭B ．[0，π)C ．3,44ππ⎡⎤⎢⎥⎣⎦ D ．[0，4π]∪[2π，34π]9．函数为R 上的可导函数，其导函数为()f x '，且()3sin cos 6f x f x x π⎛⎫=⋅+⎪⎝⎭'，在ABC ∆中，()()1f A f B ='=，则ABC ∆的形状为 A ．等腰锐角三角形B ．直角三角形C ．等边三角形D ．等腰钝角三角形10．已知函数()f x 为R 上的可导函数，且x R ∀∈，均有()()f x f x '<，则有（ ） A ．2019(2019)(0)e f f -<，2019(2019)(0)f e f < B ．2019(2019)(0)e f f -<，2019(2019)(0)f e f > C ．2019(2019)(0)e f f ->，2019(2019)(0)f e f > D ．2019(2019)(0)e f f ->，2019(2019)(0)f e f <11．设函数sin cos y x x x =+的图象上的点()00,x y 处的切线的斜率为k ，记()0k g x =，则函数()k g x =的图象大致为（ ）A ．B ．C ．D ．12．函数f （x ）=﹣12x 2+12在x=1处的切线的斜率为（ ） A ．﹣2B ．﹣1C ．0D ．1二、填空题13．设点P 是曲线3233y x x =-+上的任意一点，P 点处的切线倾斜角为σ，则σ的取值范围为____________. 14．已知函数4()ln 2f x x x xλλ=+-≥，，曲线()y f x =上总存在两点M （x 1，y 1），N （x 2，y 2）使曲线()y f x =在M 、N 两点处的切线互相平行，则x 1+x 2的取值范围为_______． 15．在曲线3211333y x x x =-+-的所有切线中，斜率最小的切线方程为______． 16．若直线y kx b =+是曲线ln 3y x =+的切线，也是曲线ln(1)y x =+的切线，则b =______17．函数在处的切线与直线垂直，则a 的值为______．18．若以曲线()y f x =上任意一点(,)M x y 为切点作切线l ，曲线上总存在异于M 的点11(,)N x y ，以点N 为切点作线1l ，且1//l l ，则称曲线()y f x =具有“可平行性”，下列曲线具有可平行性的编号为__________．（写出所有的满足条件的函数的编号） ①1y x=②3y x x =- ③cos y x = ④2(2)ln y x x =-+ 19．设()()()sin 2',''32f x x xf f x f x f ππ⎛⎫⎛⎫=+=⎪ ⎪⎝⎭⎝⎭是的导函数，则___________. 20．过点()1,1-与曲线()32f x x x =-相切的直线方程是__________．三、解答题21．已知函数f (x )＝13x 3－2x 2＋3x (x ∈R)的图象为曲线C . (1)求过曲线C 上任意一点切线斜率的取值范围；(2)若在曲线C 上存在两条相互垂直的切线，求其中一条切线与曲线C 的切点的横坐标的取值范围．22．已知函数()mf x mx x=-，()2ln g x x =. （1）当2m =时，求曲线()y f x =在点(1(1))f ，处的切线方程； （2）当1m =时，判断方程()()f x g x =在区间(1)+∞，上有无实根；（3）若(1]x e ∈，时，不等式()()2f x g x -<恒成立，求实数m 的取值范围. 23．求下列函数的导数： （1）()(1sin )(14)f x x x =+-； （2）()21x xf x x =-+. 24．设函数()bf x ax x=-，曲线y =f （x ）在点（2，f （2））处的切线方程为7x -4y -（1）求y =f （x ）的解析式；（2）证明：曲线y =f （x ）上任一点处的切线与直线x =0和直线y =x 所围成的三角形面积为定值，并求此定值．25．（1）函数()(1sin )f x x x =+的导数为()'f x ，求2f π⎛⎫' ⎪⎝⎭； （2）设l 是函数1y x=图象的一条切线，证明：l 与坐标轴所围成的三角形的面积与切点无关．26．已知函数()()1ln 1x f x x++=和()()1ln 1g x x x =--+（1）若()f x '是()f x 的导函数，求(1)f '的值 （2）当0x >时，不等式()()0g x f x kx'->恒成立，其中()g x '是()g x 导函数,求正整数k 的最大值.【参考答案】***试卷处理标记，请不要删除一、选择题 1．A 解析：A 【分析】2y kx =+是曲线()y f x =在3x =处的切线求出=(3)k f ，由图(3)=1f ，对2()()g x x f x =求导取值可得.【详解】2y kx =+是曲线()y f x =在3x =处的切线,所以切点(3,1)代入切线方程得1=(3)=3k f ，又(3)=1f 2()()g x x f x =，2()2()+()g x xf x x f x ''=，(3)6(3)+9(3)=3g f f ''∴=故选：A. 【点睛】本题考查导数的几何意义.根据导数的几何意义求参数值的思路根据导数的几何意义求参数的值时，一般是利用切点00)(P x y ，既在曲线上又在切线上构造方程组求解．2．C【分析】求函数的导数，由已知切线的方程，可得切线的斜率，求得切线的坐标，可得1a b +=，再由乘1法和基本不等式，即可得到所求最小值． 【详解】解：()y ln x b =+的导数为1y x b'=+， 由切线的方程y x a =-可得切线的斜率为1， 可得切点的横坐标为1b -，所以切点为(1,0)b -， 代入y x a =-，得1a b +=，a 、b 为正实数，则111()()22241b a b a a b a b a b a b a b+=++=+++=． 当且仅当12a b ==时，11a b+取得最小值4． 故选：C 【点睛】本题主要考查导数的应用，利用导数的几何意义以及基本不等式是解决本题的关键，属于中档题．3．A解析：A 【分析】求导得到()()'1xf x m x e =+⋅，由已知得()1f e =，()1f e '=，解得答案.【详解】()x f x mx e n =⋅+，则()()'1x f x m x e =+⋅，故()1f e =，()1f e '=，()11me n e m e e +=⎧∴⎨+=⎩，解得122m en ⎧=⎪⎪⎨⎪=⎪⎩，所以12e m n ++=. 故选：A . 【点睛】本题考查了根据切线方程求参数，意在考查学生的计算能力和转化能力.4．C解析：C 【分析】将函数()y f x =的解析式化简，求出其导数()1sin 3f x x x '=+，，然后结合导函数的符号排除错误选项即可确定导函数的图像.因为()222211sin cos cos 6226x x f x x x x =+-=-，()1sin 3f x x x '∴=+. 当03x <≤时，103x >，sin 0x >，则()1sin 03f x x x '=+>； 当3x >时，113x >，1sin 1x -≤≤，则()1sin 03f x x x '=+>. 所以，当0x >时，()1sin 03f x x x '=+>，排除ABD 选项， 故选：C. 【点睛】本题考查函数图象的识别，给定函数解析式，一般要结合函数的定义域、奇偶性、单调性（导数）、特殊值符号、零点等知识进行逐一排除，考查分析问题和解决问题的能力，属于中等题.5．A解析：A 【分析】先利用导数求切线斜率,再根据点斜式方程得切线方程,最后根据判别式为零得结果. 【详解】 1()f x x'=， 直线l 是函数()f x lnx =的图象在点(1,0)处的切线，∴其斜率为k f ='（1）1=， ∴直线l 的方程为1y x =-．又因为直线l 与()g x 的图象相切，∴211722y x y x mx =-⎧⎪⎨=++⎪⎩，消去y ，可得219(1)022x m x +-+=，得△2(1)902(4m m m =--=⇒=-=不合题意，舍去）， 故选A 【点睛】本题主要考查函数导数的几何意义,考查直线和曲线的位置关系，意在考查学生对这些知识 的理解掌握水平和分析推理能力.6．B解析：B 【解析】 【分析】由题意，求出y ＝x n ＋1(n ∈N *)在(1,1)处的切线方程，取0y =，求得n x ，再利用对数的运算性质可得答案. 【详解】由y ＝x n ＋1，可得(1)n y n x =+'，即11x y n ='=+即曲线y ＝x n ＋1(n ∈N *)在(1,1)处的切线方程为1(1)(1)y n x -=+-令0y =，得1n n x n =+ log 2 014x 1＋log 2 014x 2＋…＋log 2 014x 2 013=20141220132014122013log ()log ()1232014x x x =⋅=- 故选B 【点睛】本题考查了曲线的切线方程和对数的运算，细心计算是解题的关键，属于中档题.7．B解析：B 【分析】利用导数求出与直线23y x =+平行的曲线的切线的切点，利用点到直线的距离可得. 【详解】1y x '=,令12x =可得12x =，所以切点为1,02⎛⎫ ⎪⎝⎭. 根据题意可知1,02B ⎛⎫ ⎪⎝⎭且0m =，所以3,02A ⎛⎫- ⎪⎝⎭，此时2AB =.故选B. 【点睛】本题主要考查导数的几何意义.已知切线的斜率，结合导数可得切点.8．A解析：A 【解析】由题得cos y x '=，设切线的倾斜角为α，则，3tan cos 1tan 1[0,][,)44k x ππαααπ==∴-≤≤∴∈⋃，故选A.9．D解析：D 【解析】 【分析】求函数的导数，先求出'16f π⎛⎫= ⎪⎝⎭，然后利用辅助角公式进行化简，求出A ，B 的大小即可判断三角形的形状． 【详解】函数的导数()''cos sin 6f x x x π⎛⎫=- ⎪⎝⎭，则131''cos sin ''666662262f f f ππππππ⎛⎫⎛⎫⎛⎫⎛⎫=-=-=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭，则11'262f π⎛⎫= ⎪⎝⎭，则'16f π⎛⎫= ⎪⎝⎭，则()'sin 2cos 6f x x x x π⎛⎫=-=+⎪⎝⎭， ()cos 2cos 3f x x x x π⎛⎫=+=- ⎪⎝⎭，()()'1f A f B ==，()'2cos 16f B B π⎛⎫∴=+= ⎪⎝⎭，即1cos 62B π⎛⎫+= ⎪⎝⎭，则63B ππ+=，得6B π=，()2cos 13f A A π⎛⎫=-= ⎪⎝⎭，即1cos 32A π⎛⎫-= ⎪⎝⎭，则33A ππ-=，则23A π=， 则2366C ππππ=--=， 则B C =，即ABC 是等腰钝角三角形， 故选D ． 【点睛】本题考查三角形形状的判断，根据导数的运算法则求出函数()f x 和()'f x 的解析式是解决本题的关键．10．B解析：B 【分析】 令()()xf xg x e=，x ∈R ．()()()x f x f x g x e '-'=，根据x R ∀∈，均有()()f x f x '<，可得函数()g x 的单调性，进而得出结论． 【详解】 解：令()()x f x g x e=，x ∈R ．()()()xf x f xg x e '-'=， x R ∀∈，均有()()f x f x '<， ()g x ∴在R 上单调递增，(2019)(0)(2019)g g g ∴-<<，可得：2019(2019)(0)e f f -<，2019(2019)(0)f e f >． 故选B ． 【点睛】本题考查了利用导数研究函数的单调性、方程与不等式的解法、构造法，考查了推理能力与计算能力，属于中档题．11．A解析：A 【详解】因为sin cos ,sin cos sin cos y x x x y x x x x x x '=+=+-=， 则()cos g x x x =，该函数为奇函数，排除B 、C ，当0,2x π⎛⎫∈ ⎪⎝⎭时，()0>g x ，排除D. 故选:A12．B解析：B 【解析】 【分析】根据导数的几何意义可知(1)k f '=，求导后计算即可. 【详解】 因为()f x x '=-,所以 (1)1k f '==- ，故选B. 【点睛】本题主要考查了导数的几何意义，属于容易题.二、填空题13．【分析】设点根据导数的几何意义求得即可得到答案【详解】设点由函数可得可得即又由所以故答案为：【点睛】本题主要考查了导数的几何意义及其应用其中解答中熟记导数的几何意义准确计算是解答的关键着重考查推理与解析：20,,23πππ⎡⎫⎡⎫⋃⎪⎪⎢⎢⎣⎭⎣⎭【分析】设点00(,)P x y ，根据导数的几何意义，求得tan σ≥.【详解】设点00(,)P x y，由函数323y x =+，可得23y x '=可得020|3x x y x ='=，即tan σ≥ 又由[)0,σπ∈，所以20,,23πππ⎡⎫⎡⎫⋃⎪⎪⎢⎢⎣⎭⎣⎭. 故答案为：20,,23πππ⎡⎫⎡⎫⋃⎪⎪⎢⎢⎣⎭⎣⎭. 【点睛】本题主要考查了导数的几何意义及其应用，其中解答中熟记导数的几何意义，准确计算是解答的关键，着重考查推理与运算能力.14．【分析】求出导函数根据题意转化为对恒成立即可得解【详解】曲线上总存在两点M （x1y1）N （x2y2）使曲线在MN 两点处的切线互相平行即所以对恒成立所以x1+x2的取值范围为故答案为：【点睛】此题考查解析：()8+∞，【分析】求出导函数24()1f x x x λ'=--，根据题意转化为()()212121244x x x x x x λλ++=<对2λ≥恒成立，即可得解.【详解】4()ln 2f x x x x λλ=+-≥，，24()1f x x xλ'=--，曲线()y f x =上总存在两点M （x 1，y 1），N （x 2，y 2）使曲线()y f x =在M 、N 两点处的切线互相平行，即121212()(),,0,0f x f x x x x x ''=≠>>，2211224411x x x x λλ--=--， 22121244x x x x λλ-=-，()()212121244x x x x x x λλ++=<所以1216x x λ+>对2λ≥恒成立所以x 1+x 2的取值范围为()8+∞，. 故答案为：()8+∞，【点睛】此题考查导数的几何意义，根据导数的几何意义解决切线斜率相等的问题，求切点横坐标之和的取值范围，利用基本不等式构造不等关系求解.15．【解析】【分析】根据导数的几何意义可知在某点处的导数为切线的斜率先求出导函数利用配方法求出导函数的最小值即为切线最小斜率再用点斜式写出化简【详解】曲线时切线最小斜率为2此时切线方程为即故答案为：【点 解析：20x y -=【解析】 【分析】根据导数的几何意义可知在某点处的导数为切线的斜率，先求出导函数()f x '，利用配方法求出导函数的最小值即为切线最小斜率，再用点斜式写出化简． 【详解】曲线3211333y x x x =-+-，223y x x ∴'=-+，1x ∴=时，切线最小斜率为2，此时，32111131233y =⨯-+⨯-=．∴切线方程为22(1)y x -=-，即20x y -=．故答案为：20x y -=． 【点睛】本题主要考查了利用导数研究曲线上某点切线方程，以及二次函数的最值等基础题知识，考查运算求解能力，属于基础题．16．【分析】对两条曲线对应的函数求导设出两个切点的横坐标令它们的导数相等求出两条曲线在切点处的切线方程对比系数求得的值【详解】依题意设直线与相切切点的横坐标为即切点为设直线与相切切点的横坐标为即切点为令 解析：2ln 3-【分析】对两条曲线对应的函数求导，设出两个切点的横坐标，令它们的导数相等，求出两条曲线在切点处的切线方程，对比系数求得b 的值. 【详解】依题意，()()''11ln 3,ln 11x x x x +=+=⎡⎤⎣⎦+，设直线y kx b =+与ln 3y x =+相切切点的横坐标为0x ，即切点为()00,ln 3x x +，设直线y kx b =+与()ln 1y x =+相切切点的横坐标为1x ，即切点为()()11,ln 1x x +，令01111x x =+，解得101x x =-，故直线y kx b =+与()ln 1y x =+相切切点为()001,ln x x -.由此求出两条切线方程为()()0001ln 3y x x x x -+=-和()0001ln 1y x x x x -=-+；即001ln 2y x x x =++和000111ln y x x x x =-++，故0001ln 21ln x x x +=-++，013x =，故0ln 22ln3b x =+=-.【点睛】本小题主要考查两条曲线共切线方程的问题，考查切线方程的求法，考查导数的运算，属于中档题.17．0【解析】【分析】求函数的导数根据导数的几何意义结合直线垂直时直线斜率的关系建立方程关系进行求解即可得结果【详解】因为函数y=(x+a)ex 在x=0处的切线与直线x+y+1=0垂直所以函数y=(x+ 解析：【解析】 【分析】求函数的导数，根据导数的几何意义结合直线垂直时直线斜率的关系建立方程关系进行求解即可得结果. 【详解】 因为函数在处的切线与直线垂直，所以函数在处的切线斜率，因为，所以，解得，故答案是0. 【点睛】该题考查的是有关利用导数研究曲线上某点处的切线的问题，涉及到的知识点有两直线垂直的条件，导数的几何意义，以及函数的求导公式，属于中档题目.18．①③【解析】因为；因为不存在异于的点；因为总存在异于的点满足条件；因为不存在异于的点；所以选①③解析：①③ 【解析】 因为122111y x x x x x =-=-∴=-'≠取 ； 因为231,0y x x =-='时不存在异于M 的点N ；因为1sin sin y x x =-=-'∴总存在异于M 的点N 满足条件；因为212412(2)x x y x x x ='-+=-+，22x =不存在异于M 的点N ；所以选①③19．-1【解析】∵令可得：解得则解析：-1 【解析】∵()2(),()2()33f x sinx xf f x cosx f ππ=+'∴'=+'，令3x π=,可得：()2()333f cos f πππ'=+' ,解得1()32f π'=- ， 则1()2()1222f cosππ'=+⨯-=- 20．或【解析】由题意可得：设曲线上点的坐标为切线的斜率为切线方程为：(*)切线过点则：解得：或将其代入(*)式整理可得切线方程为：或点睛：曲线y ＝f(x)在点P(x0y0)处的切线与过点P(x0y0)的解析：20x y --=或5410x y +-= 【解析】由题意可得：()2'32f x x =-，设曲线上点的坐标为()3000,2x x x -，切线的斜率为2032k x =-，切线方程为：()()()320000232y x x x x x --=--，(*)切线过点()1,1-，则：()()()32012321x x x x ---=--，解得：01x =或012x =-将其代入(*)式整理可得，切线方程为：20x y --=或5410x y +-=.点睛：曲线y ＝f (x )“在点P (x 0，y 0)处的切线”与“过点P (x 0，y 0)的切线”的区别：前者P (x 0，y 0)为切点，而后者P (x 0，y 0)不一定为切点．三、解答题21．（1）[－1，＋∞)；（2）(－∞，2∪(1,3)∪[2∞). 【解析】试题分析：（1）先求导函数，然后根据导函数求出其取值范围，从而可求出曲线C 上任意一点处的切线的斜率的取值范围；（2）根据（1）可知k 与﹣1k的取值范围，从而可求出k 的取值范围，然后解不等式可求出曲线C 的切点的横坐标取值范围. (1)由题意得f ′(x )＝x 2－4x ＋3，则f ′(x )＝(x －2)2－1≥－1， 即过曲线C 上任意一点切线斜率的取值范围是[－1，＋∞)．(2)设曲线C 的其中一条切线的斜率为k ，则由(2)中条件并结合(1)中结论可知，111k k≥-⎧⎪⎨-≥-⎪⎩解得－1≤k ＜0或k ≥1，故由－1≤x 2－4x ＋3＜0或x 2－4x ＋3≥1， 得x ∈(－∞，2∪(1,3)∪[2∞) 22．(1) 44y x =-；(2) 内无实数根；（3）241e e ⎛⎫-∞ ⎪-⎝⎭，. 【解析】试题分析：（2）把m 的值代入后，求出f （1），求出x=1时函数的导数，由点斜式写出曲线y=f （x ）在点（1，f （1））处的切线方程；（Ⅱ）代入m 的值，把判断方程f （x ）=g （x ）在区间（1，+∞）上有无实根转化为判断函数h （x ）=f （x ）﹣g （x ）在（1，+∞）上有无零点问题，求导后利用函数的单调性即可得到答案；（Ⅲ）把f （x ）和g （x ）的解析式代入不等式，整理变形后把参数m 分离出来，x ∈（1，e]时，不等式f （x ）﹣g （x ）＜2恒成立，转化为实数m 小于一个函数在（1，e]上的最小值，然后利用导数分析函数在（1，e]上的最小值． 试题（1）2m =时，()22f x x x =-，()222f x x='+，()14f '=，切点坐标为()10，， ∴切线方程为44y x =-（2）1m =时，令()()()12ln h x f x g x x x x=-=--， ()()22211210x h x x x x-=+-=≥'，∴()h x 在()0+∞，上为增函数， 又()10h =，所以()()f x g x =在()1+∞，内无实数根. （3）2ln 2mmx x x--<恒成立，即()2122ln m x x x x -<+恒成立. 又210x ->，则当(]1x e ，∈时，222ln 1x x xm x +<-恒成立，令()222ln 1x x xG x x +=-，只需m 小于()G x 的最小值. ()()()2222ln ln 21x x x G x x-++-'=，∵1x e <≤，∴ln 0x >，∴(]1x e ，∈时，()0G x '<， ∴()G x 在(]1e ，上单调递减，∴()G x 在(]1e ，的最小值为()241eG e e =-， 则m 的取值范围是241e e ⎛⎫-∞ ⎪-⎝⎭，. 点睛：导数问题经常会遇见恒成立的问题：（1）根据参变分离，转化为不含参数的函数的最值问题；（2）若()0f x >就可讨论参数不同取值下的函数的单调性和极值以及最值，最终转化为min ()0f x >，若()0f x <恒成立，转化为max ()0f x <;（3）若()()f x g x >恒成立，可转化为min max ()()f x g x >. 23．（1）'()4cos 4sin 4cos f x x x x x ==-+--；（2）21'()2ln 2(1)x f x x =-+. 【分析】(1)利用积的导数和和差的导数法则求导.(2)利用商的导数和积的导数的法则求导. 【详解】(1)f'(x)=(1+sin x)'(1-4x)+(1+sin x)(1-4x)'=cos x(1-4x)-4(1+sin x)=cos x-4xcos x-4-4sin x.(2)f(x)=1x x +-2x =1-11x +-2x ,则f'(x)=21(1)x +-2xln 2. 【点睛】本题主要考查对函数求导，意在考查学生对该知识的掌握水平和分析推理能力. 24．(1)3()f x x x=-；(2)证明见解析. 【解析】解：(1)方程7x －4y －12＝0可化为y ＝74x －3， 当x ＝2时，y ＝12． 又f′(x)＝a ＋2b x ， 于是1222{744b a b a -=+=，解得13a b ==⎧⎨⎩故f(x)＝x －3x． (2)证明：设P(x 0，y 0)为曲线上任一点，由f′(x)＝1＋23x知，曲线在点P(x 0，y 0)处的切线方程为y －y 0＝(1＋203x )·(x －x 0)，即y －(x 0－03x )＝(1＋203x )(x －x 0)． 令x ＝0得，y ＝－06x ，从而得切线与直线x ＝0，交点坐标为(0，－06x )． 令y ＝x ，得y ＝x ＝2x 0，从而得切线与直线y ＝x 的交点坐标为(2x 0,2x 0)． 所以点P(x 0，y 0)处的切线与直线x ＝0，y ＝x 所围成的三角形面积为12|－06x ||2x 0|＝6．曲线y ＝f(x)上任一点处的切线与直线x ＝0和直线y ＝x 所围成的三角形面积为定值，此定值为6．25．（1）2；（2）证明见解析． 【分析】（1）求出()cos 1sin f x x x x '=++，即得2f π⎛⎫'⎪⎝⎭的值； （2）设切点为001,x x ⎛⎫⎪⎝⎭，先求出切线l 的方程为：()020011y x x x x -=--，再求出l 与坐标轴所围成的三角形的面积2S =，即得证. 【详解】（1）()(1sin )f x x x =+，则()[(1sin )](1sin )(1sin )cos 1sin f x x x x x x x x x x ''''=+=+++=++， 所以cos 1sin 22222f ππππ'⎛⎫=++=⎪⎝⎭； （2）设切点为001,x x ⎛⎫⎪⎝⎭， ∵1y x =，21y x'∴=-，∴切线l 的斜率201k x =-， ∴切线l 的方程为：()020011y x x x x -=--， 令0x =，得02y x =， 令0y =，得02x x =，所以l 与坐标轴所围成的三角形的面积0012222S x x =⋅⋅=， 因此l 与坐标轴所围成的三角形的面积与切点无关． 【点睛】本题主要考查导数的运算，考查导数的几何意义，意在考查学生对这些知识的理解掌握水平. 26．（1）1ln 22--；（2）3 【分析】（1）求出导函数，代入x 的值即可得到结果； （2）不等式()()0g x f x k x-'>恒成立等价于[](1)1ln(1)x x k x+++<对于0x >恒成立.【详解】（1）由题意可得()()2ln 111xx x f x x +='--+ ∴()11ln 22f '=--；（2）当0x >时，不等式()()0g x f x k x'->恒成立 即[](1)1ln(1)x x k x+++<对于0x >恒成立设[](1)1ln(1)()x x h x x+++=，则21ln(1)()x x h x x --+'=1()1011x g x x x '=-=>++，()1ln(1)g x x x =--+在区间()0,∞+上是增函数， 且()0g x =存在唯一实数根a ,满足(2,3)a ∈，即1ln(1)a a =++ 由x a >时，()0,()0g x h x '>>；0x a <<时，()0,()0g x h x '<< 知()(0)h x x >的最小值为[](1)1ln(1)()1(3,4)a a h a a a+++==+∈故正整数k 的最大值为3. 【点睛】本题考查了函数的单调性问题，考查导数的应用以及函数恒成立问题，是一道中档题．。

§导数的概念及其几何意义导数的概念导数的几何意义.理解导数的概念及导数的几何意义.(重点、难点).会求导函数及理解导数的实际意义.(重点).掌握利用导数求切线方程的方法.(难点)教材整理函数()在＝处的导数阅读教材“例”以上部分，完成下列问题.称为函数＝()瞬时变化率在点的函数＝()在点的导数，′()，记作表示通常用符号′()＝＝.设函数＝()可导，则等于( )′()′().以上都不对′()【解析】由()在＝处的导数的定义知，应选.【答案】教材整理导数的几何意义阅读教材～，完成下列问题.()在点(是曲线＝函数＝()在处的导数，，()在处())函数＝切线的斜率处的切线的斜率.反映了导数的几何意义.抛物线＝＋在点(－，)处的切线方程为.【解析】因为′＝＝(＋Δ)＝，所以＝－，故所求切线方程为＋＝.【答案】＋＝预习完成后，请将你的疑问记录，并与“小伙伴们”探讨交流：疑问：解惑：疑问：解惑：疑问：解惑：则等于( ).以上都不是()函数＝在＝处的导数是.()求函数＝＋在＝处的导数.【精彩点拨】根据导数的概念求解.【自主解答】()＝·＝·＝.()∵Δ＝－，∴＝＝，当Δ趋于时，＝趋于，∴函数＝在＝处的导数为.【答案】() ()()∵()＝＋，。

高二数学课后练习题：导数的几何意义【摘要】鉴于大家对xx十分关注，小编在此为大家整理了此文高二数学课后练习题：导数的几何意义，供大家参考!本文题目：高二数学课后练习题：导数的几何意义选修2-2 1.1 第3课时导数的几何意义一、选择题1.如果曲线y=f(x)在点(x0，f(x0))处的切线方程为x+2y-3=0，那么()A.fprime;(x0)0B.fprime;(x0)<0C.fprime;(x0)=0D.fprime;(x0)不存在[答案] B[解析]切线x+2y-3=0的斜率k=-12，即fprime;(x0)=-12<0.故应选B.2.曲线y=12x2-2在点1，-32处切线的倾斜角为()A.1B.pi;4C.54pi;D.-pi;4[答案] B[解析]∵yprime;=limDelta;xrarr;0 [12(x+Delta;x)2-2]-(12x2-2)Delta;x=limDelta;xrarr;0 (x+12Delta;x)=xthere4;切线的斜率k=yprime;|x=1=1.there4;切线的倾斜角为pi;4，故应选B.3.在曲线y=x2上切线的倾斜角为pi;4的点是()A.(0,0)B.(2,4)C.14，116D.12，14[答案] D[解析]易求yprime;=2x，设在点P(x0，x20)处切线的倾斜角为pi;4，则2x0=1，there4;x0=12，there4;P12，14.4.曲线y=x3-3x2+1在点(1，-1)处的切线方程为()A.y=3x-4B.y=-3x+2C.y=-4x+3D.y=4x-5[答案] B[解析]yprime;=3x2-6x，there4;yprime;|x=1=-3.由点斜式有y+1=-3(x-1).即y=-3x+2.5.设f(x)为可导函数，且满足limxrarr;0 f(1)-f(1-2x)2x=-1，则过曲线y=f(x)上点(1，f(1))处的切线斜率为()A.2B.-1C.1D.-2[答案] B[解析]limxrarr;0 f(1)-f(1-2x)2x=limxrarr;0 f(1-2x)-f(1)-2x=-1，即yprime;|x=1=-1，则y=f(x)在点(1，f(1))处的切线斜率为-1，故选B.6.设fprime;(x0)=0，则曲线y=f(x)在点(x0，f(x0))处的切线()A.不存在B.与x轴平行或重合C.与x轴垂直D.与x轴斜交[答案] B[解析]由导数的几何意义知B正确，故应选B.7.已知曲线y=f(x)在x=5处的切线方程是y=-x+8，则f(5)及fprime;(5)分别为()A.3,3B.3，-1C.-1,3D.-1，-1[答案] B[解析]由题意易得：f(5)=-5+8=3，fprime;(5)=-1，故应选B.8.曲线f(x)=x3+x-2在P点处的切线平行于直线y=4x-1，则P点的坐标为()A.(1,0)或(-1，-4)B.(0,1)C.(-1,0)D.(1,4)[答案] A[解析]∵f(x)=x3+x-2，设xP=x0，there4;Delta;y=3x20?Delta;x+3x0?(Delta;x)2+(Delta;x)3+Delta;x，there4;Delta;yDelta;x=3x20+1+3x0(Delta;x)+(Delta;x)2，there4;fprime;(x0)=3x20+1，又k=4，there4;3x20+1=4，x20=1.there4;x0=plusmn;1，故P(1,0)或(-1，-4)，故应选A.9.设点P是曲线y=x3-3x+23上的任意一点，P点处的切线倾斜角为alpha;，则alpha;的取值范围为()A.0，pi;2cup;23pi;，pi;B.0，pi;2cup;56pi;，pi;C.23pi;，pi;D.pi;2，56pi;[答案] A[解析]设P(x0，y0)，∵fprime;(x)=limDelta;xrarr;0 (x+Delta;x)3-3(x+Delta;x)+23-x3+3x-23Delta;x=3x2-3，there4;切线的斜率k=3x20-3，there4;tanalpha;=3x20-3≥-3.there4;alpha;isin;0，pi;2cup;23pi;，pi;.故应选A.10.(2020?福州高二期末)设P为曲线C：y=x2+2x+3上的点，且曲线C在点P处切线倾斜角的取值范围为[0，pi;4]，则点P横坐标的取值范围为()A.[-1，-12]B.[-1,0]C.[0,1]D.[12，1][答案] A[解析]考查导数的几何意义.∵yprime;=2x+2，且切线倾斜角theta;isin;[0，pi;4]，there4;切线的斜率k满足0<k<1，即0<2x+2<1，there4;-1<x<-12.二、填空题11.已知函数f(x)=x2+3，则f(x)在(2，f(2))处的切线方程为________.[答案]4x-y-1=0[解析]∵f(x)=x2+3，x0=2there4;f(2)=7，Delta;y=f(2+Delta;x)-f(2)=4?Delta;x+(Delta;x)2there4;Delta;yDelta;x=4+Delta;x.there4;limDelta;xrarr;0Delta;yDelta;x=4.即fprime;(2)=4.又切线过(2,7)点，所以f(x)在(2，f(2))处的切线方程为y-7=4(x-2) 即4x-y-1=0.12.若函数f(x)=x-1x，则它与x轴交点处的切线的方程为________.[答案]y=2(x-1)或y=2(x+1)[解析]由f(x)=x-1x=0得x=plusmn;1，即与x轴交点坐标为(1,0)或(-1,0).∵fprime;(x)=limDelta;xrarr;0 (x+Delta;x)-1x+Delta;x-x+1xDelta;x=limDelta;xrarr;0 1+1x(x+Delta;x)=1+1x2.there4;切线的斜率k=1+11=2.there4;切线的方程为y=2(x-1)或y=2(x+1).13.曲线C在点P(x0，y0)处有切线l，则直线l与曲线C的公共点有________个.[答案]至少一[解析]由切线的定义，直线l与曲线在P(x0，y0)处相切，但也可能与曲线其他部分有公共点，故虽然相切，但直线与曲线公共点至少一个.14.曲线y=x3+3x2+6x-10的切线中，斜率最小的切线方程为________.[答案]3x-y-11=0[解析]设切点P(x0，y0)，则过P(x0，y0)的切线斜率为，它是x0的函数，求出其最小值.设切点为P(x0，y0)，过点P的切线斜率k= =3x20+6x0+6=3(x0+1)2+3.当x0=-1时k有最小值3，此时P的坐标为(-1，-14)，其切线方程为3x-y-11=0.三、解答题15.求曲线y=1x-x上一点P4，-74处的切线方程.[解析]there4;yprime;=limDelta;xrarr;0 1x+Delta;x-1x-(x+Delta;x-x)Delta;x=limDelta;xrarr;0 -Delta;xx(x+Delta;x)-Delta;xx+Delta;x+xDelta;x=limDelta;xrarr;0 -1x(x+Delta;x)-1x+Delta;x+x=-1x2-12x .there4;yprime;|x=4=-116-14=-516，there4;曲线在点P4，-74处的切线方程为：y+74=-516(x-4).即5x+16y+8=0.16.已知函数f(x)=x3-3x及y=f(x)上一点P(1，-2)，过点P作直线l.(1)求使直线l和y=f(x)相切且以P为切点的直线方程;(2)求使直线l和y=f(x)相切且切点异于点P的直线方程y=g(x).[解析](1)yprime;=limDelta;xrarr;0 (x+Delta;x)3-3(x+Delta;x)-3x3+3xDelta;x=3x2-3.则过点P且以P(1，-2)为切点的直线的斜率k1=fprime;(1)=0，there4;所求直线方程为y=-2.(2)设切点坐标为(x0，x30-3x0)，则直线l的斜率k2=fprime;(x0)=3x20-3，there4;直线l的方程为y-(x30-3x0)=(3x20-3)(x-x0)又直线l过点P(1，-2)，there4;-2-(x30-3x0)=(3x20-3)(1-x0)，there4;x30-3x0+2=(3x20-3)(x0-1)，解得x0=1(舍去)或x0=-12.故所求直线斜率k=3x20-3=-94，于是：y-(-2)=-94(x-1)，即y=-94x+14.17.求证：函数y=x+1x图象上的各点处的切线斜率小于1.[解析]yprime;=limDelta;xrarr;0 f(x+Delta;x)-f(x)Delta;x=limDelta;xrarr;0 x+Delta;x+1x+Delta;x-x+1xDelta;x=limDelta;xrarr;0 x?Delta;x(x+Delta;x)-Delta;x(x+Delta;x)?x?Delta;x =limDelta;xrarr;0 (x+Delta;x)x-1(x+Delta;x)x=x2-1x2=1-1x2<1，there4;y=x+1x图象上的各点处的切线斜率小于1.18.已知直线l1为曲线y=x2+x-2在点(1,0)处的切线，l2为该曲线的另一条切线，且l1perp;l2.(1)求直线l2的方程;(2)求由直线l1、l2和x轴所围成的三角形的面积.[解析](1)yprime;|x=1=limDelta;xrarr;0 (1+Delta;x)2+(1+Delta;x)-2-(12+1-2)Delta;x=3，所以l1的方程为：y=3(x-1)，即y=3x-3.设l2过曲线y=x2+x-2上的点B(b，b2+b-2)，yprime;|x=b=limDelta;xrarr;0(b+Delta;x)2+(b+Delta;x)-2-(b2+b-2)Delta;x=2b+1，所以l2的方程为：y-(b2+b-2)=(2b+1)?(x-b)，即y=(2b+1)x-b2-2.因为l1perp;l2，所以3times;(2b+1)=-1，所以b=-23，所以l2的方程为：y=-13x-229.(2)由y=3x-3，y=-13x-229，得x=16，y=-52，即l1与l2的交点坐标为16，-52.又l1，l2与x轴交点坐标分别为(1,0)，-223，0.所以所求三角形面积S=12times;-52times;1+223=12512.【总结】2021年xx为小编在此为您收集了此文章高二数学课后练习题：导数的几何意义，今后还会发布更多更好的文章希望对大家有所帮助，祝您在xx学习愉快!更多xx：高二语文高二英语。

导数的几何意义 同步练习１．曲线122+=x y 在点)3,1(-P 处的切线方程为：（ ）Ａ．14--=x y Ｂ．74--=x y Ｃ．14-=x y Ｄ．74-=x y２．若12)21()1(lim 0-=--→∆xx f f x ，则过曲线)(x f y =上点))1(,1(f 处的切线斜率为：（ ）Ａ．2 Ｂ．1- Ｃ．1 Ｄ．2-３．2212-=x y 在点)23,1(-处的切线倾斜角为（ ） Ａ．1 Ｂ．4π Ｃ．45π Ｄ．4π-４．曲线122+=ax y 过点)3,(a ，则该曲线在该点的切线方程是（ ）Ａ．14--=x yＢ．84+=x y Ｃ．14-=x y Ｄ．444-==x y x y 或５．抛物线c bx x y ++=2在点)2,1(处的切线与其平行直线0=++c y bx 的距离是（ ）Ａ．42 Ｂ．22 Ｃ．223 Ｄ．2６．函数x y 1-=在点)2,21(-处的切线方程为＿＿＿＿＿。

７．曲线p x x y +-=422与直线1=y 相切，则______=p 。

８．若曲线32x y =上某点切线的斜率为6，求此点坐标。

９．曲线12+=x y 过点P 的切线与曲线122--=x y 相切，求点P 坐标。

１０．求曲线x x y +-=22在点)1,1(-处切线的倾斜角。

１１．求42+=x y 与10+=x y 的交点和交点处抛物线的切线方程。

参考答案１． Ｂ； 3)1(-='f 。

２．Ｂ； 根据导数定义。

３．Ｂ； 由1=切线k 可得。

４．Ｃ； 由1)(232+=a a 得)(11舍或-==a a ，再由4)1(='f 可得。

５． Ｃ；抛物线过)2,1(，所以1=+c b ；又b f +='2)1(，又由题意b b -=+2，得2,1=-=c b ；所以得切线方程1+=x y ；所以平行直线01=+-y x 与02=--y x 的距离为223。

【成才之路】2015-2016学年高中数学 第2章 2导数的概念及其几何意义课时作业 北师大版选修2-2一、选择题1．设函数f (x )在x ＝x 0处可导，则当h →0时，以下有关f x 0＋h －f x 0h的值的说法中正确的是( )A ．与x 0，h 都有关B ．仅与x 0有关而与h 无关C ．仅与h 有关而与x 0无关D ．与x 0、h 均无关 [答案] B[解析] 导数是一个局部概念，它只与函数y ＝f (x )在x 0及其附近的函数值有关，与h 无关．2．(2014·合肥一六八中高二期中)若可导函数f (x )的图象过原点，且满足lim Δx →0f ΔxΔx＝－1，则f ′ (0)＝( ) A ．－2 B ．－1 C ．1 D ．2[答案] B[解析] ∵f (x )图象过原点，∴f (0)＝0， ∴f ′(0)＝lim Δx →0 f 0＋Δx －f 0Δx ＝lim Δx →0 f ΔxΔx＝－1， ∴选B.3．曲线y ＝13x 3－2在点(－1，－73)处切线的倾斜角为( )A ．30°B ．45°C ．135°D ．－45°[答案] B[解析] Δy Δx ＝13－1＋Δx3－2－[13×－13－2]Δx＝Δx －Δx 2＋13Δx3Δx＝1－Δx ＋13(Δx )2.当Δx →0时，ΔyΔx →1，所以切线斜率k ＝1，所以倾斜角为45°.4．曲线y ＝1x上点(1,1)处的切线方程为( )A ．x ＋y －2＝0B ．x －y ＋2＝0C ．x －2y ＋1＝0D ．2x －y ＋1＝0[答案] A[解析]Δy Δx＝f 1＋Δx －f 1Δx ＝11＋Δx －1Δx ＝－11＋ΔxΔx →0时，ΔyΔx 趋于－1，∴f ′(1)＝－1，∴所求切线为x ＋y －2＝0.5．(2014·枣阳一中，襄州一中，宜城一中，曾都一中期中联考)2014年8月在南京举办的青奥会的高台跳水运动中，运动员相对于水面的高度h (m )与起跳后的时间t (s )存在函数关系h (t )＝－4.9t 2＋6.5t ＋10，则瞬时速度为0m/s 的时刻是( )A ．6598sB ．6549sC ．9865sD ．4965s [答案] A[解析] h ′(t )＝－9.8t ＋6.5，由h ′(t )＝0得t ＝6598，故选A ．二、填空题6．过点P (－1,2)，且与曲线y ＝3x 2－4x ＋2在点M (1,1)处的切线平行的直线方程为__________________．[答案] 2x －y ＋4＝0 [解析]f ′(1)＝lim Δx →031＋Δx2－41＋Δx ＋2－3×12－4×1＋2Δx＝6－4＝2∴所求直线方程为y －2＝2(x ＋1) 即2x －y ＋4＝0.7．如图，函数y ＝f (x )的图像在点P 处的切线是l ，则f (2)＋f ′(2)＝________.[答案] 98[解析] 由题图可知，直线l 的方程为：9x ＋8y －36＝0. 当x ＝2时，y ＝94，即f (2)＝94.又切线斜率为－98，即f ′(2)＝－98，∴f (2)＋f ′(2)＝98.8．抛物线y ＝14x 2在点(－2,1)处的切线方程为________；倾斜角为________．[答案] x ＋y ＋1＝0 135° [解析] f ′(－2)＝li m Δx →0 ΔyΔx＝li m Δx →014[－2＋Δx2－－22]Δx＝li m Δx →0 (－1＋14Δx )＝－1. 则切线方程为x ＋y ＋1＝0，倾斜角为135°. 三、解答题9．已知点M (0，－1)，过点M 的直线l 与曲线f (x )＝13x 3－4x ＋4在x ＝2处的切线平行．求直线l 的方程．[分析] 由题意，要求直线l 的方程，只需求其斜率即可，而直线l 与曲线在x ＝2处的切线平行，只要求出f ′(2)即可．[解析] Δy ＝13(2＋Δx )3－4(2＋Δx )＋4－(13×23－4×2＋4)＝13(Δx )3＋2(Δx )2，Δy Δx ＝13(Δx )2＋2Δx . Δx 趋于0时，ΔyΔx趋于0，所以f ′(2)＝0.所以直线l 的斜率为0，其方程为y ＝－1. 10．在曲线y ＝x 2上过哪一点的切线． (1)平行于直线y ＝4x －5； (2)垂直于直线2x －6y ＋5＝0； (3)与x 轴成135°的倾斜角． [解析] f ′(x )＝lim Δx →0f x ＋Δx －f xΔx＝lim Δx →0 x ＋Δx 2－x 2Δx＝2x ，设P (x 0，y 0)是满足条件的点． (1)因为切线与直线y ＝4x －5平行，故2x 0＝4，得x 0＝2，y 0＝4，即P (2,4)． (2)因为切线与直线2x －6y ＋5＝0垂直．故2x 0·13＝－1，得x 0＝－32，y 0＝94，即P ⎝ ⎛⎭⎪⎫－32，94. (3)因为切线与x 轴成135°的倾斜角，故其斜率为－1.即2x 0＝－1，得x 0＝－12，y 0＝14，即P ⎝ ⎛⎭⎪⎫－12，14.[点评] 设切点为P (x 0，y 0)，根据导数的几何意义，求出斜率，然后利用两直线的位置关系求出切点坐标.一、选择题1．设函数f (x )＝ax ＋3，若f ′(1)＝3，则a 等于( ) A ．2 B ．－2 C ．3 D ．－3[答案] C[解析] ∵f ′(x )＝lim Δx →0 f x ＋Δx －f xΔx＝lim Δx →0a x ＋Δx ＋3－ax ＋3Δx＝a∴f ′(1)＝a ＝3.2．设f (x )为可导函数，且满足条件lim x →0f x ＋1－f 12x＝3，则曲线y ＝f (x )在点(1，f (1))处的切线的斜率为( )A ．32B ．3C ．6D ．无法确定[答案] C [解析] lim x →0f x ＋1－f x 2x ＝12lim x →0 f x ＋1－f 1x＝12f ′(1)＝3，∴f ′(1)＝6.故选C ． 3．已知y ＝f (x )的图像如右图所示，则f ′(x A )与f ′(x B )的大小关系是( ) A ．f ′(x A )>f ′(x B ) B ．f ′(x A )<f ′(x B ) C ．f ′(x A )＝f ′(x B ) D ．不能确定 [答案] B[解析] 由导数的几何意义知，f ′(x A )、f ′(x B )分别为y ＝f (x )的图像在A 、B 两点处的切线的斜率．根据图像，知f ′(x A )<f ′(x B )．4．曲线y ＝x 3在点P 处切线的斜率为k ，当k ＝3时，P 点坐标为( ) A ．(－2，－8) B ．(－1，－1)或(1,1) C ．(2,8) D ．(－12，－18)[答案] B[解析] 设P (x 0，y 0)，则f ′(x 0)＝3x 20， 3x 20＝3，得x 0＝1或x 0＝－1， 所以坐标为P (1,1)或P (－1，－1)． 二、填空题5.如图，函数f (x )的图象是折线段ABC ，其中A ，B ，C 的坐标分别为(0,4)，(2,0)，(6,4)，则lim Δx →0 f 1＋Δx －f 1Δx＝________.[答案] －2[解析] 由导数的概念和几何意义知，lim Δx →0f 1＋Δx －f 1Δx ＝f ′(1)＝k AB ＝0－42－0＝－2.6．已知函数f (x )＝x 3－3ax (a ∈R )，若直线x ＋y ＋m ＝0对任意的m ∈R 都不是曲线y ＝f (x )的切线，则a 的取值范围为________．[答案] {a |a ∈R ，且a <13}[解析] 由题意，得f ′(x )＝3x 2－3a ＝－1无解，即3x 2－3a ＋1＝0无解．故Δ<0，解得a <13.三、解答题7．一质点的运动路程s (单位：m)是关于时间t (单位：s)的函数：s ＝－2t ＋3.求s ′(1)，并解释它的实际意义．[解析] Δs Δt＝s1＋Δt －s 1Δt＝－21＋Δt ＋3－－2×1＋3Δt＝－2(m/s)．当Δt 趋于0时，ΔsΔt 趋于－2，则s ′(1)＝－2m/s ，导数s ′(1)＝－2m/s 表示该质点在t ＝1时的瞬时速度．8.已知直线l 1为曲线y ＝x 2＋x －2在(1,0)处的切线，l 2为该曲线的另一条切线，且l 1⊥l 2.(1)求直线l 2的方程；(2)求由直线l 1、l 2和x 轴围成的三角形的面积 [解析] (1)y ′＝lim Δx →0 x ＋Δx2＋x ＋Δx －2－x 2－x ＋2Δx＝lim Δx →0 2x Δx ＋Δx 2＋ΔxΔx＝lim Δx →0(2x ＋Δx ＋1)＝2x ＋1. y ′|x ＝1＝2×1＋1＝3，∴直线l 1的方程为y ＝3(x －1)，即y ＝3x －3. 设直线l 2过曲线y ＝x 2＋x －2上的点B (b ，b 2＋b －2)， 则l 2的方程为y ＝(2b ＋1)x －b 2－2. 因为l 1⊥l 2，则有2b ＋1＝－13，b ＝－23.所以直线l 2的方程为y ＝－13x －229.(2)解方程组⎩⎪⎨⎪⎧y ＝3x －3，y ＝－13x －229.得⎩⎪⎨⎪⎧x ＝16，y ＝－52.所以直线l 1和l 2的交点坐标为(16，－52)．l 1，l 2与x 轴交点的坐标分别为(1,0)、(－223，0)．所以所求三角形的面积S ＝12×253×|－52|＝12512.。

温馨提示：此套题为Word版，请按住Ctrl,滑动鼠标滚轴，调节合适的观看比例，答案解析附后。

关闭Word文档返回原板块。

课时素养评价八导数的概念及其几何意义(20分钟·50分)一、选择题(每小题5分，共20分)1.已知函数f(x)在x=x0处可导，若=1，则f′(x0)= ( )A.-1B.-C.D.1【解析】选C.由已知可得=3=3f′(x0)=1，所以f′(x0)=.2.设函数f(x)=ax3+2，且f′(-1)=3，则a等于( )A.-1B.C.D.1【解析】选D.f′(-1)==[3a-3a·Δx+a(Δx)2]=3a.令3a=3，所以a=1.3.已知y=f(x)的图像如图所示，则f′(x A)与f′(x B)的大小关系是( )A.f′(x A)>f′(x B)B.f′(x A)<f′(x B)C.f′(x A)=f′(x B)D.不能确定【解析】选B.由导数的几何意义，f′(x A)，f′(x B)分别是切线的斜率，由图像可知f′(x A)<f′(x B).【误区警示】解答本题易出现的失误是弄不清楚曲线在点A处切线的斜率大还是在点B处切线的斜率大.4.设曲线y=ax2在点(1，a)处的切线与直线2x-y-6=0平行，则a等于( )A.1B.C.-D.-1【解析】选A.因为y′==(2a+aΔx)=2a.所以可令2a=2，所以a=1.二、填空题(每小题5分，共10分)5.设y=f(x)为可导函数，且满足条件=-2，则曲线y=f(x)在点(1，f(1))处的切线的斜率是_________.【解析】由=-2，所以f′(1)=-2，f′(1)=-4.答案：-46.根据导数的定义求得函数y=f(x)=x2+3在x=1处的导数为_________.【解析】因为Δy=f(1+Δx)-f(1)=[(1+Δx)2+3]-(12+3)=2Δx+(Δx)2，所以==2+Δx.故f′(1)=(2+Δx)=2.答案：2三、解答题(每小题10分，共20分)7.一质点做直线运动，其位移s与时间t的关系为s(t)=t2+1，该质点在2到2+Δt(Δt>0)之间的平均速度不大于5，求Δt的取值范围. 【解析】质点在2到2+Δt之间的平均速度为===4+Δt.又≤5，所以4+Δt≤5，即Δt≤1.又Δt>0，所以Δt的取值范围为(0，1].8.已知f(x)=x2，g(x)=x3，求满足f′(x)+2=g′(x)的x的值.【解析】f′(x)==2x，g′(x)==3x2.因为f′(x)+2=g′(x)，所以2x+2=3x2.即3x2-2x-2=0，解得x=或x=.(15分钟·30分)1.(5分)若直线y=kx+1与曲线y=x3+ax+b相切于点P(1，3)，则b等于( )A.3B.-3C.5D.-5【解析】选A.因为点P(1，3)既在直线上又在曲线上，所以3=k+1，且3=1+a+b，即k=2，a+b=2.根据导数的定义知y=x3+ax+b的导数为y′=3x2+a，所以3×12+a=k，所以a=-1，b=3.2.(5分)如图，函数y=f(x)的图像在点P处的切线方程是y=-2x+9，P 点的横坐标是4，则f(4)+f′(4)=_________.【解析】由题意得，f′(4)=-2，f(4)=-2×4+9=1.因此，f(4)+f′(4)=1-2=-1.答案：-13.(5分)已知二次函数f(x)=ax2+bx+c的导数为f′(x)，f′(0)>0，对于任意实数x，有f(x)≥0，则的最小值为_________.【解析】由导数的几何意义，得f′(0)===[a·(Δx)+b]=b.因为所以ac≥，又因为b>0，所以c>0.所以=≥≥=2.答案：24.(5分)若曲线y=2x2-4x+m与直线y=1相切，则m=_________.【解析】设切点坐标为(x0，1)，则f′(x0)=4x0-4=0，所以x0=1，即切点坐标为(1，1).所以2-4+m=1，即m=3.答案：35.(10分)已知曲线C：y=经过点P(0，-1)，求：(1)曲线在点P处的切线的斜率.(2)曲线在点P处的切线的方程.(3)过点O(0，0)的曲线C的切线方程.【解析】(1)将P(0，-1)代入y=中得t=-1，所以y=-.所以===，所以=，所以曲线在点P处切线的斜率为k==1.(2)曲线在点P处的切线方程为y+1=x，即x-y-1=0.(3)因为点O(0，0)不在曲线C上，设过点O的曲线C的切线与曲线C 相切于点M(x0，y0)，则切线斜率k==，因为y0=-，所以x0=-，所以切点M，切线斜率k=4，切线方程为y+2=4，即y=4x.1.曲线f(x)=x2的平行于直线x-y+1=0的切线方程为_________.【解析】f′(x)==x.因为直线x-y+1=0的斜率为1，所以x=1.所以f(1)=×12=，切点为.故切线方程为y-=1·(x-1)，即2x-2y-1=0.答案：2x-2y-1=02.已知点M(0，-1)，F(0，1)，过点M的直线l与曲线y=x3-4x+4在x=2处的切线平行.(1)求直线l的方程.(2)求以点F为焦点，l为准线的抛物线C的方程.【解析】(1)y=f(x)=x3-4x+4，所以f′(2)====0，即曲线y=x3-4x+4在x=2处的切线斜率为0，而l与此切线平行，故l的斜率也为0.又l过点M(0，-1)，所以直线l的方程为y=-1.(2)因为抛物线以点F(0，1)为焦点，y=-1为准线，设抛物线方程为x2=2py(p>0)，则=1，p=2.故抛物线C的方程为x2=4y.关闭Word文档返回原板块。

2.2.2 导数的几何意义
1、设曲线)(x f y =在某点处的导数值为0，则过曲线上该点的切线（ ）
A 、垂直于x 轴
B 、垂直于y 轴
C 、既不垂直于x 轴也不垂直于y 轴
D 、方向不能确定
2、分别求抛物线241x y =
过点（-2，1），（2，1）的切线方程。

3、已知曲线12-=x y 和其上一点，且这点的横坐标为-1，求曲线在这点的切线方程。

４、设点),(00y x 是抛物线432++=x x y 上一点，求过点),(00y x 的切线方程。

５、求抛物线241x y =
过点（4，47）的切线方程
６、曲线12)(2++=x x x f 在点M 处的切线的斜率为2，求点M 的坐标。

７、曲线22
3x y =
上哪一点的切线与直线13-=x y 平行？
参考答案：
1、B
2、答案提示：01=++y x ；01=--y x
3、答案提示：022=++y x
4、答案提示：))(32(000x x x y y -+=-
5、答案提示：0142=--y x 或049414=--y x
6、答案提示：（0，1）
7、答案提示：)2
3,1(。