折射率
- 格式:docx
- 大小:82.16 KB
- 文档页数:8

各种光的折射率排序一、引言光的折射率是指光线从一种介质进入另一种介质时,由于介质密度不同而发生的偏折程度。
不同的物质具有不同的折射率,因此在光学领域中,了解各种物质的折射率是非常重要的。
本文将对常见物质的折射率进行排序和分析。
二、空气空气是自然界中最常见的物质之一,其折射率为1.0003。
由于空气密度较低,因此光线在经过空气时会产生很小的偏折角度。
三、水水是地球上最广泛存在的液体之一,其折射率为1.33。
由于水分子密度较高,因此光线在经过水时会产生较大的偏折角度。
这也是为什么我们看到水中物体会有“错位”感觉。
四、玻璃玻璃是人工制造出来的材料,在建筑、家居等领域得到广泛应用。
其折射率约为1.5-1.9之间,具体取决于玻璃成分和制造工艺。
高端玻璃制品如水晶、钻石等折射率更高,达到2.4左右。
五、金属金属是一种良好的导电材料,其折射率较低,一般在1.5以下。
这也是为什么金属表面会反射出镜面光的原因。
不同金属的折射率也有所不同,银的折射率为0.18,黄铜为0.36。
六、晶体晶体是具有规则排列结构的物质,在光学领域中得到广泛应用。
不同晶体具有不同的折射率和双折射性质。
其中最常见的石英晶体折射率为1.544,而冰晶体的折射率则高达1.31-1.33之间。
七、塑料塑料是一种轻便、易加工的材料,在生活中得到广泛应用。
其折射率约为1.4-1.6之间,具体取决于塑料成分和制造工艺。
高端塑料制品如聚碳酸酯(PC)具有更高的折射率,可达到1.59左右。
八、结论综上所述,各种物质的折射率存在巨大的差异,不同的物质在光学应用中具有不同的特点和优劣。
因此,在进行光学设计和制造时,需要根据具体需求选择合适的材料。
[绝对折射率]:光从真空射入介质发生折射时,入射角i与折射角r的正弦之比n叫做介质的“绝对折射率”,简称“折射率”。
它表示光在介质中传播时,介质对光的一种特征。
[公式]:n=sin i/sin r=c/v由于光在真空中传播的速度最大,故其他媒质的折射率都大于1。
同一媒质对不同波长的光,具有不同的折射率;在对可见光为透明的媒质内,折射率常随波长的减小而增大,即红光的折射率最小,紫光的折射率最大。
通常所说某物体的折射率数值多少(例如水为1.33,水晶为1.55,金刚石为2.42,玻璃按成分不同而为1.5~1.9),是指对钠黄光(波长5893×10^-10米)而言。
[相对折射率]:光从介质1射入介质2发生折射时,入射角θ1与折射角θ2的正弦之比n21叫做介质2相对介质1的折射率,即“相对折射率”。
因此,“绝对折射率”可以看作介质相对真空的折射率。
它是表示在两种(各向同性)介质中光速比值的物理量。
[公式]:n21=sinθ1/sinθ2=n2/n1=v1/v2光学介质的一个基本参量。
即光在真空中的速度c与在介质中的相速v之比真空的折射率等于1,两种介质的折射率之比称为相对折射率。
例如,第一介质的折射率为n1,第二介质的折射率为n2,则n21=n2/n1称为第二介质对第一介质的相对折射率。
某介质的折射率也是该介质对真空的相对折射率。
于是折射定律可写成如下形式. n1sinθi=n2sinθt两种介质进行比较时,折射率较大的称光密介质,折射率较小的称光疏介质。
折射率与介质的电磁性质密切相关。
根据电磁理论,εr和μr分别为介质的相对电容率和相对磁导率。
折射率还与波长有关,称色散现象。
手册中提供的折射率数据是对某一特定波长而言的(通常是对钠黄光,波长为5893埃)。
气体折射率还与温度和压强有关。
空气折射率对各种波长的光都非常接近于1,例如空气在20℃,760毫米汞高时的折射率为1.00027。
在工程光学中常把空气折射率当作1,而其他介质的折射率就是对空气的相对折射率。

各种光的折射率排序1. 介质的折射率是什么?介质的折射率是指光在不同介质中传播时的速度差异所引起的光线偏折现象。
折射率决定了光线在经过介质界面时的偏折角度和传播速度的变化。
2. 光的折射率与介质的性质有关光在不同介质中的传播速度与介质的光密度有直接关系,而光密度又可以用折射率来表示。
折射率是介质的一个物理量,它描述了光在该介质中传播的速度相对于真空(或空气)的比值。
3. 各种光的折射率排序下面是各种光在空气中的折射率按照从小到大的顺序排列的列表:1.无线电波:折射率为1.000000032.微波:折射率介于1.0000和1.0003之间3.显微波:折射率介于1.0001和1.0003之间4.红外线:折射率介于1.0002和1.0004之间5.可见光(不同颜色的光波折射率不同):–紫色(波长为400-450nm):折射率介于1.520和1.530之间–蓝色(波长为450-500nm):折射率介于1.520和1.525之间–绿色(波长为500-550nm):折射率介于1.510和1.515之间–黄色(波长为550-600nm):折射率介于1.505和1.510之间–橙色(波长为600-650nm):折射率介于1.500和1.505之间–红色(波长为650-700nm):折射率介于1.495和1.500之间6.紫外线:折射率介于1.460和1.500之间7.X射线:折射率介于0.95和1.00之间8.γ射线:折射率为1.004. 介质折射率与波长的关系从以上的各种光的折射率排序可以看出,不同波长的光在介质中的传播速度是不同的,也就是折射率不同。
一般来说,光在介质中的折射率会随着波长的减小而增大。
这种现象可以用光的色散来解释。
光的色散是指光在通过透明介质时,不同波长的光被介质以不同的折射率折射的现象。
光在介质中的折射率与波长之间存在一定的关系,一般会遵循柯西公式或赫歇尔公式。
5. 折射率的影响因素介质的折射率受到多种因素的影响,包括温度、压力、密度、物质的相态等。
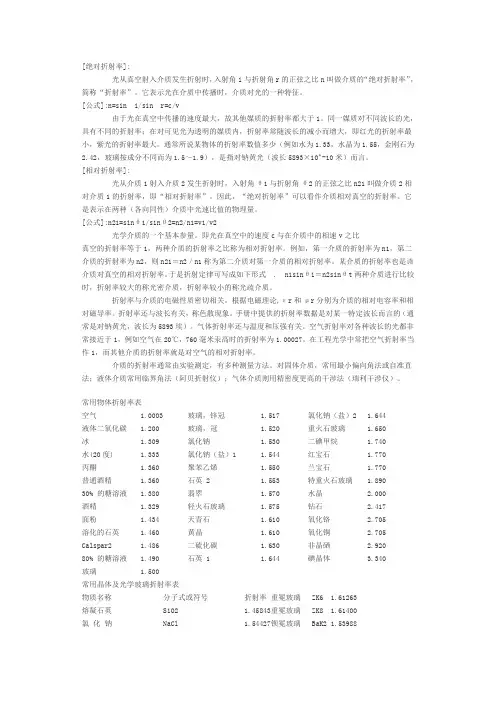
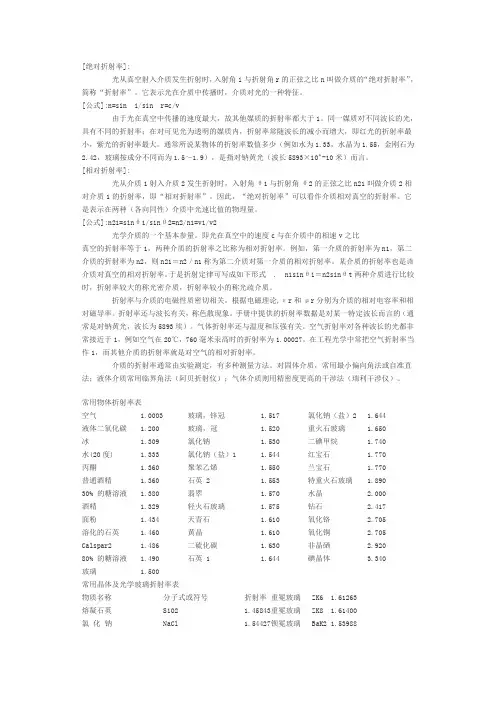
![常用折射率表[最新]](https://uimg.taocdn.com/5db013a668dc5022aaea998fcc22bcd126ff4231.webp)
[绝对折射率]:光从真空射入介质发生折射时,入射角i与折射角r的正弦之比n叫做介质的“绝对折射率”,简称“折射率”。
它表示光在介质中传播时,介质对光的一种特征。
[公式]:n=sin i/sin r=c/v由于光在真空中传播的速度最大,故其他媒质的折射率都大于1。
同一媒质对不同波长的光,具有不同的折射率;在对可见光为透明的媒质内,折射率常随波长的减小而增大,即红光的折射率最小,紫光的折射率最大。
通常所说某物体的折射率数值多少(例如水为1.33,水晶为1.55,金刚石为2.42,玻璃按成分不同而为1.5~1.9),是指对钠黄光(波长5893×10^-10米)而言。
[相对折射率]:光从介质1射入介质2发生折射时,入射角θ1与折射角θ2的正弦之比n21叫做介质2相对介质1的折射率,即“相对折射率”。
因此,“绝对折射率”可以看作介质相对真空的折射率。
它是表示在两种(各向同性)介质中光速比值的物理量。
[公式]:n21=sinθ1/sinθ2=n2/n1=v1/v2光学介质的一个基本参量。
即光在真空中的速度c与在介质中的相速v之比真空的折射率等于1,两种介质的折射率之比称为相对折射率。
例如,第一介质的折射率为n1,第二介质的折射率为n2,则n21=n2/n1称为第二介质对第一介质的相对折射率。
某介质的折射率也是该介质对真空的相对折射率。
于是折射定律可写成如下形式 . n1sinθi=n2sinθt两种介质进行比较时,折射率较大的称光密介质,折射率较小的称光疏介质。
折射率与介质的电磁性质密切相关。
根据电磁理论,εr和μr分别为介质的相对电容率和相对磁导率。
折射率还与波长有关,称色散现象。
手册中提供的折射率数据是对某一特定波长而言的(通常是对钠黄光,波长为5893埃)。
气体折射率还与温度和压强有关。
空气折射率对各种波长的光都非常接近于1,例如空气在20℃,760毫米汞高时的折射率为1.00027。
在工程光学中常把空气折射率当作1,而其他介质的折射率就是对空气的相对折射率。

折射率折射系数折射率,也被称为折射系数,是一个非常重要的光学概念,它在我们日常生活中起着至关重要的作用。
顾名思义,折射率指的是光线从一个介质(比如空气)射入到另一个介质(比如水或者玻璃)时的折射效应。
它不仅仅是科学研究中的一个重要参数,同时也在实际应用中有着许多指导意义。
首先,折射率对于我们理解光在不同媒介中传播速度的变化非常关键。
根据斯涅尔定律,光线在从一种介质射入另一种介质时,会发生折射现象,同时伴随着传播速度的变化。
折射率正是描述这种速度变化的参数。
不同的介质对光的传播速度有不同的影响,折射率的数值大小能够展示出这种影响程度,从而帮助我们理解和预测光的传播路径。
其次,折射率对于光学器件设计和工程应用非常关键。
在设计透镜、光纤等光学器件时,折射率是一个重要的参考参数。
通过调整折射率,我们可以控制光线在器件内的传播路径和聚焦效果。
这种能够控制光传播的能力为我们的日常生活带来了许多便利,比如在相机镜头中使用不同的透镜材料,可以实现景深调节和焦点调整,从而拍摄出更加清晰和美丽的照片。
折射率还与光学现象密切相关,比如反射、折射、色散等。
当光线从一种介质射入到另一种介质时,由于折射率的不同,光线会发生偏折现象,这就是被称为折射。
而在光线从一种介质射入到另一种介质时,也可能会发生一部分光线的反射现象,其中折射率也扮演了重要的角色。
此外,折射率与色散现象也有密切的关系。
不同频率的光会以稍微不同的速度在介质中传播,这就导致了光在经过某些介质时会发生色散现象,即白光分解成七彩的光谱。
总之,折射率是光学研究中一项重要的物理量,它对于理解光的传播、设计光学器件以及解释光学现象都具有重要的指导意义。
在今后的科学研究和工程应用中,我们应该继续深入研究和探索折射率的性质,以推动光学领域的进步和应用的发展。

折射率与波长的公式
折射率是物质在光线作用下,光线从一种介质中进入另一种介质时,折射率定义了光线如何变向的量度。
折射率是一种物理量,它可以用来比较两种介质(或者同一种介质中不同波长的光)的光学性能。
折射率公式是用来表示折射率与光的波长的关系的,它的形式是:折射率=n(λ)=n0+n1*λ+n2*λ2+...
其中,n0是指介质的全局折射率,它与物质的性质有关,而n
1、n2等是物质折射率随波长变化的系数,可以用于表示
物质折射率随波长变化规律的程度。
折射率公式是描述折射率和波长之间关系的,它可以用来计算介质的全局折射率和折射率随波长变化的系数。
折射率公式的应用不仅仅是用来计算折射率,还可以用来研究物质的性质,因为折射率与物质的性质是密切相关的。
折射率公式的应用也可以用来计算光的传播路径,因为折射率可以用来描述光在物质中的折射角度。
同样,折射率公式也可以用来解决光线在介质中的衍射、反射和折射等问题。
折射率公式是一种重要的物理公式,它可以用来描述折射率与波长之间的关系,以及光在介质中的传播路径等。
折射率公式的应用可以用来研究物质的性质、计算光的传播路径及解决光线在介质中的衍射、反射和折射等问题。

光学折射率和光的全反射光学折射率是描述光在介质中传播时发生偏折的性质的一个重要参数。
光的传播速度在不同介质中会发生变化,这会导致光线的传播方向发生偏折,即折射。
光学折射率是用来衡量介质对光的折射能力的指标。
1. 光学折射率的定义光学折射率(Refractive Index)是光线由真空(或空气)射入某一介质中时,在两种介质边界上的入射角和折射角之间的比值。
一般用n 表示,即n = sin(i) / sin(r),其中i为入射角,r为折射角。
2. 折射定律根据折射定律,光线从一个介质射入另一个介质时,入射角、折射角和两个介质的折射率之间存在着特定的数学关系。
折射定律可以用数学表达式n1 * sin(i) = n2 * sin(r)表示,其中n1和n2分别为两个介质的折射率,i为入射角,r为折射角。
3. 光的全反射当光从一种折射率较大的介质射入折射率较小的介质界面时,如果入射角超过一定的临界角,光将不再折射,而是发生全反射。
全反射是指光线完全被反射回折射率较大的介质中。
4. 临界角的定义临界角是指光线由折射率较大的介质射入折射率较小的介质时,使得折射角等于90°的入射角。
当入射角大于临界角时,光将发生全反射。
5. 光的全反射的应用光的全反射在光学技术中有广泛的应用。
其中一个重要的应用是光纤通讯。
光纤中的光信号可以通过多次发生全反射而一直传播到目标位置,实现远距离的高速传输。
另外,全反射还可以用于设计光学棱镜、光学透镜和光纤传感器等光学器件。
6. 折射率和材料特性的关系折射率与材料的物理特性有密切的关系。
常见材料的折射率一般都是介于1和2之间的数值,且随波长的变化而变化。
不同材料的折射率差异决定了它们在光学器件中的应用。
例如,石英具有较高的折射率,适用于光学透镜和棱镜的制作,而光纤通讯中常用的是折射率较小的光纤材料。
总结:光学折射率是描述介质对光的折射能力的重要参数,由入射角和折射角之间的比值确定。
[绝对折射率]:光从真空射入介质发生折射时,入射角i与折射角r的正弦之比n叫做介质的“绝对折射率”,简称“折射率”。
它表示光在介质中传播时,介质对光的一种特征。
[公式]:n=sin i/sin r=c/v由于光在真空中传播的速度最大,故其他媒质的折射率都大于1。
同一媒质对不同波长的光,具有不同的折射率;在对可见光为透明的媒质内,折射率常随波长的减小而增大,即红光的折射率最小,紫光的折射率最大。
通常所说某物体的折射率数值多少(例如水为1.33,水晶为1.55,金刚石为2.4 2,玻璃按成分不同而为1.5~1.9),是指对钠黄光(波长5893×10^-10米)而言。
[相对折射率]:光从介质1射入介质2发生折射时,入射角θ1与折射角θ2的正弦之比n21叫做介质2相对介质1的折射率,即“相对折射率”。
因此,“绝对折射率”可以看作介质相对真空的折射率。
它是表示在两种(各向同性)介质中光速比值的物理量。
[公式]:n21=sinθ1/sinθ2=n2/n1=v1/v2光学介质的一个基本参量。
即光在真空中的速度c与在介质中的相速v之比真空的折射率等于1,两种介质的折射率之比称为相对折射率。
例如,第一介质的折射率为n1,第二介质的折射率为n2,则n21=n2/n1称为第二介质对第一介质的相对折射率。
某介质的折射率也是该介质对真空的相对折射率。
于是折射定律可写成如下形式 . n1sinθi=n2sinθt两种介质进行比较时,折射率较大的称光密介质,折射率较小的称光疏介质。
折射率与介质的电磁性质密切相关。
根据电磁理论,εr和μr分别为介质的相对电容率和相对磁导率。
折射率还与波长有关,称色散现象。
手册中提供的折射率数据是对某一特定波长而言的(通常是对钠黄光,波长为5893埃)。
气体折射率还与温度和压强有关。
空气折射率对各种波长的光都非常接近于1,例如空气在20℃,760毫米汞高时的折射率为1.00027。
在工程光学中常把空气折射率当作1,而其他介质的折射率就是对空气的相对折射率。

光的折射与折射率的计算折射是光线从一种介质传播到另一种介质时方向发生改变的现象。
这种现象是由于光在不同介质中传播速度不同引起的。
而折射率则是用来描述光在不同介质中传播速度差异的物理量。
1. 折射定律光的折射是遵循折射定律的,即入射角、折射角和折射率之间的关系。
根据折射定律,可以得到以下公式:n1 * sin(θ1) = n2 * sin(θ2)其中,n1和n2分别代表光线从两个介质传播过程中的折射率,θ1和θ2分别代表光线在两个介质之间的入射角和折射角。
2. 折射率的计算方法折射率是一个介质的特性,用于描述光在该介质中传播的速度相对于真空中的速度。
一般情况下,光在真空中的速度近似为3 × 10^8 m/s。
对于不同介质而言,其折射率的计算方法也不相同。
以下是一些常见介质的折射率计算方法:2.1 真空折射率由于真空中的光速近似为3 × 10^8 m/s,所以其折射率为1。
2.2 水的折射率水是生活中常见的介质之一,其折射率与光的波长有关。
一般来说,可使用康奈尔关系式进行计算:n(λ) = A + B / (λ^2 - C)其中,n(λ)表示波长为λ的光在水中的折射率。
A、B、C是实验测得的常数。
2.3 玻璃的折射率玻璃是常见的透明介质,其折射率也与波长有关。
常用的计算方法是使用柯西方程:n(λ) = A + B / (λ^2 + C)其中,n(λ)表示波长为λ的光在玻璃中的折射率。
A、B、C是实验测得的常数。
3. 折射率与光的频率和波长的关系折射率与光的频率和波长之间存在一定的关系。
根据光的速度公式:v = c / n其中,v表示光的速度,c表示光在真空中的速度,n表示介质的折射率。
可以推导得到:c / v = n = λ / λ0其中,λ表示光的波长,λ0表示真空中的波长。
由上述公式可以看出,折射率与光的频率和波长成反比。
折射率越大,光的速度越慢。
4. 光的折射在实际生活中的应用光的折射在实际生活中有着广泛的应用。

常见材质折射率光在物质中传播时会发生折射现象,而折射率是描述光在不同材质中传播速度差异的物理量。
不同材质的折射率不同,对光的传播和折射产生不同的影响。
以下将介绍一些常见材质的折射率及其特点。
1. 空气:空气的折射率约为1,是光在自由空间中的参考折射率。
空气对光的传播速度影响较小,因此光在空气中传播较快。
2. 水:水的折射率约为1.33,相较于空气,水对光的传播速度减慢。
这也是为何在水中观察到的物体会出现偏移的原因。
3. 玻璃:玻璃的折射率在1.5左右,具有较高的透光性。
玻璃在光学器件中广泛应用,如镜片和透镜等。
4. 金属:金属的折射率较高,通常大于2。
这是因为金属对光的吸收较强,光在金属中传播时会受到较大的阻碍。
5. 木材:不同种类的木材折射率有所差异,一般在1.5左右。
木材对光的传播有一定的衰减作用,因此木材的透光性较差。
6. 塑料:常见的塑料材料如聚乙烯和聚丙烯等,折射率约为1.5。
塑料具有良好的透光性,常用于光学器件和眼镜等制品中。
7. 晶体:晶体的折射率较高,且具有双折射现象。
晶体的折射率与光的入射方向、种类以及晶格结构等因素有关。
8. 大气层:大气层中折射率变化较大,随着空气密度的变化而变化。
此特性是彩虹、日晕等自然现象产生的原因之一。
折射率是光学研究中的重要参数,对于光在不同材质中的传播和折射现象有着重要的影响。
不同材质的折射率差异导致了光在不同材质中的传播速度和路径的改变,从而产生了许多有趣的光学现象。
在实际应用中,了解不同材质的折射率有助于设计和制造光学器件,提高其性能和效率。
不同材质的折射率决定了光在材质中的传播速度和路径,对于光学研究和应用具有重要意义。
通过研究不同材质的折射率,我们可以更好地理解和利用光的传播和折射特性,为光学技术的发展和应用提供更广阔的空间。

光在两介质中传播速率的比值称为折射率. 一般分为相对折射率和绝对折射率. 假若平面电磁波入射到两种均匀的各向同性介质的界面上,从第一种介质入射到界面的波将分成两个波,一股透入第二种介质,方向发生改变,称为折射波. 第二股反射回第一种介质,称为反射波.光波从第一种介质透入第二种介质后方向发生改变的现象称为光的折射. 如图所示,θi ,θt 分别称为入射角和折射角. 以v 1、v 2分别表示光在介质1和2中的速率. 入射线、折射线和界面的法线位于同一平面上,并且有1221sin sin n v v t i ==θθ,这就是折射定律.n 12是与入射角θi 无关的常数,它的值与光的频率有关. n 12称为由介质1向介质2折射的相对折射率。
绝对折射率表示光从真空(或空气)中射入某种媒质时发生偏折程度的数值。
常用n 表示。
绝对折射率数值等于入射角正弦值与折射角正弦值的比值。
或等于真空中的光速与在媒质中的传播速度的比值. 若以n1和n2分别表示介质1和2的绝对折射率,那么折射定律可写为12sin sin n n t i =θθ.折射定律是1621年Snell 首先从实验上建立起来的,所以也称为Snell 定律. 折射率n 与介电常数ε及磁导率μ之间的关系由Maxwell 公式εμ=n 给出.n 与光频率ω的关系称光的色散关系.对于电导率σ不为零的介质,其折射率应由复折射率n c =n-ik 表示,这里n 就是我们前面说的透明介质中的折射率.而k 称为消光系数,它与吸收系数α的关系为α=2ωk/c ,这里c 是真空中的光速.这时n 和k 与介质的σ和ε等的关系可表示为⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧-⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧+⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+=14121141212/1222/122ωεπσεωεπσεk n当光在各向异性的晶体材料中传播时,由于介电常数ε为一个二级张量,由Fresnel 方程知,对某一给定的波法矢,允许有两个独立的平面波在各向异性介质中传播,这两个波有不同的折射率,不同的相速度和不同的偏振态,而且两个偏振方向互相垂直,这就是双折射现象. 光在各向异性介质中的折射率,可用折射率椭球来形象地描述.为了更好的理解折射率,我们需要从微观的角度了解折射率的本质。
常见介质的折射率介绍折射率是光线从一种介质射入另一种介质时,光线传播速度的相对改变。
不同介质的折射率不同,这是由于介质的光学性质和分子结构的差异所导致的。
本文将探讨一些常见介质的折射率,并解释其对光的传播和折射的影响。
空气空气是我们日常生活中最常见的介质之一。
在常温常压下,空气的折射率约为1.0003。
这意味着光线在从真空中射入空气时,传播速度几乎不受影响。
因此,我们通常可以忽略空气对光的折射的影响。
水水是另一个常见的介质,其折射率约为1.333。
相比于空气,光线在从空气射入水中时,传播速度会减慢。
这导致光线的传播方向发生改变,我们常见的折射现象就是由此引起的。
例如,当我们将一根笔放入水中时,看起来它的位置发生了变化,这是由于光线在水中的传播速度比在空气中慢,导致光线的折射。
玻璃玻璃是一种常见的固体介质,其折射率取决于玻璃的成分和结构。
普通玻璃的折射率约为1.5左右。
不同类型的玻璃具有不同的折射率,这是由于它们的化学成分和制备工艺的差异所导致的。
例如,光学玻璃的折射率通常较高,可达到1.6或更高。
这使得光学玻璃成为制造透镜和光学器件的理想材料。
金属金属是一种特殊的介质,其折射率通常为复数。
在可见光范围内,金属的折射率的实部很小,而虚部很大。
这意味着金属对可见光的传播和折射几乎没有影响,大部分光线被金属吸收和反射。
这就是为什么金属看起来有光泽,并且能够反射光线的原因。
气体除了空气之外,其他气体也具有不同的折射率。
例如,二氧化碳的折射率约为1.00045,氮气的折射率约为1.00029。
不同气体的折射率差异较小,通常情况下可以忽略不计。
然而,在某些特殊情况下,例如光学测量或气体传感器中,气体的折射率可能需要考虑。
固体除了玻璃和金属之外,其他固体材料也具有不同的折射率。
例如,钻石的折射率约为2.42,石英的折射率约为1.46。
这些固体材料的折射率通常较高,使其成为制造光学器件和宝石的理想选择。
结论不同介质的折射率对光的传播和折射起着重要的作用。
[绝对折射率]:光从真空射入介质发生折射时,入射角i与折射角r的正弦之比n叫做介质的“绝对折射率”,简称“折射率”。
它表示光在介质中传播时,介质对光的一种特征。
[公式]:n=sin i/sin r=c/v由于光在真空中传播的速度最大,故其他媒质的折射率都大于1。
同一媒质对不同波长的光,具有不同的折射率;在对可见光为透明的媒质内,折射率常随波长的减小而增大,即红光的折射率最小,紫光的折射率最大。
通常所说某物体的折射率数值多少(例如水为1.33,水晶为1.55,金刚石为2.42,玻璃按成分不同而为1.5~1.9),是指对钠黄光(波长5893×10^-10米)而言。
[相对折射率]:光从介质1射入介质2发生折射时,入射角θ1与折射角θ2的正弦之比n21叫做介质2相对介质1的折射率,即“相对折射率”。
因此,“绝对折射率”可以看作介质相对真空的折射率。
它是表示在两种(各向同性)介质中光速比值的物理量。
[公式]:n21=sinθ1/sinθ2=n2/n1=v1/v2光学介质的一个基本参量。
即光在真空中的速度c与在介质中的相速v之比真空的折射率等于1,两种介质的折射率之比称为相对折射率。
例如,第一介质的折射率为n1,第二介质的折射率为n2,则n21=n2/n1称为第二介质对第一介质的相对折射率。
某介质的折射率也是该介质对真空的相对折射率。
于是折射定律可写成如下形式. n1sinθi=n2sinθt两种介质进行比较时,折射率较大的称光密介质,折射率较小的称光疏介质。
折射率与介质的电磁性质密切相关。
根据电磁理论,εr和μr分别为介质的相对电容率和相对磁导率。
折射率还与波长有关,称色散现象。
手册中提供的折射率数据是对某一特定波长而言的(通常是对钠黄光,波长为5893埃)。
气体折射率还与温度和压强有关。
空气折射率对各种波长的光都非常接近于1,例如空气在20℃,760毫米汞高时的折射率为1.00027。
在工程光学中常把空气折射率当作1,而其他介质的折射率就是对空气的相对折射率。
不同介质的折射率
折射率是光线从空气或真空进入不同介质(如水和玻璃)时的弯曲程度。
不同介质的折射率可能不同,这可能影响到光线的传播,影响到我们看到的物体和图像。
下面我们来分步骤阐述不同介质的折射率。
1. 什么是折射率?
折射率是光线通过不同介质时发生的折射现象产生的量度,它表示在光线传播过程中光速改变的程度。
折射率是一个标量,通常用n 表示,单位是无量纲。
2. 折射率如何计算?
当光线从一个介质中进入另一个介质时,它的速度会改变,从而产生折射。
折射率的计算公式是n=sin(入射角)/ sin(折射角),其中入射角是指入射光线与法线的夹角,折射角是指折射光线与法线的夹角。
3. 不同介质的折射率有何不同?
不同介质的折射率不同,因为光线在不同介质中的速度不同。
例如,空气的折射率约为1.00,水的折射率约为1.33,玻璃的折射率约为1.52。
4. 折射率如何影响我们观察物体和图像?
折射率越高,光线越容易被弯曲,因此在高折射率的介质中,物体和图像会看起来更扭曲或变形。
例如,当我们将一根笔倒立放在玻璃杯里时,笔看起来会弯曲,这是因为光线在玻璃中的折射率高于空气。
此外,在眼睛中,晶状体的折射率使得光线聚焦在视网膜上,从而产生清晰的图像。
当晶状体的折射率发生变化时(如老年人出现白内障),视觉可能会变得模糊不清。
总之,不同介质的折射率是光在介质中传播的重要特性,它可以
影响我们对物体和图像的观察,进而影响我们的生活和健康。
了解不同介质的折射率可以帮助我们更好地了解光的行为和属性。
折射率公式与相关资料
折射率定义式:n=sinα/sinβ,折射率的补充公式:1、n=c/v;c 指的是光在真空中的速度,v指的是光在该介质中的速度。
2、n=1/sinC;C指的是该介质的临界角。
什么是折射率
折射率,光在真空中的传播速度与光在该介质中的传播速度之比。
材料的折射率越高,使入射光发生折射的能力越强。
折射率越高,镜片越薄,即镜片中心厚度相同,相同度数同种材料,折射率高的比折射率低的镜片边缘更薄。
折射率与介质的电磁性质密切相关。
根据经典电磁理论,εr和μr分别为介质的相对电容率和相对磁导率。
折射率还与频率有关,称色散现象。
光由相对光密介质射向相对光疏介质,且入射角大于临界角,即可发生全反射。
负折射率
负折射率(介电常数和磁导率同时为负)的问题是近年来国际上非常活跃的一个研究领域。
当电磁波在负折射率材料中传播时,电场E、磁场B和波矢k三者构成左手螺旋关系,因而负折射率材料又称为左手性材料(left-handed materials)。
Veselago1968年首次在理论设想了左手型材料。
Pendry在1996年与1999年分别指出可以用细金属导线及有缝谐振环阵列构造介电常数ε和磁导率μ同时为负的人工媒质。
2001年,Smith等人沿用Pendry的方法,构造出了介电常数与磁导率同时为负的人工媒质,并首次通过实验观察到了微波波段的电磁波通过这种人工媒质与空气的交界面时发生的负折射现象。
尽管初
期人们对Smith等人的实验有许多争论,但2003年以来更为仔细的实验均证实了负折射现象。
折射率浅释
折射率是物体表面发出光线与入射光线之间的变化程度,也叫做光学系数。
它可以用来衡量物体对折射光线的反射或者折射程度。
一般来说,折射率越大,物体越具有光学透明性,可以折射出更多的光束。
折射率的数值取决于物体的表面状态,也可以看作是分子的结构,如果分子更为密集,其表面的折射率也会更高。
一般来说,折射率不少于200,表面的折射率很大,光线可以完全透过物体的表面而折射到另一侧,同时,它又没有严重影响光线透过物体的角度。