当前位置：文档之家 › 2020年高中物理竞赛辅导课件★★静电场的高斯定理

2020年高中物理竞赛辅导课件★★静电场的高斯定理

  • 格式：ppt
  • 大小：2.04 MB
  • 文档页数：13

下载文档原格式

  / 13

合集下载

2020年华科附中高中物理竞赛辅导课件(09静电场)D高斯定理解题(共13张PPT)

2020年华科附中高中物理竞赛辅导课件(09静电场)D高斯定理解题(共13张PPT)

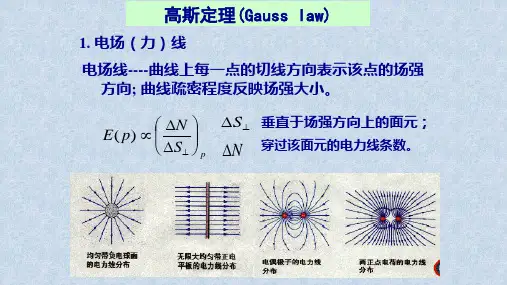
2º例8、例9说明点电荷的电
场在 r0 时, E.
R
o E
oR R
o E
oR
r r
36
例10. 求均匀带电直线的电场
E
S
rr EdS
1
0
V
dV
分布, 已知单位长度的电荷为 。
解：由电荷分布可知该电场具有轴对称性
取半径为r, 高为h的同轴高斯圆柱面
通过该面的电通量
r
h
+
例10. 求均匀带电直线的电场
2º静电场中任一闭合曲面S，若有 则S面上的 E 处处为零。
r
S E
r dS
0
，
3º若闭合曲面 S 上各点的场强为零时，则S面 内必定未包围电荷。
4º三个相等的点电荷置于等边 三角形三个顶点上，以三角 形的中心为球心作一球面S， 如图所示，能用高斯定理求 S面上的场强吗？
q
q
q
S
41
r er
1
0
h
对有限长的棒
不成立
+
37
讨论：
E
20r
体密度
1ºr0, E？
rR
无限长均匀带电圆柱体 无限长均匀带电圆柱面
E
E
2 0
r
0
2º两平行输电线的电场分布？
3º同轴电缆的电场？
ra E0
r
r
E rE
E
arb
E
20r
rb E0
ab E
r
r
38
例11.无限大薄平板均匀带电，面电荷密度+ ， 求 场强分布?
E S E dS E 4 r2
又
E

高二物理竞赛课件：静电场的高斯定理

高二物理竞赛课件：静电场的高斯定理

第八章 真空中的静电场
dS
+
8 – 2 静电场的点高电斯荷定在理任意封闭曲面内(定性分析) 第八章 真空中的静电场
由于电场线的连续性，且S1与S2、S3之间没有其他电荷， 因此穿过球面S1的电场线数目必与穿过任意曲面S2和S3 的电场线数目相同，与闭合曲面的形状无关，即
e s1
es2
es3
dΦ1 E1 dS1
q
4 π 0
d S1＇ r2
q d 0
4 π
0
dΦ2 E2 dS2
q
4 π 0
dS
＇
2
r2
q d 0
4 π 0
E2
q
dS2
dS1
E1
dΦ1
dΦ 2
0
e
E dS 0
S
8 – 2 静电场的高斯定理
第八章 真空中的静电场
由多个点电荷产生的电场
E E1 E2
在点电荷 q 和 q 的静电场中，做如下的三
个闭合面
S1 ,
S2 ,
S3 , q
求通过各闭合面的电通量
.
Φe1
E dS
S1
0
q
q
Φe2 0
Φe3
q
0
S1
S2 S3
8 – 2 静电场用的高高斯斯定定理理计算场强
第八章 真空中的静电场
i）分析对称性
ii）根据对称性，选择合适的高斯面。
高 斯 面
E dS
1
S
0
n
qi
i 1
总结
1）高斯面上的电场强度为所有内外电荷的总电场强度. 2）高斯面为封闭曲面. 3） dS 的正方向为曲面的外法线方向(垂直于曲面向 外)，因此，穿出高斯面的电通量为正，穿入为负.

2020年南师附中高中物理竞赛辅导课件08真空中的静电场(E高斯定理应用举例)

2020年南师附中高中物理竞赛辅导课件08真空中的静电场(E高斯定理应用举例)

S3
S3
由高斯定理有 E2rh h
0
E 2 0r
或 E
r
2 0r2
[例8]一无限大,厚为b,体电荷密度为P的 均匀带电板,求板内.板外电场的分布.
解:a:板内.因中间面上电场为零
选立方体为高斯面,上.下.前
↑ 后四个面上电通量 为零. → △S △S X E E • d S 2 E S
E2S1
S1 0
得 E 2 0
E
S2
S3
E S1
方向垂直于板面向外
[例7]求均匀带正电的无限长细棒的场强
分布。设棒的电荷线密度为
解：电场分布具有轴对称
r S1
h
性，任一点处的场强方向 垂直于棒辐射向外
S3
P 以棒为轴作半径为r、长为
S 2 h的圆柱闭合面为高斯面
E SE Ed dss S E1 E d ds s S E 2 E d 2s rS hE 3 d s
THE END 祝大家竞赛顺利、学业有成
谢谢观看！
再高深的学问也是从字母学起的。 在人生道路上，走上坡路要昂首阔步，走下坡路要谨小慎微，走阳关道要目视前方，走羊肠路要俯视脚下。 为了你，很多事我不一定会，但我在努力学。 希望是生命的源泉，失去它生命就会枯萎。 危机二字的正解是危险和机会，但大多数人只看到危险，鲜有人看到机会，所以成功赚到大钱的人并不多。 当你无法从一楼蹦到三楼时，不要忘记走楼梯。要记住伟大的成功往往不是一蹴而就的，必须学会分解你的目标，逐步实施。 见义不为，无勇也。——《论语·为政》 人生里面总是有所缺少，你得到什么，也就失去什么，重要的是你应该知道自己到底要什么。追两只兔子的人，难免会一无所获。
r
R
E

高二物理竞赛静电场的高斯定理PPT(课件)

高二物理竞赛静电场的高斯定理PPT(课件)

2）电场线的疏密程度表示该处场 “无限长”均匀带电直线的场强
解：建立如图坐标系，O为直线中点
强的大小 ——相当于点电荷q的电场
在圆环上任取长为dl的电荷元dq 球面上各环带元在 点的元场强的矢量和
——相当于点电荷q的电场 2）电场线的疏密程度表示该处场强的大小
E dN
A
B
EB
E
——环心处点电荷q的电场
静电场的高斯定理
一、电场线:在电场中画一系列曲
线，使得：
1、曲线上每一点的切向方向表示 ——环心处点电荷q的电场
“无限大”均匀带电平面的场强 电场是连续分布的，分立电场线只是一种形象化的方法
该点的场强方向； 2）电场线的疏密程度表示该处场强的大小
解：建立如图坐标系，O为直线中点
EA
在盘上取半径r，宽度dr 细圆环
度dr 细圆环
则 dq 2rdr
dE
1
xdq
i
40 (x2 r 2 )3/2
1
x 2rdr
i
40 (x2 r 2 )3/2
E
1 40
(
x2
qx R
2
)3
/
2
i
dq 2rdr
各细圆环在P点的电场强度方向相同
dr
O
r

R
2 x R r d r
E dE P
dE
P o
x dqdy q
dE
d E
1
L
d
y
r
0
40 r 2
E d Exi d Ey j d E cos i d E sin j
各细圆环在P点的电场强度方向相同
y 在圆环上任取长为dl的电荷元dq

2020年高中物理竞赛辅导课件：电磁学(真空中的静电场)03高斯定理解题(共18张PPT)

2020年高中物理竞赛辅导课件：电磁学(真空中的静电场)03高斯定理解题(共18张PPT)

S
右底
q内 A 0 0
由高斯定理，得
E 20
与到平面的 距离无关
矢量式：E
n0
20 平面法向单位矢量
(指离平面)
[思考]①结果对于<0是否成立? (Yes)
②平行板电容器的电场?
+ -
E E 0
ⅠⅡⅢ
E
2 20
0
Note: 高斯面：电荷分布球对称——球面； 电荷分布轴对称或二维平移对称—— 柱面.
E
r
20 R
r0
2
r0
20r
(r R) (r R)
Er曲线： E
O
E1/r
R
r
[例1-8] 无限大均匀带电平面的电场
LL
A S
设面电荷密度为(>0)
对称性→① E平面,②与平 面平等面距两的侧各E点对称E分相布同.,③在
高斯面S：底面积为A的闭合 圆柱面
E dS 2 E dS 2EA
q内 L
0
0
由高斯定理，得
E
E
20r
O
矢量式： E
r0
20r
E1/r
r
[思考]①结果对于<0是否成立? (Yes) ②无限长均匀带电圆柱面？ 设轴线方向单位长度带电荷，则
E
0
20r
r0
Er曲线： E
(r R) (r R)
E1/r
OR
rLeabharlann ③无限长均匀带电圆柱体？ 设轴线方向单位长度带电荷，则
②若q位于立方体的中心处，结果？
2.求 E
——用于电荷分布的对称性很高(球、无限长 圆柱、无限大平面等)的情形
[例1-6] 均匀带电球面的电场

2020年华科附中高中物理竞赛辅导课件(09静电场)C静电场的高斯定理(共15张PPT)

2020年华科附中高中物理竞赛辅导课件(09静电场)C静电场的高斯定理(共15张PPT)

（1）E为均匀场
r 1º设场中有一平面S，SE
或面法线方向
nr
//
r E
该面的电通量：
2º若 nr与Er成 角
E
=
S
E
E= SEcos S E
n
SS
90o E 0
90o E 0
24
（2）E 为非均匀场
任意曲面S上的电通量
取面积元dS 其上的电通量
d
E
EdS r
cros
E dS
nr
高斯定律的用途
1º可用该定律求对称分布的电场。
2º已知场强分布时，可用该定律求任一区域的电 荷、电势分布。
3º卡文迪许就是用高斯定律来证明库仑定律的平 方反比关系，这说明它们不是相互独立的定律。
33
r dS
1
0
qi
S内
设真空中有一点电荷q，在q 的电场中，
(3) 若球面S 或任意曲面S不包围电荷q
穿入的
穿出的
S S
电场线
电场线
q
rr rr
E SE dS S E dS = 0
即:曲面外的电荷对曲面的电通量无贡献
30
证明：
E
r
S E
r dS
1
0
qi
S内
(4) 若在同一空间有q1 、q2…… qn电荷系
2020
全国高中物理竞赛
华科附中辅导课件 （含竞赛真题练习）
第3节 静电场的高斯定理 Gauss Law of Electrostatic Fields
一、静电场的高斯定理
1.电场线（E线） ——静电场的形象描述
一系列曲线 +q
q
电场线上每点切线的方向表示该点场强的方向

2020年南师附中高中物理竞赛辅导课件08真空中的静电场(E高斯定理应用举例)

身体健康， 名人之所以能够成为名人，是因为他们在同伴嬉乐或休息时不停地攀登；凡人之所以成为凡人，是因为别人忙于攀登时他却安然入睡。
只有在患难的时候，才能看到朋友的真心。——克雷洛夫 沉湎于希望的人和守株待兔的樵夫没有什么两样。 不求做的最好，但求做的更好。
学习进步！ 失败是什么？没有什么，只是更走近成功一步；成功是什么？就是走过了所有通向失败的路，只剩下一条路，那就是成功的路。
2020年
高中物理学奥林匹克竞赛
考前辅导
2020 江苏南京
四.高斯定理应用举例 一般步骤: 1.分析电场所具有的对称性质 2.选择适当形状的闭合曲面为高斯面 3.计算通过高斯面的电通量
4.令电通量等于高斯面内的电荷代数和除
以o，求出电场强度
[例5]求均匀带正电球体内外的场强分布。 设球体半径为R，带电量为Q
若现在就觉得失望无力，未来那么远你该怎么扛。 在幸运时不与人同享的，在灾难中不会是忠实的友人。——伊索 对待生命要认真，对待生活要活泼。 自然界没有风风雨雨，大地就不会春华秋实。
r
R
E
0R
(4
Q
3)R3
4r2E内
r3 R3
Q
0
得
或
r
E内
Qr
4 0R3
Q
E内40R3 r
[例6]求均匀带正电的无限大平面薄板的
场强分布。设电荷面密度为
E
E
解：电场的分布具有 面对称性
高斯面取为两底与板 面对称平行，侧面与 板面垂直的圆柱形闭 合面
ESEdsS 1 E d sS 2E d sS E 3d s
←b→
=∑q/ε0 = ρ △S 2X/ε0
∴E=ρ x/ε0 (︱x︳﹤b/2)

高二物理竞赛课件：电场的高斯定理


qi内
E dS i
S
0
E
ds
S
2. 高斯定理关系式的导出 思路：1）以点电荷场为例
2）推广到一般 推导： 1）场源电荷是电量为Q的点电荷
高斯面包围点电荷，如图 通过该高斯面的电通量？ 根据电力线的连续性 等于以点电荷为球心的 任意半径的球面的电通量
Qr
S
dS
E
E
+Q
r
计算通过球面的电通量： 通过球面任一面元 的电通量是
[例] 如图，点电荷q位于 立方体的一角，则通过 侧面ABCD的电通量 e=.
q
A
B
D C
解：增补成一个大立方体，q位于其中心.
由高斯定律和对称分析：
e
q
24 0
静电场的高斯定理
1)通过任意面积 元的 电通量
de E dS
其值有正、负，取决于面 元法线与场强方向的夹角
dS E
2)通过任意曲面的电通量：
把曲面分成许多个面积元
每一面元处视为匀强电场
e de E dS E cosθdS
S
S
S
3)通过闭合面的电通量
e
E dS
S
e E dS
q1 q2 qn 0 0
0 0
0
1
0
n
qi
i1
1
0
qi
i (内 ）
qi内
E dS i
S
0
讨论
qi内
1)闭合面内、外电 荷的贡献
E dS i
S
ε0
对闭合面处的 E 都有贡献
对电通量 E dS 的贡献有差别
S
只有闭合面内的电量对电通量有贡献

高二物理竞赛高斯定理课件(共14张PPT)


③ 解决由场强求电荷分布的问题。
高斯定律的内容
静电场中任意闭合曲面 S 的电通量 e , 等于该
曲面所包围的电荷的代数和 除以 0 ,qi 与闭合曲面
外电荷无关。
1
e
s
E ds
0
qi
S内
S: 高斯面 qi: S内所有电荷电量的代数和
高斯定律的证明（分4步）
(1) 包围点电荷 q 的同心球面 S 的电通量等于
有
曲面
q
0
任
q
S S球面
(3) 点电荷q在闭合曲面 S 外 的电通量为零。
电力线在无电荷处连续，进入与
穿出S面的电力线数量相同
q
e E dS 0 S
S
(4) 当闭合曲面内有多个点电荷时，电通量等于它
们单独存在时的电通量的代数和。
S
E
ds
1
0
qi
S内
• Note：
1> 式中的 E是指高斯面上各处的 ，E
• ••
• •
•
••
E
P
例1 求均匀带电球面内外场强分布。
解：对称性分析：电场分布是球对称的。
球对称分布----同一球面上E的大小相等，方向沿 球的半径。
高斯面选取----选半径为r的同心球面为高斯面。
(1) 球面外任一点P 处的场强（ r > R ）
通过 P 点作球面 S1，则S1面上的场
强处处相等，且场强方向与球面S1 外
以点电荷为中心作半径为 r 的球面:
q
de E dS 4 0r 2 dS
E
e
de
s
s
q
4 0r 2 ds

高二物理竞赛课件：高斯定理(108张PPT)

（1）r < R
E
四、均匀带电圆柱面的电场。
沿轴线方向单位长度带电量为λ
（1）r < R 高 斯 面
E
四、均匀带电圆柱面的电场。
沿轴线方向单位长度带电量为λ
（1）r < R
E 2π r l = 0
E
4. 均匀带电圆柱面的电场。
沿轴线方向单位长度带电量为λ
（1）r < R
E 2π r l = 0 ... E = 0
第三节 高斯定理
一、电力线
一、电力线
电力线（E）线：在电场中画一组曲线， 曲线上每一点的切线方向与该点的电场方向 一致，这一组曲线称为电力线。
一、电力线 电力线（E）线：在电场中画一组曲线， 曲线上每一点的切线方向与该点的电场方向 一致，这一组曲线称为电力线。
E
一、电力线
电力线（E）线：在电场中画一组曲线， 曲线上每一点的切线方向与该点的电场方向
高斯面
. s E dS = s E dS cos00
E
=
E
s
dS
= E 4π r 2
=Σ q i ε/ O
=0
++
+ +
+R
rr
+ +q
+
+
+
+
+
+++ +
一、均匀带电球面的电场
（1）r < R
高斯面
. s E dS = s E dS cos00
E
=
E
s
dS
= E 4π r 2
=Σ q i ε/ O
+
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
S内
设真空中有一点电荷q，在q 的电场中，
(1) 取以q为中心r为半径的球面S
该S上的电通量为：
E
q
4 0r 2
er
E S E dS
er || n
E
S
q
4 0r 2
er
dS
4S4q0qr02r24SdSr
2
Sr
q
E
S E dS
q
0
1
0
q
S内
28
证明：
E
S E
dS
1
0
qi
S内
设真空中有一点电荷q，在q 的电场中，
2º引入电场线, 只是为了形象理解电场 E ， 实际上 E 是连续分布于空间。
26
3.真空中静电场的高斯定理
——静电场的基本规律之一
（1）高斯定理的表述 静电场中任何一闭合曲面的电通量，等于
该曲面所包围的电荷的代数和的0分之一倍。
数学表达式
E
S E
dS
1
0
qi
S内
27
证明：
E
S E
dS
1
0
qi
第3节 静电场的高斯定理 Gauss Law of Electrostatic Fields
一、静电场的高斯定理
1.电场线（E线） ——静电场的形象描述
一系列曲线 +q
q
电场线上每点切线的方向表示该点场强的方向
22
定义
电直场于中的E任 单意位一面点积处上，电通场过线该根处数垂 = E
即
E
dN dS
S 面上的总通量
n
r E dS
S
E dE S E dS
当S为闭合曲面时
E S E dS
闭合面的法线方向规定：
E 0
自内向外为法线的正方向
E 0
25
注：
E 0
1º E S E dS
E 0
表示净穿出(入)闭合面的电场线的总根数
E 0 有净电场线从曲面内向外穿出 E 0 有净电场线从曲面外向内穿入
穿入的 电场线
穿出的 电场线
S的电荷对曲面的电通量无贡献
30
证明：
E
S E
dS
1
0
qi
S内
(4) 若在同一空间有q1 、q2…… qn电荷系
任意点的电场强度为
E E1 E2 En
S q2
取任意闭合面S，其电通量为
q1
qn
E S E dS
（1）E为均匀场
1º设场中有一平面S，SE 或面法线方向n // E
该面的电通量： E = S E
2º若 n与E成 角
E= SEcos S E
n
SS
90o E 0
90o E 0
24
（2）E 为非均匀场
任意曲面S上的电通量
取面积元dS 其上的电通量
dE EdS cos E dS
（也称电场线密度）
dS
E
电场线的特征
（1）起于正电荷止于负电荷，有头有尾，不 会在无电荷处中断。
（2）在没有电荷的空间里，任何两条电场线 不会相交。
（3）静电荷的电场线不会形成闭合曲线。
23
2.电通量 E
定义：通过电场中任一给定面的电场线总根数， 就是该面的电通量E。
E的单位 N m2 / C
若 qi 0 E 0 有净电场线到闭合面内终止
说明静电场是有源场
正电荷是电场的源头 负电荷是电场的尾闾
高斯定律的用途
1º可用该定律求对称分布的电场。
2º已知场强分布时，可用该定律求任一区域的电 荷、电势分布。
3º卡文迪许就是用高斯定律来证明库仑定律的平 方反比关系，这说明它们不是相互独立的定律。
S(E1 E2 ... En) dS
S E1 dS S E2 dS ... S En dS
1 2 n 由单个点电荷的结论
1
0
qi
S内
qi`在S内
qj不在S内
定理得证！
i
qi
0
j 0
31
注意
E
S E
dS
1
0
qi
S内
1ºE只决定于S面包围的电荷， S面外的电荷对
E无贡献。
33
(2) 设想任意闭合面S，且S与S包围同
一个点电荷q， 由电场线的连续性可知：
SE dS S E dS
1
0
q
S内
er || n
S SS
v EE rr
qq
看出
电通量与球面半径、 闭合曲面形状无关。
29
证明：
E
S E
dS
1
0
qi
S内
设真空中有一点电荷q，在q 的电场中，
(3) 若球面S 或任意曲面S不包围电荷q
r
2º封闭面S 上的场强 E 是由S内的电荷产生，而
与S外r 的电荷无关吗？ E —— 是由全部电荷共同产生的合场强
qi 移动，E、E 变否？ 曲面S内
3º若S内的电荷是连续分布 带电体的体积
E
S E
dS
1
0
V
dV
32
（2）高斯定理的意义 反映电场的基本性质
E
S E
dS
1
0
qi
S内
若 qi 0 E 0 有净电场线从闭合面内发出