当前位置：文档之家 › 20201128空间向量与立体几何(同步)

20201128空间向量与立体几何(同步)

  • 格式：pdf
  • 大小：296.25 KB
  • 文档页数：5

下载文档原格式

  / 5

合集下载

高中数学第1章空间向量与立体几何1.1.1空间向量及其线性运算课件新人教A版选择性必修第一册

高中数学第1章空间向量与立体几何1.1.1空间向量及其线性运算课件新人教A版选择性必修第一册


1.
类型 共线(平行)向量
共面向量
如果表示若干空间向量的有向线段所
在的直线 互相平行或重合 ,那么这些
向量叫做共线向量或平行向量
平行于同一个平面的向量,叫
定义
做共面向量
共线向量也叫平行向量,注意与两直线
重合和平行的区别
如果两个向量a,b不共线,那么
充要 对任意两个空间向量a,b(b≠0),a∥b的充 向量p与向量a,b共面的充要条
1.定义.
在空间,我们把具有 大小 和 方向
小叫做空间向量的 长度或模 .
的量叫做空间向量,空间向量的大
2.空间向量及其模的表示方法.
空间向量用字母a,b,c,…表示.若向量a的起点是A,终点是B,则向量a也可以
记作
,其模记为|a|或 | |.
3.空间向量的相关概念.
对于任意向量a,均有0∥a
算时,务必要注意和向量、差向量的方向,必要时可采用空间向量的自由平
移获得更准确的结果.
(2)化简空间向量的常用思路:
①分组:合理分组,以便灵活运用三角形法则、平行四边形法则进行化简.
②多边形法则:在空间向量的加法运算中,若是多个向量求和,还可利用多
边形法则,若干个向量的和可以将其转化为首尾相接的向量求和.
1
1
+ 2 =-a+b+2c.
规律方法
空间向量线性运算的技巧与思路
(1)空间向量加法、减法运算的两个技巧:
①巧用相反向量:向量加减法的三角形法则是解决空间向量加法、减法运
算的关键,灵活运用相反向量可使有关向量首尾相接,从而便于运算.
②巧用平移:利用三角形法则和平行四边形法则进行向量的加法、减法运
空间向量与立体几何PPT教学课件

空间向量与立体几何PPT教学课件


3）射影
已知向量 AB＝a和轴l，e是l上与l同方向的单位向量。
作点A在l上的射影A1 , 作点B在l上的射影B1，
则 A1B1叫做向量 AB在轴l上的或在e方向上的正射影，
简称射影。 A1B1 AB cosa, e a e
B
e
A1
B1
l
A
注意：AB 是轴l上的正射影,A1B1是一个可正可负的实数， 它的符号代表向量 AB 与l的方向的相对关系，大小代
第二章 《空间向量与立体几何》
一.空间向量的运算
b
OaA
B
b
a
结论：空间任意两个向量都是共面向量，所以它们可用 同一平面内的两条有向线段表示。 因此凡是涉及空间任意两个向量的问题，平面向量中有 关结论仍适用于它们。
类比思想 数形结合思想
平面向量
空间向量
概念 定义 表示法 相等向量
具有大小和方向的量
| b |2 b b b12 b22 b32
注意：此公式的几何意义是表示长方体的对 角线的长度。
（2）空间两点间的距离公式
终点坐标减 在空间直角坐标系中，已知 A起(x1点, y坐1 ,标z1)、
B(x2 , y2 , z2 ) ，则 AB ( x2 x1 , y2 y1 , z2 z1)
PA n d
n
N D1 F
C1
A1
E M B1
D
Cy
A
B
x
立体几何中的向量方法——坐标法
问题1：已知：△ABC为正三角形，EC⊥平面ABC,
且EC,DB在平面ABC同侧，CE=CA=2BD.求证：
平面ADE⊥平面ACE.
z
E
⑴怎样建立适当的空间直角坐标系？
(完整版)空间向量与立体几何知识点归纳总结(2),推荐文档

(完整版)空间向量与立体几何知识点归纳总结(2),推荐文档

空间向量与立体几何知识点归纳总结一．知识要点。

1. 空间向量的概念：在空间，我们把具有大小和方向的量叫做向量。

注：（1）向量一般用有向线段表示同向等长的有向线段表示同一或相等的向量。

（2）向量具有平移不变性2. 空间向量的运算。

定义：与平面向量运算一样，空间向量的加法、减法与数乘运算如下（如图）。

;;OB OA AB a b =+=+ BA OA OB a b =-=- ()OP a R λλ=∈运算律：⑴加法交换律：a b b a+=+⑵加法结合律：)()(c b a c b a++=++⑶数乘分配律：ba b aλλλ+=+)(运算法则：三角形法则、平行四边形法则、平行六面体法则3. 共线向量。

（1）如果表示空间向量的有向线段所在的直线平行或重合，那么这些向量也叫做共线向量或平行向量，平行于，记作。

ab b a//（2）共线向量定理：空间任意两个向量、（≠），//存在实数λ，使＝λa bb 0 a b a。

b （3）三点共线：A 、B 、C 三点共线<=>AC AB λ=<=>)1(=++=y x OB y OA x OC 其中（4）与共线的单位向量为a a 4. 共面向量（1）定义：一般地，能平移到同一平面内的向量叫做共面向量。

说明：空间任意的两向量都是共面的。

（2）共面向量定理：如果两个向量不共线，与向量共面的条件是存在实,a b p ,a b数使。

,x y p xa yb =+（3）四点共面：若A 、B 、C 、P 四点共面<=>ACy AB x AP +=<=>)1(=++++=z y x OC z OB y OA x OP 其中5. 空间向量基本定理：如果三个向量不共面，那么对空间任一向量，存在,,a b cp 一个唯一的有序实数组，使。

,,x y z p xa yb zc =++若三向量不共面，我们把叫做空间的一个基底，叫做基向量，,,a b c {,,}a b c,,a b c 空间任意三个不共面的向量都可以构成空间的一个基底。

高中数学人教A版选择性必修第一册第一章空间向量与立体几何1.1空间向量及其运算课件

高中数学人教A版选择性必修第一册第一章空间向量与立体几何1.1空间向量及其运算课件

• 2.直观想象：向量运算的几何意义；
学习重难点
• 重点：理解空间向量的概念
• 难点：掌握空间向量的运算及其应用
空间向量及其运算
向量
平面向量VS空间向量
左图是一个做滑翔运动员的场景，
可以想象在滑翔过程中，飞行员会受到
来自不同方向大小各异的力，例如绳索
的拉力，风力，重力等，显然这些力不
在同一个平内。
向量．
另外，利用向量加法的交换律和结合律，还可
以得到:有限个向量求和，交换相加向量的顺序，其
和不变.
A'
B'
D
A
C
B
知识点二 空间向量的加减运算及运算律
探 对任意两个空间向量与，如果=λ (λ∈R)，与有什么位置关系?反过来，
究 与有什么位置关系时，=λ?
类似于平面问量共线的充要条件，对任意两个空间向量, (≠0)， ∥
联想，用平面向量解决物理问题的方法，能否把平面向量推广
到空间向量，从而利用向量研究滑翔运动员呢？
下面我们类比平面向量，研究空间向量，先从空间上的概念和
表示开始。
知识点一 空间向量的概念
思考1
类比平面向量的概念，给出空间向量的概念.
在空间，把具有大小和方向的量叫做空间向量。
空间向量的大小叫做向量的长度或模.
―→ ―→ ―→
(2)AA′＋ AB ＋B′C′.
解
→
→
→
→
→
→
AA′ ＋AB ＋B′C′ ＝(AA′ ＋AB )＋B′C′ ＝
→
→
→
→
→
AB′＋B′C′＝AC′.向量AD′、AC′如图所示.
课堂检测
如图，E，F分别是长方体ABCD -A'B'C'D'的棱AB，CD的中点．
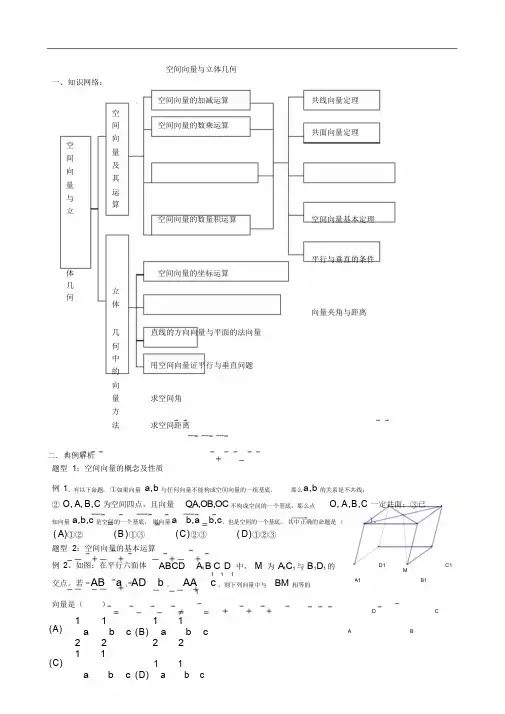
高中数学选修2-1-空间向量与立体几何

高中数学选修2-1-空间向量与立体几何

空间向量与立体几何一、知识网络：空间向量的加减运算共线向量定理空空间向量与立间向量及其运算空间向量的数乘运算共面向量定理空间向量的数量积运算空间向量基本定理平行与垂直的条件体空间向量的坐标运算几何立体向量夹角与距离几直线的方向向量与平面的法向量何中的用空间向量证平行与垂直问题向量求空间角方法求空间距离二．典例解析题型1：空间向量的概念及性质例1、有以下命题：①如果向量a,b与任何向量不能构成空间向量的一组基底，那么a,b的关系是不共线；②O, A, B,C 为空间四点，且向量OA,OB,OC不构成空间的一个基底，那么点O, A,B,C 一定共面；③已知向量a,b,c 是空间的一个基底，则向量a b,a b,c，也是空间的一个基底。

其中正确的命题是（）。

( A)①②(B)①③(C)②③( D)①②③题型2：空间向量的基本运算例2、如图：在平行六面体A BCD A1B C D 中，M 为A1C1 与B1D1 的1 1 1 D1 C1M交点。

若AB a ，A D b ，A A c ，则下列向量中与BM 相等的1A1 B1向量是（）D C(A) 1 1a b c (B)2 21 1a b c2 2A B(C) 1 11 1a b c (D) a b c2 2 2 2例3、已知： a 3m 2n 4p 0,b (x 1)m 8n 2 yp, 且m, n, p不共面. 若a ∥b , 求x, y 的值.例4、底面为正三角形的斜棱柱ABC－A1B1C1 中，D为AC的中点，求证：AB1∥平面C1BD.（三）强化巩固导练1、已知正方体ABCD—A1B1C1D1 中，点 F 是侧面CDD1C1 的中心，若，求x－y 的值.AF AD xAB y AA1 在平行六面体ABCD 中，M为AC与BD的交点，若A1 B1 a，A1 D1 b，A1 A c，则下列向量中A1B C D1 1 12、与相等的向量是( ) 。

B1M1 1 1 1 1 1 1 1A．a＋b＋c B．a＋b＋cC． a b＋c D． a b＋c2 2 2 2 2 2 2 23、（2009 四川卷理）如图，已知正三棱柱ABC A B C的各条棱长都相等，M 是侧棱CC1 的中点，则1 1 1AB和BM异面直线所成的角的大是。

2020版高中数学第三章空间向量与立体几何3.1.1空间向量的线性运算(第1课时)课件

2020版高中数学第三章空间向量与立体几何3.1.1空间向量的线性运算(第1课时)课件

减法
跟踪训练
A
归纳小结
归纳小结
2．熟练应用三角形法则和平行四边形法则 (1)利用三角形法则进行加法运算时，注意“首尾相连” 和向量的方向是从第一个向量的起点指向第二个向量的终点． 进行减法运算时，注意“共起点”，差向量的方向是从减向量 的终点指向被减向量的终点． (2)平行四边形法则一般用来进行向量的加法运算． 注意：平行四边形的两条对角线所表示的向量恰为两邻边 表示向量的和与差．
第三章 空间向量与立体几何
3.1.1 空间向量的线性运算
引入课题
F1
F3
F2
已知|F1|=2000N, |F2|=2000N, |F3|=2000N, 这三个力两两之间的夹角 都为60°, 它们的合力的大小为多少N?
三个力的特点是： 三力既有大小又有方向， 但不在同一平面上. 所以解决这类问题， 需要空间知识.
C
向量的加减法统一 在平行四边形中
知识点五：数乘运算的概念
λ>0 方向
λ<0 大小 运算律
典例分析
[思路探索] 可根据向量相等的两个条件来进行判断， 任何一条不具备，则两向量不相等．
典例分析
【解析】 命题①，
据向量相等的定义，要保证两个向量相等， 不仅模要相等，而且方向还要相同，故①错； 命题②符合两个向量相等的条件，②正确； 命题③正确； 命题④，任意两个单位向量只是模相等， 方向不一定相同，故④错． 【答案】 ②③
空间向量
知识点一：空间向量的概念
(1)定义：空间中具有 大小 和 方向 的量叫做向量．
(2)表示：
B
有向线段
向 量
几何表示
A
的 表 代数表示
示
知识点一：空间向量的概念
新教材高中数学第一章空间向量与立体几何2空间向量在立体几何中的应用3直线与平面的夹角课件新

新教材高中数学第一章空间向量与立体几何2空间向量在立体几何中的应用3直线与平面的夹角课件新


=
探究点三 利用空间向量求直线与平面的夹角
例 如图，在四棱锥 − 中，底面为直角梯形， ∥ ，∠ = 90∘
，Байду номын сангаас⊥底面，且 = = = 2，，分别为，的中点
.
（1） 求与平面所成的角；
[答案] 如图所示，以为原点，, , 的方向分别为轴，轴，轴的
角.
⒉数学运算——能用向量法求直线
与平面的夹角.
要点一 直线与平面的夹角的概念
1.直线与平面的夹角的定义
如果一条直线与一个平面垂直，则称这条直线与这个平面所成的角为①
∘
90
______；如果一条直线与一个平面平行，或直线在平面内，则称这条直线与
0∘
这个平面所成的角为②_____.
射影
平面的斜线与它在平面内的③_______所成的锐角，称为这条斜线与平面所

⋅

=
0
由൝
得ቊ
取＝1，则＝ − 1，∴ ＝(1,0, −1)，∵
+ = 0,
⋅ = 0
cos⟨, ⟩ =
⋅
||||
=
−2
8× 2
=
1
2
1
− ，
2
∴ sin = |cos < , > | = . 又0∘ ≤ ≤ 90∘ ，∴ = 30∘ .
∵ ∩ 1 = ，，1 ⊂平面1 1 ，
∴ ⊥平面1 1 ，
故∠1 为1 与平面1 1 所成的角.
易知在Rt △ 1 中， =
∴ sin∠1 =
∴ ∠1 =
π
.
6
1
，
2
3
，1
2
高中数学第三章空间向量与立体几何本章整合课件新人教B版选修2

高中数学第三章空间向量与立体几何本章整合课件新人教B版选修2

所以点 A 到平面 MBC
|·|
||
=
综合应用
专题一
专题二
专题三
(2) = (−1,0, 3), = (−1, − 3, 2 3).
设平面 ACM 的法向量为 n1=(x,y,z),
1 ⊥ ,
- + 3 = 0,
由
得
-- 3 + 2 3 = 0,
1 ⊥
解得 x= 3, = , 取n1=( 3, 1,1).
②证明能够在平面内找到一个向量与已知直线的方向向量共线;
③利用共面向量定理,即证明直线的方向向量与平面内的两个不
共线向量是共面向量.
(3)证明面面平行的方法:
①转化为线线平行、线面平行处理;
②证明这两个平面的法向量是共线向量.
综合应用
专题一
专题二
专题三
(4)证明线线垂直的方法是证明这两条直线的方向向量互相垂直.
则 P(0,− 3, 2), (0, − 3, 0), (1,0,0), (0, 3, 0).
所以 = (1, 3, −2), = (0,2 3, 0).
设 PB 与 AC 所成角为 θ,
则 cos θ=
·
||||
=
6
2 2×2 3
=
6
.
4
2
3
真题放送
1
(3)解:由(2)知BC = (−1, 3, 0).
但线段AB 与 A1B1 不重合;
π
②错误.a·b<0,即 cos<a,b><0⇒ <<a,b>≤π,而钝角的取值范
围是
π
,π
2
2
;
③错误.当 λ=0 时,λa=0 不能作为直线 l 的方向向量;
选修2-1空间向量与立体几何同步讲义

选修2-1空间向量与立体几何同步讲义


令 y1＝－1 得 x1＝1，z1＝0，∴n1＝(1，－1，0)． 由 → n2·BC＝0， －2x2＋2y2＝0， 得 → n2·CC1＝0， －y2＋ 3z2＝0. 3 3 ，∴n2＝(1，1， )． 3 3
令 y2＝1，得 x2＝1，z2＝
∴n1·n2＝1－1＋0＝0，∴n1⊥n2. ∴平面 A1AD⊥平面 BCC1B1.
2
卓越个性化教学讲义
1 1 M(0，1， )，N( ，1，1)，D(0，0，0)，A1(1，0，1)，B(1，1，0)， 2 2
→ 1 1 → → 于是MN＝( ，0， )，DA1＝(1，0，1)，DB＝(1，1，0)， 2 2
设平面 A1BD 的法向量是 n＝(x，y，z)， 则 n·DA1＝0，且 n·DB＝0，得
卓越个性化教学讲义
A．(1，2，3) B．(1，3，2) C．(2，1，3) D．(3，2，1) )． 2． 若 u＝(2， －3， 1)是平面α的一个法向量， 则下列向量中能作为平面α的法向量的是( A．(0，－3，1) B．(2，0，1) C．(－2，－3，1) D．(－2，3，－1)
3．若平面α与β的法向量分别是 a＝(1，0，－2)，b＝(－1，0，2)，则平面α与β的位置关系 是 A．平行 B．垂直 C．相交不垂直 D．无法判断 ( )．
＝(x，y，z)，则 x∶y∶z＝________． 11． 如图所示， 在正方体 ABCD－A1B1C1D1 中， M、 N 分别是 C1C、 B1C1 的中点． 求证： MN∥ 平面 A1BD. 证明 法一 如图所示，以 D 为原点，DA、DC、DD1 所在直
线分别为 x 轴、y 轴、z 轴建立空间直角坐标系，设正方体的 棱长为 1，则可求得
∴MN∥DA1，而 MN⊄平面 A1BD，DA1⊂平面 A1BD，∴MN∥平面 A1BD.
高中数学第二章空间向量与立体几何本章整合课件北师大选修2_1

高中数学第二章空间向量与立体几何本章整合课件北师大选修2_1


专题一 专题二 专题三
证明:如图所示,以 D 为坐标原点,直线 DA,DC,DD1分别为 x 轴、 y 轴、z 轴建立空间直角坐标系,
则E
������ 3
,
������ 3
,0
,F
0,
������ 3
,
2������ 3
,故������������ =
-
������ 3
,0,
2������ 3
.
又������������=(0,a,0)显然为平面 BB1C1C 的一个法向量,而������������ ·
0,
π 2
.
专题一 专题二 专题三
2.直线与平面的夹角. 求直线和平面所成的角有传统法和向量法两种.传统法关键是找 斜线在平面内的射影,从而找出线面角;向量法则可建立空间直角 坐标系,利用向量的运算求解. 3.平面间的夹角. 求平面间的夹角也有传统法和向量法两种.传统法是找到两平面 夹角的平面角,然后解这个角所在的三角形或多边形;向量法是建 立空间直角坐标系,用两平面的法向量研究两平面的夹角,但要结 合图形认真判断.
由 ������·������1������ = 0, 即 ������1-������1 -������1������ = 0, ������·������1������ = 0, ������1������ = 0.
令 x1=1,则 m=(1,1,0),而 n=λ������������1=(0,0,λa). 故 m·n=0,即平面 O1DC 与平面 ABCD 的法向量垂直,故平面 O1DC⊥平面 ABCD.
专题一 专题二 专题三
(2)解:由(1)可知,������������ =
1 3
,0,
新教材2023高中数学第一章空间向量与立体几何1.4空间向量的应用1.4.1用空间向量研究直线平面的

新教材2023高中数学第一章空间向量与立体几何1.4空间向量的应用1.4.1用空间向量研究直线平面的

建立空间直角坐标系.
由已知得 A
N 0,
3 1
,
2 4
1
- ,0,0
2
1
,B1 ,0,1
2
,B
1
,0,0
2
.
因为 M 为 BC 中点,所以 M
1
4
,C 0,
3
,0
2
1
3
, ,0
4 4
3 1
, ,1 =(1,0,1),
4 4
1
1
所以·1 =- +0+ =0.
4
4
所以= - ,
所以⊥1 ,所以 AB1⊥MN.
所以·1 =(-1,1,0)·(1,1,1)=0,
·1 =(-1,0,1)·(1,1,1)=0,
所以⊥1 ,⊥1 ,即 PB1⊥CP,PB1⊥
CA.
因为 CP∩CA=C,且 CP⊂平面 PAC,CA⊂平面 PAC,
所以直线 PB1⊥平面 PAC.
3.同类练如图,在四棱锥 P-ABCD 中,PA⊥
∴MN⊥OP,故 B 正确;
对于 C,如图,作出空间直角坐标系,设正方体棱长
为 2,则 M(2,2,2),N(0,2,0),O(1,1,0),P(0,0,1),=
(-2,0,-2),=(-1,-1,1),·=0,∴满足 MN⊥OP,故 C
正确;
对于 D,如图,作出空间直角坐标系,设正方体棱长为 2,
关直线的方向向量;
②找出平面内两条相交直线的方向向量,并分别用基
向量表示;
③分别计算有关直线的方向向量与平面内相交直线
的向量的数量积,根据数量积为 0,证得线线垂直,然后由线
面垂直的判定定理得出结论.

新教材2023高中数学第一章空间向量与立体几何1.2空间向量基本定理课件新人教A版选择性必修第一册


1
21
2
| | = a.
9
6
5.如图所示,已知平行六面体 ABCDA1B1C1D1,设=a,=b,1 =c,P 是 CA1 的
中点,M 是 CD1 的中点.用基底{a,b,c}表示
以下向量:
(1); (2).
解:如图,连接 AC,AD1.
正方向建立空间直角坐标系.
【思考】
(1)对于情境Ⅰ
,在空间中,如果用三个不共面向量 a,b,c 代
替两两垂直的向量 i,j,k,你能得出什么结论?
提示:对于空间任一向量 p,存在唯一的有序实数组
(x,y,z),使得 p=xa+yb+zc 成立.
(2)对于情境Ⅱ,是否存在实数组(x,y,z),使得 p=xe1+ye2+
所以{,, }能作为空间的一个基底.
方法规律
判断基底的基本思路及方法
(1)基本思路:判断三个空间向量是否共面,若共面,则不能
构成基底;若不共面,则能构成基底.
(2)方法:①若存在零向量,则不能作为基底;若存在一个向
量可以用另外的向量线性表示,则不能构成基底.
②假设 a=λb+μc(λ,u∈R),通过运算得到关于 λ,μ 的方程组,
1
1 1
'+ - =a+ b- c.
2
2
2 2
3.同类练已知平行六面体 OABC-O1A1B1C1,=a,1 =b,
=c,若 D 是四边形 OABC 的对角线的交点,则1 = (
)
1 1
1
1
1
1
A.-a+b+c
B.-b- a- c
C. a-b- c

【优质精选】中小学课件空间向量与立体几何课件.ppt


uuur AD
(2,
1,
4)
(4,
2,
0)
6
uuur uuur cos(AB, AD)
6
3 105
uuur u2uu1r2 5 105
sin BAD 1 9 32 105 35
SYABCD | AB | | AD | sin BAD 8 6 P
例3：如图在四棱锥P—ABCD中
底面ABCD是正方形，侧棱PD⊥
u v 2、设平面 பைடு நூலகம் 的法向量分别为 ， ，根据下
列条件判断 ， 的位置关系：
(((213)))uuu
(((12,,22,,32,,255))),,,vvv
(6,4,4) (2,4,4)
(3,1,4)
3、棱长为a的正方体ABCD—A1B1C1D1中，在棱
DD1上是否存在点P使B1D⊥面PAC？
uuur AP
uuur AD
(1,
2, 1)
(4,
2,
0)
0
，
∴ AP AB，AP AD，又 AB I AD A，AP 平 面
，
∴ uuAurB是C平D面
的法向量．
AP
ABCD
uuur | AB |
(2)2 (1)2 (4)2。
uuur 21 | AD |
42 22 02 2 5
。uAuBur
（四）、小结：本课主要探析了1、
直线的方向向量与平面的法向量 的概念与
求法；2、用方向向量和法向量判定线面位
置关系的方法。要求大家理解和掌握并会
熟练运用。
（五）、作业布置：复资P132中2、4、
5、6题。
五、教学反思
.

2020版高中数学第三章空间向量与立体几何3.1.1空间向量的线性运算课件新人教B版选修2_1


等于
A.1
√B.2
C.3
D.4
解析 对于①A→B与C—1D→1，③A→D1与C→1B长度相等，方向相反，互为相反向量； 对于②A→C1与B→D1长度相等，方向不相反； 对于④A→1D与B→1C长度相等，方向相同.故互为相反向量的有 2 对.
(2)如图，在长方体ABCD－A′B′C′D′中，AB＝3， AD＝2，AA′＝1，则分别以长方体的顶点为起点和终 点的向量中： ①单位向量共有多少个？ 解 由于长方体的高为 1，所以长方体的四条高所对应的向量A—A→′，A—′→A，B—B→′，
(1)A—A→′－C→B； 解 A—A→′－C→B＝A—A→′－D→A＝A—A→′＋A→D＝A—D→′.
(2)A—A→′＋A→B＋B—′—C→′.
解 A—A→′＋A→B＋B—′—C→′＝(A—A→′＋A→B)＋B—′—C→′＝A—B→′＋B—′—C→′＝A—C→′. 向量A—D→′，A—C→′如图所示.
＝12a＋23[－12a＋c＋21(b－c)] ＝16a＋13b＋31c.
核心素养之逻辑推理
HEXINSUYANGZHILUOJITUILI
对空间向量的有关概念理解不清致误
典例 下列说法中，错误的个数为
①若两个空间向量相等，则表示它们有向线段的起点相同，终点也相同；
②若向量A→B，C→D满足|A→B|＝|C→D|，A→B与C→D同向，则A→B>C→D；
＝(A→A1＋A→D)＋12A→B
＝a＋c＋12b.
(2)A→1N； 解 A→1N＝A→1A＋A→N
＝－A→A1＋A→B＋12A→D ＝－a＋b＋21c.
(3)M→P＋N→C1. 解 M→P＋N→C1＝(M→A1＋A—1D→1＋D→1P)＋(N→C＋C→C1)

2020高中数学 第章 空间向量与立体几何

3.1。

1 空间向量及其线性运算3.1.2 共面向量定理学习目标核心素养1。

了解空间向量与平面向量的联系与区别，掌握空间向量的线性运算及其性质，理解共线向量定理．(重点)2.了解向量共面的含义，理解共面向量定理．3。

能运用共面向量定理证明有关线面平行和点共面的简单问题。

1。

通过平面向量与空间向量的对比，培养逻辑推理素养．2。

借助共线、共面向量，提升直观想象与数学运算素养.1．空间向量及其线性运算（1)空间向量在空间，把既有大小又有方向的量叫做空间向量．（2)空间向量的线性运算空间向量的定义(或法则）2（1）共线向量如果表示空间向量的有向线段所在的直线互相平行或重合，那么这些向量叫做共线向量或平行向量．向量a与b平行，记作a∥b,规定零向量与任意向量共线．（2）共线向量定理对空间任意两个向量a，b(a≠0）,b与a共线的充要条件是存在实数λ，使b＝λa.3．共面向量（1）能平移到同一平面内的向量叫做共面向量．（2)共面向量定理如果两个向量a，b不共线，那么向量p与向量a，b共面的充要条件是存在有序实数组(x,y)，使得p＝x a＋y b.思考:(1)空间中任意两个向量一定是共面向量吗？(2）若空间任意一点O和不共线的三点A,B，C，满足错误!＝错误!错误!＋错误!错误!＋错误!错误!，则点P与点A，B，C是否共面？［提示］（1)空间中任意两个向量都可以平移到同一个平面内,成为同一个平面的两个向量，因此一定是共面向量．(2)由错误!＝错误!错误!＋错误!错误!＋错误!错误!得错误!－错误!＝错误!（错误!－错误!）＋错误!（错误!－错误!)即错误!＝错误!错误!＋错误!错误!，因此点P与点A,B,C共面．1．已知空间四边形ABCD中，错误!＝a，错误!＝b,错误!＝c，则错误!＝( ) A．a＋b－c B．－a－b＋cC．－a＋b＋c D．－a＋b－cC[错误!＝错误!＋错误!＋错误!＝错误!－错误!＋错误!＝－a＋b＋c.]2．在下列条件中，使M与A，B，C一定共面的是( )A。

空间向量与立体几何PPT课件


如图，以点O为原点，建立空间直角坐标 系，
设A(x1，y1，z1)，B(x2，y2，z2)，C(x3，y3， z3)， 由点O在底面上的射影G为△ABC的中心可得
网络构建
专题归纳
高考真题
点 G 的坐标为(x1＋x32＋x3，y1＋y32＋y3，z1＋z32＋z3)．
而O→A＋O→B＋O→C＝(x1＋x2＋x3，y1＋y2＋y3，z1＋z2＋z3)， ∴O→G＝13O→A＋13O→B＋13O→C. 点评：由二维到三维，任意一个向量可以用三个不共面的 向量线性表示，求这样的表示式的常用方法有几何法(即 上面的解法一)和代数法(即引入坐标，上面的解法二)．
网络构建
专题归纳
高考真题
专题二 向量法解决共线、共面问题
向量作为数学运算的一种重要工具，在解决立体几何 问题中有着广泛的应用．如向量共线定理有两方面的应 用：一是利用定理证明向量共线(或三点共线、线线平行)； 二是逆用，即已知两个向量共线，那么其中一个向量必然 可用另一个向量线性表示．
【例2】已知：E、F、G、H分别是空间四边形ABCD的边 AB、BC、CD、DA的中点， 求证：(1)E、F、G、H四点共面； (2)BD∥平面EFGH.
∴以 D 为原点，DA 为 x 轴，DC 为 y 轴，DD′为 z 轴，建立空 间直角坐标系．
∴A′(1，0，2)，E(0，1，1)，F(12，0，0)，G(1，1，12)．
(1)A′ →E＝(－1，1，－1)，D→B＝(1，1，0)，D→E＝(0，1，1)，
网络构建
专题归纳
高考真题
由A′ →E·D→B＝1＋(－1)＝0 ，A′→E·D→E＝1＋(－1)＝0 得：
是 BD、BC 的中点，CA＝CB＝CD＝BD ＝2，AB＝AD＝ 2. (1)求证：AO⊥平面BCD； (2)求点E到平面ACD的距离．

高中数学空间向量与立体几何空间向量在立体几何中的应用空间中的平面与空间向量同步


究 释 疑
对于平面α上任意一点B，向量A→B一定与向量n垂直，即n·A→B＝0，从
作 业
难
而可知平面α的位置可由n和A唯一确定．
返
首
页
12/10/2021
第八页，共五十七页。
课
情
堂
境
小
导 学
(3)如果v是直线l的一个方向向量，n是平面α的一个法向量，则
结 提
探
新 知
n∥v⇔
l⊥α
，n⊥v⇔
l∥α，或l⊂α
12/10/2021
第十页，共五十七页。
课
情 境
1．思考辨析(正确的打“√”，错误的打“×”)
堂 小
导 学
(1)已知直线l垂直于平面α，向量a与直线l平行，则a是平面α的
结 提
探
新 知
一个法向量．
素
( )养
(2)若直线l是平面α外的一条直线，直线m垂直于l在平面α内的投 课
合
时
作 探
影，则l与m垂直．
合
时
作 探
且垂直于向量n的平面．
分 层
究
作
释
业
疑
难
返 首 页
12/10/2021
第二十七页，共五十七页。
2．用向量法证明空间线面垂直关系的关键是什么？
课
情 境
[提示]
设直线 l，m 的方向向量分别为 a＝(a1，a2，a3)，b＝(b1，
堂 小
导
结
学 探
b2，b3)，平面 α，β 的法向量分别为 u＝(u1，u2，u3)，v＝(v1，v2，v3)，
课
合
时
作 探
(1)n是一个非零向量．
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

AB AD 2 (Ⅰ)求证: AO 平面 BCD;
(Ⅱ)求异面直线 AB 与 CD 所成角的余弦值; (Ⅲ)求点 E 到平面 ACD 的距离.
A
D O
B
C
E

5、如图,已知 P 为矩形 ABCD 所在平面外一点,PA 平面 ABCD,E、F 分别是 A B．PC 的中点.
(Ⅰ)求证:EF∥平面 PAD;
空间向量与立体几何
1. 已知向量 a (0, 2,1) ， b (1,1,2) ，则 a 与 b 的夹角为 （A）0° （B）45° （C）90° （D）180°
（）
2、已知向量 a＝（1，1，0），b＝（－1，0，2），且 k a＋b 与 2 a－b 互相垂直，则 k 的值
是（
）
A． 1
B． 1 5
(Ⅱ)求证:EF CD;
6、如图,在棱长为 1 的正方体 ABCD—A1B1C1D1 中,点 E 是棱 BC 的中点,点 F 是棱 CD 的 中点｡
(1)求证:D1E⊥平面 AB1F; (2)求二面角 C1—EF—A 的余弦值｡
4
7、在直平行六面体 AC1 中, ABCD 是菱形, DAB 60 , AC BD O , AB AA1 .
x
E
y B
图2
2
3、如图，四棱锥 P ABCD 中， 底面 ABCD 为矩形， PD 底面 ABCD，AD=PD，
E，F 分别 CD、PB 的中点。
（Ⅰ）求证：EF 平面 PAB；
xC
F
（Ⅱ）设 AB= 2 BC，求 AC 与平面 AEF 所成角的正弦值。 B
图3
z P
E
D
A y
4、如图,四面体 ABCD 中,O、E 分别是 B D．BC 的中点, CA CB CD BD 2 ,
1
空间向量练习题
1、 在棱长为 1 的正方体 ABCD A1B1C1D1 中， 求（1）平面 ACD1 的法向量 n 。（2）点 A1 到平面 ACD1 的距离。
D1 z A1
C1 B1
（3）直线 AA1 与平面 ACD1 所成角的余弦值。 （4）二面角 D1 AC D 的余弦值。
C
D A
y B
b
=（3，
,
15
）平行，则λ等于
2
6、在棱长为
1
的正方体
ABCD—A1B1C1D1
中，E、F
分别是
D1D，DB
的中点，G
在棱
CD
上
CG=
1 4
CD，
H 是 C1G 的中点.
（1)求证：EF⊥B1C;
(2)求 EF 与 C1G 所成角的余弦值;
(3)求 FH 的长.
7、正方体 ABCD—A1B1C1D1 中，E 为 CD 的中点 （1）求证：EB1⊥AD1；（2）求 D1E 与 A1C 所成角的余弦值.
C． 3 5
D． 7 5
3、已知点 A（3，-5，7），点 B（1，-4，2），则 AB 的坐标是___ _______，AB 中点坐标是 __________。
4.
已知
a
=（3，-3，-1），b
=（2，0，3），c
=（0，0，2），求
a
·（
b
+
c
）=__________。
5.
已知向量
a
=（2，-3，5）与向量
B
O M A
D C
5
x 图1
2、如图，在长方体 ABCD A1B1C1D1 中，AD= AA1 =1，AB=2，
点 E 在棱 AB 上移动。
（Ⅰ）证明： D1E A1D ；
（Ⅱ）当 E 为 AB 的中点时，求点 E 到面 ACD1 的距离；
（Ⅲ）AE
等于何值时，二面角
D1
EC
D
的大小为
4
。
z
D1
C1
A1
B1
C
D A
(1)求证: C1O // 平面 AB1D1 ; (2)求证:平面 AB1D1 平面 ACC1A1 ;
D1 A1
C1 B1
(3)求直线 AC 与平面 AB1D1 所成角的大小.
D
C
A
O B
8、如图,在四棱锥 O ABCD 中,底面 ABCD 是边长为1的菱 形, ABC , OA 底面 ABCD , OA 2 , M 为 4 OA 的中点, N 为 BC 的中点. (Ⅰ)证明:直线 MN // 平面 OCD ; (Ⅱ)求异面直线 AB 与 MD 所成角的大小; (Ⅲ)求点 B 到平面 OCD 的距离.