考虑竖向地震效应的模态Pushover分析方法

不同的建筑可以选择不同的性能指标，同一建筑对不同的地面运动可以选择 不同的性能指标，举例如表所示：
定义一个性能指标
地震地面运动
小震 中震 大震
可用 （Operational）
建筑性能水准
立即居住 （Immediate Occupation）
生命安全 （Life Safety）
√
结构稳定 （Structural Stability）
非线性静力分析（1）
（Nonlinear Static Procedure）
Pushover方法从本质上说是一种静力分析方法，对结构 进行静力单调加载下的弹塑性分析。 在结构分析模型上沿高度施加某种规定分布形式且逐渐 增加的侧向力或侧向位移，构件如有开裂或屈服，修改其 刚度，直至结构模型控制点达到目标位移或结构倾覆为止 的过程。控制点一般指建筑物顶层的形心位置；目标位移 为建筑物在设计地震力作用下的最大变形。
Pushover方法于1975年由Freeman等提出， 以后有发展但未引起更多的重视。90年代美国 科学家和工程师提出了基于性能 （Performance-based）及基于位移 （Displacement-based） 的设计方法，引起 了日本和欧洲同行的极大兴趣，从而导致 Pushover方法重新激起广大学者和设计人员 的兴趣，美国ATC-40、FEMA-273&274、日 本、中国等国家规范采纳
一些非线性计算机程序（如DRAIN－2DX（Powell et.al.1992））可以不需要迭 代而直接进行Pushover分析，下面描述的方法对于这样的程序不适用。当使用线 性计算机程序（如ETABS，SAP2000，RISA（RISA 1993）时，下面描述的过程 可以用于构建Pushover曲线：

静力弹塑性分析(Pushover分析)■简介Pushover分析是考虑构件的材料非线性特点，分析构件进入弹塑性状态直至到达极限状态时结构响应的方法。

Pushover分析是最近在地震研究及耐震设计中经常采用的基于性能的耐震设计(Performance-BasedSeismicDesign,PBSD)方法中最具代表性的分析方法。

所谓基于性能的耐震设计就是由用户及设计人员设定结构的目标性能(targetperformance)，并使结构设计能满足该目标性能的方法。

Pushover分析前要经过一般设计方法先进行耐震设计使结构满足小震不坏、中震可修的规范要求，然后再通过pushover分析评价结构在大震作用下是否能满足预先设定的目标性能。

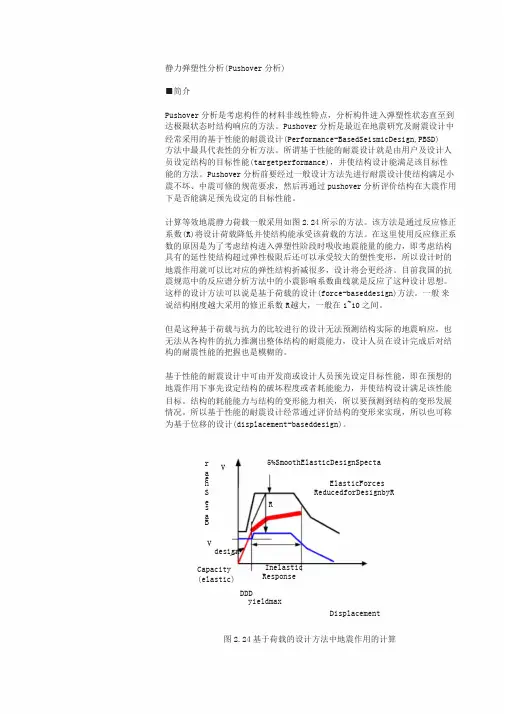
计算等效地震静力荷载一般采用如图2.24所示的方法。

该方法是通过反应修正系数(R)将设计荷载降低并使结构能承受该荷载的方法。

在这里使用反应修正系数的原因是为了考虑结构进入弹塑性阶段时吸收地震能量的能力，即考虑结构具有的延性使结构超过弹性极限后还可以承受较大的塑性变形，所以设计时的地震作用就可以比对应的弹性结构折减很多，设计将会更经济。

目前我国的抗震规范中的反应谱分析方法中的小震影响系数曲线就是反应了这种设计思想。

这样的设计方法可以说是基于荷载的设计(force-baseddesign)方法。

一般来说结构刚度越大采用的修正系数R越大，一般在1~10之间。

但是这种基于荷载与抗力的比较进行的设计无法预测结构实际的地震响应，也无法从各构件的抗力推测出整体结构的耐震能力，设计人员在设计完成后对结构的耐震性能的把握也是模糊的。

基于性能的耐震设计中可由开发商或设计人员预先设定目标性能，即在预想的地震作用下事先设定结构的破坏程度或者耗能能力，并使结构设计满足该性能目标。

结构的耗能能力与结构的变形能力相关，所以要预测到结构的变形发展情况。

所以基于性能的耐震设计经常通过评价结构的变形来实现，所以也可称为基于位移的设计(displacement-baseddesign)。

PUSHOVER分析方法全攻略作为一种常用的风险评估方法，PUSHOVER分析（Pushover Analysis）是一种基于位移的结构性能评估方法，可用于评估结构在地震等外部力作用下的破坏性能。

PUSHOVER分析的基本原理是通过对结构进行逐步加载，计算结构的位移响应，并在每个加载级别上评估结构的非弹性变形。

其中，位移响应与荷载之间的关系被表示为荷载位移曲线（Load-displacement Curve），曲线上的各点对应于结构在不同荷载水平上的位移响应。

为了进行PUSHOVER分析，以下是一些主要步骤和技术，供参考：1.结构模型准备首先，需要准备一个精确的结构模型，包括准确的几何形状、结构材料性质以及荷载。

模型可以通过各种建模软件进行创建，如ETABS、SAP2000等。

2.定义截面性能曲线对于每个结构构件，需要定义其截面的性能曲线。

这些曲线一般采用双切模型（Bi-linear Model）或多切模型（Multi-linear Model）来表示构件的力-位移响应。

3.建立非线性弹簧模型根据结构的截面性能曲线，需要建立每个构件的非线性弹簧模型。

这些弹簧模型可以通过弹簧刚度系数和屈服强度等参数来表示。

4.定义加载方式定义结构的加载方式，包括单项或多项加载。

在推进分析中，通常采用单项加载，即逐步增加水平荷载。

5.设定分析参数根据需要，设定分析的参数，包括推进步长、最大推进步数以及各构件的水平刚度。

6.进行PUSHOVER分析根据设定的加载方式和分析参数，进行PUSHOVER分析。

在每个加载步骤中，计算结构的位移响应，并绘制荷载位移曲线。

7.评估结构性能根据荷载位移曲线，评估结构的性能，包括塑性铰的形成、破坏模式以及结构的侧向刚度退化等。

8.修正分析结果在分析过程中，根据实际情况对模型进行修正。

例如，在形成塑性铰后，可以调整结构的刚度或强度参数。

9.分析结果报告最后，将分析结果整理成报告，包括结构的性能评估、塑性铰的位置和破坏模式等信息。

m i d a s C i v i lm i d a s C i v i lm i d a s C i v i l图2.8.38 基于位移设计法的结构抗震性能评价m i d a s C i v i l示。

m i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i l1n λ- : 前一步骤(n-1)的荷载因子1λ : 第1荷载步的荷载因子nstep : 总步骤数i : 等差增量步骤号当前步骤的外力向量如下。

0n n λ=⋅P P(10)(3) 第3阶段: 最终步骤的荷载增量(n nstep =) 最终荷载步骤(nstep )的外力向量如下、0nstep nstep λ=⋅P P ; 1.0nstep λ= (11)图2.8.43 自动调整荷载步长的例题(荷载因子结果)m i d a s C i v i l2. 点击步长控制选项 > 增量控制函数定义步长控制函数m i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lm i d a s C i v i lATC-40中对不同结构响应类型规定了谱折减系数的下限值(参见表2.8.7)。

静力非线性分析方法（Nonlinear Static Procedure），也称Pushover分析法，是基于性能评估现有结构和设计新结构的一种方法。

静力非线性分析是结构分析模型在一个沿结构高度为某种规定分布形式且逐渐增加的侧向力或侧向位移作用下，直至结构模型控制点达到目标位移或结构倾覆为止的过程。

控制点一般指建筑物顶层的形心位置；目标位移为建筑物在设计地震力作用下的最大变形。

Pushover方法的早期形式是“能力谱方法”（Capacity Spectrum Method, CSM），基于能量原理的一些研究成果，试图将实际结构的多自由度体系的弹塑性反应用单自由度体系的反应来表达，初衷是建立一种大震下结构抗震性能的快速评估方法。

从形式上看，这是一种将静力弹塑性分析与反应谱相结合、进行图解的快捷计算方法，它的结果具有直观、信息丰富的特点。

正因为如此，随着90年代以后基于位移的抗震设计（Displacement-Based Seismic Design, DBSD）和基于性能（功能）的抗震设计（Performance-Based Seismic Design, PBSD）等概念的提出和广为接受，使这种方法作为实现DBSD和PBSD的重要工具，得到了重视和发展。

这种方法本身主要包含两方面的内容：计算结构的能力曲线（静力弹塑性分析）、计算结构的目标位移及结果的评价。

第一方面内容的中心问题是静力弹塑性分析中采用的结构模型和加载方式；第二方面内容的中心问题则是如何确定结构在预定水平地震作用下的反应，目前可分为以ATC-40为代表的CSM和以FEMA356为代表的NSP（Nonlinear Static Procedure，非线性静力方法），CSM的表现形式是对弹性反应谱进行修正，而NSP则直接利用各种系数对弹性反应谱的计算位移值进行调整，两者在理论上是一致的。

在一些文献中只将第一方面的内容称为Pushover，不包括计算目标位移和结果评价的内容。

载和变振型加载。
(a)倒三角形加载
(b)抛物线加载
(c)均匀加载
(d)变振形加载
由于在一种固定荷载分布方式作用下不可能预测结构构件的各种变 形情况，因此建议至少用两种固定的侧向荷载分布方式来进行弹塑性分 析。较低的结构可采用倒三角形加载和基本振形加载方式中的一种，与 均匀加载组成两种加载方式； 高层结构可采用基本振形加载，与均匀加 载或变振型加载方式中的一种组成两种加载方式。
00.1
(Tg T
)
2max
[20.21(T5Tg)]max
T (s)
Tg
5T g
6.0
目标位移的确定
等效单自由度体系的周期为
Teq 2
M 2
K
xyrMr Qyr
当结构进入塑性阶段以后，结构的固有黏滞阻尼及滞回阻尼会导 致结构在运动过程中产生耗能的作用，因此需要对需求谱进行折减。
eqe 0
0
ED 4EE
(d)变振形加载
变振型加载（自适应加载，SRSS法） 利用前一步加载获得的结构周期与振型，采用振型分解反应谱法确定
结构各楼层的层间剪力，再由各层层间剪力反算出各层的水平荷载，
作为下一步施加的水平荷载模式，考虑了地震过程中结构上惯性力的
分布，比较合理但工作量大为增加。
（3）随着侧向荷载的增加，结构薄弱部位的构件达到屈服，此时对屈 服的构件的刚度予以修正，然后继续增加侧向荷载直至有新的构件屈服。 1: 将已达到抗弯强度的梁、柱、剪力墙等受弯构件的末端设置为铰接点; 2: 将楼层上已达到抗剪强度的剪力墙去掉; 3: 将已经屈曲、且屈曲后强度下降很快的支撑构件去掉; 4: 对于那些刚度己降低，但可承受更多荷载的构件，则修改其刚度特性。
Sa Vb

静力弹塑性分析方法-Gen 730版
北京迈达斯技术有限公司
CCooppyyriigghht tⓒⓒ20200-0200-0270M0ID3 AMSIIDnAfoSrmIantfionrmTaetcihonnoloTgeycChnoo.,lLotdg.y
内容目录
• 1 大震分析程序简介 • 2、MIDAS/Gen适用范围 • 3、 pushover分析原理 • 4、操作流程详解 • 5、 常见问题与解答
可以做墙元。——操作便利，但 人为可干预性较弱。
Copyright ⓒ2000-2007MIDAS Information Technology Co., Ltd.
2、MIDAS/Gen适用范围
高层结构 空间结构 体育场
Copyright ⓒ2000-2007MIDAS Information Technology Co., Ltd.
分析目的： Pushover分析前要经过一般设计方法先进行耐震设计使结构满足小震不
坏、中震可修的规范要求，然后再通过pushover分析评价结构在大震作用下 是否满足预先设定的目标性能。如：
1、通过pushover分析得到结构能力曲线。与需求谱曲线比较，判断结 构是否能够找到性能点，从整体上满足设定的大震需求性能目标。
Copyright ⓒ2000-2007MIDAS Information Technology Co., Ltd.
1、主要大震分析程序
方法
优缺点
应用程序 主要特点
1、优点：方法简单，便于理解。与动力时
静力弹塑性 程分析法相比，Pushover方法概念清晰， 实施相对简单，能使设计人员在一定程度
分析
性能点处基底剪力、控制点的位移。可与小震下基底剪力及控制点位移 比较，判断大震pushover分析结果的合理性。一般为3～4倍。

9
水平荷载分布模式
Fi Wi i1
W
i i 1
n
Vb Fi old
i1
Фi1为结构第一振型对应于第“i”层的值；Vb为上 一步计算中得到的结构基底剪力；Fiold为上一步计算的 第“i”层的层间力。 考虑多个振型时采用SRSS方法进行振型组合，按振 型参与系数进行比例化。每层的侧向力增量按下式计算：
Fi Wi hik Wi hik
i 1 n
Vb
式中，Wi、hi分别为第i层的楼层荷载代表值和层高，k为力的 形状控制参数，是结构基本周期的函数：
1.0 k 1.0 (T 0.05) / 2 2.0 T 0.5s 0.5s T 2.5s T 2.5s
层间位移角，构件的变形、材料应力等；还可以得到结构的开 裂屈服记录，把这些性态参数与结构在一定的性态水准下所要 求的能力进行对比，从而可以估计结构在地震作用下，是否满 足一定的性态要求）。
两个关键点：水平荷载分布模式、目标位移的确定 5
水平荷载分布模式
（1） 均匀分布荷载模式（Uniform Distribution） 这种分布模式认为侧向力沿结构的高度是均匀分布， 不考虑每层结构重量的不同，进行Pushover分析时，每 一步施加在楼层的侧向力由下式确定：
Fi Vb / N
式中，△Vb为每一步施加荷载时结构的基底剪力，由结 构总的基底剪力除以总的加载步数给出；N为结构的总 层数。
6
水平荷载分布模式
（2） 倒三角形分布（Inverse Triangular Distribution or Linear Distribution） 这种分布模式认为荷载沿高度为线性分布，每一步施 加于楼层“i”的侧向力为：

《Push-over方法具体实现中的几个问题讨论》Push- over方法是近年来在国外得到广泛应用的一种结构抗震能力评价新方法，既考虑了计算的简便性，避免了以往非线性动力分析的繁琐，又兼顾了构件的弹塑性性能，具有良好的准确性，成为目前抗震设计方法研究热点。

国内外许多组织将其纳入抗震规范，如美国的ATC-40、欧洲的Eurocodes 8规范以及我国的《建筑抗震设计规范》（GB 50011-2001）等。

建立合理的分析模型、确定施加水平荷载的加载模式、构件截面的屈服内力以及停止加载的条件是实现Push- over方法的关键。

《Push-over分析法及其与非线性动力分析法的对比》Push-over法正是顺应了这些要求，近些年兴起的一种地震分析方法。

它主要是作为一种结构抗震性能的评估方法，而不是作为设计结构构件的替换方法。

它可以帮助我们更好地了解结构的内部反应机制，给出有关结构强度极限、相应变形、强度分配不连续性以及可能遭受严重破坏的部位等有关信息。

《Push-over分析方法在双柱桥墩抗震性能评价上的应用》对于桥梁结构抗震分析主要是对墩柱抗震性能的研究。

目前常用的方法包括线弹性反应谱法、弹塑性动力时程分析法、等效静力分析法等。

线弹性反应谱法由于难以正确反映结构开裂后的非弹性阶段的特性，其应用范围受到一定限制；弹塑性时程分析方法由于需要准备包括场地地震波等在内的大量数据，且其计算繁琐，难以在实际工程应用中广泛推广；等效静力分析方法由于其计算过程简单、而且实用因而在桥梁抗震分析中已得到广泛应用。

Push-over方法则是应用最多的等效静力分析方法，但目前国内在这方面的研究很少。

有关Push-over分析方法的思想其实在很早时就已提出，当时主要用于理论研究。

Imbsen和Penzien等提出用于桥梁的抗震能力评估。

1975年,Freeman等人在Push-over分析方法中引入了地震需求谱和能力谱曲线的概念,发展了Push-over分析方法，并促进了Push-over分析方法在结构抗震性能评估等方面的应用推广。

分析
上了解结构在强震作用下的反应，迅速找 到结构的薄弱环节，从而完善抗震设计。
（push-over）2、不足：和实际结构的动力大震反应有一
定差异，只能定性进行计算和整体把握，
作为大震设计的参考。
MIDAS/Gen
能直接做剪力墙结构——实现便 利，结果稳定，易于掌控。
SAP2000、ETABS
适用于杆系结构——墙需用支撑 框架代替，实现起来较复杂。
领域，方法还不够成熟。因为以上原因，
不容易得到稳定和满意的结果，因此目前 也只能作为参考。
ABAQUS
采用纤维墙元模型——程序复杂， 价格昂贵，需组建专业团队。
MIDAS/Gen
适用于杆系结构——大跨场馆、 框架等，采用先进的纤维模型。
Perform 3D PKPM系列
采用纤维墙元模型——全英文、 手动命令输入，对操作者要求高， 适用于科研院校等。
30.00
40.00
Displacement
Cs接近0.0时，将自动终止分析
荷载增量很难获 得稳定解
可以获得稳定 解的区段
第19页/共50页
当前刚度比
分析模型
変位増分
4、操作流程详解-定义推覆工况
位移控制结果： 可获得稳定解
荷载控制结果：屈服后的刚度为0.0，所以无法获 得稳定解
Gen V730(NEW)
点“全选”按钮 可自动勾选构件
别忘了最后 更新配筋
第10页/共50页
4、操作流程详解-配筋输入
对于墙，“排序” 选为“墙号＋ 层”， “更新配 筋”项激活
第11页/共50页
4、操作流程详解-配筋输入
方法2：用户自定义配筋结果
特点：在设计-钢筋混凝土构件设计参数-编辑验算用梁（柱、墙）截面参数，输入验 算用截面，构件的最终实配配筋结果以此为准。可在方法一更新后配筋的基础上修改。

PUSHOVER分析方法在结构抗震分析中的探讨摘要：在介绍静力弹塑性分析方法的基本原理和实施过程的基础上，阐述了其发展概况，并通过分析其中个别有代表性的Push-over分析方法，以及这种方法在目前建筑结构抗震过程中的应用，简要评述了push-over 分析方法的优点以及存在的不足，指出了进一步研究发展的方向。

关键词：静力弹塑性，抗震性能，反应谱，能力谱，push-over1前言建筑结构抗震反应分析一般采用底部剪力法、振型分解反应谱法、弹塑性时程分析法等几种计算方法。

前两者属于弹性分析方法，计算简便，求解效率高，但是它们不能真实地反映建筑结构在强震过程中的非线性响应。

弹塑性时程法虽被认为是目前结构弹塑性分析方法中最可靠的方法，但是由于其分析技术复杂，计算工作量大，并且许多问题在理论上还有待进一步地改进，因此弹塑性时程法通常仅限于理论分析和研究，应用尚不普及。

静力弹塑性分析方法既考虑了计算的简便性，又考虑结构在地震作用下的非线性响应特性，是目前一种比较经济可行的结构非线性分析方法。

静力塑性分析方法分为两步:其一是对结构进行推覆分析，其二是根据结构推覆分析的结果评估结构的抗震性能。

结构推覆分析的关键是能够比较真实地模拟地震作用下结构的弹塑性性能和变形特征;结构抗震性能的评估多采用能力谱方法和结构性能指标。

能力谱方法实质上是通过地震反应谱曲线和结构能力谱曲线的叠加来评估结构在给定地震作用下的结构的反应特征。

抗震性能评估是在结构推覆分析的基础之上评估结构在给定地震作用下的响应特征，是静力弹塑性分析的重要组成部分。

结构的性能评估一般有结构性能指标(应力、位移和能量等)和能力谱设计方法两种评估形式。

结构性能指标也可以应用于结构弹塑性动力时程分析结果的评估。

接下来将简要的介绍静力弹塑性分析方法的基本原理和分析过程，并指出其分析过程中的优点和不足之处。

2 静力弹塑性分析的基本假定随着人们对结构弹塑性行为的认识加深和出于经济因素的考虑，广大学者和设计人员希望利用结构的弹塑性行为来抵御强震作用，确保结构“大震不倒”，以及针对不同的地震强度结构处于不同的弹塑性阶段时，保证结构“中震可修”，这些都要求设计者对结构进行弹塑性分析。

2 静力弹塑性 Push-over 分析方法的基本假定
1） 多自由度体系结构与其等效单自由度体系的力—位移关 系如图 1 所示，根据对此图分析所得到的结论，可忽略地震作用 过程中高阶振型的贡献，只考虑第一振型的影响。
2） 在地震反应过程中，楼板在自身平面内的刚度无限大，平 面外刚度可不考虑。
3 静力弹塑性 Push-over 分析方法的原理
用 Push-over 分析为原理的抗震设计考虑了结构因高度变化产
算例［J］． 工程力学，2006，23（ z2） ： 131-140．
The basic principle and application of Push-over analysis method in seismic analysis
弹性变形的影响。
设计软件 SAP2000 中文版知识选讲［C］． 2014．
Байду номын сангаас
5 结语
［2］ 北京金土木软件技术有限公司． SAP2000 中文版使用指南
本文介绍了 Push-over 分析方法的基本原理，对 Push-over 分
［M］． 北京： 人民交通出版社，2006．
析方法同静力弹性分析和时程分析方法进行对比，得出了以下 ［3］ 汪梦甫，周锡元． 关于结构静力弹塑性分析（ pushover） 方法
结论：
中的几个问题［J］． 结构工程师，2002（ 4） ： 71-72．
1） 在侧向荷载的逐渐加载作用下，结构的薄弱环节就会发生 ［4］ 北京金土木软件技术有限公司． Pushover 分析在建筑工程
破坏，通过对加载 构 件 的 分 析，了 解 和 分 析 结 构 的 变 形 和 受 力 情
抗震设计中的应用［M］． 北京： 中国建筑工业出版社，2010．

抗震设计中的Push-over分析方法存在的问题摘要：主要写了抗震设计中的push-over分析方法存在的问题及解决措施关键词：抗震设计，push-overabstract: mainly wrote the seismic design of the push-over analysis method to solve the existing problems and measures keywords: seismic design, push-over中图分类号： tu352.1+1 文献标识码：a 文章编号：前言：push-over analysis静力弹塑性分析，它是相对于动力弹塑性分析（弹塑性时程分析）的另外一种结构弹塑性分析方法。

在罕遇地震作用下，抗震结构会部分进入塑性状态，而弹性分析不能预测屈服后内力和变形的分布，必须进行弹塑性分析，才能知道结构的弹塑性变形能力，检验结构是否满足大震作用下的功能要求。

push-over分析方法较弹塑性动力分析，易于为工程设计人员所掌握。

这种方法既可得到有用的静力分析结果，又可很方便地利用其得到的层剪力—层间位移骨架曲线进行动力时程分析。

push-over分析方法在现阶段是可行的、而且在定量分析上是具有积极意义的，在应用过程中也会逐步完善。

新的抗震规范已经明确的提出采用push-over分析方法进行大震下的弹塑性变形验算。

关于push-over分析方法的研究和工程实例已经很多，但由于其本身计算假定的局限性，有很多问题尚未解决，有很多结构形式也并不适用于push-over方法进行分析。

如果盲目的采用push-over 方法进行设计，会产生较大隐患。

本文从push-over原理出发，对一些push-over分析中容易产生的问题做一简单介绍，希望引起设计者的重视。

1、几种push-over分析方法的适用范围push-over分析中有两个关键的环节：结构目标位移的确定、水平荷载模式的选择。

（4）累加各个加载阶段的力和变形，就可以获得所有构件在所有加载阶段的总内力和总变形。不断重复步骤(3)直到结构 的侧向位移达到预定的目标位移，或者结构中出现的塑性铰过多成为机构。
(a)倒三角形加载
(b)抛物线加载
均匀加载
Pj

V n
(c)均匀加载
此模式适宜于刚度与质量沿高度分布较均匀，且薄弱层为底层的结构。
(d)变振形加载
(a)倒三角形加载
(b)抛物线加载
(c)均匀加载
(d)变振形加载
倒三角加载（底部剪力法模式）
Pj
Wjhj
n
V
Wi hi
i 1
此模式适宜于高度不大于40米，以剪切变形为主且刚度与质量沿高度分布较均匀的结构。
由Pushover方法基本假定（2）可知，结构的高度变形由结
构的形状向量{Φ}表示，并且在整个加载过程中，结构的形
状向量是固定不变的。
假定结构的相对位移向量可由结构顶点位移xtop 和形状向量
{Φ}表示：
x xtop
[M ] xtop [C] xtop R [M ]I xg (t)
Push-over的基本问题可以概括为三个方面:
如何求得结构的能力曲线? 如何确定结构的目标位移? 如何对计算结果进行评价?
结构能力曲线的计算包括两个方面的主要内容 一 计算模型的建立 二 侧向力的分布形式
结构计算模型—纤维模型
基于平截面假定，将梁柱的内力-变形关系转化成混凝土与钢筋的单轴应力-应变关系。
静力弹塑性(Pushover)分析方法
静力推覆分析是结构分析模型在一个沿结构高度为某种 规定分布形式且逐渐增加的侧向力或侧向位移作用下，采用 荷载控制或位移控制的方式，在加载过程中根据构件屈服程 度不断调整结构刚度矩阵，直至结构模型控制点达到目标位 移或结构倾覆为止，得到结构的基底剪力—顶点位移能力谱 曲线。

■静力弹塑性分析方法（ PUSHOVER 分析方法）简介静力弹塑性分析也称PUSHOVER 分析方法，是指在结构上施加竖向荷载并保持不变，同时施加某种分布的水平荷载，该水平荷载单调增加，构件逐步屈服，从而得到结构在横向静力作用下的弹塑性性能。

主要步骤为：（1）按通常做法建立结构模型，包括几何尺寸、物理参数等；（2）根据单元种类（梁、柱、支撑、剪力墙等）和材料类型（钢、钢筋混凝土），确定各单元塑性铰性质（恢复力模型），根据受力形式可分为轴压、弯曲、剪切、压弯铰。

一般程序将塑性铰集中在杆件两端，并不考虑沿杆长的分布，轴压铰集中在杆件中央；（3）施加全部竖向荷载；（4）确定结构的目标位移；（5）选择合适的水平加载模式，施加在结构上，逐渐增加水平荷载，结构构件相继屈服，随之修改其刚度（程序自动完成），直到达到结构目标位移，对结构性能进行评判。

■静力弹塑性分析的原理MIDAS 程序提供的pushover 的分析方法，主要基于两本手册，一本是由美国应用技术委员会编制的《混凝土建筑抗震评估和修复》（ATC —40），另一本是由美国联邦紧急管理厅出版的《房屋抗震加固指南》（FEMA273／274）。

程序中FEMA 较本构关系和性能指标就来自于（FEMA273／274），而pushover 方法的主干部分，即分析部分采用的是能力谱法CSM ，来自于ATC 一40 (1996)和FEMA-273(1997)。

其主要步骤如下：（1）用单调增加水平荷载作用下的静力弹塑性分析，计算结构的基底剪力b V 一顶点位移n u 曲线（图1（a ））。

（2）建立能力谱曲线：对不很高的建筑结构，地震反应以第一振型为主，可用等效单自由度体系代替原结构。

因此，可以将b V —n u 曲线转换为谱加速度aS 一谱位移d S 曲线，即能力谱曲线（图l （b ））。

图1 pushover 曲线和能力谱之间的转换（3）建立需求谱曲线需求谱曲线分为弹性和弹塑性两种需求谱。

顶端位移关系曲
线 ) 。M 表示结构质量矩阵。 ( 3) 将 pushover曲线简化为双折线曲线 ( 如图 1 ( a ) 所示 ) 。一种简化方法是首先估 计基底屈服剪力 Vbny , 取 60 % Vbny 处的割线刚度作为有效初始刚度, 然后逐步迭代, 直到误差小于预定范围。 ( 4) 利用公式 ( 1), 将简化的 pushover曲线转化为 n 阶振型弹塑性单自由度体系力 - 位移曲线 ( 如图 1b 所示 )。 F sn = 显然, F sn /L sn与 D n 的屈服值表达式如下: F sny Vbny u rny = * , D ny = Ln Mn n rn ( 2) Vbn
51
向量 表示 , 且在整个地震反应过程中 , 不管结构的变形大小 , 形状向量 over方法不能考虑高阶振型的贡献, 难以应用到高层结构中。 方法 模态 pushover方法 (M PA)
[ 1]
保持不变。显然, 传统的 push -
Chopra( 2001) 及其合作者基于结构动力学理论, 考虑高阶振型对结构的影响 , 提出的一种新的 pushover 。该方法采用各阶振型的固定水平荷载模式对结构进行推覆分析, 最 后采用一定法则 ( 如 SRSS) , 确定多阶振型影响的结构目标位移。由于该方法考虑了结构的高阶振型影响, 与实际情况更为符合 , 能使计算精度相对提高 , 但是该方法在计算各阶振型等效单自由度体系的弹塑性静力 反应时 , 水平荷载仍取固定不变模式 , 还是难以解决传统 pushover 方法中假定二所带来的问题。为此 , 本文 通过考虑结构屈服后地震作用发生变化这一特性, 对该方法进行了改进。
引言
上个世纪 90 年代 , 美国科学家和工程师提出了基于性态及基于位移的设计方法。该方法一经提出, 立 即引起全世界各国科学家的关注, 有望代替规范中传统的基于承载力的抗震设计方法。作为结构非线性反 应的简化计算方法, Pushover Analysis( POA ) 由于其相对较高的精度及简单的工作量引起了广大学者和设计 人员的兴趣 , 该方法得到了深入的研究和广泛的应用。简单地说 , POA 方法的优点集中体现在两个方面: 1 . 它较底部剪力法和振型分解反应谱法考虑了结构的弹塑性特征 ( 材料非线性 ) , 精度较高; 2 . 它较非线性 时程分析法计算简单 , 工作量较小。总之 , 在实际的工程设计中, 往往要求计算方法具有一定的精度 , 同时应 力求简单和规范。 Pushover方法正具备这个条件, 因而才在全世界范围内得到了蓬勃发展和广泛应用 , 甚至 在有些国家已经被抗震实际规范所采用。 然而, 传统 pushover方法的理论基础是建立在两个基本假定上的: 1 . 结构的响应与一等效单自由度体系 ( SDOF )相关。在实际计算中 , 通常假定结构的反应仅由结构的第 1 振型控制。 2 . 结构沿高度的变形由形状

第28卷第2期铁 道 学 报Vol.28　No.2 2006年4月J OU RNAL OF T H E CHINA RA IL WA Y SOCIET Y April2006文章编号:100128360(2006)022*******基于模态分析的Push2over方法在桥梁抗震分析中的应用王克海,　李　茜(交通部公路科学研究院,北京　100088)摘　要:采用非线性时程分析是计算结构地震响应较为严格的分析方法,但它存在工作量大、计算复杂等问题。

目前土木工程中常采用非线性的静力分析(Push2over分析)来评价在地震作用下结构的抗震性能。

均匀分布、倒三角形分布的侧向荷载分布模式,适用于刚度大或第一阶振型为主的结构,为了考虑高阶振型的影响,本文提出了基于模态分析的Push2over方法,并将其应用到桥梁抗震分析中。

这种方法需要分析结构的动力特性,尤其是振型贡献率。

选出振型贡献率比较高的振型,并以此为基础,依据“侧向荷载分布模式与地震时结构惯性力的分布情况应尽量保持一致”的原则,参考《公路工程抗震设计规范》(J TJ004—89)可得到对应各振型的侧向荷载,在对主要振型进行组合后,即可获得进行Push2over分析的侧向荷载分布模式。

本文采用基于模态分析的Push2over方法对一实桥进行抗震性能分析,结果表明选取主要振型参与计算与采用全部振型计算的结果基本吻合,不仅考虑了高阶振型的影响,又消除了其他次要振型的干扰,因此这种方法应用于桥梁抗震性能评价是可行的。

关键词:Push2over方法;模态分析;桥梁抗震分析中图分类号:U442.5 文献标识码:AMode2based Push2over Method Applied to Aseism atic Analysis of B ridgesWAN G Ke2hai,　L I Qian(Research Institute of Highway,t he Ministry of Communications,Beijing100088,China)Abstract:Nonlinear time2history analysis is a more rigorous met hod to estimate seismic response of st ruct ure. Because of large workload and complex p rocedure,at p resent,Push2over analysis is used widely.Uniform force dist ribution and t riangular force dist ribution are suitable for t he rigid st ruct ures or st ruct ures whose1st2mode is main,In order to consider t he effect s of t he high modes,Push2over met hod based on mode analysis is given in t his paper and applied to aseismatic analysis of bridges.This met hod t hat p ut forward in t his paper needs to a2 nalysis t he dynamic characteristics of t he st ruct ures,especially mode cont ribution ratio.Based on t he main mode shapes t hat t he mode contribution ratio s are higher t han expected and t he principia t hat dist ribution of t he lateral forces should be in accordance wit h t he inertial dist ribution in t he eart hquake as far as possible,t he dis2 t ribution of t he lateral load corresponding to t he each selected mode shape according to t he equation specified in The Highway Engineering Seismic Design Specifications(J TJ004—89).In t his paper,evaluating aseismatic performance of t he bridge is done by using mode2based Push2over met hod.The result s indicate t hat combining modes selected and combining all modes accord wit h each ot her.The met hod t hat is gotten lateral forces by an2 alyzing t he modal cont ribution ratios to do Push2over analysis not only considers t he high modes effect,but also avoids t he dist urbing of t he secondary modes,so it’s a available met hod to estimate t he aseismic capacity of t he bridges.K ey w ords:p ush2over met hod;mode analysis;aseismatic analysis of bridges收稿日期:2005209205;修回日期:2005211210基金项目:西部交通建设科技项目(200231800028)作者简介:王克海(1964—),男,山西平遥人,副研究员,工学博士。