三讲：初等数论3——同余的性质和应用

初中数学竞赛教程《同余3》同余是数论中一个重要的概念，也是初中数学竞赛中常考的知识点之一、同余关系可以帮助我们解决一些整数求余的问题，同时也有一些重要的应用，如模运算、同余方程等。

本文将介绍同余的基本概念、性质以及应用。

一、同余的基本概念同余的定义：设a、b为任意两个整数，m为一个正整数，如果m整除(a-b)，则称a与b对于模m同余，记作a≡b(mod m)，读作a与b模m 同余。

二、同余的性质1. 自反性：对于任意整数a，有a≡a(mod m)。

证明：因为m整除（a-a），所以a与a对于模m同余。

2. 对称性：若a≡b(mod m)，则b≡a(mod m)。

证明：由a≡b(mod m)，得m整除a-b，又由整除的性质，得m整除-(a-b)，即m整除b-a，所以b≡a(mod m)。

3. 传递性：若a≡b(mod m)，b≡c(mod m)，则a≡c(mod m)。

证明：由a≡b(mod m)和b≡c(mod m)，得m整除a-b和b-c所以m整除（a-b）+（b-c），即m整除a-c，所以a≡c(mod m)。

三、同余的应用1. 求余数：当m=10时，对一个正整数n，n≡a(mod 10)的意义就是n的个位数是a。

比如，1234≡4(mod 10)。

2. 模运算：同余关系可以推广到任意的四则运算和乘幂运算中。

比如，对于任意整数a、b，若a≡b(mod m)，那么对于任意整数c，有(a+c)≡(b+c)(mod m)和(a-c)≡(b-c)(mod m)。

另外，如果a≡b(mod m)，则a^k≡b^k(mod m)。

3. 同余方程：同余方程是指形如ax≡b(mod m)的方程，其中a、b、m是已知的整数，x是未知的整数。

同余方程在密码学、计算机算法等领域有广泛的应用。

解同余方程的方法一般有试错法、中国剩余定理等。

在解同余方程时，我们要先求出模m意义下的倒数，一般记作b^-1，满足b*b^-1≡1(mod m)。

数论中的同余定理与同余方程的解法数论是研究整数性质和整数运算规律的数学分支。

同余定理和同余方程是数论中重要的概念和工具。

本文将介绍同余定理的基本思想和应用，以及解决同余方程的常见方法。

一、同余定理同余是指两个整数除以同一个数所得的余数相等。

同余定理是数论中的一个基本理论，用于刻画整数之间的关系。

设a、b和n都是整数，n>0，我们称a与b关于模n同余，记作a≡b(mod n)，当且仅当n|(a-b)。

同余定理可以分为以下几条：1. 同余的基本性质（1）自反性：a≡a(mod n)（2）对称性：若a≡b(mod n)，则b≡a(mod n)（3）传递性：若a≡b(mod n)，b≡c(mod n)，则a≡c(mod n)2. 同余的运算性质（1）加法：若a≡b(mod n)，c≡d(mod n)，则a+c≡b+d(mod n)（2）减法：若a≡b(mod n)，c≡d(mod n)，则a-c≡b-d(mod n)（3）乘法：若a≡b(mod n)，c≡d(mod n)，则a*c≡b*d(mod n)3. 同余的整除性质若a≡b(mod n)，则m|a的充分必要条件是m|b。

同余定理不仅在数论中有重要应用，还广泛用于密码学、计算机科学等领域。

二、同余方程的解法同余方程是形如ax≡b(mod n)的方程，其中a、b和n为已知整数，x 为未知整数。

解同余方程可以通过以下几种方法：1. 借助同余定理直接解法：若gcd(a,n)|b，方程ax≡b(mod n)存在解。

具体解法为，求出gcd(a,n)的一个解d，然后将方程两边同时除以d，得到新方程a'x≡b' (mod n')，其中a'、b'和n'为新方程的系数，满足gcd(a',n')=1，然后再求解新方程，最后合并得到原方程的所有解。

2. 中国剩余定理：中国剩余定理是解决同余方程组的一种有效方法。

初等数论 第二章 同 余同余的概念是高斯（Gauss ）在1800年左右给出的.同余是数论中的一个基本概念。

本章除介绍同余的基础知识外，还要介绍它的一些应用。

第一节 同余的基本性质与应用(一)定义1 给定正整数m ，如果整数a 与b 之差被m 整除，则称a 与b 对于模m 同余，或称a与b 同余，模m ，记为a ≡b (mod m)，此时也称b 是a 对模m 的同余。

如果整数a 与b 之差不能被m 整除，则称a 与b 对于模m 不同余，或称a 与b 不同余，模m ，记为a ≡/b (mod m)。

定理1 下面的三个叙述是等价的：(ⅰ) a ≡ b (mod m)；(ⅱ) 存在整数q ，使得a = b + qm ；即mq b a =-，亦即)(|b a m -(ⅲ) 存在整数q 1，q 2，使得a = q 1m + r ，b = q 2m + r ，0 ≤ r < m 。

证明 留作习题。

定理2 同余具有下面的性质：(1) （反身性） a ≡ a (mod m)；(2) （对称性） a ≡ b (mod m) ⇒ b ≡ a (mod m)；(3) （传递性） a ≡ b ，b ≡ c (mod m) ⇒ a ≡ c (mod m)定理3 设a ，b ，c ，d 是整数，并且a ≡ b (mod m)，c ≡ d (mod m)， (1) 则(4) （同余式相加） a + c ≡ b + d (mod m)；(5) （同余式相乘）ac ≡ bd (mod m)。

【证明】 (4) 由式(1)及定义1可知m ∣a - b ，m ∣c - d ，因此m ∣(a + c) - (b + d)，此即结论(ⅰ)；(5) 由式(1)及定理1可知，存在整数q 1与q 2使得a =b + q 1m ，c =d + q 2m ，因此ac = bd + (q 1q 2m + q 1d + q 2b)m ，再利用定理1，推出结论(ⅱ)。

初等数论（三）--同余基本性质：（1） 反身性：(mod )a a m ≡（2） 对称性：若(mod ),a b m ≡则(mod ),b a m ≡（3） 传递性：如果(mod ),a b m ≡(mod ),b c m ≡那么(mod ),a c m ≡以上三个性质说明∙“同余是一个等价关系，Z 中元素可以按照模m 分成m 个类，粗略地讲，用一类中的元素可以认为是相同的”（4） 如果(mod ),a b m ≡(mod ),c d m ≡那么(mod ),(mod ),a c b d m ac bd m ±≡±≡（5） 如果(mod ),a b m ≡那么(mod ),n n a b m ≡（6） 如果(mod )ac ab m ≡，不一定有(mod )c b m ≡（整数之间的乘法消去律不一定成立），（7） 若(mod ),ac bc m ≡则mod (,)m a b c m ⎛⎫≡ ⎪⎝⎭。

因此，(,)1c m =时，才会有(mod )a b m ≡。

例1.若质数5,p ≥并且21p +也是质数，证明：41p +是合数。

例2.对于任何n 个整数的集合，存在一个子集，该子集的元素之和被n 整除。

例3.证明表达式23,95x y x y ++按照相同的,x y 被17整除。

例4.设3p ≥为奇质数且111...21a p b +++=-， 证明：p a 。

作业：证明：3131421x x ++++被7整除。

例5.30对夫妻围着圆桌而坐。

证明：至少有两名妻子到各自丈夫的距离相等。

例6.设(,)1a m =，证明方程(mod )ax b m ≡在{0,1,2,3,...,1}m -中有唯一解。

例7.设01,,,,1,2,3,...n n a b x N x ax b n -∈=+=。

证明：数列12,,....,,...n x x x 不可能都是质数。

例8.证明方程2222x y z xyz ++=只有一个整数解0x y z ===。

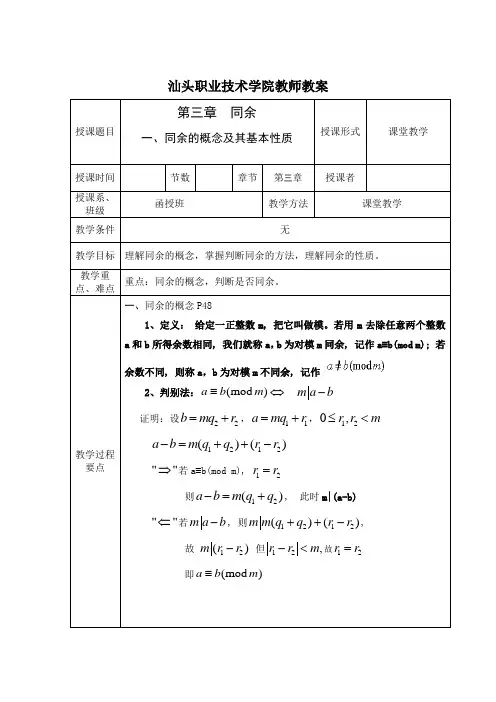
汕头职业技术学院教师教案授课题目第三章同余一、同余的概念及其基本性质授课形式课堂教学授课时间节数章节第三章授课者授课系、班级函授班教学方法课堂教学教学条件无教学目标理解同余的概念，掌握判断同余的方法，理解同余的性质。

教学重点、难点重点：同余的概念，判断是否同余。

教学过程要点一、同余的概念P481、定义：给定一正整数m, 把它叫做模。

若用m去除任意两个整数a和b所得余数相同, 我们就称a，b为对模m同余, 记作a≡b(mod m); 若余数不同, 则称a，b为对模m不同余, 记作2、判别法：(mod)a b m≡⇔m a b-证明：设22b mq r=+，11a mq r=+，120,r r m≤<1212()()a b m q q r r-=++-""⇒若a≡b(mod m),12r r=则12()a b m q q-=+, 此时m|(a-b)""⇐若m a b-, 则1212()()m m q q r r++-,故12()m r r-但12,r r m-<故12r r=即(mod)a b m≡kα特别地，若(mod )i i a b m ≡，则0(mod )nnii i i i i a x b x m ==≡∑∑a aa⇔33、弃九法（只能判断错误的结论，不能判断结论是否正确）整除的一切正整数2条件作用：求余数，除所得的余数。

(mod )pa p ≡(mod )p ，p 为质数t a 叫循环节，真分数ab（1,(,)b a a b >>=6max{,}αβ=12999t =9933999000b b •=178171610.178-==。

同余问题知识点讲解数论中的同余问题同余问题是数论中的一个重要知识点，也是各大数学竞赛和小升初考试必考的奥数知识点。

因此，学好同余问题对学生来说非常重要。

许多孩子都接触过同余问题，但也有不少孩子说“遇到同余问题就基本晕菜了！”。

同余问题主要包括带余除法的定义，三大余数定理（加法余数定理、乘法余数定理和同余定理），以及中国剩余定理和弃九法原理的应用。

带余除法的定义及性质一般地，如果a是整数，b是整数（b≠0），若有a÷b=q……r，也就是a＝b×q＋r，且0≤r＜b，我们称上面的除法算式为一个带余除法算式。

其中，当r=0时，我们称a可以被b整除，q称为a除以b的商或完全商；当r≠0时，我们称a不可以被b整除，q称为a除以b的商或不完全商。

一个完美的带余除法讲解模型可以将带余除法的概念用一个图形化的模型来解释。

假设有一堆书，共有a本，这个a可以理解为被除数。

现在要求按照b本一捆打包，那么b就是除数的角色。

经过打包后共打包了c捆，那么这个c就是商，最后还剩余d本，这个d就是余数。

这个图能够让学生清晰的明白带余除法算式中4个量的关系，并且可以看出余数一定要比除数小。

三大余数定理1.余数的加法定理a与b的和除以c的余数，等于a,b分别除以c的余数之和，或这个和除以c的余数。

例如：23，16除以5的余数分别是3和1，所以23+16=39除以5的余数等于4，即两个余数的和3+1.当余数的和比除数大时，所求的余数等于余数之和再除以c的余数。

例如：23，19除以5的余数分别是3和4，故23+19=42除以5的余数等于3+4=7除以5的余数，即2.2.余数的乘法定理a与b的乘积除以c的余数，等于a,b分别除以c的余数的积，或者这个积除以c所得的余数。

例如：23，16除以5的余数分别是3和1，所以23×16除以5的余数等于3×1=3.当余数的和比除数大时，所求的余数等于余数之积再除以c的余数。