分层随机抽样(答案)

分层随机抽样 ( 答案 )分层随机抽样一、单项选择题1、分层抽样设计效应知足（B）A 、deff 1B、deff 1C、deff 1D、deff 12、分层抽样的特色是（A）A、层内差异小，层间差异大B、层间差异小，层内差异大C、层间差异小D、层内差异大3、下边的表达式中错误的选项是（D）A、f h1B、n h nC、W h1D、N h 14、在给定花费下预计量的方差V ( y st ) 达到最小，或许对于给定的预计量方差V 使得总花费达到最小的样本量分派称为（C）A、常数分派B、比率分派C、最优分派 D 、奈曼分派5、最优分派（V opt）、比率分派（V prop）的分层随机抽样与相同样本量的简单随机抽样度之间的关系式为（ A）A、V V VB、Vopt prop srs prop （ V srs）的精V Vopt srsC 、VpropV opt V srsD、VsrsV prop V opt6、下边哪一种样本量分派方式属于比率分派？( A)n h nn h N h S h c hA 、NB、nLN hN h S hc hC 、 n h N h S hnLN h S hh 1D、 n h W h S hnLW h S hh 1h 17、下边哪一种样本量分派属于一般最优分派？( B)A 、nhn n hLN hShc h N hNB 、nN h S hc hC 、n h N h S hnLN h S hh 1D、n h W h S hnLW h S hh 1h 1二、多项选择题1. 分层抽样又被称为 ( BC )A. 整群抽样B. 种类抽样C.分类抽样D.系统抽样E.逆抽样2. 在分层随机抽样中， 当存在可利用的协助变量时，为了提升预计精度，能够采纳（ BCD ）A. 分层比预计B.结合比预计C.分别回归预计D.结合回归预计E.分别简单预计3.样本量在各层的分派方式有 ( ABCD )A. 常数分派B.比率分派C.最优分派 D.奈曼分派 E.等比分派4.分层抽样的长处有 ( ABCDE )A.在检查中能够对各个子整体进行参数预计B. 易于分工组织及逐级汇总C. 能够提升预计量的精度D.实行方便 E.保证样本更拥有代表性5.对于分层数确实定，下边说法正确的有( CE)A. 层数多一些比较好B.层数少一些比较好 C. 层数一般以不超出 6 为宜D. 层数一般以 4 层为最好E.应当充分考虑花费和精度要求等因向来确立层数6.下边哪一种样本量分配方式属于奈曼分派 ?( CD A.)n h n B. n h N h S h / c h C. N h N n L Nh S h / c hh 1n k N h S hn LN h S hh 1D. n h W h S hE. n h W h S h / c hn L n LW h S h W h S h / c hh 1 h 17.过后分层的合用处合有 (ABCD )A.各层的抽样框没法获取B.几个变量都适合于分层，而要进行预先的多重交错分层存在必定困难C.一个单位究竟属于哪一层要等到样本数据采集到此后才知道D.整体规模太大，预先分层太费事E.一般场合都能够合用三、名次解说1. 分层随机抽样2. 自加权3. 最优分派四、简答题1.简述分层随机抽样相对于简单随机抽样的长处。

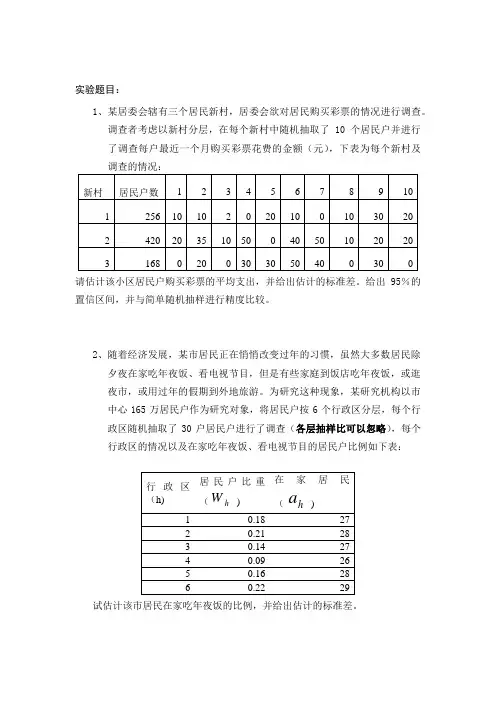
实验题目：1、某居委会辖有三个居民新村，居委会欲对居民购买彩票的情况进行调查。

调查者考虑以新村分层，在每个新村中随机抽取了10个居民户并进行了调查每户最近一个月购买彩票花费的金额（元），下表为每个新村及调查的情况：请估计该小区居民户购买彩票的平均支出，并给出估计的标准差。

给出95％的置信区间，并与简单随机抽样进行精度比较。

2、随着经济发展，某市居民正在悄悄改变过年的习惯，虽然大多数居民除夕夜在家吃年夜饭、看电视节目，但是有些家庭到饭店吃年夜饭，或逛夜市，或用过年的假期到外地旅游。

为研究这种现象，某研究机构以市中心165万居民户作为研究对象，将居民户按6个行政区分层，每个行政区随机抽取了30户居民户进行了调查（各层抽样比可以忽略），每个行政区的情况以及在家吃年夜饭、看电视节目的居民户比例如下表：试估计该市居民在家吃年夜饭的比例，并给出估计的标准差。

9.030273011===a p933.030283022===a p9.030273033===a p 867.030263044===a p933.030283055===a p 967.030293066===a p867.0*09.09.0*14.0933.0*21.09.0*18.0+++==∑pw p hHhst923.0967.0*22.0933.0*16.0≈++06.0*933.0*301*1.0*9.0*301*)1(1)(ˆ21.018.0222+=--=∑p p nf w p hhhhhhstV067.0*933.0*301*133.0*867.0*301*1.0*9.0*301*16.009.014.0222+++838.322.042033.0*967.0*301*-=+P:[)(ˆ96.1p pststV±]=[0.923±1.96*838.34-]=[0.866,0.979]。

1简单随机抽样、系统抽样、分层抽样含答案2.1.1 简单随机抽样、系统抽样、分层抽样1．简单随机抽样的定义设一个总体含有N个个体，从中逐个不放回地抽取n个个体作为样本(n≤N)，如果每次抽取时总体内的各个个体被抽到的机会都相等，就把这种抽样方法叫做简单随机抽样．2．简单随机抽样的分类?抽签法?简单随机抽样???随机数法3．简单随机抽样的优点及适用类型简单随机抽样有操作简便易行的优点，在总体个体数不多的情况下是行之有效的．4．系统抽样的概念先将总体中的个体逐一编号，然后按号码顺序以一定的间隔k进行抽取，先从第一个间隔中随机地抽取一个号码，然后按此间隔依次抽取即得到所求样本．5．系统抽样的步骤假设要从容量为N的总体中抽取容量为n的样本，步骤为：(1)先将总体的N个个体编号．有时可直接利用个体自身所带的号码，如学号、准考证号、门牌号等．NN(2)确定分段间隔k，对编号进行分段．当(n是样本容量)是整数时，取k＝；nn(3)在第1段用简单随机抽样确定第一个个体编号l(l≤k)；(4)按照一定的规则抽取样本．通常是将l加上间隔k得到第2个个体编号(l＋k)，再加k得到第3个个体编号(l＋2k)，依次进行下去，直到获取整个样本．6．分层抽样的概念在抽样时，将总体分成互不交叉的层，然后按照一定的比例，从各层独立地抽取一定数量的个体，将各层取出的个体合在一起作为样本，这种抽样方法是一种分层抽样．7．分层抽样的适用条件分层抽样尽量利用事先所掌握的各种信息，并充分考虑保持样本结构与总体结构的一致性，这对提高样本的代表性非常重要．当总体是由差异明显的几个部分组成时，往往选用分层抽样的方法．一、选择题1．抽签法中确保样本代表性的关键是( )A．制签B．搅拌均匀C．逐一抽取D．抽取不放回答案B 解析由于此问题强调的是确保样本的代表性，即要求每个个体被抽到的可能性相等．所以选B.2．下列抽样实验中，用抽签法方便的有( )A．从某厂生产的3 000件产品中抽取600件进行质量检验B．从某厂生产的两箱(每箱15件)产品中抽取6件进行质量检验C．从甲、乙两厂生产的两箱(每箱15件)产品中抽取6件进行质量检验D．从某厂生产的3 000件产品中抽取10件进行质量检验答案B- 1 -解析A总体容量较大，样本容量也较大不适宜用抽签法；B总体容量较小，样本容量也较小可用抽签法；C中甲、乙两厂生产的两箱产品有明显区别，不能用抽签法；D总体容量较大，不适宜用抽签法．3．为调查参加运动会的1 000名运动员的年龄情况，从中抽查了100名运动员的年龄，就这个问题来说，下列说法正确的是( ) A．1 000名运动员是总体B．每个运动员是个体C．抽取的100名运动员是样本D．样本容量是100答案D 解析：此问题研究的是运动员的年龄情况，不是运动员，故A、B、C错，故选D.4．用简单随机抽样方法从含有10个个体的总体中，抽取一个容量为3的样本，其中某一个体a“第一次被抽到”的可能性，“第二次被抽到”的可能性分别是( )***-*****A.，B.，C.，D.，***-**********答案A5．某会议室有50排座位，每排有30个座位．一次报告会坐满了听众．会后留下座号为15的所有听众50人进行座谈．这是运用了( )A．抽签法B．随机数表法C．系统抽样D．有放回抽样答案C解析从第1排到第50排每取一个人的间隔人数是相同的，符合系统抽样的定义．6．要从已经编号(1～50)的50枚最新研制的某种型号的导弹中随机抽取5枚来进行发射试验，用系统抽样方法确定所选取的5枚导弹的编号可能是( )A．5,10,15,20,25 B．3,13,23,33,43 C．1,2,3,4,5 D．2,4,8,16,32 答案B解析由题意知分段间隔为10.只有选项B中相邻编号的差为10，选B. 7．有40件产品，其中一等品10件，二等品25件，次品5件，现从中抽出8件进行质量分析，问应采取何种抽样方法( ) A．抽签法B．随机数表法C．系统抽样D．分层抽样答案D 8．某城市有学校700所．其中大学20所，中学200所，小学480所，现用分层抽样方法从中抽取一个容量为70的样本，进行某项调查，则应抽取中学数为( )A．70 B．20 C．48 D．2700答案B 由于＝10，即每10所学校抽取一所，又因中学200所，所以抽取200÷10＝7020(所)．9．下列问题中，最适合用分层抽样方法抽样的是( )A．某电影院有32排座位，每排有40个座位，座位号是1～40.有一次报告会坐满了听众，报告会结束以后为听取意见，要留下32名听众进行座谈B．从10台冰箱中抽出3台进行质量检查C．某乡农田有山地8 000亩，丘陵12 000亩，平地24 000亩，洼地4 000亩，现抽取农田480亩估计全乡农田平均产量D．从50个零件中抽取5个做质量检验答案C解析A的总体容量较大，宜采用系统抽样方法；B的总体容量较小，用简单随机抽样法比较方便；C总体容量较大，且各类田地的产量差别很大，宜采用分层抽样方法；D与B类似．10．要从其中有50个红球的1 000个球中，采用按颜色分层抽样的方法抽取100个进行分析，则应抽取红球的个数为( ) - 2 -A．5个B．10个C．20个D．45个*****答案A解析由题意知每＝10(个)球中抽取一个，现有50个红球，应抽取＝5(个)．*****11．在简单随机抽样中，某一个个体被抽到的可能性( )A．与第几次抽样有关，第一次抽到的可能性大一些B．与第几次抽样无关，每次抽到的可能性相等C．与第几次抽样有关，最后一次抽到的可能性大些D．与第几次抽样无关，每次都是等可能的抽取，但各次抽取的可能性不同答案B解析由简单随机抽样的特点知与第n次抽样无关，每次抽到的可能性相等．二、填空题12．福利彩票的中奖号码是从1～36个号码中选出7个号码来按规则确定中奖情况，这种从36个号码中选7个号码的抽样方法是________．答案抽签法13．用随机数表法进行抽样，有以下几个步骤：①将总体中的个体编号；②获取样本号码；③选定随机数表开始的数字，这些步骤的先后顺序应该是________．(填序号)答案①③②14．某班级共有学生52人，现根据学生的学号，用系统抽样的方法，抽取一个容量为4的样本，已知3号、29号、42号同学在样本中，那么样本中还有一个同学的学号为________．答案16解析用系统抽样的方法是等距离的．42－29＝13，故3＋13＝16.15．某农场在三种地上种玉米，其中平地210亩，河沟地120亩，山坡地180亩，估计产量时要从中抽取17亩作为样本，则平地、河沟地、山坡地应抽取的亩数分别是________．*****答案7,4,6解析应抽取的亩数分别为210×＝7,120×＝4,180×＝6.***-*****016．将一个总体分为A、B、C三层，其个体数之比为5∶3∶2.若用分层抽样方法抽取容量为100的样本，则应从C中抽取________个个体．答案20解析由题意可设A、B、C中个体数分别为5k,3k,2k，所以C中抽取个体数为2k×100＝20.5k＋3k＋2k17．某工厂生产A、B、C、D四种不同型号的产品，产品数量之比依次为2∶3∶5∶1.现用分层抽样方法抽出一个容量为n的样本，样本中A种型号有16件，那么此样本的容量n为________．答案88解析在分层抽样中，每一层所抽的个体数的比例与总体中各层个体数的比例2＋3＋5＋1是一致的．所以，样本容量n＝×16＝88.2- 3 -。

2.1.1 简单随机抽样、系统抽样、分层抽样1．简单随机抽样的定义设一个总体含有N 个个体，从中逐个不放回地抽取n 个个体作为样本(n≤N)，如果每次抽取时总体内的各个个体被抽到的机会都相等，就把这种抽样方法叫做简单随机抽样．2．简单随机抽样的分类简单随机抽样⎩⎨⎧ 抽签法随机数法3．简单随机抽样的优点及适用类型 简单随机抽样有操作简便易行的优点，在总体个体数不多的情况下是行之有效的．4．系统抽样的概念先将总体中的个体逐一编号，然后按号码顺序以一定的间隔k 进行抽取，先从第一个间隔中随机地抽取一个号码，然后按此间隔依次抽取即得到所求样本．5．系统抽样的步骤假设要从容量为N 的总体中抽取容量为n 的样本，步骤为：(1)先将总体的N个个体编号．有时可直接利用个体自身所带的号码，如学号、准考证号、门牌号等．(2)确定分段间隔k，对编号进行分段．当Nn(n是样本容量)是整数时，取k＝Nn ；(3)在第1段用简单随机抽样确定第一个个体编号l(l≤k)；(4)按照一定的规则抽取样本．通常是将l加上间隔k得到第2个个体编号(l＋k)，再加k得到第3个个体编号(l＋2k)，依次进行下去，直到获取整个样本．6．分层抽样的概念在抽样时，将总体分成互不交叉的层，然后按照一定的比例，从各层独立地抽取一定数量的个体，将各层取出的个体合在一起作为样本，这种抽样方法是一种分层抽样．7．分层抽样的适用条件分层抽样尽量利用事先所掌握的各种信息，并充分考虑保持样本结构与总体结构的一致性，这对提高样本的代表性非常重要．当总体是由差异明显的几个部分组成时，往往选用分层抽样的方法．一、选择题1．抽签法中确保样本代表性的关键是( )A．制签B．搅拌均匀C．逐一抽取D．抽取不放回答案 B 解析由于此问题强调的是确保样本的代表性，即要求每个个体被抽到的可能性相等．所以选B.2．下列抽样实验中，用抽签法方便的有( )A．从某厂生产的3 000件产品中抽取600件进行质量检验B．从某厂生产的两箱(每箱15件)产品中抽取6件进行质量检验C．从甲、乙两厂生产的两箱(每箱15件)产品中抽取6件进行质量检验D．从某厂生产的3 000件产品中抽取10件进行质量检验答案B解析A总体容量较大，样本容量也较大不适宜用抽签法；B总体容量较小，样本容量也较小可用抽签法；C中甲、乙两厂生产的两箱产品有明显区别，不能用抽签法；D总体容量较大，不适宜用抽签法．3．为调查参加运动会的1 000名运动员的年龄情况，从中抽查了100名运动员的年龄，就这个问题来说，下列说法正确的是( )A．1 000名运动员是总体B．每个运动员是个体C．抽取的100名运动员是样本D．样本容量是100答案 D 解析：此问题研究的是运动员的年龄情况，不是运动员，故A、B、C错，故选D.4．用简单随机抽样方法从含有10个个体的总体中，抽取一个容量为3的样本，其中某一个体a“第一次被抽到”的可能性，“第二次被抽到”的可能性分别是( )A.110，110B.310，15C.15，310D.310，310答案A5．某会议室有50排座位，每排有30个座位．一次报告会坐满了听众．会后留下座号为15的所有听众50人进行座谈．这是运用了( )A．抽签法B．随机数表法C．系统抽样D．有放回抽样答案C解析从第1排到第50排每取一个人的间隔人数是相同的，符合系统抽样的定义．6．要从已经编号(1～50)的50枚最新研制的某种型号的导弹中随机抽取5枚来进行发射试验，用系统抽样方法确定所选取的5枚导弹的编号可能是( )A．5,10,15,20,25 B．3,13,23,33,43 C．1,2,3,4,5 D．2,4,8,16,32答案B解析由题意知分段间隔为10.只有选项B中相邻编号的差为10，选B.7．有40件产品，其中一等品10件，二等品25件，次品5件，现从中抽出8件进行质量分析，问应采取何种抽样方法( )A．抽签法B．随机数表法C．系统抽样D．分层抽样答案D8．某城市有学校700所．其中大学20所，中学200所，小学480所，现用分层抽样方法从中抽取一个容量为70的样本，进行某项调查，则应抽取中学数为( )A．70 B．20 C．48 D．2答案B由于70070＝10，即每10所学校抽取一所，又因中学200所，所以抽取200÷10＝20(所)．9．下列问题中，最适合用分层抽样方法抽样的是( )A．某电影院有32排座位，每排有40个座位，座位号是1～40.有一次报告会坐满了听众，报告会结束以后为听取意见，要留下32名听众进行座谈B．从10台冰箱中抽出3台进行质量检查C．某乡农田有山地8 000亩，丘陵12 000亩，平地24 000亩，洼地4 000亩，现抽取农田480亩估计全乡农田平均产量D．从50个零件中抽取5个做质量检验答案C解析A的总体容量较大，宜采用系统抽样方法；B的总体容量较小，用简单随机抽样法比较方便；C总体容量较大，且各类田地的产量差别很大，宜采用分层抽样方法；D与B类似．10．要从其中有50个红球的1 000个球中，采用按颜色分层抽样的方法抽取100个进行分析，则应抽取红球的个数为( )A．5个B．10个C．20个D．45个答案A解析由题意知每1000100＝10(个)球中抽取一个，现有50个红球，应抽取5010＝5(个)．11．在简单随机抽样中，某一个个体被抽到的可能性( )A．与第几次抽样有关，第一次抽到的可能性大一些B．与第几次抽样无关，每次抽到的可能性相等C．与第几次抽样有关，最后一次抽到的可能性大些D．与第几次抽样无关，每次都是等可能的抽取，但各次抽取的可能性不同答案B解析由简单随机抽样的特点知与第n次抽样无关，每次抽到的可能性相等．二、填空题12．福利彩票的中奖号码是从1～36个号码中选出7个号码来按规则确定中奖情况，这种从36个号码中选7个号码的抽样方法是________．答案抽签法13．用随机数表法进行抽样，有以下几个步骤：①将总体中的个体编号；②获取样本号码；③选定随机数表开始的数字，这些步骤的先后顺序应该是________．(填序号)答案①③②14．某班级共有学生52人，现根据学生的学号，用系统抽样的方法，抽取一个容量为4的样本，已知3号、29号、42号同学在样本中，那么样本中还有一个同学的学号为________．答案16解析用系统抽样的方法是等距离的．42－29＝13，故3＋13＝16.15．某农场在三种地上种玉米，其中平地210亩，河沟地120亩，山坡地180亩，估计产量时要从中抽取17亩作为样本，则平地、河沟地、山坡地应抽取的亩数分别是________．答案7,4,6解析应抽取的亩数分别为210×17510＝7,120×17510＝4,180×17510＝6.16．将一个总体分为A、B、C三层，其个体数之比为5∶3∶2.若用分层抽样方法抽取容量为100的样本，则应从C中抽取________个个体．答案20解析由题意可设A、B、C中个体数分别为5k,3k,2k，所以C中抽取个体数为2k5k＋3k＋2k×100＝20.17．某工厂生产A、B、C、D四种不同型号的产品，产品数量之比依次为2∶3∶5∶1.现用分层抽样方法抽出一个容量为n的样本，样本中A种型号有16件，那么此样本的容量n为________．答案88解析在分层抽样中，每一层所抽的个体数的比例与总体中各层个体数的比例是一致的．所以，样本容量n＝2＋3＋5＋12×16＝88.。

全国⼤学⽣市场调查⼤赛题库试题答案及解析试题答案及解析※第⼀部分（），共70⼩题，70.0分。

1、随机变量中，出现次数最多的变量值是该变量的（）。

（1.0分）A. 众数B. 中位数C. 极值D. 均值正确答案：A试题解析：2、⼩刘想对Z市⼈⼝居住情况进⾏⼀个调查，因此，他把Z市随机地分成了⼏个情况相似的区域，然后从中选取了10个区域并对这些区域的家庭情况进⾏了全⾯的调查。

在这个例⼦中，⼩刘运⽤的是（）。

（1.0分）A. 分层随机抽样B. 分群随机抽样C. 判断抽样D. 整群抽样正确答案：D试题解析：3、抽样效率是指两个抽样⽅案在样本容量相同的情况下的（）。

（1.0分）A. 样本⽐例之⽐B. 抽样平均误差之⽐C. 样本均值之⽐D. 抽样⽅差之⽐正确答案：D试题解析：4、在实际⼯作中，市场调查分析⽅法主要有两种，即定性分析法和（）。

（1.0分）A. 归纳分析法B. 定量分析法C. ⽐较分析法D. 演绎分析法正确答案：B试题解析：5、变量测量尺度的类型包括（）。

（1.0分）A. 间隔尺度．长短尺度．名义尺度B. 顺序尺度．名称尺度．长短尺度C. 名称尺度．间隔尺度．长短尺度D. 间隔尺度．顺序尺度．名义尺度正确答案：D试题解析：6、某商品的100件样品中，测得的优质品为98件，则样本优质品成数为（）。

（1.0分）A. 100%B. 98%C. 2%7、下列描述直⽅图与条形图差别的说法不正确的是（）。

（1.0分）A. 条形图⽤于展⽰分类数据，直⽅图⽤于展⽰数值型数据B. 条形图⽤⾼度表⽰类别变化的多少，宽度则固定，表⽰类别C. 直⽅图的各矩形和条形图的各条形都是连续排列的D. 直⽅图中的矩形⽤⾼度表⽰频数或频率，⽤宽度表⽰各组组距正确答案：C试题解析：8、⼩王对⾹槟酒的消费情况进⾏了⼀次调研。

她界定了三个不同层次的收⼊阶段，然后规定调研⼈员对每个收⼊阶层中特定数量的⼈群进⾏访谈，这种抽样⽅法属于（）。

（1.0分）A. 分群抽样B. 配额抽样C. 任意抽样D. 随机抽样正确答案：B试题解析：9、某银⾏想知道平均每户活期存款余额和估计其总量，根据存折账号的顺序，每50本存折抽出⼀本登记其余额。

《9.1.2 分层随机抽样》教学设计【教材分析】本节《普通高中课程标准数学教科书-必修二（人教A版）第九章《9.1.2 分层抽样》，本节的主要内容在本章的结构上，通过大背景的“串联”，从大背景中不断提出新问题，从而通过问题链进行探究学习，合理选择抽样方法的必要性并掌握分层抽样方法。

从而发展学生的直观想象、逻辑推理、数学建模的核心素养。

【教学目标与核心素养】1.数学建模：结合实际问题情景，理解分层抽样的必要性和重要性；2.逻辑推理：学会用分层抽样的方法从总体中抽取样本；3.直观想象：对简单随机抽样、分层抽样方法进行比较，揭示其相互关系．4.数学运算：总体平均数的估计方法【教学重点】：理解分层抽样的基本思想和适用情形.．【教学难点】：掌握分层抽样的实施步骤，会计算总体平均数．【教学过程】抽样调查最核心的问题是样本的代表性，简单随机抽样是使总体中每一个个体都有相等的机会被抽中，但因为抽样的随机性，有可能会出现比较“极端”的样本，二、问题探究例如,在对树人中学高一年级学生身高的调查中,可能出现样本中50个个体大部分来自高个子或矮个子的情形,这种“极端”样本的平均数会大幅度地偏离总体平均数,从而使得估计出现较大的误差.能否利用总体中的一些额外信息对抽样方法进行改进呢？在对树人中学高一年级学生身高的调查中，采取简单随机抽样的方式抽取了50名学生。

1.抽样调查最核心的问题是什么？2.会不会出现样本中 50 个个体大部分来自高个子或矮个子的情形？3.为什么会出现这种“极端样本”？4.如何避免这种“极端样本”？样本代表性;会;抽样结果的随机性个体差异较大;分组抽样，减少组内差距在树人中学高一年级的 712 名学生中，男生有 326 名、女生有 386 名。

样本量在男生、女生中应如何分配？假设某地区有高中生2400人，初中生10900人，小学生11000人，此地教育部门为了了解本地区中小学的近视情况及其形成原因，要从本地区的小学生中抽取1%的学生进行调查，你认为应当怎样抽取样本？80604020你认为哪些因素影响学生视力？抽样要考虑哪些因素？分层抽样每一层抽取的样本数=一般地，按一个或多个变量把总体划分成若干个子总体，每个个体属于且仅属于一个子总体，在每个子总体中独立地进行简单随机抽样，再把所有子总体中抽取的样本合在一起作为总样本，这样的抽样方法称为分层随机抽样（stratified random sampling），每一个子总体称为层.在分层随机抽样中，如果每层样本量都与层的大小成比例，那么称这种样本量的分配方式为比例分配.×总样本量做一做1.下列问题中，最适合用分层抽样抽取样本的是( )A．从10名同学中抽取3人参加座谈会B．某社区有500个家庭，其中高收入的家庭125个，中等收入的家庭280个，低收入的家庭95个，为了了解生活购买力的某项指标，要从中抽取一个容量为100的样本C．从1 000名工人中，抽取100名调查上班途中所用时间D ．从生产流水线上，抽取样本检查产品质量【解析】A 中总体个体无明显差异且个数较少，适合用简单随机抽样；C 和D 中总体个体无明显差异且个数较多，适合用系统抽样；B 中总体个体差异明显，适合用分层抽样． 【答案】 B2．某公司生产三种型号的轿车，产量分别是1 200辆，6 000辆和2 000辆，为检验该公司的产品质量，现用分层抽样的方法抽取46辆进行检验，这三种型号的轿车依次应抽取________辆、________辆、________辆. 【解析】 三种型号的轿车共9 200辆，抽取样本为46辆，则按469 200＝1200的比例抽样，所以依次应抽取1 200×1200＝6(辆)，6 000×1200＝30(辆)，2 000×1200＝10(辆)．【答案】 6 30 10 1.分层抽样的步骤2.分层抽样的特点有哪些？【提示】 (1)分层抽样适用于已知总体是由差异明显的几部分组成的；(2)分成的各层互不交叉；(3)各层抽取的比例都等于样本容量在总体中的比例，即nN，其中n 为样本容量，N 为总体容量．3. 计算各层所抽取个体的个数时，若N i ·n N的值不是整数怎么办？【提示】 为获取各层的入样数目，需先正确计算出抽样比n N ，若N i ·nN 的值不是整数，可四舍五入取整，也可先将该层等可能地剔除多余的个体． 探究3 分层抽样公平吗？第1层的总体平均数和样本平均数为:第2层的总体平均数和样本平均数为:总体平均数和样本平均数为:由于用第一层的样本平均数 可以估计第１层的总体平均数 ，第二层的样本平均数 可以估计第2层的总体平均数,因此我们可以用估计总体平均数对各层样本平均数加权（层权）求和;分层随机抽样如何估计总体平均数12m...==X X X X M++11Mii XM =∑12...m x x x x m++==11mi i x m =∑12N ...==Y Y Y Y N++11Ni i Y N =∑12...m y y y y n++==11mi i y n =∑11M Niii i X YM X NY M NW X Y M NM N M N M N==++===+++++∑∑11m ni ii i x ymx ny m nx y m nm n m n m nω==++===+++++∑∑x X y Y Mx Ny M Nx y M N M N M N+=++++W 11M Ni ii i x yw m n==+=+∑∑m nx y m n m n=+++=m n m n M N M N +=+M m M N m n =++N n M N m n =++M Nx y M N M N=+++到男生女生平均身高分别为170.2cm和160.8cm。