不定积分练习题

第一节 不定积分的概念与性质例题：计算下列不定积分：1．dx x ⎰22．dx x⎰13．设曲线通过点()2,1，且其上任一点处的切线斜率等于这点横坐标的两倍，求此曲线的方程 4．dx x ⎰31 5．dx xx ⎰1 6．()dx xx 52-⎰ 7．dx x x ⎰28．()dx xx ⎰-231 9．()dx x e x⎰-cos 3 10．dx e xx ⎰2 11．dx x ⎰2tan12．dx x⎰2sin213．dx x x ⎰2cos 2sin 12214．dx x x x ⎰+++132224 15．dx x x x ⎰--12224 习题：1．利用求导运算验证下列等式：（1）C x x dx x +++=+⎰)1ln(1122（2）C xx dx x x+-=-⎰111222（3）C x x dx x x x +++=++⎰11arctan )1)(1(22 （4）C x x dx x ++=⎰sec tan ln sec （5）C x x x dx x x ++=⎰cos sin cos（6）C x x dx x e x+-=⎰)cos (sin 21sin 2．求下列不定积分（1）dx x⎰31（2）dx x x ⎰（3）⎰xdx （4）dx x x ⎰32（5）⎰xx dx2（6）dx x mn ⎰（7）dx x ⎰35 （8）dx x x ⎰+-)23(2（9）⎰ghdx 2（g 是常数） （10）()dx x⎰+221（11）()()d x x x ⎰-+113 （12）⎰xx dx 2（13）dx x e x⎰⎪⎭⎫ ⎝⎛+32 （14）dx x x ⎰⎪⎪⎭⎫ ⎝⎛--+221213 （15）dx xe e xx⎰⎪⎪⎭⎫ ⎝⎛--1 （16）dx e xx ⎰3 （17）dx xxx ⎰⋅-⋅32532 （18）()dx x x x ⎰-tan sec sec （19）dx x ⎰2cos2（20）⎰+x dx 2cos 1 （21）dx x x x ⎰-sin cos 2cos （22）dx xx x⎰22sin cos 2cos （23）dx x ⎰2cot （24）()dx ⎰θ+θθsec tan cos（25）dx x x ⎰+122 （26）dx x x x ⎰++123234 3．一曲线通过点()3,2e ，且任一点处的切线斜率等于该点横坐标的倒数，求该曲线的方程．4．证明函数)12arcsin(-x 、)21arccos(x -和x x-1arctan 2都是21xx -的原函数．第二节 换元积分法例题求下列不定积分1、dx x ⎰2cos 2 2、dx x ⎰+2313、dx x x ⎰+32)2( 4、dx xe x ⎰225、dx x x ⎰-21 6、dx x a ⎰+2217、dx x a ⎰-221 8、dx x a ⎰-2219、dx x x ⎰+)ln 21(1 10、dx xe x⎰311、dx x ⎰3sin 12、dx x x ⎰52cos sin13、dx x ⎰tan 14、dx x ⎰2cos15、dx x x ⎰42cos sin 16、dx x ⎰6sec17、dx x x ⎰35sec tan 18、dx x ⎰csc19、dx x ⎰sec 20、dx x x ⎰sin 3cos 21、dx x a ⎰-22 22、dx ax ⎰+22123、dx a x ⎰-221 24、dx x x a ⎰-422 25、⎰+942x dx 26、⎰-+21xx dx27、()dx x xx ⎰+-22322练习1、在下列各式等号右端的空白处填入适当的系数，使等式成立：（1）=dx )(ax d ； （2）=dx )37(-x d ；（3）=xdx )(2x d ； （4）=xdx )5(2x d ； （5）=xdx )1(2x d -； （6）=dx x 3 )43(2-x d ；（7）=dx e x 2 )(2xe d （8）dx e x 2-= )1(2x e d -+（9）=dx 23sin )23(cos x d （10）=xdx )ln 5(x d （11）=xdx)ln 53(x d -（12）=+21x dx )3(arctan x d （13）=-21xdx)arcsin 1(x d -（14）=-21x xdx )1(2x d -2、求下列不定积分（1）dt e t⎰5 （2）dx x ⎰-3)23(（3）⎰-x dx 21 （4）⎰-332x dx（5）dx e ax bx⎰-)(sin （6）dt tt ⎰sin（7）dx xex ⎰-2（8）dx x x ⎰)cos(2（9）dx xx⎰-232 （10）dx x x ⎰-4313 （11）dxx x x ⎰+++5212 （12）dt t t ⎰ϕ+ωϕ+ω)sin()(cos 2 （13）dx x x ⎰3cos sin （14）dx x x xx ⎰-+3cos sin cos sin（15）dx x x ⎰⋅210sec tan （16）⎰x x x dxln ln ln（17）⎰-221)(arcsin xx dx（18）dx xx ⎰-2arccos 2110（19）⎰+⋅+2211tan x xdxx （20）dx x x x ⎰+)1(arctan （21）dx x x x⎰+2)ln (ln 1 （22）⎰x x dx cos sin （23）dx xx x ⎰sin cos tan ln （24）dx x ⎰3cos （25）dt t ⎰ϕ+ω)(cos 2（26）dx x x ⎰3cos 2sin（27）dx x x ⎰2cos cos （28）dx x x ⎰7sin 5sin（29）dx x x ⎰sec tan 3（30）⎰-+x x e e dx（31）dx xx⎰--2491 （32）dx x x ⎰+239 （33）⎰-122x dx （34）⎰-+)2)(1(x x dx（35）dx x x x ⎰--22 （36）⎰-222xa dx x（37）⎰-12x x dx （38）⎰+32)1(x dx（39）dx x x ⎰-92 （40）⎰+xdx 21 （41）⎰-+211xdx （42）⎰-+21xx dx（43）dx x x x ⎰++-3212 （44）dx x x ⎰++223)1(1第三节 分部积分法例题 求下列不定积分1、dx x x ⎰cos2、dx xe x⎰3、dx x x ⎰ln4、dx x ⎰arccos5、dx x x ⎰arctan6、dx x e x⎰sin7、dx x ⎰3sec 8、dx e x⎰练习 求下列不定积分（1）⎰xdx x sin （2）dx x ⎰ln（3）dx x ⎰arcsin （4）dx xe x⎰-（5）dx x x ⎰ln 2（6）dx x e x ⎰-cos（7）dx x ex⎰-2sin 2 （8）dx x x ⎰2cos（9）dx x x ⎰arctan 2 （10）dx x x ⎰2tan（11）dx x x ⎰cos 2（12）dt te t ⎰-2（13）dx x ⎰2ln （14）dx x x x ⎰cos sin（15）dx x x ⎰2cos 22 （16）dx x x ⎰-)1ln( （17）dx x x ⎰-2sin )1(2（18）dx xx⎰23ln（19）dx e x ⎰3（20）dx x ⎰ln cos（21）dx x ⎰2)(arcsin （22）dx x e x ⎰2sin（23）dx x x ⎰2ln （24）dx ex ⎰+93其他有关有理函数与无理函数的不定积分计算问题：例题：1、dx x x x ⎰+-+6512 2、dx x x x x ⎰++++)1)(12(223、dx x x x ⎰---)1)(1(32 4、dx x x x ⎰++)cos 1(sin sin 1 5、dx x x ⎰-16、⎰++321x dx 7、dx x x x ⎰+11练习：（1）dx x x ⎰+33（2）dx x x x ⎰-+-103322 （3）dx x x x ⎰+-+5212 （4）⎰+)1(2x x dx（5）dx x ⎰+133 （6）dx x x x ⎰-++)1()1(122 （7）⎰+++)3)(2)(1(x x x xdx（8）dx xx x x ⎰--+3458 （9）⎰++))(1(22x x x dx（10）dx x ⎰-114（11）⎰+++)1)(1(22x x x dx （12）dx x x ⎰++)1()1(22（13）dx x x x ⎰++--222)1(2（14）⎰+x dx 2sin 3 （15）⎰+x dx cos 3 （16）⎰+x dxsin 2 （17）⎰++x x dx cos sin 1 （18）⎰+-5cos sin 2x x dx（19）⎰++311x dx（20）dx x x ⎰+-11)(3（21）dx x x ⎰++-+1111 （22）⎰+4x x dx （23）x dx x x ⎰+-11 （24）⎰-+342)1()1(x x dx本章复习题计算下列不定积分：1、⎰-x dx cos 452、⎰+942x x dx 3、dx x x ⎰+2)43(4、dx x ⎰4sin5、⎰-942x dx 6、dx x x ⎰++52127、dx x ⎰+9228、dx x ⎰-2329、dx x e x⎰cos 210、dx x x ⎰2arcsin11、⎰+22)9(x dx 12、⎰x dx 3sin 13、dx x e x ⎰-3sin 214、dx x x ⎰5sin 3sin 15、dx x ⎰3ln 16、dx xx ⎰-117、dx x ⎰+22)1(118、dx x x ⎰-11219、dx x x ⎰+2)32(20、dx x ⎰6cos 21、dx x x⎰-22222、dx x ⎰+cos 52123、⎰-122x x dx24、dx x x ⎰+-1125、dx x x x ⎰--+125226、⎰-+21x x xdx27、dx x x ⎰+2442528、⎰--x x e e dx 29、dx x x⎰-3)1(30、dx x a x ⎰-66231、dx x x x ⎰++sin cos 1 32、dx x x ⎰ln ln33、dx x x x ⎰+4sin 1cos sin 34、dx x ⎰4tan 35、⎰+)4(6x x dx 36、dx x a x a ⎰-+37、⎰+)1(x x dx 38、dx x x ⎰2cos 39、⎰+xedx 140、⎰-122x xdx41、⎰+)1(24x x dx 42、dx x x ⎰sin 43、dx x ⎰+)1ln(244、dx x x ⎰32cos sin 45、dx x ⎰arctan46、dx x x ⎰+sin cos 147、dx x x ⎰+283)1(48、dx x x x ⎰++234811 49、⎰-416x dx 50、dx x x ⎰+sin 1sin 51、dx x x x ⎰++cos 1sin 52、dx xx x x e x ⎰-23sin cos sin cos 53、dx x x x x⎰+)(3354、⎰+2)1(x e dx 55、dx e e e e x x x x ⎰+-+124356、dx e xe x x⎰+2)1( 57、dx x x ⎰++)1(ln 2258、⎰+32)1(ln x x 59、dx x x ⎰-arcsin 1260、dx xx x ⎰-231arccos61、dx x x ⎰+sin 1cot 62、⎰x x dx cos sin 363、⎰+x x dxsin )cos 2(64、dx x x x x ⎰+cos sin cos sin65、dx x x ⎰-)1(12。

不定积分专题试题（含答案）一、填空题1、若⎰==__)(sin cos )()('dx x xf u f u F ，则 C x F +)(sin2、设)(x f 的一个原函数为x x tan ，则⎰=___)('dx x xf C x xx +-tan 2sec 2 3、若)1()(ln '2>=x x x f ，则___)(=x f C e x +2214、_____1)2(=--⎰xx dxC x +--1arctan 25、设x x f ln )(=，则____)('=⎰--dx ee f x x C x +6、___sin cos 2222=+⎰xb x a dx C x a bab +)tan arctan(1 7、已知边际收益为x 230-，则收益函数为___ 230x x -8、=-+=⎰⎰dx x xf C x dx x f )1()(22，则若______ C x +--22)121（9、____)2ln 1(12=+⎰dx x x C x +2ln arctan10、若____1)1()()(2=⋅+=⎰⎰dx xxf C u F du u f ，则 C xF +-)1(二、选择题1、函数x x e 3的一个原函数为（ B ）A 、)3ln 1()3(+xe B 、3ln 1)3(+xeC 、3ln 3xe D 、3ln 3xe2、求dx x ⎰-42时，为使被积函数有理化，可作变换（C ）Ａ、t x sin 2= B 、t x tan 2= C 、t x sec = D 、42-=t x3、若x ln 是函数)(x f 的原函数，那么)(x f 的另一个原函数是BA 、ax lnB 、ax a ln 1C 、x a +lnD 、2)ln 21x （4、函数__)(_)()()(2D x F x x x f =+=的一个原函数A 、334xB 、334x xC 、)(3222x x x + D 、)(322x x x +5、__)(_)(cos )1cos 1(2D x d x =-⎰A 、C x x +-tanB 、C x anx +-cos tC 、C x x+--cos 1 D 、C x x +--cos cos 1三、计算题 1、⎰+)1(x x dxC x +arctan 2 2、dx x x ⎰-234 C x x +-+--3)4(443223、dx xx⎰-31 C x x x x x x +-++----666656711ln 3625676 4、dx e x x 23-⎰ C e e x x x +----22212125、dx x x ⎰+241 C x x x ++-arctan 336、dx xx ⎰22cos sin 1C x x +-cot tan 7、dx ex ⎰-12 C x ex +---)112(128、dx x )arcsin (2⎰ C x x x x ar x +--+2arcsin 12)sin c (229、xdx ⎰3tan C x x++cos ln 2tan 210、⎰-dx x x 123 C x x +-+-13)1(232 11、dx x x 23)(ln ⎰ C x x x x x ++-32ln 8)(ln 4442412、⎰dx x )sin(ln C x x x +-)]cos(ln )[sin(ln 213、dx x f x f ⎰)()(' )(2x f +C 14、dx ex ⎰+211C e e x x +++-+1111ln 2122 15、dx x x ⎰sin C x x x x x +-+-sin )2(6cos )6(2 四、证明题：设)(x f 的原函数)(x F 非负，且1)0(=F ，当x x F x f x 2sin )()(02=≥时，有，试证14sin 412sin )(2+-=x x xx f不定积分练习题1基础题 一．填空题 1.不定积分：⎰=_____x x dx22.不定积分：dx x ⎰-2)2(=______3.不定积分： dx x x x)11(2⎰-=_______ 4.不定积分：dx x ⎰-2)2(=__________5.不定积分：dx xe x)32(⎰+=_______ 6.一曲线通过点)3,e (2，且在任一点处的切线斜率等于该点的横坐标的倒数，则该曲线的方程为____________________7.已知一个函数)x (F 的导函数为2x 11-，且当1x =时函数值为π23，则此函数为_______________ 8.=+⎰x d )x 1x ( ________ 9. 设1()f x x=，则()f x dx '=⎰ 10.如果xe -是函数()f x 的一个原函数，则()f x dx =⎰11. 设21()ln(31)6f x dx x c =-+⎰,则()f x = . 12. 经过点(1,2),且其切线的斜率为2x 的曲线方程为 .13. 已知()21f x x '=+,且1x =时2y =,则()f x = .14. (103sin )xx x dx +-=⎰ .15.222()a x dx +=⎰. 16.3321(1)x x dx x-+-=⎰ . 二．选择题 1、，则设x d x1I 4⎰=I =（ ） c x 3 1)D ( c x 3 1)C ( cx 3 1)B ( c x 4)A (3335++-+-+--- 2、的一个原函数为则，设 )x (fx 1 1)x (f 2-=( )()arcsin ()arctan A x B x x 1 x 1 ln 2 1)C (+- x1x 1 ln 2 1)D (-+ 3、函数x 2 cos π的一个原函数为 （ ） (A) x 2 sin 2 ππ (B) x 2 sin 2 ππ- （C ）x 2 sin 2ππ (D) x2 sin 2ππ- 4、设f(x) 的一个原函数为F(x)， 则⎰=dx )x 2(f （ ）(A) F(2x)+ C (B) F( 2 x )+ C (C)C )x 2(F2 1+ (D) 2F( 2 x )+ C 5.设3()lnsin 44f x dx x C =+⎰，则()f x =（ ）。

求下列不定积分：知识点：直接积分法的练习——求不定积分的荃本方法。

思路分析：利用不定积分的运算性质和荃本积分公式，査接求出不定积分!★(1),旅思路：被积函敌|:,由积分表中的公式(2)可解。

K 77T 八★⑶思路:根裾不定积分的线性性质，将被积函数分为两项，分别积分。

解：j<2x +.K 2Wt = j2,rfA + f.rdv = -L.+lx i +C ★⑷J 仮(.丫-3皿 思酪:根拐不定积分的线性性质，将被积函薮分为两项，分别积分。

J7xU-3)rfv = |x-dv-3jA"dv = ^.v* -2.V-+C★★⑸『竺上竺旦厶息」廉:观察到3xJ3.E=w+ 1后，根拐不定积分的线性性质，将被积函数分项，分别积分。

丿 ~-V+ 1 ~~.C+ 1~"*A x 2+11 ,根据不定积分的线性性质，将被积函数分项，分别积分。

解：JI ' 心=j rfv-j ]:心=A -arctan .v+C.注.容島看出(5)(6)两題的解SI 思绝是一致的• 一般地，如果被积函数为一个有理的假分丈.谨常先将其分解为一个荃或加上或 减去一个真分丈的形丈.再分项积分.★(7) |(三二+W 心思路:分项积分。

4-~-r^ = J 'z£v -|-^<tv + 3|x 'rfv-4j.t u rfv★(8)上3 2 思路:分项积分。

■ J< ] 3 - F k£v = 3j J , dx-2jdr = 3arctan .v-2arcsinx + C.★★⑺j 后眾小思路:皿着看到皿頁=严—“直接积分。

解：J 厶斥曲Y = =加+ U息话:根据不定积分的线性性质，将被积函数分为两项，分别积分。

X ，.思路:注意到r_ JI + x* x l+x 2 l+.r 1+x 2 解: ★⑵ =x + arctan .v + C解：严小+认=★★(10) I忌路:裂项分项积分。

1、求下列不定积分1) dx ~^2 x3) (x 2)2dx5) 2 3x5 2x3xdx7) (2e x 3)dxx2、求下列不定积分（第一换元法）31) (3 2x) dx不定积分(A)2)4)6)8)dxx2. x2Jdxxcos2x .dx2 . 2cos xsin x(1 x xdxxdx32 3xx In xln(In x)4)5)dx6)dx cosxs in x27) xcos(x )dx 8) 3x31 x4dx9)sin x ,3 dxcos x10) —L X—dx<9 4x211)dx2x2 1312) cos xdx13) sin 2xcos3xdx 14)tan3 xsecxdx15)17)x32dx9 x16)10 2arccosx、1 x2dxc 23 cos x 4sin 218) arctan x dx7x(1 x)-dxx3、求下列不定积分（第二换元法）4、求下列不定积分（分部积分法）1) xSnxdx 2) arcs in xdx2 3) x In xdx2x・x 4) e sin dx21) 一dxx、1 x22) sin 一xdx3) ■^Ldx4) --dx,(ax0)5) 6)dx 1 .2x7)dxx d x28)dxdx5) x1 2 arctanxdx6) x2cosxdx7)In2 xdx 8)x2 cos2 - dx2 5、求下列不定积分(有理函数积分)1)3x . dxx 32)2x 3 」飞dxx2 3x 103)dxx(x21)(B)1、一曲线通过点(e2,3),且在任一点处的切线斜率等于该点的横坐标的倒数，求该曲线的方程。

1 32、已知一个函数F(x)的导函数为----------- ，且当x 1时函数值为-------------------------------- ，试求此函数。

2 21 x 23、 证明：若 f(x)dx F(x) c ,贝 U1f (ax b)dx F(ax b) c,(a 0)。

习题课（六）内容： 不定积分的概念及积分方法基本要求：1．理解原函数与不定积分的概念。

2．掌握不定积分的性质及不定积分与导数的关系。

3．掌握不定积分的积分方法。

4．会求简单的有理函数、无理函数、三角函数有理式的不定积分。

内容与方法精讲：一． 原函数与不定积分的概念1． 原函数定义：在区间I 上，若)()(x f x F ='（即dx x f x dF )()(=），称函数)(x F 是函数)(x f 在区间I 上的一个原函数。

2． 原函数存在的条件：若函数)(x f 在区间I 上连续。

则)(x f 在区间I 上有原函数。

3． 不定积分：函数)(x f 在区间I 上的所有原函数C x F +)(称为)(x f 在区间I 上的不定积分，记作⎰+=C x F dx x f )()(.4． 不定积分与导数的关系：（1） 先积分再求导（或微分）⎰=')(])([x f dx x f ，或 ⎰=dx x f dx x f d )(])([； （2） 先求导（或微分）再积分C x F dx x F +='⎰)()(，或 ⎰+=C x F x dF )()(. 5． 不定积分的线性性：（1）⎰⎰=dx x f k dx x kf )()(；（2）⎰⎰⎰±=±dx x g dx x f dx x g x f )()()]()([.二．基本积分公式（略） 三．不定积分的方法1． 拆项积分法：利用不定积分的线性性，将一个复杂的不定积分拆成若干个基本积分公式中的积分，从而进行积分。

（关键体现在拆项上，例如：通过有理化；利用三角公式；在分子上加一项，减一项等都是常用的手段）。

2． 凑微分法：C x F x d x f dx x x f +=='⎰⎰)]([)()]([)()]([ϕϕϕϕϕ.主要用来解决复合函数的积分（确切地说是复合函数与之间变量导数之积的积分）。

不定积分练习题(一)1.不定积分：⎰=_____xxdx 22.不定积分：dx x ⎰-2)2(=______3.不定积分： dx x x x )11(2⎰-=_______ 4.不定积分：dx x ⎰-2)2(=__________5.不定积分：dx xe x )32(⎰+=_______6.一曲线通过点)3,e (2，且在任一点处的切线斜率等于该点的横坐标的倒数，则该曲线的方程为____________________7.已知一个函数)x (F 的导函数为2x 11-，且当1x =时函数值为π23，则此函数为_______________8.=+⎰x d )x 1 x ( ________9. 设1()f x x=，则()f x dx '=⎰ 10.如果x e -是函数()f x 的一个原函数，则()f x dx =⎰11. 设21()ln(31)6f x dx x c =-+⎰,则()f x = .12. 经过点(1,2),且其切线的斜率为2x 的曲线方程为 .13. 已知()21f x x '=+,且1x =时2y =,则()f x = .14. (103sin x x dx +=⎰ . 15. 222()a x dx +=⎰ . 16. 3(1x x dx -+=⎰ .1、，则设x d x1I 4⎰= I =（ ）c x3 1)D ( c x 3 1)C ( cx 3 1)B ( c x 4)A (3335++-+-+--- 2、222222的一个原函数为则，设 )x (fx 1 1)x (f 2-=( ) ()arcsin ()arctan A x B x x1 x 1 ln2 1)C (+- x 1x 1 ln 2 1)D (-+ 3、函数x 2 cosπ的一个原函数为 （ ） (A) x 2 sin2 ππ (B) x 2 sin 2 ππ- （C ）x 2 sin 2ππ (D) x2 sin 2ππ- 4、设f(x) 的一个原函数为F(x)， 则⎰=dx )x 2(f （ ）(A) F(2x)+ C (B) F(2 x )+ C (C) C )x 2(F 2 1+ (D) 2F(2 x )+ C 5.设3()ln sin 44f x dx x C =+⎰，则()f x =（ ）A. cot 4xB. cot 4x -C. 3cos 4xD. 3cot 4x6. 若()f x 为可导、可积函数，则（ ）A. ()()f x dx f x '⎡⎤=⎣⎦⎰ B. ()()d f x dx f x ⎡⎤=⎣⎦⎰C. ()()f x dx f x '=⎰D. ()()df x f x =⎰7. 设C F(x) dx )x (f +=⎰ ，则 =⎰dx )cosx ( f sinx （ ）(A)C )sinx ( F + (B) C )sinx ( F +- (C) C )cosx ( F +- (D) sin x ( cosx ) C F + 8.设()F x 是()f x 在(),-∞+∞上的一个原函数,且()F x 为奇函数,则()f x 是 ( ) A ．偶函数 B ． 奇函数 C ． 非奇非偶函数 D ．不能确定9.已知()f x 的一个原函数为cos x ,()g x 的一个原函数为2x ,则()f g x ⎡⎤⎣⎦的一个原函数为 ( ) A ．2x B ． 2cos x C ． 2cos x D ．cos x 10.设2x e -是()f x 的一个原函数,则()02()limx f x x f x x∆→-∆-=∆ ( )A ．22x e -B ．-28x e -C ．22x e --D ．24x e - 11. 21(),()1f x f x x=-设则的一个原函数为 ()arcsin ()arctan 1111()ln ()ln 2121A x B x x x C D x x -+⎛⎫⎛⎫ ⎪ ⎪+-⎝⎭⎝⎭不定积分练习题(二)1.=⎰x d x tan 2__________．2.x d 1x1x 3x 3224⎰+++＝ ． 3.⎰+)x 1 ( x dx2 = ______________________________．4. dx e 1 1x ⎰-+= 5.=⎰dx x 2cos x12 ．6.设 )x (f 的一个原函数 xx sin 为，则 =⎰dx )x (f ．7.设 )x (f 的一个原函数为 ln x ， 则⎰+dx )x 21(f ______________．8.设)x (f 的一个原函数为 lnx , 则=')x (f _______________． 9.，的一个原函数为若x ln x )x (f =)x (f 则______ _______．1. =+-=⎰I x d 1e1e I xx ，则设（ ） c )1e ( ln )B ( c )1e ( ln )A (x x +++- c x )1e ( ln 2)C (x +-+ c )1e ( ln x 3x )D (x ++-　2. 设f(x)的一个原函数是F(x) ，则⎰+dx )b ax (f ＝（ ） (A) F(ax ＋b)＋c (B) aF(ax+b)+c (C)b ax )b ax (F +++c (D)a 1F(ax+b)+c3. =-+=⎰⎰dx )x 1 ( f x c x sin dx )x (f 2，则若（ ）(A)c )x 1 ( sin 22+- (B)c )x 1 ( sin 22+--(C) c )x 1 ( sin 2 12+- (D) c )x 1 ( sin2 12+-- 4.不定积分：21( 1 ) cos d sinx x x +=⎰ （ ） (A) C x sin 1x +-(B) Cx sin 1x ++ (C) C x sin 1x sin +-(D) Cx sin 1x sin ++ 5. 不定积分：⎰=x x de e sin （ ）(A) C e cos x + (B) C e cos x +- (C) C e arccosx + (D) C e arccos x +- 6. 不定积分：⎰+e 1 dxx＝（ ） (A)c e 1 ln x ++）（ (B) c e 1 ln x++-）（ (C) ce 1 e ln x x ++ (D)c e 1 1 ln x ++ 7. 设x 2 tan k )x (f = 的一个原函数是) x 2 cos ( ln32 ，则常数 =k （ ）(A) 3 2 - (B) 3 2 (C) 34 - (D) 3 41.⎰++dx )1x 2sin( )1x 2(cos 2求．2.求不定积分 4(1)xdx x +⎰．3.求不定积分dx)x 1( x3⎰-．不定积分练习题(三)1. 2x xe dx -=⎰( ).(a) x e c -+, (b)212x e c -+, (c)212x e c --+, (d) 2x e c --+.2. 2x e dx ⎰=( )(a) 2x e c +, (b) 212x e c +, (c) 2x e , (d) 212x e .3. 221(2)dx x =+⎰( )(a) arctan 2x c +, (b) arctan 2x , (c) arcsin 2x , (d) arcsin 2x c +. 4. 22sec 2xdx =⎰( )(a)tan 2x c +, (b) tan 2x , (c) tan x , (d) tan x c +.5.(1)n x dx +=⎰ .6. cos(34)x dx +=⎰ .7.= . 8. x e dx -=⎰ .9.1sin 2xdx ⎰= . 10.(2)x x dx -=⎰ . 11.2= . 12.12dx x =-⎰. 不定积分练习题(四)1. 设()xf x e -=,则()ln f x dx x'⎰=( )A ． 1x -c + B ． ln x c -+ C ． 1c x+ D ． ln x c + 2. 若()f x 的一个原函数为2ln x ,则()x f x dx '=⎰( )A ．2ln ln x x c -+B ．22ln ln x x c ++C ．22ln ln x x c -+D ．2ln ln x x c ++ 3. 设()()ln 1ln f x x x '=+,则()f x =( )A ．22xx xe c ++ B ．()212xx x e c -++ C ．22xx xe c -+ D ．()212xx x e c --+4. 2cos xdx x=⎰( ) A ． tan ln cos x x x c -+ B ． tan ln cos x x x c ++ C ． tan ln sin x x x c -+ D ． tan ln sin x x x c ++ 5. ()2211dx x x=+⎰ ( )A ．1arctan x c x ++ B ． 1arctan x c x -+ C ． 1arctan x c x --+ D ．1arctan x c x-++6. ,I I ==设则( )()arcsin;()arcsin n ()arcsin ;()arcsin x xA a cB a c a ax xC a cD ca a -- 7. ,I I ==设则( )22();()arctan ;(().A cB cC cD c -++8. ,x xdxI I e e-==+⎰设则( ) ()()arctan ;()arctan ;()x x x xxxA e e cB e cC e cD e e c ----+++++9.10(23),I x dx I =-=⎰设则( )991111()10(23);()20(23);11()(23);()(23).2211A x c B x c C x c D x c -+-+-+-+ 10. I I ==设则( ) ()2ln(1.(2ln(1.(2ln(1.()2ln(1.A cB cC cD c -+++-+11.1d ,1x xe I x I e -==+⎰设则( ) ()ln(1)()ln(1);()2ln(1);()2ln(1).x x xxA e cB e cC e x cD x e c -++++-+-++12. sin cos d ,I x x x I ==⎰设则( )2211()sin ;()cos ;2211()cos 2;()cos 244A x cB x cC x cD x c-+++-+ 13.求下列不定积分：dxx ⎰-3)23( ⎰-dxx32dx3dt tt ⎰sin⎰)ln(ln ln x x x dx ⎰x x dx sin cos ⎰-+x x e e dxdx x x )cos(2⎰ dx x x ⎰-4313 dx x x⎰3cos sin dx x x ⎰--2491 ⎰-122x dx dx x ⎰3cos ⎰xdx x 3cos 2sin ⎰xdx x sec tan 3dx x x ⎰+239 dx x x ⎰+22sin 4cos 31 dx x x⎰-2arccos 2110 dx x x x ⎰+)1(arctan dx xx ⎰+211 dxx ⎰sin ⎰+32)1(x dx⎰+x21dx inxdx xs ⎰ ⎰xdxarcsin⎰xdxx ln 2dx x e x⎰-2sin 2⎰xdx arctan x 2 ⎰xdx x cos 2 ⎰xdx 2ln dx x x 2cos 22⎰ ⎰-++dx x x x 103322 ⎰+)1(2x x dx⎰+dx xx211arctandx x ⎰-2sin 1 dx xa x x ⎰-2 ⎰+dx x xe x232arctan )1( ⎰+x x dx sin 2)2sin( ⎰-dx e xe x x1dx e e x x ⎰2arctan dx x x x x ⎰+cos sin cos sin 14. 设)(x f 的一个原函数为xxsin ，求⎰'dx x f x )(。

第4章不定积分习题4-11.求下列不定积分：知识点：直接积分法的练习——求不定积分的基本方法。

思路分析：利用不定积分的运算性质和基本积分公式，直接求出不定积分！★(1)思路:52x-=，由积分表中的公式（2）可解。

解：532223x dx x C --==-+⎰★(2)dx-⎰思路:根据不定积分的线性性质，将被积函数分为两项，分别积分。

解：1141113332223()24dx x x dx x dx x dx x x C ---=-=-=-+⎰⎰⎰⎰★(3)22xx dx +⎰（）思路:根据不定积分的线性性质，将被积函数分为两项，分别积分。

解：2232122ln 23x xxx dx dx x dx x C +=+=++⎰⎰⎰（）★(4)3)x dx -思路:根据不定积分的线性性质，将被积函数分为两项，分别积分。

解：3153222223)325x dx x dx x dx x x C -=-=-+⎰⎰★★(5)4223311x x dx x +++⎰思路:观察到422223311311x x x x x ++=+++后，根据不定积分的线性性质，将被积函数分项，分别积分。

解：42232233113arctan 11x x dx x dx dx x x C x x ++=+=++++⎰⎰⎰ ★★(6)221x dx x +⎰思路:注意到222221111111x x x x x +-==-+++，根据不定积分的线性性质，将被积函数分项，分别积分。

解：2221arctan .11x dx dx dx x x C x x=-=-+++⎰⎰⎰ 注：容易看出(5)(6)两题的解题思路是一致的。

一般地，如果被积函数为一个有理的假分式，通常先将其分解为一个整式加上或减去一个真分式的形式，再分项积分。

★(7)x dx x x x ⎰34134（-+-）2 思路:分项积分。

解：3411342x dx xdx dx x dx x dx x xx x --=-+-⎰⎰⎰⎰⎰34134（-+-）2 ★(8)23(1dx x -+⎰思路:分项积分。

不定积分（Ａ）１、求下列不定积分１）⎰2x dx２）⎰x x dx 2３）dx x ⎰-2)2( ４）dx xx ⎰+221５）⎰⋅-⋅dx x x x 32532 ６）dx xx x⎰22sin cos 2cos７）dx x e x)32(⎰+８）dx x x x)11(2⎰-２、求下列不定积分（第一换元法）１）dx x ⎰-3)23( ２）⎰-332xdx３）dt tt ⎰sin ４）⎰)ln(ln ln x x x dx５）⎰xx dxsin cos ６）⎰-+x x e e dx７）dx x x )cos(2⎰ ８）dx x x ⎰-4313 ９）dx xx⎰3cos sin 10）dx x x ⎰--2491 11）⎰-122x dx 12）dx x ⎰3cos13)⎰xdx x 3cos 2sin 14)⎰xdx x sec tan 315) dx x x ⎰+239 16)dx x x ⎰+22sin 4cos 3117)dx xx ⎰-2arccos 2110 18)dx x x x ⎰+)1(arctan3、求下列不定积分（第二换元法）１）dx xx⎰+211 ２）dx x ⎰sin３）dx x x ⎰-42 ４）⎰>-)0(,222a dx xa x５）⎰+32)1(x dx ６）⎰+xdx 21７）⎰-+21xx dx ８）⎰-+211xdx４、求下列不定积分（分部积分法）１）inxdx xs ⎰ ２）⎰xdx arcsin３）⎰xdx x ln 2４）dx xe x⎰-2sin 2５）⎰xdx x arctan 2 ６）⎰xdx x cos 2７）⎰xdx 2ln ８）dx x x 2cos 22⎰５、求下列不定积分（有理函数积分）１）dx x x ⎰+33２）⎰-++dx x x x 1033223）⎰+)1(2x x dx（Ｂ） １、一曲线通过点)3,(2e ，且在任一点处的切线斜率等于该点的横坐标的倒数，求该曲线的方程。

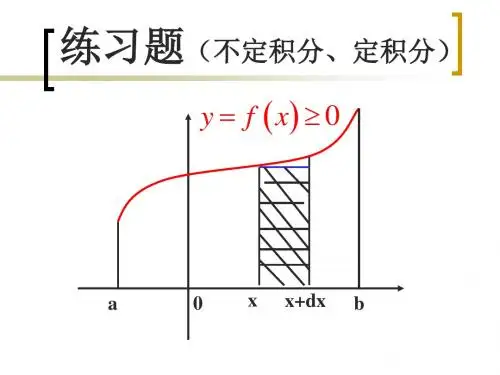
不定积分练习题1. 计算下列不定积分：∫(x^3 + 2x^2 - 5x + 1)dx。

2. 求不定积分：∫(3/x^2)dx。

3. 计算不定积分：∫(1/(1+x^2))dx。

4. 求下列函数的原函数：∫(sin(x) + cos(x))dx。

5. 计算不定积分：∫(1/√(1-x^2))dx。

6. 求下列函数的原函数：∫(x^2 * e^x)dx。

7. 计算不定积分：∫(1/(1-x))dx。

8. 求不定积分：∫(1/(1+x^2)^2)dx。

9. 计算不定积分：∫(tan(x))dx。

10. 求下列函数的原函数：∫(x * sin(x))dx。

11. 计算不定积分：∫(1/(1+√x))dx。

12. 求不定积分：∫(1/(1-x^2)^3)dx。

13. 计算不定积分：∫((1-x^2)^(1/2))dx。

14. 求不定积分：∫((1+x)^(-1/2))dx。

15. 计算不定积分：∫(1/(1+x^4))dx。

16. 求下列函数的原函数：∫(x^4 * e^(-x))dx。

17. 计算不定积分：∫(1/(x^2 * (1+x)))dx。

18. 求不定积分：∫((1-x)^(1/3))dx。

19. 计算不定积分：∫(1/(1+x^3))dx。

20. 求下列函数的原函数：∫(x * ln(x))dx。

21. 计算不定积分：∫(1/(1-x^3))dx。

22. 求不定积分：∫(1/(1+x^6))dx。

23. 计算不定积分：∫(1/(1-x^4))dx。

24. 求不定积分：∫(1/(1+x^10))dx。

25. 计算不定积分：∫(1/(1-x^6))dx。

第三章复习X.1 积分换元的几种形式1． 利用三角函数代换，变根式积分为三角有理式积分求⎰-dx x x 229解 令t x sec 3=，则tdt t dx tan sec 3⋅= 于是⎰-dx x x 229⎰⎰=⋅=dt tttdt t t t sec tan tan sec 3sec 9tan 322.9|9|ln 9|393|ln sin |tan sec |ln )cos (sec 221221C xx x x C xx x xC t t t dt t t +---++---+=+-+=-=⎰练习 求⎰-+221)1(xxxdx2． 倒代换（即令tx1=） 设n m ,分别为被积函数的分子、分母关于x 的最高次数，当1>-m n 时，可以考虑使用倒代换。

求⎰>+)0(222a xa xdx解 令tx 1=，则dt t dx 21-=，于是原式⎰⎰⎰++-=+-=⎪⎭⎫⎝⎛-⋅⎪⎭⎫ ⎝⎛+=12)1(1111122222222222t a t a d a t a tdt dt t t a tC xa a x C a t a ++-=++-=2222221 练习⎰-+dx x xx 11223． 指数代换（适用于被积函数)(x f 由x a 所构成的代数式）令t ax=，.ln 1tdt a dx ⋅=求⎰++xx x dx 4212解 令t x=2，t dt dx ⋅=2ln 1 原式⎰⎰++=⋅⋅++=43)21(2ln 12ln 1122t dtt dt t t t CC t C t t t d x ++=++=++⋅=⎪⎪⎭⎫⎝⎛+++=+⎰312arctan 2ln 32312arctan 2ln 322321arctan 322ln 123)21()21(2ln 1122练习 求⎰+++6321x x xee e dxX.2 有理函数的积分一、有理函数的积分形为mm m m nn n n b x b x b x b a x a x a x a x Q x P ++++++++=----11101110)()( ， （1）其中m 和n 都是非负整数；n a a a a ,,,,210 及m b b b b ,,,,210 都是实数，并且0,000≠≠b a 。

不定积分例题及答案求下列不定积分：知识点：直接积分法的练习——求不定积分的基本方法。

思路分析：利用不定积分的运算性质和基本积分公式，直接求出不定积分！ ★(1)2xx思路: 被积函数522xx x-，由积分表中的公式（2）可解。

解：5322223x dx x Cxx--=-+⎰ ★(2)3(x dxx⎰思路:根据不定积分的线性性质，将被积函数分为两项，分别积分。

解：1141113332223()()24dx x x dx x dx x dx x x C x--=-=-=-+⎰⎰⎰⎰3x ★(3)22x x dx +⎰（）思路:根据不定积分的线性性质，将被积函数分为两项，分别积分。

解：2232122ln 23x x x x dx dx x dx x C +=+=++⎰⎰⎰（）★(4)(3)x x dx -思路:根据不定积分的线性性质，将被积函数分为两项，分别积分。

解：315322222(3)325x dx x dx x dx x x C -=-=-+⎰⎰x ★★(5)4223311x x dxx +++⎰思路:观察到422223311311x x x x x ++=+++后，根据不定积分的线性性质，将被积函数分项，分别积分。

解：42232233113arctan 11x x dx x dx dx x x Cx x ++=+=++++⎰⎰⎰ ★★(6)221x dx x +⎰思路:注意到222221111111x x x x x +-==-+++，根据不定积分的线性性质，将被积函数分项，分别积分。

解：2221arctan .11x dx dx dx x x C x x =-=-+++⎰⎰⎰注：容易看出(5)(6)两题的解题思路是一致的。

一般地，如果被积函数为一个有理的假分式，通常先将其分解为一个整式加上或减去一个真分式的形式，再分项积分。

★(7)x dx x x x ⎰34134（-+-）2思路:分项积分。

不定积分练习题4月10日不定积分练习题基础题 一．填空题 1.不定积分：⎰=_____xxdx22.不定积分：dx x ⎰-2)2(=______ 3.不定积分： dx x x x)11(2⎰-=_______ 4.不定积分：dx x ⎰-2)2(=__________ 5.不定积分：dx xe x )32(⎰+=_______ 二．选择题 1、，则设x d x1I 4⎰=I =（ ）c x3 1)D ( c x 3 1)C ( cx 3 1)B ( c x 4)A (3335++-+-+--- 2、的一个原函数为则，设 )x (fx 1 1)x (f 2-=( ) ()arcsin ()arctan A x B x x 1 x 1ln 2 1)C (+- x1x 1 ln 2 1)D (-+ 3、函数x 2 cos π的一个原函数为 （ ）(A) x 2 sin 2 ππ (B) x 2 sin 2 ππ- （C ）x 2 sin 2ππ (D) x2 sin 2ππ-4、设f(x) 的一个原函数为F(x)， 则⎰=dx )x 2(f （ ）(A) F(2x)+ C (B) F(2 x)+ C (C)C )x 2(F 2 1+ (D) 2F(2 x )+ C5.设3()ln sin 44f x dx x C =+⎰，则()f x =（ ）。

A . cot 4xB . cot 4x -C . 3cos4xD . 3cot 4x6. 若()f x 为可导、可积函数，则（ ）。

A . ()()f x dx f x '⎡⎤=⎣⎦⎰ B . ()()d f x dx f x ⎡⎤=⎣⎦⎰C .()()f x dx f x '=⎰D .()()df x f x =⎰7. 设CF(x) dx )x (f +=⎰ ，则=⎰ dx )cosx ( f sinx （ ）(A)C )sinx ( F + (B) C )sinx ( F +- (C) C )cosx ( F +- (D) sin x ( cosx ) C F +8.设()Fx 是()f x 在(),-∞+∞上的一个原函数,且()F x 为奇函数,则()f x 是 ( )A ．偶函数B ． 奇函数C ． 非奇非偶函数D ．不能确定 9.已知()f x 的一个原函数为cos x ,()g x 的一个原函数为2x ,则()f g x ⎡⎤⎣⎦的一个原函数为 ( )A ．2x B ． 2cosx C ． 2cos x D ．cos x10.设2xe-是()f x 的一个原函数,则()02()limx f x x f x x∆→-∆-=∆ ( )A ．22xe - B ．-28xe- C ．22xe -- D ．24xe-11. 21(),()1fx f x x =-设则的一个原函数为()arcsin ()arctan 1111()ln ()ln 2121A x B x x x C D x x -+⎛⎫⎛⎫ ⎪ ⎪+-⎝⎭⎝⎭ 4月15日不定积分练习题基础题 一．填空题1.=⎰x d x tan 2__________．2.x d 1x1x 3x 3 224⎰+++＝ ． 3.⎰+)x 1 ( x dx2= ______________________________． 4.dx e 1 1x ⎰-+= 5.=⎰dx x 2cos x12 ．6.设 )x (f 的一个原函数 xx sin 为，则 =⎰dx )x (f ．7.设 )x (f 的一个原函数为 ln x ， 则⎰+dx )x 21(f ______________．8.设)x (f 的一个原函数为 lnx , 则=')x (f _______________．9.，的一个原函数为若x ln x )x (f =)x (f 则______ _______．二．选择题1. =+-=⎰I x d 1e1e I xx ，则设（ ） c )1e ( ln )B ( c )1e ( ln )A (x x +++- c x )1e ( ln 2)C (x +-+ c )1e ( ln x 3x )D (x ++-　2. 设f(x)的一个原函数是F(x) ，则⎰+dx )b ax (f ＝（ ）(A) F(ax ＋b)＋c (B) aF(ax+b)+c (C)b ax )b ax (F +++c (D)a 1F(ax+b)+c3. =-+=⎰⎰dx )x 1 ( f x c x sin dx )x (f 2，则若（ ）(A)c )x 1 ( sin 22+- (B)c )x 1 ( sin 22+--(C)c )x 1 ( sin 2 12+- (D) c )x 1 ( sin2 12+-- 4.不定积分：21( 1 ) cos d sinx x x +=⎰ （ ）(A) C x sin 1x +-(B) Cx sin 1x ++ (C) C x sin 1x sin +-(D) Cx sin 1x sin ++ 5. 不定积分：⎰=x x de e sin （ ）(A) C e cos x+ (B) C e cos x+- (C) C e arccos x+ (D) C e arccos x+-6. 不定积分：⎰+e 1 dxx＝（ ） (A)c e 1 ln x++）（ (B) c e 1 ln x++-）（ (C) c e 1 e ln x x ++ (D) ce 1 1ln x++ 7. 设x 2 tan k )x (f = 的一个原函数是) x 2 cos ( ln32 ，则常数 =k （ ） (A)3 2- (B) 3 2 (C) 34 - (D) 3 4综合题 1.⎰++dx )1x 2sin( )1x 2(cos 2求．2.求不定积分 4 (1) xdx x +⎰．3.求不定积分dx)x 1( x3⎰-．4月18日不定积分练习题基础题： 1. 2x xe dx -=⎰( ).(a) xe c -+, (b)212x e c -+, (c)212x e c --+, (d) 2x e c --+.2. 2x e dx ⎰=( )(a) 2x e c +, (b) 212x e c +, (c) 2x e , (d) 212x e .3. 221(2)dx x =+⎰( ) (a) arctan 2x c +, (b) arctan 2x , (c) arcsin 2x , (d) arcsin 2x c +. 4. 22sec 2xdx =⎰( )(a)tan 2x c +, (b) tan 2x , (c) tan x , (d) tan x c +. 5.(1)n x dx +=⎰ . 6. cos(34)x dx +=⎰ . 7.=⎰.8. x e dx -=⎰ . 9.1sin2xdx ⎰= .10.(2)x x dx -=⎰ . 11.2= .12.12dx x =-⎰ .4月19日不定积分练习题基础题：1. 设()x f x e -=,则()ln f x dx x'⎰=( )A ． 1x -c + B ． ln x c -+ C ． 1c x+ D ． ln x c + 2. 若()f x 的一个原函数为2ln x ,则()x f x dx '=⎰( )A ．2ln ln x x c -+B ．22ln ln x x c ++C ．22ln ln x x c -+D ．2ln ln x x c ++ 3. 设()()ln 1ln f x x x '=+,则()f x =( )A ．22xx xe c ++ B ．()212xx x e c -++ C ．22xx xe c -+ D ．()212xx x e c --+ 4. 2cos xdx x=⎰( ) A ． tan ln cos x x x c -+ B ． tan ln cos x x x c ++ C ． tan ln sin x x x c -+ D ． tan ln sin x x x c ++ 5. ()2211dx x x=+⎰ ( )A ．1arctan x c x ++ B ． 1arctan x c x -+ C ． 1arctan x c x --+ D ．1arctan x c x -++6.,I I ==设则( )()arcsin;()arcsin n ()arcsin ;()arcsin x x A a c B a c a ax xC a cD ca a -- 7. ,I I ==设则( )22()(arctan ;();(().A cB cC cD c -++-8. ,x xdxI I e e-==+⎰设则( ) ()()arctan ;()arctan ;()x x x xxxA e e cB e cC e cD e e c ----+++++9.10(23),I x dx I =-=⎰设则( )991111()10(23);()20(23);11()(23);()(23).2211A x c B x c C x c D x c -+-+-+-+ 10.I I ==设则( )()2ln(1.(2ln(1.(2ln(1.()2ln(1.A c B c C c D c -+++-+ 11.1d ,1x xe I x I e -==+⎰设则( ) ()ln(1)()ln(1);()2ln(1);()2ln(1).x x xxA e cB e cC e x cD x e c -++++-+-++12. sin cos d ,I x x x I ==⎰设则( )2211()sin ;()cos ;2211()cos 2;()cos 244A x cB x cC x cD x c-+++-+ 13.求下列不定积分：dx x ⎰-3)23(⎰-dx x32dx3⎰)ln(ln ln x x x dx⎰x x dx sin cos ⎰-+x x e e dxdx x x )cos(2⎰dx x x ⎰-4313dx x x⎰3cos sindx xx ⎰--2491⎰-122x dxdx x ⎰3cos⎰xdx x 3cos 2sin⎰xdx x sec tan3dx x x⎰+239dx x x ⎰+22sin 4cos 31dx xx ⎰-2arccos 2110dx x x x ⎰+)1(arctandx xx ⎰+211dx x ⎰sin⎰+32)1(x dx⎰+x21dxinxdx xs ⎰⎰xdx xln 2dx x e x⎰-2sin 2 ⎰xdx arctan x 2⎰xdx xcos 2⎰xdx 2lndx xx 2cos 22⎰ ⎰-++dx x x x 103322 ⎰+)1(2x x dx⎰+dx xx211arctandx x ⎰-2sin 1 dx xa xx⎰-2 ⎰+dx x xe x 232arctan )1(⎰+xx dxsin 2)2sin(⎰-dx e xe xx 1dx e e xx⎰2arctandx xx xx ⎰+cos sin cos sin14. 设)(x f 的一个原函数为xxsin ，求⎰'dx x f x )(。

不定积分1、定义 原函数如果 ( )'= f (x ) ，则 ( )是 f (x ) 的一个原函数。

不定积分 ⎰f (x )dx = f (x ) 的所有原函数= f (x ) 的一个原函数+C 。

注： ⎰F '(x )dx = F (x )+ c ， ⎰dF (x )= F (x )+ c(⎰ f (x )dx )' = f (x )， d (⎰ f (x )dx )= f (x )dx例 1、设 f ( x ) 的一个原函数为 xe x ，则 f '( x ) = ( )．A ． e x ( x +1)B ． e x ( x + 2)C ． e x ( x -1)D ． e x ( x - 2)例 2、设 f ( x ) 的一个原函数为 xe x ，则 ⎰f '( x ) dx =则 ⎰ f (2 x - 1)dx =2、基本公式 1、 ⎰kdx = kx + c (k 为常数)2、 ⎰x a dx = 1 x a +1 + c (a ≠ -1)a + 13、 ⎰ 1 dx = ln x + cx⎰e x dx = e x+ c4、⎰a x dx = 1 a x + cln a⎰ 1 dx = ln x + a + cx + a⎰ 1 dx = arctan x + c 5、 1+ x 2⎰ 1 1 xdx =+ ca 2 + x 2 a⎰ 1 1dx =+ cx 2 - a 2 2amx + n m (2x + b ) n - mb主要解决 ⎰ dx = ⎰( 2 + 2)dx x 2 2 + bx 2+ bx + c+ bx + c x + c x⎰ = arcsin x + c1 - x⎰ 1 x= arcsin + ca a 2 - x 26、⎰= ln x + a 2 + x 2 ca + x⎰= ln x + x 2 - a 2+ cx 2 - a 2m (2ax + b ) n - mb主要解决 ⎰ dx = ⎰( 2a + 2a )dx ax ax + bx + c ax + bx + c + bx + c⎰ s in xdx = - cos x + c ⎰ cos xdx = sin x + c⎰ s ec xdx = ⎰ cos 1 x dx = ln sec x + tan x + c ⎰ csc xdx = ⎰ sin 1 x dx = ln csc x - cot x + c= - ln csc x + cot x + c⎰ sec 2 xdx = ⎰1dx = tan x + c cos 2x⎰ csc 2 xdx = ⎰ sin 1 x dx = - cot x + c⎰ tan xdx = - ln cos x + c ⎰ cot xdx = ln sin x + c ⎰ s ec x tan xdx = sec x + c⎰ csc x cot xdx = - csc x + c3、基本方法1、 凑 (解决复合函数问题)⎰ f ( ) dx = ? ⎰ f ( )( )'dx = ? ⎰ f ( ) d ( )如果被积函数含有复合函数 f (ϕ( x )) ，想办法在被积函数中凑出 ϕ'( x ) ，形成⎰ f (ϕ ( x ))ϕ '( x ) dx = ⎰ f (ϕ ( x )) d ϕ( x )例如：⎰ (3 + 2 x ) 2 dx = 1 ⎰ (3 + 2 x ) 2 ⋅ 2 dx = 1 ⎰ (3 + 2 x ) 2 ⋅ (3 + 2 x ) 'dx = 1 ⎰ (3 + 2 x ) 2 d (3 + 2 x )2 2 2⎰ ln x dx = ⎰ ln x (ln x )'dx = ⎰ln xd (ln x )x⎰ xe x 2dx = 1 ⎰ e x 2( x 2 )'dx = 1 ⎰ e x 2dx 222⎰ 2 x + 3dx = ⎰ ( x 2 + 3 x - 4) -1 ( x 2 + 3 x - 4)' dx = ⎰( x 2 + 3 x - 4) -1 d ( x 2 + 3 x - 4)x 2 + 3 x - 42 x +3 1⎰= ⎰( x 2 + 3 x - 4) -d ( x 2+ 3 x - 4)2x 2 4+ 3 x -例： 计算不定积分 ⎰cos (ln x ) + 2 x 21+ x 2dxx解： ⎰ cos (ln x ) + 2 x 21+ x 2dx = ⎰ cos (ln x ) d ln x + ⎰d (1 + x 2 )1 + x 2x23= sin(ln x ) + (1 + x 2 ) + C23计算不定积分 ⎰1 dx ．x (2 + 3ln x )解：．原式 = 1 ⎰1 (2 + 3ln x )'dx = 1 ⎰1 d (2 + 3ln x )2 23 + 3ln x 3 + 3ln x= 1 ⎰ 1 d (2 + 3ln x ) = 1 ln 2 + 3ln x + C3 2 + 3ln x 32、 换 解决根号= t ；被积函数中含有 ax + b ，令ax + b ，令 x = a sin t , (- π ≤ t ≤ π )2 222a 2 - x 2 = a cos t d x = a cos tdt，令 x = a tan t , (-π< t < π )2222a 2 + x 2 = a sec t dx = a sec 2 tdtx 2 - a 2 , 令 x = a sec tπ)当 x ∈ ( a , +∞) x 2 - a 2= a tan t dx = a sec t tan tdt t ∈(0,2π当 x ∈ ( -∞, - a) x 2 - a 2= - a tan t dx = a sec t tan tdt t ∈( , π )2 倒代换，令 x = 1 dx = - 1 dt 化去被积函数是分式时分母中含有的 x n 项。