第十一章 自适应均衡

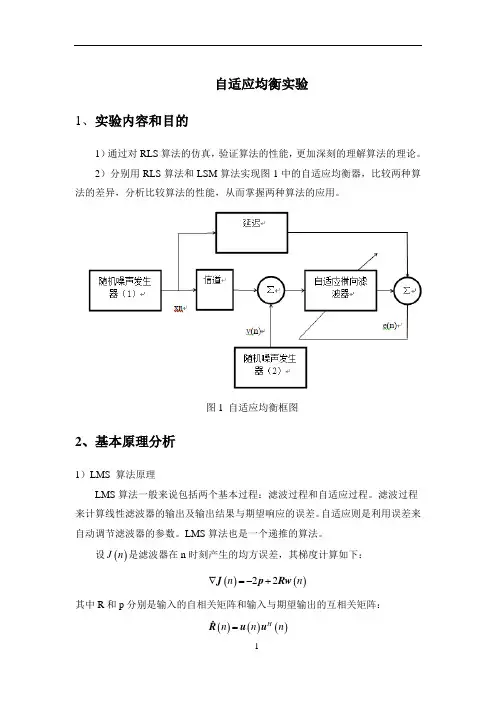
自适应均衡实验1、实验内容和目的1）通过对RLS 算法的仿真，验证算法的性能，更加深刻的理解算法的理论。

2）分别用RLS 算法和LSM 算法实现图1中的自适应均衡器，比较两种算法的差异，分析比较算法的性能，从而掌握两种算法的应用。

图1 自适应均衡框图2、基本原理分析1）LMS 算法原理LMS 算法一般来说包括两个基本过程：滤波过程和自适应过程。

滤波过程来计算线性滤波器的输出及输出结果与期望响应的误差。

自适应则是利用误差来自动调节滤波器的参数。

LMS 算法也是一个递推的算法。

设()J n 是滤波器在n 时刻产生的均方误差，其梯度计算如下：()()22n n ∇=-+J p Rw其中R 和p 分别是输入的自相关矩阵和输入与期望输出的互相关矩阵：()()()ˆH n n n =Ru u()()()*ˆn n n =pu d 则梯度向量的瞬态估计为：()()()()()()*ˆˆ22H n n n n n n ∇=-+J u d u u w 由最速下降算法可以得到抽头向量更新的递推关系式：()()()()()()*ˆˆˆ1Hn n n n n n μ⎡⎤+=+-⎣⎦w w u d u w整个LMS 算法归纳总结如下： 参数设置：M=抽头数（滤波器长度） μ=步长参数 m a x20MS μ<<其中max S 是抽头输入功率谱密度的最大值，而滤波器长度M 为中到大 初始化：如果知道抽头权向量()n w 的先验知识，则用它来选择()ˆ0w 的合适值，否则令()ˆ00=w。

更新滤波过程：()()()ˆH y n n n =wu ()()()e n d n y n =- ()()()()*ˆˆ1n n n e n μ+=+ww u 2）RLS 算法原理RLS 算法是一个递归的过程，递归最小二乘问题的正则方程可用矩阵写为()()()ˆn n n =Φwz 其中n 是可测数据的可变长度，()n Φ更新抽头输入的自相关矩阵，()n z 是抽头输入与期望响应之间的互相关向量，()ˆn w 是抽头的权值向量。

§3-2 自适应均衡技术(Adaptive Equalization Techniques)Review ：分集有哪两层含义？合并的方式有哪几种？各自的基本思想是什么？分集是如何分类的？一、均衡基础（Fundamentals of Equalization ）====》 如何补偿信道的多径衰落？均衡本质：产生与信道相反的特性，用来抵消信道的时变多径传播特性引起的码间串扰。

均衡不用增加传输功率和带宽，即可改善移动通信链路的传输质量。

均衡重在消除码间串扰，而分集重在消除深度衰落的影响。

均衡适用于信号不可分离多径且时延扩展远大于符号宽度的情况。

均衡有两个基本途径：1、频域均衡，它使包括均衡器在内的整个系统的总传输函数满足无失真传输的条件(即H(w)=1)。

它往往是分别校正幅频特性和群时延特性，模拟通信（序列均衡）通常采用这种频域均衡法。

2、时域均衡，就是直接从时间响应考虑，使包括均衡器在内的整个系统的冲激响应满足无码间串扰的条件(即h(t)=)(t δ)。

数字移动通信面临的信号是时变信号，因此通常采用这种时域均衡法，来达到整个系统无码间串扰。

随着码率的提高，时域均衡愈来愈复杂，研究热点逐步转入频域均衡。

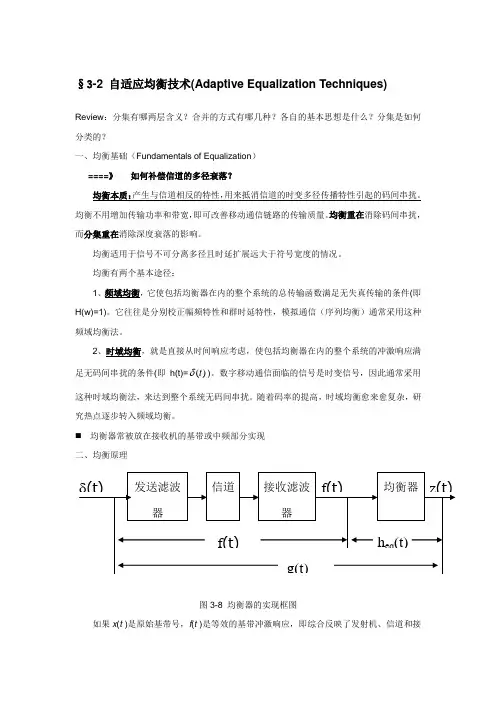
均衡器常被放在接收机的基带或中频部分实现二、均衡原理图3-8 均衡器的实现框图如果x (t )是原始基带号，f (t )是等效的基带冲激响应，即综合反映了发射机、信道和接收机的射频、中频部分的总的传输特性，g (t )是发射机、信道、接收机的射频、中频部分和均衡器四者的等效冲激响应。

均衡器的期望输出值为原始信息x (t )。

假定n b (t )= 0，则g (t )必须满足下式：)()()()(t t h t f t g eq δ=⊗=-------（3-8）其频域表达式如下：1)()(=f F f H eq -------（3-9）式（3-9）的物理意义：将经过信道后的信号中频率衰落大的频谱部分进行增强，衰落小的部分进行削弱，以使所收到频谱的各部分衰落趋于平坦，相位趋于线性。

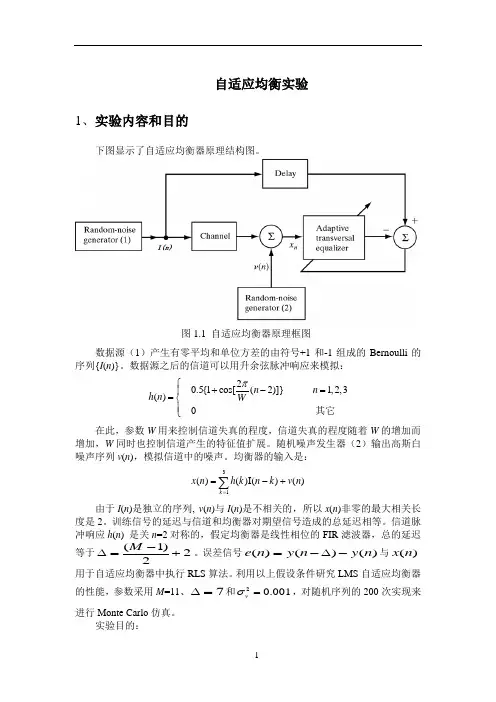
自适应均衡实验1、实验内容和目的下图显示了自适应均衡器原理结构图。

数据源（1）产生有零平均和单位方差的由符号+1和-1组成的Bernoulli 的序列{I (n )}。

数据源之后的信道可以用升余弦脉冲响应来模拟：20.5{1cos[(2)]}1,2,3()0n n h n Wπ⎧+-=⎪=⎨⎪⎩其它在此，参数W 用来控制信道失真的程度，信道失真的程度随着W 的增加而增加，W 同时也控制信道产生的特征值扩展。

随机噪声发生器（2）输出高斯白噪声序列v (n )，模拟信道中的噪声。

均衡器的输入是：31()()I()()k x n h k n k v n ==-+∑由于I (n )是独立的序列, v (n )与I (n )是不相关的，所以x (n )非零的最大相关长度是2。

训练信号的延迟与信道和均衡器对期望信号造成的总延迟相等。

信道脉冲响应h (n ) 是关n =2对称的，假定均衡器是线性相位的FIR 滤波器，总的延迟等于(1)22M -∆=+。

误差信号()()()e n y n y n =-∆-与()x n 用于自适应均衡器中执行RLS 算法。

利用以上假设条件研究LMS 自适应均衡器的性能，参数采用M =11、7∆=和20.001vσ=，对随机序列的200次实现来进行Monte Carlo 仿真。

实验目的：图1.1 自适应均衡器原理框图● 掌握RLS 算法原理及处理流程，分析对比不同信道参数与算法参数对RLS 性能的影响。

● 分析对比RLS 算法与LMS 算法的性能。

2、基本原理分析2.1 最小均方（LMS ）算法LMS 算法是一种以期望响应和滤波器输出信号之间误差的均方值最小为准则的,依据输入信号在迭代过程中估计梯度矢量，并更新权系数以达到最优的自适应迭代算法，其显著特点和优点是它的简单性。

这种算法不需要计算相应的相关矩阵，也不需要进行矩阵运算。

LMS 算法是一种线性自适应滤波算法，是最简单的均衡算法。

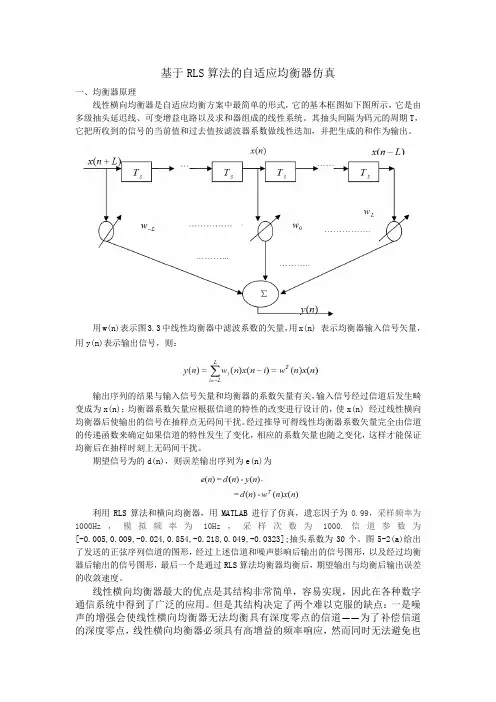
基于RLS算法的自适应均衡器仿真一、均衡器原理线性横向均衡器是自适应均衡方案中最简单的形式，它的基本框图如下图所示，它是由多级抽头延迟线、可变增益电路以及求和器组成的线性系统。

其抽头间隔为码元的周期T，它把所收到的信号的当前值和过去值按滤波器系数做线性迭加，并把生成的和作为输出。

用w(n)表示图3.3中线性均衡器中滤波系数的矢量，用x(n) 表示均衡器输入信号矢量，用y(n)表示输出信号，则：输出序列的结果与输入信号矢量和均衡器的系数矢量有关，输入信号经过信道后发生畸变成为x(n)；均衡器系数矢量应根据信道的特性的改变进行设计的，使x(n) 经过线性横向均衡器后使输出的信号在抽样点无码间干扰。

经过推导可得线性均衡器系数矢量完全由信道的传递函数来确定如果信道的特性发生了变化，相应的系数矢量也随之变化，这样才能保证均衡后在抽样时刻上无码间干扰。

期望信号为的d(n)，则误差输出序列为e(n)为利用RLS算法和横向均衡器，用MATLAB进行了仿真，遗忘因子为0.99，采样频率为1000Hz，模拟频率为10Hz，采样次数为1000.信道参数为[-0.005,0.009,-0.024,0.854,-0.218,0.049,-0.0323];抽头系数为30个。

图5-2(a)给出了发送的正弦序列信道的图形，经过上述信道和噪声影响后输出的信号图形，以及经过均衡器后输出的信号图形，最后一个是通过RLS算法均衡器均衡后，期望输出与均衡后输出误差的收敛速度。

线性横向均衡器最大的优点是其结构非常简单，容易实现，因此在各种数字通信系统中得到了广泛的应用。

但是其结构决定了两个难以克服的缺点：一是噪声的增强会使线性横向均衡器无法均衡具有深度零点的信道——为了补偿信道的深度零点，线性横向均衡器必须具有高增益的频率响应，然而同时无法避免也会放大噪声；二是线性均衡器与接收信号的幅度信息关系密切，而幅度会随着多径衰落信道中相邻码元的改变而改变，因此滤波器抽头系数的调整不是独立的。

自适应均衡
在自适应均衡算法中，有两种常用的方法：最小均方（Least Mean Square，LMS）和递归最小二乘（Recursive Least Squares，RLS）。

这两种方法都是迭代式的算法，通过不断调整权值来逼近信号的均衡状态。

LMS算法是基于梯度下降法的一种算法，它通过不断调整权值来减小均方误差。

算法的核心思想是通过对误差信号和输入信号的相关性进行估计，来更新权值。

LMS算法简单易于实现，但收敛速度较慢，准确性也相对较低。

相比之下，RLS算法是一种基于递归估计的算法，它使用信号的统计特性来进行加权最小二乘估计。

相对于LMS算法，RLS算法在准确性和收敛速度方面具有更好的性能。

但RLS算法由于计算复杂度较高，适用范围相对较窄。

无论是LMS算法还是RLS算法，在实际应用中都需要根据具体的场景和要求进行参数的调整和优化。

例如，可以通过改变步长参数、阻尼因子等来改进算法的性能。

此外，还可以利用自适应均衡算法的特点来进行前向和反馈滤波，实现音频信号的去噪、回声消除等应用。

总的来说，自适应均衡算法是一种强大的信号处理技术，可以用于消除信号中的失真和噪声。

通过选择合适的算法和参数，可以有效提高信号质量，并满足不同场景下的需求。

随着计算力的提升和新的算法的研发，自适应均衡技术也将在更广泛的领域中得到应用。

自适应均衡算法LMS 研究一、自适应滤波原理与应用所谓自适应滤波器，就是利用前一时刻已获得的滤波器参数等结果，自动地调节现时刻的滤波器参数，以适应信号和噪声未知的或随时间变化的统计特性，从而实现最优滤波。

根据环境的改变，使用自适应算法来改变滤波器的参数和结构。

1.1 均衡器的发展及概况均衡是减少码间串扰的有效措施。

均衡器的发展有史已久，二十世纪60 年代前，电话信道均衡器的出现克服了数据传输过程中的码间串扰带来的失真影响。

但是均衡器要么是固定的，要么其参数的调整是手工进行。

1965年，Lucky在均衡问题上提出了迫零准则，自动调整横向滤波器的权系数。

1969年，Gerhso和Porkasi，Milier分别独立的提出采用均方误差准则(MSE)°1972年，ungeboekc将LMS算法应用于自适应均衡。

1974年，Gedard 在kalmna滤波理论上推导出递推最小均方算法RLS(Recursive least-squares) 。

LMS类算法和RLS类算法是自适应滤波算法的两个大类。

自适应滤波在信道均衡、回波抵消、谱线增强、噪声抑制、天线自适应旁瓣抑制、雷达杂波抵消、相参检测、谱估计、窄带干扰抑制、系统辨识、系统建模、语音信号处理、生物医学、电子学等方面获得广泛的应用。

1.2 均衡器种类均衡技术可分为两类：线性均衡和非线性均衡。

这两类的差别主要在于自适应均衡器的输出被用于反馈控制的方法。

如果判决输出没有被用于均衡器的反馈逻辑中，那么均衡器是线性的；如果判决输出被用于反馈逻辑中并帮助改变了均衡器的后续输出，那么均衡器是非线性的。

LMS梯度RLS LMS 梯度RLS LMSRLS 快速RLS 平方根RLSRLS 快速RLS 平方根RLSRLS 快速RLS 平方根RLS算法图1.1均衡器的分类1.3自适应算法LMS算法LMS算法是由widrow和Hoff于I960年提出来的,是统计梯度算法类的很重要的成员之一。