计算题总复习题概论
- 格式:doc
- 大小:578.50 KB
- 文档页数:8

《计算概论》期中考试复习题一、选择题1.冯·诺伊曼计算机工作原理的设计思想是 B 。
A. 程序设计B. 存储程序C. 算法设计D. 程序编制2.衡量存储器容量大小的基本单位是 A 。
A. bitB. ByteC. KBD. MB3.光盘中的信息必须首先调入 A 后才能被CPU使用。
A. RAMB. BIOSC. CMOSD. Hard Disc 4.以下不是应用层协议的是 B 。
A. HTTPB. TCPC. SMTPD. FTP5.下列关于图像的说法中错误的是 C 。
A. 位图是由一些排成行列的像素组成的B. 矢量图主要存储绘制图形的数学描述C. MPEG是关于静态图像的压缩编码标准D. 矢量图的放大或缩小都不会损失图形的信息。
6.让计算机完成某种功能的指令序列称为 B 。
A. 文档B. 程序C. 语言D. 系统7.我们平常使用的电脑显示器所使用的颜色模型是 C 。
A. YUVB. CMYC. RGBD. VGA 8.下图所示的插头可以连接到PC机主板上的 C 接口。
A. COMB. RJ-45C. USBD. PS/29.对处于还原状态的Windows应用程序窗口,不能实现的操作是 D 。
A. 最小化B. 最大化C. 移动D. 旋转10.下面属于音频格式文件的是 B 。
A. JPG格式B. MP3格式C. A VI格式D. GIF格式11.将两个局域网进行互联的设备是 A 。
A. 路由器B. 网卡C. 集线器D. 调制解调器12.闪存属于 B 类型存储器。
A. RAMB. ROMC. DDRD. CD13.下列网络传输层协议中,适合进行视频、影像等实时信息类型传输的是 B 。
A. TCPB. RTPC. IPD. UDP14.计算机系统中,___B_____是计算机资源的管理者。
A. 硬件系统B. 操作系统C. 应用软件D. 驱动程序15.多任务操作系统通过___C_____实现程序并发执行。
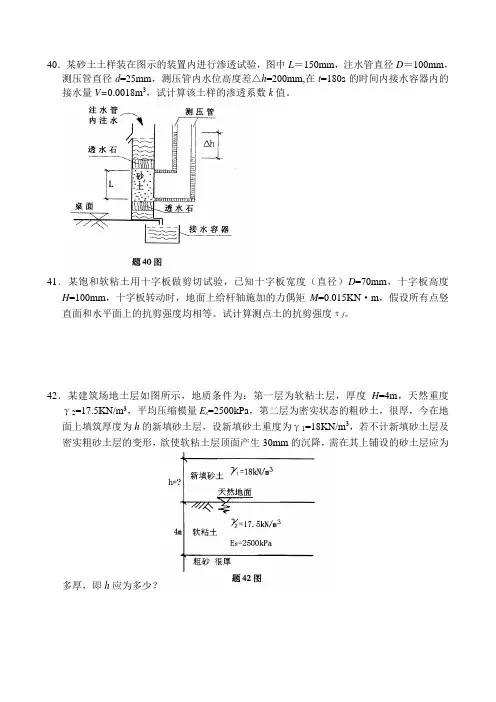
40.某砂土土样装在图示的装置内进行渗透试验,图中L=150mm,注水管直径D=100mm,测压管直径d=25mm,测压管内水位高度差△h=200mm,在t=180s的时间内接水容器内的接水量V=0.0018m3,试计算该土样的渗透系数k值。
41.某饱和软粘土用十字板做剪切试验,已知十字板宽度(直径)D=70mm,十字板高度H=100mm,十字板转动时,地面上给杆轴施加的力偶矩M=0.015KN·m,假设所有点竖直面和水平面上的抗剪强度均相等。
试计算测点土的抗剪强度τf。
42.某建筑场地土层如图所示,地质条件为:第一层为软粘土层,厚度H=4m,天然重度γ2=17.5KN/m3,平均压缩模量E s=2500kPa,第二层为密实状态的粗砂土,很厚,今在地面上填筑厚度为h的新填砂土层,设新填砂土重度为γ1=18KN/m3,若不计新填砂土层及密实粗砂土层的变形,欲使软粘土层顶面产生30mm的沉降,需在其上铺设的砂土层应为多厚,即h应为多少?43.如图所示的条形基础,宽度b=2.5m,持力层的地基承载力标准值f k=195kPa,其它指标见图。
计算现有基底尺寸和埋深条件下的地基承载力设计值f。
44.在某地基中取土样进行直接剪切试验,测得破坏时剪切破坏面上的应力如下表所列,试根据测试结果确定土的抗剪强度指标;若该地基中某点的小主应力σ=100kPa,试问当该3点的大主应力σ=200kPa时该点是否剪切破坏。
1法向应力σ(kPa)50.000 100.000 200.000 300.000剪应力τ(kPa)22.466 34.933 59.866 84.79845.如图所示挡土墙,墙高H=6m,墙背光滑、垂直、填土面水平,填土由两层土组成,第一层为粗砂,第二层为粘土,各层土的物理力学指标见图,试绘出主动土压力沿墙高的分布图,并求出主动土压力E a的值。
40.某砂土的内摩擦角︒=ϕ34,当土中某点的大主应力1σ=330kPa ,小主应力3σ=100kPa 时,试判断该点的应力状态是否达到极限平衡。
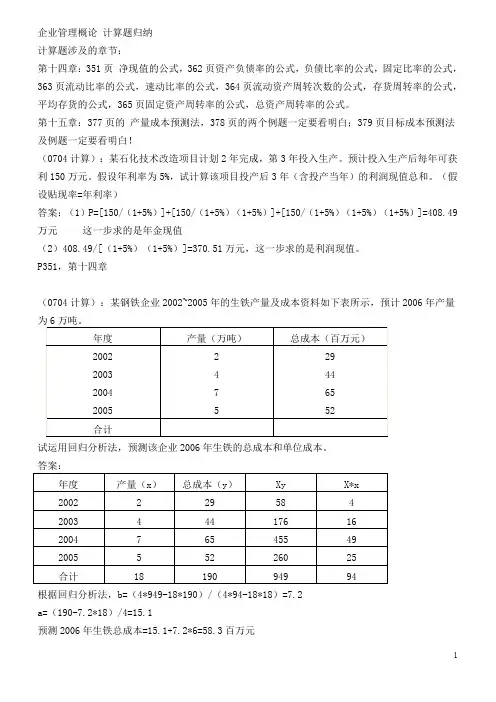
企业管理概论计算题归纳计算题涉及的章节:第十四章:351页净现值的公式,362页资产负债率的公式,负债比率的公式,固定比率的公式,363页流动比率的公式,速动比率的公式,364页流动资产周转次数的公式,存货周转率的公式,平均存货的公式,365页固定资产周转率的公式,总资产周转率的公式。
第十五章:377页的产量成本预测法,378页的两个例题一定要看明白;379页目标成本预测法及例题一定要看明白!(0704计算):某石化技术改造项目计划2年完成,第3年投入生产。
预计投入生产后每年可获利150万元。
假设年利率为5%,试计算该项目投产后3年(含投产当年)的利润现值总和。
(假设贴现率=年利率)答案:(1)P=[150/(1+5%)]+[150/(1+5%)(1+5%)]+[150/(1+5%)(1+5%)(1+5%)]=408.49万元这一步求的是年金现值(2)408.49/[(1+5%)(1+5%)]=370.51万元,这一步求的是利润现值。
P351,第十四章(0704计算):某钢铁企业2002~2005年的生铁产量及成本资料如下表所示,预计2006年产量试运用回归分析法,预测该企业2006年生铁的总成本和单位成本。
根据回归分析法,b=(4*949-18*190)/(4*94-18*18)=7.2a=(190-7.2*18)/4=15.1预测2006年生铁总成本=15.1+7.2*6=58.3百万元预测2006年生铁单位成本=58.3/6=9.72百万元 P379,第十五章(0607计算):某机械制造企业生产A、B两种系列的产品,根据其2006年第三季度15000台A系列产品A1、A2、A3的生产任务,通过计算下表中的X、Y和Z,对该企业下述各月的主生产计划进行补充和完善。
解析:从表中可以看出,一共三个月,每个月分四周进行生产,7、8、9三个月的月计划生产量分别是4000、5000、6000,而每个月中各周各产品的计划量也是已知的,故用本月计划产量减去已知的本月其他周的生产量即是未知数。

计量经济学复习资料——概论⼀元和多元线性回归习题概论、⼀元线性回归、多元线性回归习题⼀、单项选择题1. 总体回归线是指( ) A )样本观测值拟合的最好的曲线 B )使残差平⽅和最⼩的曲线C )解释变量X 取给定值时,被解释变量Y 的样本均值的轨迹D )解释变量X 取给定值时,被解释变量Y 的条件均值或期望值的轨迹2. 指出下列哪⼀变量关系是确定函数关系⽽不是相关关系? () A. 商品销售额与销售价格 B. 学习成绩总分与各门课程成绩分数 C. 物价⽔平与商品需求量 D. ⼩麦亩产量与施肥量3. 经济计量分析⼯作的基本⼯作步骤是-() A .设定理论模型→收集样本资料→估计模型参数→检验模型B .设定模型→估计参数→检验模型→应⽤模型C .理论分析→数据收集→计算模拟→修正模型D .确定模型导向→确定变量及⽅程式→应⽤模型4. 若⼀元线性回归模型Y=β1+β2X +u 满⾜经典假定,那么参数β1、β2的普通最⼩⼆乘估计量β^1、β^2是所有线性估计量中( )A )⽆偏且⽅差最⼤的B )⽆偏且⽅差最⼩的C )有偏且⽅差最⼤的D )有偏且⽅差最⼩的5. 在⼀元线性回归模型Y=β1+β2X +u 中,若回归系数β2通过了t 检验,则表⽰( ) A )β^2≠0 B )β2≠0 C )β2=0 D )β^=06. 在多元线性回归模型Y=β1+β2X 2+β3X 3 +β4X 4+u 中,对回归系数βj (j=2,3,4)进⾏显著性检验时,t 统计量为( )A )()jjSe ββ?? B )()j j Se ββ C )()j j Var ββ D )()j j Var ββ??7. 在⼆元线性回归模型中,回归系数的显著性t 检验的⾃由度为( )。
A. n B. n-1 C. n-2 D. n-38. 普通最⼩⼆乘法要求模型误差项u i 满⾜某些基本假定,下列结论中错误的是( )。
A. E(u i )=0 B. E(2i u )=2i σC. E(u i u j )=0D. u i ~N(0.σ2)9. 对模型Yi=β0+β1X1i+β2X2i+µi 进⾏总体显著性F 检验,检验的零假设是( ) A. β1=β2=0 B. β1=0 C. β2=0 D. β0=0或β1=010. 在多元线性回归中,判定系数R 2随着解释变量数⽬的增加⽽() A.减少 B .增加 C .不变 D .变化不定11. 已知三元线性回归模型估计的残差平⽅和为8002=∑te,估计⽤样本容量为24=n ,则随机误差项t u 的⽅差估计量2S 为( )。
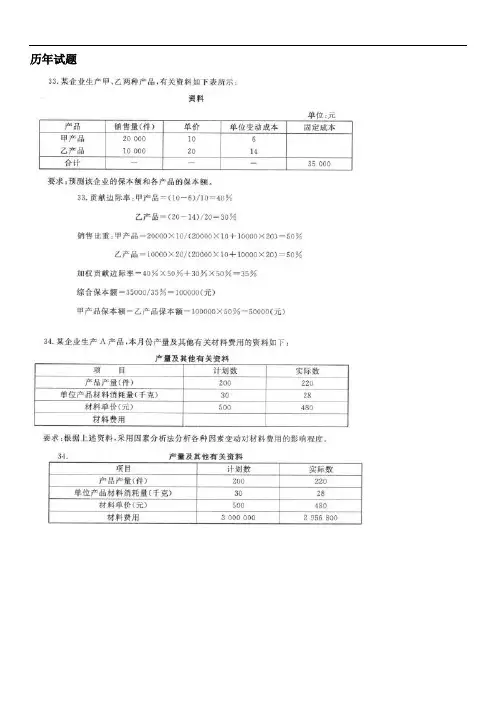
历年试题4、某企业只产销一种产品,本年单位变动成本为6元,变动成本总额为84000元,获营业利润18000元;若该企业计划下一年度变动成本率仍维持本年度的40%,其它条件不变。
要求:预计下一年度的保本销量及保本销售额。
解:本年销量=84000÷6=14000(单位)本年销售收入=84000÷40%=210000(元)单价=210000÷14000=15(元)固定成本=(15-6)×14000-18000=108000(元)保本销量=108000÷(15-6)=12000(单位)保本额=12000×15=180000(元)3.某种产品经两道工序完成,原材料随加工进度陆续投入。
原材料消耗定额为:第一道工序70%,第二道工序30%。
月末在产品数量为:第一道工序300件,第二工序300件。
该月完工产品140件。
月初和本月发生的费用为:原材料费用2900元,加工费用1350元。
要求:(1)计算该种产品两道工序的完工率。
(2)计算该种产品月末在产品的约当产量。
(3)按约当产量比例分配计算完工产品和月末在产品的原材料费用和加工费用。
(4)计算完工产品和月末在产品的成本。
3(1)该产品两道工序的完工率:第一工序 70%×50%=35%第二工序 70%+30%×50%=85%(2)月末在产品约当产量:第一工序 300×35%=105(件)第二工序 300×85%=255(件)月末在产品约当产量合计=105+255=360(件)(3)原材料费用分配率=2900/(140+360)=5.8(元)完工产品原材料费用=140×5.8=812(元)在产品原材料费用=360×5.8=2088(元)加工费用分配率=1350/(140+360)=2.7(元)完工产品加工费用=140×2.7=378(元)在产品加工费用=360×2.7=972(元)(4)完工产品成本=812+378=1190(元)在产品成本=2088+972=3060(元)复习资料11.某企业只生产一种产品,预计单价为2000元,销售量为3000件,税率为10%,成本利润率为20%。

1.某人将镍铬-镍硅补偿导线极性接反。
当炉温控制于800℃时。
若热电偶接线盒处温度为50℃,仪表接线端子温度为40℃,测量结果和实际相差多少?答案:如补偿导线接反,则仪表的电势为E(800、40)=E×(800、0)-E(50、0)-[E(50、0)-E(40、0)]=33.28-2.02-2.02+1.61=30.85mV但仪表示值仍按正常接法指示,即E(800、40)=E(t、0)-E(40、0)=0于是得30.85=E(t、0)-1.61E(t、0)=32.46mV查得t=780℃即比800℃指示低20℃2.一真空压力表量程范围为-100~500kPa,校验时最大误差发生在200kPa,上行程和下行程时校准表指示为194kPa和205kPa,问该表是否满足其1.0级的精度要求?答案:变差=[△max/(量程上限-量程下限)]×100%=(205-194)/[500-(-100)]×100%=1.83%>1.0%,所以不满足1.0级精度要求。
3.一台1151绝对压力变送器,量程范围为0~80kPa(绝压),校验时采用刻度范围为100~0kPa标准真空压力计,若当地大气压力为98kPa,则当变送器输出为12mA时,真空压力计指示的读数为多少?答案:设变送器输入压力为P绝时,输出电流为12mA,则P绝/(80-0)×16+4=12,P 绝=40KPa,根据P真空=P大气-P绝=98-40=58KPa,所以真空压力计的读数为58KPa,变送器的输出为12mA。
4.计算如图下所示的压力式液位计的调校量程范围及迁移量,已知h1=5m,h2=1m,ρ=1.0g/cm3答案:由图可知,液位计测量量程为:P=pgh1=1.0×9.8×5=49KPa;迁移量A=pgh2=1.0×9.8×1=9.8KPa,所以仪表调校量程范围为9.8—58.8KPa。
企业管理概论计算题专题一、技术与价值工程——综合评价法 1、公式:加权分数比较 2、实例:某公司2009年计划对一套设备进行更新。
甲、乙、丙三个厂家可以提供性能接近,价格相当的该种设备。
公司在选购设备时,需要从生产性(能力)、安全性、经济性、环保性四个方面对设备进行综合评价。
公司将各项评价因素的权重分别设定为0、4,0、3,0、2,0、1,并请9位业内专家对甲、乙、丙厂商的设备从上述四方面进行评分,各项评分的试根据综合评分法决定设备选购方案。
解答:(1)甲:90×0.4+60×0.3+40×0.2+30×0.1=36+18+8+3=65 (2)乙:60×0.4+90×0.3+60×0.2+40×0.1=67 (3)丙:70×0.4+70×0.3+90×0.2+50×0.1=72因为丙厂家的综合评分最高,所以最终选择丙厂家。
二、对投资方案的经济评价1、投资盈利率:投资盈利率=年平均盈利率/投资总额×100%2、投资回收率:投资回收率=(年平均盈利额+折旧)/投资总额×100%3、投资回收期:投资回收期=投资总额/年平均盈利实例:某新能源建设项目的投资总额为4000万元,建成后年折旧率为5%,预计年平均盈利800万元。
计算下列指标: (1)投资盈利率。
(2)投资回收率。
(3)投资回收期。
解答:(1)投资盈利率=8000000÷40000000×100%=20%(2)投资回收率=(8000000+40000000×5%)÷40000000=25% (3)投资回收期=40000000÷8000000=5年4、现金净流量现值:10(1)nttt p r p==+∑P 0表示净现值;Pt 表示各年现金净流量;t 表示投资项目存在年数;r 表示贴现率。

经济学概论补充计算题 (包括微观和宏观)Chap 2 需求、供给和均衡价格(含弹性理论)1. 已知某一时期内某商品的需求函数Q D = 50 -5 P ,供给函数为Q S = -10 + 5 P 。
(1) 求均衡价格P e ,和均衡数量Q e ;(2) 假定供给函数不变,由于消费者收入水平提高,使需求函数变为Q D = 60 - 5 P 。
求出相应的均衡价格P e 和均衡数量Q e ;(3) 假定需求函数不变,由于生产技术水平提高,使供给函数变为Q S = - 5 + 5 P 。
求出相应的均衡价格P e 和均衡数量Q e ;(4) 利用(1)、(2)、(3),说明需求变动和供给变动对均衡价格和均衡数量的影响。
2.某公司生产的A 产品的需求函数为Q = 500 - 2 P 。
(1) 假定公司销售A 产品200吨,其价格应为多少?(2) 如果公司按180元/吨的价格出售,其销售量为多少? 总收益如何变化? (3) 需求的价格弧弹性是多少?3. 某商品价格为100元时,销量为5000件,由此开始,价格每提高10元,销量减少500件。
(1)用公式表示商品销售量y 与价格 x 之间的函数关系。
(2)当价格为130元时,该商品的销售量是多少? (3)当价格提高到多少元时,该商品就卖不出去?Chap 3消费者行为理论1.假设某消费者的均衡如图3.2所示。
其中,横轴OX 1和纵轴OX 2分别表示商品l 和商品2的数量,线段AB 为消费者的预算线, 曲线I 为消费者的无差异曲线,E 点为均 衡点。
已知商品1的价格P 1 = 2。
(1) 求消费者的收入; (2) 求商品2的价格; (3) 写出预算线方程; (4) 求预算线的斜率;Chap 4 生产理论 (期末重点)1.某企业在短期生产中的生产函数为L L L Q 2402423++-=,计算企业在下列情况下的L 的取值范围: (1) 在第I 阶段; (2) 在第II 阶段;(3) 在第III 阶段。

例 1. 旅客航程为:MOW-CA- X/BJS-CA- MNL;全 程使用C 舱,OW 运价;在MOV 付款、出票。
计算全 程运价。
(LCF:USD; (N1)2 )解: 查运价表知 MOW - MNL 的OV V C 舱,FE 航线 的直达运价为 NUC 2110.00 I. TPM 计算如下: MOW3600 X/BJS CA 1797 MNL CA 5397II. 运价构成如下FCPNUCMOW-MN 的FE 航线的 MPM 为6166英里MOW-BJS 勺FE 航线的 TPM 为 3600, BJS-MNL 的EH 航线的TPM 为1797;MOWMNL C OW (FE)2110.00 例 3.旅客航程为:SHA-CA- BKK-TG- KHI-PK- ISB-SV- JED 全程使用C 舱运价;在SHA M 款、 LCF:CNY运价表: SHA-JED出票。
计算全程运价。
IROE:7.2069(H 10)0; C OW EH NUC MPM2009.82 EH 6045 Y146 RULE Y146I. TPM计算如下: MPMFE 6166SHA TPM 53971786 BKK CA EMA NIL2302 KHI TG EMS M701 ISB PK HIP NIL2227 JED SV RULE NIL6316AF NUC 2110.00II.运价构成如下: CHECK NAFCP SHAJEDAF NUC 2110.00NUC C OW (EH)2009.82 IROE x 1.00 (N 1)2RULE Y146 LCF USD 2110.00MPM EH 6045 例2. 旅客航程为:CAN -CZ- KUL-MH- CAI 全程使用 TPM 6316Y 舱运价;在CAN#款, 出票。
计算全程运价。
IROE EMA -700 = 5616 E/KHIISB 7.2069 ;(H10)0 ; LCF:CNY EMS M 运价表 :Y OW EH NUC MPM HIP NIL CAN-CAI 2009.82 EH 6081 RULE NIL I. TPM 计算如下:AF NUC 2009.82 CANCHECK NA1601 KUL CZ TOTAL NUC 2009.82 4938 CAI MH IROE x 7.2069 (H 10)0 6539LCFCNY 14490解:运价计算过程列表如下: II.运价构成如下:FCPNUC RULE MPM TPMEMA EMS HIP RULE AF CANCAI Y OW (EH) 2009.82 NIL EH 6081 6539 NIL 6539/6081 = 1.07531 10 MNILNIL2009.82 x 1.10 = NUC 2210.80 CHECK NATOTAL IROE LCF NUC 2210.80 x 7.2069 (H 10)0 CNY 159403024 BJS CAXMN1313 TY0 CA 306 HKG CZ 5493 AKL JL 5968 PAR CX 98306274II. 运价构成如下 FCP XMNPARFCP KHIAKL NUC C 0W (EH)2635.29 NUC C 0W (EH)1567.11 RULE Y146 RULE Y277 MPM EH 8157 MPM EH 9849 TPM 6274 TPM 9830EMANILEMA NIL EMS MEMS MHIP HKGPAR HIP BJSAKL C 0W (EH)NUC 2182.71 RULE Y146 RULEY277 AF NUC 2857.85AF NUC 2182.71CHECK BHC NILCHECK BHC NILT0TAL 2857.85 + 4.23 = NUC 2862.08 T0TAL NUC 2182.71IR0E x 7.2069 (H 10)0 IR0E x 51.700089 (H 10)0 LCF CNY 20630LCF PKR 11285010)0 ; LCF:PKR运价表: C 0W EH NUC MPM 情况1 :旅客在BJS 和TYO 中途分程; SEL-AKL 1784.02 EH 7196 情况2 :旅客仅在BJS 中途分程,在TYC 中转 BJS-AKL 2182.71 运价表: C 0W EH NUC MPM HKG-AKL 2329.61KHI-AKL 1567.11 EH 9849 Y277 解:运价计算过程列表如下: KHI-BJS 785.10 Y277 I. TPM 计算如下KHI-TY0 1107.92 Y277 SELBJS-TY0 792.51 Y277 567 BJS CA BJS-AKL 2182.71 Y277 1239 HKG CA TY0-AKL 2988.92 Y277 5699 AKL CX 情况1 :旅客在BJS 和TYO 中途分程; 7505例 4. 旅客航程为: KHI-CA- BJS-CA- TYO-JL- AK ;L 全 程使用C 舱运价;在KHI 付款,出票。

《计算机概论》老师画的重点简答题答案第二章习题复习题1(简述冯?诺依曼原理,冯?诺依曼结构计算机包含哪几部分部件,其结构以何部件为中心,答:冯?诺依曼理论的要点包括:指令像数据那样存放在存储器中,并可以像数据那样进行处理;指令格式使用二进制机器码表示;用程序存储控制方式工作。
这3条合称冯?诺依曼原理冯?诺依曼计算机由五大部分组成:运算器、控制器、存储器、输入设备、输出设备,整个结构一般以运算器为中心,也可以以控制器为中心。
(P52-P55)8(试解释下列基本概念:机器语言、汇编语言、高级语言。
答:机器语言,最早的计算机只有机器语言,计算机能直接执行用机器语言所编的程序。
机器语言是由二进制代码表示的计算机机器指令和数据组合而成。
汇编语言,到 50 年代,人们想出了用一些具有一定含义的文字、符号和数字,按规定的格式来表示各种不同的机器指令,称为“助记符”。
例如,用“ADD”表示加法,“MOV”表示数据传输等。
再用这些助记符来编写程序,这就是汇编语言。
高级语言,也称为算法语言,它定义了一套基本符号以及怎样使用这套基本符号设计程序的规则。
算法语言比较接近数学语言,与具体机器无关,直接学习该高级语言的规则就可以使用计算机解决自己的问题,例如C、C++、Java等。
(P45-P48)9(计算机软件系统可以分为哪几类,答:计算机软件系统可以分为系统软件和应用软件两大类。
(P64)22、运用所学知识,试分析哈佛结构对比冯诺依曼结构具备哪些优点,答:哈佛结构与冯?诺依曼结构的主要区别在于其将指令和数据分别进行存储管理,而两者基本组成是相同的。
由于结构上的区别,哈佛结构的微处理器通常具有较高的执行效率,其程序指令和数据指令分开组织和存储的,执行时可以预先读取下一条指令。
哈佛结构采用程序和数据空间独立的体系结构,目的是为了减轻程序运行时的访存瓶颈。
哈佛结构在并行性上要优于冯?诺依曼结构,但其实现相对复杂,在早期应用较少。
西安邮电大学2012秋《概率论与数理统计》期末试题评分标准注意:本试题解答时有可能用到以下数值8413.0)0.1(,9217.0)14.1(,0301,2)35(975.0===ΦΦt .995.0)645.1(,975.0)96.1(,5080.0)02.0(,5793.0)2.0(====ΦΦΦΦ一、填空题(每空3分,共30分) 1.已知,81)(,41)()(===AB P B P A P 则=)(B A P85. 85)()()(1)(1)()(=+--=-==AB P B P A P B A P B A P B A P2.设随机变量X 服从泊松分布,且),2()1(===X P X P 则==)4(X P232-e . 0)2(),2(!2!1)1(2=-⇒=====--λλλλλλX P eeX P ,故22432!42)4(--===e e X P 3.设随机变量X 服从参数为2的指数分布,则XeX Y 22-+=的数学期望为23. 23421222)()(2)(0222=+=+=+=⎰+∞---dx e e eE X E Y E x x X4.设随机变量X 和Y 相互独立,且),4,1(~),1,0(~N Y N X 令Y X Z +=2,则~Z )8,1(N .1)()(2)(=+=Y E X E Z E ,)8,1(~,8)()(4)(N Z Y D X D Z D ⇒=+=.5.将一根长为1的木棒随机地截成长度分别为X 和Y 的两段,则X 和Y 的相关系数=XY ρ 1- .)()1(),(),cov()1,cov()1,cov(,1X D X D X D X X X X X X Y =--=-=--=,故1-=XY ρ6.设随机变量X 和Y 的数学期望分别为2-和2,方差分别为1和4,其相关系数5.0-=XY ρ则根据切比雪夫不等式有()6≥+Y X P 的最小上界为121. 2415.0)()(),cov(-=⨯⨯-==Y D X D Y X XY ρ,0)2(2)(=-+=+Y X E ,3241)(=-+=+Y X D , 故()1213636=≤≥+Y X P . 7.设10021,,,ξξξ 独立且同分布,其概率密度均为⎩⎨⎧≤>=-000)(x x e x f x,依据中心极限定理,则()≈<+++10210021ξξξ P )02.0(Φ或508.0 .100)(10011001==⎪⎭⎫ ⎝⎛∑∑==i i i i E E ξξ,100)(10011001==⎪⎭⎫ ⎝⎛∑∑==i i i i D D ξξ,故=⎪⎭⎫ ⎝⎛<∑=1021001i i P ξ5793.0)2.0(10100102101001001=≈⎪⎪⎪⎪⎭⎫⎝⎛-<-∑=Φξi iP 8.设4321,,,X X X X 是来自正态总体)4,0(N 的样本,令()()243221X X X X Y -++=, cY Z =,要使)2(~2χZ ,则=c81. 因0)(,0)(4321=-=+X X E X X E 842)()(4321=⨯=-=+X X D X X D ,故81=c9.记总体X 的标准差为cm 3,现从中抽取出容量为36的样本,其样本平均数cm x 642=,则)(X E =μ的置信度为95.0的置信区间为 []98.642,02.641 .10.设总体X 服从参数为)0(>λλ的泊松分布,1021,,,X X X 是来自该总体的样本,则λ的最大似然估计量为=λˆ ∑=101101i i k . ()λλλλλλ101011010110102211101101!1!,,,-=-=-∑=∑=⎪⎪⎭⎫ ⎝⎛======∏∏eA k e e k k X k X k X P i i i iik i i k i i k ,故 λλ10ln ln 101-⎪⎭⎫ ⎝⎛∑+==i i k A L ,令010101=-∑==λλi ik d dL 得最大似然估计量∑==101101ˆi i k λ. 二、计算题(共70分)11(10分).设随机变量X 的密度函数为⎪⎩⎪⎨⎧<≤-<≤=othersx xa x xx f 02110)(,试求:(1)常数a ;(2)X 的分布函数)(x F .解:(1)由()212321)(2110=⇒=-+=-+=⎰⎰⎰∞∞-a a dx x a xdx dx x f .…………………………5分(2)()⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧≤<≤-+-=---+=-+<≤=<=⎰⎰⎰x x x x x x dt t tdt x t tdt x x F x x 112112221)1(221210200)(2211020.……5分12(10分).设二维随机变量),(Y X 服从平面区域{}x y x y x D ≤≤≤=,10),(上的均匀分布,(1)求随机变量X 的概率密度函数;(2)求条件密度函数)(x y f XY .解:由已知,D 的面积为1,故有⎩⎨⎧≤≤≤=otherx y x y x f 0,101),(. ………………2分(1)⎪⎩⎪⎨⎧≤≤===⎰⎰-∞∞-other x xdy dy y x f x f x xX 0102),()(. ………………4分(2)()100121)(),()(≤≤⎪⎩⎪⎨⎧≤==x othery xx f y x f x y f X X Y . ………………4分13(12分).设二维随机变量),(Y X 的概率密度函数为⎩⎨⎧<<<<--=othery x y x A y x f 010,10),(,试求:(1)常数a ;(2)X 和Y 是否相关?为什么?(3))(Y X D +.解:(1)由()12121),(1010=--=--=⎰⎰⎰⎰∞∞-∞∞-A dxdy y x A dxdy y x f 知,2=A .…………4分 (2)()12521213112),()(101=⋅--=--==⎰⎰⎰⎰∞∞-∞∞-dxdy y x x dxdy y x xf X E ,同理:125)(=Y E ,…2分 ()2125),()()(125125),(⎪⎭⎫⎝⎛-=-=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=⎰⎰∞∞-∞∞-dxdy y x xyf y E x E XY E Y X E Y X Cov ,…1分()()⎰⎰⎰⎰==⋅-⋅-=--=--=10122210192184313131212122)(dxdy y x y x xy dxdy y x xy XY E ,…1分 01296253914492514421442592),(≠=⋅⋅-⋅=-=Y X Cov ,故X 和Y 不相关. …………1分 (3)()()1232131413222)(10123210122=⋅--=--=--=⎰⎰⎰⎰dxdy y x x x dxdy y x x X E ,同理,123)(2=X E . []1449125123)()()(222=⎪⎭⎫ ⎝⎛-=-=X E X E X D ,同理:1449)(=Y D . …………2分 64825377912962531449212962532)()(),(2)()()(+=⎪⎭⎫ ⎝⎛+⨯=⨯++=++=+Y D X D Y X Cov Y D X D Y X D . …………1分14(10分).设X 和Y 是相互独立的随机变量,其密度函数分别为⎩⎨⎧≤≤=otherx x f X 0101)(,⎩⎨⎧≤>=-00)(y y e y f yY ,令Y X Z +=,求Z 的概率密度函数.解:当0<z 时,由0)()(=≤+=z Y X P z F Z 知,此时有0)(=z f Z . …………3分当10<<z 时,z z z zx zzx z Z e e e dx e edx ez f ------=-==⋅=⎰⎰1)1(1)(00)(, …………4分 当z <1时,)1(1)(11)(-==⋅=----⎰⎰e edx e edx ez f zx zx z Z ,故⎪⎩⎪⎨⎧≤-<<-≤=--z e e z e z z f z z Z 1)1(10100)( …………3分15(8分).设二维随机变量),(Y X 的分布律为YX1 2 31 γ 91 181231α β问γβα,,分别取什么值时,X 和Y 相互独立?.解:由已知得方程组γγγ=⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛++3118191; ααγ=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛++9118191ββγ=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛++18118191; 1213118191=+++=+++++γβαγβα. …………4分整理并求解得:⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧==⇒=++=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+==⇒=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+==⇒=+-91181211816118191916161310181212ββγβαββγααααγγγγγor or or …………4分 经验证,两组解都满足题给条件(含第三个方程).16(12分).设总体X 的分布密度为⎪⎩⎪⎨⎧≤≤=otherx x f 001);(θθθ,其中0>θ是未知参数,现已抽得n X X X ,,,21 ,(1)求θ的矩估计量1ˆθ;(2)令{}n X X X nn ,,,max 1ˆ212 +=θ,验证1ˆθ和2ˆθ都是θ的无偏估计量;(3)比较1ˆθ和2ˆθ哪个更有效. 解:(1)21)(0θθθ==⎰dx xX E ,令X X E =)(,得矩估计量X 2ˆ1=θ. …………4分 (2)因⎪⎩⎪⎨⎧≤≤=otherx xx F 00)(θθ,则⎪⎩⎪⎨⎧≤≤⎪⎭⎫ ⎝⎛=≤≤≤=otherx x x X x X x X P x F nn 00),,,,()(21ˆ2θθθ ,故密度函数为⎪⎩⎪⎨⎧≤≤=-otherx nx x f nn 00)(1ˆ2θθθ,{}()θθθθθθ=++=+=+=+-⎰01012121111,,,max 1)ˆ(n n n n n x n n n n dx nx x n n X X X E n n E . ()()θθθ===⎪⎭⎫ ⎝⎛=∑∑∑===ni n i i n i i n X E n X n E E 111122212ˆ. 故1ˆθ和2ˆθ都是θ的无偏估计量. …………4分 (3)()()()1243412222222θθθθθθ-=-=-=-=⎰dx xX E XE X D iii .()()n n X D n D ni ni i31244ˆ2122121θθθ===∑∑==.{}(){}(){}()[]n n n X X X E X X X E n n X X X D n n D ,,,max ,,,max 1,,,max 1)ˆ(21222122122222 -⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛+=θ⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+-+⎪⎭⎫ ⎝⎛+=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+-⎪⎭⎫⎝⎛+=⎰-222222012212111θθθθθn n n n n n n n dx nx x n n nn .()()()()()()()22222222222122112211121θθθθ+=++-+=++-+=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+-+⎪⎭⎫ ⎝⎛+=n n n n n n n n n n n n n n n n n n n .()()2221)2(1)2(131ˆˆθθθθ+-=⎥⎦⎤⎢⎣⎡+-=-n n n n n n D D .可见,当1>n 时,2ˆθ比1ˆθ更有效. ………4分17(8分).假定某厂生产一种钢索,它的断裂强度)(2cm kg ξ服从正态分布)40,(2μN ,从中选取一个容量为9的样本,得)(7802cm kg x =,问:对于05.0=α,能否据此样本认为这批钢索的断裂强度为)(8002cm kg ?解:对于给定的05.0=α构造假设800:0=μH ;800:0=μH …………3分若800:0=μH 成立,则)1,0(~340800940800N X X Z -=-=. …………3分 对于题给样本有5.140320940800780-=⨯-=-=Z 。
地球概论复习题一、选择题1. 地球的形状最接近于以下哪个几何体?A. 立方体B. 球体C. 椭球体D. 圆柱体2. 地球的赤道半径约为多少千米?A. 6000B. 6200C. 6400D. 66003. 地球的自转周期是多久?A. 24小时B. 48小时C. 72小时D. 96小时4. 地球的公转周期是多久?A. 365天B. 365.25天C. 366天D. 366.25天5. 地球的自转轴与公转轨道平面的夹角约为多少度?A. 23°B. 30°C. 45°D. 60°二、填空题1. 地球的极半径约为______千米。
2. 地球的赤道周长约为______千米。
3. 地球的表面积约为______平方千米。
4. 地球的体积约为______立方千米。
5. 地球的平均密度约为______克/立方厘米。
三、简答题1. 简述地球自转的地理意义。
2. 简述地球公转的地理意义。
3. 地球的内部结构是如何划分的?4. 地球的大气层有哪些主要层?5. 什么是地球的磁极?它与地理极有何不同?四、论述题1. 论述地球自转和公转对气候的影响。
2. 论述地球内部结构对地球表面活动的影响。
3. 论述地球大气层对地球环境的作用。
五、计算题1. 如果地球的自转速度增加到每24.5小时转一圈,试计算新的赤道周长。
2. 假设地球的体积增加到原来的1.5倍,而质量保持不变,计算新的地球平均密度。
六、案例分析题1. 根据地球的自转和公转,分析不同纬度地区的季节变化。
2. 以地球的内部结构为基础,分析地震和火山活动的形成机制。
七、实验题1. 设计一个实验来模拟地球的自转和公转。
2. 通过实验探究地球大气层对太阳辐射的影响。
八、综合题1. 结合地球的形状、自转和公转,解释为什么地球上会有昼夜变化和季节变化。
2. 综合地球的内部结构、大气层和磁场,分析地球作为一个生命支持系统的复杂性。
43.甲汽车制造公司2009年5月购进原材料取得的增值税专用发票上注明的税额为810万元,当月销售汽车含增值税销售额8000万元,当月进口一台汽车检测设备,在海关缴纳增值税85万元,已知甲公司适用增值税率17%。
根据以上条件计算当月应纳增值税。
(计算结果保留小数点后两位)答:(1)销项税额: (万元)(2)准予抵扣的进项税额:810+85=895(万元)(3)当月应纳增值税额:当月销项税额-当月可抵扣进项税额=1162.39-895=267.39(万元)43.某汽车生产企业为增值税一般纳税人,生产的A型小汽车的销售单价(含增值税)为每辆10万元。
2009年2月份购销情况如下:(1)销售小汽车100辆,取得的运输发票上注明运费47000元。
(2)公司购进零配件、原材料增值税专用发票上注明的税款为85万元。
已知小汽车的增值税率为17%,运输费用的进项税额扣除率为7%。
要求:计算该企业当月应缴纳的增值税。
(计算结果精确到小数点后2位)答:本月应纳的增值税:本月的销项税=(10×100)÷(1+17%)×17%=145.30(万元)本月可抵扣的进项税=85+4.7×7%=85.33(万元)本月应纳税=145.30-85.33=59.97(万元)43.退休人员王某2011年5月收入如下:退休金4000元,体育彩票奖金30000元,稿酬3000元,演讲报酬3000元。
请计算王某当月应缴纳的个人所得税数额(要求答出计算过程)。
答:(1)偶然所得应纳税额=应纳税所得额×适用税率=每次收入额×20%体育彩票奖金应缴纳个人所得税:3000×20%=6000元(2)稿酬所得每次收入不超过4000元的,减除费用800元,其余额为应纳税所得额。
应纳税额=应纳税所得额×适用税率稿酬所得应缴纳个人所得税:(3000-800)×20%×(1-30%)=308元(3)劳务报酬所得每次收入不超过4000元的,减除费用800元,其余额为应纳税所得额。
06959工程经济概论题库一、单项选择题1.为组织和管理生产所发生的各项费用属于【】A.制造费用B.管理费用C.财务费用D.销售费用2.在市场价格失真时,经济分析中所用的价格应是【】A.零售价格B.批发价格C.出厂价格D.影子价格3.土地使用权属于【】A.递延资产B.固定资产C.无形资产D.流动资产4.企业利润总额与资本金总额的比率称为【】A.销售收入利润率B.资本金利润率C.产值利润率D.成本费用利润率5.对特定消费品或消费行为的流转额或流转量所征的税称为【】A.营业税B.增值税C.消费税D.所得税6.间接以增值额为计税依据的方法是【】A.扣额法B.扣税法C.从价法D.从量法7.整付现值系数是【】A.(F/A,i,n)B.(F/P,i,n)C.(A/P,i,n)D.(P/F,i,n)8.在工程经济分析中,应采用【】A.单利法B.复利法C.固定利率法D.浮动利率法9.已知方案A、B、C,其投资KA<KB<KC,设其差额投资内部收益率满足△IRRA-B<i0,△IRRB-C>i0,△IRRA-C<i0,(io为标准投资收益率),则方案从优到劣的排队顺序为【】A.C-A-BB.B-A-CC.A-B-CD.B-C-A10.评价技术改造项目部经济效益应着重考察其【】A.投资规模B.项目投资C.技术投入D.增量投资11.用产品表示的工程项目年综合生产能力是【】A.生产规模B.销售规模C.经济规模D.计划规模12.机会研究的主要任务是提出投资方向的【】A.依据B.建议C.可行性D.决议13.尚处于理论研究或实验研究阶段的新产品称为【】A.实验室新产品B.试制新产品C.试销新产品D.正式生产新产品14.某产品N,其销售额为800万元,总成本费用650万元,占用资金400万元,合理的资金利润率为35%,那么该产品属于【】A.低资金利润率型产品B.资金积压型产品C.低销售利润率型产品D.高资金利润率型产品15.由有形磨损所决定的设备的使用寿命称为【】A.自然寿命B.技术寿命C.经济寿命D.折旧寿命16.由于自然力的作用而导致的设备磨损称为【】A.第Ⅰ种形式的有形磨损B.第Ⅱ种形式的有形磨损C.第Ⅰ种形式的无形磨损D.第Ⅱ种形式的无形磨损17.用低劣化数值法计算出来的最优更新期是设备的【】A.物理寿命B.技术寿命C.经济寿命D.会计寿命18.在固定制造费用差异分析中,实际固定制造费与预算固定制造费的差额称为【】A.固定制造费用差异B.固定制造费用能力差异C.固定制造费用开支差异D.固定制造费用效率差异19.在标准成本的分类中,以现有的生产技术和经营管理水平处于最佳状态为基础而确定的标准成本称为【】A.现时标准成本B.基准标准成本C.理想标准成本D.能实现良好业绩的标准成本20.在生产成本的执行控制中,减少不必要的加班属于【】A.制造费用控制B.工资率控制C.材料价格控制D.工时控制1.无形资产一般按规定的期限分期摊销,没有规定期限的,按不少于( A )年摊销A 10B 9C 8D 62、价值工程的最重要的特征是( B )A、效益分析B、功能分析C、成本分析D、收益分析3、生产成本的事前控制主要是( C )A、事前计划B、事前分析C、标准制定D、事前决策4、不应冲销当期的销售收入的是(D )A、销售退回B、销售折让C、销售折扣D、销售收入5、下列各项中不属于增值税的税率是( A )A、18%B、基本税率C、低税率D、零税率二、简答题1.当测得值中系统误差与随机误差同时存在时,若测量次数足够多,则各次测量绝对误差的算术平均值为。
1、电荷为+q 和-2q 的两个点电荷分别置于x =1 m 和x =-1 m 处.一试验电荷置于x 轴上何处,它受到的合力等于零?2、如图所示的长空心柱形导体半径分别为1R 和2R ,导体内载有电流I ,设电流均匀分布在导体的横截面上。
求(1)导体内部各点的磁感应强度。
(2)导体内壁和外壁上各点的磁感应强度。
3、如图所示,有一根长直导线,载有直流电流I ,近旁有一个两条对边与它平行并与它共面的矩形线圈,以匀速度v沿垂直于导线的方向离开导线.设t =0时,线圈位于图示位置,求(1) 在任意时刻t 通过矩形线圈的磁通量Φ ; (2) 在图示位置时矩形线圈中的电动势E 。
4、在复色光照射下的单缝衍射图样中,其中某一未知波长光的第3级明纹极大位置恰与波长为nm 600=λ光的第2级明纹极大位置重合,求这种光波的波长。
5、求线电荷密度为λ的无限长均匀带电直线的电场强度分布。
6、A 和B 为两个正交放置的圆形线圈,其圆心相重合。
A 线圈半径m R A 2.0=,10=A N 匝,通有电流A I A 10=;B 线圈半径m R B 1.0=,20=B N 匝,通有电流A I B 5=。
求两线圈公共中心处的磁感应强度。
7、电流为I 的无限长直导线旁有一弧形导线,圆心角为1200,几何尺寸及位置如图所示。
求当圆弧形导线以速度v 平行于长直导线方向运动时,弧形导线中的动生电动势。
Ia bvl8、一衍射光栅,每厘米200条狭缝,每条狭缝宽为a=2×10-3 cm ,在光栅后放一焦距f=1 m的凸透镜,现以λ=600 nm (1 nm =10-9 m)的单色平行光垂直照射光栅,求:(1) 单缝a 的单缝衍射中央明条纹宽度为多少? (2) 在该宽度内,有几个光栅衍射主极大?9、一均匀带电半圆环,半径为R ,电量为Q ,求环心处的电势10、一无限长的载流导线中部被弯成圆弧形,并用同样的直导线将B A ,两点连接,如图B07所示,圆弧形半径为cm R 3=,导线中的电流为A I 2=。
求圆弧形中心O 点的磁感应强度。
11、一同轴电缆由中心导体圆柱和外层导体圆筒组成,两者半径分别为1R 和2R ,导体圆柱的磁导率为1μ,筒与圆柱之间充以磁导率为2μ的磁介质。
电流I 可由中心圆柱流出,由圆筒流回。
求每单位长度电缆的自感系数。
12、在通常亮度下,人眼瞳孔直径约为3 mm ,若视觉感受最灵敏的光波长为550 nm (1 nm = 10-9 m),试问:(1) 人眼最小分辨角是多大?(2) 在教室的黑板上,画的等号的两横线相距2 mm ,坐在距黑板10 m 处的同学能否看清?13、一半径为R ,均匀带电Q 的球面,试求:(1A OBθ内、外各点的电势。
14、在同一平面内有一长直导线和一矩形单匝线圈,线圈的长边与长直导线平行,如图所示。
若直导线中的电流为A I 201=,矩形线圈中的电流为A I 102=,求矩形线圈所受的磁场力。
15、一圆形线圈A 由50匝细导线绕成,其面积为4cm 2,放在另一个匝数等于100匝、半径为20cm 的圆形线圈B 的中心,两线圈同轴。
设线圈B 中的电流在线圈A 所在处激发的磁场可看作匀强磁场。
求: (1)两线圈的互感;(2)当线圈B 中的电流以50A/s 的变化率减小时,线圈A 中的感生电动势的大小。
16、波长500nm(1nm=10-9m)的单色光垂直照射到宽度a 为0.25 mm 的单缝上,单缝后面放置一凸透镜,在凸透镜的焦平面上放置一屏幕,用以观测衍射条纹.今测得屏幕上中央明条纹一侧第三级暗条纹和另一侧第三级暗条纹之间的距离为d 为12 mm ,求凸透镜的焦距f 。
17、一半径为R ,圆心角为2π/3的圆环上均匀分布电荷+Q ,求环心处的电场强度。
18、如图所示,长直电缆由半径为R 1的导体圆柱与同轴的内外半径分别为R 2、R 3的导体圆筒构成,电流沿轴线方向由一导体流入,从另一导体流出,设电流强度I 都均匀地分布在横截面上。
求距轴线为r 处的磁感应强度大小(∞<<r 0)。
19、设想利用水流通过地磁场所产生的动生电动势来探测海洋中水的运动。
假设在某处海水中地磁场的竖直分量为0.70×10-4T ,将两个电极插入与水流方向垂直的水中,两电极相距200m 。
如果与两电极相连的灵敏伏特计测出电势差为7.0mV 。
求海水的流速。
20、在双缝干涉实验装置中,屏幕到双缝的距离D 远大于双缝之间的距离d ,对于钠黄光(nm 3.589=λ),产生的干涉条纹,相邻两明条纹的角距离(即相邻两明条纹对双缝中心处的张角)为︒20.0。
(1)对于什么波长的光,这个双缝装置所得相邻两条纹的角距离比用钠黄光测得的角距离大%10?(2)假想将此装置浸入水中(水的折射率33.1=n ),用钠黄光垂直照射时,相邻两明条纹的角距离有多大?21、电荷q 均匀分布在长为2l 的细杆上,求在杆外延长线上与杆端距离为a 的P 点的电势(设无穷远处为电势零点)。
22、无限长细导线弯成如图所示的形状,其中c 部分是在xoy 平面内半径为R 的半圆,试求通以电流I 时O 点的磁感应强度。
23、电子感应加速器中的磁场在直径为0.50m 的圆柱形区域内是匀强的,若磁场的变化率为1.0×10-2 T/s .试计算离开中心0.10m ,0.50m ,1.0m 处各点的感生电场场强。
24、在光栅夫琅禾费衍射中,已知光栅上每厘米刻有3200刻痕,透镜焦距为1m ,现用单色光垂直照射光栅,测得第3级明纹的衍射角为300,求1)入射光波长;2)第二级明纹距中央明纹的距离。
Pa O 2lx d x25、如图所示,两个点电荷+q 和-3q ,相距为d . 试求:(1) 在它们的连线上电场强度0 E的点与电荷为+q 的点电荷相距多远?(2) 若选无穷远处电势为零,两点电荷之间电势U =0的点与电荷为+q 的点电荷相距多远?26、如图所示,半径为R 的木球上绕有密集的细导线,线圈平面彼此平行,且以单层线圈均匀覆盖住半个球面。
设线圈的总匝数为N ,通过线圈的电流为I ,求球心O 的磁感强度。
27、电磁“涡流”制动器由一导电率为γ 和厚度为d 的圆盘组成,此盘绕通过其中心的轴转动,且有一覆盖面积为l 2的磁场B 垂直于圆盘,如图所示若面积l 2在离r 处,当圆盘角速度为ω时,试说明使圆盘慢下来的道理。
dωlrB28、以波长为694nm 的红宝石激光作双缝干涉实验,双缝间距为0.6mm 。
求距双缝3m 的屏幕上相邻两明纹间的距离。
29、两个带等量异号电荷的均匀带电同心球面,半径分别为R 1=0.03 m 和R 2=0.10 m .已知两者的电势差为450 V ,求内球面上所带的电荷。
+q-3qxdx' xO30、如图,一均匀带电长直圆柱体,电荷体密度为ρ,半径为R 。
若圆柱绕其轴线匀速旋转,角速度为ω,求:(1)圆柱体内距轴线r 处的磁感应强度的大小;(2)两端面中心的磁感应强度的大小。
31、一面积为S 的单匝平面线圈,以恒定角速度ω在磁感强度k t B Bωsin 0=的均匀外磁场中转动,转轴与线圈共面且与B 垂直( k为沿z 轴的单位矢量).设t =0时线圈的正法向与k同方向,求线圈中的感应电动势.32、用波长为589.3nm 的光做牛顿环实验,测得某一明环半径为1.0mm ,其外第四个明环的半径为3.0mm ,求实验中所用的平凸透镜的凸面曲率半径。
33、一半径为R 的带电球体,其电荷体密度分布为4πRqr=ρ (r ≤R ) (q 为一正的常量) ρ = 0 (r >R )试求:(1) 带电球体的总电荷;(2) 球内、外各点的电场强度;(3) 球内、外各点的电势。
34、两根直导线与铜环上B A ,两点连接,如图所示,并在很远处与电源相连接。
若圆环的粗细均匀,半径为r ,直导线中电流I 。
求圆环中心处的磁感应强度。
35、无限长通电导线与一矩形线框共面(尺寸如图所示),导线中的电流t I I ωsin 0=,求线框的感应电动势。
36、折射率为1.52的照相机镜头的表面上涂有一层厚度均匀的折射率为1.38的MgF 2增透膜,如果此膜只适用于波长为550nm 的光,则此膜的最小厚度为多少?若所涂MgF 2为增反膜,则此膜的最小厚度为多少?电场强度E37、实验表明,在靠近地面处有相当强的电场,垂直于地面向下,大小约为100 N/C ;在离地面 1.5 km 高的地方,E也是垂直于地面向下的,大小约为25N/C 。
(1) 假设地面上各处E都是垂直于地面向下,试计算从地面到此高度大气中电荷的平均体密度;(2) 假设地表面内电场强度为零,且地球表面处的电场强度完全是由均匀分布在地表面的电荷产生,求地面上的电荷面密度.(已知:真空介电常量0ε=8.85×10-12 C 2·N -1·m -2)38、如图一圆柱形无限长导体,磁导率为μ,半径为R ,通有沿轴线方向的均匀电流I ,求:(1)导体内任一点的B H 、和M ;(2)导体外任一点的B H 、。
x d x dabE(2)SE 2∆SE 1(1) h39、一螺线管长300mm,截面直径为15mm,共绕2000匝,当导线中通有电流为2A时,线圈中铁芯的相对磁导率为1000,不考虑端点效应,求管中心的磁能密度和所储存的磁场能量。
40、在双缝干涉实验中,波长 =550 nm的单色平行光垂直入射到缝间距d=2×10-4 m的双缝上,屏到双缝的距离D=2 m.求:(1) 相邻明纹的间距及中央明纹两侧的第5级明纹中心的间距;(2) 用一厚度为e=6.6×10-5 m、折射率为n=1.58的玻璃片覆盖其中一缝后,零级明纹将移到原来的第几级明纹处?(1 nm = 10-9 m)。