下载文档原格式
反射系数引言反射是物理学中一个重要的现象，它指的是光、声波或其他波动传播中的一部分能量从一种介质中传播到另一种介质时被折射或吸收的过程。
而反射系数则是描述反射率的一个数值化指标。
本文将介绍反射系数的概念、计算方法以及其在不同领域的应用。
一、概念反射系数是指光或其他波动在从一种介质到另一种介质传播时，与前一种介质界面发生反射的能量占总能量的比率。
一般用R表示。
在光学中，反射系数是描述光的反射能力的重要参数。
在声学中，反射系数则是描述声波在不同介质间传播时的反射情况的参数。
二、计算方法计算反射系数需要考虑光或波动在两个介质之间传播时的折射、透射和反射等现象。
根据光的几何光学原理，反射系数可以通过以下公式计算：R = (n1 - n2) ^ 2 / (n1 + n2) ^ 2其中，n1和n2分别表示两种介质的折射率。
反射系数的取值范围在0到1之间，越接近1表示反射越强，越接近0表示反射越弱。
三、应用领域1. 光学反射系数在光学中有广泛的应用。
光的反射能力对于材料的颜色、光泽度以及光学分析等起着重要的作用。
通过改变材料的反射系数，可以调节光线对物体的反射和透射能力，实现光线的控制和调节。
在光学设备的设计中，反射系数也是重要的考虑因素之一。
2. 声学反射系数在声学中同样具有重要的应用。
声波在不同介质间传播时，会发生反射、折射和透射等现象，反射系数可以用来描述声波在不同介质间的反射情况。
通过控制反射系数，可以调节声波在空间中的传播和反射，从而达到改善音质、降低噪音等目的。
3. 建筑在建筑学中，反射系数被用来描述建筑材料的反射特性。
不同材料的反射系数对建筑的保温、隔热、能源利用等方面有着重要影响。
通过选择具有较高或较低反射系数的材料，可以实现建筑结构的热管理，提高建筑的能源效率。
4. 材料科学在材料科学领域，反射系数常用于表征材料的光学特性。
通过测量材料的反射系数，可以了解其光学平均自由程、折射率等参数，为材料的性质分析和应用提供重要的数据。
地震反演方法概述地震反演：由地震信息得到地质信息的过程；地震反射波法勘探的基础在于：地下不同地层存在波阻抗差异，当地震波传播有波阻抗差异的地层分界面时，会发生反射从而形成地震反射波。
地震反射波等于反射系数与地震子波的褶积，而某界面的法向入射反射系数就等于该界面上下介质的波阻抗差与波阻抗和之比。
也就是说，如果已知地下地层的波阻抗分布，我们可以得到地震反射波的分布，即地震反射剖面。
即由地层波阻抗剖面得到地震反射波剖面的过程称为地震波阻抗正演，反之，由地震反射剖面得到地层波阻抗剖面的过程称为地震波阻抗反演。
叠前反演主要是指AVO反演，通过AVO反演，可以获得全部的岩石参数，如：岩石密度、纵横波速度、纵横波阻抗、泊松比等。
叠前反演与叠后反演的根本区别在于叠前反演使用了未经叠加的地震资料。
多道叠加虽然能够改善资料的品质，提高信噪比，但是另一方面，叠加技术是以动校正后的地震反射振幅、波形等特征不随炮检距变化的假设为基础的。
实际上，来自同一反射点的地震反射振幅在不同炮检距上是不同的，并且反射波形也随炮检距的变化而发生变化。
这种地震反射振幅、波形特征随炮检距的变化关系很复杂，主要原因就在于不同炮检距的地震波经过的地层结构、弹性性质、岩性组合等许多方面都是不同的。
叠加破坏了真实的振幅关系，同时损失了横波信息。
叠前反演通过叠前地震信息随炮检距的变化特征，来揭示岩性和油气的关系。
叠前反演的理论基础是地震波的反射和透射理论。
理论上讲，利用反射振幅随入射角的变化规律可以实现全部岩性参数的反演，提取纵波速度、横波速度、纵横波速度比、岩石密度、泊松比、体积模量、剪切模量等参数。
叠后地震剖面相当于零炮检距的自激自收记录。
与叠前反演不同，叠后反演只能得到纵波阻抗。
虽然叠后反演与叠前反演相比有很多不足之处，但由于其技术方法成熟完备，到目前为止，叠后反演仍然是主流的反演类型，是储层预测的核心技术。
介绍几种叠后反演方法：1）道积分：利用叠后地震资料计算地层相对波阻抗（速度）的直接反演方法。
第一章绪论1.1概述声全息场变换是一种利用声场空间某一区域已知的声场分布,如复声压、复振速分布来预报另一区域声场特性，包括声源表面、近场及远场的各种声学标量场和向量场的分布的技术。
它可以解决一些利用常规的理论和实验方法不便或尚难解决的问题。
本文讨论的就是一种主动声全息技术：利用SFT（空间傅立叶变换）进行任意角度下声反射系数的反演，以及对利用这一理论进行的一次原理实验的分析。
1.2 一种任意入射角反射系数反演技术]4[声学材料的声特性测量主要包括声管中的小样测量和自由场中的大样测量两种。
前者给出小样材料的法向反声特性。
经过几十年的努力，这方面的测量技术已经基本成熟，并已形成了有关的测量标准。
而后者不仅能够给出大样材料或声反射面的法向反声特性，更重要的是，自由场测量还可以给出测向特性，这在实际工作中是很需要的。
关于自由场中任意入射角反射系数的测量方法已经不少了。
大致可归纳为以下几类]2[：（1）表面声压法：在待测材料表面上测得其复声压，再与位于空间同一点上全反射材料上测得的声压相比较。
（2）干涉图法：应用几何反射理论，可以通过位于待测材料前的声波干涉图得到反射系数。
（3）信号分离法：使用脉冲或相关技术，测量一待测材料表面上对一测试信号的响应声压，再分离入射和反射信号以- 1 -- 2 -得到反射系数。
（4） 双微音器法： 通过置于待测材料表面附近的两个微音器之间的一个传播方程来测量，可计算得反射系数。
随着信号处理计算机应用技术的迅速发展，使近场声全息技术应用于声学材料或声反射面的反声特性的测量成为可能。
Tamura 首先引用了这种技术，提出了一种新的测量方法，即利用SFT （Spatial Fourier Transform 空间傅立叶变换）来测量任意角的反射系数。
这种方法需要测量两个声全息面上的复声压，再利用ＳＦＴ将每个全息面上的复声压分解为平面波成分。
而待测材料上的入射与反射平面波可利用平面波传播理论通过计算分离开。
地震反演技术简介在上世纪70~80年代，地震反演作为地球物理学的一个重要进展得到了广泛的赞扬，获得广泛应用；地震反演技术能够帮助解释人员确定地层单元而不仅仅是通过反射波确定地层单元的边界，而且能直接进行深度域成图。
在一个竞争的市场环境中，开发出了很多不同的反演算法，在基本递归反演方法的基础上不断取得进进展，一下简要介绍几种基本的地震反演方法。
主要分三大类：1、基于地震数据的声波阻抗反演：其结果有两种：相对阻抗反演（常说的道积分）与绝对阻抗反演。
主要算法有：递归反演（早期的地震反演算法）与约束稀疏脉冲反演（优化的地震反演算法）。
这种反演受初始模型的影响小，忠实于地震数据，反映储层的横向变化可靠；但分辨率有限，无法识别10米以下的薄砂层。
2、基于模型的测井属性反演：此种反演可以得到多种测井属性的反演结果，分辨率较高（可识别2-6米的薄层砂岩）；但受初始模型的影响严重，存在多解性，只有井数多（工区内至少有10口以上的井，分布合理，且要求反演的属性与阻抗相关），才能得到较好的结果。
3、基于地质统计的随机模拟与随机反演：此种算法可以进行各种测井属性的模拟与岩性模拟，分辨率高（可识别2-6米的薄层砂岩），能较好的反映储层的非均质性，受初始模型的影响小，在井点处忠实于井数据，在井间忠实于地震数据的横向变化，最终得到多个等概率的随机模拟结果；但要求工区内至少有6-7口井，且分布较合理，才能得到好的模拟结果。
道积分道积分技术出现，为广大少井无井地区岩性及油气预测提供了新的途径，它能得到类似于虚速度测井的新方法，其结果对应于地层的波阻抗，它最大优点是不像虚速度测井那样依赖于井的资料和地球物理学家的经验。
尽管道积分剖面不能像GLOG波阻抗剖面那样反映地层绝对速度，而只能反映其相对速度大小，但是它反映出的层位与GLOG剖面是一样的，甚至在反映的细节上还比它多，对薄层识别也非常有利，因此道积分剖面能用于岩性和油气层解释。
第二章地震反演技术地震反射波法的基础是由于地下不同的地层存在着波阻抗的差异，从而形成了反射波法。
所以从本质上来讲，地震反演的目标就是根据已经获得的地震反射波形，以已知地质规律和钻井、测井资料为约束，对地下岩层空间结构和物理性质所进行的成像（求解），广义的地震反演包含了地震资料处理解释的整个内容。
波阻抗反演是利用地震资料反演地层波阻抗（或）速度的地震特殊处理解释技术。
与地震模式识别预测油气、神经网络预测地层参数、振幅拟合预测储层厚度等统计性方法相比，波阻抗反演具有明确的物理意义，是储层岩性预测、油藏特征描述的确定性方法，在实际应用中取得了明显的地质效果，因此地震反演通常特指波阻抗反演。
李庆忠院士指出：“波阻抗反演是高分辨率地震资料处理的最终表达方式”，说明了波阻抗反演在地震技术中的特殊地位。
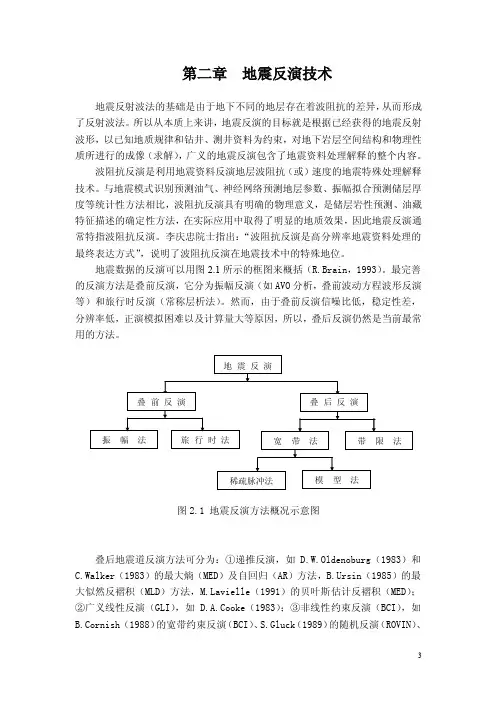
地震数据的反演可以用图2.1所示的框图来概括（R.Brain，1993）。
最完善的反演方法是叠前反演，它分为振幅反演（如AVO分析，叠前波动方程波形反演等）和旅行时反演（常称层析法）。
然而，由于叠前反演信噪比低，稳定性差，分辨率低，正演模拟困难以及计算量大等原因，所以，叠后反演仍然是当前最常用的方法。
图2.1 地震反演方法概况示意图叠后地震道反演方法可分为：①递推反演，如D.W.Oldenoburg（1983）和C.Walker（1983）的最大熵（MED）及自回归（AR）方法，B.Ursin（1985）的最大似然反褶积（MLD）方法，vielle（1991）的贝叶斯估计反褶积（MED）；②广义线性反演（GLI），如 D.A.Cooke（1983）；③非线性约束反演（BCI），如B.Cornish （1988）的宽带约束反演（BCI）、S.Gluck（1989）的随机反演（ROVIN）、R.D.Martinez（1988）的多参数约束反演（包括BCI、WLI和LCI）。
根据反演结果的频带特性又可分为：①带限法（如GLI、合成声波测井）；②稀疏脉冲法（如MED、AR、MLD、BED方法等）；③模型法（如BCI、ROVIN、LCI、Strata和Jason 方法等）。
杨氏模量和泊松比反射系数近似方程及叠前地震反演近年来，随着石油勘探技术的飞速发展，地震反演技术作为一种重要的勘探技术已经得到了广泛的应用。
在反演过程中，选择合适的反射系数模型是比较重要的，目前杨氏模量和泊松比反射系数近似方程是一种比较常用的方法。
本文的主要内容是阐述这种反射系数近似方程，以及它在叠前地震反演中的应用。
杨氏模量和泊松比反射系数近似方程的基本原理是，以杨氏模量和泊松比作为反射系数的参数，以一定的函数形式表达出反射系数，而这种反射系数更接近于真实地质结构中的真实反射系数。
具体而言，在参数方程中，杨氏模量M和泊松比μ被表达为：M=M0（1-2μ）/（1+2μ），μ=（M-M0）/（M+M0），其中M0为背景杨氏模量，M为地层杨氏模量。
而反射系数R的表达式为：R=(1-2μ)2/((1+2μ)2-4μ)。
从上面的分析可以看出，杨氏模量和泊松比反射系数近似方程的优点在于它能够捕捉到地质结构中的杨氏模量和泊松比变化，从而更好地模拟出反射系数。
在叠前地震反演中，杨氏模量和泊松比反射系数近似方程也可以用来计算叠前地震反射系数。
叠前地震反演的基本原理是把叠前地震反射系数看作一个三维反射系数地图，根据物理原理预先定义出一套反射系数模型，再根据杨氏模量和泊松比反射系数近似方程计算出反射系数，并用函数的形式表示出叠前地震反射系数地图，从而得到一套较真实的反射系数模型。
总之，杨氏模量和泊松比反射系数近似方程是一种比较常见的方法，它可以用来模拟地质结构，同时可以用来计算叠前地震反射系数，从而更加真实地反映地质结构。
本文讨论了杨氏模量和泊松比反射系数近似方程，以及它在叠前地震反演中的应用。
杨氏模量和泊松比反射系数近似方程可以用来描述地质结构，而在叠前地震反演中，也可以用这种方法构建一套更加真实的反射系数模型，从而更好地实现勘探目标。
反射特征模拟反演（VOLV）xcz地震反射特征模拟反演•地震反射特征模拟反演技术是一种针对薄层地质体预测的新思路，基本原理是从地震数据中去除子波从而得到反射率。
对于具有高信噪比的地震数据，可以解决远小于调谐厚度的薄层预测问题。
处理成果可以通过切片演化或时窗提取的方式，预测薄储层展布及其连通关系。
•Portniaguine和Castagna在2005年探讨了一种叠后谱反演方法，可以解决在小于调谐厚度时的薄层预测问题。
这个方法更多的从地质上意义上去考虑，而不是数学上的假设。
其重点在于通过分频方法来获取局部频谱信息（Castagna，等，2003年；Portniaguine，Castagna，2004年）。
这种谱反演或者薄层反演最终输出为反射系数序列，其视分辨率要远高于输入的地震数据，可以用来对薄储层进行精细的描述和刻画。
该方法在商业上称为ThinMan，是一种全新提取反射信息的方式，去除子波时并不会加大高频段的噪音，而地震分辨率却是得到了相应的提升。
地震反射特征模拟反演•我们基于该原理，对方法适当做了改进，作为岩相分析和储层预测方法之一镶嵌到iLoop油藏-地球物理综合研究平台上，用于与其它方法综合分析、研究复杂岩相、薄储层分布。
模块操作界面见图地震反射特征模拟反演•该方法主要包括两个步骤：首先是从地震数据中精细计算时变、空变子波。
这里井控参与还是有必要的，如果没有任何井，则采用统计的方法来计算子波；然后从地震数据中去除第一步计算得到的子波，这里采用了谱约束下的地震反演方法，约束条件来源于频谱分解计算过程。
•该方法在处理的过程中没有任何初始地质模型或解释方案参与，道与道计算方式无需初始模型和边界连续条件的约束，这是与常规反演方法的根本区别。
另外，该方法在频带范围内仍可以提高频率而不扩大噪音，传统的反褶积方法则做不到这一点。
•利用该技术对研究区三维地震数据进行处理，得到反射特征模拟反演数据体，并与井信息结合，综合开展岩相解释、薄储层预测。
地球物理反演简介引言自从我们这个行业诞生以来，地球物理学家就一直致力于求解反演问题。
在地球物理勘探中，解释人员总是基于地面观测数据如地震记录或势场记录来推断地下特性。
他们事先在头脑中形成一个粗糙的反映地面记录形成过程的模型，解释时通过这个粗糙的模型根据实际观测到的地面记录重构地下特性。
按现代的说法，这种根据观测数据推断地下特性的工作就是求解所谓的“反演问题”。
相反，“正演问题”就是在给定地下特征和特定的物理定律成立的前提下确定所能记录到的数据。
直到20世纪60年代初地球物理反演才真正在地球物理学家的头脑中扎下了根。
从那时开始，人们就尝试开展定量的和通用的地球物理反演，所采取的方法是一方面求助于理论的扩展，另一方面借助于计算机的能力将这些理论付诸实际应用。
应该指出，理论和计算机算法无论如何不可能替代最终裁决人——地球物理解释人员来决定最终反演结果是否有意义。
或许我们的子孙后代在写第22世纪的评论文章时会谈到机器在没有人的干预下已经解决了反演问题。
但就目前而言，所谓的“无监督地球物理反演”仍然是一个梦。
按照上述很广义的反演问题定义，我们在处理中心应用的那些熟悉的算法都可以看作地球物理数据的转换程序。
例如，地震偏移就是试图根据地震记录重建实际的地下地层形态（Gardner,1985）。
地层反射系数的反演可以通过预测反褶积衰减多次波反射来实现（Peacock 和Treitel,1969），或通过地层脉冲响应中一次波和多次波的模拟来实现（Lines 和Treitel,1984）。
振幅随偏移距的变化（AVO）（Castagna 和Backus,1993）处理包括地面振幅测量结果的岩性反演等等。
反演能处理不同类型的地球物理数据。
由此，人们能够将不同的地球物理数据集（诸如地震、势场和井中数据）与同一个地层模型同步地或顺序地进行拟合（如Lines等，1988）。
其它反演的例子很多，不胜枚举。
在每一种情况下，我们都假定物理定律是成立的。
反射系数反演原理提高地震资料分辨率一直是地震资料数字处理工作者的追求目标。
高分辨率地震资料数据处理的关键环节就是压缩地震子波，或者去除地震波在地下传播过程中干涉、调谐等效应对地下地层的影响，拓宽有效地震信号的频带范围，特别是较为准确地拓宽高频成分。
薄层的识别和厚度估计是当前地震石油勘探领域的主要研究方向。
薄层反射系数反演方法也就应运而生。
早在1999年Partyka在发表的文章中提出应用时频分析方法计算薄层厚度，即为薄层陷频法，他认为少数几个反射系数谱不像是长时窗反射系数谱一样是白噪，在频率域存在周期性的陷频规律，地震道的谱就是反射系数谱与子波谱的乘积，消去子波谱就能显示出陷频谱，从而进行薄层厚度的计算。
2001年K.J.Marfurt提出用滑动时窗的频谱分析方法计算多种频率相关的属性进行储层厚度定性解释，对薄窄河道展布规律进行描述。
上述两种方法尝试利用频谱分解的结果来求取薄层厚度，但如果地震频带宽度不足以清晰识别谱峰和陷频变化规律时，谱分解对于分辩薄层还是存在困难，这也推动了新方法的发展，无需精确识别频宽内的波峰和波谷，即为谱反演方法。
2005年Portniaguine和Castagna提出了一种叠后谱反演方法，来解决在小于调谐厚度时的薄层预测问题。
这个方法更多的从地质上去考虑，而不是数学上的假设。
其重点在于通过分频方法来获取局部频谱信息。
这种谱反演或薄层系数反演方法最终输出的为反射系数序列，其视分辨率要远高于输入的地震数据，可以用来对薄储层进行精细的描述和刻画。
并指出了该方法具有不需要任何先验模型、反射系数的数学假设、层位约束，也不需要井资料强制约束等优点，并可用来分辨小于调谐厚度的薄层[5,6]。
之后很多学者在谱反演方面做出很多研究成果。
Puryear和Castagna (2008)对谱反演理论给出了详细的说明，主要包括Widess楔形模型理论，把反射系数序列分解成偶分量和奇分量，发展了一种新的谱反演算法[7]。
Satinder Chopra, John Castagna和Yong Xu(2009)由谱反演所得的反射系数算出了波阻抗剖面，并将其应用到了层厚的确定和地层学解释中[8,9]。
袁三一博士和王尚旭教授等（2009）提出了一种相对快速的谱反演系数反演混合技术，其采用求解的算法是Particle Swarm Optimization (PSO)，粒子群算法和Levenberg - Marquardt(L-M)[10,11]。
Kelyn Paola Castaño 和 Germ án Ojeda(2010)采用遗传算法和模拟退火优化算法来求解Castagna 教授的基于反射系数序列奇偶原理的谱反演目标函数，并指出遗传算法效果比模拟退火算法稍好[12]。
1. Widess 模型1973年的薄层反射Widess 模型认为地震分辨率极限为1/8波长，如图1中所示，Widess 模型与30Hz 雷克子波褶积后峰值频率与层厚关系。
频率域内地震频谱振幅在1/4波长达到最大，当层薄至1/8波长时地震波形及频率不会再有明显变化，振幅逐渐减小。
实际情况下，假设条件是难以保证，顶底反射系数比不可能是连续变化的，不同反射系数比下峰值振幅、峰值频率与厚度的关系也不尽相同如图2。
图3奇偶分量峰值振幅、峰值频率与厚度的关系我们利用Chung和Lawton(1995)提出的方程计算了峰值振幅和峰值频率，图3分别表示为随层厚减薄时由奇部、偶部形成的反射系数对模型峰值振幅及峰值频率的变化。
根据这种模型的分析，显示了在偶部序列占优时奇部序列和偶部序列主峰振幅和频率的随层厚的变化特征，同时也显示了总的主频变化特征。
当薄层的顶底界面处反射系数并不相等、极性也不相反时，可以看到在小于调谐频率的一半时主频会随着层薄而减小。
这种变化的转折点位置取决于序列中偶部和奇部反射系数的相对大小。
与Widess模型相反的是，在层厚小于该点后，主频还依赖于地层厚度。
这说明与以往观点对比，地层响应对薄层更敏感。
由于奇偶分量峰值振幅、峰值频率随层厚的变化规律的确定性，地震资料的主频确定的情况下，对于单层厚度的地震模型，可以通过奇偶分解的方式，准确预测小于调谐厚度下的薄层厚度。
反射系数经过奇偶分解之后，奇分量与偶分量的主频随地层厚度变化是一个确定关系，通过这种关系，在主频已知的情况下可进行厚度的预测。
图4 单层厚度模型奇偶分解预测厚度图3. 谱反演的目标函数谱反演的原理就是根据时间域褶积模型，从地震记录中去除地震子波的影响，进而得到反射系数序列。
在时间域内一个脉冲对的表达为(如图5)：1121()()()g t r t t r t t T δδ=-+-- (1)其中1r 为层顶部反射系数，2r 为层底部反射系数，t 为时间位置，1t 为顶部反射的时间位置，T 为层厚度。
图5 两层反射率模型将分析点放在层的中心点位置，进行傅立叶变换后，用三角法则进行化简约去t ，得到：()2cos()2sin()e o g f r fT r fT ππ=+ (2)基于褶积原理，),(f t s 是地震数据，),(f t w 是已知的子波。
()⎰-+=wwt t o e dt t fT t ir t fT t r f t w f t s ]}sin[)()](cos[)({),(),(ππ (3)最后整理得到单层目标函数：()()()()()()()(),,,Re ,/,cos Im ,/(,)sin wHw wl w e o t e e f t t f o o t O r r T t a S t f W t f r t fT t dt df a S t f W t f r t fT t dt ππ-=⎡⎤⎧⎫⎪⎪⎢⎥-+⎡⎤⎡⎤⎨⎬⎣⎦⎣⎦⎢⎥⎪⎪⎩⎭⎢⎥⎧⎫⎢⎥⎪⎪-⎡⎤⎡⎤⎨⎬⎢⎥⎣⎦⎣⎦⎪⎪⎢⎥⎩⎭⎣⎦⎰⎰⎰ (4) 目标函数中，()(),/,S t f W t f 可以认为是反褶积过程，在这里我们假设子波是已知。
子波的正确与否将很大程度上影响反演的结果，因此子波的提取是一个非常重要的过程。
但是我们对于子波往往是不知道的，如果子波知道了，反射系数也就知道了。
因此我们做的是尽可能的使子波接近于真实子波。
厚度T,我们在反射系数中可以认为是第一层和最后一层的距离，第二层和倒数第二层的距离，依次类推。
在信号的奇偶分解中 我们可以认为是进行奇偶分解的信号对之间的距离。
以上的推导都是基于窗口中心位置的坐标为零，但实际上数据都是从零开始的，而窗口的中心位置坐标不可能为零，而是半个窗口的位置。
因此我们实际应用中应该对上面的推导加一时移。
实部和虚部时移后的谱可以表示为：2Im[()]2sin()cos(2)2cos()sin(2)i f t o e e g f r fT f t r fT f t πππππ∆=∆+∆ (5) 2Re[()]2cos()cos(2)2sin()sin(2)i f t e o e g f r fT f t r fT f t πππππ∆=∆-∆ (6)多层的目标函数变为：()()()()()(){}()()()(){}002()cos cos22sin 22sin cos22()c ,,,Re ,/,sin Im ,/(,)sin os 2wHwl e o e o t e f t f o o e O r r T t a S t f W t f fT t f t fT t f t dt df a S t f W t f fT t f t fT t r t r t r t r t f t dt ππππππππ+⎡⎤⎡⎤⎣⎦⎣⎦⎡⎤⎡⎤=⎡⎤⎧⎫⎪⎪-∆∆+⎡⎤⎢⎥⎨⎬⎣⎦⎪⎪⎢⎥⎩⎭⎢⎥⎧⎫⎪⎪⎢⎥-∆-∆⎡⎤⎨⎬⎣⎦⎢⎥⎪⎪⎩⎭⎣⎦⎦⎣⎣⎦⎰⎰⎰(7)其中，w t 为半个窗口的宽度；e a ，o a 为平衡参数。
其矩阵形式，形如：1111212233112233(()/())cos(2t )cos(2t )cos (()/())(()/())(()/())(()/())(()/())(()/())(()/())m m m m real X f W f f f real X f W f real X f W f real X f W f imag X f W f imag X f W f imag X f W f imag X f W f ππ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥-⎢⎥⎢⎥-⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦31n 1122232n 2132333n 3123n 112131(2t )cos(2t )cos(2t )cos(2t )cos(2t )cos(2t )cos(2t )cos(2t )cos(2t )cos(2t )cos(2t )cos(2t )cos(2t )cos(2t )sin(2t )sin(2t )sin(2t )sin(2m m m m f f f f f f f f f f f f f f f f f ππππππππππππππππππ123n 1122232n 2n 132333n 3123n (t )(t )(t )t )sin(2t )sin(2t )sin(2t )sin(2t )(t )sin(2t )sin(2t )sin(2t )sin(2t )sin(2t )sin(2t )sin(2t )sin(2t )m m m m r r r f f f f f r f f f f f f f f ππππππππππππ⎡⎤⎢⎥⎢⎥⎢⎥⎡⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎦(8)通常地震道采样点数远大于反射系数的个数，因此谱反演理论一部分就是为了解决(8)式的超定线性方程组求解的适定性和稳定性问题。
通常的迭代计算流程如下：图6 反射系数迭代计算流程任何反演方法都是一个系统工程，许多小环节的处理手段都会影响到反演的结果，子波提取、噪声及初始模型选取都对反演结果有影响。
在实际地震数据的处理中，反演过程大致包含以下几步：步骤一、子波提取，精细提取时变子波；步骤二、从地震数据中去除子波，提取计算反射系数的奇部和偶部；步骤三、根据稀疏脉冲反演计算初始反射系数的方法，反演出高频成分；步骤四、高频成分与奇部、偶部反射系数，由权重函数控制，组合出完整的宽频反射系数体。
