第二十四章圆小结与复习剖析

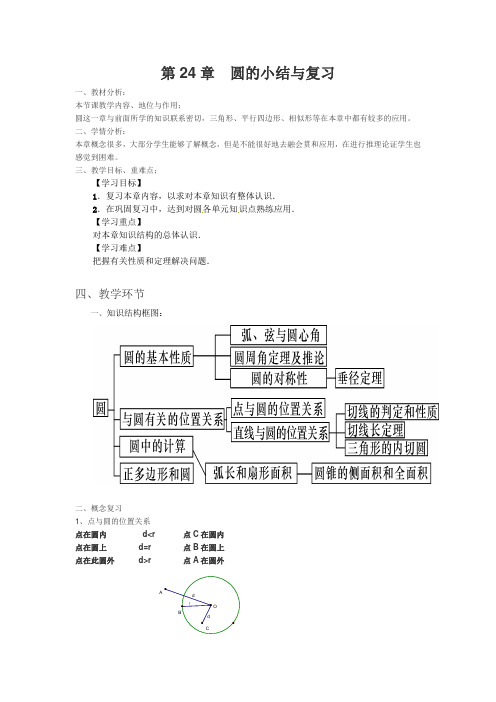
第二十四章《圆》小结一、本章知识结构框图二、本章知识点概括（一）圆的有关概念1、圆（两种定义）、圆心、半径；2、圆的确定条件：①圆心确定圆的位置，半径确定圆的大小；②不在同一直线上的三个点确定一个圆。

3、弦、直径；4、圆弧（弧）、半圆、优弧、劣弧；5、等圆、等弧，同心圆；6、圆心角、圆周角；7、圆内接多边形、多边形的外接圆；8、割线、切线、切点、切线长；9、反证法：假设命题的结论不成立，由此经过推理得出矛盾，由矛盾断定所作假设不正确，从而得到原命题成立。

（二）圆的基本性质1、圆的对称性①圆是轴对称图形，任何一条直径所在的直线都是它的对称轴。

*②圆是中心对称图形，圆心是对称中心。

2、圆的弦、弧、直径的关系①垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的两条弧。

②平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧。

* [引申] 一条直线若具有：Ⅰ、经过圆心；Ⅱ、垂直于弦；Ⅲ、平分弦；Ⅳ、平分弦所对的劣弧；Ⅴ、平分弦所对的优弧，这五个性质中的任何两条，必具有其余三条性质，即“知二推三”。

（注意：具有Ⅰ和Ⅲ时，应除去弦为直径的情况）3、弧、弦、圆心角的关系①在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等。

②在同圆或等圆中，如果两条弧相等，那么它们所对的圆心角相等，所对的弦相等。

③在同圆或等圆中，如果两条弦相等，那么它们所对的圆心角相等，所对的弧相等。

归纳：在同圆或等圆中，两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量也相等。

4、圆周角的性质①定理：在同圆或等圆中，同弧或等弧所对圆周角相等，都等于这条弧所对的圆心角的一半。

②在同圆或等圆中，如果两个圆周角相等，它们所对的弧一定相等。

③推论：半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径。

（三）与圆有关的位置关系1、点与圆的位置关系设⊙O的半径为r，OP=d则：点P在圆内d<r；点P在圆上d=r；点P在圆外d>r.2、直线与圆的位置关系设⊙O的半径为r，圆心O到l的距离为d则：直线l与⊙O相交d<r 直线和圆有两个公共点；直线l与⊙O相切d=r 直线和圆只有一个公共点；直线l与⊙O相离d>r 直线和圆没有公共点。

第24章 圆的小结与复习一、教材分析： 本节课教学内容、地位与作用； 圆这一章与前面所学的知识联系密切，三角形、平行四边形、相似形等在本章中都有较多的应用。

二、学情分析：本章概念很多，大部分学生能够了解概念，但是不能很好地去融会贯和应用，在进行推理论证学生也感觉到困难。

三、教学目标、重难点；【学习目标】1．复习本章内容，以求对本章知识有整体认识． 2．在巩固复习中，达到对圆各单元知识点熟练应用．【学习重点】对本章知识结构的总体认识．【学习难点】把握有关性质和定理解决问题．四、教学环节一、知识结构框图：二、概念复习 1、点与圆的位置关系点在圆内 d<r 点C 在圆内点在圆上 d=r 点B 在圆上点在此圆外 d>r 点A 在圆外2、直线与圆的位置关系•直线与圆相离d>r 无交点•直线与圆相切d=r 有一个交点•直线与圆相交d<r 有两个交点3、垂径定理垂径定理：垂直于弦的直径平分这条弦并且平分这条弦所对的两条弧推论：（1）平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧；（2）弦的垂直平分线经过圆心，并且平分弦所对的两条弧；以上共3个定理，简称2推3定理：此定理中共5个结论中，只要知道其中2个即可推出其它3个结论，即：①AB是直径②AB⊥CD ③CE=DE ④⑤①②③④⑤或①③②④⑤或……4、圆心角定理•圆心角定理：在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等，所对弦的弦心距相等此定理也称1推3定理，即上述四个结论中，只要知道其中的1个相等，则可以推出其它的3个结论也即：①∠AOB=∠DOE ②AB=DE ③OC=OF ④①②③④或②①③④……即：∠AOB=2∠ACB5、圆周角定理的推论：推论1：在同圆或等圆中,同弧或等弧所对的圆周角相等，相等的圆周角所对的弧也相等。

即：∠C=∠D推论2：半圆或直径所对的圆周角是直角；90°的圆周角所对的弦是直径即：在⊙O中，∵AB是直径或∵∠C=90°∴∠C=90°∴AB是直径6、圆内接四边形圆的内接四边形定理：圆的内接四边形的对角互补，外角等于它的内对角.即：在⊙O中，∵四边形ABCD是内接四边形，∴∠C+∠BAD=180°，B+∠D=180°，∠DAE=∠C7、切线的性质与判定定理（1）性质定理：圆的切线垂直于过切点的半径（如上图）∵MN是切线∴MN⊥OA（2）判定定理：经过半径外端并且垂直于这条半径的直线是圆的切线两个条件：过半径外端且垂直半径，二者缺一不可即：∵MN⊥OA且MN过半径OA外端∴MN是⊙O的切线切线长定理切线长定理： 从圆外一点引圆的两条切线，它们的切线长相等，圆心与这一点的连线平分两条切线的夹角. 即：∵PA 、PB 是的两条切线，∴PA=PB ，PO 平分∠BPA8、圆内接正多边形的计算（1）正三角形1::2弧长、扇形面积公式（1）弧长公式： （2）扇形面积公式：三、随堂训练 学生把通过“自学互研”得出的结论展示出来，并将疑难问题板演到黑板上由学生进行讨论，老师最后再予以点评。

第二十四章圆小结与复习1.12.23.3圆是轴对称图形有无数条对称轴过圆心的每一条直线，过圆中一点最长的弦是直径最短的弦是与垂直的弦，弧的度数等于它所对的圆心角的度数，圆周角定理一条弧所对的圆周角等于它所对的圆心角的一半。

第二十四章圆小结与复习2017-10-30 13:32:47 | #1楼第二十四章圆小结与复习24.1.1圆一、圆的概念1、圆的定义：（1）（2）2、圆的特征（1）（2）3、确定圆的条件：圆心、半径二、圆的有关概念弦、直径、虎半圆、优虎劣虎等圆、同心圆、等虎弦心距（10个）注：1、直径是弦，但弦不是直径2、半圆是虎但弧不是半圆三、圆的对称性1、圆是轴对称图形，有无数条对称轴（过圆心的每一条直线）2、圆是中心对称图形，圆心是对称中心（也是旋转对称图形，具有旋转不变性） 24.1.2垂径定理1、以下五个条件任意两个，均可得出其余三个：（1）过圆心的直线（2）垂直于弦（3）平分弦（4）平分优弧（5）平分劣弧（强调平分的弦不是直径）2、常用辅助线：连半径、做弦心距3、过圆中一点P最长的弦是直径，最短的弦是与OP垂直的弦4、垂径定理常常与勾股定理合用求值。

24.1.3虎弦、圆心角、弦心距1、圆心角：2、弧的度数等于它所对的圆心角的度数。

3、四者关系、推论：（前提：在同圆或等圆中）24.14圆周角1、圆周角:①②2、圆周角定理：一条弧所对的圆周角等于它所对的圆心角的一半。

3、圆周角定理的推论：（1）同弧或等弧所对的圆周角相等；在同圆或等圆中，相等圆周角所对的弧也相等。

（2）半圆（或直径）所对圆周角是直角，90°的圆周角所对的弦是直径，所对的弧是半圆。

（给直径想直角；给90°圆周角想直径）（3）在同圆或等圆中，同弦或等弦所对的圆周角相等或互补。

（同侧：相等;异侧：互补）（4）如果三角形一边上的中线等于这条边的一半，那么这个三角形是直角三角形。

注：1、有弧找角、有角找弧是证明弧相等、角相等的常用思想。

第24章圆小结与复习、圆的概念集合形式的概念：i、圆可以看作是到定点的距离等于定长的点的集合;2、圆的外部：可以看作是到定点的距离大于定长的点的集合;3、圆的内部：可以看作是到定点的距离小于定长的点的集合轨迹形式的概念:1、圆：至U定点的距离等于定长的点的轨迹就是以定点为圆心，定长为半径的圆;（补充）2、垂直平分线：到线段两端距离相等的点的轨迹是这条线段的垂直平分线（也叫中垂线）；3、角的平分线：到角两边距离相等的点的轨迹是这个角的平分线；4、到直线的距离相等的点的轨迹是：平行于这条直线且到这条直线的距离等于定长的两条直线；5、到两条平行线距离相等的点的轨迹是：平行于这两条平行线且到两条直线距离都相等的一条直线。

练习题：一个圆的直径为8cm，到圆心的距离为则该点在圆_______________三、直线与圆的位置关系1、直线与圆相离— d • r = 无交点;2、直线与圆相切— d =r―有一个交点;3、直线与圆相交—d r―有两个交点;1、点在圆内— d :: r—点C在圆内;2、点在圆上― d = r―点B在圆上;3、点在圆外— d r—点A在圆外;5cm,、点与圆的位置关系练习题：、一个点到圆的最短距离为 3cm ，到圆的最长距离为 9cm ，则这个圆的半径为四、垂径定理垂径定理：垂直于弦的直径平分弦且平分弦所对的弧。

推论1：（ 1）平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧;（2）弦的垂直平分线经过圆心，并且平分弦所对的两条弧； （3）平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧以上共4个定理，简称2推3定理：此定理中共 5个结论中，只要知道其中 2个即可推出其它3个结论，即:六、圆周角定理①AB 是直径② AB _CD③CE =DE ④弧BC =弧BD⑤弧AC =弧AD中任意2个条件推出其他3个结论。

推论2：圆的两条平行弦所夹的弧相等。

即:在O O 中，T AB // CD•••弧 AC 二弧 BD五、圆心角定理圆心角定理：同圆或等圆中，相等的圆心角所对的弦相等，所对 的弧相等，弦心距相等。

第二十四章圆（小结与复习）一、学习目标：1. 了解圆的有关概念，探索并理解垂径定理，探索并认识圆心角、弧、•弦之间的相等关系的定理，探索并理解圆周角和圆心角的关系定理．2. 探索并理解点和圆、直线与圆以及圆与圆的位置关系：了解切线的概念，•探索切线与过切点的直径之间的关系，能判定一条直线是否为圆的切线，会过圆上一点画圆的切线．3. 进一步认识和理解正多边形和圆的关系和正多边的有关计算．4. 熟练掌握弧长和扇形面积公式及其它们的应用；•理解圆锥的侧面展开图并熟练掌握圆锥的侧面积和全面积的计算．二、学习重点、难点：1. 重点:1．平分弦（不是直径）的直径垂直于弦，•并且平分弦所对的两条弧及其运用．2．在同圆或等圆中，相等的圆心角所对的弧相等，•所对的弦也相等及其运用．3．在同圆或等圆中，同弧或等弧所对的圆周角相等，•都等于这条弧所对的圆心角的一半及其运用．4．半圆（或直径）所对的圆周角是直角，90•°的圆周角所对的弦是直径及其运用．5．不在同一直线上的三个点确定一个圆．6．直线L和⊙O相交⇔d<r；直线L和圆相切⇔d=r；直线L和⊙O 相离⇔d>r及其运用．7．圆的切线垂直于过切点的半径及其运用．8．•经过半径的外端并且垂直于这条半径的直线是圆的切线并利用它解决一些具体问题．9．从圆外一点可以引圆的两条切线，它们的切线长相等，•这一点和圆心的连线平分两条切线的夹角及其运用．10．两圆的位置关系：d与r1和r2之间的关系：外离⇔d>r1+r2；外切⇔d=r1+r2；相交⇔│r2-r1│<d<r1+r2；内切⇔d=│r1-r2│；内含⇔d<│r2-r1│．11．正多边形和圆中的半径R、边心距r、中心角θ之间的等量关系并应用这个等量关系解决具体题目．12．n°的圆心角所对的弧长为L=180n R π，n°的圆心角的扇形面积是S扇形=2360n R π及其运用这两个公式进行计算．13．圆锥的侧面积和全面积的计算． 2. 难点:1．垂径定理的探索与推导及利用它解决一些实际问题．2．弧、弦、圆心有的之间互推的有关定理的探索与推导，•并运用它解决一些实际问题．3．有关圆周角的定理的探索及推导及其它的运用． 4．点与圆的位置关系的应用．5．三点确定一个圆的探索及应用．6．直线和圆的位置关系的判定及其应用．7．切线的判定定理与性质定理的运用．8．切线长定理的探索与运用．9．圆和圆的位置关系的判定及其运用．10．正多边形和圆中的半径R 、边心距r 、中心角θ的关系的应用． 11．n 的圆心角所对的弧长L=180n R π及S 扇形＝2360n R π的公式的应用．12．圆锥侧面展开图的理解． 三、学习过程： (一)自主学习1.在同圆或等圆中的弧、弦、圆心角、有什么关系？一条弧所对的圆周角和它所对的圆心角有什么关系？2.垂径定理的内容是什么？推论是什么？3.点与圆有怎样的位置关系？直线和圆呢？圆和圆呢？怎样判断这些位置关系？请你举出这些位置关系的实例？4.圆的切线有什么性质？如何判断一条直线是圆的切线？5.正多边形和圆有什么关系？你能用正多边形和等分圆周设计一些图案吗？6.举例说明如何计算弧长、扇形面积、圆锥的侧面积和全面积？（二）合作探究例1：如图，P 是⊙O 外一点，PAB 、PCD 分别与⊙O 相交于A 、B 、C 、D.(1)PO 平分∠BPD ；(2)AB =CD ；(3)OE ⊥CD ，OF ⊥AB ；(4)OE =OF .从中选出两个作为条件，另两个作为结论组成一个真命题，并加以证明，与同伴交流.ABPOE FCD例2：如图，AB 是⊙O 的弦，OA OC ⊥交AB 于点C ，过点B 的直线交OC 的延长线于点E ，当BE CE =时，直线BE 与⊙O 有怎样的位置关系？并证明你的结论．例3：（1）如图，圆心角都是90°的扇形OAB 与扇形OCD 叠放在一起，•OA=3，OC=1，分别连结AC 、BC ，则圆中阴影部分的面积为（ ） A ．12π B ．π C ．2π D ．4π（2）如图,在Rt △ABC 中，∠C=90°,AC=1,BC=2．以边BC 所在直线为轴，把△ABC 旋转一周,得到的几何体的侧面积是 A ．π B ．2π C ．5π D ．25π（三）巩固练习1.教材120页复习题24第1题。

前言：
该教学设计（教案）由多位一线国家特级教师根据最新课程标准的要求和教学对象的特点结合教材实际精心编辑而成。

实用性强。

高质量的教学设计（教案）是高效课堂的前提和保障。

（最新精品教学设计）
第二十四章《圆》小结
一、本章知识结构框图
二、本章知识点概括
（一）圆的有关概念
1、圆（两种定义）、圆心、半径；
2、圆的确定条件：
①圆心确定圆的位置，半径确定圆的大小；
②不在同一直线上的三个点确定一个圆。

3、弦、直径；
4、圆弧（弧）、半圆、优弧、劣弧；
5、等圆、等弧，同心圆；
6、圆心角、圆周角；
7、圆内接多边形、多边形的外接圆；
- 1 -。

第２４章《圆》复习与小结【学习目标】1．梳理本章知识，使知识系统化；2．能利用圆的重要性质与切线的性质、判定进行证明和计算.３.掌握正多边形的有关计算，掌握弧长、扇形面积、圆锥侧面积的计算.【学习重点】梳理本章知识，圆的性质和切线的判定、性质【学习难点】综合运用几何知识证明与计算，感悟数形结合、分类讨论思想.【学习过程】一、知识梳理：学生自学课本第１２１—１２２页内容（一）知识结构图：（二）圆的重要性质：（请结合图形回忆有关定理）１. 垂径定理及推论：２.圆心角、弧、弦：３.圆周角定理及推论：４.圆内接四边形性质：OED C'BAA'OCAOB1（三）与圆有关的位置关系：1．点与圆的位置关系:设⊙O 的半径为r ，OP=d 则： 点P 在圆内； 点P 在圆上； 点P 在圆外.2．直线与圆的位置关系设⊙O 的半径为r ，圆心O 到l 的距离为d 则： 直线l 与⊙O 相交 直线和圆有两个公共点； 直线l 与⊙O 相切 直线和圆只有一个公共点； 直线l 与⊙O 相离直线和圆没有公共点.３.切线的判定：（两种思路） ４.切线的性质 ５. 切线长定理（四）正多边形的计算：正多边形的计算→直角三角形的计算（中心角αn ，边长a n ，半径R n ，边心距r n ，周长l n ，面积S n ）（五）扇形、圆柱和圆锥的相关计算公式1、扇形：（1）弧长公式：180n Rlπ=；（2）扇形面积公式： 213602n R S lR π== 2、圆柱：DCBAOCBAOEDCBABODCBAOECBADOBAO母线长底面圆周长C 1D 1DC30°DOB AC（1）圆柱侧面展开图 2S S S =+侧表底=222rh r ππ+（2）圆柱的体积：2V r h π=（2）圆锥侧面展开图 （1）S S S =+侧表底=2Rr r ππ+（2）圆锥的体积：213V r h π=（六）本章常用数学思想： .二，典例精析：1.如图，AB 是⊙O 的切线，B 为切点，圆心在AC 上，∠A =30°，D 为»BC的中点．(1)求证:AB =BC ；(2)求证:四边形BOCD 是菱形．【解题反思】： . 2.如图，在△ABC 中，∠ABC =90°，D 是边AC 上的一点，连接BD ，使∠A =2∠1，E 是BC 上的一点，以BE 为直径的⊙O 经过点D . （1）求证：AC 是⊙O 的切线；（2）若∠A =60°，⊙O 的半径为2，求阴影部分的面积.（结果保留根号和π）【解题反思】： . 3.如图，在平面直角坐标系中，以点O 为圆心，半径为2的圆与y 轴交于点A ，点P （4，2）是⊙O 外一点，连接AP ，直线PB 与⊙O 相切于点B ，交x 轴于点C. （1）证明PA 是⊙O 的切线；（2）求点B的坐标.４．如图1，一辆汽车的背面，有一种特殊形状的刮雨器，忽略刮雨器的宽度可抽象为一条折线OAB，如图2所示，量得连杆OA长为10cm，雨刮杆AB长为48cm，∠OAB=120°．若启动一次刮雨器，雨刮杆AB正好扫到水平线CD的位置，如图3所示．（1）求雨刮杆AB旋转的最大角度及O、B两点之间的距离；（结果精确到0.01）（2）求雨刮杆AB扫过的最大面积．（结果保留π的整数倍）【解题反思】： .5.如图，在半径为2的扇形AOB中，∠AOB=90°，点C是弧AB上的一个动点（不与点A、B重合）OD⊥BC，OE⊥AC，垂足分别为D、E．（1）当BC=1时，求线段OD的长；（2）在△DOE 中是否存在长度保持不变的边？如果存在，请指出并求其长度，如果不存在，请说明理由；（3）设BD =x ，△DOE 的面积为y ，求y 关于x 的函数关系式，并写出它的定义域．【解题反思】： . 三、巩固与应用：1.如图，以AB 为直径的⊙O 与弦CD 相交于点E ，且AC =2，AE =，CE =1．则弧BD 的长是（ ）A ．B ．C ．D ．2.如图，半圆O 的直径AB=10cm ，弦AC=6cm ，AD 平分∠BAC ，则AD 的长为（ ） A.cmB ．cmC ．cmD ． 4cm3.如图所示，ABC △是的内接三角形，AC BC =，D 为中上一点，延长DA至点E ，使CE CD =．（1）求证：AE BD =；（2）若AC BC ⊥，求证：2AD BD CD +=．四、小结： 1.理解记忆有关概念和定理；２.领会“两头凑”的探究方法. 五、作业：必做：课本P124习题T9、１０、1３、1５、１６；选做：《作业精编》相应练习.。