第三章真值表的判断作用

真值表名词解释真值表是计算机科学中的一个重要概念，它可以用来设计计算机中的程序。

真值表是用来确定真假的表格，它的功能就是将输入的真假的数据转换成指定的输出。

一个真值表可以通过将真假的条件成对地列出来，然后按照相应的规则来确定真假，从而实现一个程序的功能。

一个真值表可以由一到多个变量组成，每一个变量都有相应的取值，比如0或1。

一般而言，在一个普通的真值表中，0表示假，1表示真，但也可以使用其他的取值来表示真和假，比如Yes和No。

对于一个真值表，输入的真假的数据可以通过真假的规则确定输出的结果，每一组输入数据可以按照特定的规则确定一个输出，从而实现真假的判断。

一个真值表可以用来控制一个计算机程序的运行，可以用来解决多种问题，比如数学、科学和工程等。

真值表中的参数可以按照不同的模式来执行，比如逻辑模式、数学模式和统计模式等。

每一种模式都有自己的输入和输出。

比如逻辑模式可以以如下规则输入：如果A 等于B，那么结果就是真；如果A不等于B，那么结果就是假。

统计模式的输入可以是：如果X大于Y，那么结果就是真；如果X不大于Y，那么结果就是假。

真值表在计算机系统中起着重要作用，它可以帮助我们控制不同的计算机程序，实现复杂的功能。

真值表可以提供更多精度，可以更好地处理不同的数据，而这也是程序设计和计算机编程中非常重要的一点。

在程序设计中，真值表是一种非常常用的工具，它可以提高程序的运行效率和准确性。

真值表的使用方法很简单，只需要将真假的参数输入，然后按照指定的规则确定真假，然后输出指定的结果。

真值表可以很容易地理解，同时也可以用来解决很多复杂的问题。

总之，真值表是计算机科学中一个非常重要的概念，它可以帮助我们更好地控制计算机程序，实现复杂的功能。

真值表的使用方法简单易懂，只需要按照规则输入数据，然后输出指定的结果，从而提高了程序的准确性和运行效率。

第3章[题3.1] 分析图P3.1电路的逻辑功能，写出Y 1、、Y 2的逻辑函数式，列出真值表，指出电路完成什么逻辑功能。

[解]BCAC AB Y BCAC AB C B A ABC Y ++=+++++=21)(B 、C 为加数、被加数和低位的进位，Y 1为“和”，Y 2为“进位”。

[题3.2] 图P3.2是对十进制数9求补的集成电路CC14561的逻辑图，写出当COMP=1、Z=0、和COMP=0、Z=0时，Y 1～Y 4的逻辑式，列出真值表。

[解]（1）COMP=1、Z=0时，TG 1、TG 3、TG 5导通，TG 2、TG 4、TG 6关断。

3232211 , ,A A Y A Y A Y ⊕===， 4324A A A Y ++=（2）COMP=0、Z=0时，Y 1=A 1， Y 2=A 2， Y 3=A 3， Y 4=A 4。

COMP =0、Z=0的真值表从略。

[题3.3] 用与非门设计四变量的多数表决电路。

当输入变量A 、B 、C 、D 有3个或3个以上为1时输出为1，输入为其他状态时输出为0。

[解] 题3.3的真值表如表A3.3所示，逻辑图如图A3.3所示。

ABCD D ABC D C AB CD B A BCD A Y ++++= BCD ACD ABC ABC +++=B C D A C D A B D A B C ⋅⋅⋅=[题3.4] 有一水箱由大、小两台泵M L 和M S 供水，如图P3.4所示。

水箱中设置了3个水位检测元件A 、B 、C 。

水面低于检测元件时，检测元件给出高电平；水面高于检测元件时，检测元件给出低电平。

现要求当水位超过C 点时水泵停止工作；水位低于C 点而高于B 点时M S 单独工作；水位低于B 点而高于A 点时M L 单独工作；水位低于A 点时M L 和M S 同时工作。

试用门电路设计一个控制两台水泵的逻辑电路，要求电路尽量简单。

[解] 题3.4的真值表如表A3.4所示。

逻辑学真值表法
逻辑学真值表法是一种常用的推理方法，它可以帮助我们研究、解释和理解复杂的或超越思维能力的问题。

它是一种基于逻辑规则的知识表示法，为给定的条件和结果构建一种以真值表的形式运算的推导系统，从而完成推理和判断工作。

绘制真值表是实现此类推理的基本步骤。

真值表一般由有终止性的几个命题组成，每个命题都有两个可能的真假值，即真和假。

通过将这些真假值进行组合，可以确定输入命题和输出命题者之间的关系。

结果，关于给定条件或结论的结论可以提出。

在使用逻辑学真值表法之前，必须先弄清楚问题当中的信息，以及我们要得到的结果。

通常，我们需要将问题表达成操作，接着写出信息和推测，再将命题连接起来，用Negation，Disjunction，Conjunction和implication来构建命题，从而明确解决问题的思路。

接着，就可以使用真值表来回答问题了。

简而言之，要使用逻辑学真值表法来解决问题，必须首先明确问题的描述，然后将问题表达为的操作和命题，最后通过真值表法得出答案。

真值表法是一种有效的推理方法，掌握了它，就可以有效地解决复杂的问题，从而提高求解能力和解决问题的速度。

因此，它是一种有效的学习工具，是非常重要的数学和逻辑学知识。

命题逻辑的真值表和范式命题逻辑是研究命题（陈述句）之间的逻辑关系的一种逻辑学分支。

在命题逻辑中，我们使用真值表和范式来表示和分析命题的逻辑结构。

本文将介绍真值表和范式在命题逻辑中的重要性和应用。

一、真值表真值表是用来表示和计算命题的真假值情况的一种工具。

它列举了命题中每个命题变量的可能取值情况，并根据命题之间的逻辑运算规则计算出整个命题的真假值。

真值表通常由命题变量和逻辑运算符组成。

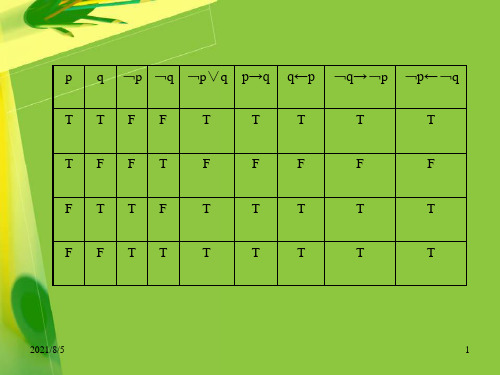
例如，对于两个命题变量P和Q，我们可以构建如下的真值表：P | Q | P∧Q | P∨Q | P→Q | P↔Q----------------------T | T | T | T | T | T----------------------T | F | F | T | F | F----------------------F | T | F | T | T | F----------------------F | F | F | F | T | T在真值表中，"T"代表命题的真值为真，"F"代表命题的真值为假。

通过观察真值表，并根据命题之间的逻辑运算规则，我们可以推断出命题之间的逻辑关系。

例如，P∧Q表示P与Q的合取，只有当P和Q 都为真时，合取才为真。

类似地，P∨Q表示P与Q的析取，只要P和Q中至少有一个为真，析取就为真。

真值表为我们提供了一种清晰的逻辑分析工具，能够帮助我们理解和推理命题之间的逻辑关系。

二、范式范式是用来简化和表示复杂命题的一种方法。

它将命题表示为若干个简单命题之间的逻辑连接，并以逻辑运算符为界限构成。

在命题逻辑中，最常见的范式有析取范式（DNF）和合取范式（CNF）。

析取范式将命题表示为若干个合取式之间的析取，而合取范式将命题表示为若干个析取式之间的合取。

例如，对于命题P、Q和R，我们可以将它们表示为析取范式和合取范式。

析取范式（DNF）：(P∧Q∧¬R)∨(¬P∧Q∧R)∨(¬P∧¬Q∧R)合取范式（CNF）：(P∨¬Q∨¬R)∧(¬P∨Q∨¬R)∧(¬P∨Q∨R)范式的使用可以帮助我们简化和理解复杂的逻辑表达式。

第三章真值表的判定作用第一节重言式矛盾式可满足式一、真值联结词比较下面两个例子1、如果天下雨，那么地上湿。

2、如果2+2=4，那么北京是个大城市。

第一例我们听起来就觉得顺耳，符合我们的语言习惯。

第二句我们听起来觉得有点别扭，不符合我们的语言习惯。

这就说明我们平时说“如果……那么……”时除了考虑前后件的真假以外，还考虑了前后件之间意义上的联系。

但是从现代逻辑的观点看，这两个命题都是正确的。

因为现代逻辑撇开了命题间意义上的联系，仅研究命题间的真假关系。

由于现代命题逻辑和传统逻辑一样都属二值逻辑，真和假是命题仅有的两个值，统称“真值”，因此，复合命题与肢命题之间在真假方面的联系，就是真值联系。

所谓真值联结词是指仅仅表示复合命题与肢命题之间真假关系的联结词。

基本的真值联结词有五个1、否定（并非）┒2、合取（并且）∧3、析取（或者）∨4、蕴涵（如果……那么……）→5、等值（当且仅当……才）←二、真值形式定义：真值形式是指由真值联结词和命题变项所构成的形式结构。

第二章所讲的所有的复合命题的形式结构和复合命题推理的形式结构都是真值形式。

但是第五章中的讲的性质命题和第六章所讲的关系的命题不是真值形式。

例：P∧q （P∧q）→P 是真值形式但 SAP aRb 不是真值形式真值形式是命题形式的一部分。

最基本的真值形式有五种1、否定式：┒P2、合取式：P∧q3、析取式：P∨q4、蕴涵式：P→q5、等值式：P←q其他的真值形式都是由这五种基本真值形式构成的。

三、重言式、矛盾式、可满足式（一）重言式的定义如果一真值形式不论其中的变项赋什么值，这个真值形式的值总是真的，这样的真值形式叫做重言式。

（重言式）如P∨ ┑q，P→P等等（二）矛盾式的定义如果一真值形式不论其中的变项赋什么值，这个真值形式的值总是假的，这样的真值形式就叫矛盾式。

（永假式）如P∧ ┑q（三）可满足式的定义如果一真值形式当其中的变项赋不同的值后，这个真值形式的值在有些情况下是真的，在有些情况下是假的，那么这样的真值形式就是可满足式。