下载文档原格式
板壳理论课程设计第一部分 学习心得第二部分文克勒地基上的基础板解题法题目：文克勒地基上的四边简支薄板中心受集中荷载的解法设文克勒地基上放置一个正方形薄板，边长为a=1.6m,厚度0.08m δ=，如图所示，四边均为简支边，在薄板的中心受有集中力的作用，0 1.07F e N =。
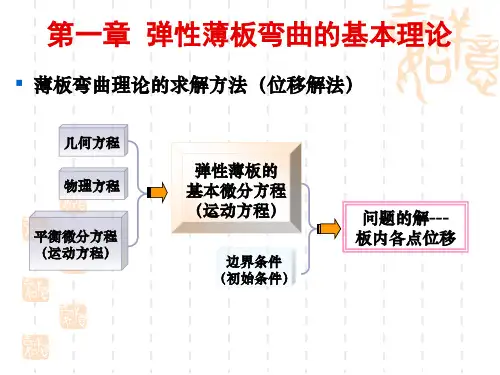
取薄板弹性模量E =205a GP ，泊松比0.3μ=，1k = ，取坐标轴如图所示， 方法1——纳维解法当并无支座沉陷时，其边界条件为(((( 把挠度w 的表达式取为如下的重三角级数：11sin sin mn m n m x n yw A a b ππ∞∞===∑∑（1）其中的m 和n 都是任意正整数。
显然，上列的边界条件都能满足。
将式（1）代入弹性曲面的微分方程4D w q ∇=中，但是在薄板承受横向荷载而发生挠度时，弹性地基将对薄板作用一定的分布反力，即所谓弹性抗力。
在文克勒地基中，地基对薄板所施反力的集度P ，是和薄板的挠度w 成正比而方向相反，即p kw =-，这样，薄板所受横向分布力的总集度将为p q +，因此薄板弹性曲面的微分方程oX须改变成为4k qD w wD D∇+=此时，将荷载q也展为同一形式的级数，即（2）将式（1）和式（2）代入微分方程4k qD w wD D∇+=中，即得002242224sin sin()a bmnm x n yq dxdyab a bAm nD ka bπππ=++⎰⎰（3）当薄板在任意一点(),ξη受集中荷载F时，可以得到当薄板在任意一点(),ξη受集中荷载F时，可以用微分面积dxdy上的均布荷载Fdxdy来代替分布荷载q，于是除了在(),ξη处的微分面积上等于Fdxdy以外，在其余各处都等于零。
22421122sin sin4sin sin()m nm nF m x n ya bwm nab a bD ka bπξπηπππ∞∞===++∑∑（4）由题意，当集中荷载作用在薄板中心时，中心处()0.8,0.8的挠度最大，将坐标点()0.8,0.8代入式（4）,结果如下图所示00114sin sin sin sina bm nm x n y m x n yq q dxdyab a b a bππππ∞∞==⎡⎤=⎢⎥⎣⎦∑∑⎰⎰解得max 3.092e w =-方法2——差分法2.1网格（4*4）差分法用4*4网格求解4a h ⎛⎫= ⎪⎝⎭。
板壳理论课程设计对工科各专业说来，弹性力学的任务和材料力学、结构力学的任务一样，是分析各种结构或其构件在弹性阶段的应力和位移，校核它们是否具有所需的强度和刚度，并寻求或改进它们的计算方法。
然而，它们之间还存在着一些不同。
材力中，基本上只研究杆状结构，即长度远大于高度和宽度的构件。
而材料力学中主要研究的是这种构件在拉压、剪切、弯曲、扭转作用下的应力和位移。
结构力学中，主要是在材料力学的基础上研究杆状构件所组成的结构，即杆件系统。
至于非杆状结构，则是弹性力学的主要研究内容。
在弹性力学中，研究杆状结构一般都不用诸如一些关于构建的从8主要是研0.1m均布载荷为q=得到结果如下：纳维解法四边简支的正方形薄板，四边无支座沉陷时，边界条件为把挠度表示为如下的重三角级数：代入弹性曲面的微分方程，得A，须将式子右边展为与左边同样的重三角，即为求出系数mn得到与(b)式对比，得当薄板受到均布载荷时，q 成为0q ，则式(d)积分成为则得到：对挠度表达式的后部运用Matlab 进行编程迭代，在确定收敛之后，可以得到：厚度为0.2m 时：● 其中，◆ 差分方程： 化简后得：改为矩阵形式，为： 得到：厚度为0.2m 时： 厚度为0.1m 时： 厚度为0.05m 时： 厚度为0.01m 时：● 有限元法厚度为0.2m时：创建壳实体，在材料赋定时确定厚度，得到在中心点有最大位移创建3D实体，得到在中心点有最大位移：厚度为0.1m时：创建壳实体，在材料赋定时确定厚度，得到在中心点有最大位移 厚度为0.05m时：创建壳实体，在材料赋定时确定厚度，得到在中心点有最大位移创建3D实体，得到在中心点有最大位移：厚度为0.01m时：创建壳实体，在材料赋定时确定厚度，得到在中心点有最大位移创建3D实体，得到在中心点有最大位移：●。
板壳理论课程设计对工科各专业说来，弹性力学的任务和材料力学、结构力学的任务一样，是分析各种结构或其构件在弹性阶段的应力和位移，校核它们是否具有所需的强度和刚度，并寻求或改进它们的计算方法。
然而，它们之间还存在着一些不同。
材力中，基本上只研究杆状结构，即长度远大于高度和宽度的构件。
而材料力学中主要研究的是这种构件在拉压、剪切、弯曲、扭转作用下的应力和位移。
结构力学中，主要是在材料力学的基础上研究杆状构件所组成的结构，即杆件系统。
至于非杆状结构，则是弹性力学的主要研究内容。
在弹性力学中，研究杆状结构一般都不用诸如一些关于构建的形变状态或应力分布的假定，因而得到的结果就比较精确。
从8个方程8个未知量，到圣维南原理、相容方程；从逆解法、半逆解法到差分法、变分法，邱老师的课讲的十分生动，同学们也听得十分认真。
到弹性力学下册，也就是板壳理论，主要是研究薄板的小挠度变形及其应力、应变。
求解四边简支矩形薄板在载荷下的挠度，以及矩形薄板的莱维法解及一般解法。
另外，变厚度矩形和圆形薄板的挠度求解问题。
差分法中引进了较为精确的边界条件以及在均布载荷和集中载荷下的不同解法。
在课程设计的过程中，在自学Matlab 的过程中完成了纳维解法中挠度表达式的表示和循环收敛过程，并且完成了差分法中不同网格划分下的差分方程化为矩阵形式后的求解过程。
除此之外，还学会了使用ABAQUS 创建板并定义厚度以减少同等情况下创建实体添加边界条件不准确对计算结果产生的影响。
尽管和差分法与精确解的误差分析相比，误差还是比较大，但相比于创建三维实体并在底边添加约束条件相比，误差还是减少了很多。
在计算过程中，先是采用厚度0.2m 薄板，有限元方法的误差过大，而当把薄板的厚度改为0.1m 时，误差变小。
两种厚度的薄板都进行了同样的计算。
四边简支的薄板在均布载荷作用下位移的最大值，薄板的尺寸为长宽高：110.1⨯⨯ ，均布载荷为21000/q N m = ，弹性模量E=205GPa ，泊松比=0.3μ， 分别用：纳维法、差分法以及有限元方法进行求解并比较求得的结果。
板壳理论课程设计对工科各专业说来，弹性力学的任务和材料力学、结构力学的任务一样，是分析各种结构或其构件在弹性阶段的应力和位移，校核它们是否具有所需的强度和刚度，并寻求或改进它们的计算方法。
然而，它们之间还存在着一些不同。
材力中，基本上只研究杆状结构，即长度远大于高度和宽度的构件。
而材料力学中主要研究的是这种构件在拉压、剪切、弯曲、扭转作用下的应力和位移。
结构力学中，主要是在材料力学的基础上研究杆状构件所组成的结构，即杆件系统。
至于非杆状结构，则是弹性力学的主要研究内容。
在弹性力学中，研究杆状结构一般都不用诸如一些关于构建的形变状态或应力分布的假定，因而得到的结果就比较精确。
从8个方程8个未知量，到圣维南原理、相容方程；从逆解法、半逆解法到差分法、变分法，邱老师的课讲的十分生动，同学们也听得十分认真。
到弹性力学下册，也就是板壳理论，主要是研究薄板的小挠度变形及其应力、应变。
求解四边简支矩形薄板在载荷下的挠度，以及矩形薄板的莱维法解及一般解法。
另外，变厚度矩形和圆形薄板的挠度求解问题。
差分法中引进了较为精确的边界条件以及在均布载荷和集中载荷下的不同解法。
在课程设计的过程中，在自学Matlab 的过程中完成了纳维解法中挠度表达式的表示和循环收敛过程，并且完成了差分法中不同网格划分下的差分方程化为矩阵形式后的求解过程。
除此之外，还学会了使用ABAQUS 创建板并定义厚度以减少同等情况下创建实体添加边界条件不准确对计算结果产生的影响。
尽管和差分法与精确解的误差分析相比，误差还是比较大，但相比于创建三维实体并在底边添加约束条件相比，误差还是减少了很多。
在计算过程中，先是采用厚度0.2m 薄板，有限元方法的误差过大，而当把薄板的厚度改为0.1m 时，误差变小。
两种厚度的薄板都进行了同样的计算。
四边简支的薄板在均布载荷作用下位移的最大值，薄板的尺寸为长宽高：110.1⨯⨯ ，均布载荷为21000/q N m = ，弹性模量E=205GPa ，泊松比=0.3μ， 分别用：纳维法、差分法以及有限元方法进行求解并比较求得的结果。
得到结果如下：纳维解法四边简支的正方形薄板，四边无支座沉陷时，边界条件为()()()()000,0,0,0,x x a y y b w w w w ======== 22022220220,0,0,0.x x a y y bw x w x w y w y ====⎛⎫∂= ⎪∂⎝⎭⎛⎫∂= ⎪∂⎝⎭⎛⎫∂= ⎪∂⎝⎭⎛⎫∂= ⎪∂⎝⎭把挠度表示为如下的重三角级数：11sinsin mn m n m x n yw A a bππ∞∞===∑∑()a代入弹性曲面的微分方程，得22242211sin sin mn m n m n m x n y D A q a b a b πππ∞∞==⎛⎫+= ⎪⎝⎭∑∑ ()b为求出系数mn A ，须将式子右边展为与左边同样的重三角，即11sinsin mn m n m x n yq C a bππ∞∞===∑∑ ()c 得到1sin d sin 2ain n m x a n yq x C a bππ∞==∑⎰sinsin d d 4a bij m x n y abq x y C a b ππ=⎰⎰与(b)式对比，得2224224sinsin d d abmn m x n yq x y a b A m n abD ab πππ=⎛⎫+ ⎪⎝⎭⎰⎰ ()d 当薄板受到均布载荷时，q 成为0q ，则式(d)积分成为()()00000002sinsin d d sin d sin d 1cos 1cos aba b m x n yq x y a b m x n y q x y a b q ab m n mnπππππππ==--⎰⎰⎰⎰则得到：26221,3,5,1,3,5,22sinsin 16m n m x n yq a b w D m n mn ab πππ∞∞===⎛⎫+ ⎪⎝⎭∑∑对挠度表达式的后部运用Matlab 进行编程迭代，在确定收敛之后，可以得到：厚度为0.2m 时： 2.7053e-08w =厚度为0.1m 时： 2.1642e-07w =厚度为0.05m 时：1.73106w e =- 厚度为0.01m 时：2.1638e-04w =● 差分法4*4网格划分：差分方程：0001232312223213333444444208(4)2(4)0208(2)2(2)()208(2)2()()()()()q a D q a D q a D w w w w w w w w w w w w w w w w -++=-+++-=-++-+-= 化简后得：00123123123444444203288241621620()()()q a D q a Dq a Dw w w w w w w w w -+=-+-=-+=其中，()32121E D δμ=- 化为矩阵形式：140232032818241614216201w q a w D w -⎡⎤⎧⎫⎡⎤⎪⎪⎛⎫⎢⎥⎢⎥--=⎨⎬ ⎪⎢⎥⎢⎥⎝⎭⎪⎪⎢⎥⎢⎥-⎣⎦⎩⎭⎣⎦ 得到结果：厚度为0.2m 时：1230.26821.0e-070.19510.1422w w w ⎧⎫⎡⎤⎪⎪⎢⎥=⨯⎨⎬⎢⎥⎪⎪⎢⎥⎩⎭⎣⎦厚度为0.1m 时：1230.21461.0e-060.15610.1138w w w ⎧⎫⎡⎤⎪⎪⎢⎥=⨯⎨⎬⎢⎥⎪⎪⎢⎥⎩⎭⎣⎦ 厚度为0.05m 时：123 0.17171.0e-05 0.1248 0.0910w w w ⎧⎫⎡⎤⎪⎪⎢⎥=⨯⎨⎬⎢⎥⎪⎪⎢⎥⎩⎭⎣⎦ 厚度为0.01m 时：1230.21461.0e-030.15610.1138w w w ⎧⎫⎡⎤⎪⎪⎢⎥=⨯⎨⎬⎢⎥⎪⎪⎢⎥⎩⎭⎣⎦◆ 8*8网格划分： 差分方程：4012344023********032516438404527381653208(4)2(4)48208(2)2(22)(2)8208(22)2(2)(22)8208(2)2(22)(20)8208(q a w w w w D q a w w w w w w w w w D q a w w w w w w w w D q a w w w w w w w w D w w ⎛⎫-++= ⎪⎝⎭⎛⎫-+++++++= ⎪⎝⎭⎛⎫-++++++= ⎪⎝⎭⎛⎫-+++++++= ⎪⎝⎭-404862579259406593810440784529740859********)2()(0)8208(22)2(2)(2)08208(2)2(2)(2)8208()2()()8q a w w w w w w w w w w D q a w w w w w w w D q a w w w w w w w D q a w w w w w w w w w w D ⎛⎫+++++++++++= ⎪⎝⎭⎛⎫-++++++= ⎪⎝⎭⎛⎫-++++-= ⎪⎝⎭⎛⎫-+++++++-= ⎪⎝⎭4096810595794010********(0)2()()8208(2)2()(22)8q a w w w w w w w w w D q a w w w w w D ⎛⎫-+++++++-= ⎪⎝⎭⎛⎫-++-= ⎪⎝⎭化简后得：4012344012345740123456840123456782342032840000008825168600008216224162020088420162840080388q a w w w w D q a w w w w w w D q a w w w w w w w D q a w w w w w w w w D w w w ⎛⎫-++++++++= ⎪⎝⎭⎛⎫-+--++++++= ⎪⎝⎭⎛⎫-++-+++++= ⎪⎝⎭⎛⎫-++-+-+++= ⎪⎝⎭+--+4056789403456894024578940345678910567823828308002216200416080084019162080028282088000038819q a w w w w w D q a w w w w w w D q a w w w w w w D q a w w w w w w w w D w w w w ⎛⎫-+-++= ⎪⎝⎭⎛⎫+++-+++-+= ⎪⎝⎭⎛⎫++-+++-++= ⎪⎝⎭⎛⎫+++-+-+-+= ⎪⎝⎭++++-+-+409104068910880000020216188q a w w D q a w w w w D ⎛⎫-= ⎪⎝⎭⎛⎫+++++++--= ⎪⎝⎭改为矩阵形式，为：20 -32 8 4 0 0 0 0 0 0 -8 25 -16 -8 6 0 1 0 0 0 2 -16 22 4 -16 2 0 2 0 0 1 -8 4 20 -16 2 -8 4 0 0 0 3 -8 -8 23 -8 2 -8 3 0 0 0 2 2 -16 20 0 4 -16 2 0 1 0 -8 4 0 19 -16 2 0 0 0 1 2 -8 2 -8 20 -8 1 0 0 0 0 3 -8 1 -8 21 -8 0 0 0 0 0 2 0 2 -16 18⎡123445067891011111181111w w w w w q a w D w w w w ⎧⎫⎤⎡⎤⎪⎪⎢⎥⎢⎥⎪⎪⎢⎥⎢⎥⎪⎪⎢⎥⎢⎥⎪⎪⎢⎥⎢⎥⎪⎪⎢⎥⎢⎥⎪⎪⎢⎥⎢⎥⎪⎪⎛⎫=⎢⎥⎢⎥⎨⎬ ⎪⎝⎭⎢⎥⎢⎥⎪⎪⎢⎥⎢⎥⎪⎪⎢⎥⎢⎥⎪⎪⎢⎥⎢⎥⎪⎪⎢⎥⎢⎥⎪⎪⎢⎥⎢⎥⎪⎪⎢⎥⎢⎥⎪⎪⎣⎦⎣⎦⎩⎭ 得到：厚度为0.2m 时：12345678910 0.2700 0.2511 0.2335 0.1956 0.1820 1.0e-07 0.1421 0.1083 0.1009 0.0790 0.0441w w w w w w w w w w ⎧⎫⎧⎫⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪=⨯⎨⎬⎨⎬⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎭⎩⎭厚度为0.1m 时：12345678910 0.2160 0.2008 0.1868 0.1565 0.1456 1.0e-06 0.1137 0.0867 0.0807 0.0632 0.0353w w w w w w w w w w ⎧⎫⎧⎫⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪=⨯⎨⎬⎨⎬⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎭⎩⎭厚度为0.05m 时：123456789100.17280.16070.14940.12520.1165 1.0e-050.09100.06930.06460.05060.0282w w w w w w w w w w ⎧⎫⎧⎫⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪=⨯⎨⎬⎨⎬⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎭⎩⎭厚度为0.01m 时：123456789100.21600.20080.18680.15650.1456 1.0e-030.11370.08670.08070.06320.0353w w w w w w w w w w ⎧⎫⎧⎫⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪=⨯⎨⎬⎨⎬⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎭⎩⎭ ● 有限元法厚度为0.2m 时：创建壳实体，在材料赋定时确定厚度，得到在中心点有最大位移max 3.6788w e =-创建3D 实体，得到在中心点有最大位移：max 5.4628w e =-厚度为0.1m 时：创建壳实体，在材料赋定时确定厚度，得到在中心点有最大位移max 2.4437w e =-厚度为0.05m 时：创建壳实体，在材料赋定时确定厚度，得到在中心点有最大位移max 2.4054w e =-创建3D 实体，得到在中心点有最大位移：max 2.1664w e =-厚度为0.01m时：创建壳实体，在材料赋定时确定厚度，得到在中心点有最大位移max 2.4054w e=-创建3D实体，得到在中心点有最大位移：max 2.1664w e=-●结果对比厚度为0.2m时：厚度为0.1m时：厚度为0.05m时：厚度为0.01m时：。
