曲墙式衬砌计算

拱形曲墙式衬砌结构计算一、基本资料某一级公路隧道，结构断面如下图，围岩级别为Ⅴ级，围岩容重γ=20KN/m3，围岩的弹性抗力系数K=0.2×106 kN/m，衬砌材料C20混凝土，弹形模量E h =2.6×107kPa，重度γh=23 KN/m3。

衬砌结构断面（尺寸单位：cm）二、荷载确定1、根据《公路隧道设计规范》的有关计算公式，围岩竖向均布压力：q=0.45 × 2S-1 γω式中：S——围岩级别，此处S=5；γ——围岩容重，此处γ=20 kN/m3；ω——跨度影响系数，ω=1+i (B-5)，毛洞跨度lm=11.81+2×0.1=12.01m，式中0.1为一侧平均超挖量;lm=5～15m时，i=0.1,此处ω=1+0.1×（12.01-5）=1.701所以，有：q=0.45×25-1×20×1.701=244.944(kPa) 此处超挖回填层重忽略不计。

2、围岩水平均布压力：e=0.25q=0.25×244.944=61.236（kPa）三、衬砌几何要素1、衬砌几何尺寸内轮廓线半径： r=5.4039m内径r所画圆曲线的终点截面与竖直轴的夹角：φ=113⁰拱顶截面厚度d=0.5 m ；拱底截面厚度dn=0.5m。

外轮廓线半径： R=r+d=5.9039m拱轴线半径： r′=r+0.5d=5.6539m拱轴线各段圆弧中心角：θ=113⁰2、半拱轴线长度S及分段轴长△SS =θ r′/180⁰=113⁰×3.14×5.6539/180⁰=11.1451（m）将半拱轴长度等分为8段，每段轴长为：△S=S/8=11.1451/8=1.3931（m）3、各分块接缝（截面）中心几何要素（1）与竖直轴夹角ɑiɑ1=Δθ=θ/8=113⁰/8=14.125⁰ɑ2=ɑ1+Δθ=14.125⁰+14.125⁰=28.25⁰ɑ3=ɑ2+Δθ=28.25⁰+14.125⁰=42.375⁰ɑ4=ɑ3+Δθ=42.375⁰+14.125⁰=56.5⁰ɑ5=ɑ4+Δθ=56.5⁰+14.125⁰=70.625⁰ɑ6=ɑ5+Δθ=70.625⁰+14.125⁰=84.75⁰ɑ7=ɑ6+Δθ=84.75⁰+14.125⁰=98.875⁰ɑ8=ɑ7+Δθ=98.875⁰+14.125⁰=113⁰（2）接缝中心点坐标计算X 1=r′sinɑ1=5.6539×sin14.125⁰=1.3798(m)X 2=r′sinɑ2=5.6539×sin28.25⁰=2.6761(m)X 3=r′sinɑ3=5.6539×sin42.375⁰=3.8106(m)X 4=r′sinɑ4=5.6539×sin56.5⁰=4.7147(m)X 5=r′sinɑ5=5.6539×sin70.625⁰=5.3337(m)X 6=r′sinɑ6=5.6539×sin84.75⁰=5.6302(m)X 7=r′sinɑ7=5.6539×sin98.875⁰=5.5862(m)X 8=r′sinɑ8=5.6539×sin113⁰=5.2044(m)y 1=r′(1-cosɑ1)=5.6539×(1-cos14.125⁰)=0.1709(m)y 2=r′(1-cosɑ2)=5.6539×(1-cos28.25⁰)=0.6734(m)y 3=r′(1-cosɑ3)=5.6539×(1-cos42.375⁰)=1.4771(m)y 4=r′(1-cosɑ4)=5.6539×(1-cos56.5⁰)=2.5333(m)y 5=r′(1-cosɑ5)=5.6539×(1-cos70.625⁰)=3.7782(m)y 6=r′(1-cosɑ6)=5.6539×(1-cos84.75⁰)=5.1366(m)y 7=r′(1-cosɑ7)=5.6539×(1-cos98.875⁰)=6.5262(m)y 8=r′(1-cosɑ8)=5.6539×(1-cos113⁰)=7.8631(m)当然也可以在下图中直接量出xi 、yi衬砌结构计算图示四、计算位移1、单位位移用辛普生法近似计算，按计算列表进行，单位位移的计算见表1。

曲墙式衬砌结构计算步骤1. 确定断面形状；截面厚度；2. 确定弹性抗力区的范围及分布规律： 1） 按照拱顶圆弧圆心确定b ϕ位置；2） 按照ab 32确定最大抗力h σ位置，以该点的法线与隧道断面的平分线的交点为基准点o ，连接ob ，此时ob 与隧道平分线的夹角作为抗力计算的实际b ϕ，h i b ϕϕϕ≤≤。

3. 计算主动荷载作用下的内力：1） 由主动荷载的分布在去掉多余约束后，单独考虑主动荷载引起的结构内力，画出内力图o ipip N M 、0。

计算模型为“悬臂曲梁”； 2） 计算墙底在单位力矩作用下的转角位移akI 11=β 3） 按照内力图，可以知道墙底弯矩oap M ，计算由此产生的墙底转角o ap β=1βo ap M 。

轴力oipN 引起竖向位移，由于结构对称，不影响结构内力计算（不考虑）；4） 计算拱顶单位未知力引起的结构内力1M 、2M ，画出弯矩图； 5） 计算位移系数ik δ和自由项ip ∆，其中 ds EI M M ⎰=1111δ≈∑∆IE s 1（1） ds EI M M ⎰==212112δδ≈∑∆IyE s （2） ds EI M M ⎰=2222δ≈∑∆Iy E s 2（3）ds EI M M oipp ⎰=∆11≈∑∆IM E s oip（4） ds EIM M o ipp ⎰=∆22≈∑∆IyM E s oip（5）6） 按照基本方程的泛函形式)()(0)()(021222212110111221111=+∆++++=+∆++++ap p p p ap p p p f f X f X f X X ββδβδββδβδ （6）计算出基本未知力p X 1、p X 2； 7） 主动荷载作用下内力计算o ipi p ip oipi p p ip N X N M y X X M +=++=φcos 221 （7）4. 计算弹性抗力引起的结构内力 1） 计算最大弹性抗力公式 σδδσh hp h k k -=1 弹性抗力的大小与hp δ、σδh 有关，计算hp δ、σδh 需要知道主动荷载作用下的ip M 、单位最大抗力作用下的σi M 和单位力单独作用下的ih M 。

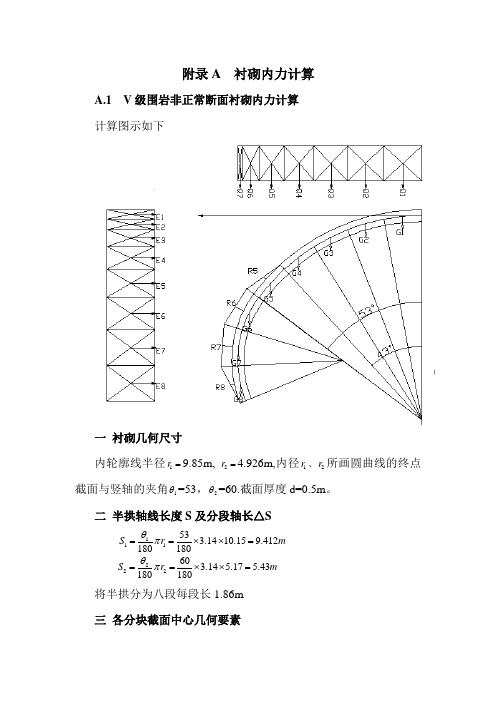
附录A 衬砌内力计算A.1 V 级围岩非正常断面衬砌内力计算 计算图示如下一 衬砌几何尺寸内轮廓线半径1r =9.85m, 2r =4.926m,内径1r 、2r 所画圆曲线的终点截面与竖轴的夹角1θ=53，2θ=60.截面厚度d=0.5m 。

二 半拱轴线长度S 及分段轴长△S111533.1410.159.412180180S r m θπ==⨯⨯=222603.14 5.17 5.43180180S r m θπ==⨯⨯= 将半拱分为八段每段长1.86m 三 各分块截面中心几何要素各分块截面中心几何要素计算原理3-8，结果见单位位移计算表。

四 主动荷载作用下的内力计算 ①单位位移表A1 单位位移计算表61171 1.86279.88315.540103.3510S E I δ-∆==⨯=⨯⨯∑ 61271.86913.24250.705103.3510S y E I δ-∆==⨯=⨯⨯∑ 262271.865161.227286.564103.3510S y E I δ-∆==⨯=⨯⨯∑ 计算精度校核为：角度闭合差为零。

26337(1) 1.867267.593403.514103.3510S y E I δ-∆+==⨯=⨯⨯∑ 661112222(15.54250.705286.564)10403.51410δδδ--++=+⨯+⨯=⨯闭合差为零 ②载位移根据《公路隧道设计规范》Ⅴ级围岩中二次衬砌承担70%的外荷载，则q=515.837kpa,e=72.849kpa.每一分块上的作用力： 竖向力：i i GE eh a =，由计算图示得i b 如下：b1=1.88,b2=1.83,b3=1.71,b4=1.53,b5=1.3,b6=0.92,b7=0.25.水平力：i i E eh =，由计算图示得i h 如下：h1=0.17,h2=0.52,h3=0.84 h4=1.14,h5=1.4,h6=1.71,h7=1.93,h8=1.91.自重力：G=d ×△S ×r=1.86×0.7×24.5=31.899KN.各分块上集中力对下一截面的力臂由计算图示量得，分别计为Q a 、E a 、G a ，由上述公式得，各外力及其力臂如下表：表 A2 外力及相应力臂组合计算图示，计算各分块如下：表A3 0p M 计算表表A4 0p N 计算表08802280880000888820.5320.53()515.837(8.686)242418948.39672.84913.4426581.44722()682.2418948.3966581.447682.2423212.083q e g i i gi p q e gB B M qx e M H M G x x a M M M M =--=-⨯-=-=-=-⨯=-=--+=-=++=---=-∑从A3得到08p M =-23343.37 闭合差23343.3723212.08100%0.56%23212.083-∆=⨯=③主动荷载位移表A5主动荷载位移计算表16170026271.863527885.468195876.626103.35101.8618217417.0841011474.501103.3510sp p p spp p M M M s ds EI E I M M yM s ds EI E I --∆∆===-⨯=-⨯⨯∆∆===-⨯=-⨯⨯∑⎰∑⎰计算精度校核：6612(195876.6261011474.501)101207351.12710p p --∆+∆=-+⨯=-⨯67(1) 1.8621745302.5521207351.127103.3510p sp y M S E I -+∆∆==-⨯=-⨯⨯∑ 闭合差△=0五 载位移——单位弹性抗力及摩擦力引起的位移 （1）各接缝处的抗力强度度抗力上零点假设在接缝4，4b 42.2=αα=。

第一章绪论1. 隧道:构筑在离地面一定深度的岩层或土层中用作通到底建筑物2. 隧道分类:按周围介质分：岩石隧道和土层隧道;按用途不同分：交通隧道和市政工程隧道3. 公路隧道：穿越公路路线障碍物的交通隧道4. 公路隧道的主要特点:(1)断面形状复杂：宽而扁，高：宽<=1.; 常有特殊构造：岔洞，紧急停车带回车区，以及双连拱隧道，小间距隧道，双层隧道;(2) 荷载形式单一：主要是围岩压力，方向不会改变;(3)附属设施多：通风,照明,交通信号,消防,监控设施5. 断面几何形状:考虑功能和经济的两方面:马蹄形,圆形(盾构开挖),拱形(山岭隧道),双连拱(浅埋土层,地形受限),矩形(沉管法,城市隧道)6.. 衬砌的结构类型分为四类:整体式砼衬砌;装配式衬砌;锚喷支护衬砌;复合式衬砌7.. 整体式砼衬砌又可分为:半衬砌;厚拱薄墙衬砌;直墙拱形衬砌;曲墙拱形衬砌(1)半衬砌:适用于岩石较坚硬并且整体稳定或基本稳定的围岩; 对于侧压力很大的较软岩层或土层,为避免直墙承受较大压力,采用落地拱(2)厚拱薄衬砌:适用于水平压力很小的情况,拱脚较厚,边墙较薄(3) 直墙拱形衬砌:铁路隧道常用,竖向压力较大,水平侧压力不大(4)曲墙拱形衬砌:地质条件差,岩石破碎松散和易于坍塌地段8. 装配式衬砌:用于盾构法施工,深埋法施工,TBM 法施工9. 锚喷支护衬砌:喷混凝土和加锚杆两方法的统称。

常用方法：喷混凝土，钢筋网喷混凝土，锚杆喷混凝土，钢筋网锚杆混凝土，钢纤维喷混凝土;特点：有很强时效性，新奥法和挪威法10. 复合式衬砌：主要应用于含水量较多的地段，外层为锚喷支护，中间有一层防水层，内层多为整体式衬砌，新奥法多采用11. 初始地应力场由两种力系组成:自重应力分量;构造应力分量影响因素：一类是和地壳的运动，地下水的变化以及人类活动等因素有关12. 构造应力场：区域性明显，测试方法：解析反演法，原位测试法(1)地质的构造过程不公改变了地质的重力应力场，而且还有一总分残余在岩体内(2) 构造应力场在一定深度内普遍存在且多为水平分量(3)构造应力具有明显的区域性和时间性13. 作用在隧道结构上的荷载分为三类:主要荷载(就是长期作用的荷载,包括地层压力,围岩弹性抗力,结构自重力,回填岩土重力，地下静水压力及使用荷载); 附加荷载(指非经常作用的荷载，包括施工荷载，灌浆压力，局部落石以及有温度变化或砼收缩引起的温度应力和收缩用力) ;特殊荷载(一些偶然发生的荷载，如炮弹冲击力和爆炸时产生激波压力，地震力，车祸时冲撞力)14. 形变压力: 由岩体变形所产生的挤压力;15. 松散压力: 岩体坠落、滑移、坍塌所产生的重力16. 围岩压力：形变压力和松散压力统称为围岩压力17. 影响围岩压力的因素：a岩土的重力b岩体的结构c.地下水的分布d.隧道洞室的形状和尺寸e. 初始地应力18•确定围岩压力的方法：a•现场量测b•理论估算c工程类比法19•常用的围岩分类方法：a岩石坚固系数分类法b•太沙基理论c•铁路围岩分类法d•人工岩石洞室围岩分类法e.水工隧道围岩分类法20. 隧道结构计算的任务：就是采用数学力学的方法，计算分析在隧道修筑的整个过程中 (包括竣工，运营)a.隧道围岩及衬砌的强度 b.刚度和稳定性，为隧道的设计及施工提供具体设计参数21. 隧道的计算方法可分为三大部分： a.刚体力学法b.结构力学法(荷载位移法)c.连续介质力学法(地层结构法)22. 附：19 世纪后期，砼材料与钢材料的出现，地下结构的建造于计算进入地下连续拱形框架结构阶段，而计算的理论基础为线弹性结构力学；地下连续拱形框架结构式一种超静定弹性结构系统，荷载为地层压力，优点：以结构力学原理为计算理论基础缺点：没有考虑地层对衬砌结构变形所产生的弹性抵抗力23. 如果人工考虑隧道衬砌和地层的相互作用，地下结构的计算方法仅分为结构力学方法和连续介质力学方法24. 造成隧道结构计算结果不能直接应用的主要原因:(1) 围岩的物理力学参数无法准确确定(2)隧道的荷载量级很大,无法准确给出(3) 围岩自承能力除受围岩自身条件影响外,还受施工方法、时间、支护形式、洞室几何尺寸等的影响( 4)围岩本构关系复杂和屈服性准则不完善性，使围岩自承能力无法发挥第二章隧道结构计算的结构力学法1. 在分析过程中首先要确定地层压力，然后计算衬砌在地层压力和其他荷载作用下的内力分布，最后根据内力分布对衬砌结构断面进行验算2. 荷载结构法和计算地表结构所采用的结构力学方法基本相同，主要差别是衬砌结构在变形过程中要受到周围介质的限制，分为力法与位移法3. 拱形半衬砌隧道的结构计算： ( 1)半衬砌结构可简化为弹性固定平面无铰拱(计算模型) (2)拱顶截面建立位移协调方程，由拱顶截面的位移协调方程得拱脚处的位移和转角( 3) 将拱脚位移和转角方程代入拱顶截面位移协调方程，得关于未知力X1 ，X2 的线性代数方程组，可得拱顶截面未知力( 4)各截面强度校核4. 拱形曲墙隧道的结构计算： (1)假定弹性抗力为镰刀形分布，拱形曲墙式衬砌的计算模型为墙角弹性固定而两侧受周围约束的无铰拱( 2)通过h点的变形协调条件计算弹性抗力bh(3)计算主动荷载作用下衬砌的内力(4) b h=1时衬砌的内力⑸求出最大抗力值b h(6)用叠加的方法求出衬砌内任一点的内力5. 拱形曲墙隧道的结构计算模型：竖向荷载所引起的侧墙部分的变形，将受到侧面围岩的约束，形成一个抗力区，这里假定弹性抗力为镰刀形，其量值用 3 个特征值控制：抗力上零点对一般与对称中线夹角为40°-60°；抗力下零点在拱脚处；最大抗力点h 在衬砌最大跨度处，一般在抗力区2/3 处6. 拱形直墙隧道的局部变形法:在分析拱形直墙式隧道结构时,需将拱圈与直墙分开考虑,拱圈是一个拱脚弹性固定的无铰拱,弹性抗力假定为二次抛物线分布,边墙视为弹性地基梁,全部抗力有文克勒假设确定,墙顶和拱脚弹性固结,墙脚与基岩间有较大的摩擦力,无水平位移发生,他在基岩的作用视为刚性体7•外荷载产生的位移卩hp和直墙拱的结构计算:(1)由弹性地基梁公式，计算系数卩1, 3 1,卩2, 3 2(墙顶位移)(2)由主动荷载及单位弹性抗力所产生的h点位移计算单位弹性抗力所产生的位移h b (3)由口hp和口h b求得弹性抗力b h (4)根据任一截面i处的内力表达式得拱的截面内力( 5)求出直梁的内力( 6)校核8•隧道衬砌结构计算的矩阵力法计算步骤：(1)计算［F0］(2)计算［丫SX］并将其转化为［丫SX］'⑶计算［丫SP］并将其转化为［丫SP］' (4)计算［Fxx］,［Fxp］(5)计算赘余力{x} (6)计算衬砌单元节点{s} ( 7)计算衬砌节点位移{ S }9•隧道衬砌结结构计算的矩阵位移法计算步骤：(1)计算衬砌单元刚度位移矩阵( 2)计算链杆刚度( 3)计算墙底支座的刚度矩阵( 4)集成总体刚度矩阵,并计算各元素值( 5)消去已知位移( 6)计算节点位移( 7)计算单元节点力10•拱形直墙计算模型：拱圈是一个拱脚弹性固定的无铰拱，拱圈弹性抗力假定为二次抛物线分布,边墙视为弹性地基梁,全部抗力由文壳勒假设确定。