当前位置：文档之家 › 八年级数学上学期人教版优质课件-12.3 第2课时 角平分线的判定

八年级数学上学期人教版优质课件-12.3 第2课时 角平分线的判定

  • 格式：ppt
  • 大小：1.22 MB
  • 文档页数：26

下载文档原格式

  / 26

合集下载

人教版数学八年级上册12.3.2 角平分线的判定课件(共22张PPT)

人教版数学八年级上册12.3.2 角平分线的判定课件(共22张PPT)
BE=CF，
E
B
D
┐
A
FC
DB=DC，
∴Rt△BDE≌Rt△CDF（HL）. ∴DE=DF.
∴即AD是∠BAC的平分线.
12.3.2 角平分线的判定
二 三角形的内角平分线
探究1
分别画出以下三角形的三个内角的角平分线，你发现了什么？
A
A
A
B
C
┐
B
C
B
C
三角形的三条角平分线相交于一点，且交点位于三角形的内部.
针对训练
1.如图，在直角△ABC 中，AC＝BC，∠C ＝90°，AP 平分∠BAC，BD
平分∠ABC；AP，BD 交于点 O，过点 O 作 OM⊥AC 于点 M，若 OM
＝4.
(1) 求点 O 到△ABC 三边的距离和；
B
解：如图，过点 O 作 ON⊥BC 于点 N,过点
O 作 OE⊥AB 于点 E,
A. 110° B. 120° C. 130°
D. 140°
解析：由于 O 到△ABC 三边的距离相等， 故 O 是三条内角平分线的交点， 即 BO，CO 都是内角的平分线，
12.3.2 角平分线的判定
则∠OBC＝1∠ABC，∠OCB＝1∠ACB.
2
2
∵∠ABC＋∠ACB＝180°－∠A＝180°－40°＝140°，
∴FG=FM.
G
同理可得∴FM=FH. ∴FG=FH， ∴点F在∠BAC的平分线上．
M H
12.3.2 角平分线的判定
3.如图，∠B=∠C=90°，M是BC的中点，DM平分∠ADC. 求证：AM是∠DAB的平分线. 解：如图，作MN⊥AD于N，
∵DM平分∠ADC，∠C=∠DNM=90°

人教版八年级上册第12章全等三角形12.3角的平分线的判定课件(共21张PPT)

人教版八年级上册第12章全等三角形12.3角的平分线的判定课件(共21张PPT)

•9、要学生做的事，教职员躬亲共做；要学生学的知识，教职员躬亲共学；要学生守的规则，教职员躬亲共守。2021/9/102021/9/10Friday, September 10, 2021 •10、阅读一切好书如同和过去最杰出的人谈话。2021/9/102021/9/102021/9/109/10/2021 4:30:01 AM •11、只有让学生不把全部时间都用在学习上，而留下许多自由支配的时间，他才能顺利地学习……（这）是教育过程的逻辑。2021/9/102021/9/102021/9/10Sep-2110-Sep-21 •12、要记住，你不仅是教课的教师，也是学生的教育者，生活的导师和道德的引路人。2021/9/102021/9/102021/9/10Friday, September 10, 2021
知识点：角的平分线的判定 【例1】课本练习题
课堂导学
【答案】证明：过点P作PD⊥AN, PE⊥AM， PF⊥CB，垂足分别为D，E，F. ∵CP平分∠MCB，PE⊥AM，PF⊥CB. ∴PE＝PF，同理，PD＝PF. ∴PD＝PE，∴AP平分∠BAC. 【点拔】涉及证角平分线问题，常作角两边 的垂线段．再推证两条垂线段相等．
13、He who seize the right moment, is the right man.谁把握机遇，谁就心想事成。2021/9/102021/9/102021/9/102021/9/109/10/2021 •14、谁要是自己还没有发展培养和教育好，他就不能发展培养和教育别人。2021年9月10日星期五2021/9/102021/9/102021/9/10 •15、一年之计，莫如树谷；十年之计，莫如树木；终身之计，莫如树人。2021年9月2021/9/102021/9/102021/9/109/10/2021 •16、教学的目的是培养学生自己学习，自己研究，用自己的头脑来想，用自己的眼睛看，用自己的手来做这种精神。2021/9/102021/9/10September 10, 2021 •17、儿童是中心，教育的措施便围绕他们而组织起来。2021/9/102021/9/102021/9/102021/9/10

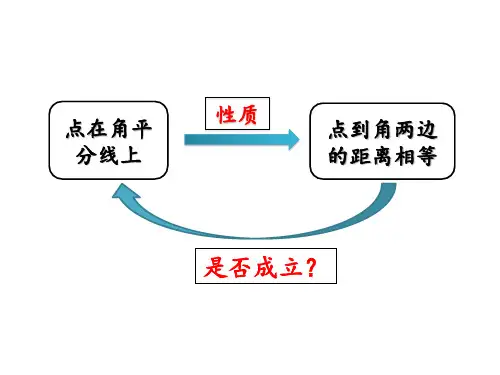
人教版八年级数学上册12.3.2角平分线的判定课件

人教版八年级数学上册12.3.2角平分线的判定课件

D NP
F M
同理，PE=PF.
B
E
C
∴PD＝PE=PF.
即点P到三边AB、BC、CA的距离相等.
结论想：一三想，角点形P在的∠三A的条平角分平线上分吗线？交这说于明一三点角， 并形且的三这条点角到平分三线边有的什距么关离系相？等.
3、如图所示是一块三角形的草坪，现要在草坪上建 一凉亭供大家休息，要使凉亭到草坪三条边的距离相
∵BD=CD，BE=CF ∴ Rt△BDE ≌ Rt△CDF（HL） ∴DE=DF ∴ AD平分∠BAC
如图，DE⊥AB于E，DF⊥AC于F，若BD=CD，BE=CF （1）求证：AD平分∠BAC； （2）猜想写出AB+AC与AE之间的
等量关系并给予证明.
（2）猜想：AB+AC=2AE 证明：由（1）得AD平分∠BAC
等，凉亭的位置应选在( C )
A.△ABC的三条中线的交点 B.△ABC三边的中垂线的交点 C.△ABC三条角平分线的交点 D.△ABC三条高所在直线的交点 4、如图，∠AOB=70°，QC⊥OA于C， QD⊥OB于D，若QC=QD，则∠AOQ=__3_5_°
1.角的内部到角的两边的距离相等的点在角的平分线上
解得x 2.5 在图上取OD 2.5cm， A
DS
B
C
D点即为集贸市场的位置
2、如图，△ABC的角平分线BM，CN相交于点P。 求证：点P到三边AB、BC、CA的距离相等
证明：过点P作PD⊥AB于D， PE⊥BC于E，PF⊥AC于F
∵BM是△ABC的角平分线， 点P在BM上， ∴PD=PE.
A
用符号语言表示为：
A
∵ PD⊥OA，PE⊥OB, PD＝PE．

人教版八年级上册12.3 第2课时 角平分线的判定 课件(共13张PPT)

人教版八年级上册12.3 第2课时 角平分线的判定 课件(共13张PPT)
第十二章 全等三角形
12.3 角的平分线的性质 第2课时
角平分线的判定
学习目标
1.理解角的内部到角两边距离相等的点在角的平分线上（角的判定）； 2.能利用角的判定定理解决简单的几何问题。
复习回顾
问题1：关于角平分线，你知道什么？ 问题2：角平分线性质的文字语言和几何语言？
复习回顾
角的平分线的性质: 角的平分线上的点到角的两边的距离相等.
. 一处
B. 两处
C. 三处
D. 四处
分析: 由于没有限制在何处选址，故要求的地址共有四处.
巩固新知
2. 如图，△ABC 中，∠C = 90°，AD 是△ABC 的角平分线， DE⊥AB 于 E，F 在 AC 上 BD=DF. 求证：CF=EB.
证明：∵AD 平分∠CAB， DE⊥AB，∠C＝ 90°（已知），
角的平分线上的点到角的两边的距离相等.
O
用数学语言表示为：
∵ QD⊥OA，QE⊥OB，点 Q 在∠AOB 的平分线上．
∴ QD＝QE．
A D
Q EB
探究新知
证明: ∵ PD⊥OA，PE⊥OB(已知)， ∴ ∠PDO＝∠PEO＝ 90°(垂直的定义) . 在Rt△PDO 和Rt△PEO 中 PO＝PO(公共边)， PD=PE， ∴ Rt△PDO ≌ Rt△PEO(HL) . ∴ ∠ POD＝∠POE. ∴点P在∠AOB 的平分线上.
总结新知
结论: 角的内部到角的两边距离相等的点在角的平分线上.
几何语言:
∵OC 是∠AOB 的平分线，PD⊥OA，PE⊥OB， ∴PD=PE (角的平分线上的点到角的两边的距离相等).
探究新知
反过来，到一个角的两边的距离相等的点是否一定在这个 角的平分线上呢？

八年级数学上册 第十二章 《角平分线的判定》课件 人教版

八年级数学上册 第十二章 《角平分线的判定》课件 人教版

A
B
P
D
C
挑战自我
5、如图，点A、点B、点C分别是三位同学所在座 位，要在三点构成的△ABC内部确定一个点P存放 一个神秘礼盒，使点P到三边AB、AC、BC的距离 相等，这个点应取于何处？
三角形的三条角平分线 交于一点，这个点到三角形 三边的距离相等。
D F
.P
E
挑战自我
6、如图，BD=CD，DE⊥AB，DF⊥AC，垂足分别为E，
作业布置：创优P31-32
谢谢指导！
A M
Q
O
N
B
小试锋芒
判断正误：
2、已知：Q 到OA 的距离等于2 cm， 且Q 到OB 距离等于2 cm，则Q 在∠AOB 的平分线上． A
M
Q
O
N
B
小试锋芒
3、如图，DE⊥AB于点E，DF⊥BC于点F， 且DE＝DF，若∠DBC＝55°，则∠ABC＝______.
小试锋芒
4、如图，已知AB//CD，∠BCD=100°，点P到 AB、BC的距离相等，则∠PBC＝______.
已知：PD⊥OA，PE⊥OB，垂足分 别为D，E，PD =PE．
求证：P在∠AOB的平分线上．
新知探究
角平分线的判定
角的内部到角的两边的距离相等的 点在角的平分线上
几何语言 ∵PD⊥OA，PE⊥OB， PD = PE ∴点P 在∠AOB的平分线上 （OP 平分 ∠AOB）．
小试锋芒
判断题：
1、如图，若QM =QN，则OQ 平分∠AOB。
§12.3.2 角平分线的判定
情境引入
如图，长沙最近多雨水天气，要在S 区一点P放 置一个雨量器测量降水量，使它到两条路的距离相 等. 这个放置点应取于何处？

人教版八年级上册 12.3 角的平分线的判定(共18张PPT)

人教版八年级上册 12.3 角的平分线的判定(共18张PPT)

•
填空：
A
练一练 12
(1). ∵∠1= ∠2,DC⊥AC, DE⊥AB
E
∴__D_C__=_D_E____
(__在__角__平__分___线__上__的___点__到__角___的__两__边__的_C__距__离__相D___等__)
B
(1). ∵DC⊥AC ,DE⊥AB ,DC=DE
∴_∠__1_=_∠__2___
B
等的点在角的平分线上
。 ∵ PDOA PEOB
PD = PE
\ OP 是 AOB的平分线
用途：判定一条射线是角平分线
•
9、要学生做的事，教职员躬亲共做； 要学生 学的知 识，教 职员躬 亲共学 ；要学 生守的 规则， 教职员 躬亲共 守。20 21/8/10 2021/8/10Tues day , August 10, 2021
(_到__一__个__角__的__两__边__的__距__离__相__等__的__点__，__在__这__个__角__平__分__线__上__。)
应用角平分线性质定理的逆定理
判断题： （1）如图，若QM =QN，则OQ 平分∠AOB；( X )
A M
Q
O
N
B
应用角平分线性质定理的逆定理
判断题：
（2）如图，若QM⊥OA 于M，QN⊥OB 于N，则
• 2、Our destiny offers not only the cup of despair, but the chalice of opportunity. (Richard Nixon, American President )命运给予我们的不是失望之酒，而是机会之杯。二〇二一年六月十七日2021年6月17日星期四

新人教版八年级上册课件：第12章 12.3角平分线的性质和判定(共66张PPT)


D
A
证明：作射线OP
∵
PD ^ OA
\
PE ^ OB
O E
P
PDO PEO 90
OP = OP （公共边） PD = PE （ 已 知 ）
在 Rt△PDO 和Rt△PEO 中，
B
\ RtPDO≌ RtPEO （ HL） \ AOP BOP （全等三角形的对应角相等） \ 点P在 AOB 角的平分线上
OM=ON， MC=NC， OC=OC， ∴ △OMC≌ △ONC（SSS） ∴∠MOC=∠NOC Ｂ 即：OC平分∠AOB
A Ｍ
Ｃ
Ｎ
Ｏ
角的平分线上的点到这个角的两边的距离相等。 已知：如图，OC是∠AOB的平分线，点P在OC上，
PD⊥OA，PE⊥OB，垂足分别是D，E。 求证：PD=PE 证明：∵ PD⊥OA，PE⊥OB（已知）
D
C
F A E B N
课堂小结
1、画一个已知角的角平分线； 及画一条已知直线的垂线；
2、角平分线的性质：
角的平分线上的点到角的两边的距离相等． 3、角平分线的判定结论： 到角的两边的距离相等的点在角平分线上。
判定：到角的两边的距离相 等的点在角的平分线上。
用数学语言表示为：
∵ QD⊥OA，QE⊥OB，QD＝QE ∴点Q在∠AOB的平分线上． 性质：角的平分线上的点到角的两边的距离 相等. 用数学语言表示为： ∵ QD⊥OA,QE⊥OB,点Q在∠AOB的平分线上 ∴ QD＝QE
B C E
怎样找三角形内到三角形三边距离相等的点？
如图，△ＡＢＣ的∠Ｂ的外角的平分线ＢＤ与∠Ｃ 的外角的平分线ＣＥ相交于点Ｐ．
求证：点Ｐ到三边ＡＢ、ＢＣ、ＣＡ所在直线的距离 相等．

人教版八年级数学上册12.3 角的平分线的性质 课件

【课本P50 练习 第1题】
随堂演练
4.已知：如图，在△ABC中，AD是∠BAC的角平分线，且 BD=CD，DE⊥AB，DF⊥AC.垂足分别为E、F.求证：EB=FC. 证明：∵AD是∠BAC的角平分线，DE⊥AB，DF⊥AC
∴ DE=DF， ∠DEB=∠DFC=90 °， 在Rt△BDE 和 Rt△CDF中，
BD=CD， DE=DF ， ∴ Rt△BDE ≌ Rt△CDF（HL）. ∴ EB=FC.
课堂小结
角平分线
尺规 作图
性质
依据：SSS
一个点： 角平分线上的点 二距离： 点到角两边的距离 两相等： 两条垂线段相等
添加辅助 线解题
过角平分线上一点向 两边作垂线段
12.3 角的平分线的性质
角平分线的判定
(2) 分别以点M，N为圆心．大于 1 MN的长为半径画弧，两弧在 2 ∠AOB的内部交于点C．
A M
(3) 画射线OC．射线OC即为所求．
C
O
B
N
思考
1.为什么以大于
1 2
MN的长为半径作弧？
2.两弧的交点一定在∠AOB的内部吗？
A M
C
O
NB
结论
1.如果以小于 1 MN的长为半径作弧，所作的两弧
AD=AB，
CD=CB，
D
∴△ACD≌△ACB（SSS）
∴∠DAC=∠BAC.
∴AE平分∠DAB.
A
B C E
知识点一 用尺规作角的平分线
已知：∠AOB. 求作：∠AOB的平分线.
A
思考 如果没有平分角的仪器， 我们用尺规作图也能画 出一个角的平分线吗？
O
B
知识点一 用尺规作角的平分线

数学人教版八年级上册数学第十二章12.3角的平分线的判定 PPT课件


新知应用
例3 如图, ∠B=∠C=90°, M是BC的中点, DM平分∠ADC． (2) 线段CD、AB、AD间有怎样的关系?
解: (2)CD+AB=AD; 理由如下: ∵ME⊥AD, MC⊥CD, ∴∠C=∠DEM=90°, 在Rt△DCM和Rt△DEM中
DM=DM,
MC=ME, ∴Rt△DCM≌Rt△DEM(HL), ∴CD=DE,
新知应用
例2 如图, 已知∠CBD和∠BCE的平分线相交于点F, 求证: 点F在∠DAE的平分线上．
证明: 过点F作FG⊥AE, FH⊥AD, FM⊥BC, 垂足为G, H, M.
∵点F在∠BCE的平分线上, FG⊥AE, FM⊥BC.
∴FG=FM.
A
同理可得, ∴FM=FH,
∴FH =FG , ∴点F在∠DAE的平分线上.
课堂总结
内容
角平分线的 判定定理
作用
结论
角的内部到角两边距离相等的点在 这个角的平分线上.
判断一个点是否在角的平分线上.
三角形的三条角平分线相交于三角 形内一点.
感谢聆听
D N
P
∴PD=P点EP. 在∠A的平分线上.
B
同理PE=PF.
E
结∴论P:D=三PE角=形PF的. 三条角平分线交于一点, 称为三角
即点P形到的三边内A心B,, B并C,且CA这的点距到离三相边等.的距离相等.
F M
C
新知应用
例1 如图, 在△ABC中, 点O是△ABC内一点, 且点O到△ABC三边 的距离相等．若∠A=40°, 则∠BOC的度数为( )A
A D
则∠AOC与∠BOC 是否相等?
C
P
O
E

人教版八年级上册数学精品系列角平分线的判定PPT


D
A
在Rt△PDO和Rt△PEO 中，
OP=OP，
O
P
PD= PE，
∴Rt△PDO≌Rt△PEO（ HL）.
E B
∴∠AOP=∠BOP（全等三角形的对应角相等）.
∴点P在∠AOB 的平分线上.
★判定定理： 角的内部到角的两边的距离相等的点在角的平分线上.
▼应用所具备的条件： （1）位置关系：点在角的内部；
CN相交
证明：过点P作PD、PE，PF分 别垂直于AB、BC，CA，垂足 分别为D、E、F.
A
ND
F
P
M
∵BM是△ABC的角平分线，
点P在BM上，
B
∴PD=PE.同理PE=PF.
∴PD=PE=PF.
即点P到三边AB、BC、CA的距离相等.
C E
人教版八年级上册数学课件 12.3 第2课时 角平分线的判定(共23张PPT)
(2)若△ABC的周长为32，求△ABC的面积.
解：连接OC.
SABC SAOC SBOC SAOB
1 AB OE 1 BC ON 1 AB OM
2
2
2
1 OM (AB BC OM ) 2
1 4 32 64
A
2
B
O
P
DM
C
人教版八年级上册数学课件 12.3 第2课时 角平分线的判定(共23张PPT)
（2）数量关系：该点到角两边的距离相等.
A
▼定理的作用：判断点是否在角平分线上. D
C
▼应用格式：
P
∵ PD⊥OA,PE⊥OB，PD=PE. O
E
B
∴点P 在∠AOB的平分线上.
人教版八年级上册数学课件 12.3 第2课时 角平分线的判定(共23张PPT)
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

几何语言描述： ∵ OC平分∠AOB， 且PD⊥OA， PE⊥OB.
∴ PD= PE. 不必再证全等
A D
P到OA的距离
C 角平分线上的点
P
O
E
B P到OB的距离
2.我们知道，角平分线上的点到角的两边的距离相 等.那么到角的两边的距离相等的点是否在角的平 分线上呢？
到角的两边的距离相等的点在角的平分线上.
PE的距离与到PF的距离相等，判断AD是否平分
∠BAC，并说明理由．
解：AD平分∠BAC．理由如下： ∵D到PE的距离与到PF的距离相等， ∴点D在∠EPF的平分线上． ∴∠1＝∠2．
又∵PE∥AB，∴∠1＝∠3． B E
(
A
34 P
12 DFC
同理，∠2＝∠4．
∴∠3＝∠4，∴AD平分∠BAC．
3.已知：如图，OD平分∠POQ，在OP、OQ边上取 OA＝OB，点C在OD上，CM⊥AD于M，CN⊥BD于 N.求证：CM＝CN. 证明：∵OD平分线∠POQ， ∴∠AOD=∠BOD. 在△AOD与△BOD中， ∵OA=OB，∠AOD=∠BOD，OD=OD， ∴△AOD≌△BOD. ∴∠ADO=∠BDO. ∵CM⊥AD，CN⊥BD， ∴CM=CN.
你能证明这 个结论吗？ 发现：过交点作三角形三边的垂线段相等
证明结论
已知：如图，△ABC的角平分线BM，CN相交于点P，
求证：点P到三边AB，BC，CA的距离相等.
证明：过点P作PD，PE，
PF分别垂直于AB，BC， CA，垂足分别为D，E，F.
∵BM是△ABC的角平分线，
A
ND
F
P
M
点P在BM上，
周长
2
例2 如图，在△ABC中，点O是△ABC内一点，且点O
到△ABC三边的距离相等．若∠A＝40°，则∠BOC的
度数为( A ) A．110° B．120°
C．130°
解D析．：14由0°已知，O到三角形三边的距离
相等，所以O是内心，即三条角平分线
的交点，AO，BO，CO都是角平分线， 所∠B以C有O＝∠C∠BAOC＝O＝∠AB∠12 OAC＝B，∠12 ABC， ∠ABC＋∠ACB＝180°－40°＝140°，
八年级数学上（RJ）
第十二章 全等三角形
12.3 角的平分线的性质
第2课时 角平分线的判定
导入新课
讲授新课
当堂练习
课堂小结
学习目标
1.理解角平分线判定定理.(难点） 2.掌握角平分线判定定理内容的证明方法并应用其解题. （重点） 3.学会判断一个点是否在一个角的平分线上.
导入新课
复习回顾
1.叙述角平分线的性质定理 角的平分线上的点到角的两边的距离相等.
讲授新课
一 角平分线的判定 问题：交换角的平分线的性质中的已知和结论，你能
得到什么结论，这个新结论正确吗？
角平分线的性质：
A
角的平分线上的点到角的两边的距离相等. D
几何语言：
C
∵ OC平分∠AOB，
O
且PD⊥OA， PE⊥OB
P
E
B
∴ PD= PE 猜想:
思考：这个结 论正确吗？
角的内部到角的两边距离相等的点在角的平分线上．
P
∵ PD⊥OA,PE⊥OB，PD=PE. O
E
B
∴点P 在∠AOB的平分线上.
典例精析
例1：如图，要在S区建一个贸易市场，使它到铁路 和公路距离相等， 离公路与铁路交叉处500米，这 个集贸市场应建在何处（比例尺为1︰20000）？
O
解：作夹角的角平分线OC，
截取OD=2.5cm ,D即为所求.
D S
C
方法点拨：根据角平分线的判定定理，要求作的点到 两边的距离相等，一般需作这两边直线形成的角的平 分线，再在这条角平分线上根据要求取点.
二 三角形的内角平分线 活动1 分别画出下列三角形三个内角的平分线，你 发现了什么？
发现：三角形的三条角平分线相交于一点
活动2 分别过交点作三角形三边的垂线，用刻度尺量一 量，每组垂线段，你发现了什么？
B
∴PD=PE.同理PE=PF.
C E
∴PD=PE=PF.
即点P到三边AB，BC，CA的距离相等.
想一想：点P在∠A的平分线上吗？这说明三角形
的三条角平分线有什么关系？
A
点P在∠A的平分线上.
D
N
F
P
M
B
C
E
结论：三角形的三条角平分线交于一点，并且
这点到三边的距离相等.
变式1：如图，在直角△ABC中，∠C＝90°，AP平分
P E
B
∴∠AOP=∠BOP（全等三角形的对应角相等）.
∴点P在∠AOB 角的平分线上.
知识总结
判定定理：
角的内部到角的两边的距离相等的点在角的平分线上.
应用所具备的条件： （1）位置关系：点在角的内部；
（2）数量关系：该点到角两边的距离相等.
A
定理的作用：判断点是否在角平分线上. D
C
应用格式：
∠OBC＋∠OCB＝70°， ∠BOC＝180°－70°＝110°.
方法总结
由已知，O 到三角形三边的距离相等，得O是 内心，再利用三角形内角和定理即可求出∠BOC的 度数．
归纳总结
角的平分线的性质 角的平分线的判定
图形C PFra bibliotekC P
已知 条件
结论
OP平分∠AOB PD⊥OA于D PE⊥OB于E
PD=PE
PD=PE PD⊥OA于D PE⊥OB于E
OP平分∠AOB
当堂练习
1. 如图，某个居民小区C附近有三条两两相交的道路 MN、OA、OB，拟在MN上建造一个大型超市，使得 它到OA、OB的距离相等，请确定该超市的位置P.
A
M
小区C
P
O
N
B
2. 如图所示，已知△ABC中，PE∥AB交BC于点E，
PF∥AC交BC于点F，点P是AD上一点，且点D到
证明猜想
已知：如图，PD⊥OA，PE⊥OB，垂足分别是D、E， PD=PE.求证：点P在∠AOB的角平分线上.
证明：作射线OP，∵PD⊥OA,PE⊥OB. ∴∠PDO=∠PEO=90
D
A
在°R，t△PDO和Rt△PEO 中，
OP=OP（公共边），O PD= PE（已知 ），
∴Rt△PDO≌Rt△PEO（ HL）.
解：连接OC
SABC SAOC SBOC SAOB
1 AB OE 1 BC ON 1 AB OM
2
2
2
1 OM ( AB BC OM ) 2
1 4 32 64
A
2
B
O
P
DM
C
知识与方法
1.应用角平分线性质： 存在角平分线 条件 涉及距离问题
2.联系角平分线性质：
距离
面积 s 1 ch
∠BAC，BD平分∠ABC;AP,BD交于点O，过点O作 OM⊥AC,若OM＝4,
(1)求点O到△ABC三边的距离和.
B
12
O
P
A
DM
C
温馨提示：不存在垂线段———构造应用
变式1：如图，在直角△ABC中，∠C＝900，AP平分 ∠BAC，BD平分∠ABC;AP,BD交于点O，过点O作 OM⊥AC,若OM＝4. (2)若△ABC的周长为32，求△ABC的面积.