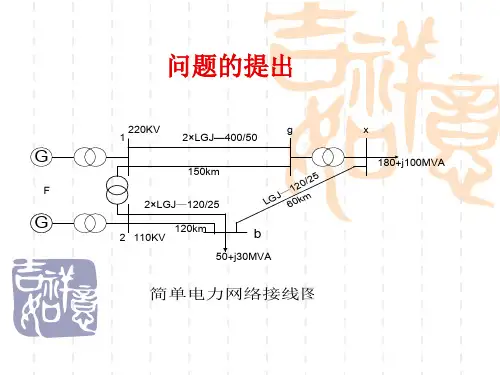
简单电网潮流计算
- 格式:ppt
- 大小:192.00 KB
- 文档页数:20





电气工程师-专业基础(发输变电)-电气工程基础-4.3简单电网的潮流计算[单选题]1.高压电网中,影响电压降落纵分量的是()。
[2018年真题]A.电压B.电流C.有功功率D(江南博哥).无功功率正确答案:D参考解析:由电压降落纵分量计算公式ΔU=(PR+QX)/U可知,在高压输电线路参数中,电压基本恒定,电抗要比电阻大得多。
若忽略线路电阻,上式变为:ΔU=QX/U。
因此,影响电压降落纵分量的主要因素是无功功率Q。
[单选题]2.额定电压110kV的辐射型电网各段阻抗及负荷如图4-3-1所示,已知电源A的电压为121kV,若不计电压降落的横分量,则B点电压是()。
[2018年真题]图4-3-1A.105.5kVB.107.4kVC.110.5kVD.103.4kV正确答案:A参考解析:已知不同点电压和功率求潮流分布。
先假设全网电压为额定电压,即110kV,由末端往首端推功率,求出S A。
已知末端功率S C=-(8+j6)MVA,可以推出S B、S A分别为:S B=S C+ΔS BC+S′B=-(8+j6)+[(82+62)/1102]×(10+j20)+(40+j30)=(32.08+j24.17)MVAS A=S B+ΔS AB=32.08+j24.17+[(32.082+24.172)/1102]×(20+j40)=(34.75+j29.5)MVA又因为:ΔU AB=(PR+QX)/U=(34.75×20+29.5×40)/121=15.5kV;则:U B=U A-ΔU AB=121-15.5=105.5kV。
[单选题]3.图4-3-2各支路参数为标幺值,则节点导纳Y11、Y22、Y33、Y44分别是()。
[2018年真题]图4-3-2A.-j4.4,-j4.9,-j14,-j10B.-j2.5,-j2.0,-j14.45,-j10C.j2.5,j2,j14.45,j10D.j4.4,j4.9,-j14,-j10正确答案:A参考解析:根据节点电压法,分别计算节点导纳Y11、Y22、Y33、Y44为:Y11=Y10+Y12+Y13=j0.1-j2.5-j2=-j4.4Y22=Y20+Y12+Y23=j0.1-j2.5-j2.5=-j4.9Y33=Y13+Y30+Y23+Y34=-j2+j0.5-j2.5-j10=-j14Y44=Y34=-j10[单选题]4.线路末端的电压降落是指()。

简单电力系统分析潮流计算电力系统潮流计算是电力系统分析中的一项重要任务。
其目的是通过计算各个节点的电压、电流、有功功率、无功功率等参数,来确定系统中各个元件的运行状态和互相之间的相互影响。
本文将介绍电力系统潮流计算的基本原理、计算方法以及应用。
潮流计算的基本原理是基于电力系统的节点电压和支路功率之间的网络方程。
通过对节点电压进行迭代计算,直到满足所有支路功率平衡方程为止,得到系统的运行状态。
潮流计算的基本问题可以表示为以下方程组:P_i = V_i * (G_i * cos(θ_i - θ_j ) + B_i * sin(θ_i -θ_j )) - V_j * (G_i * cos(θ_i - θ_j ) - B_i * sin(θ_i -θ_j )) (1)Q_i = V_i * (G_i * sin(θ_i - θ_j ) - B_i * cos(θ_i -θ_j )) - V_j * (G_i * sin(θ_i - θ_j ) + B_i * cos(θ_i -θ_j )) (2)其中,P_i为节点i的有功功率注入;Q_i为节点i的无功功率注入;V_i和θ_i分别为节点i的电压幅值和相角;V_j和θ_j分别为节点j的电压幅值和相角;G_i和B_i分别为支路i的导纳的实部和虚部。
对于一个电力系统,如果知道了节点注入功率和线路的导纳,就可以通过潮流计算求解出各节点的电压和功率。
这是一种不断迭代的过程,直到系统达到平衡状态。
潮流计算的方法有多种,常见的有高斯-赛德尔迭代法、牛顿-拉夫逊迭代法等。
其中,高斯-赛德尔迭代法是最常用的一种方法。
高斯-赛德尔迭代法的思想是从已知节点开始,逐步更新其他节点的电压值,直到所有节点的电压值收敛为止。
具体步骤如下:1.初始化所有节点电压的初始值;2.根据已知节点的注入功率和节点电压,计算其他节点的电压值;3.判断节点电压是否收敛,如果收敛则结束计算,否则继续迭代;4.更新未收敛节点的电压值,返回步骤2高斯-赛德尔迭代法的优点是简单有效,但其收敛速度较慢。



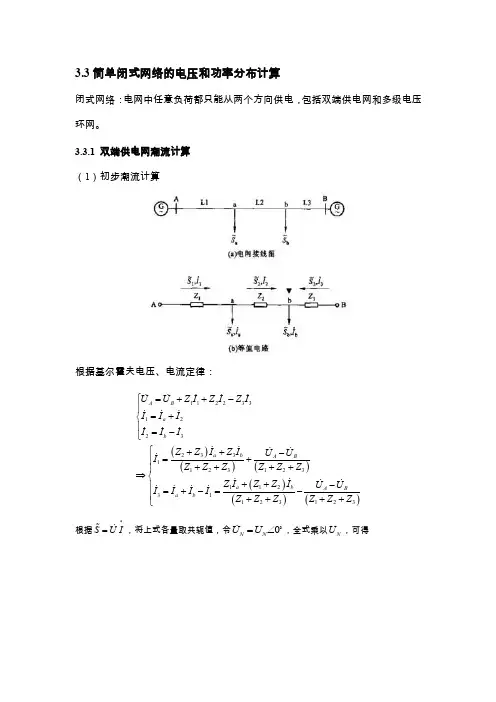
3.3简单闭式网络的电压和功率分布计算闭式网络:电网中任意负荷都只能从两个方向供电,包括双端供电网和多级电压环网。
3.3.1 双端供电网潮流计算 (1)初步潮流计算根据基尔霍夫电压、电流定律:()()()()()()1122331223233112312311231123123A B a b a b A Ba b A Ba b U U Z I Z I Z I I I I I I I Z Z I Z I U U I Z Z Z Z Z Z Z I Z Z I U U I I I I Z Z Z Z Z Z ⎧=++-⎪=+⎨⎪=-⎩⎧++-=+⎪++++⎪⇒⎨++-⎪=+-=-⎪++++⎩根据*S U I = ,将上式各量取共轭值,令0N NU U =∠ ,全式乘以N U ,可得其中1LD S 和3LD S —供载功率,LS —循环功率。
获得电源输出功率1S 和3S 后,进而可以求出各段线路上的传输功率,从而可以判断各段线路上传输功率的实际方向(确定功率分点——实际的双端供电点,分为有功功率分点、无功功率分点)。
(2)最终潮流计算初步潮流计算后,在功率分点将网络打开,分为两个开式电网(当有功功率分点和无功功率分点不一致时,常选电压较低的分点将电网打开。
鉴于高压电网中,电压损耗主要由无功功率流动所致,无功功率分点电压往往低于有功功率分点电压,故一般选取无功功率分点将电网打开)。
开式电网潮流计算:已知终端电压和始端电压,采用迭代法计算。
几点说明:(1) 环网(A BU U = )——无循环功率。
(2) 35KV 及以下电网,可以忽略线路功率损耗,因此初步潮流分布就是最终潮流分布。
(3) 均一电网(C i i X R =常数),供载功率为在均一网中,有功功率和无功功率的分布彼此独立,且可以只利用各线段的电阻(或电抗)分别计算。
对于电压等级和导线截面相同的均一网,有功功率和无功功率的分布仅由线路长度决定。
—线路的电压降落和功率损耗—变压器的电压降落和功率损耗—辐射网潮流计算—环网潮流计算*电力系统潮流计算是指节点电压和支路功率分布的计算。
详细地讲,电力系统潮流计算就是根据给定的某些运行条件(比如:有功、无功负荷,发电机的有功出力,发电机母线电压大小等)和电力系统接线方式,求解电网中各母线的电压、各条线路和各台变压器中的功率及功率损耗。
*标志电网电压运行水平的指标(1)电压降落—指线路始、末两端电压的相量差即:(2)电压损耗(或电压损失)—指线路始、末两端电压的数量差,即:U1–U2或(3)电压偏移—指线路始端或末端电压与线路额定电压的数值差,即:U1–U N 及 U2–U N或*线路的电压降落和功率损耗取,则电压降落为:相量图:如果取,则当采用Π型等值电路时,必须考虑并联导纳支路的功率:电压降落:三相功率损耗:注意:公式中的功率为三相功率,并且为直接流入或流出阻抗的功率;电压为线电压。
如果功率为容性,即,则有关公式中的无功功率符号要改变,为:*变压器的电压降落和功率损耗与线路的计算类似。
比如,已知功率和电压则:*放射式电网的潮流计算放射式电网可以简化为末端有一个集中负荷时的线路(或包括变压器):首先作等值电路:或如果已知末端功率和电压,则如果已知末端功率和首端电压,则可以先假设末端电压为U2=U N,由末端起求电网的功率损耗和功率分布,然后用U1和功率分布从始端起求末端节点的电压。
在第六、八讲的习题中,已知线路末端功率为10 MW,cosφ2=0.95滞后或超前,这时的无功功率即为感性或容性。
滞后:φ2 = cos-10.95 =18.195°Q2 = P2tgφ2 = 3.287 Mvar超前:*树枝式电网的潮流计算对于树枝式(或链式、主干式)电网,也仍然需要作等值电路:树枝式电网往往已知末端功率和首端电压,求潮流时可以先假设全网电压为额定电压U N,由末端起求电网的功率损耗和功率分布,最后用U1和功率分布从始端起求其它各节点的电压。
简单配电网的潮流计算电力系统正常运行状况下,运行、管理和调度人员需要知道在给定运行方式下各母线的电压是否满意要求,系统中的功率分布是否合理,元件是否过载,系统有功、无功损耗各是多少等等状况。
为了了解这些运行状况就需要进行潮流计算。
潮流计算:依据已知的负荷(功率)及电源电压计算出其它节点的电压和元件上的功率分布。
潮流计算是电力系统中最基本、最常用的一种汁算。
开式网:只有一端电源供电的网络。
一.计算中的两种类型:1.同一电压等级的开式网计算 2.不同电压等组的开式网计算二.计算中的三种状况:1.已知末端电压和功率,求首端电压和功率采纳将电压和功率由已知点向未知点逐段递推计算的方法。
即已知和,求和,见图1。
图1 已知末端电压和功率,求首端电压和功率(1)功率计算:2)电压计算:(3)对功率和电压交替计算,求和对于110kV及以下的网络,在计算电压损耗时常略去横重量,使计算进一步简化。
在计算时需留意变压器两侧参数与电压的归算。
2.已知首端电压和功率,求末端电压和功率即已知和,求和,这种状况的电路见图2。
图2 已知首端电压和功率,求末端电压和功率(1)功率计算:2.电压计算:(3)对功率和电压交替计算:求和3.已知末端功率和首端电压,求首端功率和末端电压(常见)即已知和,求末端和首端,这种状况的电路见图3。
图 3 已知末端功率和首端电压,求首端功率和末端电压近似计算(常用):精确计算:不断迭代!(1)设定各节点电压等于其额定电压:(2)与第一种状况一样求出功率分布:(3)与其次种状况一样求出各节点电压分布:常见的状况是给出开式配电网的末端负荷与首端电压。
对于这种状况可进一步简化计算,不必进行反复递推。
设全网为额定电压(一般可将全网参数归算到同一个电压等级),由网络末端向首端推算各元件的功率损耗和功率分布,而不计算电压;待求得首端功率后,再由给定的首端电压与求得的首端功率、网络各处的功率分布,从首端向末端推算各元件电压损耗和各母线(节点)电压,此时不再重新计算功率损耗与功率分布。