第三章简单电力系统的潮流计算汇总
- 格式:doc
- 大小:1.40 MB
- 文档页数:17







第3章简单电力系统的潮流计算简单电力系统的潮流计算是电力系统运行中的重要环节,主要用于分析电力系统中各节点的电压、功率等参数的分布和变化情况,以保证系统的稳定运行和优化调度。
本章主要介绍了简单电力系统的潮流计算的基本原理和方法。
首先,简单电力系统的潮流计算是基于电力系统节点电压相等、功率平衡和潮流方向一致的基本假设。
在计算过程中,需要对电力系统进行建模和等效处理。
电力系统的节点可以分为发电节点、负荷节点和平衡节点。
发电节点表示电力系统的发电机节点,负荷节点表示电力系统的负载节点,平衡节点表示电力系统的节点电压保持不变。
潮流计算主要通过节点潮流方程和支路潮流方程进行求解。
节点潮流方程是基于潮流方向一致和功率平衡的基本原理,用于计算电力系统的节点电压。
支路潮流方程用于计算电力系统的支路电流。
节点潮流方程和支路潮流方程可以通过潮流计算矩阵的形式表示。
潮流计算的求解方法主要有迭代法和直接法两种。
迭代法是将潮流计算问题转化为非线性方程组的求解问题,常用的迭代法有高斯-赛德尔迭代法和牛顿-拉夫逊迭代法。
直接法是通过高斯消元法或LU分解法直接求解潮流计算矩阵的方程组,计算速度较快但适用范围较窄。
在潮流计算中,还需要考虑电力系统中的各种约束条件,如节点电压范围、支路功率限制等。
这些约束条件可以通过潮流计算的目标函数中引入惩罚项的方式来处理,最终得到满足约束条件的潮流计算结果。
总之,简单电力系统的潮流计算是电力系统运行和调度中的重要环节,通过对电力系统的节点电压、功率等参数进行分析和计算,可以保证电力系统的稳定运行和优化调度。
潮流计算的基本原理和方法主要包括节点潮流方程和支路潮流方程的求解,以及迭代法和直接法的计算方法。
同时,需要考虑电力系统中的各种约束条件,以保证潮流计算结果的合理性和可行性。


第3章简单电力系统潮流计算第3章是关于简单电力系统潮流计算的内容。
潮流计算是电力系统静态分析的基础,用于分析电力系统中各个节点的电压、功率和电流等参数的分布和变化情况。
本章主要介绍了潮流计算的基本原理、潮流方程的建立及其求解方法。
首先,潮流计算的基本原理是利用电压与功率之间的耦合关系,通过建立潮流方程来计算电力系统中各个节点的电压和功率。
潮流方程是基于电流的守恒方程和电压的Kirchhoff定律,其中包括节点功率平衡方程、支路功率方程和节点电压和节点功率之间的关系等。
为了建立潮流方程,首先需要确定电力系统的拓扑结构,即节点和支路之间的连接关系。
然后,根据节点和支路的电压和功率关系,可以得到节点功率平衡方程和支路功率方程。
节点功率平衡方程表示电力系统中各个节点的功率之和为零;支路功率方程表示电力系统中各个支路的功率与电压和电流之间的关系。
在求解潮流方程时,可以使用迭代法、牛顿-拉夫逊法、高斯-赛德尔法等方法。
迭代法是最常用的方法,主要包括直接迭代法和间接迭代法。
直接迭代法先将支路功率方程转化为节点电压和节点功率之间的关系,然后通过迭代计算更新节点电压和节点功率,直到收敛。
间接迭代法则通过反复迭代计算节点电压和节点功率之间的关系来求解潮流方程。
潮流计算的结果可以用来分析电力系统的运行状态和负荷情况,评估电力设备的运行性能和潜在问题,并为电力系统的规划和调度提供支持。
潮流计算还可以用于电力系统的故障分析和稳定分析等,对电力系统的稳定性和可靠性进行评估。
总结来说,第3章简单电力系统潮流计算介绍了潮流计算的基本原理、潮流方程的建立及其求解方法。
潮流计算是电力系统静态分析的基础,可以用于分析电力系统中各个节点的电压、功率和电流等参数的分布和变化情况,对电力系统的运行和规划提供支持。
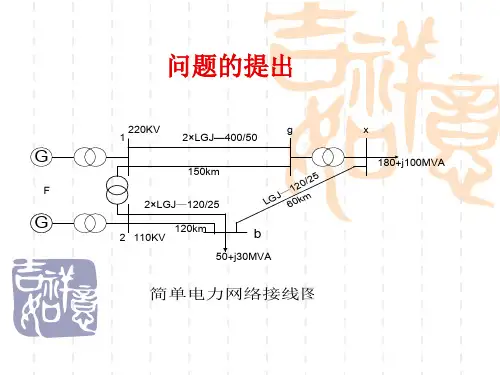
第三章 简单电力系统的潮流计算本章介绍简单电力系统潮流计算的基本原理和手工计算方法,这是复杂电力系统采用计算机进行潮流计算的基础。
潮流计算是电力系统分析中最基本的计算,其任务是对给定的运行条件确定系统的运行状态,如各母线上的电压、网络中的功率分布及功率损耗等。
本章首先通过介绍网络元件的电压降落和功率损耗计算方法,明确交流电力系统功率传输的基本规律,然后循序渐进地给出开式网络、配电网络和简单闭式网络的潮流计算方法。
3.1 单一元件的功率损耗和电压降落电力网络的元件主要指线路和变压器,以下分别研究其功率损耗和电压降落。
电力线路的功率损耗和电压降落1.线路的功率损耗线路的等值电路示于图3-1。
U 1S 'S 2S 1B Q ∆j Q ∆j 2Bj 2Bj X I I 1I 2I 2U R图3-1 线路的等值电路图中的等值电路忽略了对地电导,功率为三相功率,电压为线电压。
值得注意的是,阻抗两端通过的电流相同,均为I ,阻抗两端的功率则不同,分别为S '和S ''。
电力线路传输功率时产生的功率损耗既包括有功功率损耗,又包括无功功率损耗。
线路功率损耗分为电流通过等值电路中串联阻抗时产生的功率损耗和电压施加于对地导纳时产生的损耗,以下分别讨论。
1) 串联阻抗支路的功率损耗电流在线路的电阻和电抗上产生的功率损耗为222L L L 22j (j )(j )P Q S P Q I R X R X U ''''+∆=∆+∆=+=+ (3-1) 若电流用首端功率和电压计算,则22L 21(j )P Q S R X U ''+∆=+ (3-2) 从上式看出,串联支路功率损耗的计算非常简单,等同于电路课程中学过的I 2乘以Z 。
值得注意的是,由于采用功率和电压表示电流,而线路存在功率损耗和电压损耗,因此线路两端功率和电压是不同的,在使用以上公式时功率和电压必须是同一端的。
第一章 简单电力系统的分析和计算一、基本要求掌握电力线路中的电压降落和功率损耗的计算、变压器中的电压降落和功率损耗的计算;掌握辐射形网络的潮流分布计算;掌握简单环形网络的潮流分布计算;了解电力网络的简化。
二、重点内容1、电力线路中的电压降落和功率损耗图3-1中,设线路末端电压为2U 、末端功率为222~jQ P S +=,则 (1)计算电力线路中的功率损耗① 线路末端导纳支路的功率损耗: 2222*222~U B j U Y S Y -=⎪⎭⎫ ⎝⎛=∆ ……………(3-1)则阻抗支路末端的功率为: 222~~~Y S S S ∆+=' ② 线路阻抗支路中的功率损耗: ()jX R U Q P Z I S Z +'+'==∆2222222~ ……(3-2) 则阻抗支路始端的功率为: Z S S S ~~~21∆+'=' ③ 线路始端导纳支路的功率损耗: 2121*122~U B j U Y S Y -=⎪⎭⎫⎝⎛=∆ …………(3-3)则线路始端的功率为: 111~~~Y S S S ∆+'=~~~图3-3 变压器的电压和功率~2•U(2)计算电力线路中的电压降落选取2U 为参考向量,如图3-2。
线路始端电压 U j U U U δ+∆+=21 其中 222U X Q R P U '+'=∆ ; 222U R Q X P U '-'=δ ……………(3-4)则线路始端电压的大小: ()()2221U U U U δ+∆+=………………(3-5)一般可采用近似计算: 222221U X Q R P U U U U '+'+=∆+≈ ………………(3-6)2、变压器中的电压降落和电能损耗图3-3中,设变压器末端电压为2U 、末端功率为222~jQ P S +=,则~~~图3-3 变压器的电压和功率~(1)计算变压器中的功率损耗 ① 变压器阻抗支路的功率损耗:()T T T ZT jX R U Q P Z I S ++==∆2222222~ ……(3-7) 则变压器阻抗支路始端的功率为:ZT S S S ~~~21∆+='② 变压器导纳支路的功率损耗: ()*2211YT T T S YU G jB U ∆==+ ………(3-8)则变压器始端的功率为: YT S S S ~~~11∆+'= 。
(2)计算变压器中的电压降落变压器始端电压: TT U j U U U δ+∆+=21 其中 222U X Q R P U TT T +=∆, 222U R Q X P U T T T -=δ ……………(3-9)则变压器始端电压的大小: ()()2221T T U U U U δ+∆+=…………(3-10)一般可采用近似计算: 222221U X Q R P U U U U TT T ++=∆+≈ …………(3-11)3、 辐射形网络潮流计算潮流(power flow )计算是指电力网络中各节点电压、各元件流过的电流或功率等的计算。
辐射形网络潮流计算主要有两种类型:(1)已知同一端点的电压和功率求潮流分布,采用逐段推算法;逐段推算法:根据已知端点的电压和功率,逐段推算电网各点电压和功率。
参看例3-1 。
(2)已知不同端点的电压和功率求潮流分布,采用逐步渐进法。
逐步渐进法:首先设已知功率端点的电压为)0(i U ,运用该点已知的功率i S 和)0(iU 推算电网潮流;再由另一端点已知电压jU和求得的功率)1(jS 推算电网各点电压;以此类推,反复推算,逐步逼近结果。
逐步渐进法的近似算法:首先设电网未知点的电压为N U ,运用已知的功率计算电网功率分布;再由另一端点已知电压U 和求得的各点功率计算电网电压分布。
参看例3-3 。
4、环式网络的近似功率分布计算将最简单的环式网络简化,并将电源节点一分为二得到等值环式网络的等值电路如图3-4。
其两端电压大小相等、相位相同。
231231'2Z 1Z 3Z图3-4 等值环式网络的等值电路环式网络的近似功率分布:3*2*1**33*32*2~~~Z Z Z Z S Z Z S S a +++⎪⎭⎫ ⎝⎛+= ………………(3-12) 3*2*1**21*3*12~~~Z Z Z Z Z S Z S S b ++⎪⎭⎫⎝⎛++= ………………(3-13) 223~~~S S S a -= ………………(3-14)5、两端供电网络的近似功率分布计算将最简单的两端供电网络简化,得到两端供电网的等值电路如图3-5。
其两端电压大小不等、相位不同,41U U ≠ 。
2312342Z 1Z 3Z C~图3-5 两端供电网的等值电路由于两端电压14U U ≠,它们之间存在相量差 14dU U U =-,就使得由节点1到节点4产生了一个循环功率,以C S 表示循环功率 3*2*1**~Z Z Z U d U S N c ++=………………(3-15)两端供电网络中,各线路中流过的功率可以看作是两个功率分量的叠加。
其一为两端电压相等时的环式网络的近似功率;另一为循环功率(注意循环功率的方向与dU 的取向有关)。
两端供电网络的近似功率分布:c a S Z Z Z Z S Z Z S S ~~~~3*2*1**33*32*2++++⎪⎭⎫ ⎝⎛+= ………………(3-16)c b S Z Z Z Z Z S Z S S ~~~~3*2*1**21*3*12-++⎪⎭⎫⎝⎛++= ………………(3-17) 223~~~S S S a -= ………………(3-18)由此可见,区域性开式网络与区域性闭式网络在计算上的不同点就在于功率分布的计算,后者的功率分布是分两步完成的。
当网络各线段的R/X 值相等时,称之为均一网络。
这类网络在不计功率损耗影响时,自然功率分布的有功分量和无功分量是互不影响的。
这时,他们是按电阻或电抗分布的,即1ni iB i A PR P R =∑∑=1ni iBi A Q R Q R =∑∑=………………(3-19)1ni iA i B PR P R =∑∑=1ni iAi A Q R Q R =∑∑=………………(3-18)将式(3-18)中的电阻换为相应的电抗也是正确的,特别是全网导线截面相同时,功率的自然分布按长度分布,即1niBi i Al l S S=∑∑=1niAi i Bl l S S=∑∑=………………(3-19)应该注意:环流高鼓功率的计算与网络是否均一无关。
可以证明:在闭式电力网络中,欲使有功功率损耗最小,应使功率分布按电阻分布,即:1niBi i A optl R S S=⋅∑∑=1niAi i B optl R S S=⋅∑∑=………………(3-20)由此可见:均一网络功率的自然分布也就是有功损耗最小时的分布。
因此,在进行网络规划设计时,应使网络接近均一。
对于非均一网络,要达此目的,必须采用一定的措施。
6、地方电力网络的计算电压为35kV 及以下的网络称为地方电力网。
这种电力网由于其自身的特点(电压较,线路较短,传输功率相对较小,等等),在计算时可大大简化。
一般可作如下简化:a 、 可不计线路电容的影响,线路的等值电路仅为一个串联阻抗;b 、 计算功率分布和电压分布时,可不计功率损耗的影响,并用网络额定电压;c 、 计算电压分布时,可不计电压降落横分量(这对110kV 网络同样适用),这时,电压降落纵分量近似等于电压损耗,即∑∑==+≈+≈∆nj j j j j j j nj j jjX I R I X Q RP 11j N)sin cos (3)(V 1V ϕϕ式中 j j Q P ----通过线段j 负荷功率的有功分量(real power component)和无功分量(reactive power component );--j j X R 线段j 的电阻和电抗--j j I ϕcos 流过线段j 的负荷电流及功率因数(power factor) --N V 网络额定电压(rated voltage) n --计算网络的线段数d 、 有的线段具有较均匀分布的负荷,计算时可用一个集中负荷来代替,其大小等于均匀分布负荷的总和,其位置居均匀分布线段的中点,如图所示。
bc p P •=(a)(b)图 3-6 具有均匀分布负荷的地方电力网(a )原网络 (b )等值网络7、电力网络的简化实际的电力网络是一个较复杂的网络。
一般在计算之前,须简化网络的等值电路,即使在利用计算机进行计算时,也须如此。
例如,将变电所和发电厂用运算负荷和运算功率代替,将若干电源支路合并为一个等值电源支路,移置中间复负荷,网络结构的等值变换(如星形←→三角形网络的等值变换),网络分块,等等。
任何简化的计算都有两个过程,其一是简化,其二是还原。
所有上述简化的方法皆可以从参考书[1]、[2]、[3]、[4]中找到,这里不再重复。
掌握网络简化的技巧对于网络特性的计算和分析是十分有益的。
三、例题分析例3-1: 电力网络如图所示。
已知末端负荷MVA j S 25.1115~+=,末端电压36 kV ,计算电网首端功率和电压。
20MVA 110/38.5 kVLGJ —120 80 km解: (1)选取 110kV 作为电压的基本级,计算网络参数,并画出等值电路。
(计算过程略)~~ 电力网络的等值电路~~~~(2)计算潮流分布根据画出的电力网络等值电路可见:已知末端功率MVA j S 25.1115~3+= ,将已知 末端电压36 kV 归算到电压基本级,则有 kV U 85.1025.38110363=⨯= 。
本网为辐射形电网,并且已知末端的功率和电压,求潮流分布,因此采用逐段推算法进行计算。
① 计算变压器阻抗上的功率损耗()()MVA j j jX R U Q P S T T ZT 11.216.05.6393.485.10225.1115~222232323+=+⨯+=++=∆ 则变压器阻抗始端功率MVA j j j S S S ZT 36.1316.1511.216.025.1115~~~33+=+++=∆+='② 计算变压器阻抗上的电压损耗kV U X Q R P U T 67.785.1025.6325.1193.415333=⨯+⨯=+=∆则变压器始端电压 kV U U U T 52.11067.785.10232=+=∆+= ③ 计算变压器导纳上的功率损耗()()MVA j j U jB G S T T YT 6.006.052.110105.4995.4~2622+=⨯⨯+=+=∆-④ 计算线路末端导纳上的功率损耗MVar j j U B j S Y 34.152.110101.12~24222-=⨯⨯-=-=∆-则线路阻抗末端的功率MOAj j j j S S S S Y YT 62.1222.1534.16.006.036.1316.15~~~~232+=-+++=∆+∆+'='⑤ 计算线路阻抗上的功率损耗()()MOA j j jX R U Q P S Z 056.1691.0336.2152.11062.1222.15~222222222+=+⨯+=+'+'=∆⑥ 计算线路阻抗上的电压损耗kV U X Q R P U 74.652.1103362.126.2122.15222=⨯+⨯='+'=∆则线路始端电压 kV U U U 26.11774.652.11021=+=∆+= ⑦ 计算线路始端导纳上的功率损耗MVar j j U B j S Y 51.126.117101.12~24211-=⨯⨯-=-=∆-则线路始端功率MVA j j j j S S S S Y Z 16.1291.1551.1056.1691.062.1222.15~~~~121+=-+++=∆+∆+'=例3-2: 如图10kV 三相配电线路。