非对称加密技术的教学
- 格式:doc
- 大小:31.00 KB
- 文档页数:6



非对称加密技术一、问题的提出非对称加密技术是电子商务安全的基础,是电子商务安全课程的教学重点。
笔者查阅许多电子商务安全教材、网络安全教材,发现这些教材过于注重理论,涉及具体操作较少,内容不够通俗易懂。
笔者认为,学生掌握非对称加密技术,需要学习以下四个方面:图形直观认识、RSA File演示软件直观操作、RSA算法直接计算、PGP的实际应用。
二、非对称加密图形直观认识非对称密码体制也叫公钥加密技术,该技术就是针对私钥密码体制的缺陷提出来的。
在公钥加密系统中,加密和解密会使用两把不同的密钥,加密密钥向公众公开,解密密钥只有解密人自己知道,非法使用者根据公开的加密密钥无法推算出解密密钥,顾其可称为公钥密码体制。
非对称密码体制的加密模型如图所不O 非对称加密的优势:一方面解决了大规模网络应用中密钥的分发和管理问题。
如采用对称加密进行网络通信,N个用户需要使用N/2个密钥,而采用对称加密体制,N个用户只需要N对密钥。
另一方面实现网络中的数字签名。
对称加密技术由于其自身的局限性,无法提供网络中的数字签名。
公钥加密技术由于存在一对公钥和私钥,私钥可以表征惟一性和私有性,而且经私钥加密的数据只能用与之对应的公钥来验证,其他人无法仿冒。
三、RSA File演示软件直观操作利用一款RSA F订e演示软件可向学生直观展示非对称加密解密过程。
其步骤如下:第一,点击图标,生成密钥对,公钥保存为,私钥保存为。
第二,新建文本,输入内容“RSA演示”。
第三,点击加密图标,装载公钥,然后载入明文文件,点击加密文件按钮,生成密文“”。
若将密文扩展名改为TXT,打开将全是乱码。
第四,点击解密图标,装载私钥,然后载入密文文件,点击解密文件按钮,生成明文“”。
第五,对比“”和“”文本内容一致。
通过RSA F订e演示软件操作,学生对密钥对的生成,加密解密操作基本掌握,但对于用公钥加密,用私钥解密这一现象还是不明白,此时还需通过RSA算法来进一步解释。



常⽤加密算法学习总结之⾮对称加密公开密钥密码学(英语:Public-key cryptography)也称⾮对称式密码学(英语:Asymmetric cryptography)是密码学的⼀种演算法。
常⽤的⾮对称加密算法有 RSA DSA ECC 等。
⾮对称加密算法使⽤公钥、私钥来加解密。
公钥与私钥是成对出现的。
多个⽤户(终端等)使⽤的密钥交公钥,只有⼀个⽤户(终端等)使⽤的秘钥叫私钥。
使⽤公钥加密的数据只有对应的私钥可以解密;使⽤私钥加密的数据只有对应的公钥可以解密。
⾮对称加密通信过程下⾯我们来看⼀看使⽤公钥密码的通信流程。
假设Alice要给Bob发送⼀条消息,Alice是发送者,Bob是接收者,⽽这⼀次窃听者Eve依然能够窃所到他们之间的通信内容。
⑴ Alice与bob事先互不认识,也没有可靠安全的沟通渠道,但Alice现在却要透过不安全的互联⽹向bob发送信息。
⑵ Alice撰写好原⽂,原⽂在未加密的状态下称之为明⽂ plainText。
⑶ bob使⽤密码学安全伪随机数⽣成器产⽣⼀对密钥,其中⼀个作为公钥 publicKey,另⼀个作为私钥 privateKey。
⑷ bob可以⽤任何⽅法传送公钥publicKey 给Alice,即使在中间被窃听到也没问题。
⑸ Alice⽤公钥publicKey把明⽂plainText进⾏加密,得到密⽂ cipherText⑹ Alice可以⽤任何⽅法传输密⽂给bob,即使中间被窃听到密⽂也没问题。
⑺ bob收到密⽂,⽤私钥对密⽂进⾏解密,得到明⽂ plainText。
由于其他⼈没有私钥,所以⽆法得知明⽂;如果Alice,在没有得到bob私钥的情况下,她将重新得到原⽂。
Processing math: 100%RSARSA是⼀种⾮对称加密算法,是由罗纳德·李维斯特(Ron Rivest)、阿迪·萨莫尔(Adi Shamir)和伦纳德·阿德曼(Leonard Adleman)在1977年⼀起提出,并以三⼈姓⽒开头字母拼在⼀起组成的。

非对称加密算法流程下载温馨提示:该文档是我店铺精心编制而成,希望大家下载以后,能够帮助大家解决实际的问题。
文档下载后可定制随意修改,请根据实际需要进行相应的调整和使用,谢谢!并且,本店铺为大家提供各种各样类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,如想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by theeditor. I hope that after you download them,they can help yousolve practical problems. The document can be customized andmodified after downloading,please adjust and use it according toactual needs, thank you!In addition, our shop provides you with various types ofpractical materials,such as educational essays, diaryappreciation,sentence excerpts,ancient poems,classic articles,topic composition,work summary,word parsing,copy excerpts,other materials and so on,want to know different data formats andwriting methods,please pay attention!非对称加密算法是一种加密方式,它需要两个密钥,一个是公开密钥,另一个是私有密钥。

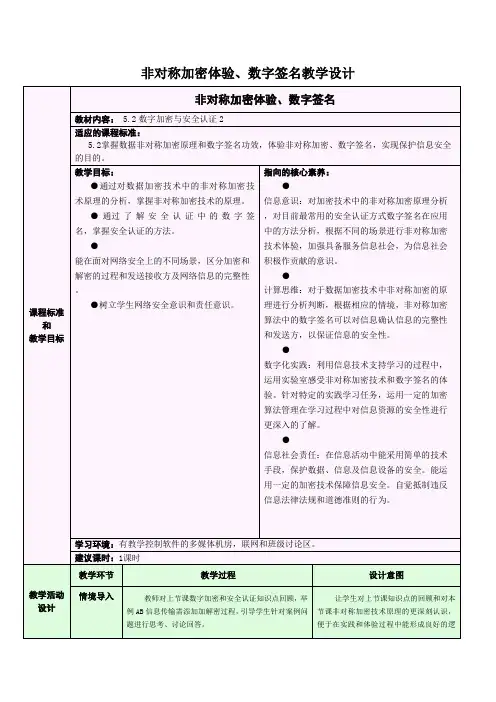

1.1 非对称密钥加密技术1.1.1 实训目的通过使用PGP软件实现数据加密和数字签名,理解非对称密钥加密的原理,学会对文件内容、电子邮件进行加密和数字签名,保障信息安全。
1.1.2 实训任务客户公司的业务大部分都是靠电子邮件与合作伙伴进行交流的,但是发生过这样一起事故,当公司按照一个合作伙伴电子邮件的要求发了一批商品到对方,而对方却说商品型号发错了,经调查,公司确实是按电子邮件的要求发的货,而对方却不承认电子邮件中的商品型号。
现在需要设置一个安全的电子邮件交流手段,不仅能对数据进行加密,还要能够防止数据被篡改,防止发送者抵赖。
1.1.3 背景知识1. 非对称密钥加密加密算法有两大类:对称密钥加密和非对称密钥加密。
在对称密钥加密技术中,加密和解密使用的是同一个密钥,由于难于通过常规的渠道进行安全的密钥传递,例如不能通过电子邮件安全地传递密钥,因此在电子商务等领域对称密钥加密技术受到了很大的限制。
非对称密钥加密也叫公开密钥加密(Public Key Encryption),在加密和解密时使用不同的密钥,加密时使用的密钥和解密时使用的密钥形成一个密钥对,用其中的一个密钥加密的密文只能用另一个密钥解密,而不能由其它密钥(包括加密用的密钥)解密。
通常一个密钥指定为“公钥”,可以对外公布,另一个则指定为“私钥”,只能由密钥持有人保管。
公开密钥加密技术解决了密钥的发布和管理问题,是目前商业加密通信的核心。
使用公开密钥技术,进行数据通信的双方可以安全地确认对方身份和公开密钥,提供通信的可鉴别性。
因此,公开密钥体制的建设是开展电子商务的前提。
非对称密钥加密算法主要有RSA、DSA、DiffieHellman、PKCS、PGP等。
使用非对称密钥加密技术,可以实现下述目的:♦保密性:信息除发送方和接受方外不被其他人窃取;♦完整性:信息在传输过程中不被篡改;♦身份认证:接收方能够通过数字证书来确认发送方的身份;♦不可否认性:发送方对于自己发送的信息不能抵赖。

非对称加密算法流程一、非对称加密算法的基本概念。
1.1 非对称加密算法呢,那可是加密世界里的一个“神器”。
它不像对称加密算法,只用一个密钥。
非对称加密有一对密钥,一个是公钥,一个是私钥。
这就好比是一把锁配了两把不同的钥匙,公钥就像是可以到处给人用的那把,谁都能拿着它来加密信息;而私钥呢,那可是自己藏得严严实实的宝贝,只有用这个私钥才能解开用公钥加密的信息。
1.2 这种算法的出现,真的是给信息安全带来了“翻天覆地”的变化。
以前担心密钥在传输过程中被窃取,现在有了非对称加密,公钥可以公开传播,安全性大大提高了。
二、非对称加密算法的加密流程。
2.1 发送方要获取接收方的公钥。
这就像是要给朋友寄一个超级机密的包裹,得先知道朋友给的那个专门用来寄包裹(加密)的地址(公钥)。
这个公钥的获取途径有很多,可以从专门的密钥服务器上获取,也可以直接由接收方发送过来。
2.2 然后呢,发送方就用这个公钥对要发送的信息进行加密。
这一步就像是把机密包裹按照那个特殊地址(公钥)的要求进行包装,包装好之后,这个信息就变成了一堆看不懂的乱码。
在这个过程中,即使有坏人在中间拦截了这个加密后的信息,他没有私钥,那也是干瞪眼,就像“热锅上的蚂蚁——团团转”,根本不知道这堆乱码到底是什么内容。
2.3 加密后的信息就可以在网络上传输了,这个时候,就像这个包裹在快递的路上,不用担心被偷看,因为除了接收方的私钥,谁也解不开。
三、非对称加密算法的解密流程。
3.1 接收方收到加密后的信息后,就轮到私钥出场了。
接收方用自己藏得好好的私钥来对信息进行解密。
这就像是用只有自己有的特殊钥匙打开那个包裹,只有这把钥匙才能让包裹恢复成原来的样子。
3.2 整个过程中,非对称加密算法就像是一个忠诚的卫士,守护着信息的安全。
它的这种独特的加密解密方式,让信息在网络这个复杂的环境里能够安全地传递。
就好比在一个鱼龙混杂的江湖里,有了非对称加密算法这个“武林高手”的保护,信息就能够安然无恙地到达目的地。
数据加密中非对称加密算法的使用方法数据安全在当今信息时代显得尤为重要。
为了保护数据的隐私和完整性,加密技术起到了至关重要的作用。
非对称加密算法作为一种常用的加密技术,广泛应用于数据传输和存储中。
本文将介绍非对称加密算法的使用方法,以帮助读者更好地了解和应用此项技术。
非对称加密算法,也被称为公钥加密算法,与对称加密算法不同,它使用一对密钥:公钥和私钥。
公钥用于加密信息,任何人都可以获得和使用公钥,而私钥则用于解密信息,只有私钥的拥有者可以使用。
非对称加密算法能够有效解决密钥交换和密钥管理的问题,增强数据的安全性。
首先,了解非对称加密算法的一些常见的应用场景。
非对称加密算法通常用于以下情况:1. 安全数据的传输:在网络通信中,非对称加密算法可以用于加密敏感数据的传输,确保数据在网络中传输的过程中不会被窃取或更改。
2. 数字签名:非对称加密算法能够生成数字签名,用于验证数据的真实性和完整性。
数字签名可以保证数据在传输过程中没有被篡改,并确认发送方的身份。
这在电子商务和电子合同等场景中非常重要。
3. 密钥分发:非对称加密算法可以用于安全地分发对称加密算法的密钥。
在对称加密算法中,双方必须共享相同的密钥,而非对称加密算法可以用于安全地分发和交换对称加密算法的密钥。
接下来,我们将详细介绍非对称加密算法的使用方法。
1. 生成密钥对非对称加密算法使用一对密钥,即公钥和私钥。
首先,我们需要生成一对密钥。
通常情况下,生成密钥对的过程由加密算法库自动完成。
生成密钥对时,我们需要注意以下几点:- 密钥的长度:密钥的长度决定了加密算法的安全性。
一般来说,密钥越长,破解的难度就越大。
常用的非对称加密算法有RSA和ECC,它们的密钥长度一般为1024到4096位。
- 密钥的保管:私钥是非对称加密算法中最重要的部分,一定要妥善保管,确保只有合法的用户能够访问私钥。
2. 加密数据一旦我们生成了密钥对,就可以开始加密数据了。
非对称加密算法使用公钥加密数据,只有拥有相应私钥的用户能够解密数据。
国家高等职业教育网络技术专业教学资源库计算机网络安全技术与实施课程资源子库学习情境2:实训指导2.1-1 利用PGP实施非对称加密实训指导2.1-1一、实训题目:利用利用PGP实施非对称加密。
二、实训目的:1. 掌握利用PGP实施非对称加密的方法;2. 能够对文件在网传传输过程中提供完整性保护;3. 能够合理选用加密算法,区分对称与非对称加密。
三、实训要求:1. 掌握PGP软件的安装与使用方法;2. 学会利用Apocalypso软件进行非对称加密的方法;3. 熟悉建立FTP服务器的方法和过程。
四、实训网络场景或网络拓扑结构:网络拓扑结构图如下:五、实训步骤:1. PGP软件的安装步骤一:解压缩后,双击或运行安装程序后,进入安装界面,显示欢迎信息,选择“NEXT”,然后出现许可协议,这里阅读后选择接受,即“YES”,进入提示安装PGP所需要的系统、以及软件配置情况的界面,建议阅读一下,特别是那条警告信息:“Warning:Export of this software may be restricted by the U.S. Government(此软件的出口受美国政府的限制)。
继续点NEXT按钮,出现创建用户类型的界面,选择“NEXT”。
步骤二:安装程序会提示用户,是否已经有了密钥,如果安装过PGP可能计算机中存在密钥,这就可以再利用了。
如果没有安装过PGP则这里选择如下图所示中的,“No I’m a new user”,然后选择“NEXT”,出现程序的安装目录,建议将PGP安装在安装程序默认的目录,也就是系统盘内,程序很小。
再次点“NEXT”按钮,出现选择PGP组件的窗口,安装程序会检测你系统内所安装的程序,如果存在PGP可以支持的程序,它将自动为你选中该支持组件,如图所示。
PGP可以和Outlook结合完成邮件的加密。
步骤三:安装过程按提示选择“NEXT”,重启系统即可完成安装。
重新启动系统进后,系统会启动PGP许可验证,PGP已经在开始->所有程序->启动,加入了启动项。
非对称密钥中对文件进行加密的方法一、前言非对称密钥加密算法是一种常用的加密方式,它采用了公钥和私钥两个不同的密钥进行加密和解密操作。
其中,公钥可以随意分发给任何人使用,而私钥则必须保持机密性。
在非对称密钥中对文件进行加密,需要先生成一对公私钥,然后使用公钥对文件进行加密,再使用私钥进行解密。
二、生成公私钥1. 选择一个合适的非对称加密算法,如RSA、ECC等。
2. 生成一对公私钥。
这里以RSA算法为例:a. 随机选择两个大质数p和q,并计算它们的积n=p*q。
b. 计算欧拉函数φ(n)=(p-1)*(q-1)。
c. 随机选择一个整数e(1<e<φ(n)),使得e与φ(n)互质。
d. 计算d=d^-1 mod φ(n),其中d满足ed≡1(mod φ(n))。
e. 公钥为{e,n},私钥为{d,n}。
三、文件加密1. 将待加密的文件读入内存中。
2. 将文件内容转换成数字形式。
可以使用哈希函数或编码方式将文件内容转换成一个大整数m。
3. 使用公钥{e,n}对m进行加密,得到密文c=c^e mod n。
4. 将密文c写入文件中保存。
四、文件解密1. 将加密后的文件读入内存中。
2. 将文件内容转换成数字形式,得到密文c。
3. 使用私钥{d,n}对c进行解密,得到明文m=m^d mod n。
4. 将明文m转换成原始文件内容,并保存到文件中。
五、安全性考虑1. 选择合适的非对称加密算法和参数。
一般来说,RSA算法使用2048位或以上长度的密钥比较安全。
2. 保护好私钥。
私钥是解密的关键,必须妥善保管。
可以将私钥保存在加密芯片中或者使用密码保护等方式来增强安全性。
3. 防止中间人攻击。
公钥需要分发给其他人使用,但是公钥可能被篡改或者伪造。
可以使用数字证书等方式来验证公钥的真实性。
六、总结非对称密钥加密算法是一种常用的加密方式,在实际应用中广泛使用。
在对文件进行加解密时,需要先生成一对公私钥,然后使用公钥对文件进行加密,再使用私钥进行解密。
非对称加密算法的实现一、设计内容、算法原理非对称密码系统即公钥密码系统,主流分为基于大整数分解难度,基于离散对数计算难度和椭圆曲线公钥密码三类。
本次实验主要介绍RSA 、ELG 加密。
二、RSA1).RSA 公钥密码算法原理和过程:Alice 要求Bob 将信息m 用RSA 方法加密传送回来,Alice 找到大素数p,q , 令n=pq , 取a >1满足 (,())1a n ϕ=,再找d 使得1(mod ())da n ϕ≡,然后Alice 将n 、a 作为加密密钥(公钥)发送给Bob, 这里p,q ,d ,()n ϕ都是私钥,要求保密,用作解密。
Bob 将原文m <<n 加密得到密文(mod )a A E m n ≡,并将密文E A 传送给 Alice 。
Alice 收到后,计算 ()1()()(mod )d d a d ad n k A A A D E E m m m m n ϕ+≡≡≡≡≡得到原文m 。
这里大素数要求足够大,通常要求是大于100位的十进制数。
有资料表明,几十位的素数构造的RSA 公钥密码系统是不安全的。
因为位数较多,加密效率就不够高,因此,通常用来加密对称密码的密钥,例如,加密序列密码的密钥。
Maple 简介:Maple 是一个具有强大符号运算能力、图形处理能力的交互式计算机代数系统,它可以进行各种科学计算和数学推理,它的高精度数值计算能力对于处理大数的计算和素性判定有其独特的功能。
它适合于所有需要科学计算的人.。
RSA 算法可以实现数字签名。
B 向A 进行签名,则1、B 不能否认进行了签名2、A 不能篡改B 的签名设A (如网站)的公钥为A E ,私钥为A D B(签名者)的公钥为 B E ,私钥为B D ,B 的原文m , B 用B D 作用m , 得到B D (m ),再用A 提供的A E 作用,得到 (())A B E D m C =,B 将C 和B E 发给A, A 收到后,先用A D 作用于C 再用B E 作用 (())(((()))B A B A A B E D C E D E D mm ==。
对称加密和非对称加密的流程对称加密和非对称加密是现代密码学中两种常见的加密算法。
它们在保护数据的安全性方面发挥着重要的作用。
本文将分别介绍对称加密和非对称加密的流程以及它们的特点和应用。
一、对称加密的流程对称加密是一种使用相同密钥进行加密和解密的加密算法。
其流程如下:1. 密钥生成:加密方生成一个密钥,该密钥将用于加密和解密数据。
2. 明文加密:加密方使用密钥将明文进行加密。
加密过程中,明文会被分割成固定大小的数据块,并对每个数据块进行加密。
3. 密文传输:加密后的密文通过网络或其他传输方式发送给解密方。
4. 密文解密:解密方使用相同的密钥对接收到的密文进行解密。
解密过程与加密过程相反,将密文转换为明文。
对称加密的特点是加密和解密的速度快,适用于大规模数据的加密。
然而,对称加密的安全性依赖于密钥的安全性,因此在密钥的传输和管理上需要特别注意。
对称加密算法有很多种,常见的有DES、AES等。
它们的安全性和加密效率各有差异,可以根据实际需求选择合适的算法。
二、非对称加密的流程非对称加密是一种使用公钥和私钥进行加密和解密的加密算法。
其流程如下:1. 密钥生成:解密方生成一对密钥,包括公钥和私钥。
公钥用于加密数据,私钥用于解密数据。
2. 公钥传输:解密方将公钥传输给加密方。
在传输过程中,公钥不需要保密,可以通过网络等方式进行传输。
3. 明文加密:加密方使用接收到的公钥对明文进行加密。
加密过程与对称加密不同,非对称加密一次只能加密一个数据块。
4. 密文传输:加密后的密文通过网络或其他传输方式发送给解密方。
5. 密文解密:解密方使用自己的私钥对接收到的密文进行解密。
解密过程与加密过程相反,将密文转换为明文。
非对称加密的特点是密钥的生成和传输相对较为安全,可以解决对称加密中密钥安全性的问题。
然而,非对称加密的速度较慢,不适合加密大规模数据。
因此,通常会结合对称加密和非对称加密的方式,使用非对称加密来传输对称加密的密钥,从而兼顾了安全性和效率。
非对称加密技术的教学探讨
一、问题的提出
非对称加密技术是电子商务安全的基础,是电子商务安全课程的教学重点。
笔者查阅许多电子商务安全教材、网络安全教材,发现这些教材过于注重理论,涉及具体操作较少,内容不够通俗易懂。
笔者认为,学生掌握非对称加密技术,需要学习以下四个方面:图形直观认识、
rsa file演示软件直观操作、rsa算法直接计算、pgp的实际应用。
二、非对称加密图形直观认识
非对称密码体制也叫公钥加密技术,该技术就是针对私钥密码体制的缺陷提出来的。
在公钥加密系统中,加密和解密会使用两把不同的密钥,加密密钥(公开密钥)向公众公开,解密密钥(秘密密钥)只有解密人自己知道,非法使用者根据公开的加密密钥无法推算出解密密钥,顾其可称为公钥密码体制。
非对称密码体制的加密模型如图所示。
非对称加密的优势:一方面解决了大规模网络应用中密钥的分发和管理问题。
如采用对称加密进行网络通信,n个用户需要使用n (n-1)/2个密钥,而采用对称加密体制,n个用户只需要n对密钥。
另一方面实现网络中的数字签名。
对称加密技术由于其自身的局限性,无法提供网络中的数字签名。
公钥加密技术由于存在一对
公钥和私钥,私钥可以表征惟一性和私有性,而且经私钥加密的数据只能用与之对应的公钥来验证,其他人无法仿冒。
三、rsa file演示软件直观操作
利用一款rsa file演示软件可向学生直观展示非对称加密解密过程。
其步骤如下:
第一,点击图标,生成密钥对,公钥保存为1.puk,私钥保存为2.prk。
第二,新建rsa.txt文本,输入内容“rsa演示”。
第三,点击加密图标,装载公钥1.puk,然后载入明文文件rsa.txt,点击加密文件按钮,生成密文“rsa.txt.enc”。
若将密文扩展名改为txt,打开将全是乱码。
第四,点击解密图标,装载私钥2.prk,然后载入密文文件rsa.txt.enc,点击解密文件按钮,生成明文“rsa.dec.txt”。
第五,对比“rsa.txt”和“rsa.dec.txt”文本内容一致。
通过rsa file演示软件操作,学生对密钥对的生成,加密解密操作基本掌握,但对于用公钥加密,用私钥解密这一现象还是不明白,此时还需通过rsa算法来进一步解释。
四、rsa算法直接计算
rsa算法基于一个十分简单的数论事实:将两个大素数相乘十分容易,但想要对其乘积进行因式分解却极其困难,因此可以将乘积公开作为加密密钥。
1.rsa加密算法
(1)选取两个大素数p和q,并计算乘积n(n=pq)。
(2)任意选取一个大整数e,e与ф(n)=(p-1)*(q-1)互质,整数e用作加密密钥。
(3)确定解密密钥d,由d*e=1 mod((p-1)*(q-1)),根据e,p 和q可以容易地计算出d;
(4)若用整数x表示明文,整数y表示密文(x,y均小于n),则加解密运算为:
加密:y = xe mod n
解密:x = yd mod n
注意,其中d和n也互素。
e和n是公开密钥,d是秘密密钥。
两个素数p和q保密。
2.相关数学背景知识
(1)素数:素数是一大于1,且只能被1和这个数本身整除的整数。
素数是无限的。
例如,2,3,5,7……等。
(2)两个数互为素数:指的是它们除了1之外没有共同的因子。
也可以说这两个数的最大公因子是1。
例如:4和9、13和27等。
(3)模变换:两个数相模,如a模n运算,它给出了a的余数,余数是从0到n-1的某个整数,这种运算称为模运算。
3.算法的具体实现
(1)为了方便计算,我们选取素数p=3和q=11,则n=pq =3*11=33。
(2)ф(n)=(p-1)(q-1)=2*10=20。
(3)从[0,ф(n)-1]中,即[0,19]之间任意选取加密密钥e = 3,且e和ф(n)互素。
(4)求解密密钥d。
将公式ed=1modф(n)转换成形式ed=k*ф(n)+1,即3d=k*20+1,将0,1,2,3…依次代入k,求出d。
取k=0,得d=1/3;不满足d为整数;
取k=1,得d=7;满足d为整数条件;
取k=2时,得d=41/3,不满足d为整数;
取k=3时,得d=61/3,不满足d为整数条件;
取k=4时,得d=81/3=27,满足d为整数条件;
……
若明文x=15,n=33,e=3,d=7,
加密:y=xe mod n= 153 mod 33=9
解密:x=yd mod n = 97 mod 33= 15
也可取d=27,通过电脑附件中的计算器计算如下:
解密:x=yd mod n=927 mod 33= 58149737003040059690390169 mod 33=15
通过手工计算rsa加密算法,让学生更直观更深层理解非对称加密原理。
rsa的安全来源于n足够大,我们测试中使用的n是非常小的,根本不能保障安全性,当前小于1024位的n已经被证明是不安全
的,最好使用2048位的。
通过一款“攻击rsa算法-分解n-求素数因子”软件可以快速实现因式分解,为获得足够大的n及d 、e,我们可以通过rsakit、rsatool之类的工具测试。
rsa简捷,但计算速度比较慢,通常加密中并不是直接使用rsa 来对所有的信息进行加密,最常见的情况是随机产生一个对称加密的密钥,然后使用对称加密算法对信息加密,之后用rsa对刚才的加密密钥进行加密。
五、pgp的实际应用
pgp是美国pgp公司开发的基于rsa公开密钥体制的邮件加密软件,在电子商务事务中得到广泛的应用。
付费的pgp个人版软件可实现邮件加密解密,这里采用免费的pgp8.1汉化版实现对文件的加密解密、签名及验证签名。
具体操作如下:
第一,启动pgp key,创建学生密钥对xues@,并导出公钥。
第二,导入老师的公钥“laoshi公钥.asc”。
第三,新建word文档,录入文本“我是××号学生,完成pgp
作业”→复制文本→打开pgpmail中的“加签并签名”图标→选择剪贴板→选择接收人laoshi@→输入自己的密码→确定。
第四,将结果粘贴到文本中提交上来、同时还要提交学生的公钥。
老师导入自己的私钥,选择pgpmail中的“解密/效验”图标,输入自己的密码解密文本,实现对接收者身份的验证;若导入学生
的公钥,则显示签名者的信息,实现对发送者身份的验证。
通过pgp的实际应用,利用两个密钥实现对发送方和接收方身份的认证问题,让学生掌握非对称加密技术。
通过图形、实操、算法分析、实际应用由浅入深,由理论到实践不断深化学习非对称加密技术。