下载文档原格式
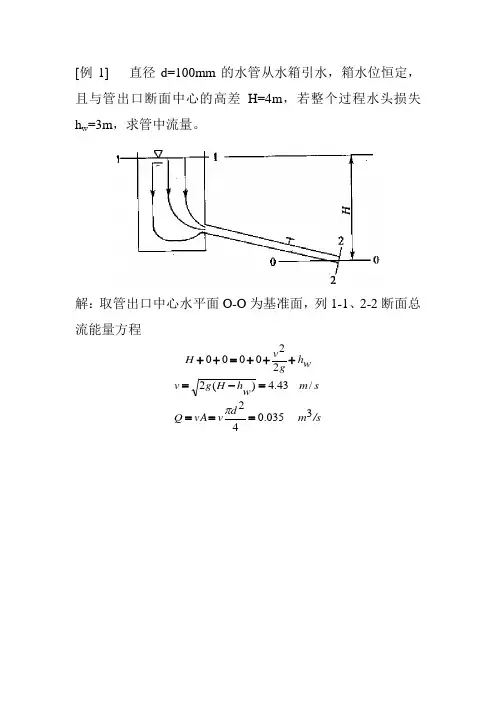
第三章 流体运动学本章在连续介质假设下，讨论描述流体运动的方法，根据运动要素的特性对流动进行分类。
本章的讨论是纯运动学意义上的，不涉及流动的动力学因素。
连续方程是质量守恒定律对流体运动的一个具体约束，也在本章的讨论范围之中。
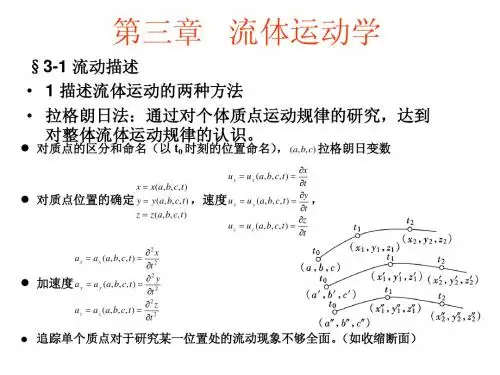
§3—1 描述流动的方法一. 拉格朗日法和欧拉法● 拉格朗日法是质点系法，它定义流体质点的位移矢量为：r r a b c t =(,,,)，其中(,,)(,,,)a b c r a b c t =0是拉格朗日变数，即t 0时刻质点的空间位置，用来对连续介质中无穷多个质点进行编号，作为质点标签。
● 欧拉法是流场法，它定义流体质点的速度矢量场为：u u x y z t =(,,,)，其中(,,)x y z 是空间点（场点）。
流体的其它物理特性和运动要素也都用对应于时间与空间域的场的形式描述。
二. 流体质点的加速度、质点导数● 在拉格朗日观点下，流体质点加速度的求法是比较简单的。
求速度和加速度只须将位移矢量直接对时间求一、二阶导数即可，求导时a,b,c 作为参数不变，意即跟定流体质点。
u r t rt a u t u t r t =====d d ,d d ∂∂∂∂∂∂22.● 欧拉法中流体质点加速度的表达必须特别注意，求加速度需要跟定流体质点，于是 x,y,z均随 t 变，而且),,(d ),,d(z y x u u u tz y x =，所以加速度 u u tz u u y u u x u u t u t z z u t y y u t x x u t u t u a z y x)(d d d d d d d d ∇⋅+=+++=+++==∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂. ● 建立 t 时刻和 t+dt 时刻的流场图，假设一流体质点在 t 时刻位于场点 M ，t + dt 时刻它到达场点M ’，在 t+dt 时刻的流场图上再标上与点M 处于同一位置的场点M 1，此时有另一个流体质点占据该场点。
