离散数学第七章第五节详解
- 格式:ppt
- 大小:265.50 KB
- 文档页数:13

离散数学第七章计数离散数学7.1基本计数原理1.加法原理2.乘法原理离散数学加法原理加法原理又称为和计数原理,也称和规则,存在三种表述形式,其本质是说,整体等于其部分之和。
①若集合某是不相交非空子集S1,S2,…,Sm的并,则|某|=m|Si1i|②若E1,E2,…,Em是彼此互斥事件,并且E1发生有e1种方式,E2发生有e2种方式,…,Em发生有em种方式,则E1或E2或…或Em发生有e1+e2+…+em种方式。
应该指出的是,事件E1和E2互斥是说,E1和E2发生但两者不能同时发生。
离散数学③如果选择事物O1有n1种方法,选择事物O2有n2种方法,…,选择事物Om有nm种方法,并且选择诸事物方法不重叠,则选取O1或O2或…或Om有n1+n2+…+nm种方法。
离散数学加法原理例7.1.1一个学生想选修一门数学课或一门生物学课,但不能同时选修两门课。
如果该生对5门数学课和3门生物学课具有选课条件,试问该生有多少方式来选修课程?离散数学乘法原理乘法原理又称有序计数原理,也称积规则,类似加法原理,也有三种表述形式。
①若S1,S2,…,Sm是非空集合,则笛卡尔m积S1S2…Sm的元素个数是|Si|i1②若事件E1,E2,…,Em发生分别有e1,e2,…,em种方式,并且诸事件是独立的,则事件E1或E2或··m依次发生有e1e2…em·或E种方式。
离散数学乘法原理③如果选取事物O1,O2,…,Om分别有n1,n2,…,nm种方法,并且选取诸事物方法不重叠,则事物O1与O2与…与Om依次选取有n1n2…nm种方法。
离散数学乘法原理例7.1.2一个学生要选修两门课,第一门课在上午4小时内任选1小时,第二门课在下午3小时内也可任选1小时,试问该生有多少种可能的时间安排?离散数学乘法原理例7.1.3计数因特网地址。
在由计算机的物理网络互连而构成的因特网中,每台计算机的网络连接被分配一个因特网地址。

离散数学左孝凌第七章答案【篇一:离散数学(左孝凌)课后习题解答(详细)】1.下列句子中,哪些是命题?哪些不是命题?如果是命题,指出它的真值。
⑴中国有四大发明。
⑵计算机有空吗⑶不存在最大素数。
⑷ 21+3 V5。
(5)老王是山东人或河北人。
⑹2与3都是偶数。
⑺小李在宿舍里。
⑻这朵玫瑰花多美丽呀!⑼请勿随地吐痰!⑽圆的面积等于半径的平方乘以。
何只有6是偶数,3才能是2的倍数。
⑫雪是黑色的当且仅当太阳从东方升起。
㈣如果天下大雨,他就乘班车上班。
解:⑴⑶⑷⑸⑹⑺⑽⑪㈣㈣是命题,其中(1)(3)⑽㈣是真命题,⑷⑹⑫是假命题,⑸⑺㈣的真值目前无法确定;⑵⑻⑼不是命题。
2.将下列复合命题分成若干原子命题。
⑴李辛与李末是兄弟。
⑵因为天气冷,所以我穿了羽绒服。
⑶天正在下雨或湿度很高。
⑷刘英与李进上山。
⑸王强与刘威都学过法语。
⑹如果你不看电影,那么我也不看电影。
⑺我既不看电视也不外出,我在睡觉。
⑻除非天下大雨,否则他不乘班车上班。
解:⑴本命题为原子命题;⑵p:天气冷;q:我穿羽绒服;⑶p:天在下雨;q:湿度很高;⑷p:刘英上山;q:李进上山;⑸p:王强学过法语;q:刘威学过法语;⑹p:你看电影;q:我看电影;⑺p:我看电视;q:我外出;r:我睡觉;⑻p:天下大雨;q:他乘班车上班。
3.将下列命题符号化。
⑴他一面吃饭,一面听音乐。
⑵3是素数或2是素数。
⑶若地球上没有树木,则人类不能生存。
⑷8是偶数的充分必要条件是8能被3整除。
⑸停机的原因在于语法错误或程序错误。
⑹四边形abcd是平行四边形当且仅当它的对边平行。
⑺如果a和b是偶数,则a+b是偶数。
解:⑴p:他吃饭;q:他听音乐;原命题符号化为:p人q⑵p:3是素数;q:2是素数;原命题符号化为:pv q⑶p:地球上有树木;q:人类能生存;原命题符号化为:?p-?q⑷p:8是偶数;q:8能被3整除;原命题符号化为:p?q⑸p:停机;q:语法错误;r:程序错误;原命题符号化为:qv r—p⑹p:四边形abcd是平行四边形;q:四边形abcd的对边平行;原命题符号化为:p?q。


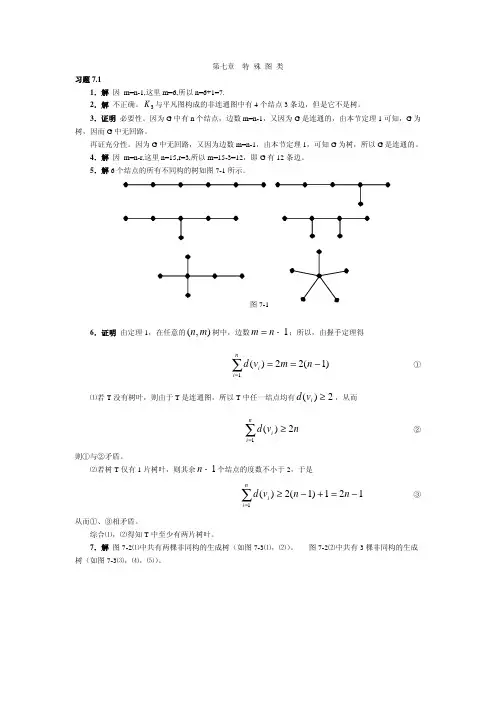
第七章 特 殊 图 类习题7.11.解 因 m=n-1,这里m=6,所以n=6+1=7.2.解 不正确。
与平凡图构成的非连通图中有4个结点3条边,但是它不是树。
3K 3.证明 必要性。
因为G 中有n 个结点,边数m=n-1,又因为G 是连通的,由本节定理1可知,G 为树,因而G 中无回路。
再证充分性。
因为G 中无回路,又因为边数m=n-1,由本节定理1,可知G 为树,所以G 是连通的。
4.解 因 m=n-r,这里n=15,r=3,所以m=15-3=12,即G 有12条边。
5.解6个结点的所有不同构的树如图7-1所示。
图7-16.证明 由定理1,在任意的树中,边数),(m n 1−=n m;所以,由握手定理得)1(22)(1−==∑=n m v d ni i①⑴若T 没有树叶,则由于T 是连通图,所以T 中任一结点均有,从而2)(≥i v d n v d ni i2)(1≥∑= ②则①与②矛盾。
⑵若树T 仅有1片树叶,则其余1−n个结点的度数不小于2,于是121)1(2)(1−=+−≥∑=n n v d ni i③从而①、③相矛盾。
综合⑴,⑵得知T 中至少有两片树叶。
7.解 图7-2⑴中共有两棵非同构的生成树(如图7-3⑴,⑵)。
图7-2⑵中共有3棵非同构的生成树(如图7-3⑶,⑷,⑸)。
⑵⑴⑶⑷ ⑸图7-38.解 在图7-4中共有8棵生成树,如图7-5⑴~⑻所示,第i 生成树用表示。
,,,)8,,2,1( =iT i 7)(8=T W 8)()(61==T W T W 6)()(52==T W T W )()(73==T W T W 9)(4=T W 。
其中T 2,T 5是图中的最小生成树。
9.解 最小生成树T 如图7-7所示,W (T )=18。
a bc da b cda ba bcdabc d⑴⑵⑶⑷⑸⑹⑺ ⑻图7-5图7-4图7-6图7-7习题7.21.解 不一定是。
如图7-8就不是根树.2.解 五个结点可形成3棵非同构的无向树,如图7-9⑴,⑵,⑶所示。
![第7章 图论 [离散数学离散数学(第四版)清华出版社]](https://uimg.taocdn.com/58b7923143323968011c9244.webp)


离散数学习题答案习题二及答案:(P38)5、求下列公式的主析取范式,并求成真赋值: (2)()()p q q r ⌝→∧∧解:原式()p q q r ⇔∨∧∧q r ⇔∧()p p q r ⇔⌝∨∧∧()()p q r p q r ⇔⌝∧∧∨∧∧37m m ⇔∨,此即公式的主析取范式, 所以成真赋值为011,111。
6、求下列公式的主合取范式,并求成假赋值: (2)()()p q p r ∧∨⌝∨解:原式()()p p r p q r ⇔∨⌝∨∧⌝∨∨()p q r ⇔⌝∨∨4M ⇔,此即公式的主合取范式, 所以成假赋值为100。
7、求下列公式的主析取范式,再用主析取范式求主合取范式: (1)()p q r ∧∨解:原式()(()())p q r r p p q q r ⇔∧∧⌝∨∨⌝∨∧⌝∨∧()()()()()()p q r p q r p q r p q r p q r p q r ⇔∧∧⌝∨∧∧∨⌝∧⌝∧∨⌝∧∧∨∧⌝∧∨∧∧ ()()()()()p q r p q r p q r p q r p q r ⇔⌝∧⌝∧∨⌝∧∧∨∧⌝∧∨∧∧⌝∨∧∧ 13567m m m m m ⇔∨∨∨∨,此即主析取范式。
主析取范式中没出现的极小项为0m ,2m ,4m ,所以主合取范式中含有三个极大项0M ,2M ,4M ,故原式的主合取范式024M M M ⇔∧∧。
9、用真值表法求下面公式的主析取范式: (1)()()p q p r ∨∨⌝∧ 解:公式的真值表如下:由真值表可以看出成真赋值的情况有7种,此7种成真赋值所对应的极小项的析取即为主析取范式,故主析取范式1234567m m m m m m m ⇔∨∨∨∨∨∨习题三及答案:(P52-54)11、填充下面推理证明中没有写出的推理规则。
前提:,,,p q q r r s p ⌝∨⌝∨→结论:s证明:① p 前提引入②p q⌝∨前提引入③ q ①②析取三段论④q r⌝∨前提引入⑤ r ③④析取三段论⑥r s→前提引入⑦ s ⑤⑥假言推理15、在自然推理系统P中用附加前提法证明下面推理:(2)前提:()(),()∨→∧∨→p q r s s t u结论:p u→证明:用附加前提证明法。



图论部分第七章、图的基本概念7. 1无向图及有向图无向图与有向图多重集合:元素可以重复出现的集合无序积:{(x, y) |定义无向图Q<K£>,其中(1) 顶点集$0,元素称为顶点(2) 边集F为k&f的多重子集,其元素称为无向边,简称边.例如,如图所示,其中心⑷,…,心,&{(旳,匕),(匕,匕),(迫,方),(乃,方),(迫,%), (s, %),(必,%)} 定艾有向图E>,其中(1) $同无向图的顶点集,元素也称为顶点(2) 边集F为的多重子集,其元素称为有向边,简称边.用无向边代替0的所有有向边所得到的无向图称作Q的基图,右图是有向图, 试写出它的!/和F注意:图的数学定艾与图形表示,在同构(待叙)的意狡下是一一对应的通常用G表示无向图,0表示有向图,也常用G泛指无向图和有向图,用6表示无向边或有向边.K6), E(G, Eg G和D的顶点、集,边集.77阶图:”个顶点的图有限图:K F都是有穷集合的图零图:吕0平凡图:1阶零图空图:^=0顶点和边的关联与相邻:定狡设e*,v)是无向图G^<V f E>的一条边,称v…匕为e*的端点,©与v, ( 16)关联.若Vi H V”则称故与Vi ( v)的关联次数为1;若匕=匕,则称6为环,此时称◎与匕的关联次数为2;若匕不是鸟端点, 则称鼓与匕的关联次数为0.无边关联的顶点称作孤立点.定义设无向图=<V, E>, v if K e“e《E,若©,匕)e£;则称乙匕相邻;若% &至少有一个公共端点,则称6, 8/相邻.对有向图有类似定义.设6二〈乙匕〉是有向图的一条边,又称匕是牧的始点,V」是6的终点,K邻接到Vj.匕邻接于Vi.邻域和关联集邻域和关联集设无向图^veV(G)”的邻域谑克匕(6A3"(G)A亦}1 的闪邻域2V(V)=M V)U{V)丫的关联集7(v)=fej族要(G>e与咲联}设有向图空厲蚀)1的后绅元集石(护{边煖玖刀人今炉訪⑹付妙、的先驱元集纭(忙甸頰匕(D)人Y细>“(C)人T1的邻域E(v)=“e)u巧(巧'的丙邻域jv D(v) = 1V23(v)U{v}顶点的度数设G=<V,E>为无向图,keKy的度数(度)〃3): #作为边的端点次数之和悬挂顶点:度数为1的顶点悬挂边:与悬挂顶点关联的边G 的最大度zl(Q 二max {〃(“)| i/e HG的最小度&Q=min{d(访| keH例如〃(%)二3, 〃(乃)二4, 6/(I/.) =4,zl(6)=4, J(6)=1, r4是悬挂顶点,g是悬挂边,设^=<K £>为有向图,reKi/的出度dW: y作为边的始点次数之和1/的入度力3) :#作为边的终点次数之和1/的度数(度)〃3):#作为边的端点次数之和d(v)~ / (#) + d(v)。