《算法设计与分析》(全)

《算法设计与分析》实验指导书本书是为配合《算法分析与设计实验教学大纲》而编写的上机指导，其目的是使学生消化理论知识，加深对讲授内容的理解，尤其是一些算法的实现及其应用，培养学生独立编程和调试程序的能力，使学生对算法的分析与设计有更深刻的认识。

上机实验一般应包括以下几个步骤：（1）、准备好上机所需的程序。

手编程序应书写整齐，并经人工检查无误后才能上机。

（2）、上机输入和调试自己所编的程序。

一人一组，独立上机调试，上机时出现的问题，最好独立解决。

（3）、上机结束后，整理出实验报告。

实验报告应包括：题目、程序清单、运行结果、对运行情况所作的分析。

本书共分阶段4个实验，每个实验有基本题和提高题。

基本题必须完成，提高题根据自己实际情况进行取舍。

题目不限定如下题目，可根据自己兴趣爱好做一些与实验内容相关的其他题目，如动态规划法中的图象压缩，回溯法中的人机对弈等。

其具体要求和步骤如下：实验一分治与递归（4学时）一、实验目的与要求1、熟悉C/C++语言的集成开发环境；2、通过本实验加深对递归过程的理解二、实验内容：掌握递归算法的概念和基本思想，分析并掌握“整数划分”问题的递归算法。

三、实验题任意输入一个整数，输出结果能够用递归方法实现整数的划分。

四、实验步骤1．理解算法思想和问题要求；2．编程实现题目要求；3．上机输入和调试自己所编的程序；4．验证分析实验结果；5．整理出实验报告。

一、实验目的与要求1、掌握棋盘覆盖问题的算法；2、初步掌握分治算法二、实验题：盘覆盖问题：在一个2k×2k个方格组成的棋盘中，恰有一个方格与其它方格不同，称该方格为一特殊方格，且称该棋盘为一特殊棋盘。

在棋盘覆盖问题中，要用图示的4种不同形态的L型骨牌覆盖给定的特殊棋盘上除特殊方格以外的所有方格，且任何2个L型骨牌不得重叠覆盖。

三、实验提示void chessBoard(int tr, int tc, int dr, int dc, int size) {if (size == 1) return;int t = tile++, // L型骨牌号s = size/2; // 分割棋盘// 覆盖左上角子棋盘if (dr < tr + s && dc < tc + s)// 特殊方格在此棋盘中chessBoard(tr, tc, dr, dc, s);else {// 此棋盘中无特殊方格// 用t 号L型骨牌覆盖右下角board[tr + s - 1][tc + s - 1] = t;// 覆盖其余方格chessBoard(tr, tc, tr+s-1, tc+s-1, s);}// 覆盖右上角子棋盘if (dr < tr + s && dc >= tc + s)// 特殊方格在此棋盘中chessBoard(tr, tc+s, dr, dc, s);else {// 此棋盘中无特殊方格// 用t 号L型骨牌覆盖左下角board[tr + s - 1][tc + s] = t;// 覆盖其余方格chessBoard(tr, tc+s, tr+s-1, tc+s, s);}// 覆盖左下角子棋盘if (dr >= tr + s && dc < tc + s)// 特殊方格在此棋盘中chessBoard(tr+s, tc, dr, dc, s);else {// 用t 号L型骨牌覆盖右上角board[tr + s][tc + s - 1] = t;// 覆盖其余方格chessBoard(tr+s, tc, tr+s, tc+s-1, s);}// 覆盖右下角子棋盘if (dr >= tr + s && dc >= tc + s)// 特殊方格在此棋盘中chessBoard(tr+s, tc+s, dr, dc, s);else {// 用t 号L型骨牌覆盖左上角board[tr + s][tc + s] = t;// 覆盖其余方格chessBoard(tr+s, tc+s, tr+s, tc+s, s);}}一、实验目的与要求1、熟悉二分搜索算法；2、初步掌握分治算法；二、实验题1、设a[0:n-1]是一个已排好序的数组。

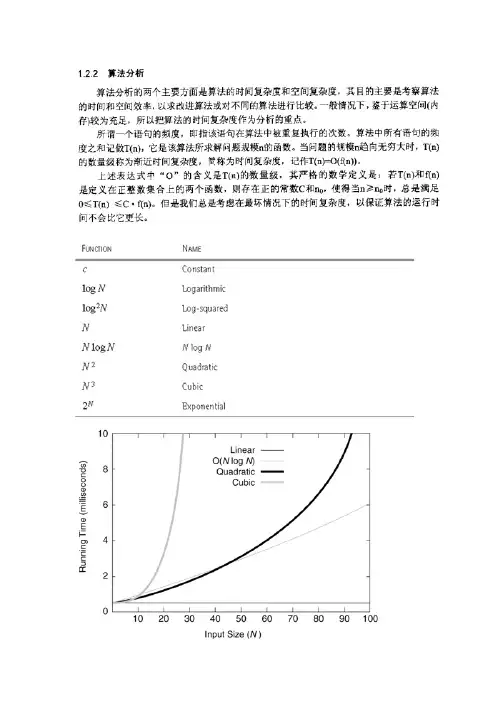
O(1)Temp=i;i=j;j=temp;以上三条单个语句的频度均为1，该程序段的执行时间是一个与问题规模n无关的常数。

算法的时间复杂度为常数阶，记作T(n)=O(1)。

如果算法的执行时间不随着问题规模n的增加而增长，即使算法中有上千条语句，其执行时间也不过是一个较大的常数。

此类算法的时间复杂度是O(1)。

O(n^2)2.1. 交换i和j的内容sum=0；（一次）for(i=1;i<=n;i++) （n次）for(j=1;j<=n;j++) （n^2次）sum++；（n^2次）解：T(n)=2n^2+n+1 =O(n^2)2.2.for (i=1;i<n;i++){y=y+1; ①for (j=0;j<=(2*n);j++)x++; ②}解：语句1的频度是n-1语句2的频度是(n-1)*(2n+1)=2n^2-n-1f(n)=2n^2-n-1+(n-1)=2n^2-2该程序的时间复杂度T(n)=O(n^2). O(n)2.3.a=0;b=1; ①for (i=1;i<=n;i++) ②{s=a+b;③b=a;④a=s;⑤}解：语句1的频度：2,语句2的频度：n,语句3的频度：n-1,语句4的频度：n-1,语句5的频度：n-1,T(n)=2+n+3(n-1)=4n-1=O(n).O(log2n )2.4.i=1; ①while (i<=n)i=i*2; ②解：语句1的频度是1,设语句2的频度是f(n), 则：2^f(n)<=n;f(n)<=log2n取最大值f(n)= log2n,T(n)=O(log2n )O(n^3)2.5.for(i=0;i<n;i++){for(j=0;j<i;j++){for(k=0;k<j;k++)x=x+2;}}解：当i=m, j=k的时候,内层循环的次数为k当i=m时, j 可以取0,1,...,m-1 , 所以这里最内循环共进行了0+1+...+m-1=(m-1)m/2次所以,i从0取到n, 则循环共进行了: 0+(1-1)*1/2+...+(n-1)n/2=n(n+1)(n-1)/6所以时间复杂度为O(n^3).我们还应该区分算法的最坏情况的行为和期望行为。

黄宇《算法设计与分析》课后习题解析（⼆）第2章：从算法的视⾓重新审视数学的概念2.1：(向下取整)题⽬：请计算满⾜下⾯两个条件的实数的区间解析：根据向下取整的含义，令，讨论a的取值范围即可解答：令，则可得：即：故的取值区间为：2.2: (取整函数)题⽬：证明：对于任意整数,（提⽰：将n划分为）。

解析：根据提⽰将n进⾏划分，根据取整函数的定义⽤k表⽰取整函数，即可证明；证明如下：因为对于任意整数,可划分为，则:① ；② ；综上：对于任意整数,, 得证；2.3: (斐波拉契数列)对于斐波拉契数列，请证明：1）题⽬：是偶数当且仅当n能被3整除解析：由斐波拉契数列的递归定义式，容易联想到数学归纳法；证明如下：（采⽤数学归纳法）i)当n = 1,2,3时，依次为1，1，2，符合命题；ii)假设当（k>=1）时命题均成⽴，则：① 当n = 3k+1时，是奇数，成⽴；② 当n = 3k+2时，是奇数，成⽴；③ 当 n = 3(k+1)时，是偶数，成⽴；综上：归纳可得为偶数当且仅当，得证;2）题⽬：x x =1+a (0<a <1)x =1+a (0<a <1)⌊x ⌋=1⇒⌊x ⌋=21⌊x ⌋=2⌊1+a +22a ⌋=1a +22a <1⇒0<a <−21⇒1<a +1<⇒21<x <2x (1，)2n ≥1⌈log (n +1)⌉=⌊logn ⌋+12≤k n ≤2−k +11n ≥12≤k n ≤2−k +11k +1=⌈log (2+k 1)⌉≤⌈log (n +1)⌉≤⌈log (2)⌉=k +1k +1=>⌈log (n +1)⌉=k +1k =⌊log (2)⌋≤k ⌊logn ⌋≤⌊log (2−k +11)⌋=k =>⌊logn ⌋=k n ≥1⌈log (n +1)⌉=k +1=⌊logn ⌋+1F n F n n ≤3k F =n F +n −1F =n −2F +3k F =3k −1>F 3k +1F =n F +3k +1F =3k >F 3k +2F =n F +3k +2F =3k +1>F 3k +3F n 3∣n F −n 2F F =n +1n −1(−1)n +1解析：同1）理，容易联想到数学归纳法证明如下：（采⽤数学归纳法）i)当n = 2时，, 易知成⽴；ii)假设当 n = k 时命题成⽴，① 若k = 2m, 则,当n = k+1 = 2m+1时，要证命题成⽴，即证： => ,代⼊递推式, 得：, 易知是恒等式，故命题成⽴；②当 k=2m+1时，同①理可证命题成⽴；综上：归纳可得，得证；2.4：(完美⼆叉树)给定⼀棵完美⼆叉树，记其节点数为，⾼度为，叶节点数为，内部节点数为1）题⽬：给定上述4个量中的任意⼀个，请推导出其他3个量解析：根据完美⼆叉树的结构特点易得解答：（仅以已知⾼度h推导其他三个量为例，其余同理）已知⾼度为h，可得：节点数：叶节点数：内部节点数：2）题⽬：请计算完美⼆叉树任意⼀层的节点个数：① 如果任意指定深度为的⼀层节点，请计算该层节点个数；② 如果任意指定⾼度为的⼀层节点，请计算该层节点个数；解析：根据完美⼆叉树的结构特点易得（注意节点深度和节点⾼度是互补的，相加为树⾼）解答：① ; ② ;2.5: (⼆叉树的性质)对于⼀棵⾮空的⼆叉树T，记其中叶节点的个数为，有1个⼦节点的节点个数为，有两个⼦节点的节点个数为1）题⽬：如果T是⼀棵2-tree，请证明。

常用算法设计方法要使计算机能完成人们预定的工作，首先必须为如何完成预定的工作设计一个算法，然后再根据算法编写程序。

计算机程序要对问题的每个对象和处理规则给出正确详尽的描述，其中程序的数据结构和变量用来描述问题的对象，程序结构、函数和语句用来描述问题的算法。

算法数据结构是程序的两个重要方面。

算法是问题求解过程的精确描述，一个算法由有限条可完全机械地执行的、有确定结果的指令组成。

指令正确地描述了要完成的任务和它们被执行的顺序。

计算机按算法指令所描述的顺序执行算法的指令能在有限的步骤内终止，或终止于给出问题的解，或终止于指出问题对此输入数据无解。

通常求解一个问题可能会有多种算法可供选择，选择的主要标准是算法的正确性和可靠性，简单性和易理解性。

其次是算法所需要的存储空间少和执行更快等。

算法设计是一件非常困难的工作，经常采用的算法设计技术主要有迭代法、穷举搜索法、递推法、贪婪法、回溯法、分治法、动态规划法等等。

另外，为了更简洁的形式设计和藐视算法，在算法设计时又常常采用递归技术，用递归描述算法。

一、迭代法迭代法是用于求方程或方程组近似根的一种常用的算法设计方法。

设方程为f(x)=0，用某种数学方法导出等价的形式x=g(x)，然后按以下步骤执行：（1）选一个方程的近似根，赋给变量x0；（2）将x0的值保存于变量x1，然后计算g(x1)，并将结果存于变量x0；（3）当x0与x1的差的绝对值还小于指定的精度要求时，重复步骤（2）的计算。

若方程有根，并且用上述方法计算出来的近似根序列收敛，则按上述方法求得的x0就认为是方程的根。

上述算法用C程序的形式表示为：【算法】迭代法求方程的根{ x0=初始近似根；do {x1=x0；x0=g(x1)；/*按特定的方程计算新的近似根*/} while ( fabs(x0-x1)>Epsilon)；printf(“方程的近似根是%f\n”，x0)；}迭代算法也常用于求方程组的根，令X=（x0，x1，…，x n-1）设方程组为：x i=g i(X) (I=0，1，…，n-1)则求方程组根的迭代算法可描述如下：【算法】迭代法求方程组的根{ for (i=0;i<n;i++)x[i]=初始近似根;do {for (i=0;i<n;i++)y[i]=x[i];for (i=0;i<n;i++)x[i]=gi(X);for (delta=0.0,i=0;i<n;i++)if (fabs(y[i]-x[i])>delta) delta=fabs(y[i]-x[i])；} while (delta>Epsilon)；for (i=0;i<n;i++)printf(“变量x[%d]的近似根是%f”，I，x[i])；printf(“\n”)；}具体使用迭代法求根时应注意以下两种可能发生的情况：（1）如果方程无解，算法求出的近似根序列就不会收敛，迭代过程会变成死循环，因此在使用迭代算法前应先考察方程是否有解，并在程序中对迭代的次数给予限制；（2）方程虽然有解，但迭代公式选择不当，或迭代的初始近似根选择不合理，也会导致迭代失败。

5..证明等式gcd(m,n)=gcd(n,m mod n)对每一对正整数m,n都成立.Hint:根据除法的定义不难证明:●如果d整除u和v, 那么d一定能整除u±v;●如果d整除u,那么d也能够整除u的任何整数倍ku.对于任意一对正整数m,n,若d能整除m和n,那么d一定能整除n和r=m mod n=m-qn；显然，若d能整除n和r，也一定能整除m=r+qn和n。

数对(m,n)和(n,r)具有相同的公约数的有限非空集，其中也包括了最大公约数。

故gcd(m,n)=gcd(n,r)6.对于第一个数小于第二个数的一对数字,欧几里得算法将会如何处理?该算法在处理这种输入的过程中,上述情况最多会发生几次?Hint:对于任何形如0<=m<n的一对数字,Euclid算法在第一次叠代时交换m和n, 即gcd(m,n)=gcd(n,m)并且这种交换处理只发生一次.7.a.对于所有1≤m,n≤10的输入, Euclid算法最少要做几次除法?(1次)b. 对于所有1≤m,n≤10的输入, Euclid算法最多要做几次除法?(5次)gcd(5,8)习题1.21.(农夫过河)P—农夫W—狼G—山羊C—白菜2.(过桥问题)1,2,5,10---分别代表4个人, f—手电筒4. 对于任意实系数a,b,c, 某个算法能求方程ax^2+bx+c=0的实根,写出上述算法的伪代码(可以假设sqrt(x)是求平方根的函数)算法Quadratic(a,b,c)//求方程ax^2+bx+c=0的实根的算法//输入:实系数a,b,c//输出:实根或者无解信息D←b*b-4*a*cIf D>0temp←2*ax1←(-b+sqrt(D))/tempx2←(-b-sqrt(D))/tempreturn x1,x2else if D=0 return –b/(2*a)else return “no real roots”else //a=0if b≠0 return –c/belse //a=b=0if c=0 return “no real numbers”else return “no real roots”5.描述将十进制整数表达为二进制整数的标准算法a.用文字描述b.用伪代码描述解答：a.将十进制整数转换为二进制整数的算法输入：一个正整数n输出：正整数n相应的二进制数第一步：用n除以2，余数赋给Ki(i=0,1,2...)，商赋给n第二步：如果n=0，则到第三步，否则重复第一步第三步：将Ki按照i从高到低的顺序输出b.伪代码算法DectoBin(n)//将十进制整数n转换为二进制整数的算法//输入：正整数n//输出：该正整数相应的二进制数，该数存放于数组Bin[1...n]中i=1while n!=0 do {Bin[i]=n%2;n=(int)n/2;i++;}while i!=0 do{print Bin[i];i--;}9.考虑下面这个算法,它求的是数组中大小相差最小的两个元素的差.(算法略) 对这个算法做尽可能多的改进.算法MinDistance(A[0..n-1])//输入:数组A[0..n-1]//输出:the smallest distance d between two of its elements习题1.31.考虑这样一个排序算法,该算法对于待排序的数组中的每一个元素,计算比它小的元素个数,然后利用这个信息,将各个元素放到有序数组的相应位置上去.a.应用该算法对列表‖60,35,81,98,14,47‖排序b.该算法稳定吗?c.该算法在位吗?解:a. 该算法对列表‖60,35,81,98,14,47‖排序的过程如下所示:b.该算法不稳定.比如对列表‖2,2*‖排序c.该算法不在位.额外空间for S and Count[]4.(古老的七桥问题)习题1.41.请分别描述一下应该如何实现下列对数组的操作,使得操作时间不依赖数组的长度. a.删除数组的第i 个元素(1<=i<=n)b.删除有序数组的第i 个元素(依然有序) hints:a. Replace the i th element with the last element and decrease the array size of 1b. Replace the ith element with a special symbol that cannot be a value of the array ’s element(e.g., 0 for an array of positive numbers ) to mark the i th position is empty. (―lazy deletion ‖)第2章 习题2.17.对下列断言进行证明:(如果是错误的,请举例) a. 如果t(n )∈O(g(n),则g(n)∈Ω(t(n)) b.α>0时,Θ(αg(n))= Θ(g(n)) 解:a. 这个断言是正确的。

《算法设计与分析》教案算法设计与分析是计算机科学与技术专业的一门核心课程，旨在培养学生具备算法设计、分析和优化的能力。

本课程通常包括算法基础、算法设计方法、高级数据结构以及算法分析等内容。

本教案主要介绍了《算法设计与分析》课程的教学目标、教学内容、教学方法和评价方法等方面。

一、教学目标本课程的教学目标主要包括以下几个方面：1.掌握算法设计的基本思想和方法。

2.熟悉常见的算法设计模式和技巧。

3.理解高级数据结构的原理和应用。

4.能够进行算法的时间复杂度和空间复杂度分析。

5.能够使用常见的工具和软件进行算法设计和分析。

二、教学内容本课程的主要教学内容包括以下几个方面：1.算法基础：算法的定义、性质和分类，时间复杂度和空间复杂度的概念和分析方法。

2.算法设计方法：贪心算法、分治算法、动态规划算法、回溯算法等算法设计思想和方法。

3.高级数据结构：堆、树、图等高级数据结构的原理、实现和应用。

4.算法分析：渐进分析法、均摊分析法、递归方程求解等算法分析方法。

5. 算法设计与分析工具：常见的算法设计和分析工具，如C++、Java、Python和MATLAB等。

三、教学方法本课程采用多种教学方法结合的方式，包括讲授、实践和讨论等。

1.讲授：通过教师讲解理论知识，引导学生掌握算法的基本思想和方法。

2.实践：通过课堂上的编程实验和课后作业，培养学生动手实践的能力。

3.讨论：通过小组讨论和学生报告，促进学生之间的交流和合作，提高学习效果。

四、评价方法为了全面评价学生的学习情况，本课程采用多种评价方法，包括考试、作业和实验报告等。

1.考试：通过期中考试和期末考试，检验学生对算法设计和分析的理解和掌握程度。

2.作业：通过课后作业，检验学生对算法设计和分析的实践能力。

3.实验报告：通过编程实验和实验报告，检验学生对算法设计和分析工具的应用能力。

五、教学资源为了支持教学工作，我们为学生准备了如下教学资源：1.课件：编写了详细的教学课件，包括理论知识的讲解和案例分析。

《算法设计与分析》试卷1一、多项选择题（每空2分, 共20分）:1.以下关于算法设计问题的叙述中正确的是__________。

A.计算机与数值问题的求解——方程式求根、插值问题、数值积分、函数逼近等有关B.利用计算机无法解决非数值问题C.计算机在解决分类、语言翻译、图形识别、解决高等代数和组合分析等方面的数学问题、定理证明、公式推导乃至日常生活中各种过程的模拟等问题中, 主要进行的是判断、比较, 而不是算术运算D、算法设计与分析主要研究对象是非数值问题, 当然也包含某些数值问题2.算法的特征包括_________。

A.有穷性B、确定性C.输入和输出D.能行性或可行性3、以下描述是有关算法设计的基本步骤:①问题的陈述②算法分析③模型的拟制④算法的实现⑤算法的详细设计⑥文档的编制, 应与其它环节交织在一起其中正确的顺序是__________。

A.①②③④⑤⑥B.①③⑤②④⑥C.②④①③⑤⑥D.⑥①③⑤②④4.以下说法正确的是__________。

A.数学归纳法可以证明算法终止性B.良序原则是证明算法的正确性的有力工具C. x = 小于或等于x的最大整数（x的低限）D. x = 小于或等于x的最大整数（x的高限）5、汉诺塔（Hanoi）问题中令h（n）为从A移动n个金片到C上所用的次数, 则递归方程为__________, 其初始条件为__________, 将n个金片从A柱移到C柱上的移动次数是__________；设菲波那契（Fibonacci）数列中Fn为第n个月时兔子的对数, 则有递归方程为__________, 其中F1=F2=__________。

A.Fn=Fn-1+Fn-2 B、h（n）= 2h（n-1）+1C.1 D、h（1）= 1E、h（n）=2n-1F、06.在一个有向连通图中（如下图所示）, 找出点A到点B的一条最短路为____ ______。

A.最短路: 1→3→5→8→10, 耗费: 20B、最短路：1→4→6→9→10, 耗费：16C.最短路: 1→4→6→9, 耗费: 12D.最短路: 4→6→9→10, 耗费: 13二、填空（每空2分, 共20分）:1.快速排序法的基本思想是重新排列关键字, 把一个文件分成两个文件, 使得第一个文件中所有元素均小于第二个文件中的元素；然后再对两个子文件进行同样的处理。

《算法设计与分析》《算法设计与分析》是计算机科学中探讨算法设计和分析的一门课程。

本书深入浅出地介绍了算法的基本概念、常见的算法设计技巧以及常用的算法分析方法。

书中涵盖了排序算法、图算法、动态规划、贪心算法等多个领域，通过详细且实用的案例，帮助读者深入理解每个算法的原理和应用场景。

第二部分重点介绍了排序算法。

排序是计算机科学中最基本也是最常用的算法之一、本书详细讲解了冒泡排序、选择排序、插入排序、快速排序等各种排序算法的原理和实现方法，并对它们的时间和空间复杂度进行了分析。

通过对比不同排序算法的优缺点，读者将能够选择最适合具体问题的排序算法。

第三部分介绍了图算法。

图是计算机科学中常见的数据结构，广泛应用于网络、社交网络等领域。

本书详细介绍了图的基本概念、表示方法和遍历算法，包括深度优先和广度优先。

同时，还介绍了最短路径算法、最小生成树算法和拓扑排序等图算法的原理和实现方法，为读者提供了解决实际问题的思路和方法。

第四部分介绍了动态规划和贪心算法。

动态规划和贪心算法是算法设计中常用的两种思想。

本书通过实例讲解了动态规划和贪心算法的基本原理和应用场景，详细介绍了背包问题、最长公共子序列、最优二分查找等经典问题的动态规划解法。

同时，还介绍了活动选择问题、马尔可夫决策过程等贪心算法的原理和实现方法，为读者提供了灵活运用动态规划和贪心算法解决实际问题的能力。

总结来说，《算法设计与分析》全面而深入地介绍了算法设计和分析的基本概念、常用技巧和方法。

本书既适合计算机科学专业的学生学习，也适合计算机从业人员进一步提升算法设计能力和解决实际问题的能力。

通过学习本书，读者将能够掌握各种常见算法的设计和分析方法，提高解决实际问题的能力，为进一步学习和研究算法领域奠定坚实基础。

HUNAN CITY UNIVERSITY 算法设计与分析课程设计题目：求最大值与最小值问题专业：学号：姓名：指导教师：成绩：二0年月日一、问题描述输入一列整数，求出该列整数中的最大值与最小值。

二、课程设计目的通过课程设计，提高用计算机解决实际问题的能力，提高独立实践的能力，将课本上的理论知识和实际有机的结合起来，锻炼分析解决实际问题的能力。

提高适应实际，实践编程的能力。

在实际的编程和调试综合试题的基础上，把高级语言程序设计的思想、编程巧和解题思路进行总结与概括，通过比较系统地练习达到真正比较熟练地掌握计算机编程的基本功，为后续的学习打下基础。

了解一般程序设计的基本思路与方法。

三、问题分析看到这个题目我们最容易想到的算法是直接比较算法：将数组的第 1 个元素分别赋给两个临时变量：fmax:=A[1]; fmin:=A[1]; 然后从数组的第 2 个元素 A[2]开始直到第 n个元素逐个与 fmax 和 fmin 比较，在每次比较中，如果A[i] > fmax，则用 A[i]的值替换 fmax 的值；如果 A[i] < fmin，则用 A[i]的值替换 fmin 的值；否则保持 fmax（fmin）的值不变。

这样在程序结束时的fmax、fmin 的值就分别是数组的最大值和最小值。

这个算法在最好、最坏情况下，元素的比较次数都是 2(n-1)，而平均比较次数也为 2(n-1)。

如果将上面的比较过程修改为：从数组的第 2 个元素 A[2]开始直到第 n 个元素，每个 A[i]都是首先与 fmax 比较，如果 A[i]>fmax,则用 A[i]的值替换 fmax 的值；否则才将 A[i]与 fmin 比较，如果 A[i] < fmin，则用 A[i]的值替换 fmin 的值。

这样的算法在最好、最坏情况下使用的比较次数分别是 n-1 和 2(n-1),而平均比较次数是 3(n-1)/2,因为在比较过程中，将有一半的几率出现 A[i]>fmax 情况。