高频电子线路—张肃文(第四版)
- 格式:doc
- 大小:196.50 KB
- 文档页数:23

高频电子线路复习例题一(嘿嘿整理2012年6月)第一章绪论一、填空题1.无线通信系统一般由信号源、__________、__________、___________、输出变换器五部分组成。
2.人耳能听到的声音的频率约在__________到__________的范围内。
(20HZ、20KHZ )3.调制有_________、__________、_________三种方式。
(调幅、调频、调相)4.无线电波在空间的传播方式有________、_________、__________三种。
(地波、天波、直线波)二、简答或作图题1.画出无线通信调幅发射机原理框图,并说明各部分的作用,同时画出波形示意图和频谱示意图。
2. 画出超外差接收机方框图,并说明各部分的作用,同时画出波形示意图和频谱示意图。
3.在接收设备中,检波器的作用是什么?试画出检波器前后的信号波形。
4. 通信系统由哪些部分组成?各组成部分的作用是什么?答:通信系统由输入、输出变换器,发送、接收设备以及信道组成。
输入变换器将要传递的声音或图像消息变换为电信号(基带信号);发送设备将基带信号经过调制等处理,并使其具有足够的发射功率,再送入信道实现信号的有效传输;信道是信号传输的通道;接收设备用来恢复原始基带信号;输出变换器将经过处理的基带信号重新恢复为原始的声音或图像。
第三章选频网络1、串联谐振和并联谐振的特征,以及失谐时表现出的特性。
如:LC回路并联谐振时,回路_阻抗___最大,且为纯__电阻__。
当所加信号频率高于并联谐振回路谐振频率时,回路失谐,此时,回路呈容性,电流超前电压。
2、由于信号源内阻或负载电阻的影响,将使谐振回路的品质因数Q ,选频特性,通频带。
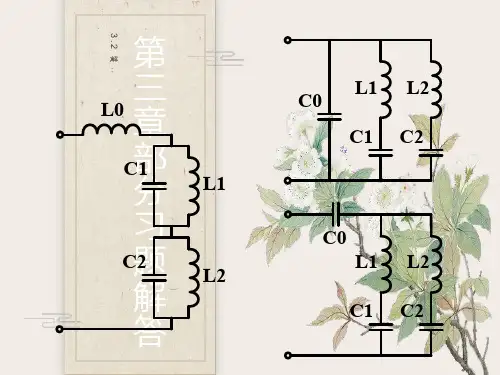
3、课后题 3.54、课后题 3.65、课后题 3.76、课后题 3.97、课后题 3.13有一耦合回路如图,已知试求:1)回路参数L1、L2、C1、C2和M;2)图中a 、b两端的等效谐振阻抗ZP;3)初级回路的等效品质因数Q1’;4)回路的通频带BW;解:由已知条件可知两个回路的参数是全同的,即L1=L2,C1=C2,Q1=Q2 ;1)由得:又由于发生临界耦合时因此2)由于发生了临界耦合,所以R f1=R 1=20Ω 此时ab 两端的等效 谐振阻抗为纯阻,即3)初级回路的等效品质因数为4)初级回路本身的品质因数为因此可得出通频带为 :,试计算回=5k L R ,=10k R =20pF, 2C =20pF, 1C =5pF,C =100,0Q =0.8uH,L 所示电路为一等效电路,其中18-2图8.路的谐振频率、谐振电阻。



6.5.1 馈电线路 6.5.2 输出、输入与级间耦合回路 频电子线路》(第四版)张肃文主编高等教育出版以上的高频功率放大器的电路仅仅是其原理图。
欲使高频功率放大器正常工作于丙类某一最佳状态,与小信号谐振放大器同样,必须有正确的直流通路和交流通路。
除此之外,还要尽量减少功率传输中的损耗。
这就涉及其馈电线路的实现问题。
图 6.5.1 对不同频率电流的等效电路频电子线路》(第四版)张肃文主编高等教育出版频电子线路》(第四版)张肃文主编高等教育出图 6.5.2 集电极电路的两种馈电形式版图 6.5.3 基极馈电的两种形式频电子线路》(第四版)张肃文主编高等教育出图 6.5.3 几种常用的产生基极偏压的方法版图 6.5.5 放大器与负载之间用四端网络耦合 1. 输出匹配网络 ①使负载阻抗与放大器所需要的最佳阻抗相匹配,以保证放大器传输到负载的功率最大,即它起着匹配网络的作用。
②抑制工作频率范围以外的不需要频率,即它应有良好的滤波作用。
③有效地传送功率到负载,但同时又应尽可能地使这几个电子器件彼此隔离,互不影响。
频电子线路》(第四版)张肃文主编高等教育出版图 6.5.6 复合输出回路 1. 输出匹配网络 频电子线路》(第四版)张肃文主编 高等教育出版图 6.5.7 等效电路 1. 输出匹配网络 虽然阻抗变换网络类型很多,但是,都可以等效成一个标准的并联谐振回路。
下面就等效成的标准并联谐振回路分析其功率传输效率。
图中,r ’为等效到谐振回路的负载电阻,r 1为谐振回路本身的损耗电阻。
功率电子器件送至回路的总回路送至负载的功率=k η)(12k 2k r r r '+'=I I r r r '+'=1r r r '+-=111L 1Q -=p p '1R R -=频电子线路》(第四版)张肃文主编高等教育出版图 6.5.10 晶体管等效电路 2. 输入匹配网络与级间耦合网络 1)中间放大级工作于过压状 态,此时它等效为一个理想电 压源,其输出电压几乎不随负 载变化。

第三章(pF)).(L C H)(.QR则L Ω取R Δf f Q (kHz)Δf MHz解:f..159101*********1159********10010100101010121010990101211362620603670036700=⨯⨯⨯⨯===⨯⨯⨯====⨯⨯===⨯-⨯==--ωμω时,产生并联谐振。
C L 或ωC L )当(时,产生串联谐振。
C L 或ωC L )当(时,产生并联谐振。
C L 或ωC L )当解:(22021101220211012202110111311211123======-ωωωR R C L R )LC ωL(j ωR )LC ωLR(j ωC L R C j ωR L j ωR )C j ωL)(R j ω(R 证明:Z =+=-+-++=+++++=-2112111133220020020000 )()()()()())()()()())318010404501053514321121535100160512405354501605151431223202222μH .C C L 故采用后一个不合理舍去pF -得C C C 由pF得C C C 由解:=⨯+⨯⨯⨯⨯='+==+=⨯+=+=⨯+--ω。
L C C ’()()()()mV V Q V V mA .R V I μH ..C L ..R C 解:Q-Sm Com Lom -om om --21210121220510111210100105114321121251010010511432115330312260200126000=⨯⨯====⨯===⨯⨯⨯⨯===⨯⨯⨯⨯⨯⨯==-ωω()()()()()()Ωj ..j .C jR Z Ω.....Q LQ L R pF C pF .L C C C C .V V Q μH .C 解:L X X X X X X X S C 7967471020010143217471747100102531014321052102531014322001001025310143211100101025310100101432116312606666000626200122620-=⨯⨯⨯⨯-=-==⨯⨯⨯⨯-⨯⨯⨯⨯=-==→=⨯⨯⨯⨯==+⋅====⨯⨯⨯⨯==------ωωωωω()()()。
21k Ω0.5R ,R ,故0.5Q Q ,则f 22f 因2Δ320105105552310023100101501052220105010514321173000.70.7660036700012620电阻所以应并上='='∆⨯='=⨯⨯-⨯⨯===⨯⨯===⨯⨯⨯⨯⨯==--.f Δf Q ξΔf f Q μH ..C ω解:L . ∑===-g Q CωΔf f C πf C πΔf 证明:..070007022483()()()()()()()()MHz ...Q f Δf .....L ωR Q k Ω..R C C C C R R R k Ω..C LQ R MHz ....LC πf pF .C C C C C C C 解:C L .L P i P i 4812281064122281080106411432108858855202020209201092010202010801006411031810801432121318202020202020593607066302021102126121260102102=⨯===⨯⨯⨯⨯⨯⨯===⨯⎪⎭⎫⎝⎛++=⎪⎪⎭⎫ ⎝⎛++==⨯+⨯⨯===⨯⨯⨯⨯===++++=++++=--∑∑----)))R Z 30Z 20Z 1123f1f1f1===-解:)()()()())()()()()()()))())()()()()()()Ω.j .j ..Z M Z j ..j C L j R Z pF .L C kHz .R ρf Q f Δf .R R L Q k ΩC R R L Z Ω..R M Z μH ..ηR M pF .L C C μH .ρL L 解:f .f f f P 8437680100201018310143210020101771014321101591014322011771015910950143211522810201022224252020101591014323251015920201015920201018310143221831014322011591015910143211159101432101133266222011126662*********2322022361100706611101112611112662201160116261201216301121-=+⨯⨯⨯⨯==+=⎪⎭⎫⎝⎛⨯⨯⨯⨯-⨯⨯⨯⨯+=⎪⎪⎭⎫⎝⎛'-+==⨯⨯⨯⨯⨯='='=⨯⨯====+⨯⨯⨯⨯=+==⨯⨯+⨯=+==⨯⨯⨯⨯===⨯⨯⨯===⨯⨯⨯⨯====⨯⨯===----------ωωωωωωωωω()100101410222002010159105010159153367.00111236=⨯=∆==→=∴=Ω=⨯⨯⨯⨯==---f f Q M R R C R L R f P 解:)()()()()()()()))013.02001122211222005101001032510102402051010010205101011632207.067101671012671120126722011=⨯-⨯+=⋅-+=∆=⨯⨯===⨯==Ω=+⨯⨯=+=Ω=⨯==-----Q f f R LQ R M k R RL R R M R 解:f ab f ηηωωηωω5.75.22303021103001010112118.111020*********.325.22115.2225.11103001010112111732332001230233200=-='-=→=⎪⎪⎭⎫⎝⎛⨯⨯+=⎪⎪⎭⎫ ⎝⎛∆+==⨯⨯⨯⨯⨯⨯==='→=⎪⎪⎭⎫ ⎝⎛⨯⨯'+=⎪⎪⎭⎫ ⎝⎛∆'+=--Q Q Q Q f f Q I I C Q R Q Q ff Q I I 解:ω()⎩⎨⎧==→⎪⎪⎩⎪⎪⎨⎧+==-μL μH L 并联联谐C L L ω串联联谐C L ω解:12537511218321212第四章5102501050501501时,5012.1102501020501501时,20491025010501501时,154266200266200266200=⎪⎪⎭⎫ ⎝⎛⨯⨯⨯+=⎪⎪⎭⎫ ⎝⎛+===⎪⎪⎭⎫ ⎝⎛⨯⨯⨯+=⎪⎪⎭⎫ ⎝⎛+===⎪⎪⎭⎫ ⎝⎛⨯⨯+=⎪⎪⎭⎫ ⎝⎛+==-TT T f f ββMHz f f f ββMHz f f f ββMHz f βββ当当解:当()()()()()()()()()()()()()()()()()()()()mS j .j .j b a jb a g r C j b a jb a C j g g r C j g y mS j .j b a jb a g y mS j .j .j b a jb a C j g y mS .j ..j .j b a jb a C j g y ..r ωC b .g r a pF ..πf g C mS ..r βg mS .βI g mb bc b c b c b m b b c b ce oe m fe c b cb re e b e b ieb b e b e b b b T m eb eb m E e b 68.0049.01011.01107.377011031014321733.3327.371011.01107.37187.00187.01011.0110310143241189501011.01102410143210754.010701024101432110754070112410250143210737273710754050754015026112674223127222222322221272222127322127363300+=⎪⎭⎫ ⎝⎛+-⨯⨯⨯+⨯⨯⨯⨯≈⎪⎭⎫⎝⎛+-+≈+-+++=-=+-⨯⨯=+-=--=+-⨯⨯⨯⨯⨯-≈+-+-=+=+-⨯⨯⨯⨯⨯+⨯=+-+=≈⨯⨯⨯⨯⨯==≈⨯⨯+=+==⨯⨯⨯⨯===⨯⨯===+⨯=+=---''''''--''--''-''-''-'-''ωωωωω解:()()()()4124142701010042104010041704070121101241104221104210124212422124284--=⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫ ⎝⎛-==⋅⎪⎪⎭⎫ ⎝⎛-==⎪⎪⎭⎫⎝⎛+=⎪⎪⎭⎫ ⎝⎛⋅⎪⎪⎭⎫ ⎝⎛-==⎪⎪⎭⎫⎝⎛+=⎪⎪⎭⎫⎝⎛-m mmm ...r m .m.mvo v m .m.mvo v Δf Δf K Qf Δf f ΔfQ A A Qf Δf f Δf Q A A 故得令得解:令()()()()()()()()()1103101045952110830081020010286021830082501020025010237952258854tan 2tan 431100316116570316107102316104107102105228113151********5228104525025052281028604110200411023723710410010710211250205250205943326662262621222206070666022632162626222166001345213231>>⨯⨯+⨯+⨯⨯⨯=+'++=⨯⨯+⨯=+='-=--=+==⎪⎭⎫⎝⎛-=⎪⎪⎭⎫ ⎝⎛-==⨯===⨯⨯⨯⨯⨯⨯======⨯⨯⨯⨯===⨯⨯+⨯⨯+⨯=++==⨯⨯⨯⨯⨯========-----------------∑-...y y ξg g g g S μS ....p g p g g ..ξ..Q Q K MH ...Q f Δf ..π.L ωg Q ..A A ....g y p p A μS ..g p g p g g μS ..πL Q ωg .N N p .N N p refe L oe ie s ie p L oo re fe L Z L .ΣL vo po Σfevo ie oe p p ϕϕ解:()()()()()()()()()()()()()()()()()()()()7221698266804238225025668042479479610444454782122259044546104422610441222565197445412212243822502578213445410158010410710143222782115802438303015801503008203010037010370104107101432100111104444447070707041707041704147044436260070222122222156600..-.A A ..A A ....f ΔΔf A A kHz ...Δf f ΔkHz .Δf f ΔkHz ..Δf Δf ..A A kHz ....f Lg ωΔf .....g y p p A mS .......g p g p R g g mS ...L ωQ g vovo vo vo..vo vo......vo vo .fevo ie oe p p =='-=='='=⨯='='=-=-'=-='=⨯-=⋅-=====⨯⨯⨯⨯⨯⨯⨯===+⨯⨯===⨯+⨯++=+++==⨯⨯⨯⨯⨯⨯==---∑∑∑-解:()()()()不能满足解:9.1K 522106250110511432121625011830500114r0.1122620221<=⨯⨯⨯⨯⨯===⨯+=+=--∑∑μH ....C πf L pF ..C p C C oe()74.73.05.24.364.265.2144220=⨯+==-refe S vo C y A ω解:()()()()()()()163910601046522260104910100410465274104921040574513114910010100010465210620574513491001010001046521020100440574513100010044100012051373118607311873118118101000104652111741030706123121206321123320202236123601012222236112563423612231201.K kH .Q f Δf πg C ωQ ..g y p p A μS π...Q C ωg p g μS πQ C ωg g pF ..C p C C pF C C C .L L L L μH πC ωL .r Z L .L fevo i o i o ==⨯⨯===⨯⨯⨯⨯⨯===⨯⨯⨯⨯⨯===∴=⨯⨯⨯⨯+⨯⨯⎪⎭⎫ ⎝⎛=+==⨯⨯⨯⨯+⨯=+==⨯⎪⎭⎫⎝⎛+=+==+=+==⨯+⨯+=++==⨯⨯⨯⨯==----------,则。