下载文档原格式
【最新整理，下载后即可编辑】高频电子第五版(pF)).(L C H)(.QR则L Ω取R Δf f Q (kHz)Δf MHz解：f..159101*********1159********10010100101010121010990101211362620603670036700=⨯⨯⨯⨯===⨯⨯⨯====⨯⨯===⨯-⨯==--ωμω时，产生并联谐振。
C L 或ωC L )当(时，产生串联谐振。
C L 或ωC L )当(时，产生并联谐振。
C L 或ωC L )当解：(22021101220211012202110111311211123======-ωωωR R C L R )LC ωL(j ωR )LC ωLR(j ωC L R C j ωR L j ωR )C j ωL)(R j ω(R 证明：Z =+=-+-++=+++++=-2112111133220020020000)()()()()())()()()())318010404501053514321121535100160512405354501605151431223202222μH .C C L 故采用后一个不合理舍去pF -得C C C 由pF得C C C 由解：=⨯+⨯⨯⨯⨯='+==+=⨯+=+=⨯+--ω。
L C C ’()()()()mV V Q V V mA .R V I μH ..C L ..R C 解：Q-Sm Com Lom -om om --21210121220510111210100105114321121251010010511432115330312260200126000=⨯⨯====⨯===⨯⨯⨯⨯===⨯⨯⨯⨯⨯⨯==-ωω()()()()()()Ωj ..j .C jR Z Ω.....Q LQ L R pFC pF .L C C C C .V V Q μH .C 解：L X X X X X X X S C 7967471020010143217471747100102531014321052102531014322001001025310143211100101025310100101432116312606666000626200122620-=⨯⨯⨯⨯-=-==⨯⨯⨯⨯-⨯⨯⨯⨯=-==→=⨯⨯⨯⨯==+⋅====⨯⨯⨯⨯==------ωωωωω()()()。
高频电子第五版(pF)).(L C H)(.QR则L Ω取R Δf f Q (kHz)Δf MHz解：f..159101*********11591014321010010100101010121010990101211362620603670036700=⨯⨯⨯⨯===⨯⨯⨯====⨯⨯===⨯-⨯==--ωμω时，产生并联谐振。
C L 或ωC L )当(时，产生串联谐振。
C L 或ωC L )当(时，产生并联谐振。
C L 或ωC L )当解：(22021101220211012202110111311211123======-ωωωR R C L R )LC ωL(j ωR )LC ωLR(j ωC L R C j ωR L j ωR )C j ωL)(R j ω(R 证明：Z =+=-+-++=+++++=-2112111133220020020000)()()()()())()()()())318010404501053514321121535100160512405354501605151431223202222μH .C C L 故采用后一个不合理舍去pF -得C C C 由pF得C C C 由解：=⨯+⨯⨯⨯⨯='+==+=⨯+=+=⨯+--ω。
L C C ’()()()()mV V Q V V mA .R V I μH ..C L ..R C 解：Q-Sm Com Lom -om om --21210121220510111210100105114321121251010010511432115330312260200126000=⨯⨯====⨯===⨯⨯⨯⨯===⨯⨯⨯⨯⨯⨯==-ωω()()()()()()Ωj ..j .C jR Z Ω.....Q LQ L R pF C pF .L C C C C .V V Q μH .C 解：L X X X X X X X S C 7967471020010143217471747100102531014321052102531014322001001025310143211100101025310100101432116312606666000626200122620-=⨯⨯⨯⨯-=-==⨯⨯⨯⨯-⨯⨯⨯⨯=-==→=⨯⨯⨯⨯==+⋅====⨯⨯⨯⨯==------ωωωωω()()()。
高频电子线路课后题解答 主编 张肃文前三章课后题不重要,不会出考题.(pF)).(L C H)(.QR则L Ω取R Δf f Q (kHz)Δf MHz解：f..159101*********1159101432101001010010101012101099010121136262063670036700=⨯⨯⨯⨯===⨯⨯⨯====⨯⨯===⨯-⨯==--ωμω时，产生并联谐振。
C L 或ωC L )当(时，产生串联谐振。
C L 或ωC L )当(时，产生并联谐振。
C L 或ωC L )当解：(22021101220211012202110111311211123======-ωωωR R C L R )LC ωL(j ωR )LC ωLR(j ωC L R C j ωR L j ωR )C j ωL)(R j ω(R 证明：Z =+=-+-++=+++++=-2112111133220020020000)()()()()())()()()())31801040450105351432112153510016051240535450160515143122322222μH .C C L 故采用后一个不合理舍去pF -得C C C 由pF得C C C 由解：=⨯+⨯⨯⨯⨯='+==+=⨯+=+=⨯+--ω。
L C C ’()()()()mV V Q V V mA .R V I μH ..C L ..R C 解：Q-Sm Com Lom -om om --21210121220510111210100105114321121251010010511432115330312260200126000=⨯⨯====⨯===⨯⨯⨯⨯===⨯⨯⨯⨯⨯⨯==-ωω()()()()()()Ωj ..j .C jR Z Ω.....Q LQ L R pFC pF .L C C C C .V V Q μH .C 解：L X X X X X X X S C 7967471020010143217471747100102531014321052102531014322001001025310143211100101025310100101432116312606666000626200122620-=⨯⨯⨯⨯-=-==⨯⨯⨯⨯-⨯⨯⨯⨯=-==→=⨯⨯⨯⨯==+⋅====⨯⨯⨯⨯==------ωωωωω()()()。
一•填空题1. 为了改善系统性能，实现信号的有效传输及信道的复用,通信系统中广泛采用调制技术。
2. 用待传输的基带信号去改变高频载波信号某一参数的过程，称为调制,用基带信号去改变载波信号的幅度，称为调幅。
3. 无线电波传输方式大体可分为沿地面传播（地播）,沿空间直线传播（空间播）, 依靠电离层传播（电播）。
4. 非线性器件能够产生新的频率分量,具有频率变换作用。
1. LC并联回路谐振时阻抗为最大且为纯电阻,当频率高于谐振频率而失谐时，阻抗将减小,并呈容性。
2. 小信号谐振放大器以谐振回路作为负载,它不仅有放大作用,还有选频作用。
3. 矩形系数K0.1是用来说明小信号选频放大器选择性好坏的性能指标，其值越接近于2,放大器的选择性越好。
单调谐放大器的KO.l^lOo4. 电路中同一端口的宜号功率与噪吏功率之比，称为信噪比，其值越大，噪声的影响就越小。
1. 丙类谐振功率放大器的特点是：晶体管基级偏压VbbvUbe（on）,集电极电流为余弦脉冲，其导通角0小于90°,故放大器具有很高的效率；放大器负载采用LC谐振网络,用以滤出谐波,实现阻抗匹配获得大功率输出。
2. 丙类谐振功率放大器工作在临界状态，当负载回路等效电阻Re减小时，放大器将进入欠压状态,此时输出功率减小,管耗增大。
3. 谐振功率放大器中晶体管工作进入包河区，集电极电流脉冲出现巴陷，称为过压状态。
4. 谐振功率放大器集电极直流馈电电路有里僮和并馈两种形式。
5. 传输线变压器与普通变压器相比较，其主要特点是工作频带极宽,能量以传输线和变压器方式传输。
1. 反馈镇正弦波振荡器主要由放大电路,正反馈网络,选频网络等部分组成。
2. 设放大电路的放大倍数为A,反馈网络的反馈系数为F,则正弦波振荡器的振幅平衡条件是AF=1,相位平衡条件是（n二0,1, 2, ........................................ ）。
高频电子线路〔用于学习之间交流，不得用于出版等商业用处！〕第2章习题答案2-1某一并联谐振回路的谐振频率f 0＝1MHz ，要求对990kHz 的干扰信号有足够的衰减，问该并联回路应如何设计？解 为了有效滤除990kHz 的干扰信号，应使它位于通频带之外。
假设取BW 0.7＝20kHz ，那么由通频带与回路Q 值之间的关系有502010007.00===BW f Q因此应设计Q ＞50的并联谐振回路。
2-2试定性分析题图2-2所示的电路在什么情况下呈现串联谐振或并联谐振状态。
解 题图2-2〔a 〕中L 1C 1或L 2C 2之一呈并联谐振状态，那么整个电路即为并联谐振状态。
假设L 1C 1与L 2C 2呈现为容抗，那么整个电路可能成为串联谐振。
题图2-2〔b 〕只可能呈现串联谐振，不可能呈现并联谐振状态。
题图2-2〔c 〕只可能呈现并联谐振，不可能呈现串联谐振状态。
2-3有一并联回路，其电感、电容支路中的电阻均为R 。
当C L R =时〔L 和C 分别为电感和电容支路的电感值和电容值〕，试证明回路阻抗Z 与频率无关。
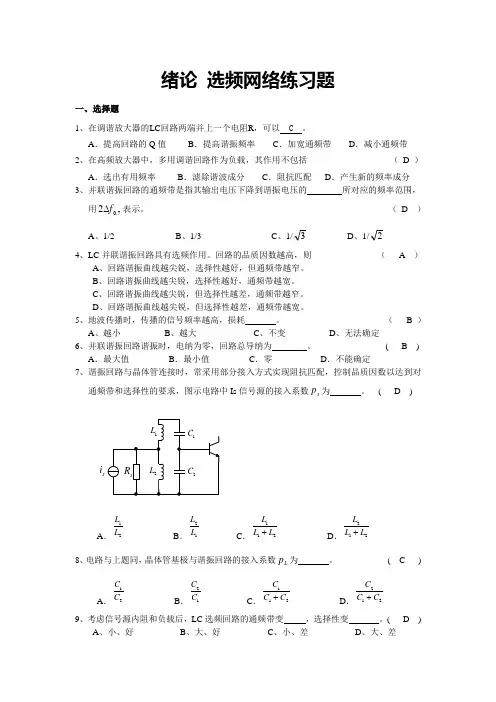
解 ()()()⎪⎭⎫ ⎝⎛-++⎪⎪⎭⎫⎝⎛-+⎪⎭⎫ ⎝⎛+=⎪⎭⎫⎝⎛-++⎪⎭⎫ ⎝⎛-+=C L j R R C R LR j C L R R C j R L j R C j R L j R Z abωωωωωωωω11121112212121 要想使Z ab 在任何频率下，都呈现纯阻性，就必须使分子与分母的相角相等，亦即必须有2121121R R C L CL R R C R LR +-==-ωωωω 上式化简得C R C L LR C L 2122222-=⎪⎪⎭⎫ ⎝⎛-ω 要使上式在任何频率下都成立，必有0222=-LR C L 或 C L R =2 0212=-C R C L 或 CL R =1 因此最后得CLR R ==212-4有一并联回路在某频段内工作，频段最低频率为535kHz ，最高频率为1605kHz 。
绪论 选频网络练习题一、选择题1、在调谐放大器的LC 回路两端并上一个电阻R ，可以 C 。
A ．提高回路的Q 值B ．提高谐振频率C ．加宽通频带D ．减小通频带2、在高频放大器中，多用调谐回路作为负载，其作用不包括 （ D ）A ．选出有用频率B ．滤除谐波成分C ．阻抗匹配D ．产生新的频率成分3、并联谐振回路的通频带是指其输出电压下降到谐振电压的 所对应的频率范围， 用7.02f ∆表示。
（ D ）A 、1/2B 、1/3C 、1/3D 、1/24、LC 并联谐振回路具有选频作用。
回路的品质因数越高，则 （ A ）A 、回路谐振曲线越尖锐，选择性越好，但通频带越窄。
B 、回路谐振曲线越尖锐，选择性越好，通频带越宽。
C 、回路谐振曲线越尖锐，但选择性越差，通频带越窄。
D 、回路谐振曲线越尖锐，但选择性越差，通频带越宽。
5、地波传播时，传播的信号频率越高，损耗 。
（ B ）A 、越小B 、越大C 、不变D 、无法确定6、并联谐振回路谐振时，电纳为零，回路总导纳为 。
( B )A ．最大值B ．最小值C ．零D ．不能确定7、谐振回路与晶体管连接时，常采用部分接入方式实现阻抗匹配，控制品质因数以达到对通频带和选择性的要求，图示电路中Is 信号源的接入系数s p 为 。
( D )s iA ．12L LB ．21L LC ．112L L L +D ．212L L L +8、电路与上题同，晶体管基极与谐振回路的接入系数L p 为 。
( C )A ．12C CB ．21C C C ．112C C C +D ．212C C C +9、考虑信号源内阻和负载后，LC 选频回路的通频带变 ，选择性变 。
( D )A 、小、好B 、大、好C 、小、差D 、大、差10、LC 组成并联谐振回路，谐振频率LC f o π21=，把它串接在电路中，就能阻止频率为多少的信号通过。
（ A ） A ． 不为o f B ．o f C ．大于o f D ．小于o f11、如图所示，将负载L R 等效到ab 两端L R '= 。
绪论 选频网络练习题一、选择题1、在调谐放大器的LC 回路两端并上一个电阻R ，可以 C 。
A ．提高回路的Q 值B ．提高谐振频率C ．加宽通频带D ．减小通频带2、在高频放大器中，多用调谐回路作为负载，其作用不包括 （ D ）A ．选出有用频率B ．滤除谐波成分C ．阻抗匹配D ．产生新的频率成分3、并联谐振回路的通频带是指其输出电压下降到谐振电压的 所对应的频率范围，用7.02f ∆表示。
（ D ）A 、1/2B 、1/3C 、1/3D 、1/24、LC 并联谐振回路具有选频作用。
回路的品质因数越高，则 （ A ）A 、回路谐振曲线越尖锐，选择性越好，但通频带越窄。
B 、回路谐振曲线越尖锐，选择性越好，通频带越宽。
C 、回路谐振曲线越尖锐，但选择性越差，通频带越窄。
D 、回路谐振曲线越尖锐，但选择性越差，通频带越宽。
5、地波传播时，传播的信号频率越高，损耗 。
（ B ）A 、越小B 、越大C 、不变D 、无法确定6、并联谐振回路谐振时，电纳为零，回路总导纳为 。
( B )A ．最大值B ．最小值C ．零D ．不能确定7、谐振回路与晶体管连接时，常采用部分接入方式实现阻抗匹配，控制品质因数以达到对通频带和选择性的要求，图示电路中Is 信号源的接入系数s p 为 。
( D )s iA ．12L LB ．21L LC ．112L L L +D ．212L L L +8、电路与上题同，晶体管基极与谐振回路的接入系数L p 为 。
( C )A ．12C CB ．21C C C ．112C C C +D ．212C C C +9、考虑信号源内阻和负载后，LC 选频回路的通频带变 ，选择性变 。
( D )A 、小、好B 、大、好C 、小、差D 、大、差10、LC组成并联谐振回路，谐振频率LCfoπ21=，把它串接在电路中，就能阻止频率为多少的信号通过。
（ A ）A．不为of B．of C．大于of D．小于of11、如图所示，将负载LR等效到ab两端LR'= 。
第二章选频网络注意：①有部分答案有差异；②3-1题是2-1题；③只有计算题答案和部分问答题；④答案不齐全。
(pF)).(L C H)(.QR L ΩR Δf f Q (kHz)Δf MHz:f ..159101*********11591014321010010100101010121010990101211362620603670036700=××××===×××====××===×−×==−−ωµω, .C L ωC L ) (, .C L ωC L ) ( , .C L ωC L ) :(22021101220211012202110111311211123======−ωωωR R C L R )LCωL(jωR )LC ωLR(jωC L R C jωR L jωR )C jωL)(R jω(R :Z =+=−+−++=+++++=−2112111133220020020000)()()()()())()()()())318010404501053514321121535100160512405354501605151431223202222μH .C C LpF - C C CpFC C C:=×+××××=′+==+=×+=+=×+−−ω。
L C C ’()()()()mV V Q V V mA .R V I μH ..C L ..R C :Q -Sm Com Lom -om om --21210121220510111210100105114321121251010010511432115330312260200126000=××====×===××××===××××××==−ωω()()()()()()Ωj ..j .C j R Z Ω.....Q L Q L R pF C pF .L C C C C .V V Q μH .C :L X X X X X X X S C 7967471020010143217471747100102531014321052102531014322001001025310143211100101025310100101432116312606666000626200122620−=××××−=−==××××−××××=−==→=××××==+⋅====××××==−−−−−−ωωωωω()()().21kΩ0.5R,R , 0.5Q Q , f 22f 2Δ320105105552310023100101501052220105010514321173000.70.7660036700012620电阻所以应并上=′=′∆×=′=××−××===××===×××××==−−.f Δf Q ξΔf f Q μH ..C ω :L .∑===−g QCωΔf f C πf C πΔf :..070007022483()()()()()()()()MHz ...Q f Δf .....L ωR Q kΩ..R C C C C R R R kΩ..C LQ R MHz ....LC πf pF .C C C C C C C :C L .L P i P i 4812281064122281080106411432108858855202020209201092010202010801006411031810801432121318202020202020593607066302211021261201260102102=×===××××××===×⎠⎞⎜⎝⎛++=⎟⎟⎠⎞⎜⎜⎝⎛++==×+××===××××===++++=++++=−−∑∑−−−−)))RZ 30Z 20Z 1123f1f1f1===−解：)()()()())()()()()()()))())()()()()()()Ω.j .j ..Z M Z j ..j C L j R Z pF .L C kHz .R ρf Q f Δf .R R L Q kΩC R R L Z Ω..R M Z μH ..ηR M pF .L C C μH .ρL L :f .f f f P 8437680100201018310143210020101771014321101591014322011771015910950143211522810201022224252020101591014323251015920201015920201018310143221831014322011591015910143211159101432101133266222011126662*********2322022361100706611101112611112662201160116261201216301121−=+××××==+=⎟⎠⎞⎜⎝⎛××××−××××+=⎟⎟⎠⎞⎜⎜⎝⎛′−+==×××××=′=′=××====+××××=+==××+×=+==××××===×××===××××====××===−−−−−−−−−−ωωωωωωωωω()100101410222002010159105010159153367.00111236=×=∆==→=∴=Ω=××××==−−−f f Q M R R C R L R f P ∵解：)()()()()()()()))013.02001122211222005101001032510102402051010010205101011632207.067101671012671120126722011=×−×+=⋅−+=∆=××===×==Ω=+××=+=Ω=×==−−−−−Q f f R L Q R M k R RL R R M R :f ab f ηηωωηωω5.75.22303021103001010112118.111020*********.325.22115.2225.111030010101121117323320012302332=−=′−=→=⎟⎟⎠⎞⎜⎜⎝⎛××+=⎟⎟⎠⎞⎜⎜⎝⎛∆+==××××××===′→=⎟⎟⎠⎞⎜⎜⎝⎛××′+=⎟⎟⎠⎞⎜⎜⎝⎛∆′+=−−Q Q Q Q f f Q I I C Q R Q Q f f Q I I :ω()⎩⎨⎧==→⎪⎪⎩⎪⎪⎨⎧+==−μL μH L CL L ω C L ω :12537511218321212第三章高频小信号放大器5102501050501501 ,5012.1102501020501501 ,20491025010501501 ,154266200266200266200=⎟⎟⎠⎞⎜⎜⎝⎛×××+=⎟⎟⎠⎞⎜⎜⎝⎛+===⎟⎟⎠⎞⎜⎜⎝⎛×××+=⎟⎟⎠⎞⎜⎜⎝⎛+===⎟⎟⎠⎞⎜⎜⎝⎛××+=⎟⎟⎠⎞⎜⎜⎝⎛+==−TT T f f ββMHz f f f ββMHz f f f ββMHz f βββ当当解：当()()()()()()()()()()()()()()()()()()()()mS j .j .j b a jb a g r C j b a jb a C j g g r C j g y mS j .j b a jb a g y mS j .j .j b a jb a C j g y mS .j ..j .j b a jb a C j g y ..r ωC b .g r a pF ..πf g C mS ..r βg mS .βI g m b b c b c b c b m b b c b ce oe m fe c b c b re e b e b ieb b e b e b b b T m eb eb m E e b 68.0049.01011.01107.377011031014321733.3327.371011.01107.37187.00187.01011.0110310143241189501011.01102410143210754.010701024101432110754070112410250143210737273710754050754015026112674223127222222322221272222127322127363300+=⎟⎠⎞⎜⎝⎛+−×××+××××≈⎟⎠⎞⎜⎝⎛+−+≈+−+++=−=+−××=+−=−−=+−×××××−≈+−+−=+=+−×××××+×=+−+=≈×××××==≈××+=+==××××===××===+×=+=−−−′′′′′′−−′′−−′′−′′−′′−′−′′ωωωωω解：()()()()4124142701010042104010041704070121101241104221104210124212422124284−−=⎟⎟⎠⎞⎜⎜⎝⎛−⎟⎟⎠⎞⎜⎜⎝⎛−==⋅⎟⎟⎠⎞⎜⎜⎝⎛−==⎟⎟⎠⎞⎜⎜⎝⎛+=⎟⎟⎠⎞⎜⎜⎝⎛⋅⎟⎟⎠⎞⎜⎜⎝⎛−==⎟⎟⎠⎞⎜⎜⎝⎛+=⎠⎞⎜⎜⎝⎛−m mm m ...r m .m.m vo v m .m.mvo v Δf Δf K Q f Δf f ΔfQ A A Q f Δf f Δf Q A A 故得令得解：令()()()()()()()()()1103101045952110830081020010286021830082501020025010237952258854tan 2tan 431100316116570316107102316104107102105228113151********5228104525025052281028604110200411023723710410010710211250205250205943326662262621222206070666022632162626222166001345213231>>××+×+×××=+′++=××+×=+=′−=−−=+==⎟⎠⎞⎜⎝⎛−=⎟⎟⎠⎞⎜⎜⎝⎛−==×===××××××======××××===××+××+×=++==×××××========−−−−−−−−−−−−−−−−−∑−...y y ξg g g g S μS ....p g p g g ..ξ..Q Q K MH ...Q f Δf ..π.L ωg Q ..A A ....g y p p A μS ..g p g p g g μS ..πL Q ωg .N N p .N N p refe L oe ie s ie p L oo re fe L Z L .ΣL vo po Σfe vo ie oe p p ϕϕ解：()()()()()()()()()()()()()()()()()()()()7221698266804238225025668042479479610444454782122259044546104422610441222565197445412212243822502578213445410158010410710143222782115802438303015801503008203010037010370104107101432100111104444447070707041707041704147044436260070222122222156600..-.A A ..A A ....f ΔΔf A A kHz ...Δf f ΔkHz .Δf f ΔkHz ..Δf Δf ..A A kHz ....f Lg ωΔf .....g y p p A mS .......g p g p R g g mS ...L ωQ g vo vo vo vo ..vo vo ......vo vo .fe vo ie oe p p ==′−==′=′=×=′=′=−=−′=−=′=×−=⋅−=====×××××××===+××===×+×++=+++==××××××==−−−∑∑∑−解：()()()()不能满足解：9.1K 522106250110511432121625011830500114r0.1122620221<=×××××===×+=+=−−∑∑μH ....C πf L pF ..C p C C oe ()74.73.05.24.364.265.2144220=×+==−refeS vo C y A ω解：()()()()()()()163910601046522260104910100410465274104921040574513114910010100010465210620574513491001010001046521020100440574513100010044100012051373118607311873118118101000104652111741030706123121206321123320202236123601012222236112563423612231201.K kH .Q f Δf πg C ωQ ..g y p p A μS π...Q C ωg p g μS πQ C ωg g pF ..C p C C pF C C C .L L L L μH πC ωL .r Z L .L fe vo i o i o ==××===×××××===×××××===∴=××××+××⎟⎠⎞⎜⎝⎛=+==××××+×=+==×⎟⎠⎞⎜⎝⎛+=+==+=+==×+×+=++==××××==−−−−−−−−−−，则。
