角动量角动量守恒定律
- 格式:ppt
- 大小:1.32 MB
- 文档页数:36

量子力学中的角动量与角动量守恒定律量子力学是20世纪物理学的重要进展之一,它以其奇特的原理和理论体系引起了广泛的兴趣和研究。
在量子力学中,角动量是一个重要的物理量,它在物理过程中具有很多奇异的性质。
本文将介绍量子力学中的角动量和角动量守恒定律,并探讨其在不同体系中的应用。
量子力学中的角动量是描述一个物体自旋和转动的性质。
它与经典力学中的角动量概念相似,但存在着一些重要的区别。
首先,量子力学中的角动量是离散的,即只能取某些特定的数值;而经典力学中的角动量可以取任意实数值。
其次,量子力学中的角动量是通过测量得到的,而经典力学中的角动量是确定的。
在量子力学中,角动量运算符是描述角动量的数学工具。
角动量运算符可以分为两个部分,一个部分是轨道角动量运算符,描述物体的转动;另一个部分是自旋角动量运算符,描述物体的自旋。
这两个部分的和构成了总角动量运算符。
通过对角动量运算符的求解,可以得到角动量的具体数值和方向。
角动量守恒定律是指在物理过程中,系统的总角动量守恒不变。
这个定律可以通过量子力学的数学框架来解释和证明。
系统的总角动量守恒不变意味着系统中的角动量不能被创建或者销毁,只能在不同的子系统之间转移。
这个定律在很多物理过程中都有广泛的应用,例如原子的电子能级跃迁、核反应等。
在讨论角动量守恒的过程中,我们需要了解不同体系中的角动量性质。
在轨道角动量中,角动量量子数l描述了轨道的形状和空间分布。
l的取值范围为0到n-1,其中n是主量子数。
通过角动量量子数l的不同取值,可以得到不同的轨道,例如s轨道、p轨道等。
自旋角动量主要描述物体内部的自旋状态,其量子数为s,其取值范围为±1/2。
自旋角动量是一个基本粒子的内禀属性,不同的基本粒子具有不同的自旋。
除了轨道角动量和自旋角动量,角动量还有一个重要的性质是角动量的选择定则。
角动量的选择定则规定了在特定过程中角动量的变化规律。
通过角动量选择定则,我们可以确定许多物理现象的发生概率和过程。

角动量守恒定律角动量守恒定律,也称转动动量守恒定律,是描述旋转系统中物体角动量守恒的物理定律。
它是在伽利略与牛顿的基础上,由欧拉和拉格朗日等人发展起来的。
它表明,在无外力矩作用下,一个封闭系统的总角动量守恒。
在物理学中,角动量是描述物体旋转运动的物理量。
一个物体的角动量等于其自转角速度和惯性矩的乘积。
考虑一个刚性物体,其围绕某个轴心旋转。
此时,物体的角动量L等于其自转惯性矩I和角速度ω的积,即L=Iω。
这个公式可以用来描述物体的旋转状态。
在没有外力矩作用的情况下,物体的角动量守恒。
也就是说,在这种情况下,刚体自身的角速度和惯性矩不会发生改变。
这个定律可以由牛顿第二定律的角动量形式推导出来。
当一个刚体受到外部力矩时,他的角动量就会发生变化。
这个变化量等于力矩与旋转时间的积。
一个封闭系统中的物体,在没有外部力矩作用时,总角动量守恒,即所有物体的角动量的代数和不变。
如果物体中有某一个物体受到外部力矩,那么这个物体的角动量就会发生变化,但是,由于总系y运中的总力矩为零,所以其他物体的角动量将以相反的方式发生变化,以保证总角动量守恒。
一个典型的例子是一个旋转跳板启动一个跳跃者,高度和角速度的变化取决于跳板和跳跃者的质量和形状。
在这个过程中,跳板和跳跃者的角动量守恒,因为在计算角速度和角动量时,两个物体的总和是不变的。
总之,角动量守恒定律是一种重要的动力学基本定律。
它说明,封闭系统中的角动量总和保持不变。
在硬物体的运动中往往非常有用,可以帮助计算速度、加速度和其他涉及运动的数值。
在工程学和物理学中,它被广泛地应用于旋转系统、制药生产,以及其他需要涉及转动的领域。





角动量守恒定律是什么公式有哪些
有很多的同学是非常想知道,角动量守恒定律是什幺,公式有哪些,小编整理了相关信息,希望会对大家有所帮助!
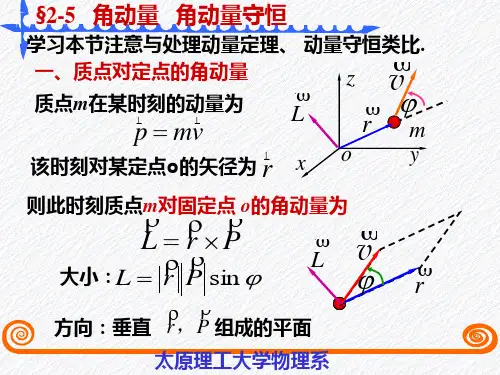
1 角动量守恒定律内容对于质点,角动量定理可表述为:质点对固定点的角动量对时间的微商,等于作用于该质点上的力对该点的力矩。
物理学的普遍定律之一。
反映质点和质点系围绕一点或一轴运动的普遍规律
如果合外力矩零(即M 外=0),则L1=L2,即L=常矢量。
这就是说,对一固定点o,质点所受的合外力矩为零,则此质点的角动量矢量保持不变。
这一结论叫做质点角动量守恒定律。
1 角量守恒公式是什幺角动量守恒定律是用来叙述刚体旋转运动的方法,要想了解它建议用和动量守恒定律类比的方法
很容易理解,我给您谢几个公式,注意他们是对应的:
1 动量:质量m,速度v,加速度a,动量mv,力F,F=ma
2 角动量:转动惯量J,角速度w,角加速度β,角动量Jw,力矩M,M=Jβ
可以看出转动惯量是“充当”质量的角色,力矩充当了力的角色
牛2:物体不受外力或合外力为0,则物体保持运动状态不变
角:旋转物体不受外力矩或和力矩为0,则物体保持旋转状态不变
以上可以看出其数学结构很统一,但是角动量中转动惯量的求法要复杂的多, 有些需要微积分基础,这里给出质点:J=mr
最后,角动量守恒定理:。

角动量定理和角动量守恒定律
角动量定理和角动量守恒定律是描述刚体运动时的两个基本定律。
下面进行简单的介绍:
1. 角动量定理
角动量定理是描述角动量变化的定律。
它表示为:物体所受外力矩等于物体角动量对时间的变化率。
即
I*ω= ΔL/Δt
其中,I 为物体的转动惯量,ω为物体的角速度,L 为物体的角动量。
这个定理表明了一个物体的角动量发生变化时,必定受到了外部的力矩作用,即力矩等于角动量的变化率。
2. 角动量守恒定律
角动量守恒定律是描述角动量不变的定律,即如果没有外部力矩作用,系统的总角动量保持不变。
即:
L = L0
其中,L 为系统的总角动量,L0 为系统在某一时刻的总角动量。
这个定律表明,如果没有外部力矩作用,那么系统的总角动量保持不变。
如果一个物体在自由运动时,角动量发生变化,那么它将会改变自身的旋转状态(比如转速、方向等)。
总之,角动量定理和角动量守恒定律是描述刚体运动和角动量变化的基本定理,可以帮助我们更好地理解物体的运动和变化规律。