电磁学第二版习题答案第一章[1]
- 格式:pdf
- 大小:270.34 KB
- 文档页数:23

程稼夫电磁学篇第一章《静电场》课后习题1-1设两个小球所带净电荷为q,距离为l,由库仑定律:由题目,设小球质量m,铜的摩尔质量M,则有:算得1-2 取一小段电荷,其对应的圆心角为dθ:这一小段电荷受力平衡,列竖直方向平衡方程,设张力增量为T:解得1-3(1)设地月距离R,电场力和万有引力抵消:解得:(2)地球分到,月球分到,电场力和万有引力抵消:解得:1-4设向上位移为x,则有:结合牛顿第二定律以及略去高次项有:1-5由于电荷受二力而平衡,故三个电荷共线且q3在q1和q2之间:先由库仑定律写出静电力标量式:有几何关系:联立解得由库仑定律矢量式得:解得1-6(1)对一个正电荷,受力平衡:解得,显然不可能同时满足负电荷的平衡(2)对一个负电荷,合外力提供向心力:解得1-7(1)设P限制在沿X轴夹角为θ的,过原点的直线上运动(θ∈[0,π)),沿着光滑直线位移x,势能:对势能求导得到受力:小量近似,略去高阶量:当q>0时,;当q<0时,(2)由上知1-8设q位移x,势能:对势能求导得到受力:小量展开有:,知1-9(1)对q受力平衡,设其横坐标的值为l0:,解得设它在平衡位置移动一个小位移x,有:小量展开化简有:受力指向平衡位置,微小谐振周期(2)1-101-11先证明,如图所示,带相同线电荷密度λ的圆弧2和直线1在OO处产生的电场强度相等.取和θ.有:显然两个电场强度相等,由于每一对微元都相等,所以总体产生的电场相等.利用这一引理,可知题文中三角形在内心处产生的电场等价于三角形内切圆环在内心处产生的电场.由对称性,这一电场强度大小为0.1-12(1)如图,取θ和,设线电荷密度λ,有:积分得(2)(3)用圆心在场点处,半径,电荷线密度与直线段相等的,张角为θ0 ()的一段圆弧替代直线段,计算这段带电圆弧产生的场强大小,可以用其所张角对应的弦长与圆弧上单位长度所产生的电场强度大小的积求得:1-13我们先分析一个电荷密度为ρ,厚度为x的无穷大带电面(图中只画出有限大),取如图所示高斯面,其中高斯面的两个相对面平行于电荷平面,面积为S,由高斯定理:算得,发现这个无穷大平面在外部产生的电场是匀强电场,且左右两边电场强度相同,大小相反.回到原题,由叠加原理以及,算得在不存在电荷的区域电场强度为0(正负电荷层相互抵消.)在存在电荷的区域,若在p区,此时x处的电场由三个电荷层叠加而成,分别是左边的n区,0到x范围内的p区,以及右边的p区,有:,算得同理算出n区时场强,综上可得1-14(1)取半径为r的球形高斯面,有:,解得(2)设球心为O1,空腔中心为O2,空腔中充斥着电荷密度为−ρ的电荷,在空腔中任意一点A处产生的电场为:(借助第一问结论)同时在A处还有一个电荷密度为+ρ则有:1-15取金属球上一面元d S,此面元在金属球内侧产生指向内的电场强度,由于导体内部电场处处为0,所以金属球上除该面元外的其他电荷在该面元处产生的电场强度为所以该面元受到其他电荷施加的静电力:球面上单位面积受力大小:半球面受到的静电力可用与其电荷面密度相等的,该半球面的截口圆面的面积乘该半球面的单位面积受力求得:1-16设轴线上一点到环心距离为x,有:令其对x导数为0:解得1-17写出初态体系总电势能:1-18系统静电势能大小为:1-19由对称性,可以认为四个面分别在中心处产生的电势,故取走后,;设BCD,ACD,ABD在P2处产生的电势为U,而ABD在P2处产生的电势为,有:;取走后:,解得1-20构造如下六个带电正方体(1到6号),它们的各面电荷分布彼此不相同,但都能通过一定的旋转从程中电荷直接相加而不重新分布).这个带电正方体各面电势完全相同,都为.容易证明,正方体内部的每一个点的电势也都为(若不然,正方体内部必存在电场线,这样的电场线必定会凭空产生,或凭空消失,或形成环状,都与静电场原理不符).故此时中心电势同样为1-21 O4处电势:O1处电势:故电势差为:1-22从对称性方面考虑,先将半球面补全为整个球面.再由电势叠加原理,即一个半球面产生的电势为它的一半,从而计算出半球面在底面上的电势分布.即1-23设上极板下版面面电荷密度为,下极板上版面面电荷密度为.取一个长方体型的高斯面,其形状是是两极板中间间隔的长方体,并且把和囊括进去.注意到金属导体内部没有电场,故这个高斯面电通量为0,其中净电荷为0,有:再注意到上下极板电势相等,其中E1方向向上,E2方向向下:再由高斯定理得出的结论:解得1-24先把半圆补成整圆,补后P、Q和O.这说明,新补上的半圆对P产生的电势为,而由于对称性,这个电势恰好也是半球面ACB对Q产生的电势.故:1-25在水平方向上,设质点质量m,电量为q:运动学:整体带入得:1-26(1)先将半球面补全为整个球面,容易计算出此时半球底面的电势.再注意到这个电势由对称的两个半球面产生的电势叠加得到,即一个半球面产生的电势为它的一半,即可求出一个半球面对底面产生的电势恒为定值,故底面为等势面,由E点缓慢移至A点外力做功为W1=0.(2)由上一问的分析知由E点缓慢移至O点外力不做功,记电势能为E,E的右下标表示所代表的点,则有:依然将半球面补为整球面,此时q在球壳内部任意一点电势能为2EO.此时对于T点,其电势能为上下两个球面叠加产生,由对称性,有:综上有W2=−W.1-27小球受电场力方程:将a与g合成为一个等效的g′:方向与竖直夹角再将加速度分解到垂直于g′和平行与g′的方向上.注意到与g′平行的分量最小为0,而垂直的分量则保持不变,故速度的最小值为垂直分量:1-28假设给外球壳带上电量q2,先考虑q2在内外表面各分布了多少.取一个以内球壳外表面和外球壳内表面为边界的高斯面,并把内球壳外表面和外球壳内表面上的电荷囊括进去,真正的高斯面边界在金属内部.由于金属内部无电场,高斯面电通量为0,高斯面内电荷总量为0,得到外球壳内表面分布了−q1电荷,外表面分布了q2+q1电荷.由电势叠加原理知球心处的电势:解得由电势叠加原理及静电屏蔽:1-29设质点初速度为v0,质量为m,加速度为a,有:,其中.设时竖直向下速度为v1,动能为Ek1,初动能为Ek0,有:解得1-30球1依次与球2、球3接触后,电量分别为.当球1、4接触时满足由于解得.注:若此处利用,略去二阶小量则可以大大简便计算,有意思的是,算出的答案与笔者考虑二阶小量繁重化简过后所得结果完全一致,这是因为在最后的表达式中没有r与a的和或差的项的缘故。

电磁学-第二版-习题答案第二版《电磁学》的习题答案:1. 第一章:电荷和电场习题1:假设有两个电荷,一个带正电量Q1,另一个带负电量Q2,在他们之间的距离为r1。
如果将Q1的电荷减小到原来的一半,同时将Q2的电荷加倍,并将它们之间的距离改为r2,那么这两个电荷之间的相互作用力是怎样改变的?解答:根据库伦定律,两个电荷之间的相互作用力正比于它们的电荷量乘积,反比于它们之间的距离的平方。
即F∝(Q1Q2)/r^2。
根据题目,Q1变为原来的一半,Q2变为原来的两倍,r由r1变为r2。
代入上述关系式,可得新的相互作用力F'为:F'∝((Q1/2)*(Q2*2))/(r2^2)。
化简上式,可得F'∝(Q1Q2)/(r2^2)。
由上式可知,新的相互作用力与原来相互作用力相等。
即新旧相互作用力大小相同。
习题2:有一组平行板电容器,两板之间的距离为d,电容的电极面积为A。
当电容器充满理想电介质时,电容器的电容是原来的多少倍?解答:当电容器充满理想电介质时,电容的电容量由电容公式C=εA/d得到。
其中,ε为电介质的相对介电常数。
而当电容器未充满电介质时,电容的电容量为C0=ε0A/d。
其中,ε0为真空的介电常数。
所以,电容器充满电介质时,电容与未充满时的电容C0比较,即C/C0=ε/ε0。
所以,电容器电容是原来的ε/ε0倍。
2. 第二章:电荷的连续分布习题1:在距离线段中点为R的的P点,取出一个长度为l的小线段,小线段的位置如何改变时,该小线段对P点电势的贡献较大?解答:根据电场电势公式,P点电势由该小线段的电荷贡献决定。
即V=k(q/R),其中k为电场常量,q为该小线段的电荷量,R为该小线段到P点的距离。
所以,小线段对P点电势的贡献较大的情况是,当该小线段长度l较大且该小线段离P点的距离R较小的时候,即小线段越靠近P点且长度越大,对P点电势的贡献越大。
习题2:线电荷的线密度为λ,长度为L,P点到线电荷的距离为d。

精心整理第一章 静电场§1.1静电的基本现象和基本规律思考题:1、 给你两个金属球,装在可以搬动的绝缘支架上,试指出使这两个球带等量异号电荷的方向。
你可以用丝绸摩擦过的玻璃棒,但不使它和两球接触。
你所用的方法是否要求两球大小相等?答:先使两球接地使它们不带电,再绝缘后让两球接触,将用丝绸摩擦后带正电的玻璃棒靠近金属球一侧时,由于静电感应,靠近玻璃棒的球感应负电荷,较远的球感应等量的正电荷。
然后两球分开,再移去玻璃棒,两金属球分别带等量异号电荷。
本方法不要求两球大小相等。
因为它们本来不带电,根据电荷守恒定律,由于静电感应而带电时,无论两球大小是否相等,其总电荷仍应为零,2、答:3、 §1.2思考题:1、 2、 荷量q0答:q03、 4、 答:由对称性可知,圆环中心处电场强度为零。
轴线上场强方向沿轴线。
当带电为正时,沿轴线向外;当带电为负时,沿轴线向内,-----------------------------------------------------------------------------------------------------------§1.3高斯定理思考题:1、 一般地说,电力线代表点电荷在电场中运动的轨迹吗?为什么?答:一般情况下,电力线不代表点电荷在电场中运动的轨迹。
因为电力线一般是曲线,若电荷沿电力线作曲线运动,应有法向力存在;但电力线上各点场强只沿切线方向,运动电荷必定偏离弯曲的电力线。
仅当电力线是直线,且不考虑重力影响时,初速度为零的点电荷才能沿着电力线运动。
若考虑重力影响时,静止的点电荷只能沿竖直方向电力线运动。
2、 空间里的电力线为什么不相交?答:电力线上任一点的切线方向即为该点场强方向。
如果空间某点有几条电力线相交,过交点对每条电力线都可作一条切线,则交点处的场强方向不唯一,这与电场中任一点场强有确定方向相矛盾。
3、一个点电荷q放在球形高斯面的中心处,试问在下列情况下,穿过这高斯面的电通量是否改变?(1)如果第二个点电荷放在高斯球面外附近;(2)如果第二个点电荷放在高斯球面内;(3)如果将原来的点电荷移离了高斯球面的球心,但仍在高斯球面内。

第一章静电场§静电的基本现象和基本规律思考题:1、给你两个金属球,装在可以搬动的绝缘支架上,试指出使这两个球带等量异号电荷的方向。
你可以用丝绸摩擦过的玻璃棒,但不使它和两球接触。
你所用的方法是否要求两球大小相等?答:先使两球接地使它们不带电,再绝缘后让两球接触,将用丝绸摩擦后带正电的玻璃棒靠近金属球一侧时,由于静电感应,靠近玻璃棒的球感应负电荷,较远的球感应等量的正电荷。
然后两球分开,再移去玻璃棒,两金属球分别带等量异号电荷。
本方法不要求两球大小相等。
因为它们本来不带电,根据电荷守恒定律,由于静电感应而带电时,无论两球大小是否相等,其总电荷仍应为零,故所带电量必定等量异号。
2、带电棒吸引干燥软木屑,木屑接触到棒以后,往往又剧烈地跳离此棒。
试解释之。
答:在带电棒的非均匀电场中,木屑中的电偶极子极化出现束缚电荷,故受带电棒吸引。
但接触棒后往往带上同种电荷而相互排斥。
3、用手握铜棒与丝绸摩擦,铜棒不能带电。
戴上橡皮手套,握着铜棒和丝绸摩擦,铜棒就会带电。
为什么两种情况有不同结果?答:人体是导体。
当手直接握铜棒时,摩擦过程中产生的电荷通过人体流入大地,不能保持电荷。
戴上橡皮手套,铜棒与人手绝缘,电荷不会流走,所以铜棒带电。
--------------------------------------------------------------------------------------------------------------------- §电场电场强度思考题:1、在地球表面上通常有一竖直方向的电场,电子在此电场中受到一个向上的力,电场强度的方向朝上还是朝下?答:电子受力方向与电场强度方向相反,因此电场强度方向朝下。
2、在一个带正电的大导体附近P点放置一个试探点电荷q0(q0>0),实际测得它受力F。
若考虑到电荷量q0不是足够小的,则F/ q0比P点的场强E大还是小?若大导体带负电,情况如何?答:q0不是足够小时,会影响大导体球上电荷的分布。
前言:专门感激质心教育的题库与解析,和“程稼夫力学、电磁学习题答案详解”的作者先辈和血色の寂宁先辈的资料.1-1设两个小球所带净电荷为q,距离为l,由库仑定律:由题目,设小球质量m,铜的摩尔质量M,那么有:算得1-2 取一小段电荷,其对应的圆心角为dθ:这一小段电荷受力平稳,列竖直方向平稳方程,设张力增量为T:解得1-3(1)设地月距离R,电场力和万有引力抵消:解得:(2)地球分到,月球分到,电场力和万有引力抵消:解得:1-4设向上位移为x,那么有:结合牛顿第二定律和略去高次项有:1-5由于电荷受二力而平稳,故三个电荷共线且q3在q1和q2之间:先由库仑定律写出静电力标量式:有几何关系:联立解得由库仑定律矢量式得:解得1-6(1)对一个正电荷,受力平稳:解得,显然不可能同时知足负电荷的平稳(2)对一个负电荷,合外力提供向心力:解得1-7(1)设P限制在沿X轴夹角为θ的,过原点的直线上运动(θ∈[0,π)),沿着滑腻直线位移x,势能:对势能求导取得受力:小量近似,略去高阶量:当q>0时,;当q<0时,(2)由上知1-8设q位移x,势能:对势能求导取得受力:小量展开有:,知1-9(1)对q受力平稳,设其横坐标的值为l0:,解得设它在平稳位置移动一个小位移x,有:小量展开化简有:受力指向平稳位置,微小谐振周期(2)1-101-11先证明,如下图,带相同线电荷密度λ的圆弧2和直线1在OO处产生的电场强度相等.取和θ.有:显然两个电场强度相等,由于每一对微元都相等,因此整体产生的电场相等.利用这一引理,可知题文中三角形在内心处产生的电场等价于三角形内切圆环在内心处产生的电场.由对称性,这一电场强度大小为0.1-12(1)如图,取θ和,设线电荷密度λ,有:积分得(3)用圆心在场点处,半径,电荷线密度与直线段相等的,张角为θ0 ()的一段圆弧替代直线段,计算这段带电圆弧产生的场壮大小,能够用其所张角对应的弦长与圆弧上单位长度所产生的电场强度大小的积求得:1-13咱们先分析一个电荷密度为ρ,厚度为x的无穷大带电面(图中只画出有限大),取如下图高斯面,其中高斯面的两个相对面平行于电荷平面,面积为S,由高斯定理:算得,发觉那个无穷大平面在外部产生的电场是匀强电场,且左右两边电场强度相同,大小相反.回到原题,由叠加原理和,算得在不存在电荷的区域电场强度为0(正负电荷层彼此抵消.)在存在电荷的区域,假设在p区,现在x处的电场由三个电荷层叠加而成,别离是左侧的n区,0到x范围内的p区,和右边的p区,有:,算得同理算出n区时场强,综上可得1-14(1)取半径为r的球形高斯面,有:,解得(2)设球心为O1,空腔中心为O2,空腔中充满着电荷密度为−ρ的电荷,在空腔中任意一点A处产生的电场为:(借助第一问结论)同时在A处还有一个电荷密度为+ρ那么有:1-15取金属球上一面元d S,此面元在金属球内侧产生指向内的电场强度,由于导体内部电场处处为0,因此金属球上除该面元外的其他电荷在该面元处产生的电场强度为因此该面元受到其他电荷施加的静电力:球面上单位面积受力大小:半球面受到的静电力可用与其电荷面密度相等的,该半球面的截口圆面的面积乘该半球面的单位面积受力求得:1-16设轴线上一点到环心距离为x,有:令其对x导数为0:解得1-17写出初态体系总电势能:1-18系统静电势能大小为:1-19由对称性,能够以为四个面别离在中心处产生的电势,故取走后,;设BCD,ACD,ABD在P2处产生的电势为U,而ABD在P2处产生的电势为,有:;取走后:,解得1-20构造如下六个带电正方体(1到6号),它们的各面电荷散布彼此不相同,但都能通过必然的旋转从而与其它正方体形成全等:将这六个正方体形成的电场和其上的电荷全数叠加,形成一个新的带电正方体(由于是假想叠加,叠加进程中电荷直接相加而不从头散布).那个带电正方体各面电势完全相同,都为.容易证明,正方体内部的每一个点的电势也都为(假设不然,正方体内部必存在电场线,如此的电场线必然会凭空产生,或凭空消失,或形成环状,都与静电场原理不符).故现在中心电势一样为1-21 O4处电势:O1处电势:故电势差为:1-22从对称性方面考虑,先将半球面补全为整个球面.再由电势叠加原理,即一个半球面产生的电势为它的一半,从而计算出半球面在底面上的电势散布.即1-23设上极板下版面面电荷密度为,下极板上版面面电荷密度为.取一个长方体型的高斯面,其形状是是两极板中间距离的长方体,而且把和囊括进去.注意到金属导体内部没有电场,故那个高斯面电通量为0,其中净电荷为0,有:再注意到上下极板电势相等,其中E1方向向上,E2方向向下:再由高斯定理得出的结论:解得1-24先把半圆补成整圆,补后P、Q和O.这说明,新补上的半圆对P产生的电势为,而由于对称性,那个电势恰好也是半球面ACB对Q产生的电势.故:1-25在水平方向上,设质点质量m,电量为q:运动学:整体带入得:1-26(1)先将半球面补全为整个球面,容易计算出现在半球底面的电势.再注意到那个电势由对称的两个半球面产生的电势叠加取得,即一个半球面产生的电势为它的一半,即可求出一个半球面对底面产生的电势恒为定值,故底面为等势面,由E点缓慢移至A点外力做功为W1=0.(2)由上一问的分析知由E点缓慢移至O点外力不做功,记电势能为E,E的右下标表示所代表的点,那么有:仍然将半球面补为整球面,现在q在球壳内部任意一点电势能为2EO.现在关于T点,其电势能为上下两个球面叠加产生,由对称性,有:综上有W2=−W.1-27小球受电场力方程:将a 与g 合成为一个等效的g′:方向与竖直夹角再将加速度分解到垂直于g′和平行与g′的方向上.注意到与g′平行的分量最小为0,而垂直的分量那么维持不变,故速度的最小值为垂直分量:1-28假设给外球壳带上电量q2,先考虑q2在内外表面各散布了多少.取一个之内球壳外表面和外球壳内表面为边界的高斯面,并把内球壳外表面和外球壳内表面上的电荷囊括进去,真正的高斯面边界在金属内部.由于金属内部无电场,高斯面电通量为0,高斯面内电荷总量为0,取得外球壳内表面散布了−q1电荷,外表面散布了q2+q1电荷.由电势叠加原理知球心处的电势:解得由电势叠加原理及静电屏蔽:1-29设质点初速度为v0,质量为m ,加速度为a ,有:,其中.设时竖直向下速度为v1,动能为Ek1,初动能为Ek0,有:解得1-30球1依次与球2、球3接触后,电量别离为. 当球1、4接触时知足由于解得.注:假设此处利用,略去二阶小量那么能够大大简便计算,成心思的是,算出的答案与笔者考虑二阶小量繁重化简事后所得结果完全一致,这是因为在最后的表达式中没有r 与a 的和或差的项的缘故。


电磁学第二版答案第一章:电磁场的基本概念和电场定律1.问题:什么是电磁场?电磁场与电荷的关系是什么?答案:电磁场是由电荷产生的一种物质性质,可以通过施加力量或引力相互作用的方式来描述。
电磁场与电荷之间通过电场和磁场来相互作用。
电荷产生的电场是电力线从正电荷指向负电荷的线,而磁场则是呈环状绕着电流或磁体产生的。
2.问题:什么是库仑定律?请描述其数学形式。
答案:库仑定律是描述电荷之间相互作用力的定律。
其数学形式可以表示为:$F = k \\frac{Q_1Q_2}{r^2}$其中,F表示电荷之间的力,Q1和Q2分别表示两个电荷,r表示两个电荷之间的距离,k为库仑常数。
3.问题:什么是电场强度?电场强度的计算公式是什么?答案:电场强度表示单位正电荷在某点上受到的力,是描述电场场强性质的物理量。
其计算公式可以表示为:$E = \\frac{F}{q}$其中,E表示电场强度,F表示力,q表示测试电荷。
4.问题:什么是高斯定律?请描述其数学形式。
答案:高斯定律描述了电场与电荷之间的关系。
其数学形式可以表示为:$\\phi_E = \\frac{Q}{\\varepsilon_0}$其中,$\\phi_E$表示电场的通量,Q表示电荷量,$\\varepsilon_0$为真空介电常数。
第二章:静电场1.问题:什么是电势能?请描述其计算公式。
答案:电势能是指电荷在电场中的位置所具有的能量。
其计算公式为:PE=qV其中,PE表示电势能,q表示电荷量,V表示电势。
2.问题:什么是电势?请描述其计算公式。
答案:电势是描述电场中某一点电能状态的物理量。
其计算公式为:$V = \\frac{U}{q}$其中,V表示电势,U表示电势能,q表示电荷量。
3.问题:什么是电容器?请描述电容器的分类。
答案:电容器是储存电荷的装置,由两个导体之间的绝缘介质(电介质)隔开。
电容器根据结构和工作方式的不同,可以分为电容电器和分布式电容器两种类型。

第一章静电场§1.1 静电的基本现象和基本规律思考题:1、给你两个金属球,装在可以搬动的绝缘支架上,试指出使这两个球带等量异号电荷的方向。
你可以用丝绸摩擦过的玻璃棒,但不使它和两球接触。
你所用的方法是否要求两球大小相等?答:先使两球接地使它们不带电,再绝缘后让两球接触,将用丝绸摩擦后带正电的玻璃棒靠近金属球一侧时,由于静电感应,靠近玻璃棒的球感应负电荷,较远的球感应等量的正电荷。
然后两球分开,再移去玻璃棒,两金属球分别带等量异号电荷。
本方法不要求两球大小相等。
因为它们本来不带电,根据电荷守恒定律,由于静电感应而带电时,无论两球大小是否相等,其总电荷仍应为零,故所带电量必定等量异号。
2、带电棒吸引干燥软木屑,木屑接触到棒以后,往往又剧烈地跳离此棒。
试解释之。
答:在带电棒的非均匀电场中,木屑中的电偶极子极化出现束缚电荷,故受带电棒吸引。
但接触棒后往往带上同种电荷而相互排斥。
3、用手握铜棒与丝绸摩擦,铜棒不能带电。
戴上橡皮手套,握着铜棒和丝绸摩擦,铜棒就会带电。
为什么两种情况有不同结果?答:人体是导体。
当手直接握铜棒时,摩擦过程中产生的电荷通过人体流入大地,不能保持电荷。
戴上橡皮手套,铜棒与人手绝缘,电荷不会流走,所以铜棒带电。
计算题:1、真空中两个点电荷q1=1.0×10-10C,q2=1.0×10-11C,相距100mm,求q1受的力。
解:2、真空中两个点电荷q与Q,相距5.0mm,吸引力为40达因。
已知q=1.2×10-6C,求Q。
解:1达因=克·厘米/秒=10-5牛顿3、为了得到一库仑电量大小的概念,试计算两个都是一库仑的点电荷在真空中相距一米时的相互作用力和相距一千米时的相互作用力。
解:4、氢原子由一个质子(即氢原子核)和一个电子组成。
根据经典模型,在正常状态下,电子绕核作圆周运动,轨道半径是r=5.29×10-11m。
已知质子质量M=1.67×10-27kg,电子质量m=9.11×10-31kg。

电磁学第二版课后习题答案电磁学是物理学中的重要分支,研究电荷和电流的相互作用以及电磁场的产生和传播。
对于学习电磁学的学生来说,课后习题是巩固知识和提高能力的重要途径。
本文将对《电磁学第二版》课后习题进行一些解答和讨论,帮助读者更好地理解电磁学的概念和应用。
第一章:电荷和电场1. 问题:两个等量的正电荷之间的相互作用力是多少?答案:根据库仑定律,两个等量的正电荷之间的相互作用力等于它们之间的电荷量的平方乘以一个常数k,即F = kq1q2/r^2。
2. 问题:电场是什么?如何计算电场强度?答案:电场是指电荷周围的一种物理量,它描述了电荷对其他电荷的作用力。
电场强度E可以通过电场力F除以测试电荷q得到,即E = F/q。
第二章:静电场1. 问题:什么是电势能?如何计算电势能?答案:电势能是指电荷在电场中由于位置变化而具有的能量。
电势能可以通过电荷q乘以电势差V得到,即U = qV。
2. 问题:什么是电势差?如何计算电势差?答案:电势差是指单位正电荷从一个点移动到另一个点时所做的功。
电势差可以通过电场力F乘以移动距离d得到,即V = Fd。
第三章:电流和电阻1. 问题:什么是电流?如何计算电流?答案:电流是指单位时间内通过导体横截面的电荷量。
电流可以通过电荷量Q除以时间t得到,即I = Q/t。
2. 问题:什么是电阻?如何计算电阻?答案:电阻是指导体中电流流动受到的阻碍程度。
电阻可以通过电压V除以电流I得到,即R = V/I。
第四章:电路和电源1. 问题:什么是电路?如何计算电路中的电流和电压?答案:电路是指由电源、导线和电器元件组成的路径,用于电流的传输和电能的转换。
电路中的电流可以通过欧姆定律计算,即I = V/R,其中V为电压,R 为电阻。
2. 问题:什么是直流电源?什么是交流电源?答案:直流电源是指电流方向保持不变的电源,如电池。
交流电源是指电流方向周期性变化的电源,如交流发电机。
通过以上的解答和讨论,我们对电磁学的基本概念和计算方法有了更深入的了解。

第一章 习题一1、电量Q 相同的四个点电荷置于正方形的四个顶点上,0点为正方形中心,欲使每个顶点的电荷所受电场力为零,则应在0点放置一个电量q =-(1+2√2)Q/4 的点电荷。
2、在点电荷系的电场中,任一点的电场强度等于各点电荷单独在该点产生场强的矢量和,这称为电场强度叠加原理。
3、一点电荷电场中某点受到的电场力很大,则该点的电场强度E :( C )(A)一定很大 (B)一定很小 (C)可能大也可能小4、两个电量均为+q 的点电荷相距为2a ,O 为其连线的中点,求在其中垂线上场强具有极大值的点与O 点的距离R 。
解法一:22020214141aR qπεr q πεE E +=== 21E E E+=,θE θE θE E cos 2cos cos 121=+=2222042a R R a R q πε++=()2/32202a R R πεq +=E 有极值的条件是:()0222/522220=+-=a R R a πεq dR dE 即 0222=-R a ,解得极值点的位置为:a R 22=∵ ()2/722220223223a R a R πεqR dR E d +-=,而 0398402/222<-==aπεqdR E d a R ∴ 中垂线上场强具有极大值的点与O 点的距离为a R 22= 且 ()202/3220m a x 332/2/2aπεq a a a πεq E =+=解法二:θaq πεr q πεE E 2202021sin 4141===,21E E E +=+qθE θE θE E cos 2cos cos 121=+=θθaq πεcos sin 21220=)cos (cos 21320θθaq πε-=E 有极值的条件是:0)sin 3sin 2(2320=-=θθaπεq θd dE E 有极值时的θ满足:31cos 32sin 1cos 0sin 2211====θ,θ;θ,θ )cos 7cos 9(2)cos sin 9cos 2(232022022θθaπεq θθθa πεq θd E d -=-= 0)cos 7cos 9(22011320221>=-==aπεq θθa πεq θd E d θθ 032)cos 7cos 9(22022320222<-=-==aπεq θθa πεq θd E d θθ 可见 θ = θ2时,E 有极大值。

第一章静电场§静电的基本现象和基本规律思考题:1、给你两个金属球,装在可以搬动的绝缘支架上,试指出使这两个球带等量异号电荷的方向。
你可以用丝绸摩擦过的玻璃棒,但不使它和两球接触。
你所用的方法是否要求两球大小相等?答:先使两球接地使它们不带电,再绝缘后让两球接触,将用丝绸摩擦后带正电的玻璃棒靠近金属球一侧时,由于静电感应,靠近玻璃棒的球感应负电荷,较远的球感应等量的正电荷。
然后两球分开,再移去玻璃棒,两金属球分别带等量异号电荷。
本方法不要求两球大小相等。
因为它们本来不带电,根据电荷守恒定律,由于静电感应而带电时,无论两球大小是否相等,其总电荷仍应为零,故所带电量必定等量异号。
2、带电棒吸引干燥软木屑,木屑接触到棒以后,往往又剧烈地跳离此棒。
试解释之。
答:在带电棒的非均匀电场中,木屑中的电偶极子极化出现束缚电荷,故受带电棒吸引。
但接触棒后往往带上同种电荷而相互排斥。
3、用手握铜棒与丝绸摩擦,铜棒不能带电。
戴上橡皮手套,握着铜棒和丝绸摩擦,铜棒就会带电。
为什么两种情况有不同结果?答:人体是导体。
当手直接握铜棒时,摩擦过程中产生的电荷通过人体流入大地,不能保持电荷。
戴上橡皮手套,铜棒与人手绝缘,电荷不会流走,所以铜棒带电。
--------------------------------------------------------------------------------------------------------------------- §电场电场强度思考题:1、在地球表面上通常有一竖直方向的电场,电子在此电场中受到一个向上的力,电场强度的方向朝上还是朝下?答:电子受力方向与电场强度方向相反,因此电场强度方向朝下。
2、在一个带正电的大导体附近P点放置一个试探点电荷q0(q0>0),实际测得它受力F。
若考虑到电荷量q0不是足够小的,则F/ q0比P点的场强E大还是小?若大导体带负电,情况如何?答:q0不是足够小时,会影响大导体球上电荷的分布。
第一章静电场§1.1 静电的基本现象和基本规律思考题:1、给你两个金属球,装在可以搬动的绝缘支架上,试指出使这两个球带等量异号电荷的方向。
你可以用丝绸摩擦过的玻璃棒,但不使它和两球接触。
你所用的方法是否要求两球大小相等?答:先使两球接地使它们不带电,再绝缘后让两球接触,将用丝绸摩擦后带正电的玻璃棒靠近金属球一侧时,由于静电感应,靠近玻璃棒的球感应负电荷,较远的球感应等量的正电荷。
然后两球分开,再移去玻璃棒,两金属球分别带等量异号电荷。
本方法不要求两球大小相等。
因为它们本来不带电,根据电荷守恒定律,由于静电感应而带电时,无论两球大小是否相等,其总电荷仍应为零,故所带电量必定等量异号。
2、带电棒吸引干燥软木屑,木屑接触到棒以后,往往又剧烈地跳离此棒。
试解释之。
答:在带电棒的非均匀电场中,木屑中的电偶极子极化出现束缚电荷,故受带电棒吸引。
但接触棒后往往带上同种电荷而相互排斥。
3、用手握铜棒与丝绸摩擦,铜棒不能带电。
戴上橡皮手套,握着铜棒和丝绸摩擦,铜棒就会带电。
为什么两种情况有不同结果?答:人体是导体。
当手直接握铜棒时,摩擦过程中产生的电荷通过人体流入大地,不能保持电荷。
戴上橡皮手套,铜棒与人手绝缘,电荷不会流走,所以铜棒带电。
计算题:1、真空中两个点电荷q1=1.0×10-10C,q2=1.0×10-11C,相距100mm,求q1受的力。
解:2、真空中两个点电荷q与Q,相距5.0mm,吸引力为40达因。
已知q=1.2×10-6C,求Q。
解:1达因=克·厘米/秒=10-5牛顿3、为了得到一库仑电量大小的概念,试计算两个都是一库仑的点电荷在真空中相距一米时的相互作用力和相距一千米时的相互作用力。
解:4、氢原子由一个质子(即氢原子核)和一个电子组成。
根据经典模型,在正常状态下,电子绕核作圆周运动,轨道半径是r=5.29×10-11m。
已知质子质量M=1.67×10-27kg,电子质量m=9.11×10-31kg。
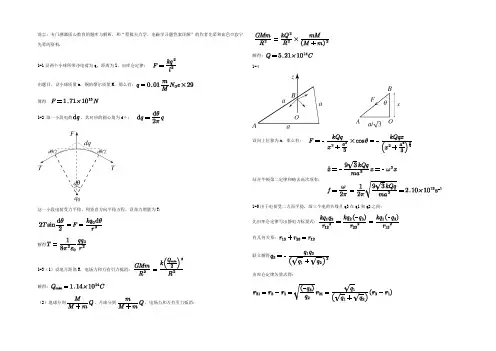
电磁学(赵凯华陈熙谋 ) 第二版课后答案1电磁学(赵凯华-陈熙谋-)--第二版-课后答案1第一章静电场§1.1静电的基本现象和基本规律计算题:1、真空中两个点电荷q1=1.0×10-10c,q2=1.0×10-11c,距离100mm,谋q1受到的力。
解:f?q1q2?10?9.0?10n(排斥力)24??0r12、真空中两个点电荷q与q,相距5.0mm,吸引力为40达因。
已知q=1.2×10-6c,求q。
求解:1超过因=克厘米/秒=10-5牛顿4??0r2fqqf??q93?10?13c24??0rq13、为了得到一库仑电量大小的概念,试计算两个都是一库仑的点电荷在真空中相距一米时的相互作用力和距离一千米时的相互作用力。
q1q2?9.0?109n(当r?1m)相当于90万吨物体的重量解:f34??0r29.0?10n(当r?1000m)相当于900kg物体的重量?14、氢原子由一个质子(即氢原子核)和一个电子组成。
根据经典模型,在正常状态下,电子拖核作圆周运动,轨道半径就是r=5.29×10-11m。
未知质子质量m=1.67×10-27kg,电子质量m=9.11×10-31kg。
电荷分别为e=±1.6×10-19c,万有引力常数g=6.67×10-11nm2/kg2。
(1)谋电子难以承受的库仑力;(2)库仑力就是万有引力的多少倍?(3)谋电子的速度。
e2?8(1)fe??8.22?10n(吸引力)4??0r21(2)fg?g解:m1m2?3.63?10?47n(吸引力)?fe/fg?2.26?10392re2?2.19?106m/s4??0mr1v21e2(3)m??v?2r4??0r由此可知,在原子范围内,与库仑力相比,万有引力完全可以略去不计5、卢瑟福实验证明:当两个原子核之间的距离小到10-15米时,它们之间的排斥力仍遵守库仑定律。