学员讲义

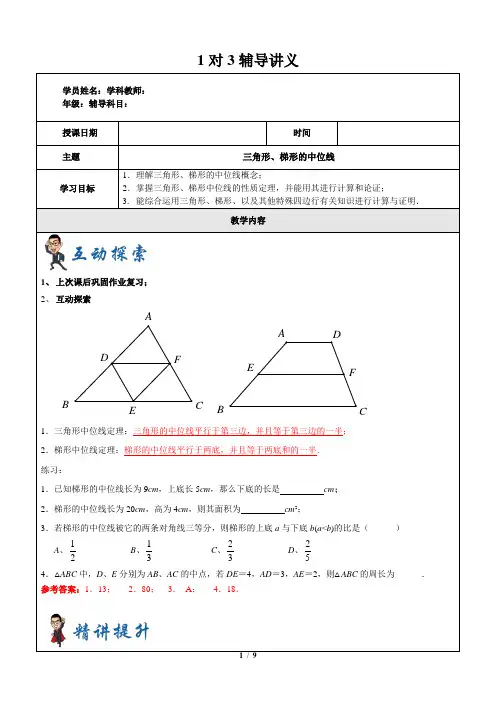
1对3辅导讲义学员姓名：学科教师： 年级：辅导科目： 授课日期时间主题三角形、梯形的中位线学习目标1．理解三角形、梯形的中位线概念；2．掌握三角形、梯形中位线的性质定理，并能用其进行计算和论证；3. 能综合运用三角形、梯形、以及其他特殊四边行有关知识进行计算与证明．教学内容1、 上次课后巩固作业复习；2、 互动探索1．三角形中位线定理：三角形的中位线平行于第三边，并且等于第三边的一半； 2．梯形中位线定理：梯形的中位线平行于两底，并且等于两底和的一半． 练习：1．已知梯形的中位线长为9cm ，上底长5cm ，那么下底的长是 cm ； 2．梯形的中位线长为20cm ，高为4cm ，则其面积为 cm ²；3．若梯形的中位线被它的两条对角线三等分，则梯形的上底a 与下底b (a <b )的比是（ ） A 、12 B 、13 C 、23 D 、254．△ABC 中，D 、E 分别为AB 、AC 的中点，若DE ＝4，AD ＝3，AE ＝2，则△ABC 的周长为______． 参考答案：1．13； 2．80； 3． A ； 4．18．EDFBCAEF AD BC【知识梳理1】三角形的中位线平行于第三边，并且等于第三边的一半 【例题精讲】例1：在梯形ABCD 中，EF 分别是对角线BD 和AC 的中点，求证：1()2EF BC AD =-参考答案：联结DF 并延长交BC 与G ，证明△ADF ≌△CGF ，再根据三角形中位线可得试一试：如图，梯形ABCD 中，AB ∥CD ，点E 、F 、G 分别是BD 、AC 、DC 的中点．已知两底的差是8，两 腰和是12，求△EFG 的周长。

参考答案：联结AE 并延长，交CD 于点H ．∵AB ∥CD ， ∴∠ABE ＝∠HDE ，∠EAB ＝∠EHD ， 又∵E 为BD 中点， ∴BE ＝DE ．∴△AEB ≌△HED ． ∴DH ＝AB ，AE ＝EH ． ∵F 为AC 中点； ∴EF ＝12HC ＝12 (CD —DH )＝ 12(CD —AB )＝4 ∵点E 、F 、G 分别是BD 、AC 、DC 的中点 ∴EG ＝12BC ， FG ＝12AD ； ∴EG+ FG ＝12(BC+AD )＝6 ∴△EFG 的周长为10例题2：问题1：我们把依次联结任意一个四边形各边中点得到的四边形叫做中点四边形．如图，在四边形ABCD 中，E 、F 、G 、H 分别是边AB 、BC 、CD 、DA 的中点，依次联结各边中点得到的中点四边形EFGH ．这个中点四边形EFGH 的形状为 ；说明理由．EFA DBC EFA D BCG FEB DCA H GFEB DCA问题2：将问题1中的四边形特殊化后，又能都到什么特殊的中点四边形？ 总结一下，完成下表：基础图形 顺次联结其各边中点所得的四边形 （在图中画出并指出四边形类型）平行四边形矩形菱形正方形梯形等腰梯形问题3：根据问题2的探究，请你总结中点四边形的形状由原四边形的什么决定的？参考答案：问题1：平行四边形； 证明：联结AC ，∵E 是AB 的中点，F 是BC 的中点， ∴EF ∥AC ，EF ＝12AC FGEHA BCDFGEHABCD同理：HG ∥AC ，HG ＝12AC ∴EF ∥HG ，EF ＝HG ， ∴四边形EFGH 是平行四边形． 问题2：略；问题3：中点四边形的形状是由原四边形对角线的数量和位置关系决定的，当原四边形对角线相等时为菱形，对角线垂直时为矩形，对角线相等且垂直时为正方形．例题3：如图，在△ABC 中，点D 是边BC 的中点，点E 在△ABC 内，AE 平分∠BAC 内，CE ⊥AE ，点F 在边AB 上，EF ∥BC ．（1）求证：四边形BDEF 是平行四边形；（2）线段BF 、AB 、AC 的数量之间具有怎样的关系？证明你所得到的结论．参考答案：（1）证明：延长CE 交AB 于点G ，∵AE ⊥CE ，∴∠AEG ＝∠AEC ＝90º，又∵∠GAE ＝∠CAE ，AE ＝AE ，∴△AGE ≌△ACE ． ∴GE ＝EC ．∵BD ＝CD ，∴DE //AB ．∵EF //BC ，∴四边形BDEF 是平行四边形．（2）解：∵四边形BDEF 是平行四边形，∴BF ＝DE ．∵D 、E 分别是BC 、GC 的中点，∴BG ＝2BF ＝2DE ． ∵△AGE ≌△ACE ，∴AG ＝AC ，∴2BF ＝AB –AG ＝AB –AC ．例题4：如图，在梯形ABCD 中，AB //CD ，AD ＝BC ，对角线AC 、BD 的交点O ，∠AOB ＝60°，又S 、P 、Q 分别是DO 、AO 、BC 的中点． 求证：△SPQ 是等边三角形．FEDBCAGFEDBCA参考答案：证明：联结CS ，BP ． ∵四边形ABCD 是等腰梯形，且AC 与BD 相交于O ， ∴可得出：△CAB ≌△DBA ， ∴∠CAB ＝∠DBA ， 同理可得出：∠ACD ＝∠BDC ，∴AO ＝BO ，CO ＝DO ． ∵∠AOB ＝60°， ∴△OCD 与△OAB 均为等边三角形． ∵S 是OD 的中点， ∴CS ⊥DO ．在Rt △BSC 中，Q 为BC 中点，SQ 是斜边BC 的中线，∴SQ ＝12BC ． 同理BP ⊥AC ． 在Rt △BPC 中，PQ ＝12BC ． 又∵SP 是△OAD 的中位线，∴SP ＝12AD ＝12BC ． ∴SP ＝PQ ＝SQ ．故△SPQ 为等边三角形※例题5：如图在△ABC 中，D 、E 分别为AB 、AC 上的点，且BD ＝CE ，M 、N 分别是BE 、CD 的中点．过 MN 的直线交AB 于P ，交AC 于Q ，线段AP 、AQ 相等吗？为什么？ 答案：AP ＝AQ ，理由：取BC 的中点H ，联结MH ，NH ． ∵M ，H 为BE ，BC 的中点，∴MH ∥EC ，且MH ＝12EC ．同理：NH ∥BD ，且NH ＝12BD ．∵BD ＝CE ，∴MH ＝NH ．∴∠HMN ＝∠HNM ； ∵MH ∥EC ，∴∠HMN ＝∠PQA ， 同理∠HNM ＝∠QP A ． ∴∠APQ ＝∠AQP ， ∴AP ＝AQ补充类试题：已知：如图，在四边形ABCD 中，AD ＝BC ，E 、F 分别是DC 、AB 边的中点，FE 的延长线分别与AD 、BCQPS OC DA BQPS OCDA BQPNMABCD E HQ PN MABCD E的延长线交于H 、G 点． 求证：∠AHF ＝∠BGF ．参考答案：联结AC ，取AC 的中点M ，再分别联结ME 、MF ， ∵E 、F 分别是DC 、AB 边的中点，∴ME ∥AD ， EM ＝12AD ， MF ∥BC ，MF ＝12BC ． ∵AD ＝BC ， ∴EM ＝MF ， ∴∠MEF ＝∠MFE ． ∵EM ∥AH ，∴∠MEF ＝∠AHF ∵FM ∥BG ，∴∠MFE ＝∠BGF ∴∠AHF ＝∠BGF1．若顺次联结四边形ABCD 各边的中点所得四边形是矩形，则四边形ABCD 一定是 的四边形； 2．如图，在梯形ABCD 中，已知AD //CB ，对角线AC ⊥BD ，且AC ＝5cm ，BD ＝12cm ，则梯形的中位线长 为 cm ；3．已知：如图，△ABC 中，D 是BC 边的中点，AE 平分∠BAC ，BE ⊥AE 于E 点，若AB ＝5，AC ＝7，求ED ．GH FEDABC MGH FE DABCDBCA4．如图，AD 平分∠BAC ，交BC 于点D ，过C 作AD 的垂线，交AD 的延长线于点E ，F 为BC 中点，联结EF ； 求证：EF //AB .参考答案：1．对角线垂直； 2．132； 3． ED ＝1，提示：延长BE ，交AC 于F 点； 4．提示：延长AB 和CE 交于G 点即可．【巩固练习】1．如图，梯形ABCD 中，E 、F 分别为腰AB 、CD 的中点，若 ∠ABC 和∠DCB 的平分线相交与线段EF 上的一点P ，当EF ＝3时，则梯形ABCD 的周长为 ；EDBCAD FEBCA2．等腰梯形的对角线互相垂直，若连接该等腰梯形各边中点，则所得图形是（ ） A 、平行四边形B 、矩形C 、菱形D 、正方形3．如图，在梯形ABCD 中，AD //BC ，E 、F 、M 分别为AB 、DC 、BC 的中点，且ME ＝ MF ． 求证：梯形ABCD 是等腰梯形．4．如图，已知BE 、CD 分别是△ABC 的角平分线，并且AE ⊥BE 于E 点，AD ⊥DC 于D 点． 求证：（1）DE ∥BC ；（2）DE ＝12(AB +AC −BC )．参考答案：1．12； 2．D ；3．联结AC ，BD ， ∵E 、F 、M 分别为AB 、DC 、BC 的中点， ∴EM ＝12AC ，MF ＝12BD ， ∵ME ＝ MF ， ∴AC ＝BD ， ∴梯形ABCD 是等腰梯形4．证明：（1）延长AD 、AE ，交BC 于F 、G ； ∵BE ⊥AG ， ∴∠AEB ＝∠BEG ＝90°；∵BE 平分∠ABG ，∴∠ABE ＝∠GBE ；∴∠BAE ＝∠BGE ； ∴△ABG 是等腰三角形；∴AB ＝BG ，即E 是AG 中点； 同理可得：D 是AF 中点； ∴DE 是△AFG 的中位线； ∴DE ∥BC ． （2）由（1）知DE 是△AFG 的中位线，∴DE ＝12FG ； PFE DBCA FEDMA BC FEDMABCED B CAGF ED BCA∵FG＝BG+CF-BC，且AB＝BG，AC＝CF；∴FG＝AB+AC-BC，即DE＝12（AB+AC-BC）【预习思考】1．菱形的两条对角线之比是2：3，面积是27，则两条对角线的长分别是和．2．如图，已知梯形ABCD的中位线为EF，且△AEF的面积为6cm2，则梯形ABCD的面积为（）A、12 cm2B、18 cm2C、24 cm2D、30 cm23．已知四边形ABCD是平行四边形，下列结论中不正确的是（）A、当AB＝BC时，它是菱形；B、当AC⊥BD时，它是菱形；C、当AC＝BD时，它是正方形；D、当∠ABC＝900时，它是矩形. 4．下列说法：①一组对边平行，另一组对边相等的四边形是平行四边形或等腰梯形。

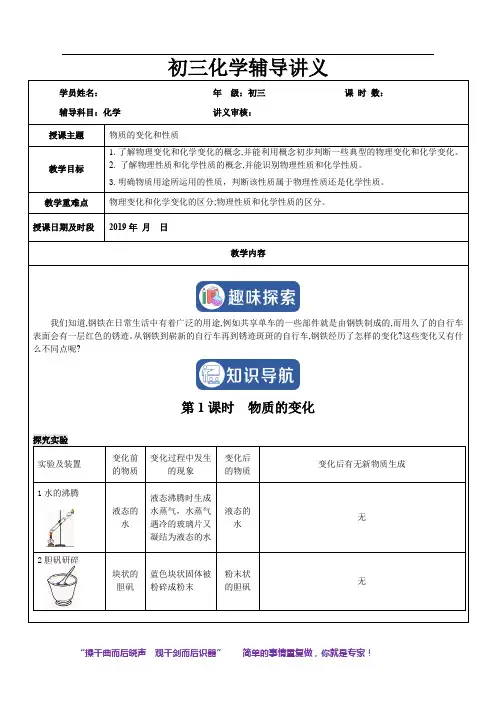
初三化学辅导讲义学员姓名：年级：初三课时数：辅导科目：化学讲义审核：授课主题物质的变化和性质教学目标1.了解物理变化和化学变化的概念,并能利用概念初步判断一些典型的物理变化和化学变化。

2. 了解物理性质和化学性质的概念,并能识别物理性质和化学性质。

3.明确物质用途所运用的性质，判断该性质属于物理性质还是化学性质。

教学重难点物理变化和化学变化的区分;物理性质和化学性质的区分。

授课日期及时段2019年月日教学内容我们知道,钢铁在日常生活中有着广泛的用途,例如共享单车的一些部件就是由钢铁制成的,而用久了的自行车表面会有一层红色的锈迹。

从钢铁到崭新的自行车再到锈迹斑斑的自行车,钢铁经历了怎样的变化?这些变化又有什么不同点呢?第1课时物质的变化探究实验实验及装置变化前的物质变化过程中发生的现象变化后的物质变化后有无新物质生成1水的沸腾液态的水液态沸腾时生成水蒸气，水蒸气遇冷的玻璃片又凝结为液态的水液态的水无2胆矾研碎块状的胆矾蓝色块状固体被粉碎成粉末粉末状的胆矾无3胆矾溶液和氢氧化钠溶液反应蓝色的硫酸铜溶液等立即生成蓝色沉淀，溶液颜色变浅，最后变为无色蓝色的氢氧化铜沉淀等有4石灰石和盐酸反应颗粒状石灰石等石灰石表面有气泡产生，且石灰石逐渐变小，烧杯中澄清石灰水变浑浊二氧化碳气体等有课堂讨论归纳总结 物理变化化学变化定义 没有生成新物质的变化（如实验1、2） 有新物质生成的变化，又叫化学反应（如实验3、4） 现象只是物质的状态、形状、大小发生改变，也可能有发光、放热等现象发生在变化过程中常伴随有发光、放热、变色、放出气体、产生沉淀等现象发生 实例水结成冰、石蜡熔化、灯泡发光、海水晒盐、碘升华等铁生锈、物质的燃烧、烧制瓷器、冶炼金属、呼吸作用、食物腐败、酒、醋的酿造等 本质区别 （判断依据） 变化过程中是否有新物质生成。

联系在物质发生化学变化的过程中，同时发生物理变化；但在发生物理变化的过程中，不一定会同时发生化学变化。

学车科目一培训讲义科目一培训讲义第一章概述一、培训内容：1、道路交通信号及其含义：（1）道路交通信号的概念；（2）组成部分：交通信号灯、交通标志、交通标线、交通警察手势信号；2、道路交通安全法律、法规和规章：（1）法律、法规出处；（2）通行原则及条件；（3）灯光的使用；（4）机动车管理；（5）机动车驾驶证管理；（6）违章处罚；（7）交通事故的处理及理赔；3、汽车构造、安全行车及文明驾驶、应急处理等知识：（1）汽车构造；（2）安全及文明驾驶；（3）应急处理常识；二、培训对象：科目一阶段学员。

会车让行会车先行双向通行靠左侧道路通行左侧绕行左侧通行最高限速最低限速解除限制速度注意行人注意儿童人行横道步行3、交通标线：按属性分为指示、警告、禁止标线3种，关键在于实线和虚线的把握。

实线:（严禁压线变道或超车）。

虚线：（可以压线变道或超车，但不能长时间压线行驶）。

虚实线：（虚线一侧准许越线超车或向左转弯，实现一侧严禁压线）。

需关注的交通标线：导向箭头减速让行线停车让行线禁止掉头（直行车辆被放行时，左转弯车辆可以进入待转区等候）机动车禁止在网状线内停留，防止交通拥堵禁止临时或长时停放车辆禁止长时停放车辆禁止临时停车的简化网状要领：（1）站位（4个）：决定指挥对象；（2）手势（8个）：代表具体内容；（以上3个手势指挥对象为正面所对车辆）直行信号减速慢行信号右转弯信号（以上3个手势指挥对象为右侧所对车辆）左转弯信号左转弯待转信号（以上2个手势指挥对象为左侧所对车辆）第三章道路交通安全法律、法规和规章一、法规出处：《中华人民共和国道路交通安全法》，所有道路交通参与者必须遵守，违反道路交通安全法律、法规关于道路通行规定的行为，属于违法行为。

二、通行原则及条件：驾驶机动车必须遵守右侧通行的原则；道路划分机动车道、非机动车道和人行道的，实行分道行驶；在没有划分机动车道、非机动车道和人行道的道路，机动车在道路中间行驶，非机动车和行人在两侧通行。

国际贸易理论与实务培训讲义第一部分：国际贸易理论概述1.1 国际贸易的定义国际贸易是指各国之间进行商品和服务的交流、买卖以及相关金融、技术、劳务等方面的交流。

1.2 国际贸易的意义国际贸易有助于优化资源配置，提高生产效率，促进经济发展，增加就业机会，促进国际关系和文化交流等。

1.3 国际贸易的形式国际贸易可以通过货物贸易、服务贸易、技术贸易、劳务贸易等形式进行。

第二部分：国际贸易的理论基础2.1 绝对优势理论由亚当·斯密提出，认为各国应专注于生产自己具有绝对优势的产品，然后通过国际贸易来获取其他产品。

2.2 比较优势理论由大卫·李嘉图提出，认为各国应专注于生产自己相对于其他国家具有比较优势的产品，从而提高整体效率。

2.3 因素禀赋理论由何苏恒提出，认为各国因其禀赋的资源差异而形成相对优势，从而决定了贸易模式和贸易方向。

2.4 国际贸易理论的发展除了以上几种经典理论外，还有新贸易理论、战略贸易理论、服务贸易理论等不断涌现的理论，为国际贸易的实践提供了更多的参考和解释。

第三部分：国际贸易的实务操作3.1 贸易政策和障碍各国采取不同的贸易政策和贸易壁垒，如关税、配额、禁止措施等，对国际贸易产生了一定的影响。

3.2 贸易促进措施为了促进国际贸易的发展，各国可以采取积极的贸易促进政策，如降低关税、取消配额、签订自由贸易协议等。

3.3 贸易协定和组织各国可以通过签订贸易协定和参加国际贸易组织来加强贸易合作和解决贸易纠纷，如世界贸易组织（WTO）、自由贸易区（FTA）等。

3.4 贸易融资和支付国际贸易涉及到跨国支付和融资问题，各国可以通过各种方式解决，如信用证、跨境支付、外汇市场等。

第四部分：国际贸易的案例分析4.1 汇率变动对国际贸易的影响汇率的波动对国际贸易有直接的影响，通过案例分析可以了解不同汇率变动情况下的贸易效果。

4.2 贸易摩擦和争端的解决国际贸易中经常发生贸易摩擦和争端，通过案例分析可以了解各种争端解决机制和效果。

学科教师辅导讲义学员编号:年级：课时数:3 学员姓名: 辅导科目:英语学科教师：课题授课时间教学目标1。

能正确听，说,读,写字母Aa Bb Cc Dd Ee 。

2.培养学生良好的朗读和书写习惯，要求读音正确，书写规范. 3。

会唱字母歌ABCsong.教学内容上节课回顾(此部分由老师们按照自己学生的进度添加，第一次课没有则不用添加）新课导入(此部分由老师们按照自己学生特点添加)模块学习（添加本次课上课的内容）Step1 Warm up教师首先说明英语单词是由26个字母组成，并且有大小写之分。

英语字母有多种不同的文字，每个字体中的字母书写方式不一样，让学生认识四线格，知道每个英语字母在四线格中占有固定的位置。

Step2 Presentation利用字母卡片，教授字母Aa,让学生注意读音，认真看口型,大写A三笔，占上下两格.小写a一笔。

占中间一行。

字母Bb,大写两笔，占一二两格，小写中间一格。

字母C的大写及d的小写都是一笔完成,大写D两笔完成。

Step3 Practice教完字母后,可让学生在练习本上进行书写练习，教师要注意指导学生正确的书写。

Step4 Consolidation字母配对游戏1、把新授字母的大小写分别写在卡片上，发给学生，然后教师或学生说出新授字母中的任意一个拿到该字母大小写的学生到讲台上来配对找朋友,并正确读出这个字母.Step5学生听录音，跟唱字母歌课堂总结1、请回顾本节课所讲的重点知识。

2、请把存在疑惑的地方提出来.过关小测试考试时间：分钟（根据学生情况进行限时测试)得分：回家作业。

机车工作计划一、机务部门与运输部门的关系整个铁路是一部联动机，机务部门必须与其他部门紧密配合，协调一致才能完成铁路运输生产任务。

在机车的日常运用中，机务部门同运输部门的关系尤为密切。

一是机车出入段或在车站停留，受车站调度或值班员指挥；二是机车在牵引列车的区段上，受列车调度员指挥；三是机务指标靠运输部门来完成。

二、机务简介机车是铁路运输的牵引动力设备，是完成铁路运输任务的基础设备之一。

铁道部机车管理工作由铁道部运输局装备部负责，它是全国机务系统的最高领导部门。

铁路局机车管理工作由机务处负责。

机务处下设机务运用、检修、设备科等业务科，分管相应的有关机车业务。

机务段是机务沿线生产单位，是机车管理工作的基层组织，按照其担当的运输生产任务、机车交路、机车检修任务及设备规模，可分为机务本段、机务折返段、机务折返点。

机务本段简称机务段，它配属有一定数量的干线机车和调机，有一整套的机车运转整备设备和一定能力的检修设备，担当一定区段内的列车牵引作业和编组站、区段站及沿线较大的中间站的调车作业，负责机车的运转整备作业和日常保养工作，担当一定的机车检修任务。

如：西安、新丰镇、安康、延安北机务段。

机务折返段，由机务段领导，一般不配属机车，仅担当本段或其他机务段折返机车的整备作业并组织乘务员正常休息。

如：华山、韩城、瑶曲、铜川南折返段。

机务折返点，又称机务整备所，它是为担当补机、调机、小运转机车的部分整备作业而设臵的，机车在折返点为等待工作仅作较短时间的停留。

如：咸阳机务整备所。

此外，为了及时处理铁路交通事故，起复机车车辆，各机务段均配属有救援列车。

一旦发生事故，救援列车可迅速出动，开通线路，恢复正常行车。

三、有关机车的基本概念1.机车分类⑴按牵引力类型分为内燃机车（DF系列）和电力机车（SS系列、HX、进口机车）。

⑵按归属权限分为配属机车和非配属机车配属机车：根据铁道部配属命令、拨交铁路局（包括自购）及机务段保管、使用，涂有局、段标志，并在资产台帐内登记的机车。

只 要 努 力 就 会 成 功 ， 加 油 ！ ① 学员姓名： 辅导课目：科学 年级：八年级 学科教师：汪老师授课日期及时段课 题 第一章《生活中的水》——水的密度学习目标1、知道如何测量固体和液体的密度2、知道密度与体积、质量之间的关系教学内容 第一章《生活中的水》——水的密度一、密 度1、定义：在物理学中，把某种物质单位体积的质量叫做这种物质的密度2、公式：密度 = 体积质量 即ρ=V m3、密度的单位：千克/米3(Kg/m 3)，克/厘米3(g/cm 3)4、密度单位的读法：千克/米3 读作：“千克每立方米；克/厘米3读作：“克每立方厘米”5、密度单位的换算关系：1g/cm 3 = 103kg/m 3， 1kg/m 3 = 10-3g/cm 36、密度的含义：① 每种物质都有它一定的密度，对同种物质来说，它的质量与体积成正比，两者的比值是一个定值 同种物质的密度与质量、体积的大小无关，密度是物质的一种特性② 不同的物质，其密度一般不同． ③ 密度与物质的种类有关，与物质的状态也有关．7、一些常见固体、液体和气体的密度见教材 注意:查密度表可知（1）铜、铁、铝的密度大小关系为ρ铜＞ρ铁 ＞ρ铝还要知道水，酒精，各种油，酱油，海水相互之间的密度比较（2）水的密度为1.0×103㎏/m 3,那么一桶水的密度是1.0×103㎏/m 3,一滴水的密度是1.0×103㎏/m 3,冰的密度为0.9×103㎏/m 3，冰的密度小于水的密度（3）固体中金属的密度大，水银虽然是液体但它是金属，所以密度也大，气体的密度小．8、密度的物理意义：水的密度为1.0×103㎏/m 3，它表示每1立方米的水的质量是1.0×103㎏【例题】:1、铅的密度是11.3 ×103千克/米3, 它所表示的意义是（ ）A. 每立方米铅的密度为11.3×103千克B. 每立方米铅的质量为11.3 ×103千克/米C. 每立方米铅的质量为11.3×103千克D. 每千克铅的体积为11.3 ×103米3只 要 努 力 就 会 成 功 ， 加 油 ！ ②【练习】：【09台州期末】甲物质密度为2.5t/m 3,乙物质密度为2.5kg/dm 3，丙物质密度为2.5g/cm 3，丁物质的密度为250kg/m 3。

初三化学辅导讲义5 学员姓名：年级：初三课时数：辅导科目：化学讲义审核：授课主题氧气教学目标1.掌握氧气的物理性质和化学性质以及常见的用途2.掌握常见物质在空气和氧气中的燃烧现象3.认识基本反应类型之一化合反应和氧化反应教学重难点常见物质在空气和氧气中的燃烧现象授课日期及时段2019年月日教学内容水里的鱼为什么能活着氧气的性质一.氧气的物理性质通常情况下，氧气是无色无味的气体；密度略大于空气；不易溶于水；思考氧气密度大于空气，集满氧气的集气瓶应该如何放置呢？答：玻璃分为光面和毛面，集气瓶正方在桌上，玻璃片毛面向下氧气不易溶于水，在水里是没有氧气的，对吗？你判断的理由是什么？答：不对，水中的鱼能生存二、氧气的化学性质氧气化学性质比较活泼。

氧气具有助燃性和氧化性。

氧气的检验方法：把一根______________伸入集气瓶中，如果带火星的木条________，证明是氧气。

化学性质要通过_化学反应_来表现，因而，观察化学实验很重要，回忆之前所学，要如何观察？观察时要注意哪【注意事项】①用砂纸把细铁丝磨成光亮的银白色，是为了除去细铁丝表面的杂质。

②将细铁丝盘成螺旋状，是为了_______________________。

③把细铁丝绕在火柴上，是为了引燃细铁丝，使细铁丝的温度达到着火点。

④待火柴快燃尽时才缓慢插入盛有氧气的集气瓶中，是为了防止___________________，保证有充足的氧气与细铁丝反应。

⑤由上向下缓慢伸进盛有氧气的集气瓶中是为了防止细铁丝燃烧时放热使氧气从集气瓶口逸出，保证有充足的氧气与细铁丝反应。

⑥集气瓶里要预先装少量水或在瓶底铺上一薄层细沙，是为了______________________四化合反应和分解反应1.化合反应：由两种或两种以上物质生成另一种物质的反应。

2.分解反应：由一种反应物生成两种或两种以上其他物质的反应叫做分解反应。

化合反应的特点是“多变一”，分解反应的特点是“一变多”。

一对一教师辅导讲义学员编号：年级：六课时次数（日期）：学员姓名：辅导科目：数学学科教师：课题六上第一单元《圆》第三课时——圆的面积授课时间：备课时间：教学目标1、复习圆的面积的相关含义，经历圆面积计算公式的推导过程，掌握圆面积计算公式。

2、熟练掌握圆和圆环面积的计算公式，能用圆的面积计算公式解决实际问题。

3、经历运用圆的有关知识计算所走弯道距离的过程，了解“跑道的弯道的部分，外圈比内圈要长”。

教学内容（包括知识点、典型例题、课后作业）知识点巩固1、圆的面积：圆所占面积的大小叫圆的面积。

2．把一个圆割成一个近似的长方形，割拼成的长方形的长相当于圆周长的一半，用字母（πr）表示，宽相当于圆的半径，用字母（r）表示，因为长方形的面积=长×宽，所以圆的面积= πr×r。

圆的面积公式：Ｓ＝πｒ²。

3．圆的面积公式：Ｓ＝πｒ²或者S=π（d÷2）²或者S=π（C÷π÷2）²4．在一个正方形里画一个最大的圆，圆的直径等于正方形的边长。

5．在一个长方形里画一个最大的圆，圆的直径等于长方形的宽。

6．一个环形，外圆的半径是R，内圆的半径是r，它的面积是S=πR²－πｒ²或S=π（R²－ｒ²）。

（其中R＝r＋环的宽度．）7．半圆的周长等于圆的周长的一半加直径。

半圆的周长与圆周长的一半的区别在于，半圆有直径，而圆周长的一半没有直径。

半圆的周长公式：Ｃ＝πd÷2＋d或Ｃ＝πr＋2r圆周长的一半=πr8．半圆面积＝圆的面积÷2公式为：Ｓ＝πｒ²÷29．在同一个圆里，半径扩大或缩小多少倍，直径和周长也扩大或缩小相同的倍数。

而面积扩大或缩小以上倍数的平方倍。

例如：在同一个圆里，半径扩大４倍，那么直径和周长就都扩大４倍，而面积扩大１６倍。

10、25．当长方形，正方形，圆的周长相等时，圆的面积最大，长方形的面积最小圆的面积公式推导1、半圆是（）图形，它有（）对称轴。

三角函数讲义的周期相等，则4.（1）要得到函数sin y x =的图象，只需将函数cos y x π⎛⎫=- ⎪3⎝⎭的图象向 平移 个单位5.已知函数)0,)(4sin()(>∈+=w R x wx x f π的最小正周期为π，将)(x f y =的图像向左平移||ϕ个单位长度，所得图像关于y 轴对称，则ϕ的一个值是 （ ）A 2π B 83π C 4πD 8π6.将函数 y = 3 cos x －sin x 的图象向左平移 m （m > 0）个单位，所得到的图象关于y 轴对称，则 m 的最小正值是 （ ）A. π6B. π3 C. 2π3D. 5π67.函数f (x )=cos x (x )(x ∈R)的图象按向量(m,0) 平移后，得到函数y =-f ′(x )的图象，则m 的值可以为 ( )A.2πB.πC.－πD.－2π8．将函数y=f （x ）sinx 的图象向右平移4π个单位，再作关于x 轴的对称曲线，得到函数y=1－2sin 2x 的图象，则 f （x ）是 （ ）A ．cosxB ．2cosxC ．SinxD ．2sinx9．若函数()θ+=x y sin 2的图象按向量)2,6(π平移后，它的一条对称轴是4π=x ，则θ的一个可能的值是A ．125π B ．3π C ．6πD ．12π七．图象1．函数πsin 23y x ⎛⎫=- ⎪⎝⎭在区间ππ2⎡⎤⎢⎥⎣⎦，的简图是 （ ）2 在同一平面直角坐标系中，函数])20[)(232cos(ππ，∈+=x x y 的图象和直线21=y 的交点个数是（A ）0 （B ）1 （C ）2 （D ）4 3.已知函数y=2sin(ωx+φ)(ω>0)在区间[0，2π]的图像如下：那么ω=A. 1B. 2ＡＢC. 1/2D. 1/34． 下列函数中，图象的一部分如右图所示的是 （ ）（A ）sin 6y x π⎛⎫=+ ⎪⎝⎭ （B ）sin 26y x π⎛⎫=- ⎪⎝⎭（C ）cos 43y x π⎛⎫=- ⎪⎝⎭ （D ）cos 26y x π⎛⎫=- ⎪⎝⎭6． 为了得到函数y ＝sin ⎝⎛⎭⎪⎫2x －π3的图象，只需把函数y ＝sin ⎝ ⎛⎭⎪⎫2x ＋π6的图象 ( ) A ．向左平移π4个长度单位 B ．向右平移π4个长度单位 C ．向左平移π2个长度单位 D ．向右平移π2个长度单位7．已知函数y ＝sin ⎝ ⎛⎭⎪⎫x －π12cos ⎝ ⎛⎭⎪⎫x －π12，则下列判断正确的是 ( )A ．此函数的最小正周期为2π，其图象的一个对称中心是⎝ ⎛⎭⎪⎫π12，0B ．此函数的最小正周期为π，其图象的一个对称中心是⎝⎛⎭⎪⎫π12，0C ．此函数的最小正周期为2π，其图象的一个对称中心是⎝⎛⎭⎪⎫π6，0D ．此函数的最小正周期为π，其图象的一个对称中心是⎝⎛⎭⎪⎫π6，0八..综合1. 定义在R 上的函数)(x f 既是偶函数又是周期函数，若)(x f 的最小正周期是π，且当]2,0[π∈x 时，x x f sin )(=，则)35(πf 的值为2． 函数f(x)22sin sin 44f x x x ππ=+--（）（）（）是 （ ） A ．周期为π的偶函数 B ．周期为π的奇函数C ． 周期为2π的偶函数D ．.周期为2π的奇函数3． 已知函数))(2sin()(R x x x f ∈-=π，下面结论错误．．的是 ( ) A. 函数)(x f 的最小正周期为2π B. 函数)(x f 在区间［0，2π］上是增函数C.函数)(x f 的图象关于直线x ＝0对称D. 函数)(x f 是奇函数4． 函数)32sin(3)(π-=x x f 的图象为C , 如下结论中正确的是①图象C 关于直线π1211=x 对称; ②图象C 关于点)0,32(π对称;③函数125,12()(ππ-在区间x f )内是增函数;。

焊接工程师培训讲义焊接工程师培训讲义（一）一、引言焊接工程师是现代制造业中重要的技术岗位之一，其工作涉及到各种焊接技术和设备的应用。

在工程领域中，焊接是一项常见且关键的技术，它将金属材料通过加热、熔化和冷却的方式连接在一起。

本课程将为大家介绍焊接的基本概念、原理、常见焊接方法以及相关技术知识，旨在帮助学员掌握焊接工程师所需的基本技能和知识。

二、焊接的基本概念1. 什么是焊接？焊接是一种通过将金属材料熔化并冷却后，实现材料之间的连接的技术。

焊接可以将金属材料连接在一起，形成稳固的结构。

2. 焊接的原理是什么？焊接的原理基于金属材料的熔化点和冷却后的结合力。

在焊接过程中，首先要加热金属材料，使其达到熔化点，然后将熔化的金属材料连接在一起，并等待其冷却后产生结合力。

3. 焊接的分类有哪些？常见的焊接分类包括电弧焊、气焊、激光焊、电阻焊、摩擦焊等。

每种焊接方法都有其独特的应用场景和技术要求。

三、焊接的常见方法1. 电弧焊电弧焊是一种利用电弧发热将金属材料熔化并冷却后连接的焊接方法。

它使用电弧产生高温，使金属材料熔化，并通过焊丝添加材料来连接工件。

2. 气焊气焊是利用氧瓶和乙炔瓶生成的气体火焰将金属材料熔化并冷却后连接的焊接方法。

气焊常用于对大型工件的焊接，如钢结构等。

3. 激光焊激光焊是利用强聚光激光束将金属材料局部加热至熔化点，并通过冷却后的结合力实现焊接的方法。

激光焊具有高能量密度、热影响区小、焊接速度快等优点。

4. 电阻焊电阻焊是利用电流通过工件产生的焊接热量将金属材料熔化，并通过加压以实现焊接连接的方法。

电阻焊常用于对小型金属零部件的连接。

5. 摩擦焊摩擦焊是通过摩擦热产生的热量将金属材料局部加热至熔化点，并通过外力将焊件连接在一起的方法。

摩擦焊可用于不同种类金属的连接。

四、焊接前的准备工作1. 检查设备和线路是否正常。

焊接前需要检查焊接设备和线路是否正常工作，如电源是否稳定，线路是否接触良好等。