理论力学实验报告指导答案
- 格式:doc
- 大小:54.00 KB
- 文档页数:47

理论⼒学课后习题答案第10章动能定理及其应⽤)习题10— 3图第10章动能定理及其应⽤ 10-1计算图⽰各系统的动能: 1 ?质量为 m ,半径为r 的均质圆盘在其⾃⾝平⾯内作平⾯运动。
在图⽰位置时,若已知圆盘上A 、B 两点的速度⽅向如图⽰, B 点的速度为v B ,■■ = 45o (图a )。
2.图⽰质量为 m i 的均质杆OA ,⼀端铰接在质量为m 2的均质圆盘中⼼,另⼀端放在⽔平⾯上,圆盘在地⾯上作纯滚动,圆⼼速度为 v (图b ) 3?质量为m 的均质细圆环半径为 R ,其上固结⼀个质量也为 m 的质点 A 。
细圆环在⽔平⾯上作纯滚动,图⽰瞬时⾓速度为⑷(图C )。
(C )解:2. 3. 1 2 J c c 2 C C -m 2v 22 2ImR 2 2 2」m (纠2 12 2 2 1 12/V\2⼝2「(⼀) 2 2 r -mr 2(VB )2 3mv B2 2r 16 12 32 m .v m 2v 2 4 jgv 2 2 2 2 2 = ]mR 2 .2 ^mR 2 2 】m (. 2R -)^2mR 2 2 2 2 2图⽰滑块A 重⼒为W 1,可在滑道内滑动,与滑块 A ⽤铰链连接的是重⼒为 W 2、长为I 的匀质V 1,杆AB 的⾓速度为? 1。
当杆与铅垂线的夹⾓为 ::时,试求系统10— 2 杆AB 。
现已知道滑块沿滑道的速度为的动能。
解:图(a ) T ⼆T A T B 1 W 1 2 , 1 W 2 21 . 2、 v 1 - ( v C J C )2 g 2 g 2W 2v .2g 1 I 2 2-■ 1) ■ v 1 -丄 I m J I W 2 2 2⼇2 “ cos ?] -1 ;-1 2 2 12 g1 1 [(W ; W )V : - W 2I2 12 W 2I 1V 1COS] 2g3 C习题10 — 2图(a) 10— 3 重⼒为F P 、半径为r 的齿轮II 与半径为R =3r 的固定内齿轮 I 相啮合。
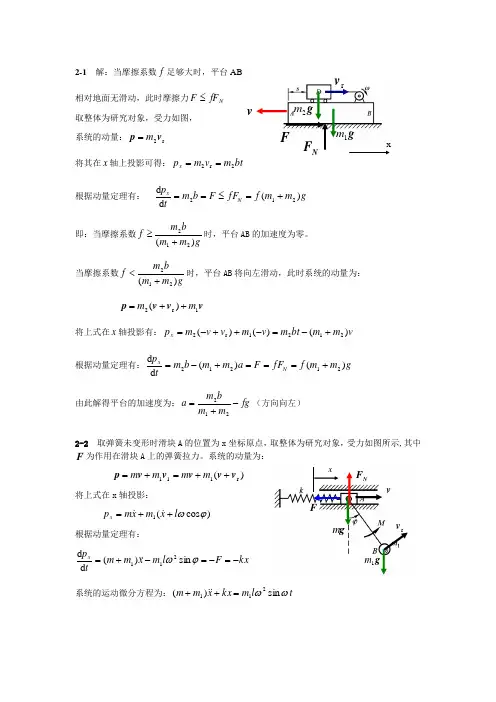
2-1 解:当摩擦系数f 足够大时,平台AB 相对地面无滑动,此时摩擦力N fF F ≤ 取整体为研究对象,受力如图, 系统的动量:r 2v p m =将其在x 轴上投影可得:bt m v m p x 2r 2==根据动量定理有:g m m f fF F b m tp N x)(d d 212+=≤== 即:当摩擦系数gm m bm f )(212+≥时,平台AB 的加速度为零。
当摩擦系数gm m bm f )(212+<时,平台AB 将向左滑动,此时系统的动量为:v v v p 1r 2)(m m ++=将上式在x 轴投影有:v m m bt m v m v v m p x )()()(2121r 2+-=-++-=根据动量定理有:g m m f fF F a m m b m tp N x)()(d d 21212+===+-= 由此解得平台的加速度为:fg m m bm a -+=212(方向向左)2-2 取弹簧未变形时滑块A 的位置为x 坐标原点,取整体为研究对象,受力如图所示,其中F 为作用在滑块A 上的弹簧拉力。
系统的动量为:)(r 111v v v v v p ++=+=m m m m将上式在x 轴投影:)cos (1ϕωl x m xm p x ++= 根据动量定理有:kx F l m xm m tp x-=-=-+=ϕωsin )(d d 211 系统的运动微分方程为:t l m kx x m m ωωsin )(211=++N Fg mg 1mFxvr vvr vN FFg 1mg 2mx2-4 取提起部分为研究对象,受力如图(a)所示,提起部分的质量为vt m ρ=,提起部分的速度为v ,根据点的复合运动可知质点并入的相对速度为r v ,方向向下,大小为v (如图a 所示)。
(a ) (b)根据变质量质点动力学方程有:v vt t t m m t t mρρr r )()(d d )(d d v g F v g F v ++=++= 将上式在y 轴上投影有:)()()()(d d 2r v vgt t F v v g vt t F tvm+-=--=ρρρ 由于0d d =tv,所以由上式可求得:)()(2v vgt t F +=ρ。

理论力学单摆参考答案理论力学单摆参考答案单摆是理论力学中一个经典的物理实验,通过对单摆的研究可以深入理解振动和周期运动的原理。
在本文中,将介绍单摆的基本概念、运动方程以及一些常见问题的解答。
1. 单摆的基本概念单摆由一个质点和一根无质量、不可伸长的细线组成。
质点在重力作用下沿着细线做简谐振动,称为单摆的摆动。
2. 单摆的运动方程假设单摆的质量为m,细线的长度为L,摆角为θ,摆动的周期为T。
根据牛顿第二定律和几何关系,可以得到单摆的运动方程:mg sinθ = mLθ'',其中θ''表示摆角的二阶导数。
这个方程描述了单摆的运动规律,可以通过求解这个方程来得到摆角随时间变化的关系。
3. 单摆的周期利用运动方程可以推导出单摆的周期公式:T = 2π√(L/g),其中g表示重力加速度。
这个公式表明,单摆的周期与摆长L和重力加速度g有关,与质点的质量m无关。
这也说明了在同一地点,不同质量的单摆摆动的周期是相同的。
4. 单摆的振幅振幅是指单摆摆动的最大摆角。
根据运动方程,可以得到单摆的振幅与总能量E有关:E = 1/2mL²θ'² + mgL(1 - cosθ)从上式可以看出,当θ=0时,E取最小值,即单摆在最低点时的总能量最小;当θ=π时,E取最大值,即单摆在最高点时的总能量最大。
振幅越大,总能量越大。
5. 单摆的简谐近似当摆角较小的时候,可以将单摆的运动近似为简谐振动。
这是因为当θ较小时,sinθ≈θ,cosθ≈1,可以将运动方程简化为:θ'' + (g/L)θ = 0这是一个简谐振动的运动方程,解为θ = A sin(√(g/L)t + φ),其中A为振幅,φ为初相位。
6. 单摆的阻尼和驱动在实际情况中,单摆的摆动会受到阻尼和驱动的影响。
阻尼是指由于空气阻力等外界因素导致振动能量逐渐减小的现象。
驱动是指外力对单摆施加的周期性作用力。

实验名称:力的合成与分解实验实验日期:2021年10月25日实验地点:物理实验室一、实验目的1. 理解力的合成与分解的概念;2. 掌握力的平行四边形法则;3. 培养实验操作能力和数据处理能力。
二、实验原理力的合成与分解是力学中的基本概念。
力的合成是指将两个或多个力合成一个力的过程,而力的分解则是指将一个力分解为两个或多个力的过程。
力的合成与分解遵循平行四边形法则,即两个力的合力可以用一个平行四边形来表示,而一个力也可以分解为两个互成一定角度的力。
三、实验器材1. 弹簧测力计;2. 力的合成与分解实验装置;3. 白纸、铅笔、直尺;4. 计算器。
四、实验步骤1. 将弹簧测力计固定在实验装置上,调整至零位;2. 用弹簧测力计分别测量两个已知力的大小和方向;3. 在白纸上按照比例尺画出两个力的矢量图,以原点为起点,分别画出两个力的方向和大小;4. 以两个力的矢量为邻边,构造一个平行四边形;5. 在平行四边形对角线上画出合力矢量,并测量其大小和方向;6. 将一个已知力分解为两个互成一定角度的力,按照比例尺画出分解后的矢量图;7. 检查分解后的两个力的合力是否与原力相等,验证力的分解原理。
五、实验数据1. 已知力F1:大小5N,方向向东;已知力F2:大小7N,方向向北;2. 合力F合:大小8.6N,方向东北方向;3. 分解力F1'和F2':F1'大小3N,方向东北方向;F2'大小5N,方向西北方向。
六、数据处理与分析1. 根据平行四边形法则,验证合力F合的大小和方向是否与两个已知力的合成结果相符;2. 验证分解力F1'和F2'的合力是否与原力F1和F2相等;3. 分析实验误差,讨论可能的原因。
七、实验结果1. 合力F合的大小和方向与两个已知力的合成结果相符;2. 分解力F1'和F2'的合力与原力F1和F2相等;3. 实验过程中存在一定的误差,可能的原因有测量工具的精度、操作不当等。

哈尔滨工业大学(威海)理论力学实验指导书张天伟力 学 实 验 室2018 年 05 月一、测量重心实验1、测量重心的重要性在地球表面附近的空间中,任何物体的各个质点都受到铅垂向下的地球引力作用,习惯称之为重力。
物体重力合力的作用点称为物体的重心。
物体的重心是力学和工程中的一个重要的概念,在许多工程问题中,物体重心的位置对物体的平衡或运动状态起着重要的作用。
如起重机的重心位置若超出某一范围,起重机工作时就会出事故;高速旋转的轴及其上各部件的重心如不在转轴轴线上,将引起剧烈振动而影响机器的寿命甚至发生事故;飞机、轮船及车辆的重心位置对他们运动的稳定性和可操控性也有极大的关系。
因此,测定物体重心的位置,在工程中有着重要的意义。
2、实验测量重心的方法及原理工程中经常遇到形状复杂或非均质的物体,此时其重心的位置可用实验方法确定。
另外,虽然设计时重心的位置计算的很精确,但由于在制造和装配时产生误差等原因,待产品制成后,其重心不在设计的范围内,也可以用实验的方法来进行重心的测定。
下面介绍两种常用的实验方法。
(1)悬吊法对于薄板形物体或具有对称面的薄零件,可将物体悬挂于任一点 A,待平衡时,设法标出线段 AB,根据二力平衡公理,重心必在此线上。
再将该物体悬挂于任一点 D,待平衡时,设法标出线段 DE,则两线段的交点 C 就是该物体的重心。
(2)称重法对于形状复杂、体积庞大的物体或由许多零件组成的物体系,常用称重法测定重心的位置。
假设物品的重心距一端的距离为 x c,为测定 x c的值,将物体一端置于台面上,一端置于磅秤上,读出磅秤的读数 F1;再将物体左右调换方向放置,读出磅秤读数 F2。
则物体的重量为:W= F1+ F2重心距离一端的距离为:3、学习目标理解重心的概念;掌握悬吊法与称量法测重心的方法;实测组合型钢试件与发动机连杆的重心位置。
4、实验工具设备及试件组合型钢挂件发动机连杆水平尺积木垫块电子秤5、实验步骤及数据处理1)顺时针旋转电源开关,打开试验台电源。
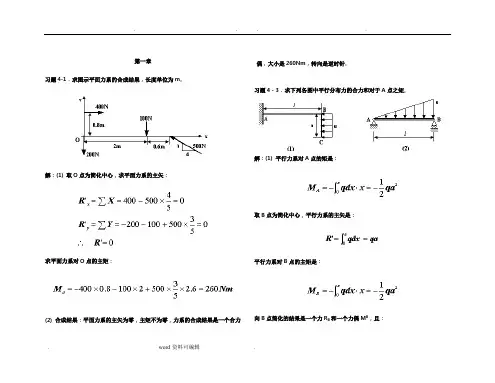
第一章习题4-1.求图示平面力系的合成结果,长度单位为m。
解:(1) 取O点为简化中心,求平面力系的主矢:求平面力系对O点的主矩:(2) 合成结果:平面力系的主矢为零,主矩不为零,力系的合成结果是一个合力偶,大小是260Nm,转向是逆时针。
习题4-3.求下列各图中平行分布力的合力和对于A点之矩。
解:(1) 平行力系对A点的矩是:取B点为简化中心,平行力系的主矢是:平行力系对B点的主矩是:向B点简化的结果是一个力R B和一个力偶M B,且:如图所示;将R B向下平移一段距离d,使满足:最后简化为一个力R,大小等于R B。
其几何意义是:R的大小等于载荷分布的矩形面积,作用点通过矩形的形心。
(2) 取A点为简化中心,平行力系的主矢是:平行力系对A点的主矩是:向A点简化的结果是一个力R A和一个力偶M A,且:如图所示;将R A向右平移一段距离d,使满足:最后简化为一个力R,大小等于R A。
其几何意义是:R的大小等于载荷分布的三角形面积,作用点通过三角形的形心。
习题4-4.求下列各梁和刚架的支座反力,长度单位为m。
解:(1) 研究AB杆,受力分析,画受力图:列平衡方程:解方程组:反力的实际方向如图示。
校核:结果正确。
(2) 研究AB杆,受力分析,将线性分布的载荷简化成一个集中力,画受力图:列平衡方程:解方程组:反力的实际方向如图示。
校核:结果正确。
(3) 研究ABC,受力分析,将均布的载荷简化成一个集中力,画受力图:列平衡方程:解方程组:反力的实际方向如图示。
校核:结果正确。
习题4-5.重物悬挂如图,已知G=1.8kN,其他重量不计;求铰链A的约束反力和杆BC所受的力。
解:(1) 研究整体,受力分析(BC是二力杆),画受力图:列平衡方程:解方程组:反力的实际方向如图示。
习题4-8.图示钻井架,G=177kN,铅垂荷载P=1350kN,风荷载q=1.5kN/m,水平力F=50kN;求支座A的约束反力和撑杆CD所受的力。

理
论
力
学
作
业
姓名:
班级:
学号:
题6—7
分析:由OA=AB=200,AC=CD=DE=AE=50,的数量关系结合相似三角形的比例关系,易得纵坐标关系yd=0.5ya,xa=xd.这样只要确定A点得运行轨迹就可以确定D点得运行轨迹。
其运行结果如下图所示:
结论:A的轨迹易得为:
x^2+y^2=200^2;
则由相似关系的D的运动方程为:X^2+(y/2)^2=200^2.
完整的代码:
clc
% w是角速度。
w=pi/5;
syms t
%x,y可以由几何知识求出。
x=200*cos(w*t);
y=100*sin(w*t);
%求速度,是x,y的一次导数
Vx=diff(x,t);
Vy=diff(y,t);
%加速度ax,ay
ax=diff(x,'t',2);
ay=diff(y,'t',2);
%一个周期的时间T
T=0:0.1:10
%在不同的区域画出各种图像x=subs(x,t,T);
y=subs(y,t,T);
Vx=subs(Vx,t,T);
Vy=subs(Vy,t,T);
ax=subs(ax,t,T);
ay=subs(ay,t,T);
figure(1)
plot(x,y)
figure(2)
plot(T,x)
figure(3)
plot(T,x,T,Vx,T,ax)
D点x轴时间曲线历程
D点的速度,加速度图象。
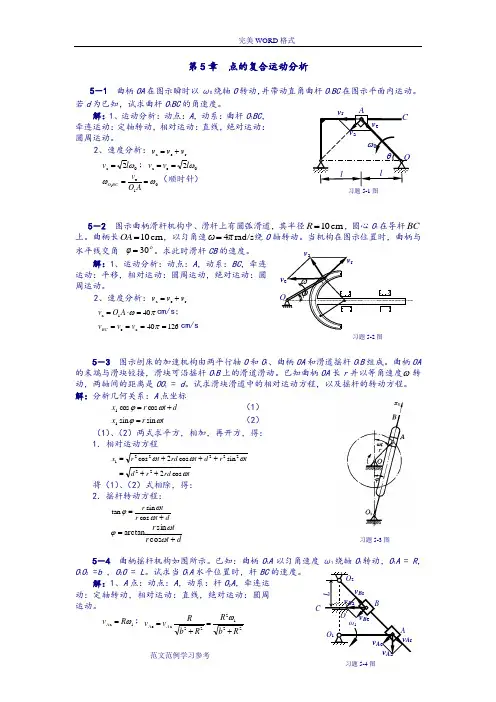
第5章 点的复合运动分析5-1 曲柄OA 在图示瞬时以ω0绕轴O 转动,并带动直角曲杆O 1BC 在图示平面内运动。
若d 为已知,试求曲杆O 1BC 的角速度。
解:1、运动分析:动点:A ,动系:曲杆O 1BC ,牵连运动:定轴转动,相对运动:直线,绝对运动:圆周运动。
2、速度分析:r e a v v v +=0a 2ωl v =;0e a 2ωl v v ==1e1ωω==AO v BCO (顺时针)5-2 图示曲柄滑杆机构中、滑杆上有圆弧滑道,其半径cm 10=R ,圆心O 1在导杆BC 上。
曲柄长cm 10=OA ,以匀角速rad/s 4πω=绕O 轴转动。
当机构在图示位置时,曲柄与水平线交角 30=φ。
求此时滑杆CB 的速度。
解:1、运动分析:动点:A ,动系:BC ,牵连运动:平移,相对运动:圆周运动,绝对运动:圆周运动。
2、速度分析:r e a v v v += πω401a =⋅=A O v cm/s ; 12640a e ====πv v v BC cm/s5-3 图示刨床的加速机构由两平行轴O 和O 1、曲柄OA 和滑道摇杆O 1B 组成。
曲柄OA 的末端与滑块铰接,滑块可沿摇杆O 1B 上的滑道滑动。
已知曲柄OA 长r 并以等角速度ω转动,两轴间的距离是OO 1 = d 。
试求滑块滑道中的相对运动方程,以及摇杆的转动方程。
解:分析几何关系:A 点坐标 d t r x +=ωϕcos cos 1 (1) t r x ωϕsin sin 1= (2) (1)、(2)两式求平方,相加,再开方,得: 1.相对运动方程trd r d t r d t rd t r x ωωωωcos 2sin cos 2cos 22222221++=+++=将(1)、(2)式相除,得: 2.摇杆转动方程: dt r tr +=ωωϕcos sin tandt r t r +=ωωϕcos sin arctan5-4 曲柄摇杆机构如图所示。

力学实验报告答案力学实验报告答案引言:力学是物理学的一个重要分支,研究物体的运动和相互作用。
在力学实验中,通过设计合适的实验装置和进行精确的测量,可以验证力学理论,并获得一些有价值的实验数据。
本文将就几个力学实验的结果和分析进行讨论,以加深对力学知识的理解。
实验一:简谐振动简谐振动是力学中的重要概念,指的是振动系统在无阻尼和无外力的情况下,受到恢复力作用而产生的振动。
我们通过实验装置模拟了简谐振动,并测量了振动周期与振幅的关系。
实验结果显示,振动周期与振幅的平方成正比。
这符合简谐振动的特性,即振动周期与振幅无关,只与振动系统的特性有关。
通过分析实验数据,我们可以得出简谐振动的周期公式:T=2π√(m/k),其中T为振动周期,m为振动系统的质量,k为恢复力系数。
实验二:牛顿第二定律牛顿第二定律是力学中的重要定律,描述了物体的加速度与作用在物体上的合力之间的关系。
我们通过实验验证了牛顿第二定律,并测量了物体的加速度与施加在物体上的力的关系。
实验结果显示,物体的加速度与施加在物体上的力成正比。
这符合牛顿第二定律的表述:F=ma,其中F为合力,m为物体的质量,a为物体的加速度。
通过分析实验数据,我们可以得出物体的加速度与施加在物体上的力的关系为:a=F/m。
实验三:动量守恒定律动量守恒定律是力学中的重要定律,描述了一个封闭系统中物体的总动量保持不变。
我们通过实验验证了动量守恒定律,并测量了碰撞前后物体的动量之和。
实验结果显示,碰撞前后物体的动量之和保持不变。
这符合动量守恒定律的表述:m1v1 + m2v2 = m1v1' + m2v2',其中m1和m2分别为两个物体的质量,v1和v2分别为碰撞前两个物体的速度,v1'和v2'分别为碰撞后两个物体的速度。
通过分析实验数据,我们可以验证动量守恒定律的成立。
结论:通过以上实验的结果和分析,我们验证了简谐振动、牛顿第二定律和动量守恒定律这几个力学理论。

成绩理论力学计算机实验报告平面桁架内力计算姓名:谢宗言学号:6011207469指导教师:叶金铎天津大学仁爱学院建筑工程系2011级土木工程四班2012年4月目录实验一、平面桁架内力计算 (4)一.实验目的: (4)二.实验内容: (4)三.实验步骤: (4)四.计算题目,计算结果与结果验证 (5)五. 学习体会与建议: ........................................... 错误!未定义书签。
实验一、平面桁架内力计算一.实验目的:1.熟悉FORTRAN软件和平面桁架计算程序的使用方法。
2.学习用文本编辑器编写原始数据文件,保存文件。
3.学习查看计算结果文件。
二.实验内容:1.使用循环节点法求平面简单桁架的杆件内力和约束反力。
2.使用循环节点法求平面复杂桁架的杆件内力和约束反力。
三.实验步骤:1. 创建计算文件夹创建平面桁架计算的文件夹,文件名可以是中文,也可以是英文或汉语拼音。
2. 原始数据文件的编辑原始数据文件的编写方法按照教材指定的方法编写,编写前要给结构编写杆号,节点号。
编辑数据文件的方法是,打开记事本,编写数据文件,数据之间用逗号或空格隔开,保存数据文件,文件的扩展名为*.DAT,或TXT,退出文本编辑器。
将编写好的数据文件以COND1命名,存入创建的计算文件名下。
3. 执行计算将计算文件TRUSS.EXE拷入计算文件名下,点击计算文件名TRUSS,执行计算(程序自动生成结果文件RESU1.DAT/ RESU1.TXT)4. 计算结果的查看用记事本打开结果文件查看计算,结果文件的扩展名为*.DAT/*.TXT。
5. 重复计算的执行首次计算(第一组数据),按上述二至四步进行,重复计算,(两组以上数据)在输入第二组数据之前,将第一组的数据,包括原始数据文件和结果文件改名,如将COND1.DAT该为C1.DAT,将RESU1.DAT该为R1.DAT。
四.计算题目,计算结果与结果验证1.习题3.3结构与载荷如图1所示,求杆的内力和支座反力。
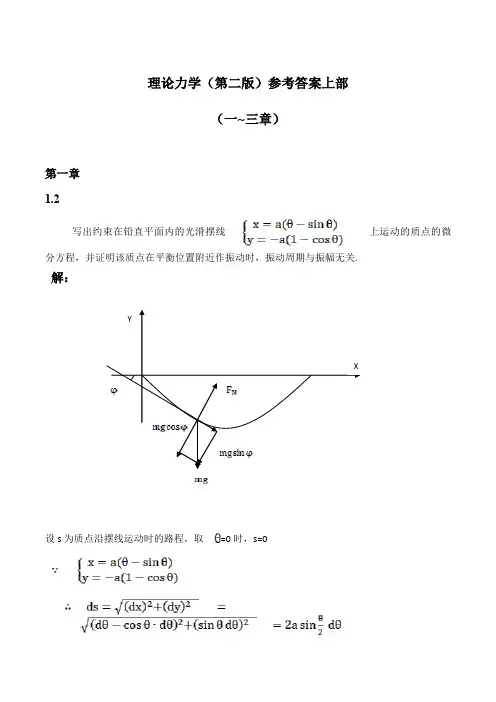
理论力学(第二版)参考答案上部(一~三章)第一章1.2写出约束在铅直平面内的光滑摆线上运动的质点的微分方程,并证明该质点在平衡位置附近作振动时,振动周期与振幅无关. 解:设s为质点沿摆线运动时的路程,取=0时,s=0S== 4 a (1)设为质点所在摆线位置处切线方向与x轴的夹角,取逆时针为正,即切线斜率=受力分析得:则,此即为质点的运动微分方程。
该质点在平衡位置附近作振动时,振动周期与振幅无关,为.1.3证明:设一质量为m的小球做任一角度θ的单摆运动运动微分方程为θθθFrrm=+)2(θθsinmgmr= ①给①式两边同时乘以dθθθθθdgdr s i n=对上式两边关于θ 积分得cgr+=θθc o s212②利用初始条件θθ=时0=θ 故cosθgc-=③由②③可解得c o sc o s2-θθθ-∙=lg上式可化为dtdlg=⨯-∙θθθcoscos2-两边同时积分可得θθθθθθθθd g l d g l t ⎰⎰---=--=020222002sin 12sin 10012cos cos 12进一步化简可得θθθθd g l t ⎰-=0002222sin sin 121由于上面算的过程只占整个周期的1/4故⎰-==02022sin2sin124T θθθθd g l t由ϕθθsin 2sin /2sin 0=两边分别对θϕ微分可得ϕϕθθθd d cos 2sin2cos=ϕθθ202sin 2sin 12cos-=故ϕϕθϕθθd d 202sin 2sin 1cos 2sin2-= 由于00θθ≤≤故对应的20πϕ≤≤故ϕϕθϕθϕθθθθπθd g l d g l T ⎰⎰-=-=202022cos 2sinsin 2sin 1/cos 2sin42sin2sin 2故⎰-=2022sin 14πϕϕK d g l T 其中2sin 022θ=K通过进一步计算可得g lπ2T =])2642)12(531()4231()21(1[224222 +⨯⨯⨯⨯-⨯⨯⨯⨯++⨯⨯++n K nn K K1.5解:如图,在半径是R的时候,由万有引力公式,对表面的一点的万有引力为, ①M为地球的质量;可知,地球表面的重力加速度g , x为取地心到无限远的广义坐标,,②联立①,②可得:,M为地球的质量;③当半径增加,R2=R+,此时总质量不变,仍为M,此时表面的重力加速度可求:④由④得:⑤则,半径变化后的g 的变化为⑥对⑥式进行通分、整理后得:⑦对⑦式整理,略去二阶量,同时远小于R ,得⑧则当半径改变 时,表面的重力加速度的变化为:。
理论力学(郝桐生)第一章习题1-1.画出下列指定物体的受力图。
解:习题1-2.画出下列各物系中指定物体的受力图。
解:习题1-3.画出下列各物系中指定物体的受力图。
解:第二章习题2-1.铆接薄钢板在孔心A、B和C处受三力作用如图,已知P1=100N沿铅垂方向,P2=50N沿AB方向,P3=50N沿水平方向;求该力系的合成结果。
解:属平面汇交力系;合力大小和方向:习题2-2.图示简支梁受集中荷载P=20kN,求图示两种情况下支座A、B的约束反力。
解:(1)研究AB,受力分析:画力三角形:相似关系:几何关系:约束反力:(2) 研究AB,受力分析:画力三角形:相似关系:几何关系:约束反力:习题2-3.电机重P=5kN放在水平梁AB的中央,梁的A端以铰链固定,B端以撑杆BC支持。
求撑杆BC所受的力。
解:(1)研究整体,受力分析:(2) 画力三角形:(3) 求BC受力习题2-4.简易起重机用钢丝绳吊起重量G=2kN的重物,不计杆件自重、磨擦及滑轮大小,A、B、C三处简化为铰链连接;求杆AB和AC所受的力。
解:(1) 研究铰A,受力分析(AC、AB是二力杆,不计滑轮大小):建立直角坐标Axy,列平衡方程:解平衡方程:AB杆受拉,BC杆受压。
(2) 研究铰A,受力分析(AC、AB是二力杆,不计滑轮大小):建立直角坐标Axy,列平衡方程:解平衡方程:AB杆实际受力方向与假设相反,为受压;BC杆受压。
习题2-5.三铰门式刚架受集中荷载P作用,不计架重;求图示两种情况下支座A、B的约束反力。
解:(1) 研究整体,受力分析(AC是二力杆);画力三角形:求约束反力:(2) 研究整体,受力分析(BC是二力杆);画力三角形:几何关系:求约束反力:习题2-6.四根绳索AC、CB、CE、ED连接如图,其中B、D两端固定在支架上,A端系在重物上,人在E点向下施力P,若P=400N,α=4o,求所能吊起的重量G。
解:(1) 研究铰E,受力分析,画力三角形:由图知:(2) 研究铰C,受力分析,画力三角形:由图知:习题2-7.夹具中所用的两种连杆增力机构如图所示,书籍推力P作用于A点,夹紧平衡时杆AB与水平线的夹角为;求对于工件的夹紧力Q和当α=10o时的增力倍数Q/P。
理论力学实验报告指导答案实验一振动测试系统组成及基本仪器使用方法1—底座; 2—支座; 3—二(三)自由度系统; 4—薄壁圆板支承螺杆;5—固定铰;6—非接触式激振器;7—薄壁圆板;8—电动式激振器;9—电机压板;10—偏心电机;11—加速度传感器;12—简支梁;13—活动铰;14—悬臂梁;15—圆支柱;16—质量;17—调压器; 18—电动式激振器支座; 19—ZK-4JCZ型激振测振仪;20—信号源; 21—计算机及虚拟仪器库; 22—打印机图1 实验装置与结构框图传感器1输入传感器2输入一道振动幅值二道振动幅值频率/功率显示值频率,周期,灵敏度调节一道,二道增益及测试方式状态设置选择及参数选择旋扫频选择方式选择灵敏度选择显示选择功率输出选择功率幅度调节信号源调节功率输出B 道功率输出A 道信号源波形输出ZK —4JCZ 型激振测振仪功能分布图ZK-4JCZ 型激振测振仪是一种多功能测量仪器。
它包括信号源、功率放大器及两个配接加速度计的测量通道,可对振动的加速度、加速度或位移进行测量。
实验二简谐振动幅值测量一、实验目的1. 了解振动信号位移、速度、加速度的关系。
2. 学会用压电式加速度传感器测量简谐振动的位移、速度、加速度幅度。
二、实验装置与仪器框图实验装置与仪器框图见图(1)图(1)实验装置与仪器框图四、实验方法1. 激振信号源输出端接电动式激振器,用电动式激振器对简支梁激振。
2. 用加速度传感器拾振,加速度传感器的输出接测振仪。
3. 开启激振信号源的电源开关,对系统施加交变正弦激振力,使系统产生振动,调整信号源的输出调节开关便可改变振幅大小。
调整信号源的输出调节开关时注意不要过载。
4. 分别用测振仪的位移X、速度V、加速度A各档进行测量和读数。
五、实验报告1. 实验数据表12. 根据位移X,按公式(2)计算速度V、加速度A。
3. 根据速度V,按公式(2)计算位移X、加速度A。
4. 根据加速度A,按公式(2)计算位移X、速度V。
静力学1-3 试画出图示各结构中构件AB 的受力图F AxF A yF B(a)(a)F AF BF BF DF D F BxF ByF BxF CF BF CF By1-4 试画出两结构中构件ABCD 的受力图1-5 试画出图a 和b 所示刚体系整体合格构件的受力图1-5a1-5bF AxF A y F DF ByF A F BxF B F AF Ax F A y F DxF Dy WT EF CxF C yWF AxF A yF BxF B yF CxF C yF DxF DyF Bx F ByT EN’F BF DF A N F AF BF D1-8在四连杆机构的ABCD 的铰链B 和C 上分别作用有力F 1和F 2,机构在图示位置平衡。
试求二力F 1和F 2之间的关系。
解:杆AB ,BC ,CD 为二力杆,受力方向分别沿着各杆端点连线的方向。
解法1(解析法)假设各杆受压,分别选取销钉B 和C 为研究对象,受力如图所示: 由共点力系平衡方程,对B 点有:∑=0x F 045cos 02=-BC F F 对C 点有:∑=0x F 030cos 01=-F F BC解以上二个方程可得:22163.1362F F F ==解法2(几何法)分别选取销钉B 和C 为研究对象,根据汇交力系平衡条件,作用在B 和C 点上的力构成封闭的力多边形,如图所示。
对B 点由几何关系可知:0245cos BC F F =对C 点由几何关系可知:0130cos F F BC =解以上两式可得:2163.1F F =F ABF BC F CD 60o F 130o F 2 F BC45o F 2F BC F ABB45oy xF CD C60o F 130o F BC x y450302-3 在图示结构中,二曲杆重不计,曲杆AB 上作用有主动力偶M 。
试求A 和C 点处的约束力。
解:BC 为二力杆(受力如图所示),故曲杆AB 在B 点处受到约束力的方向沿BC 两点连线的方向。
理论力学课后习题答案第6章刚体的平面运动分析第6章刚体的平面运动分析6-1 图示半径为r 的齿轮曲柄OA带动,沿半径为R的固定齿轮滚动。
曲柄OA以等角加速度绕轴O转动,当运动开始时,角速度= 0,转角= 0。
试求动齿轮以圆心A为基点的平面运动方程。
00解:sx A(Rr)coA001(Rr)sin 为常数,当t = 0时,== 02起始位置,P与P重合,即起始位置AP 水0平,记,则AP从起始水平位置至图示A CP CP AP位置转过习题6-1图因动齿轮纯滚,故有,即rRR r 0, A rr将代入、、得动齿轮以A为基点的平面运动方程为:y2x1R r2 (R t r)costA 2r A22(Rr)sintA 26-2 杆AB斜靠于高为h的台阶角C处,一端A以匀速v沿水平向右运动,如图所示。
试以杆与铅垂线的夹角表示杆的角速度。
解:杆AB作平面运动,点C的 B B P速度v沿杆AB如图所示。
作速度Cv和v的垂线交于点P,点P即为C C 杆AB的速度瞬心。
则角速度杆cosvcoso0000h 为 A v A v 2ABAPACh习题6-2图习题6-2解图6-3 图示拖车的车轮A与垫滚B的半径均为r。
试问当拖车以速度v前进时,轮A与垫滚B的角速度与有什么关系?设轮A和垫滚B与地面之间以及垫滚B与拖车之间无滑动。
ABvv ARR A解:B2R2R习题v = v Bv = v vv BA B6-3解图习题6-3图AB6036-4 直径为mm 的滚子在水平面上作纯滚动,杆BC一端与滚子铰接,另一端与滑块C铰接。
速度=12 rad/s,=设杆BC在水平位置时,滚子的角,=,BC=270mm。
试求该瞬时杆BC的角速度和点C的速度。
解:杆BC 的瞬P 心在点P,滚子O的瞬心在点D BC v C B vBD C B B B 12603cos30vBD B270sin30O BCBPBP O v 习题6-4图 D 8rad/svPC 习题6-4解图CBC/s 6-5 在下列机构中,那些构件做平面运动,画出它们图示位置的速度瞬心。
理论力学参考答案第5章第5章摩擦· ·47· 47·第5章摩擦一、是非题正确的在括号内打“√”、错误的打“×” 1静滑动摩擦力与最大静滑动摩擦力是相等的。
× 2最大静摩擦力的方向总是与相对滑动趋势的方向相反。
√ 3摩擦定律中的正压力即法向约束反力是指接触面处物体的重力。
× 4当物体静止在支撑面上时支撑面全约束反力与法线间的偏角不小于摩擦角。
× 5斜面自锁的条件是斜面的倾角小于斜面间的摩擦角。
√ 二、填空题1当物体处于平衡时静滑动摩擦力增大是有一定限度的它只能在0≤Fs≤Fsmax范围内变化而动摩擦力应该是不改变的。
2静滑动摩擦力等于最大静滑动摩擦力时物体的平衡状态称为临界平衡状态。
3对于作用于物体上的主动力若其合力的作用线在摩擦角以内则不论这个力有多大物体一定保持平衡这种现象称为自锁现象。
4当摩擦力达到最大值时支撑面全约束反力与法线间的夹角为摩擦角。
5重量为G的均质细杆AB与墙面的摩擦系数为0.6f如图5.12所示则摩擦力为0。
6物块B重2kNP物块A重5kNQ在B上作用一水平力F如图5.13所示。
当系A之绳与水平成30角B与水平面间的静滑动摩擦系数s102f.物块A与B之间的静滑动摩擦系数s2025f.要将物块B拉出时所需水平力F的最小值为2.37kN。
A CB G A B F 图5.12 图5.13 ·48·理论力学·48·三、选择题1如图5.14所示重量为P的物块静止在倾角为的斜面上已知摩擦系数为sfsF为摩擦力则sF的表达式为B 临界时sF的表达式为 A 。
A sscosFfP B ssinFP C sscosFfP D ssinFP NF P sF 图5.14 2重量为G的物块放置在粗糙的水平面上物块与水平面间的静摩擦系数为sf今在物块上作用水平推力P 后物块仍处于静止状态如图5.15所示那么水平面的全约束反力大小为C 。
理论力学实验报告指导答案实验一振动测试系统组成及基本仪器使用方法1—底座;2—支座;3—二(三)自由度系统;4—薄壁圆板支承螺杆;5—固定铰;6—非接触式激振器;7—薄壁圆板;8—电动式激振器;9—电机压板;10—偏心电机;11—加速度传感器;12—简支梁;13—活动铰;14—悬臂梁;15—圆支柱;16—质量;17—调压器;18—电动式激振器支座;19—ZK-4JCZ型激振测振仪;20—信号源;21—计算机及虚拟仪器库;22—打印机图1实验装置与结构框图传感器1输入传感器2输入一道振动幅值二道振动幅值频率/功率显示值频率,周期,灵敏度调节及步进,锁定旋钮一道,二道增益及测试方式状态设置选择及参数选择旋钮扫频选择方式选择灵敏度选择显示选择功率输出选择功率幅度调节信号源调节功率输出B道功率输出A道信号源波形输出ZK—4JCZ型激振测振仪功能分布图ZK-4JCZ型激振测振仪是一种多功能测量仪器。
它包括信号源、功率放大器及两个配接加速度计的测量通道,可对振动的加速度、加速度或位移进行测量。
16实验二简谐振动幅值测量一、实验目的1.了解振动信号位移、速度、加速度的关系。
2.学会用压电式加速度传感器测量简谐振动的位移、速度、加速度幅度。
二、实验装置与仪器框图实验装置与仪器框图见图(1)图(1)实验装置与仪器框图四、实验方法1.激振信号源输出端接电动式激振器,用电动式激振器对简支梁激振。
2.用加速度传感器拾振,加速度传感器的输出接测振仪。
开启激振信号源的电源开关,对系统施加交变正弦激振力,使系统产生振动,调整信号源的输出调节开关便可改变振幅大小。
调整信号源的输出调节开关时注意不要过载。
4.分别用测振仪的位移X、速度V、加速度A各档进行测量和读数。
五、实验报告1.实验数据表1频率f位移X(um)速度V(cm/s)加速度A(cm/s2)3047505660682.根据位移X,按公式(2)计算速度V、加速度A。
根据速度V,按公式(2)计算位移X、加速度A。
4.根据加速度A,按公式(2)计算位移X、速度V。
5.位移、加速度、加速度幅值的实测值与计算值有无差距?为什麽?实验三单自由度系统强迫振动的幅频特性、固有频率和阻尼的测定一、实验目的1.学会用测量单自由度系统强迫振动的幅频特性曲线。
2.学会根据幅频特性曲线确定系统的固有频率f0和阻尼比。
二、实验装置与仪器框图实验装置与仪器框图如图(1)所示。
图(1)实验装置与结构框图式(3)叫做系统的幅频特性。
将式(3)所表示的振动幅值与激振频率的关系用图形表示,称为幅频特性曲线,如图(2)b所示。
a单自由度系统的力学模型幅频特性曲线图(2)单自由度系统的力学模型与幅频特性曲线在图(2)b中,Bmax为系统共振时的振幅,f0为系统的固有频率,f1、f2为半功率点频率。
振幅最大时的频率叫共振频fa。
有阻尼时,共振频率为:fa=f0(4)当阻尼较小时,fa≈f0,故以固有频率f0作为共振频率fa。
在小阻尼情况下可得:ζ=(5)f1、f2的确定如图(2)所示。
四、实验方法1.将加速度传感器置于简支梁上,其输出端接测振仪,用来测量简支梁的振动幅值。
2.将电动式激振器接入激振信号源输出端,开启激振信号源的电源开关,对简支梁系统施加交变正弦激振力,使系统产生正弦振动。
3在激振力不变的情况下,调整激振信号源输出信号的频率,并从测振仪上读出各频率及其对应的幅值,填入表(1)。
五、实验报告1.实验数据表(1)频率f(Hz)yy振幅B(um)hh2.根据表(1)中的实验数据,用计算机MicrosoftofficesExcel(电子表格)绘制出实验中系统强拍振动的幅频特性曲线图。
3.确定系统固有频率f0。
(幅频特性曲线共振峰上最高点对应的频率近似等于系统的固有频率)。
4.确定阻尼比ζ。
按图(2)b计算0.707Amax,,然后在幅频特性曲线上确定f1、f2,利用式(5)计算阻尼比。
实验四二自由度系统各阶固有频率及主振型测定一、实验目的1.学会用共振法确定二自由度系统的各阶固有频率。
2.观察二自由度系统的各阶振型。
3.将实验所测得的各阶固有频率、振型与理论计算值相比较。
二、实验装置与仪器框图实验装置与仪器框图见图(1)图(1)实验装置与仪器框图这样一个二自由度系统具有两个固有频率。
当给系统一个激振力时,系统发生振动,该振动是两个主振型的迭加。
当激振频率等于某一阶固有频率时,系统的振动就是这一阶固有频率的主振型,而另一阶振型的影响可忽略不计。
在测定系统的固有频率时,需要连续调整激振频率,使系统出现某阶振型且振幅达到最大,此时的激振频率即是该阶固有频率。
图(2)二自由度系统的力学模型由振动理论知:M=K=0(1)系统的各阶固有频率为:一阶固有频率f1=(2)二阶固有频率f2=(3)式中:弦上集中质量m=0.0045千克弦丝张力T=()牛顿弦丝长度L=0.625米固有频率f1=ω1/2π赫兹各阶主振型如图(3)所示。
图(3)二自由度系统的主振型四、实验方法1.将非接触式激振器接入激振信号源输出端,把激振器对准钢质量块A或B,保持一定的初始间隙(约为8~10mm),使振动时激振器不碰撞质量块。
2.用1kg或2kg的重锤调整所需张力T,张力T不同,测得的固有频率不同。
3.开启激振信号源的电源开关,对系统施加交变正弦激振力,使系统产生振动,调整信号源的输出调节开关便可改变振幅大小。
调整信号源的输出调节开关时注意不要过载。
4.激振频率由低到高逐渐增加,当观察到系统出现如图(3)所示的第一阶振型且振幅最大时,激振信号源显示的频率就是系统的一阶固有频率。
依此下去,可得到如图(3)所示的第二阶振型和二阶固有频率。
五、实验报告1.将不同张力下各阶固有频率的理论计算值与实测值填入下表弦丝张力T=1×9.8(N)固有频率f1f2理论值实测值2.绘出观察到的二自由度系统振型曲线。
3.根据式(2);(3)计算出各阶固有频率理论值、理论振型,并与实测固有频率、实测振型相比较,是否一致?如有误差产生的原因在哪里?实验五连续弹性体悬臂梁各阶固有频率及主振型的测定一、实验目的1.用共振法确定连续弹性体悬臂梁横向振动时的各阶固有频率。
2.观察分析梁振动的各阶主振型。
3.将实测的各阶固有频率、振型与固有频率理论值、理论振型相比较。
二、实验装置与仪器框图实验装置与仪器框图见图(1)图(1)实验装置与仪器框图本实验取:L=18.5cmb=1cmh=0.065cmE=2×106kg/cm2p=0.0078kg/cm3各阶固有频率之比:f1:f2:f3:… (1)6.25:17.5……(3)进一步可计算出悬臂梁的一、二、三阶固有频率和振型如图(3)所示。
图(3)悬臂梁的一、二、三阶固有频率和主振型四、实验方法1.选距固定端L/4之处为激振点,将激振器端面对准悬臂梁上的激振点,保持初始间隙δ=6~8mm。
2.将非接触式激振器接入激振信号源输入端,开启激振信号源的电源开关,对系统施加交变正弦激振力,使系统产生振动,调整信号源的输出调节开关便可改变振幅大小。
调整信号源的输出调节开关时注意不要过载。
3.调整信号源,使激振频率由低到高逐渐增加,当系统出现明显的一阶主振型且振幅最大时,激振信号源显示的频率就是梁的第一阶固有频率。
找到一阶固有频率后,不再调整激振频率,只改变激振源输出功率的大小(即改变激扰力幅值大小),并观察振型随激扰力大小变化的情况。
用上述同样的方法可确定梁的二、三阶固有频率及振型。
五、实验报告1.各阶固有频率的理论计算值与实测值表1固有频率(Hz)f1f2f3理论值实测值2.绘出观察到的悬臂梁振型曲线。
3.根据式(1);(2);(3)计算出各阶固有频率理论值、理论振型,并与实测固有频率、实测振型相比较,是否一致?如有误差产生误差的原因在哪里?实验六拍振实验一、实验目的1.观察拍振现象,建立拍振的概念。
2.了解消除或减弱拍振的现象。
二、实验装置与仪器框图实验装置与仪器框图见图(1)图(1)实验装置与仪器框图三、实验原理当结构振动时,有时会产生所谓拍的现象。
什麽叫拍?如对简支梁系统施加两个频率接近、振幅不等的激振力,使系统产生振动,用测振仪测得系统的横向水平振动波形如图(2)所示,其振幅是周期地变化,这种现象就叫做拍。
总的来讲,两个频率接近、振幅不等的振动迭加就能形成拍。
根据拍振原理,设两个频率接近、振幅不等的振动为:y1=A1sin(ω1t)y2=A2sin(ω2t)图(2)拍振现象合振动y=y1+y2=A1sin(ω1t)+A2sin(ω2t)y=Asin(t+j)(1)式中:A—合振动振幅j—初相角A=j=tg-1(tgt)(2)分振动y1、y2与合振动y的波形如图(2)所示,合振动的频率及周期为f合==(3)T合==合振动的振幅随时间在最大振幅Amax与最小振幅Amin间作周期变化,就形成了拍,在拍振图形上,有最大振幅的一段叫拍的腹,最小振幅的一段叫拍的腰,腰和腹总是间隔地出现。
在单位时间内腰或腹出现的次数叫拍的频率f拍,振幅大小改变一次的时间叫拍的周期T拍。
f拍=f2-f1=(5)T拍==从(5)式可知,两个分振动的频率相差越小,拍振动的周期就越大。
四、实验方法1.将传感器置于简支梁上,用来测量简支梁振幅A。
2.用调速电机对简支梁施加频率为f1的激扰力,使之产生振幅为A1的分振动,用虚拟式FFT分析仪测量出频率f1,记下f1、A1和调压器刻度,关掉调压器。
3.用电动式激振器对简支梁施加频率为f2的激扰力,使之产生振幅为A2的分振动。
调整激振频率和幅值,满足f1A2。
记下f2、A2值。
4.分振动频率、幅值不变,用调速电机和电动式激振器同时对简支梁激振。
传感器测得的振动经测振仪变换成位移信号后输入计算机或示波器进行显示。
五、实验报告1.实验数据表(1)分振动y1分振动y2频率f1=()Hzf2=()Hz幅值A1=()umA2=()um2.绘出在计算机屏幕上观察到的拍振波形。
3.根据表(1)数据计算Amax、Amin、f合、f拍、T拍。
4.如果微微调节激振器频率f1或电机转速f2,观察拍的频率f拍的变化,实验与理论是否一致?5.对结构来讲,拍是不利的现象,如果拍的最大振幅大于允许值,则必须消除或减弱拍的现象。
你用什么方法来改变拍的现象?篇2:机械系统动力学三级项目报告机械系统动力学三级项目报告本文关键词:动力学,报告,项目,机械,系统机械系统动力学三级项目报告本文简介:机械系统动力学三级项目报告指导老师:胡波小组成员:班级:机电1班完成时间:20XX年7月4日目录一、四杆机构11、初始数据22、计算过程23、运动仿真53.1SolidWorks运动仿真53.2simulink仿真63.3MATLAB编程7二、单自由度、初始数据102、自由振动103、受迫振动机械系统动力学三级项目报告本文内容:机械系统动力学三级项目报告指导老师:胡波小组成员:班级:机电1班完成时间:20XX年7月4日目录一、四杆机构11、初始数据22、计算过程23、运动仿真53.1SolidWorks运动仿真53.2simulink仿真63.3MATLAB编程7二、单自由度101、初始数据102、自由振动103、受迫振动102.1无阻尼102.2小阻尼振动132.3临界阻尼152.4大阻尼173、受迫振动193.1无阻尼193.2有阻尼213.2Solidworks运动仿真21三、两自由度振动231、自由振动242、受迫振动26一、四杆机构针对以下连杆系统,给定初始位置和运动,求解动力学方程,绘制动力学曲线,并进行机械系统仿真。